Overview of the SAMPL5 host–guest challenge: Are we doing better?

Abstract

The ability to computationally predict protein-small molecule binding affinities with high accuracy would accelerate drug discovery and reduce its cost by eliminating rounds of trial-and-error synthesis and experimental evaluation of candidate ligands. As academic and industrial groups work toward this capability, there is an ongoing need for datasets that can be used to rigorously test new computational methods. Although protein–ligand data are clearly important for this purpose, their size and complexity make it difficult to obtain well-converged results and to troubleshoot computational methods. Host–guest systems offer a valuable alternative class of test cases, as they exemplify noncovalent molecular recognition but are far smaller and simpler. As a consequence, host–guest systems have been part of the prior two rounds of SAMPL prediction exercises, and they also figure in the present SAMPL5 round. In addition to being blinded, and thus avoiding biases that may arise in retrospective studies, the SAMPL challenges have the merit of focusing multiple researchers on a common set of molecular systems, so that methods may be compared and ideas exchanged. The present paper provides an overview of the host–guest component of SAMPL5, which centers on three different hosts, two octa-acids and a glycoluril-based molecular clip, and two different sets of guest molecules, in aqueous solution. A range of methods were applied, including electronic structure calculations with implicit solvent models; methods that combine empirical force fields with implicit solvent models; and explicit solvent free energy simulations. The most reliable methods tend to fall in the latter class, consistent with results in prior SAMPL rounds, but the level of accuracy is still below that sought for reliable computer-aided drug design. Advances in force field accuracy, modeling of protonation equilibria, electronic structure methods, and solvent models, hold promise for future improvements.

Introduction

Structure-based computer-aided drug design (CADD) methodologies are widely used to assist in the discovery of small molecule ligands for proteins of known three-dimensional structure [1–3]. Docking and scoring methods can assist with qualitative hit identification and optimization [4–6], and explicit solvent free energy methods [7–10] are beginning to show promise as an at least semi-quantitative tool to identify promising variants on a defined chemical scaffold [11–14]. However, despite numerous efforts to improve the reliability of CADD by going beyond docking and scoring methods, ligand design still includes a large component of experimental trial and error, and the reasons why CADD methods are often not predictive are unclear. Although likely sources of substantial systematic error are well known—such as inaccuracy in the energy models used and uncertainty in protonation and tautomer states—it is difficult, and perhaps impossible, to analyze systematic errors in any detail, because incomplete conformational sampling of proteins adds large, ill-characterized random error.

As a consequence, host–guest systems [15–25] are finding increasing application as substitutes for protein– ligand systems in the evaluation of computational methods of predicting binding affinities [26–28]. A host is a compound much smaller than a protein but still large enough to have a cavity or cleft into which a guest molecule can bind by non-covalent forces. Host–guest systems can be identified that highlight various issues in protein–ligand binding, including receptor flexibility, solvation, hydrogen bonding, the hydrophobic effect, tautomerization and ionization. Because host molecules tend to be more rigid and always have far fewer degrees of freedom than proteins, random error due to inadequate or uncertain conformational sampling can be dramatically reduced, allowing a tight focus on other sources of error. Additionally, host–guest systems arguably represent a minimalist threshold test for methods of estimating binding affinities, as it is improbable that a method which does not work for such simple systems could succeed for more complex proteins.

Accordingly, host–guest systems have been included in rounds 3, 4 and now 5, of the Statistical Assessment of the Modeling of Proteins and Ligands (SAMPL) project, a community-wide prediction challenge to evaluate computational methods related to CADD [29–32]. The SAMPL project has traditionally posed challenges involving not only binding affinities but also simpler physical properties, such as hydration free energies of small molecules, and, in the present SAMPL5, distribution coefficients of drug-like molecules between water and cyclohexane. Importantly, SAMPL is a blinded challenge, which means that the unpublished experimental measurements are withheld from participants until the predictions have been made and submitted. This approach avoids the risk, in retrospective computational studies, of adjusting parameters or protocols to yield agreement with the known data, leading to results which appear promising but are not in fact reflective of how the method will perform on new data. In addition, SAMPL challenges facilitate comparisons among methods, because all participants address the same problems, and the consistency of the procedures offers the possibility of comparing results from one challenge to the next, in order to at least begin to track the state of the art.

The most recent challenge, SAMPL5, included 22 host–guest systems (Fig. 1), which attracted 54 sets of predictions from seven research groups. Here, we provide an overview of this challenge and the results. (Note that many participants also have provided individual papers on their host–guest predictions, most in this same special issue, and that additional papers address the distribution coefficient challenge that also was part of SAMPL5.) The present paper is organized as follows. We first introduce the design of the current SAMPL challenge, including descriptions of the host–guest systems and measurements, information on how the challenge was organized, and the nature of the submissions. We then analyze the performance of the various computational methods, using a number of different error metrics, and compare the results with each other and with those from prior SAMPL host–guest challenges.

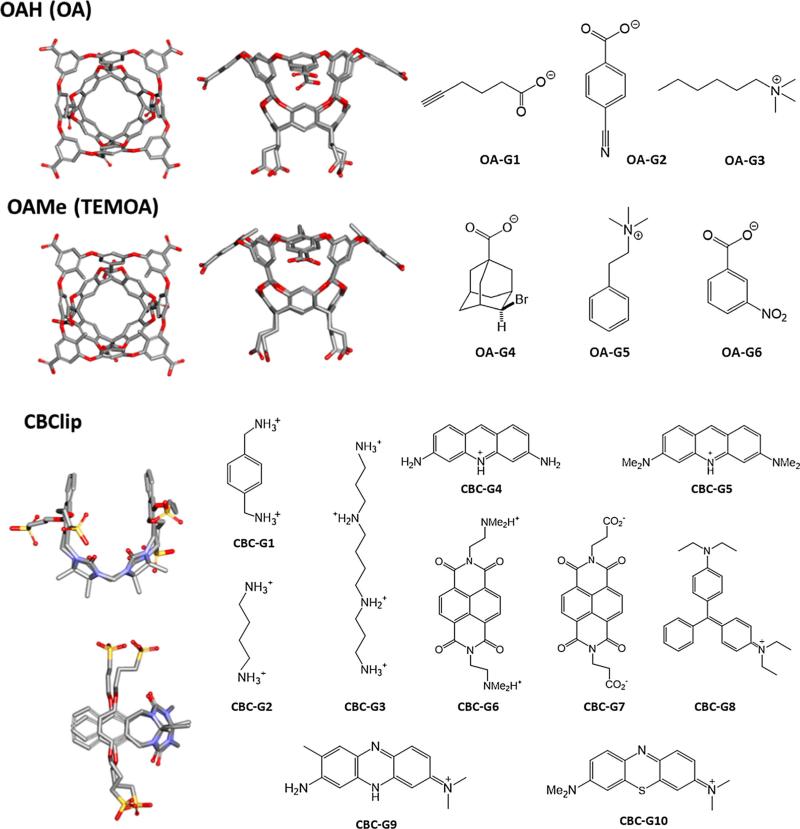
Fig. 1.

Structures of host OAH, OAMe, CBClip and their guest molecules. OA and OAMe are also known as OA and TEMOA, respectively. All host molecules are shown in two perspectives. Silver carbon, Blue nitrogen, Red oxygen, Yellow sulfur. Non-polar hydrogen atoms were omitted for clarity. OA-G1–OA-G6 are the common guest molecules for OAH and OAMe, and CBC-G1–CBC-G10 are guests for CBClip. Protonation states of all host and guest molecules shown in the figure were suggested by the organizers based on the expected pKas and the experimental pH values

Methods

Structures of Host–Guest Systems and Experimental Measurements

The SAMPL5 host–guest challenge involves three host molecules, which were synthesized and studied in the laboratories of Prof. Bruce Gibb and Prof. Lyle Isaacs, who kindly allowed the experimental data to be included in the SAMPL5 challenge before being published. The first two hosts, OAH [33] and OAMe, from the Gibb laboratory, are also known as octa-acid (OA) and tetra-endo-methyl octa-acid (TEMOA) [34, 35]. The third, CBClip [36], was developed in the Isaacs laboratory. Representative 3D structures along with the 2D drawings of their respective SAMPL5 guest molecules, are shown in Fig. 1. Host OAH was used in the SAMPL4 challenge [31], but with a different set of guests. One end of it has a wide opening to a bowl-shaped binding site, while the other end has a narrow opening that is too small to admit most guests. The bowl's opening is rimmed by four carboxylic acids, and another four carboxylic groups extend into solution from the closed end. The carboxylic groups were added to promote solubility and are not thought to interact closely with any of the guests. Host OAMe is identical to OAH, except for the addition of four methyl groups to the aromatic rings at the rim of the portal. The common guest molecules of OAH and OAMe, OA-G1–OA-G6 were chosen based on chemical diversity, solubility, and an expectation that they would exhibit significant binding to these hosts. Host CBClip is an acyclic molecular clip that is chemically related to the cucurbiturils used in previous SAMPL projects [30, 31]. It consists of two glycoluril units, each with an aromatic sidewall, and four sulfonate solubilizing groups. Ten molecules, CBC-G1–CBC-G10, were chosen as guests of CBClip, with the aim of attaining a wide range of affinities.

The experimental binding data for all three sets of host–guest systems are listed in Table 1. A 1:1 binding stoichiometry was confirmed experimentally in all cases. The binding affinities of most OAH/OAMe complexes were measured using two different techniques, NMR and ITC, and binding enthalpies are also available for the ones studied by ITC. The NMR experiments were carried out in 10 mM sodium phosphate buffer at a pH of 11.3, while the ITC experiments were performed in 50 mM sodium phosphate buffer at pH 11.5. Both sets of experiments were conducted at 298 K, except that the NMR results for OAMe-G4 were obtained at 278 K. In the SAMPL5 instruction file (see Supplementary Material), we provided expected buffer conditions for OAH/OAMe systems as “aqueous 10 mM sodium phosphate buffer at pH 11.5, at 298 K, except for OA-G6, for which the buffer was 50 mM sodium phosphate”, based on information from Dr. Gibb. Therefore, the binding affinities measured under these conditions were used for the present error analysis when-ever they are available; i.e., the ITC values for OA-G6 and NMR values for the rest. Note that OA-G4 with OAH was measured only by ITC, so this value was used in the present analysis. For the CBClip systems, the experimental studies were carried out in 20 mM sodium phosphate buffer at pH 7.4, at a temperature of 298 K. Most of the CBClip binding affinities were measured by either NMR or UV/Vis spectroscopy. However, CBC-G6 and CBC-G10 were measured by both techniques; for these, the present analysis uses the results with the highest confidence level indicated by the experimentalists: UV/Vis measurement for CBC-G6 and fluorescence for CBC-G10. Detailed experimental data for OAH and OAMe system are provided in the SAMPL5 special issue [37], and data for CBClip systems are provided elsewhere [38]. Note that a different set of numbering was used for both hosts and guests in the octa acid experimental paper.

Table 1.

Experimental standard binding affinities (ΔG°) of OAH, OAMe and CBClip (1 M standard concentration) used as references for SAMPL5 host-guest affinity predictions. All binding affinities discussed in the present work denote standard binding affinities

Compd ID	Technique	Buffer Conc (mM)	Ka (M−1)a	ΔG° (kcal/mol)b	Uncertainty (kcal/mol)
OAHc
OA-G1	NMR	10	(5.00 ± 0.07) × 103	−5.04	0.01
OA-G2	NMR	10	(1.31 ± 0.04) × 103	−4.25	0.01
OA-G3	NMR	10	(5.16 ± 0.09) × 103	−5.06	0.01
OA-G4	ITC	50	(7.43 ± 0.04) × 106	−9.37	0.00
OA-G5	NMR	10	(1.996 ± 0.005) × 103	−4.50	0.00
OA-G6	ITC	50	(8.15 ± 0.07) × 103	−5.33	0.00
OAMec
OA-G1	NMR	10	(6.94 ± 0.76) × 103	−5.24	0.05
OA-G2	NMR	10	(4.96 ± 0.37) × 103	−5.04	0.03
OA-G3	NMR	10	(2.31 ± 0.66) × 104	−5.94	0.12
OA-G4d	NMR	10	(5.58 ± 0.28) × 101	−2.38	0.02
OA-G5	NMR	10	(7.29 ± 0.33) × 102	−3.90	0.02
OA-G6	ITC	50	(2.05 ± 0.10) × 103	−4.52	0.02
CBClip
CBC-G1	NMR	20	(1.9 ± 0.1) × 104	−5.83	0.03
CBC-G2	NMR	20	70 ± 8	−2.51	0.07
CBC-G3	NMR	20	(8.8 ± 0.5) × 102	−4.02	0.03
CBC-G4	UV/VIS	20	(2.0 ± 0.1) × 105	−7.24	0.03
CBC-G5	UV/VIS	20	(1.8 ± 0.2) × 106	−8.53	0.07
CBC-G6e	UV/VIS	20	(2.2 ± 0.2) × 106	−8.64	0.05
CBC-G7	UV/VIS	20	(6.2 ± 0.2) × 103	−5.17	0.02
CBC-G8	UV/VIS	20	(3.3 ± 0.2) × 104	−6.17	0.04
CBC-G9	UV/VIS	20	(2.6 ± 0.1) × 105	−7.39	0.02
CBC-G10f	Fluorescence	20	(3.9 ± 0.2) × 107	−10.35	0.03

^aAll K_a values are reported as mean ± standard deviation (SD), where the SD was computed from the experimental replicates

^bThe uncertainties of experimental ΔG° values are reported as standard error of the mean (SEM), obtained from the experimental replicates of K_a (see Table S1)

^cFor the complete set of NMR and ITC data for OAH/OAMe systems, please see ref [37]

^dK_a values were measured at 298 K except OAMe-G4 was measured at 278 K

^eThe binding constant of CBClip-G6 measured by fluorescence titration is (2.3 ± 0.2) × 10⁶ M⁻¹

^fThe binding constant of CBClip-G10 is (2.4 ± 0.4) × 10⁷ M⁻¹ measured by UV/Vis titration and (6.6 ± 0.7) × 10⁷ M⁻¹ measured by UV/Vis competition assay

Design of the SAMPL5 host–guest challenge

The SAMPL5 challenge was organized in collaboration with the Drug Design Data Resource (D3R). The general information, detailed instructions, and input files for SAMPL5 were posted on the D3R website (https://drugdesigndata.org/about/sampl5) mostly before September 15, 2015; the information for three guest molecules in the CBClip series was added in mid-October. Submissions were accepted from registered participants until the February 2 deadline. Multiple sets of predictions were allowed for any or all of the host–guest series. Experimental measurements and error analyses of all predictions were released shortly after the submission deadline, and many participants discussed their results and the challenge at the D3R workshop held March 9–11, 2016, at University of California San Diego. All participants were invited to submit a manuscript about their calculations and results before a June 20, 2016 deadline, and the resulting papers accompany this overview in the special issue of the Journal of Computer-Aided Molecular Design.

The SAMPL5 host–guest instruction files provided the expected experimental conditions for each set of host–guest systems, including pH, buffer composition and temperature, though these were subject to adjustment because some experiments were still being done when the instructions were distributed. The instructions noted that all acidic groups of the host molecules seemed likely to be ionized at the experimental pH values (above), leading to net charges of net charges of −8, −8 and −4 for OAH, OAMe and CBClip, respectively; but also noted that this assumption was open to modification by each participant. Plausible three-dimensional coordinates of host CBClip were provided by Prof. Lyle Isaacs, while the starting 3D structures of OAH and OAMe were built and energy-minimized with the program MOE [39]. The protonation states of all guest molecules in their unbound state were also suggested, based on their expected pKas and the experimental pH values (Fig. 1), but, again, it was made clear that each participant had to make his or her own judgment regarding the ionization states and whether they remained unchanged on binding their respective hosts. The initial structures of the free guest molecules were constructed by conformational search with MOE. The resulting structures of free hosts and guests were provided in the download as PDB, mol2 and SD files. (A bond order issue in a few SD files of the free CBClip guests were reported by SAMPL users at the workshop; two submissions using the Movable Type method were adversely affected [40].) When submitting their predictions, participants were required to provide not only estimated binding free energies, but also computational uncertainties, in the form of standard errors of the mean (SEM). New in SAMPL5, participants were also invited to provide predictions of the binding enthalpies for the octa-acid host–guest systems, OA and OAMe, but this aspect of the challenge is not discussed in the present overview paper because only one group predicted enthal-pies [41].

In prior rounds of SAMPL, it was observed that participants using ostensibly equivalent force fields and simulation procedures to compute binding free energies sometimes reported rather different predictions. To help resolve such situations in case they arose in SAMPL5, participants using explicit solvent free energy methods were encouraged to submit additional “standard” runs with a prescribed set of force field and simulation parameters. The systems selected for these standard runs were OAH-G3 and OAH-G4. The input files for plausibly docked host–guest complexes solvated in TIP3P water with counterions were provided to participants in Amber [42], Gromacs [43], Desmond [44], and LAMMPS [45] formats, along with the other SAMPL5 starting data. The procedures used to ascertain that all four standard setups were equivalent across all four software packages are detailed in another paper in this issue [46].

Error analysis

Details of the experimental measurements for the host–guest complexes in SAMPL5 are available elsewhere [37, 38]; all available data were provided to the participants after the close of the challenge. For most of the OAH and OAMe cases, affinities were measured by more than one technique [37]. Some SAMPL5 participants used the averaged affinities for their error analysis, while others selected affinities measured by either NMR or ITC. It is up to the participants to determine which set of experimental affinities to use for their own analyses, as long as consistent criteria are used, rather than choosing ones that generate the best agreement with the computational estimates. In any case, given that the different affinities measured for the same host–guest pairs vary only slightly, this factor should not influence the judgement of the performance of any submissions to a significant extent. In the present paper, the error analysis for OAH and OAMe is based on comparisons with the selected NMR/ITC affinities listed in Table 1, which were chosen to best match the experimental conditions that participants were told to expect when the challenge was set. However, our statistical analyses change little on comparing instead with, for example, the average of all available affinities (ITC and NMR) for each host–guest pair. For example, the RMSE values change by at most 0.1 kcal/mol; see the error metric spreadsheet in SI. For completeness, detailed error metrics based on both sets of experimental affinities (those listed in Table 1, and averaged) are provided in the SI. The SI also provides the experimental replicates (Prof. Bruce Gibb, personal communication), which we used to estimate the experimental uncertainties in Table 1.

All binding affinity prediction sets were compared with the corresponding experimental data by four measures: root mean-squared error (RMSE), Pearson coefficient of determination (R²), linear regression slope (m), and the Kendall rank correlation coefficient (τ). Evaluating these statistics was straightforward for predictions of absolute (also known as standard) binding free energies, and the results are presented here as “absolute error metrics”. For OAH and OAMe, some submissions included only relative binding free energies, and comparing these with experiment is more complicated. One approach for handling relative free energies would be to reference all of the relative binding free energies to a single guest molecule, but then the apparent accuracy can become particularly sensitive to the quality of the calculations for the reference guest. Another approach would be to consider all pairwise free energy differences, but this becomes cumbersome and redundant. Additionally, a method is needed to compare the accuracy of relative and absolute free energy calculations on a uniform footing.

Here, we adopted an approach used in analyzing the SAMPL4 challenge [31], in which the mean signed error (MSE) of each submission set, whether relative or absolute, is subtracted from each prediction leading to “offset” binding affinity estimates. The error metrics for comparisons to experiment are less sensitive with this approach than using any particular host–guest system as a reference. We compute the offset binding free energies for each method as follows

$$\Delta G_{i,o}^{\mathrm{calc}}=\Delta G_{i,r}^{\mathrm{calc}}-MSE$$ (1)

$$MSE=\frac{1}{n}\sum _{i=1}^n\left(\Delta G_i^{\exp }-\Delta G_{i,\mathrm{r}}^{\mathrm{calc}}\right)$$ (2)

where $\Delta G_{i,r}^{\mathrm{calc}}$ is the reported (absolute or relative) binding affinity for each prediction i, $\Delta G_i^{\exp }$ is the corresponding absolute experimental binding affinity, $\Delta G_{i,o}^{\mathrm{calc}}$ is the offset binding affinity, and n is the total number of guests considered. By offsetting both relative and absolute predictions, we can make a fair comparison of their agreement with experiment. We term the error metrics computed with this approach “offset error metrics” and they are named RMSE_o, ${\mathrm{R}}_{\mathrm{o}}^2$, m_o, and τ_o.

Given the similarity of the OAH and OAMe hosts, the fact that the same guests were studied for both, and the fact that most submissions included results for both subsets, we provide error statistics for the combined OAH/OAMe datasets. Note that, in the submissions that reported relative affinities, the binding estimates of OAH-G1 and OAMe-G1 were both arbitrarily set as zero, even though the experimental binding affinities of OAH-G1 and OAMe-G1 are not identical. We addressed this problem by applying a separate MSE offset to the data for these two hosts; that is, by subtracting the MSE of the OAH subset from the OAH estimates, and the MSE of the OAMe subset from the OAMe estimates. For instance, in a combined set of OAH/OAMe predictions which contains six relative binding affinity estimates for host OAH and six for OAMe, the offset RMSE error metric, termed RMSE_o, is given by

$$RMS{E}_o=\sqrt{\frac{1}{12}\left(\sum _{i=1}^6{\left[\Delta G_i^{\exp }-\left(\Delta G_{i,\mathrm{r}}^{\mathrm{calc}}-MSE\right)\right]}_{\mathrm{OAH}}^2+\sum _{j=1}^6{\left[\Delta G_j^{\exp }-\left(\Delta G_{j,\mathrm{r}}^{\mathrm{calc}}-MSE\right)\right]}_{\mathrm{OAMe}}^2\right)}$$ (3)

We also tested how well the computational predictions performed by comparison with two simple null models, Null1 and Null2. In Null1, all binding free energies were set to 0.0 kcal/mol and the statistical uncertainty for each data point was set to 0.0 kcal/mol. In the Null2 model, the binding affinity estimate for each guest was computed via a linear regression of the experimental binding free energies versus the number of heavy atoms in the corresponding guest molecule, for identical or similar host molecules used in the SAMPL3 [30] and SAMPL4 [31] exercises; the resulting expression is ΔG = −1.11 × number of heavy atoms +5.06 (kcal/mol) for OAH and OAMe systems and ΔG = −0.25 × number of heavy atoms −1.81 (kcal/mol) for the CBClip systems. In order to simulate a real submission, we assigned a statistical uncertainty of 1.0 kcal/-mol to each data point in Null2.

In addition to evaluating how each calculation method performed in this specific challenge (i.e., the two types of error metrics described above), we wanted to provide an estimate of how well each method would perform in general. In other words, we wanted to compute error metric uncertainties which accounted for how the reported statistical error and composition of the data set influences the error metric results. The uncertainty in the error metrics was determined via bootstrap resampling with replacement. Conceptually, this involves creating thousands of hypothetical “experiment versus calculation” data sets which are consistent with the reported uncertainties, and then recording the distribution of the error metrics across all of the hypothetical sets. More specifically, we considered each data point, whether experiment or calculated, as a normal distribution centered on the reported mean value with the width determined by the reported SEM. For each bootstrap cycle, we selected a single random value from that distribution for each data point, which we term “re-sampling”. Additionally, while each bootstrap cycle always had the same total number of host–guest systems (12 for OAH/OAMe, 10 for CBClip), the composition of the data set was selected “with replacement”, meaning that in some cycles there were multiple copies of a host–guest pair, while other pairs were absent. The error metric distributions were generated with a sufficient number of bootstrap cycles, 100,000 in this case, such that the mean and standard deviation of the distributions were reproducible to the second decimal place. For submissions which did not report an uncertainty (see Tables 3, 4 footnotes), the resampling step was omitted. The code for generating the error metrics and plotting the distributions is available both in the SI and on Github.

Table 3.

Absolute and offset error metrics of binding affinity predictions for the combined OAH/OAMe datasets

Method	RMSE	Absolute error metrics			RMSEo	Offset error metrics
		R2	m	τ		${\mathrm{R}}_{\mathrm{o}}^2$	mo	τ o
Null1a	5.3 (5.3 ± 0.5)	–	–	–	1.5 (1.4 ± 0.4)	0.1 (0.2 ± 0.1)	0.1 (0.1 ± 0.1)	–
Null2b	3.5 (3.5 ± 0.8)	0.0 (0.2 ± 0.2)	0.1 (−0.4 ± 1.0)	−0.3 (−0.2 ± 0.3)	2.5 (2.6 ± 0.5)	0.0 (0.2 ± 0.2)	0.2 (−0.3 ± 1.0)	−0.2 (−0.2 ± 0.3)
APR-OPC	2.1 (2.1 ± 0.2)	0.8 (0.8 ± 0.2)	1.4 (1.5 ± 0.5)	0.6 (0.6 ± 0.2)	1.2 (1.2 ± 0.4)	0.8 (0.8 ± 0.2)	1.4 (1.5 ± 0.5)	0.6 (0.6 ± 0.2)
APR-TIP3P	1.6 (1.6 ± 0.2)	0.9 (0.9 ± 0.1)	1.4 (1.4 ± 0.2)	0.7 (0.7 ± 0.1)	0.8 (0.9 ± 0.2)	0.9 (0.9 ± 0.1)	1.4 (1.4 ± 0.2)	0.7 (0.7 ± 0.1)
BEDAM	6.1 (6.0 ± 1.0)	0.0 (0.1 ± 0.2)	0.2 (0.6 ± 1.5)	0.0 (0.1 ± 0.3)	4.4 (4.3 ± 0.6)	0.0 (0.1 ± 0.2)	0.5 (0.8 ± 1.4)	0.1 (0.1 ± 0.2)
DFT/TPSS-cc	–	–	–	–	5.3 (5.2 ± 0.8)	0.3 (0.4 ± 0.2)	2.2 (2.8 ± 1.5)	0.5 (0.5 ± 0.2)
DFT/TPSS-nc	–	–	–	–	5.5 (5.5 ± 0.8)	0.4 (0.4 ± 0.2)	2.5 (2.4 ± 1.5)	0.3 (0.3 ± 0.3)
DLPNO-CCSD(T)c	–	–	–	–	7.3 (7.2 ± 1.1)	0.4 (0.4 ± 0.2)	3.1 (2.6 ± 2.0)	0.3 (0.3 ± 0.2)
Metadynamics	3.1 (3.2 ± 0.5)	0.7 (0.5 ± 0.3)	1.2 (1.1 ± 0.6)	0.4 (0.4 ± 0.2)	1.0 (1.4 ± 0.4)	0.7 (0.5 ± 0.3)	1.0 (1.0 ± 0.5)	0.5 (0.4 ± 0.2)
MMPBSA-GAFF	3.6 (3.6 ± 0.5)	0.0 (0.2 ± 0.2)	0.3 (0.1 ± 1.1)	0.1 (0.1 ± 0.3)	3.0 (2.9 ± 0.8)	0.0 (0.2 ± 0.2)	0.3 (0.1 ± 1.1)	0.1 (0.0 ± 0.3)
MovTyp-1d	3.0 (2.9 ± 1.1)	0.0 (0.3 ± 0.3)	0.2 (−0.1 ± 0.9)	0.0 (0.0 ± 0.3)	2.2 (2.1 ± 0.7)	0.1 (0.3 ± 0.3)	0.3 (0.0 ± 0.9)	0.0 (0.0 ± 0.3)
MovTyp-2d	3.1 (2.9 ± 1.1)	0.0 (0.3 ± 0.3)	0.2 (−0.1 ± 1.1)	0.1 (0.1 ± 0.3)	2.6 (2.5 ± 0.7)	0.1 (0.3 ± 0.2)	0.4 (0.1 ± 1.0)	0.1 (0.1 ± 0.3)
TI-ps	2.7 (2.7 ± 0.9)	0.0 (0.2 ± 0.2)	0.2 (0.2 ± 1.0)	0.2 (0.2 ± 0.2)	2.2 (2.4 ± 0.8)	0.1 (0.3 ± 0.2)	0.5 (0.5 ± 0.9)	0.3 (0.2 ± 0.3)
TI-raw	2.7 (2.8 ± 0.9)	0.0 (0.2 ± 0.2)	0.2 (0.3 ± 1.1)	0.2 (0.2 ± 0.2)	2.3 (2.5 ± 0.7)	0.1 (0.2 ± 0.2)	0.5 (0.6 ± 1.0)	0.4 (0.2 ± 0.2)
HBAR	3.0 (3.0 ± 0.9)	0.0 (0.2 ± 0.2)	−0.3 (−0.2 ± 1.0)	0.1(0.1 ± 0.2)	2.4 (2.4 ± 0.7)	0.0 (0.2 ± 0.2)	0.1 (0.1 ± 0.8)	0.2 (0.2 ± 0.3)
HBAR-ps	3.0 (2.9 ± 0.9)	0.0 (0.2 ± 0.2)	−0.3 (−0.2 ± 1.0)	0.1 (0.1 ± 0.2)	2.3 (2.3 ± 0.7)	0.0 (0.2 ± 0.2)	0.1 (0.1 ± 0.8)	0.2 (0.2 ± 0.3)
HBAR-ps1	3.0 (3.0 ± 0.9)	0.0 (0.2 ± 0.2)	−0.3 (−0.2 ± 1.0)	0.1 (0.1 ± 0.3)	2.4 (2.4 ± 0.7)	0.0 (0.2 ± 0.2)	0.1 (0.1 ± 0.8)	0.2 (0.2 ± 0.3)
HBAR-ps2	2.2 (2.3 ± 0.5)	0.0 (0.1 ± 0.2)	0.0 (0.1 ± 0.7)	0.1 (0.1 ± 0.3)	1.7 (1.8 ± 0.4)	0.1 (0.2 ± 0.2)	0.3 (0.4 ± 0.5)	0.3 (0.2 ± 0.2)
SOMD-1	3.6 (3.6 ± 0.3)	0.9 (0.8 ± 0.2)	1.3 (1.2 ± 0.3)	0.5 (0.4 ± 0.2)	0.8 (0.9 ± 0.2)	0.9 (0.8 ± 0.2)	1.2 (1.1 ± 0.3)	0.5 (0.5 ± 0.2)
SOMD-2	3.6 (3.6 ± 0.3)	0.9 (0.8 ± 0.2)	1.3 (1.2 ± 0.3)	0.5 (0.4 ± 0.2)	0.8 (0.9 ± 0.2)	0.9 (0.8 ± 0.2)	1.2 (1.2 ± 0.3)	0.5 (0.5 ± 0.2)
SOMD-3	2.1 (2.1 ± 0.3)	0.9 (0.7 ± 0.2)	1.3 (1.2 ± 0.3)	0.4 (0.4 ± 0.2)	0.9 (1.0 ± 0.2)	0.9 (0.7 ± 0.2)	1.2 (1.1 ± 0.3)	0.5 (0.4 ± 0.2)
SOMD-4	10.0 (10.0 ± 0.5)	0.1 (0.2 ± 0.2)	2.0 (1.7 ± 3.1)	0.3 (0.3 ± 0.2)	9.8 (9.7 ± 1.0)	0.1 (0.2 ± 0.1)	1.9 (1.6 ± 3.1)	0.3 (0.3 ± 0.2)

The values before the parentheses are error metrics computed from the original data in the left column and the offset data in the right column. The mean values and uncertainties inside the parentheses were obtained through resampling the original data with replacement. RMSE, R², m and τ are the root mean-squared error, Pearson coefficient of determination, linear regression slope and Kendall rank correlation coefficient of the absolute error metrics, as opposed to their respective counterparts, the offset error metrics RMSE_o, ${\mathrm{R}}_{\mathrm{o}}^2$, m_o and τ_o

^aNull1 model with a constant value of 0.0 kcal/mol and no computational uncertainties

^bNull2 model based on the linear regression equation ΔG = −1.11 × number of heavy atoms +5.06 kcal/mol (based on SAMPL4 OA data); SEM was set to 1.0 kcal/mol

^cRelative binding affinities were reported; computational uncertainties were not provided

^dComputational uncertainties were not reported

Table 4.

Offset error metrics of binding affinity predictions for the separate OAH and OAMe datasets

Method	OAH				OAMe
	RMSEo	${\mathrm{R}}_{\mathrm{o}}^2$	mo	τ o	RMSEo	${\mathrm{R}}_{\mathrm{o}}^2$	mo	τ o
Null1a	1.7 (1.6 ± 0.6)	–	–	–	1.1 (1.1 ± 0.3)	–	–	–
Null2b	1.7 (1.9 ± 0.5)	0.4 (0.4 ± 0.3)	0.8 (0.4 ± 4.5)	0.4 (0.3 ± 0.3)	3.1 (3.1 ± 0.8)	0.7 (0.6 ± 0.2)	−1.5 (−1.6 ± 1.0)	−0.8 (−0.6 ± 0.2)
APR-OPC	0.7 (0.7 ± 0.2)	0.9 (0.7 ± 0.3)	1.1 (1.2 ± 2.7)	0.6 (0.5 ± 0.3)	1.6 (1.6 ± 0.6)	0.9 (0.9 ± 0.2)	2.2 (1.9 ± 0.7)	0.9 (0.7 ± 0.2)
APR-TIP3P	0.8 (0.8 ± 0.2)	1.0 (0.9 ± 0.2)	1.4 (1.5 ± 0.9)	0.6 (0.5 ± 0.3)	0.9 (0.9 ± 0.3)	0.9 (0.9 ± 0.1)	1.6 (1.5 ± 0.4)	0.9 (0.7 ± 0.2)
BEDAM	4.8 (4.7 ± 0.9)	0.0 (0.1 ± 0.2)	−0.5 (0.2 ± 18.5)	−0.1 (0.0 ± 0.3)	3.9 (3.8 ± 0.7)	0.4 (0.5 ± 0.3)	2.7 (2.1 ± 2.4)	0.3 (0.3 ± 0.4)
DFT/TPSS-cc	5.7 (5.6 ± 1.3)	0.2 (0.4 ± 0.3)	1.7 (3.7 ± 9.1)	0.5 (0.4 ± 0.3)	4.8 (4.7 ± 0.8)	0.7 (0.7 ± 0.2)	4.1 (3.9 ± 2.4)	0.3 (0.3 ± 0.4)
DFT/TPSS-nc	4.4 (4.3 ± 0.7)	0.5 (0.6 ± 0.3)	2.2 (2.0 ± 5.8)	0.3 (0.3 ± 0.4)	6.5 (6.4 ± 1.3)	0.4 (0.5 ± 0.3)	3.9 (2.7 ± 4.3)	0.3 (0.3 ± 0.4)
DLPNO-CCSD(T)c	7.0 (6.9 ± 1.3)	0.5 (0.5 ± 0.3)	3.3 (1.8 ± 9.9)	0.3 (0.3 ± 0.4)	7.6 (7.4 ± 1.7)	0.3 (0.4 ± 0.3)	3.7 (2.2 ± 5.4)	0.2 (0.2 ± 0.4)
Metadynamics	0.7 (0.9 ± 0.3)	0.9 (0.7 ± 0.3)	1.2 (1.1 ± 1.9)	0.6 (0.4 ± 0.3)	1.2 (1.6 ± 0.5)	0.3 (0.3 ± 0.3)	0.6 (0.8 ± 1.1)	0.3 (0.3 ± 0.3)
MMPBSA-GAFF	1.8 (1.8 ± 0.3)	0.5 (0.5 ± 0.3)	1.0 (1.3 ± 5.4)	0.5 (0.4 ± 0.4)	3.9 (3.7 ± 1.2)	0.4 (0.5 ± 0.3)	−1.7 (−1.2 ± 1.9)	−0.3 (−0.3 ± 0.4)
MovTyp-1d	0.8 (0.7 ± 0.2)	0.8 (0.7 ± 0.3)	1.0 (0.9 ± 2.4)	0.5 (0.4 ± 0.4)	3.1 (2.9 ± 1.0)	0.7 (0.6 ± 0.3)	−1.5 (−1.3 ± 0.9)	−0.5 (−0.4 ± 0.4)
MovTyp-2d	1.2 (1.2 ± 0.2)	0.8 (0.7 ± 0.3)	1.2 (1.4 ± 4.2)	0.9 (0.8 ± 0.2)	3.5 (3.4 ± 1.0)	0.5 (0.5 ± 0.3)	−1.7 (−1.5 ± 1.3)	−0.5 (−0.4 ± 0.4)
TI-ps	0.8 (1.3 ± 0.4)	0.8 (0.7 ± 0.2)	1.0 (1.6 ± 3.6)	0.7 (0.5 ± 0.3)	3.0 (3.1 ± 1.1)	0.2 (0.3 ± 0.3)	−0.8 (−0.4 ± 1.8)	−0.2 (−0.1 ± 0.4)
TI-raw	1.7 (1.9 ± 0.5)	0.5 (0.5 ± 0.3)	1.0 (1.7 ± 4.6)	0.6 (0.4 ± 0.3)	2.7 (2.8 ± 1.1)	0.1(0.4 ± 0.3)	−0.6 (−0.2 ± 1.7)	−0.2 (−0.1 ± 0.4)
HBAR	1.7 (1.7 ± 0.5)	0.2 (0.4 ± 0.3)	0.3 (0.7 ± 4.8)	0.5 (0.4 ± 0.3)	3.0 (2.9 ± 1.0)	0.2 (0.4 ± 0.3)	−0.9 (−0.4 ± 1.5)	−0.1 (−0.1 ± 0.4)
HBAR-ps	1.3 (1.3 ± 0.3)	0.4 (0.6 ± 0.2)	0.4 (0.8 ± 2.2)	0.6 (0.5 ± 0.3)	3.0 (2.9 ± 1.0)	0.2 (0.4 ± 0.3)	−0.9 (−0.4 ± 1.5)	−0.1 (−0.1 ± 0.4)
HBAR-ps1	1.2 (1.2 ± 0.4)	0.5 (0.6 ± 0.2)	0.5 (1.0 ± 2.0)	0.6 (0.6 ± 0.3)	3.2 (3.2 ± 1.0)	0.2 (0.4 ± 0.3)	−1.1 (−0.6 ± 1.6)	−0.2 (−0.2 ± 0.4)
HBAR-ps2	1.5 (1.5 ± 0.4)	0.3 (0.4 ± 0.2)	0.3 (0.7 ± 1.8)	0.5 (0.4 ± 0.3)	1.9 (2.0 ± 0.5)	0.0 (0.3 ± 0.3)	−0.1 (0.2 ± 1.1)	−0.1 (0.0 ± 0.4)
SOMD-1	0.8 (1.0 ± 0.4)	0.9 (0.7 ± 0.3)	1.3 (1.1 ± 1.6)	0.5 (0.4 ± 0.4)	0.7 (0.8 ± 0.3)	0.8 (0.7 ± 0.3)	1.1 (1.0 ± 0.5)	0.5 (0.5 ± 0.3)
SOMD-2	0.9 (1.0 ± 0.3)	0.9 (0.8 ± 0.3)	1.4 (1.1 ± 1.6)	0.5 (0.4 ± 0.4)	0.7 (0.8 ± 0.3)	0.8 (0.7 ± 0.3)	1.1 (1.0 ± 0.5)	0.6 (0.5 ± 0.3)
SOMD-3	1.0 (1.1 ± 0.3)	0.9 (0.7 ± 0.3)	1.3 (1.0 ± 1.7)	0.3 (0.3 ± 0.4)	0.7 (0.8 ± 0.3)	0.8 (0.7 ± 0.3)	1.1 (1.0 ± 0.5)	0.6 (0.5 ± 0.3)
SOMD-4	9.5 (9.5 ± 1.5)	0.4 (0.4 ± 0.3)	3.6 (3.5 ± 30.8)	0.5 (0.4 ± 0.3)	10.0 (9.9 ± 1.5)	0.0 (0.3 ± 0.3)	−1.4 (−0.5 ± 7.1)	0.1 (0.1 ± 0.4)
TI/BAR	1.0 (1.2 ± 0.4)	0.6 (0.6 ± 0.2)	0.6 (1.1 ± 2.5)	0.9 (0.6 ± 0.3)	–	–	–	–
MMPBSA-OPLS	–	–	–	–	3.4 (3.2 ± 1.1)	0.7 (0.6 ± 0.3)	−1.7 (−1.4 ± 1.0)	−0.6 (−0.4 ± 0.3)

The values before the parentheses are error metrics computed from the original data offset by the MSE. The mean values and uncertainties inside the parentheses were obtained through resampling the original data using replacement. The offset error metrics RMSE_o, ${\mathrm{R}}_{\mathrm{o}}^2$, m_o and τ_o are provided

^aNull1 model with a constant value 0.0 kcal/mol and no computational uncertainties

^bNull2 model based on the linear regression equation ΔG = −1.11 × number of heavy atoms + 5.06 kcal/mol (based on SAMPL4 OA data); SEM was set to 1.0 kcal/mol

^cComputational uncertainties were not reported

^dComputational uncertainties were not reported

Results

The SAMPL5 host–guest challenge received a total of 54 submissions from 7 research groups, comprising 12 submissions for host CBClip, 21 submissions for OAH and 21 submissions for OAMe. Key aspects of all prediction methods—the conformational sampling method, the force field used for the host and guest, and the water model—are summarized in Table 2. After merging submissions that used identical methods for both OAH and OAMe, the 42 OAH/OAMe submissions reduce to 20 sets of combined predictions, along with two subset predictions: TI-BAR (Table 2) for only OAH, and MMPBSA-OPLS (Table 2) for only OAMe. The conformational sampling techniques used include docking, molecular dynamics (MD) simulations with explicit or implicit solvent, and Monte Carlo methods. Compared with SAMPL3 and SAMPL4 exercises, docking was less frequently used as the sole sampling technique, but it was commonly used for obtaining the starting structures for more detailed computational approaches. Extensive use was made of generalized classical force fields with fixed charges and no explicit treatment of electronic polarizability, and methods using explicit solvent models employed chiefly the TIP3P water model [47]. However, a few methods focused less on conformational sampling and more on the quality of the energy calculations, through the use of various quantum methods. For the quantum methods to obtain configurational entropy, low-lying vibrational modes were treated by the free-rotor approximation, using the interpolation model implemented by Grimme [48]. The methods to derive affinities or relative affinities range from relatively established approaches, such as thermodynamic integration (TI) [49], Bennett acceptance ratio (BAR) [50], metadynamics [51], and MM/PBSA [52], to the more recently developed Movable Type method [53].

Table 2.

Summary of computational methods in all SAMPL5 host-guest submissions

Method	Conformational sampling	Energy model	Solvent model	SAMPL5 Refs.
OAH/OAMe
APR-OPC (C, E)	MD; docking	GAFF/RESP	OPC	[41]
APR-TIP3P (C, E)	MD; docking	GAFF/RESP	TIP3P	[41]
BEDAM (C, I)	MD	OPLS-2005	AGBNP2	[54]
DFT/TPSS-ca (Q, I)	Manual	DFT-D3 (TPSS functional)	COSMO-RS	[55]
DFT/TPSS-na (Q, I)	Manual	DFT-D3 (TPSS functional)	COSMO-RS	[55]
DLPNO-CCSD(T)a (Q, I)	Manual	DLPNO-CCSD(T)	COSMO-RS	[55]
Metadynamics (C, E)	Funnel metadynamics	GAFF/RESP	TIP3P	[56]
MMPBSA-GAFF (C, I)	MD	GAFF/RESP	PBSA; TIP3P	[56]
MMPBSA-OPLSb (C, I)	MD	OPLS/RESP	PBSA; TIP3P	[56]
MovTyp-1 (C, I)	Mixed torsion/low mode	KECSA 1	Implicit	[40]
MovTyp-2 (C, I)	Mixed torsion/low mode	KECSA 2	Implicit	[40]
TI/BARc (C, E)	MD; docking	CGenFF	TIP3P	[57]
TI-psc (C, E)	MD; docking	CGenFF	TIP3P	[57]
TI-rawc (C, E)	MD; docking	CGenFF	TIP3P	[57]
HBARd (C, E)	MD; docking	CGenFF	TIP3P	[57]
HBAR-psd (C, E)	MD; docking	CGenFF	TIP3P	[57]
HBAR-ps1d (C, E)	MD; docking	CGenFF	TIP3P	[57]
HBAR-ps2d (C, E)	MD; docking	CGenFF	TIP3P	[57]
SOMD-1e (C, E)	MD	GAFF/RESP	TIP3P	[58]
SOMD-2 (C, E)	MD	GAFF/RESP	TIP3P	[58]
SOMD-3 (C, E)	MD	GAFF/RESP	TIP3P	[58]
SOMD-4 (C, E)	MD	GAFF/RESP	TIP3P	[58]
CBClip
BAR-ab-initiof (C, E)	MD	CGenFF	TIP3P	[59]
BAR-dockf (C, E)	MD; docking	CGenFF	TIP3P	[59]
TI-ab-initiof (C, E)	MD	CGenFF	TIP3P	[59]
TI-BARf (C, E)	MD; docking	CGenFF	TIP3P	[59]
TI-dockf (C, E)	MD; docking	CGenFF	TIP3P	[59]
BEDAM (C, I)	MD	OPLS-2005	AGBNP2	[54]
MovTyp-1 (C, I)	Mixed torsion/low mode	KECSA 1	Implicit	[40]
MovTyp-2 (C, I)	Mixed torsion/low mode	KECSA 2	Implicit	[40]
SOMD-1e (C, E)	MD	GAFF/RESP	TIP3P	[58]
SOMD-2 (C, E)	MD	GAFF/RESP	TIP3P	[58]
SOMD-3 (C, E)	MD	GAFF/RESP	TIP3P	[58]
SOMD-4 (C, E)	MD	GAFF/RESP	TIP3P	[58]

APR attach-pull-release approach [60], OPC “optimal” 3-charge, 4-point rigid water model [61]; TIP3P transferable interaction potential three-point [47]; BEDAM binding energy distribution analysis method [62]; DLPNO-CCSD(T) domain based, local pair natural orbital-coupled-cluster single double and perturbative triple excitations [63]; DFT-D3 density functional theory with the latest dispersion corrections [64]; MovTyp Movable Type method [53]; SOMD single topology relative free energy calculations performed with Sire/OpenMM6.3 software [65, 66]; BAR Bennett acceptance ratio [50]; TI thermodynamic integration [49, 67]; GAFF generalized AMBER force field [68]; CGenFF CHARMM generalized force-field [69]; RESP restrained electrostatic potential [70]; OPLS-2005 optimized potentials for liquid simulations 2005 force field [71, 72]; KECSA knowledge-based and empirical combined scoring algorithm [73]; AGBNP2 analytical generalized born plus non-polar 2 [74]; COSMO-RS conductor-like screening model for real solvents [75]; MMPBSA molecular mechanics Poisson Boltzmann/solvent accessible surface area [52]. The classifications of the energy model: quantum (Q) or classical (C), as well as the solvent model: implicit (I) or explicit (E) are listed in parentheses following the name of each method

^aDLPNO-CCSD(T) and DFT/TPSS-n (n indicates neutralized) used neutralized hosts, yet fully charged guests. DFT/TPSS-c (c indicates charged) used both fully charged hosts and guests

^bThe MMPBSA-OPLS approach was only used to generate predictions for the OAMe subset

^cTI was used to compute binding affinities in both TI-raw and TI-ps. Lowest values of the computed binding free energies were reported in TI-raw. In TI-ps, possible corrections were added through calculating the relative pKa/pKb of the ligands to known analogs

^dBinding free energies in HBAR submission were computed by Hamiltonian replica exchange method (HREM) combined with the BAR method. The protonation state correction was used in HBAR-ps, HBAR-ps1 and HBAR-ps2. Results from the neutralized-only systems were reported as HBAR-ps1 and those from systems at the experimental ionic strength were reported as HBAR-ps2. TI/BAR prediction only reported binding affinities for the OAH subset based on the averaged results computed by TI and HREM/BAR for each guest

^eAll SOMD predictions were produced based on single topology relative free energy calculations combined with multistate Bennet acceptance ratio (MBAR) method, but with different protocols. SOMD-1: No corrections; SOMD-2: includes a correction term for long-range dispersion interactions; SOMD-3: same as SOMD-2, but a correction term for the use of the flat-bottom distance restraints was also applied to bring the decoupled guest to a standard concentration; SOMD-4: same as SOMD-3 but with an additional correction term for electrostatic energies

^fPredictions were generated by either TI (labeled with TI-) or HREM/BAR (label by BAR-). Also the starting structures were obtained by quantum calculations (labeled with “ab initio”) or docking (labeled with “dock”). TI/BAR reported the lowest binding affinity from either method

Error statistics

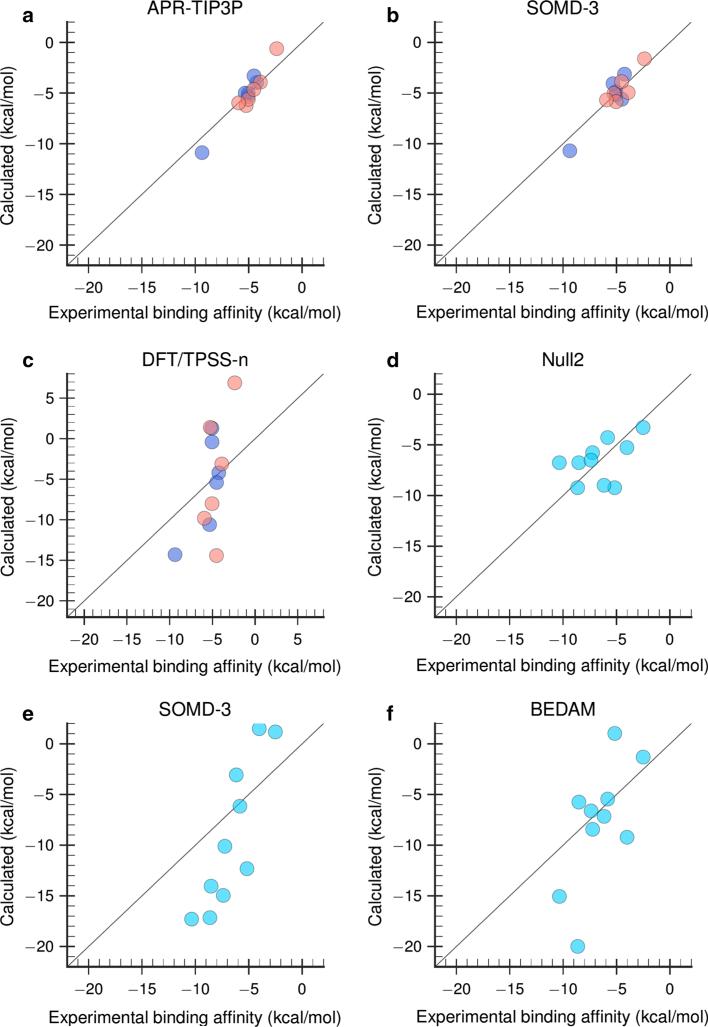
Error statistics for all 17 sets of absolute binding free energy predictions for the combined OAH/OAMe dataset are summarized in Table 3 (left-hand side) and Fig. 2. These absolute binding free energy predictions, in addition to three sets of relative binding free energy predictions: DFT/TPSS-n, DFT/TPSS-c, and DLPNO-CCSD(T), were then converted to offset binding free energies, using Eq 1, and the error statistics are presented in Table 3 (right-hand side) and Fig. 3. The offset free energy statistics for all methods for the separate OAH and OAMe sets are presented in Table 4. All 12 sets of CBClip predictions are absolute binding free energies, and error statistics for these are presented in Table 5 and Fig. 4. Scatter plots of original data and offset predictions versus experimental binding free energies for all methods and systems are provided in Figure S1 and S2 respectively.

Fig. 2.

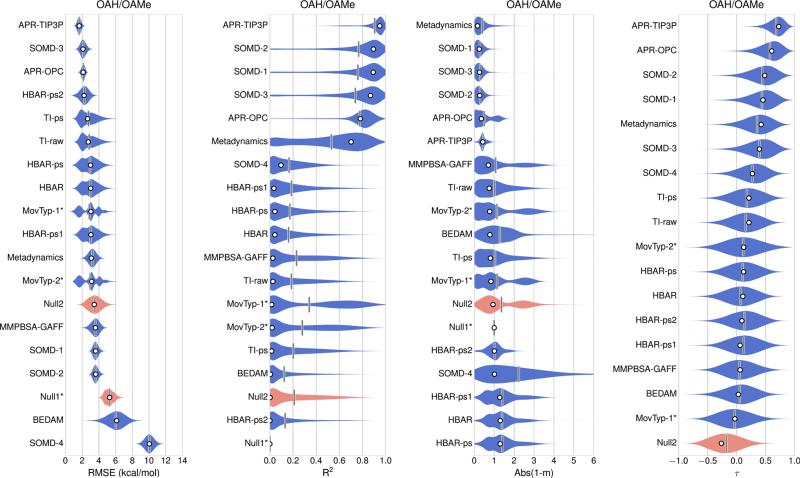
OAH/OAMe submissions ranked based on the original values of absolute error metrics (white circles), which were computed from reported binding affinities without resampling or considering any uncertainty sources. The violin plot describes the shape of the sampling distribution for each set of predictions when bootstrapping 100,000 samples with replacement, and the vertical bar represents the mean of the distribution. The computational uncertainties are absent in the Null1, MovTyp-1, and MoveTyp-2 predictions. Two null models are shown in red. The violin plot area, here and below, are normalized not to unity, but instead to give the same maximum thickness

Fig. 3.

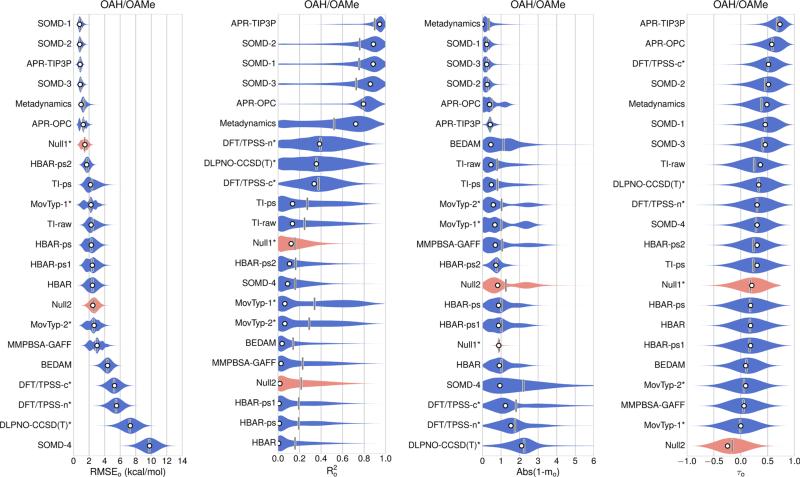
OAH/OAMe submissions ranked based on the original values of offset error metrics (white circles), which were computed from reported binding affinities without resampling or considering any uncertainty sources. The violin plot describes the shape of the sampling distribution for each set of predictions when bootstrapping 100,000 samples with replacement, and the vertical bar represents the mean of the distribution. The computational uncertainties are absent in Null1 model, MovTyp-1, MoveTyp-2 DFT/TPSS-n, DFT/TPSS-C and DLPNO-CCSD(T) predictions. Two null models are shown in red

Table 5.

Absolute error metrics of binding affinity predictions for the CBClip datasets

Method	RMSE	R2	m	τ
Null1a	6.9 (6.9 ± 0.7)	–	–	–
Null2b	2.2 (2.4 ± 0.5)	0.2 (0.2 ± 0.2)	0.4 (0.4 ± 0.3)	0.4 (0.3 ± 0.2)
BAR-ab initio	4.0 (4.0 ± 0.8)	0.0 (0.1 ± 0.1)	−0.1 (−0.1 ± 0.4)	−0.2 (−0.1 ± 0.2)
BAR-dock	4.7 (4.9 ± 1.0)	0.1 (0.1 ± 0.1)	−0.4 (−0.4 ± 0.6)	−0.2 (−0.2 ± 0.2)
TI-ab initio	4.7 (4.8 ± 0.8)	0.2 (0.2 ± 0.2)	−0.6 (−0.6 ± 0.5)	−0.2 (−0.2 ± 0.3)
TI-dock	3.4 (3.6 ± 0.7)	0.0 (0.1 ± 0.1)	−0.1 (−0.1 ± 0.5)	−0.2 (−0.1 ± 0.2)
TI/BAR	4.0 (4.0 ± 0.9)	0.0 (0.1 ± 0.1)	−0.1 (−0.1 ± 0.4)	−0.2 (−0.1 ± 0.2)
BEDAM	4.8 (4.6 ± 1.3)	0.4 (0.5 ± 0.2)	1.7 (1.8 ± 0.8)	0.4 (0.4 ± 0.2)
MovTyp-1c	3.5 (3.5 ± 0.7)	0.0 (0.1 ± 0.1)	0.0 (0.0 ± 0.3)	0.0 (0.0 ± 0.3)
MovTyp-2c	4.2 (4.1 ± 0.8)	0.0 (0.1 ± 0.1)	0.0 (0.0 ± 0.5)	0.0 (0.0 ± 0.3)
SOMD-1	6.4 (6.4 ± 0.9)	0.8 (0.7 ± 0.2)	2.7 (2.7 ± 0.5)	0.7 (0.6 ± 0.1)
SOMD-2	6.3 (6.3 ± 0.9)	0.8 (0.7 ± 0.2)	2.7 (2.7 ± 0.5)	0.7 (0.6 ± 0.1)
SOMD-3	5.7 (5.7 ± 0.7)	0.8 (0.7 ± 0.2)	2.7 (2.7 ± 0.5)	0.7 (0.6 ± 0.2)
SOMD-4	18.4 (17.7 ± 5.3)	0.5 (0.5 ± 0.3)	5.6 (5.6 ± 2.4)	0.5 (0.5 ± 0.3)

The values before the parentheses are raw error metrics computed from the original data. The mean values and uncertainties inside the parentheses were obtained through resampling the original data using replacement. The absolute error metrics RMSE, R², m and τ are provided

^aNull1 model with a constant value 0.0 and no computational uncertainties were assigned to guests

^bNull2 model based on the linear regression equation ΔG = −0.25 × number of heavy atoms −1.81 kcal/mol (based on SAMPL3 Host1 data); SEM was set to 1.0 kcal/mol

^cComputational uncertainties were not reported. Results were adversely affected by bond order issues in the provided SD files of free guests [40]

Fig. 4.

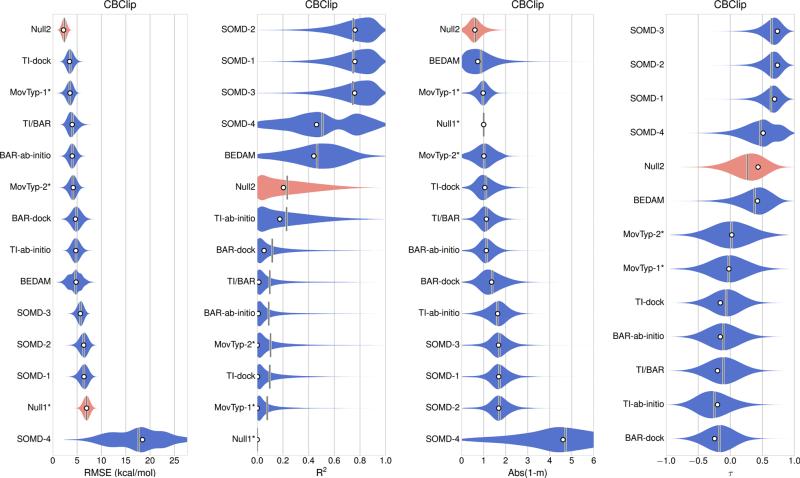
CBClip submissions ranked based on the original values of absolute error metrics (white circles), which were computed from reported binding affinities without resampling or considering any uncertainty sources. The violin plot describes the shape of the sampling distribution for each set of predictions when bootstrapping 100,000 samples with replacement, and the vertical bar represents the mean of the distribution. Two null models are shown in red. The computational uncertainties are absent in Null1 model, MovTyp-1 and MoveTyp-2 predictions

Inspection of the absolute binding free energy results for OAH and OAMe (Fig. 2; Table 3) reveals that most prediction sets outperformed both Null models for this dataset, and that comparatively favorable results were provided by several explicit solvent free energy methods with fixed charge models and the GAFF parameters [68]. The attach-pull-release (APR) method [60] with either the TIP3P or the OPC water model, performed well, as did the SOMD-3 method (Fig. 5a, b), followed closely by the SOMD-1 and SOMD-2 methods. The APR method obtains the binding free energy in terms of the reversible work to pull the guest from the host along a physical pathway [60, 76], while the SOMD calculations use the double-decoupling approach [77]. The APR-TIP3P, APR-OPC and SOMD-3 methods all yielded R² ≥ 0.8, linear regression slopes 1.3 < m < 1.4, and 1.6 ≤ RMSE ≤ 2.1 kcal/mol. The other two SOMD predictions, SOMD-1 and SOMD-2, which closely resemble SOMD-3 but use different correction protocols, provide similar correlations with experiment, but larger RMSE values, 3.6 kcal/mol. The Metadynamics method uses the funnel metadynamics approach [78] to obtain the binding free energy via the potential of mean force along a physical binding pathway, again using molecular dynamics with GAFF and TIP3P; this method also performed relatively well, with R² of 0.7, slope near 1, and RMSE of 3.1 kcal/mol. It is not immediately clear why the Metadynamics and APR-TIP3P differ, as the force fields used appear to match, but it is worth noting that the Metadynamics calculations actually provided relative binding free energies, which were converted into absolute binding free energies for submission by referring to a known octa-acid guest result from SAMPL4. The accurate absolute binding free energies cannot be obtained by Metadynamics due to the special treatment of the unbound state as a “dry state”, in which all water molecules were restrained from entering the host cavity [56].

Fig. 5.

Combined OAH/OAMe predictions with MSE offsets using a APR-TIP3P, b SOMD-3, and c DFT/TPSS-n method. CBClip predictions without MSE offset using d the Null2 model, e SOMD-3, and f BEDAM method. Purple dots OAH, red dots OAMe, cyan dots CBClip, solid black line of identity

The analysis of relative binding free energies (Fig. 3; Tables 2, 3) provides a similar overall picture, but allows the three sets of relative predictions—DLPNO-CCSD(T), DFT/TPSS-n and DFT/TPSS-c to be compared with the other predictions on an equal footing. The DFT/TPSS-n and DFT/TPSS-c predictions were generated with dispersion-corrected density functional theory calculations, in conjunction with the COSMO-RS continuum solvation model [75], while DLPNO-CCSD(T) approach used the DLPNO-CCSD(T) level of theory, again combined with COSMO-RS. Both DLOPNO-CCSD(T) and DFT/TPSS-n treated the host as neutral and the guest as fully charged, while the DFT/TPSS-c assumed charges appropriate to the experimental pH for both host and guest molecules. According to the participant, the correlations shown in DFT/TPSS-n (${\mathrm{R}}_{\mathrm{o}}^2=0.5$; Fig. 5c) and other two quantum submissions actually resulted from including the OAMe-G4 data point based on a faulty binding configuration. When the proper configuration was used in later calculations, no correlations were found with experimental data [54].

The offset error analysis also provides separate statistics for OAH and OAMe, and it is noteworthy that, despite their relatively low correlations for the OAH/OAMe combined set, the MovTyp-1 and MovTyp-2 methods yield good error statistics for the OAH subset (Table 4), with ${\mathrm{R}}_{\mathrm{o}}^2$ of 0.8 and regression slopes near 1. However, the two Movable Type methods yield anti-correlations for the OAMe subset, and this degrades the overall performance of these methods for the combined OAH/OAMe set. Similar performance deterioration by including estimates from the OAMe subset was also observed for several other methods, including Metadynamics, TI-raw and TI-ps, and to some degree for MMPBSA-GAFF predictions. Interestingly, although the Null2 model showed a large RMSE_o value of 3.1 kcal/mol and anti-correlation for the OAMe subset, it seems to be able to generate reasonable predictions for the OAH subset, with the RMSE_o value of 1.7 kcal/mol, ${\mathrm{R}}_{\mathrm{o}}^2$ value of 0.4 and m_o value of 0.8. Null2 model resembles what was observed in about one third of the predictions for OAH and OAMe systems: a method that performed well on OAH systems could totally fail on OAMe systems. It is also worth noting that methods that showed much weaker correlation for the OAMe set also yielded larger RMSE_o values for OAMe, suggesting that the narrower spread of experimental binding energies in the OAMe dataset, relative to OAH, cannot fully account for the weak correlations.

Fewer methods were applied to the CBClip set (Fig. 4; Table 5), and results are in general less favorable than those for OAH and OAMe. Indeed, the Null-2 model, which estimates affinity based on the number of guest heavy atoms, outperformed all methods in terms of RMSE and regression slope, and turned in a mid-range performance for the measures of correlation (Fig. 5d). The SOMD methods again provided high correlations with experiment, yet large regression slopes of 2.7 and RMSE values on the order of 6 kcal/mol (Table 5; Fig. 5e). The BEDAM method provided a balanced performance, with an R² value of 0.4, a RMSE value of 4.8 kcal/mol, and a regression slope of 1.7 (Table 5; Fig. 5f). MovTyp-1 and MovTyp-2 submissions showed near-zero correlations. However, according to the participant, moderate correlations and lower RMSE_o values were obtained when structures with corrected bond orders were used [40]. The remaining five sets of predictions generated by either TI or HREM/BAR approach, yielded either zero or negative correlations with experiment. One possible explanation for the worse performance of multiple methods for CBClip, versus the octa-acids, is that CBClip is acyclic and hence may be more flexible and slower to converge. However, this would presumably lead to greater scatter of the binding estimates and thus lower correlation, yet the SOMD method still showed good correlations for the CBClip set (R² ~ 0.8). Instead, the large errors in this case seem to derive from the fact that the slopes (m) are as high as 2.7 for the CBClip cases. This would suggest some systematic error, such as finite-size effects or problems in the treatment of short-range electrostatics, since the four sulfonate groups are positioned where they can interact strongly with the guests.

Comparison with SAMPL3 and SAMPL4 host–guest challenges

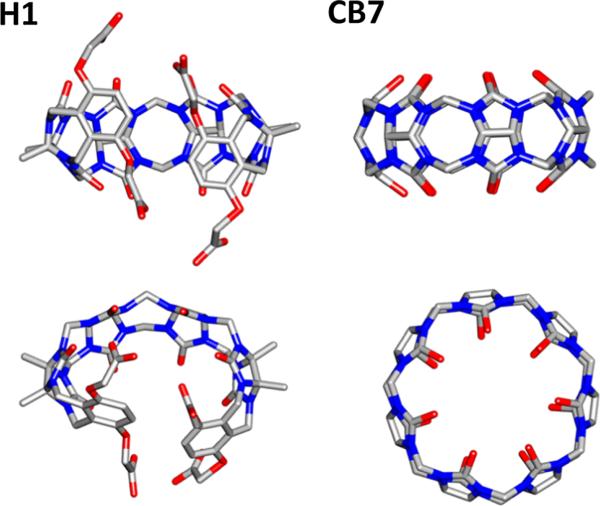
Host–guest systems were first introduced to SAMPL for the SAMPL3 challenge, and all SAMPL hosts to date have been drawn from the cucurbituril and octa-acid families of hosts, a trend which reflects the continuing data contributions of Professors Lyle Isaacs and Bruce Gibb. Although some hosts are new chemical variants, others have recurred across challenges. Thus, the current OAH host is identical to the OA host in SAMPL4; and the present CBClip resembles the glycoluril-based molecular clip Host H1 in SAMPL3 and the glycoluril host CB7 in SAMPL4. The structures of H1 and CB7 are shown in Fig. 6. In addition, some SAMPL5 participants used closely related methods to generate predictions for prior rounds of SAMPL. One may thus begin to look for trends in computational performance over time.

Fig. 6.

Structures of host H1 and cucurbit[7]uril (CB7) tested in prior SAMPL host–guest challenges. Silver carbon, Blue nitrogen, Red oxygen. Hydrogen atoms were omitted for clarity

Two methods, BEDAM and TI/BAR, applied to the present CBClip case, were also used to predict the binding affinities for the chemically related H1 in SAMPL3 [30, 79]. Both methods yielded larger RMSE values in the present study: 4.8 kcal/mol (Table 5) versus 2.5 kcal/mol in SAMPL3 for BEDAM, and 4.0 kcal/mol versus 2.6 kcal/mol for TI/BAR. However, the correlations were similar: R² values between 0.4 and 0.5 for BEDAM, and R² values near zero for TI/BAR in both SAMPL exercises.

Binding data for the octa-acid host OAH were also used in the SAMPL4 challenge [31], where this host was termed OA instead of OAH, and several identical or similar computational methods were applied to this host in both SAMPL challenges. Note that, since the error analysis in SAMPL4 was based on relative binding affinity predictions, we compared the SAMPL4 error metrics of OA with the offset error metrics of OAH in the current challenge. In particular, RMSE_o in SAMPL4 was obtained in a similar manner to RMSE_o here by using offset binding affinity estimates. The BEDAM method yielded substantially more accurate predictions for this host in SAMPL4, with R² of 0.9 then versus 0.04 now, and the offset RMSE 0.9 kcal/mol then and 4.8 kcal/mol now. It is important to note that, although the methods, energy models, solvent models and sampling techniques appear mostly the same between SAMPL3 and SAMPL5 for this approach, the more diverse guest set in SAMPL5 may pose a challenge to BEDAM's implicit solvent model. An in-depth discussion on the performance of BEDAM can be found in the SAMPL5 special issue [54].

It also seemed appropriate to compare the present DFT/TPSS-n predictions with RRHO-551 (SAMPL4 ID:551), which used DFT-D, an early version of dispersion-corrected DFT with COSMO-RS; and the DLPNO CCSD(T) predictions with RRHO-552 (SAMPL4 ID:552), which used LCCSD(T), a local coupled-cluster method with COSMO-RS [80]. Comparable performance was observed in both cases on going from SAMPL4 to SAMPL5 for the OAH set only. For the DFT methods, the prior offset RMSE, R² and regression slopes were, respectively, 5.8 kcal/mol, 0.5 and 3.9, while the current values are 4.4 kcal/mol, 0.5, and 2.2. For the coupled-cluster methods, the prior offset RMSE, R² and regression slopes were, respectively, 6.1 kcal/mol, 0.4 and 3.3, while the current values are 7.0 kcal/mol, 0.5, and 3.3. However, as mentioned above, the quantum submissions showed essentially zero correlation on the mixed OAH/OAMe set after the faulty configuration of OAMe-G4 was replaced with a more proper one [55]. Given this adjustment, the quantum methods performed worse in SAMPL5 compared with SAMPL4.

The Metadynamics approach yielded more accurate predictions in SAMPL5 than in SAMPL4 (ID:579), though it is important to note that, for this method, the hosts studied are largely distinct, and a different force field was used previously [81]. The SAMPL4 predictions with this method showed near-zero or anti-correlations for the CB7 host, whereas the SAMPL5 predictions showed moderate correlations in the OAH/OAMe combined set and fairly good agreement with experiments in the OAH subset.

Although two top-ranked SAMPL5 methods, SOMD and APR, were not tested in prior SAMPL challenges, it is of interest to compare each with one of the free energy perturbation (FEP) methods that also employed GAFF parameters, RESP charges and TIP3P water model in SAMPL4. APR-TIP3P and SOMD-1 were thus compared with FEP-526 (SAMPL4 ID: 526) [80] for the octa acid predictions. In spite of the increased chemical diversity of the SAMPL5 set of guests, all three methods performed equally well: the R² values in all three methods are no less than 0.9; the offset RMSE measures ranged from 0.8 to 0.9 kcal/mol, and slopes ranged from 1.3 to 1.5. APR-TIP3P and SOMD-1 even showed slightly better performance for the OAH/OAMe combined datasets than FEP-526 for OAH alone.

Discussion

The SAMPL5 host–guest blinded prediction challenge has provided a fresh opportunity to rigorously test the reliability of computational tools for predicting binding affinities, and the fact that host–guest systems were also used in two prior rounds of SAMPL makes it possible to look for consistencies and trends over time. A full analysis of the varied prediction methods used is beyond the scope of this overview, and readers desiring greater detail are referred to the more focused articles provided by SAMPL5 participants. However, some general observations may be made.

Overall, the reliability of methods based on explicit solvent free energy simulations and of those based on electronic structure calculations appear to be fairly consistent across SAMPL challenges, with the simulation-based methods generally providing greater reliability. However, it should be emphasized that the number of observations is still modest, even across three SAMPL rounds and that each class of methods includes multiple variants with different levels of performance. Moreover, there is significant variation in performance across different host–guest series, even within SAMPL5. Thus, predictions for the octa-acid hosts tend to be more accurate than those for CBClip, and accuracy is somewhat greater for the OAH systems than for OAMe, although OAMe differs from OAH only by the addition of four methyl groups. Based on informal discussions at the D3R/SAMPL5 workshop, it appears that the methyl groups, which are disposed around the opening of the binding site, increased difficulties in sampling guest poses in the bound state.

Even the best performing simulation-based methods in SAMPL5 yield absolute RMSE values on the order of 2 kcal/mol and tend to overestimate binding affinities (Figure S1). Previous binding calculations have shown that extensive sampling and small statistical uncertainties of binding estimates can be feasibly achieved on host–guest systems nowadays, with the aid of high-performance computing capabilities [60, 82]. Given that adequate conformational sampling can be achieved for such moderatesized systems, and that the ionization states of these systems are relatively straightforward to ascertain at the experimental pH, the errors in predictions from carefully executed calculations presumably trace to limitations in the potential functions, or force fields, used in the simulations. It should be emphasized that, if current force fields yield errors of this magnitude on host–guest systems, one should not expect to achieve any better in blinded predictions of protein-small molecule binding free energies, even with greater simulation times and a correct treatment of protonation states. Although a recent report describes encouraging results for alchemical calculations of relative protein–ligand binding free energies [11], the statistics come from a retrospective analysis, rather than from blinded prediction along the lines of those described in the present paper. The present results thus underscore the need for improvements in force field parameters and perhaps functional forms.

Electronic structure methods, such as the DFT and coupled cluster methods discussed above, offer an alternative route to improved accuracy in the potential function, since they largely avoid the need for empirical force fields. However, such methods still are, arguably, restricted by the challenge of achieving adequate conformational sampling, due to the high computational cost of evaluating the energy for each conformation. In addition, their accuracy may be limited by the fact that it is difficult to couple them to an explicit solvent model. Although implicit solvent models have predictive power for molecular systems that are essentially convex in shape (see, e.g., SAMPL5 papers regarding the calculation of distribution coefficients for drug-like molecules), it is unknown whether they can capture the properties of water in confined spaces, such as the binding sites of host molecules or proteins, well enough to provide binding free energies with kcal/mol accuracy. It seems probable that continued improvements in computer power and algorithms will make quantum methods, perhaps hybridized with classical methods, increasingly competitive with classical free energy methods. More computationally efficient methods, such as BEDAM and Movable Type, also generated some encouraging results and are amenable to continued refinement, such as through the development of improved solvent models, and the incorporation of more accurate force fields as they become available.

In the current host–guest challenge, a number of groups submitted multiple predictions, and the results often provided clear signals as to the relative merits of the various approaches tested. Indeed, the simplicity of host–guest model systems makes it relatively easy to evaluate errors and isolate their sources, and the blinded nature of the SAMPL challenges eliminates the risk of even unintentionally adjusting one's method to agree with known data. Thus, submission of multiple predictions is encouraged for future rounds of SAMPL. It is also hoped that more groups will participate, so that an even wider range of methods may be tested; additional methods may also be evaluated by participants using software developed outside their own research groups, including commercial packages.

SAMPL is a community effort. It depends on the generosity of experimentalists who make their data available on a prepublication basis, which is not always convenient, and it requires courage on the part of the computational chemists, who are making truly blinded predictions in a public setting. It is indeed encouraging that so many groups contributed to and participated in the SAMPL5 host–guest challenge, and thus to the continuing improvement of the entire field.