Stay Wet, Stay Stable? How Internal Water Helps Stability of Thermophilic Proteins

Abstract

We present a systematic computational investigation of the internal hydration of a set of homologous proteins of different stability content and molecular complexities. The goal of the study is to verify whether structural water can be part of the molecular mechanisms ensuring enhanced stability in thermophilic enzymes. Our free energy calculations show that internal hydration in the thermophilic variants is generally more favourable and that the cumulated effect of wetting multiple sites results in a meaningful contribution to stability. Moreover, thanks to a more effective capability to retain internal water some thermophilic proteins benefit of a systematic gain from internal wetting up to their optimal working temperature. Our work supports the idea that internal wetting can be viewed as an alternative molecular variable to be tuned for increasing protein stability.

Introduction

Life is found at both severe cold and hot climates. Extremophilic organisms equipped by a suitable molecular machinery challenge these extreme conditions. For instance, proteins from thermophilic bacteria or archea are stable and functional at very high temperatures¹, in some cases up to the boiling point of water, 100° C.

Thermophilic enzymes are considered as a natural template for understanding the elementary molecular factors concurring to the stability and the stability/function trade-off of proteins^1–3. Structural analysis and biochemical engineering have successfully singled out several mechanisms of thermal stabilisation. These include the location of strategic ion-pairs^4–6, optimal distribution of charged amino-acids at the surface^7,8, optimal local packing⁹. However, it is widely accepted that different molecular mechanisms can be combined, resulting in a variety of thermodynamic routes to thermal adaptation^10–12.

The design of enzymes resistant to high temperatures or other harsh conditions, e.g. pH, denaturants, is appealing in biotechnology, chemical processing and other technologies which aim to exploit the power of enzymes^13–16. The possibilities to enlarge the molecular variables so as to get tuned to achieve enhanced stability of the enzymes is therefore of practical interest.

Inspired by seminal work on globular proteins that attempted to quantify the contribution of cavity hydration on protein stability^17–19, we started examining whether internal wetting is a key stabilising factor of thermophilic proteins when compared to their mesophilic variants²⁰. The goal is to reveal an alternative strategy in protein engineering. In fact, several investigation have suggested that specific solvation could contribute to the enhanced stability of the thermophilic enzymes^21–27. Moreover, it is important to recall that thermophilic proteins generally sustain high pressure too¹. The presence of strategic internal water helps in explaining this double resistance as the effect of optimised internal packing²⁸ and extended molecular hydrogen bond patterns,which are less sensitive to temperature and pressure^22,29.

Experimentally, by applying single point mutation (which modifies the local environment of internal cavities too) it was found that buried water acts as a stabilising agent for several proteins like BPTI¹⁹, subtilisin¹⁸, lysozyme³⁰ and lipases²². However, for some other cases the opposite is true, e.g. iso-1-cytochrome³¹, protease³² and lysozyme T4 mutants¹⁷. Computational studies^33–39 have provided complementary atomistic details on water penetration and correlated the internal wetting to the chemical nature of protein pockets^36–38,40, protein stability^36,41 and their function^42–51.

How the internal wetting acts differently on stability and function of mesophilic and thermophilic homologues however has never been addressed in detail. In a seminal work Yin, Hummer and Rasaiah²⁶ investigated the hydration of the internal cavities of tetrabrachion protein from hyperthermophilic Staphylothermus marinus, whose optimal growth temperature is ~ 365K. They pointed out that at high temperature dewetting of the internal cavities leads to denaturation. Recently, some of our group members performed a comparative study between a mesophilic and hyperthermophilic G-domains^20,25,52,53. The internal hydration was found to contribute to the stability gap between the two homologues. A gain of about 1.3-2.5 kcal/mol was estimated in favour of the hyperthermophilic domain that corresponds to the shift of melting temperature of about 6 K, almost $\frac{1}{6}$ of the experimental shift between the two proteins²⁰. It was also clearly shown that internal hydration correlates to the flexibility/rigidity of the protein matrix^20,53. This finding potentially opens a new perspective to elicit the relationship among protein mechanical, thermal stabilities and hydration³.

In this work we extend our investigation and present the results of a systematic comparative study on a set of homologues of different stability contents. We used molecular dynamics (MD) simulations stretching up to hundreds of nanoseconds to explore the exchange dynamics of water penetrating inside the protein structures. On the basis of this analysis and using a convenient computational approach we estimated the hydration free energy for buried water. Our results show that thermophilic proteins can actually benefit from internal hydration to ensure their stability in a broad range of temperatures. This is caused by a more favourable interaction of water with the internal cavities and by a stronger capability to retain internal wetting in a broader window of temperatures.

Method

Systems and MD Simulations

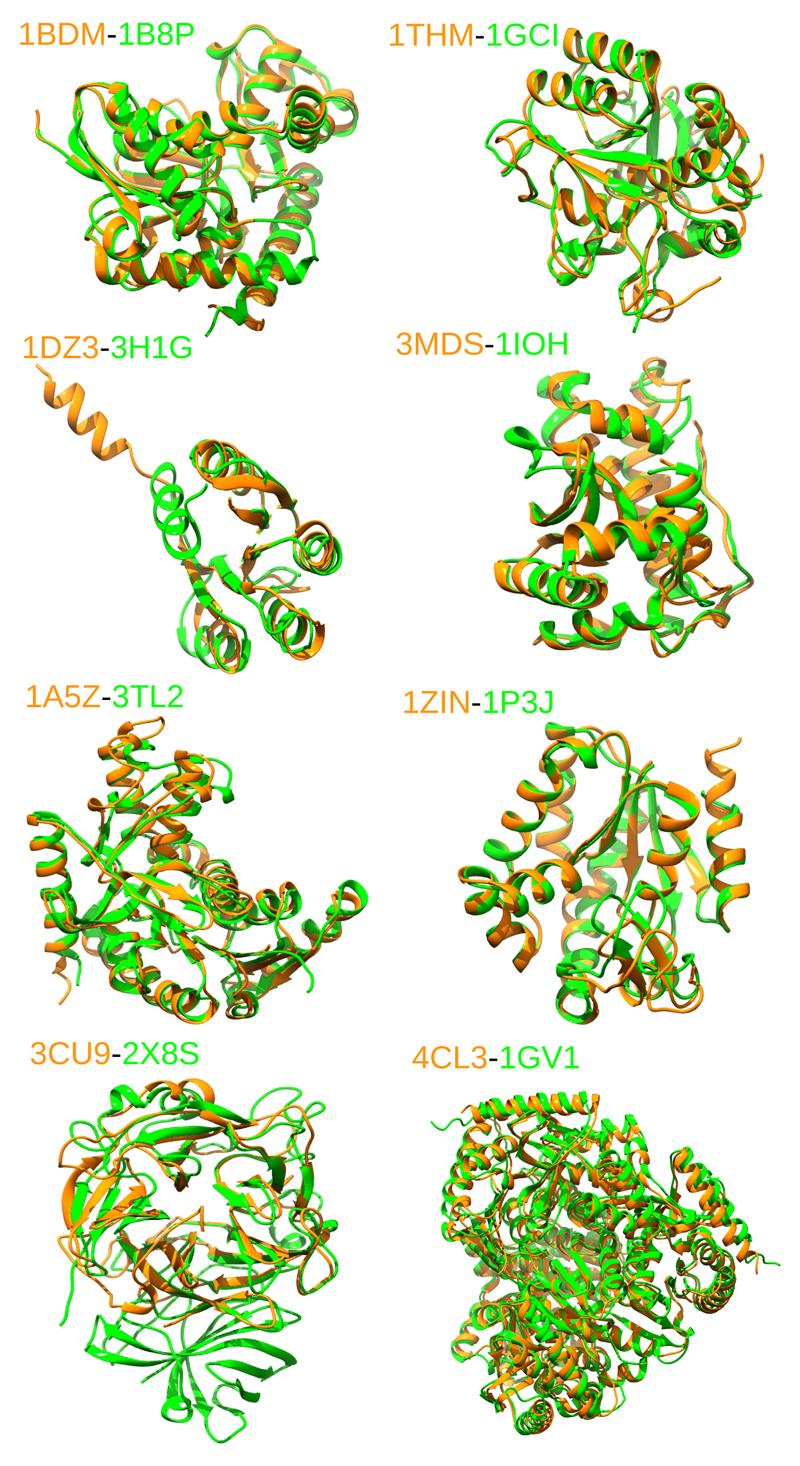
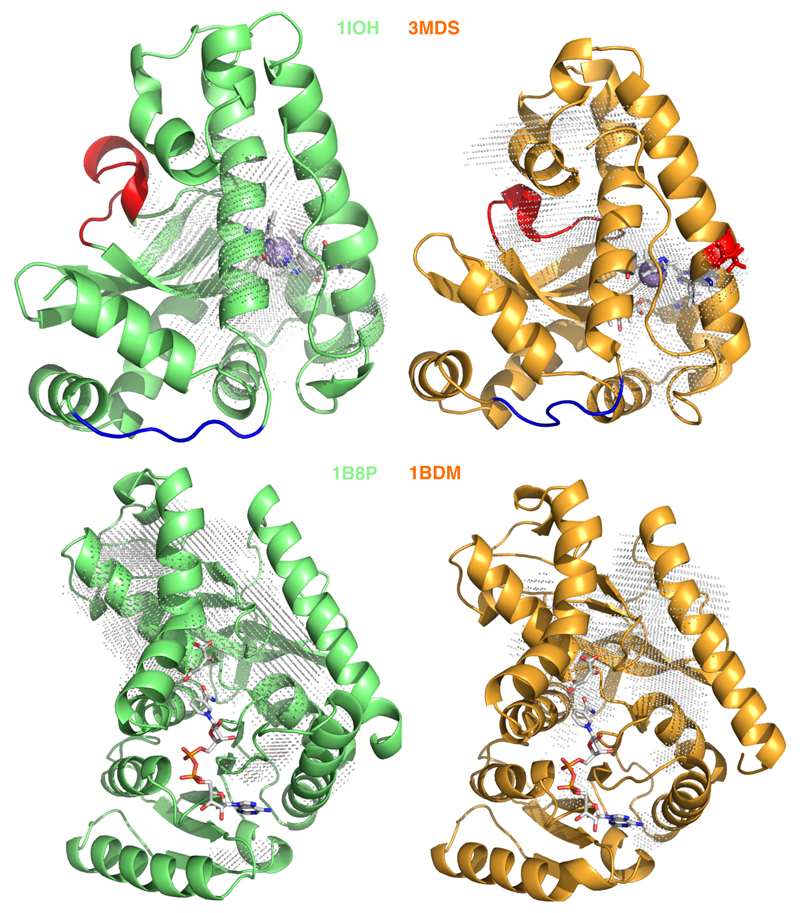
We have investigated eight pairs of homologous mesophilic/thermophilic proteins belonging to different families. As starting point we have considered the list of proteins analysed in a previous work by Pechkova et al.⁵⁴ where the authors looked for a direct correlation among thermophilicity and water content in X-ray structures. We have extended the investigation by searching in the Protein Data Bank for homologous of high structural similarity and focusing on the content of structural water. Our analysis was not conclusive and the overall results appear to be extremely dependent on the different resolutions at which the structures were resolved. In order to have a better understanding without limit ourselves to crystallographic data we have selected a pool of seven pairs for our atomistic simulations, the proteins in the selected pairs have comparable X-ray resolutions. For computational reason, the selected monomeric proteins have relatively small size, 200 to 400 amino acids. To these seven pairs, we added another one already investigated by some of us in a different context, a pair of tetrameric malate dehydrogenases⁵⁵, a second extra pair was used for sake of comparison of the free energy calculations (see below in the text), this latter is a pair of G-domains from Elongation Factor proteins²⁰.The molecular details of these systems are summarised in Table 1 and a molecular view of the structural superimposition of the eighth pairs studied specifically here is given in the Figure 1, for the G-domains we refer to²⁰. The size of the systems ranges from 123 up to 1240 amino acids, and each protein fold contains both α-helices and β structures. Three pairs belong to the malate/lactate dehydrogenase family. Out of three, for two we considered only one monomer of the multimeric protein, while for the other pair (1GV1/4CL3) all the tetrameric protein is considered. This selection helps filtering the effect of inter domain interface on water confinement.

Table 1.

Pairs of mesophilic/tehrmophilic homologues studied in this work. The optimal temperature of the host organism is reported in column 4. The number of amino acids, of water molecules solvating the protein in the simulation box, and the simulation length are reported in the last three columns. For the proteins 1B8P/1BDM and 3TL2/1A5Z the simulated monomer corresponds to the chain A in the PDB.

PDB code	Protein	Organism	Topt (C)	N. aa	Nw	Simulation length (ns)
1EFC 1SKQ (A)	G-domain EF-Tu G-domain EF-α	E. coli Sulfulobos solfataricus	37 75	196 226	7440 10673	600 600
1B8P (A) 1BDM (A)	Malate dehydrogenase Malate dehydrogenase	Aquaspirillum articum Thermus thermophilus	4-10 65	327 317	9944 8837	430 450
1GCI 1THM	Subtilisin Thermitase (subtlisin-like)	Bacillus lentus Thermoactinomyces vulgaris	10-35 55	269 279	7324 7142	410 428
3H1G 1DZ3	Chemotaxis (CheY-like) Spo0A (CheY-like)	Helicobacter pylori Geobacillus stearothermophilus	30-37 55-65	123 123	4720 6727	450 400
1I0H 3MDS	Manganese superoxide dismutase Manganese superoxide dismutase	Escherichia coli Thermus thermophilus	37-49 65	205 203	7226 6680	430 420
3TL2 (A) 1A5Z (A)	Malate dehydrogenase L-lactate dehydrogenase	Bacillus anthracis Thermotoga maritima	37 80	315 311	10014 11609	400 400
1P3J 1ZIN	Adenylate kinase Adenylate kinase	Bacillus subtilis Geobacillus stearothermophilus	25-35 55-65	212 217	6395 8461	400 400
2X8S 3CU9	L-arabinanase L-arabinanase	Bacillus subtilis Geobacillus stearothermophilus	28-30 55-65	470 314	11457 9739	210 200
1GV1 4CL3	Malate dehydrogenase Malate dehydrogenase	Chlorobium vibrioforme Chloroflexus auranticus	15-45 >50	1240 1236	35485 35422	600 600

Figure 1.

Molecular representation of the eight homologous pairs studied in this work. The mesophilic variant is coloured in green, the thermophilic variant is coloured in orange.

For each protein we performed MD simulations in aqueous solution and at ambient conditions. The proteins were modelled by the charmm22 force-field combined with charmm-TIP3P model for water⁵⁶. The proteins were placed in a simulation box ensuring a good solvation conditions, see Table 1. Crystallographic water was maintained during the system set-up. The simulations were carried out using the NAMD package⁵⁷. After an equilibration phase in the NPT ensemble, the trajectories were integrated with a time step of 2 fs in combination with the Langevin thermostat to keep the temperature constant (characteristic time of τ_T = 0.2 ps⁻¹) and sampling the canonical ensemble (NVT). Electrostatics was handled by the PME scheme with a resolution of 1 Å for the reciprocal part. The short range part of electrostatic interactions and vdW interactions were truncated at 10 Å. The configurations along the trajectories were stored with a frequency of 2 ps. The simulations were extended for about 400/600 ns. For selected pairs complementary simulations of various lengths (from 60 to 100 ns) were performed at high temperatures, namely 320,340, 360 K.

Internal Water

In order to estimate the free energy contribution of internal hydration to protein stability it is necessary, as first step, to individuate the molecules hydrating the internal sites of the protein. For this purpose we used a kinetic criterion and selected the water molecules that reside continuously in the protein hydration shell for more than 4.5 ns. In fact, it is well established that water molecules buried in protein internal cavities or pockets exchange with the external solution with a characteristic time exceeding the nanosecond^35,58–60. For each of the individuated water molecule we estimated the hydration free energy that represents the work for transferring the molecule from the external bulk solution to the protein internal site. The framework used for these calculations is discussed below. The hydration shell is defined by the water molecules which are within the spherical-cut off (r_c = 4.5 Å) from the heavy atoms of the protein. The continuous location of water in the hydration shell was monitored by the survival probability function, N_w(t), as described in Refs^20,35. The analysis of internal hydration was restricted to a representative stretch of the trajectory (~100/200 ns depending on the system and the exchange dynamics). In the specific case of the tetrameric malatate dehydrogenases (1GV1/4CL3) because of the size of the system and the presence of an internal water pool at the interface with the four domains, the kinetic cutoff was made more strict, 20 ns, in order to select buried water molecules and filter out the molecules in the internal pool. From the ensemble of long residence water molecules a smallest set constituted by the more stable molecules located in the interior of the proteins was used for the free energy calculations. The number of internal water molecules used for calculating hydration free energies is reported in Table S1, for all pairs but one, about 20 molecules per protein were used as sample.

Free energy calculations

Hydration free energy can be rigorously computed by combining the free energy perturbation (FEP) method and a localisation constraint^34,36,61. In short, a non interacting water molecule is localised in the protein reference site where it is slowly energetically coupled to the protein environment. The same procedure (without localisation) is performed for a molecule in the pure water solution. The free energy differences between the two processes corrected by the localisation contribution represents the free energy gain/penalty to hydrate the protein internal site. For a complete description we refer to the work of Rick and coworkers³⁶. However, this approach is computationally expensive and when the goal is a systematic comparison between different systems a more efficient method, although approximated, is preferred. Several strategies have been recently reported in literature^62,63.

In this work we rely on the so-called Gaussian approximation⁶⁴ that in combination with the particle insertion method provides a reasonable compromise for estimating hydration free energy. In the past, this approach was successfully tested for different molecular environments like proteins and micelles^65–67.

The excess chemical potential μ_ex associated to the hydration of a protein internal site can be written as the sum of two contributions

$${\mu }_{ex}={\mu }_{ex}^0+{\mu }_{ex}^{pw}$$ (1)

The first term on the right side represents the work to create an empty volume in the disordered protein medium capable to host a water molecule, the second term measures the free energy contribution due to the specific interactions of the molecule with the protein, i.e. electrostatic and vdW interactions. This term is formally given by the ensemble average $\frac{1}{\beta }ln{\langle e^{\beta \Delta U}\rangle }_1;$ where the contribution ΔU = U₁ − U₀ is the difference between the potential energy calculated for a given configuration assuming a fully interacting particle (final state, U₁) and a non-interacting particle (initial state, U₀). Since the initial state of the hydration process is represented by the non-interacting water molecule located in the protein site, the term U₀ = 0. The ensemble average 〈…〉₁ is evaluated in the final state representing the interacting water molecule inside the protein.

The numerical estimate of the term < e^βΔU >₁ is difficult to converge in a standard simulation because of the oscillatory nature of the exponential function, and an approximation is often used. In this work we apply the so-called Gaussian approximation that reduces the expression to

$${\mu }_{ex}^{pw}=\frac{1}{\beta }\mathit{ln}<e^{\beta \Delta U}{>}_1\approx {\langle \Delta U\rangle }_1+\frac{1}{2}\beta {\sigma }_1^2$$ (2)

where the average of ΔU and its fluctuations σ² = 〈(ΔU − 〈ΔU〉)²〉 are extracted from the simulations in the state 1, internal site hydrated. Similarly, the excess chemical potential of a water molecule in bulk can be computed. For TIP3P model at ambient condition it is estimated to be ~ 9 kcal/mol^66,67. The advantage of the Gaussian approximation is that using a single long simulation where the hydration of internal sites is sampled at once it is possible to extract the hydration free energy of the sites of interest.

The cavity term ${\mu }_{ex}^0$ can be calculated according to the Widom’s particle insertion theory⁶⁸. In previous work, Garcia and coworker showed that this term is approximately same when estimated for an internal protein site or for the bulk water, ≃ 4 kcal/mol^65,66, and differences are in the order 0.2 kcal/mol. Therefore this contribution cancels out when the total free energy difference $\Delta {\mu }_{ex}={\mu }_{ex}^{pw}-{\mu }_{ex}^{bulk}$ is calculated.

After a preliminary check, we have verified that generally the dominant contribution to the hydration free energy stems from the direct interaction of the tagged internal water with the protein matrix, so for our systematic calculations we have just considered this contribution to the interaction potential energy entering in the estimate of ${\mu }_{ex}^{pw}.$

Results and Discussion

Free energy of internal hydration

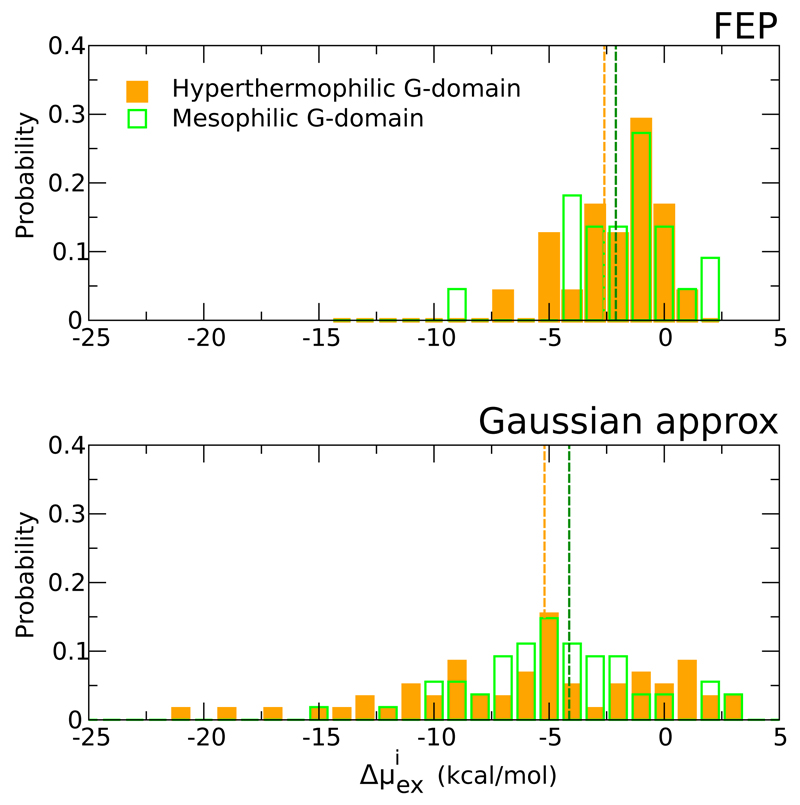
The quality of the Gaussian approximation is first verified. In a previous study²⁰ we have constructed the distribution of the per molecule hydration free energies (Δμ_ex) at ambient temperature for water buried in the internal cavities of two homologous G-domains by applying rigorous FEP calculations. We found that while the two distributions look very similar the internal hydration of the thermophilic proteins is however slightly more favourable than that of the mesophilic variant. For sake of comparison they are reported in the top panel of Figure 2. We have constructed the equivalent probability distribution by applying the Gaussian approximation. Because of the less-demanding computational cost, the calculations were performed on a larger set of internal water than in the case of FEP calculations. The final result is reported in the bottom panel of Figure 2. As observed using the FEP calculations, the distributions for the mesophilic and thermophilic species are very similar, and for the majority of the considered water molecules the location in the protein internal sites is energetically favourable. When compared to the FEP distributions, we notice that applying the Gaussian approximation, the values of the hydration free energy are more spread, ranging from +2 to -20 kcal/mol. As effect of this broadening, the average hydration free energy for the thermophilic homologue results about 3 kcal/mol more favourable than that of the mesophilic one. All the estimates of ${\mu }_{ex}^{pw}$ come with an error, estimated by block analysis, of about 0.2 kcal/mol each.

Figure 2.

Probability distribution of the free energy to transfer a single water molecule from the external solution to the interior of the G-domain proteins (∆µ_ex). Top panel refers to FEP calculations, see ref20. Bottom panel refers to calculations performed applying the Gaussian approximation.The values obtained for the mesophilic protein are reported in green and those for the thermophilic variant are in orange.

The broader shape of P (μ_ex)s, is caused by two concomitant effect, first the Gaussian approximation cannot always properly account for the tails in the distribution P (ΔU) that extend at less favourable gap values ΔU, secondly the ensemble of water used for reconstructing the free energy is larger (see last line in Table S1) and for the same water the location in several close sites are naturally included in the calculations. Note that, as reported in Figure S1, when separate states exist, thus the P(ΔU) deviates from the unimodal Gaussian-like shape, we separated the states and carried out independent calculations.

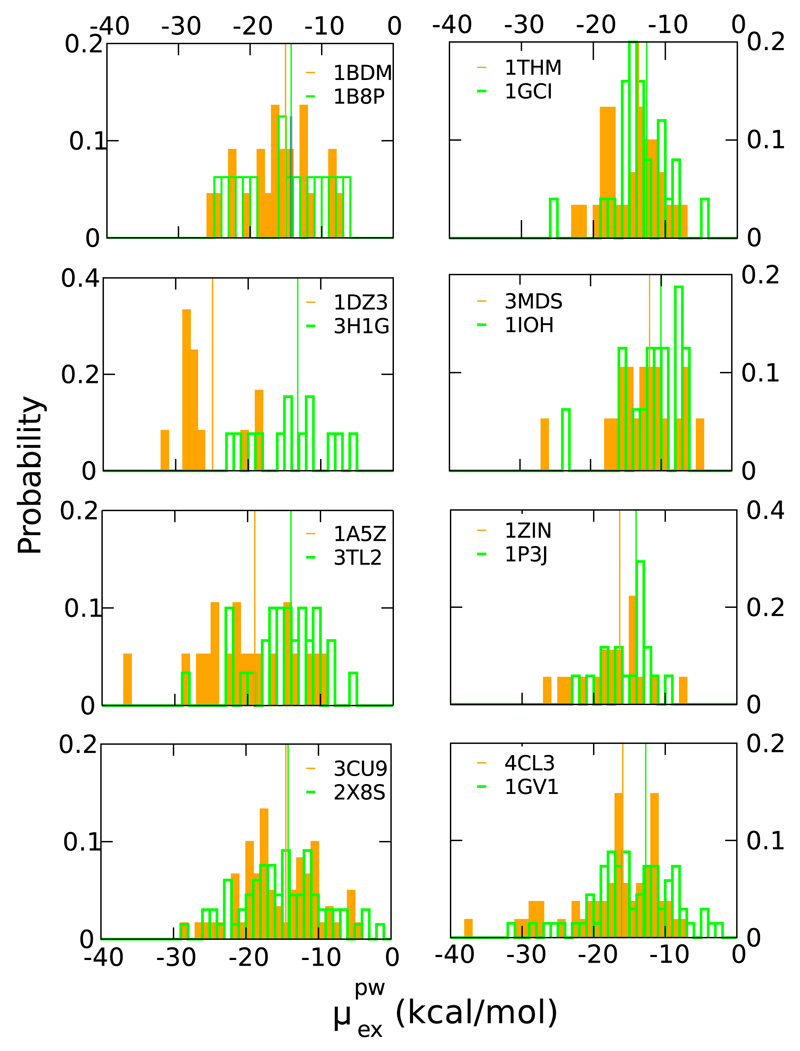
Next, we turn the attention to the set of protein pairs investigated for the first time in this work. Since we are interested in comparing the two homologues we focuses only on the term ${\mu }_{ex}^{pw},$ in fact the bulk term ${\mu }_{ex}^{bulk}$ to be subtracted to obtain the hydration free energy is the same for the two species. In Figure 3 we report the distribution of the excess chemical potential ${\mu }_{ex}^{pw}=\langle \Delta U\rangle +\frac{1}{2}\beta {\sigma }^2$ calculated for internal water for all the protein pairs. In each panel we compare the mesopihlic (green) and the thermophilic (orange) variants. For the majority of the pairs the distribution of ${\mu }_{ex}^{pw}$ extracted from the simulations of the mesophilic and of the thermophilic species are very similar and overlap. As a consequence, the per molecule free energy gain due to internal hydration is comparable between the two homologues, $\Delta {\mu }_{ex}^{pw}={\langle {\mu }_{ex}^{pw}\rangle }^T-{\langle {\mu }_{ex}^{pw}\rangle }^M$ is −2 to 0 kcal/mol. However, in a few cases the distributions of the thermophilic species is shifted toward more negative values and associated to a substantial favourable hydration free energy such that $\Delta {\mu }_{ex}^{pw}=-4$ down to −10 kcal/mol, see the pairs 1DZ3/3HIG,1A5Z/3TL2,4CL3/1GV1. This gain is associated to a specific hydrophilic characters of the internal cavities of the thermophilic proteins, for example for the pair 1DZ3/3H1G the buried water molecules are systematically linked by a higher number of hydrogen bonds, and the cavities are depleted of hydrophobic contacts (see Figure S2). The 1DZ3/3HIG pairs is a specific case, these are the smallest proteins in our data-set, the size being of 123 amino acids, and in average only one single long residence water molecule is buried in the protein matrix.

Figure 3.

Probability distribution of the excess chemical potential due to the interactions between the water molecule and the protein as calculated via the Gaussian approximation. Each panel refers to a different pair of thermophilic/mesophilic homologues. Data for the mesophiles are in green, data for the thermophiles are in orange.The average value $\langle {\mu }_{ex}^{pw}\rangle$ are indicated by the vertical lines. All averages are lower than the bulk estimate for ${\mu }_{ex}^{bulk}=-9kcal/mol$ reporting an average favourable internal hydration.

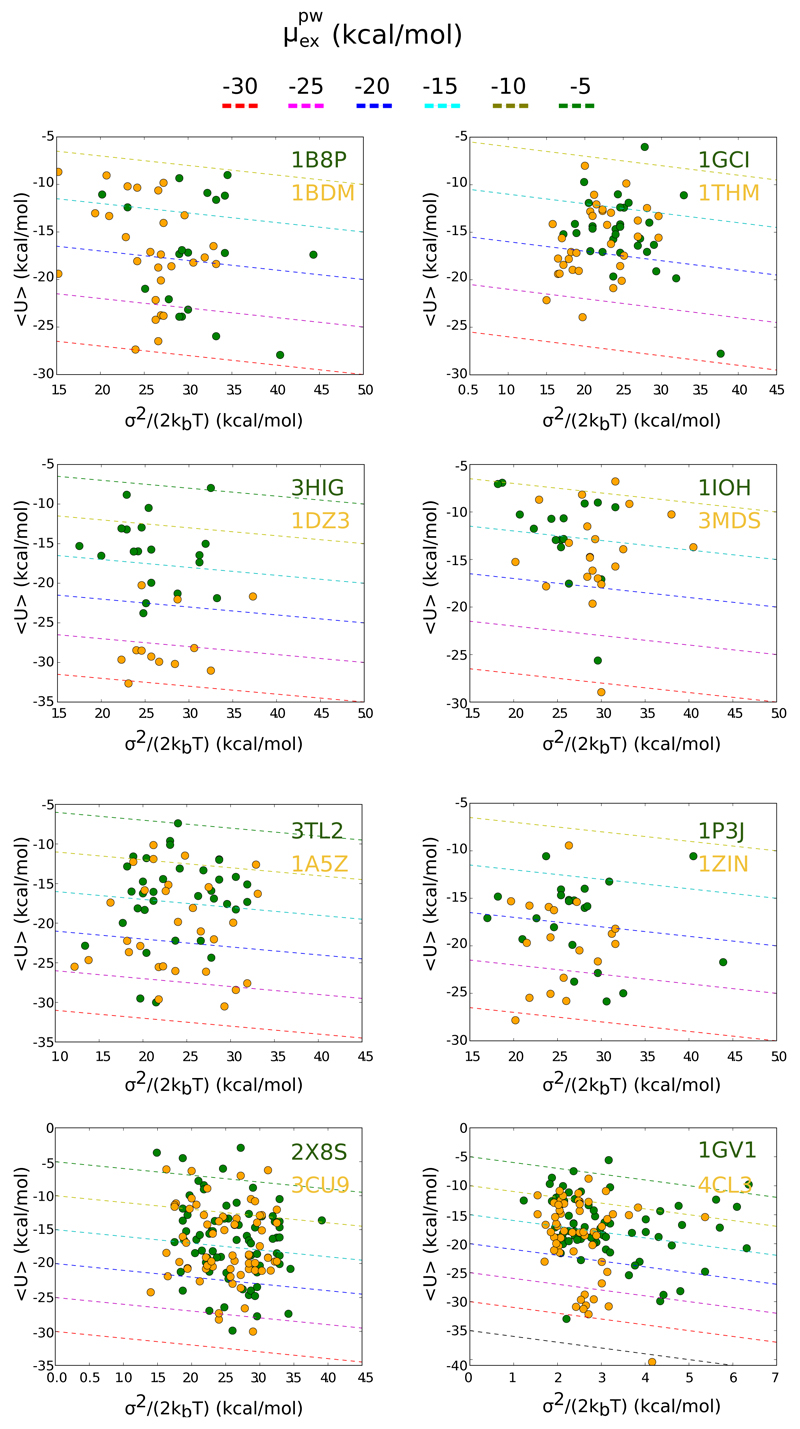
A separation of the enthalpic vs entropic contributions to ${\mu }_{ex}^{pw}$ is provided in the 2D plots presented in Figure 4. For each pair the scattered distribution of the values 〈U〉 and $\frac{{\sigma }^2}{2k_{b}T}$ is plotted. We first note that the larger hydration free energy computed for the thermophilic proteins 1A5Z, 1DZ3 and 4CL3 with respect to their mesophilic counterparts is granted by more negative potential energy terms, 〈U〉, that quantifies a favourable environment for water hydrogen bond connectivity in the protein interior. A second important results concerns the distribution of the entropic term $\frac{{\sigma }^2}{2k_{b}T}$ for the pair of the tetrameric malate dehydrogenases, 1GV1/4CL3. The fluctuations of the interaction energy are systematically larger in the mesophilic malate than in the thermophilic one, $\frac{{\sigma }^2}{2k_{b}T}$ takes values larger than 4 kcal/mol. This correlates to what observed in a recent computational investigation where the mesophilic tetrameric malate dehydrogenase (1GV1) was probed to be more flexible than the thermophilic species (4CL3) by monitoring several metrics describing protein conformation changes⁵⁵. In fact, the conformational flexibility ensures larger changes in the confinement acting on internal water as visible in larger σ²s. As noted for conformational flexibility, the shift in water confinement between the two tetrameric homologues is an effect of inter-domain interactions since for the single domains of the lactate/malate proteins of pairs 1BDM/1B8P and 3TL2/1A5Z no differences pop up. When focusing on the ensemble of systems all considered, we recover a neat trend, water/protein interactions are more favourable in average for thermophilic species than mesophilic ones, Ū = −16.4 and −13.1 kcal/mol, respectively; while the entropic penalty is comparable, (for the thermophilic proteins $\frac{{\overline{\sigma }}^2}{2k_{b}T}=2.5kcal/mol$ and for mesophilic ones $\frac{{\overline{\sigma }}^2}{2k_{b}T}=2.8kcal/mol$ The values extracted from our simulations are comparable to what computed with different approach for internal water in proteins^36,63,65.

Figure 4.

2D representation of the enthalpic and entropic contributions to ${\mu }_{ex}^{pw}$ for each pair of thermophilic (orange) and mesophilic (green) species. Dashed lines represent iso-(free energy) contours.

Stability gain from hydration

The per molecule excess chemical potential ${\mu }_{ex}^{pw}$ measures how favourable a local internal protein site is for water. However, the protein internal cavities can be solvated by multiple molecules at once. This number is highly fluctuating and depends on conformational changes of the protein^20,35,60. A practical strategy to estimate this number is to count how many of the long residence water molecules are located simultaneously in the interior of the protein. The average number obtained for the set of proteins is reported in Table 2.

Table 2.

Average per molecule excess chemical potential ${\mu }_{ex}^{pw}$ and hydration free energy $\Delta {\mu }_{ex}={\mu }_{ex}^{pw}-{\mu }^{bulk}\left({\mu }^{bulk}=-9.0\left(0.1\right)kcal/mol\right).$ The number in parenthesis indicate statistical error, estimated from propagation of standard deviations. The number of long residence water molecules residing simultaneously in the interior of the proteins at T=300 K are indicated by 〈n_w〉, the drop of internal hydration due to temperature increase is referred as Δn_w = 〈n_w〉³⁰⁰ − 〈n_w〉³⁶⁰.

Mesophile					Thermophile
Protein	${\mu }_{ex}^{pw}\left(\text{kcal}/\text{mol}\right)$	Δµex (kcal/mol)	〈nw〉	〈Δnw〉	Protein	${\mu }_{ex}^{pw}\left(\text{kcal}/\text{mol}\right)$	Δµex (kcal/mol)	〈nw〉	〈Δnw〉
1B8P	-14.3(0.1)	-5.3(0.2)	15	8	1BDM	-15.0(0.1)	-6.0(0.2)	16	10
1GCI	-12.6(0.1)	-3.6(0.2)	16	8	1THM	-13.7(0.1)	-4.7(0.2)	16	6
3H1G	-13.2(0.1)	-4.2(0.2)	1	0	1DZ3	-24.9(0.1)	-15.9(0.2)	1	0
1IOH	-10.0(0.1)	-1.0(0.2)	13	10	3MDS	-11.7(0.1)	-2.7(0.2)	13	8
3TL2	-14.0(0.1)	-5.0(02)	9	5	1A5Z	-19.0(0.1)	-10.0(0.2)	7	3
1P3J	-14.1(0.1)	-5.1(0.2)	5	4	1ZIN	-16.4(0.1)	-7.4(0.2)	5	3
2X8S	-14.2(0.1)	-5.2(0.2)	49	24	3CU9	-14.5(0.1)	-5.5(0.2)	25	13
1GV1	-12.7(0.1)	-3.7(0.2)	130	65	4CL3	-15.94(0.1)	-3.7(0.2)	135	67

For G-domain homologues discussed in the previous section²⁰ we have attempted to estimate the total contribution stemming from these molecules to the overall stability of a protein. Mainly, we were interested to evaluate the energetic gain for a protein in solution to have the internal cavities wet instead of dry, see the scheme in Figure S7. On the basis of the hydration free energy differences calculated for individual internal site with respect to bulk, the total contribution was derived by imposing the total occupation of the internal sites equal to the number of internal water estimated by considering the kinetic cut-off on the exchange dynamics. Using a tight kinetic threshold (τ_c = 15 ns) the cavities were found to host 〈n_w〉 = 4.7 molecules in both homologues, and the total hydration free energy with respect to bulk was $\Delta {\mu }_{ex}^{tot,pw}=-15.7\text{and}-17.0kcal/mol$ respectively for the mesophilic and the hyperthermophilic proteins. Therefore, a marginal contribution to the stability gap between the two proteins was associated to internal hydration, $\Delta \Delta {\mu }_{ex}^{tot,pw}=1.3kcal/mol$ in favour of the hyperthermophilic one, and quantifiable in a shift of the melting temperature of about 6 K. For a less strict condition on localisation kinetics (τ_c = 4.5 ns as used in this work) the gap in favour of the hyperthermophilic domain was larger, $\Delta \Delta {\mu }_{ex}^{tot,pw}=2.5kcal/mol.$

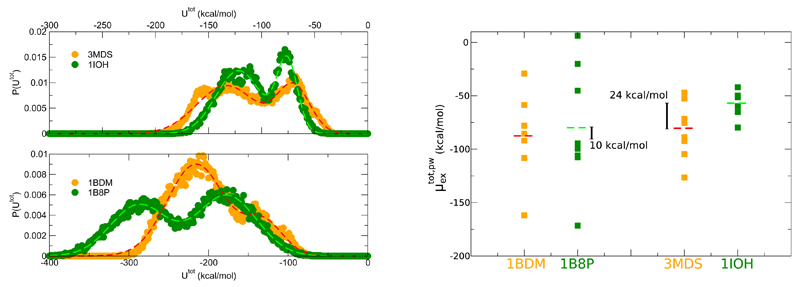
In order to address the issue for the new systems we have selected two representative pairs, 1BDM/1B8P and 3MDS/1IOH. For these pairs the per particle excess chemical potentials calculated for the mesophilic and thermophilic variants are very close and their folds are very similar structurally. Thus, we try to understand whether the collective internal hydration could give a different contribution to the stability of the highly similar protein folds. Here, by exploiting the Gaussian approximation we follow a different and somehow simpler strategy. First, the interactions with the protein of internal water molecules selected by the kinetic criterium is computed along the trajectory for the stretch of time the water is buried in the protein. At the time t this interaction energy corresponds to $U^{tot}={\displaystyle {\sum }_{i=1}^{nw}{U}_i(t){\delta }_i(t)}$ where δ_i is a function taking value of 1 if the i molecule is inside the protein and of zero otherwise and nw is the number of water molecules used for the free energy calculations. The fluctuations of U^tot are controlled by the breathing mode of the proteins and the correlated escape/penetration of the long residence water. The probability distributions of U^tot extracted from the trajectories are reported in Figure 5. We appreciated, as already observed for the G-domains, that the internal hydration is associated to multiple states, in fact all the distributions show a bimodal shape well fitted by a bi-Gaussian curve.

Figure 5.

Left. Probability distribution of the total interaction energy between internal water and the protein. A fit with a two-Gaussian function is represented as dashed lines. Right. Spectra of values of the ${\mu }_{ex}^{tot,pw}$ extracted using the Gaussian approximation for representative states of the internal hydration. Average values are represented as dashed horizontal lines and the gap estimated between the thermophilic and mesophilic proteins are indicated.

In a previous study we have highlighted²⁰ the correlation among the distribution of internal hydration states and the number of conformational states visited by the proteins and directly measured by order parameters that quantify the fluctuations of the protein matrix only, i.e. RMSD, fraction of native contacts, fraction of torsional angles. Preliminary results from cluster analysis⁵³ on the pairs 1BDM/1B8P and 3MDS/1IOH, confirm the correlation (see Figure S4). For instance, the mesophilic 1B8P is more flexible and visit a larger number of states than the thermophilic 1BDM, this flexibility is reflected in a broader distribution of internal hydration states, see Figure 5. For the pair 3MDS/1IOH, along the stretch of trajectory used for the study of internal hydration, the two proteins visit a very similar number of states, and this agrees with a similar distribution of internal hydration states. A molecular representation of selected hydration states for the pair 1BDM/1B8P is given in Figure S5.

For several stretches of the trajectory where locally the behaviour of U^tot is steady we have computed the total excess chemical potential using the Gaussian framework, ${\mu }_{ex}^{tot,pw}=\langle U^{tot}\rangle +\frac{1}{2}\beta {({\sigma }^{tot})}^2.$ This strategy allows us to focus on internal hydration states that are not altered by the in/out exchange events. The Gaussian calculations were performed for representative states that cover all the range of values experienced by U^tot, see Figure S3. In the right part of the Figure 5 we report the spectrum of the extracted values of ${\mu }_{ex}^{tot,pw}$ and of the average $\langle {\mu }_{ex}^{tot,pw}\rangle .$ For the two pairs we probe that the internal hydration provides an important contribution to the protein stability, and that this contribution is larger for the thermophilic variants than the for the mesophilic ones. Thus, even if the thermophilic and mesophilic variants host in average the same number of internal water, see Table 2, the thermophilic species have a larger gain from interior wetting. For the pair 1BDM/1B8P we have verified that the contribution of the interaction energies between the internal water molecules themselves is of a few kcal/mol, about 1% of the total interaction energy of these water with the protein.

Water retention

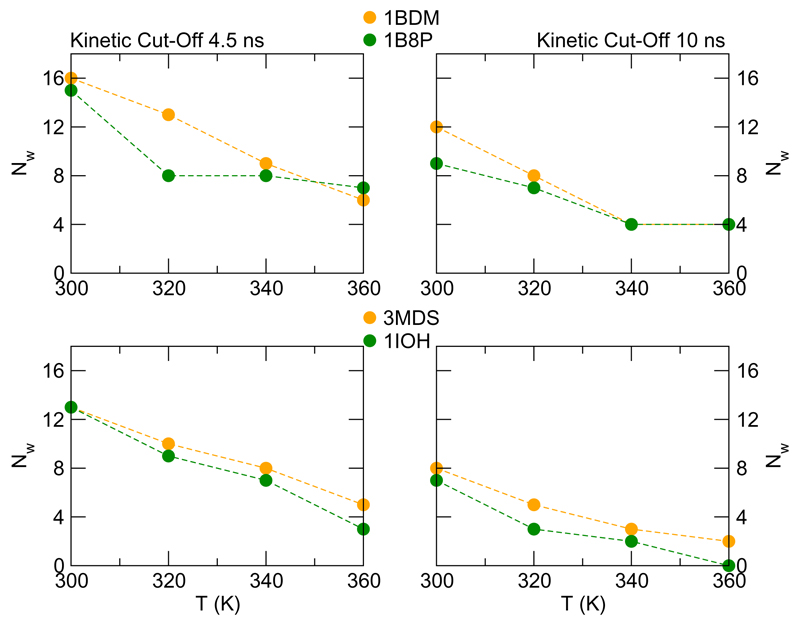
Thermophilic proteins are stable and functional at high temperature, therefore it is important to understand how internal wetting evolves upon thermal excitation approaching the optimal working conditions for these extremophiles. For the thermophilic homologues considered in this work, the optimal working temperature of the hosting organism is comprised between 60° and 90° C. For all pairs we have performed supplemental simulations at T = 360 K. The length of the generated trajectories is approximately 100 ns for each system. Using the kinetic criterium already described and accounting for thermal effect on the exchange kinetics we calculated how many long residence water molecule solvate in average the internal protein matrix at higher T. For all pairs but one (1DZ3/3H1G) temperature increase favour internal dewetting, with a drop of the amount of internal water molecules of about 40 – 70%.

In order to consider in more detail how the dewetting occurs, for the pairs 1BDM/1B8P and 3MDS/1IOH we have explored the behaviour at intermediated temperatures, including new simulations at T = 320 K and 340 K. The results obtained are summarised in Figure 6. For the pair 1BDM/1B8P the thermophilic enzyme exhibits a greater capacity of water retention upon thermal excitation and therefore can benefit of a systematic gain from internal hydration at higher temperature window encompassing its experimental optimal working temperature, T ≃ 335K. For the pair 3MDS/1IOH, water retention in the thermophilic variant is less striking although observed up to 360 K.

Figure 6.

Variation of long residence water molecules buried in the protein interior as a function of temperature. The charts in the top panel refer to the pair 1BDM/1B8P, the charts in the bottom panel refer to the pair 3MDS/1IOH. For each pair, on the left and on right charts we report the data using a kinetic cut-off of 4.5 ns and 10 ns, respectively.

Internal water, stability and function

As final step, we inquired whether the localisation of the long residence water molecules correlate to proteins functional sites. For this purpose we have constructed a spatial density map of the long residence water molecules that allows to screen the most occupied sites in the proteins structure. The general finding is that some long residence water can be in fact found in the active site but most are scattered away. The presence of long residence water in active site is not surprising per se, since on the basis of an excluded volume effect the exchange dynamics is expected to be slower than for the external hydration layer. However, what the mapping shows is that localisation of a potential stabilising factor as buried water is preferential in peripheral regions of the proteins. This can be appreciated in the set of Figure S6 (Supporting Information). For sake of example we discuss here two different cases. In the monomer of the malate dehydrogenase (pair 1BDM/1B8U) according to our kinetic cut-off no long residence water cluster is present in the binding site implying that the binding site is regularly washed up. In a previous work on malate proteins⁵⁵ it was shown that, when considered in its monomeric state, the protein loop gating the access to the binding site is highly flexible in both the mesophilic and thermophilic species, and this probably eases the turn-over of water in the site. We can also observe that in the functional multimeric state (see Figure S6) the long residence waters are largely distributed at the domain interfaces. This finding points out that for this tetrameric proteins, the stabilising water molecules play a role in the stability as well as in the internal allosteric sliding of the domains interface. On the contrary for the manganese superoxide dismutases (pair IOH/3MDS) long residence waters are found in the active site and in proximity of some residues considered key for activity and also thermal stability⁶⁹. While the presence of structural water in binding site is visible in some pairs, our finding shows -as expected- that a stability route by internal hydration could be better achieved by localising the watery bricks in region of the protein matrix not correlated to function, thus challenging stability/function trade-off. This rule-on-thumbs adds to other empirical evidences showing for example that artificial thermal stabilisation is more efficiently achieved by modifying charged residues at the protein surface because this avoids to distort the hydrophobic internal packing⁷, or that is safer to cumulate mutations far away from the active site thus avoiding function knock-out⁷⁰.

Conclusion

We have performed a systematic investigation of the role of internal hydration on protein stability by considering an ensemble of mesophilic/thermophilic homologues. The study is based on a computationally affordable framework for the estimate of internal hydration free energy. When focusing on the hydration free energy of individual water molecule, the internal cavities in thermophilic and mesophilic homologues offer, in most of the cases, an equally favourable environment to water. However, for some pairs, a marked larger favourable contribution is estimated for thermophilic variants, with diffrences among the homologues as high as 10 kcal/mol. Moreover, when considering the overall wetting of the internal sites, thus focusing on the ensemble of water simultaneously located in the interiors of the proteins, we appreciate that the contribution to the stability of thermophilic species can be rather important when compared to the mesophilic variants. The analysis of the thermal perturbation of the internal wetting performed on selected study-cases also highlights the capability of thermophilic proteins to retain to a larger extend the internal hydration state, thus making the favourable contribution to stability from internal water effective in a broader range of temperatures up to their optimal working condition. Our findings suggest, in agreement with Yutani et al.⁷¹, that the design of internal cavity hydration is a valuable strategy to be tested for creating mutants of enhanced thermal stability.

Finally, the highlighted correlation among internal wetting and the variability of protein conformational states opens a new perspective to investigate the relationship among mechanical and thermal stability, as already proposed in the context of pressure driven unfolding^38,72. For example NMR experiment could be designed^60,73 to probe the correlation among exchange kinetics, mechanical fluctuations and thermal stabilities in homologues.

Supporting Information

Supporting data for interaction energy distributions, correlation among conformational and internal hydration states, location of buried hydrated sites. This information is available free of charge via the Internet at http://pubs.acs.org.

Figure 7.

Density map of long residence water molecule overlapped to the X-ray crystallographic structure of the mesophilic (green) and thermophilic (orange) proteins. Top panel. Manganese superoxide dismutase hi lighting the position of the Manganese in the original pdb structure (sphere), the amino acids of the active site (licorice) and region individuated as key for thermal stability and function (red and blue). Bottom panel: single domain of the Malate dehydrogenase highlighting the ligand from the original pdb structure (1B8U).