Beyond Composite Endpoints Analysis: Semicompeting Risks as an Underutilized Framework for Cancer Research

Abstract

Background: Composite endpoints (CEP), such as progression-free survival, are commonly used in cancer research. Notwithstanding their popularity, however, CEP analyses suffer from a number of drawbacks, especially when death is combined with a nonterminal event (ie, progression or recurrence), exemplifying the semicompeting risks setting. We investigated the semicompeting risks framework as a complementary analysis strategy that avoids certain drawbacks of CEPs.

Methods: The illness-death model under the semicompeting risks framework was compared with standard analysis approaches: CEP analyses and (separate) univariate analyses for each component endpoint. Data from a previously published phase III randomized clinical trial in metastatic colon cancer including 1419 participants in the N9741 trial (conducted between 1997 and 2003) were used to determine the impact of the loss of information associated with combining multiple endpoints, as well as of ignoring the potentially informative role of death. A simulation study was conducted to further explore these issues.

Results: Failure to account for critical features of semicompeting risks data can lead to potentially severely misleading conclusions. Advantages of semicompeting risks analyses include a clear delineation of treatment effects on both events, the ability to draw conclusions about a patient’s joint risk of the two events, and an assessment of the dependence between the two event types.

Conclusions: Embedding and analyzing component outcomes in the semicompeting risks framework, either as a supplement or alternative to CEP analyses, represents an important, underutilized, and feasible opportunity for cancer research.

When designing clinical trials, investigators often define outcomes using a composite endpoint (CEP) for which patients are said to experience an “event” the first time they experience one of a set of predetermined events of interest (1–7). In cancer research, the canonical example of a CEP is progression-free survival (PFS). Much has been written on the advantages of using PFS as a primary endpoint (8,9), including that it is less sensitive to effects of second-line therapy than overall survival (OS) (10), it incorporates a broader range of informative events indicative of treatment quality (10), and its use shortens trials because of the potential increase in statistical power due to the increased (overall) event rate (11,12).

Despite these potential benefits, however, PFS remains controversial. In particular, progression may not always be consistently defined across or even within studies (13), and the accuracy of the measured time to progression also raises concerns as progression is typically assessed at scheduled physician visits rather than in real time (12–16). Moreover, although PFS is often interpreted as a surrogate for OS, progression and death do not necessarily correlate well, particularly for cancers characterized by long survival post-progression (13,17–22). This, in turn, could lead to misleading conclusions in either direction—researchers have found statistically significant differences between treatments based on PFS but not OS (18), and vice-versa (23–25).

PFS is also subject to a number of drawbacks associated with the use of CEPs more generally. First, because treatment effect estimates reported from CEP analyses represent a mixture of the treatment effects associated with the component endpoints, their interpretation can be complex and unintuitive (26), and even more so if the component endpoints are not of comparable importance (2). Second, when death is one of the components, its potentially informative role (ie, patients who die may have been at higher risk to experience other events even if they did not) is masked once the individual components are combined. Finally, and perhaps less well known, is that, in contrast to conventional wisdom, the use of a CEP may, in fact, result in a loss of statistical power to detect treatment effects, particularly if treatment effects differ across component endpoints and if they are in opposite directions (5). Furthermore, the degree of this power loss is also influenced by the relative frequencies of and dependence between component endpoints (6).

Each of these drawbacks can be linked to the loss of information that results from combining several outcomes into a single endpoint. Toward making full use of the available information, we present the semicompeting risks framework. As we elaborate upon, this framework provides a means for evaluating semicompeting risks data wherein the occurrence of a nonterminal event (eg, disease progression or tumor recurrence) may be influenced by a terminal event (eg, death). While the recent statistical literature is rich with methods for semicompeting risks data, they have not been widely adopted in the clinical/epidemiological literature. The purpose of this paper, therefore, is to describe and illustrate the semicompeting risks framework, as well as to contrast it with a number of standard analysis strategies. In addition, a simulation study is conducted to explore the potentially informative role that the terminal event plays in CEP analyses.

Methods

The N9741 Trial

To help illustrate semicompeting risks data analyses, we use data on 1419 participants in the N9741 trial. Briefly, N9741, conducted between 1997 and 2003 and published in 2004, was a phase III study of patients with previously untreated metastatic colorectal cancer, designed to compare combinations of the standard of care—5-fluorouracil and leucovorin (5-FU/LV)—with irinotecan (CPT-11) and oxaliplatin (OXAL) (27–29). While the trial originally had seven treatment arms, it was reconfigured in 2000 to have only three: 5-FU/LV+CPT-11, 5-FU/LV+OXAL, and OXAL+CPT-11. For consistency with previously published reports, we label these arms as A, F, and G, respectively. All participants provided written informed consent, and institutional review board approval was obtained for the study. Additional baseline characteristics of these patients can be found in Supplementary Table 1 (available online).

To illustrate the semicompeting risks framework, we consider PFS, defined as the first of: 1) tumor progression or 2) death from any cause. During follow-up, tumors were measured in N9741 approximately every six weeks for the first 42 weeks or until tumor response was confirmed. Measurements were taken every 12 weeks thereafter. Progression was defined as a greater than 25% increase in measurable tumor size, an increase in tumor size in patients who were not considered to have measurable disease, tumor measurements above 50% of the largest previously observed reduction in patients who experienced a partial response, or any new lesion (27).

Semicompeting Risks Data

Here we show how PFS, as defined, can be cast within the semicompeting risks framework (30–42). In its most general form, semicompeting risks refers to the setting when the occurrence of some so-called nonterminal event of interest is subject to some terminal event, in the sense that individuals may only experience the nonterminal event if the terminal event has not occurred. For PFS, the nonterminal event is tumor progression, with the terminal event being death. Note the distinction from the more familiar competing risks framework, in which the multiple events are typically various causes of death (43,44).

Given specific definitions for the nonterminal and terminal events, and finite follow-up, patients will ultimately be classified into one of four outcome groups: 1) those who experience neither event before being censored (ie, neither progression nor death), 2) those who experience the nonterminal event but are censored prior to experiencing the terminal event (ie, progression but no observed death), 3) those who experience the terminal event without having experienced the nonterminal event (ie, death without progression), and 4) those who experience both (ie, progression followed by death). Note that groups 2 through 54 would be combined into a single outcome category in a CEP analysis.

Statistical Analysis

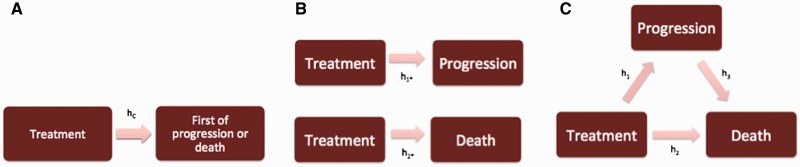
Given outcome information on the two events, an analysis could proceed in a number of ways. Here we focus on three options: 1) a composite endpoint analysis, 2) separate univariate analyses, and 3) a semicompeting risks analysis based on an illness-death model. Figure 1 provides graphical representations of these choices, with the boxes indicating “states” that a patient can be in at any given point in time and arrows indicating the transitions between states. In Figure 1A, we see that patients begin in an “initial” state (eg, time of diagnosis in N9741) and can only experience a single transition (eg, into the state of progression or death). In the subfigure, the label “h_C” refers to the hazard function that would be modeled, for instance, with a Cox model in a standard CEP analysis; the corresponding hazard ratios in the Results section are labeled “HR_C”. Instead of collapsing the two events into a single state, Figure 1B illustrates how one could build separate univariate models for the hazards for the nonterminal and the terminal events (1,45). To distinguish these transitions/hazards from the one in the CEP analysis, Figure 1B labels the hazard for the nonterminal event “h_1*” and the hazard for the terminal event “h_2*”; corresponding hazard ratios in the Results are labeled “HR_1*” and “HR_2*”. While this focuses the analysis on the component outcomes that are, arguably, more interpretable than a collapsed composite, consideration of the independent censoring assumption requires special care. For example, in separating the component outcomes for PFS, the progression model implicitly treats death as an independent censoring mechanism, and yet it may not be plausible to assume that patients who die are representative of the patients at risk for progression at that time (4). Indeed, it may be inappropriate to view death as a censoring mechanism altogether (43,44).

Figure 1.

Flowcharts illustrating the three analysis approaches described in the main text in the context of the progression-free survival (PFS) endpoint. (A) Corresponds to a composite endpoint (CEP) analysis, (B) to separate univariate analyses for the nonterminal and terminal events, and (C) to the illness-death model in the semicompeting risks framework.

Toward explicitly recognizing the potentially informative role that the terminal event may play and distinguishing between the transitions into the terminal state before and after experiencing a nonterminal event, Figure 1C provides the illness-death model representation of the semicompeting risks setting (31,37). For each of the three transitions, one can specify a model for the corresponding hazard function (eg, a Cox model). Thus, three distinct hazard ratios can be estimated to distinguish the effects of a particular covariate on each transition. For PFS, this would permit estimation of HR₁, the hazard ratio for progression; HR₂, the hazard ratio for death given that a patient has not progressed; and HR₃, the hazard ratio for death given that a progression event has occurred. Thus, in contrast to the CEP and separate univariate analyses, the illness-death model formulation makes full use of the information in the semicompeting risks data to explicitly allow the risk of the terminal event to depend on whether the nonterminal event has occurred. Furthermore, one can introduce a common patient-specific frailty, analogous to a random effect in a mixed-effects model, into each of the three models to account for dependence between the nonterminal and terminal events. Typically, the variance of these frailties, denoted θ, is used to indicate the extent of residual dependence (ie, beyond that explained by the risk factors included in the three transition-specific hazard models). While other methods have been developed for analyzing semicompeting risks data (30–41), we focus on the illness-death model because of its interpretability and the availability of software for its implementation (46,47).

Additional, detailed information about the models for each of the three analyses, as well as the software used to fit them to the N9741 data, can be found in the Supplementary Materials (available online).

Simulation Study

We conducted a simulation study to investigate hazard ratio estimates from CEP analyses, in particular to examine the influence of dependence between the nonterminal and terminal events (as characterized by θ) on the value of HR_C. Toward this, we used a fit of the illness-death model to the observed data from the N9741 trial to generate a series of simulated datasets; see Supplementary Table 2 (available online) for details. Across the simulated datasets, we varied the “true” values of HR₁ and HR₂ for Arm F, as well as the frailty variance θ. With the exception of the baseline hazard for death without progression, the remaining components of the data-generating mechanism were held at the values from the illness-death model fit (see the Supplementary Materials, available online). For death without progression, we considered two cases for the 60-month event rate: 1) 6%, based on the original fit (see Table 1); and 2) 35% (see Supplementary Table 2, available online, for details).

Table 1.

Outcomes of 1419 patients in the N9741 trial data, overall and by treatment arm, corresponding to PFS

Outcome categories	Overall	Treatment arm
		A	F	G
	No. (%)	No. (%)	No. (%)	No. (%)
Total*	1419	390	670	359
1) Progression and death	1229 (86.6)	353 (90.5)	557 (83.1)	319 (88.9)
2) Death without progression	80 (5.6)	20 (5.1)	43 (6.4)	17 (4.7)
3) Progression and censored prior to death	74 (5.2)	0 (2.6)	50 (7.5)	14 (3.9)
4) Censored prior to progression or death	36 (2.5)	7 (1.8)	20 (3.0)	9 (2.5)

^*Censoring was performed administratively at 60 months. Treatment arm A: 5-FU/LV (5-fluorouracil and leucovorin) with CPT-11 (irinotecan); treatment arm F: 5-FU/LV with OXAL (oxaliplatin); treatment arm G: OXAL with CPT-11. PFS = progression-free survival.

Table 2.

HR estimates and 95% CIs comparing treatment arms F and G to the reference arm A in the N9741 trial data based on PFS as a composite endpoint, using three analysis strategies^*

Analysis	HR (95% CI)
Composite endpoint	HRC (95% CI)
Arm F	0.68 (0.60 to 0.78)
Arm G	0.93 (0.80 to 1.07)
Univariate	HR1* (95% CI)	HR2* (95% CI)
Arm F	0.67 (0.59 to 0.77)	0.66 (0.58 to 0.75)
Arm G	0.93 (0.80 to 1.08)	0.90 (0.77 to 1.04)
Semicompeting risks	HR1 (95% CI)	HR2 (95% CI)	HR3 (95% CI)
Arm F	0.49 (0.40 to 0.60)	0.60 (0.34 to 1.09)	0.59 (0.48 to 0.72)
Arm G	0.83 (0.66 to 1.04)	0.82 (0.34 to 1.65)	0.82 (0.66 to 1.03)

^*Treatment arm A (reference arm): 5-FU/LV (5-fluorouracil and leucovorin) with CPT-11 (irinotecan); treatment arm F: 5-FU/LV with OXAL (oxaliplatin); treatment arm G: OXAL with CPT-11. CI = confidence interval; HR = hazard ratio; HR₁ = HR for progression in semicompeting risks analysis; HR_C = HR for composite endpoint; HR_1* = HR for progression in univariate analysis; HR₂ = HR for death given that progression has not occurred in semicompeting risks analysis; HR_2* = HR for death in univariate analysis; HR₃ = HR for death given that progression has occurred in semicompeting risks analysis; PFS = progression-free survival.

Results

Observed Outcome Data

Table 1 presents the observed outcomes for the 1419 patients in N9741 across the four outcome groups, where administrative censoring was applied at 60 months. We see, for example, that for PFS the majority of patients (1229, 86.6%) experienced both progression and death. Supplementary Figures 1 and 2 (available online) display the timing of these outcomes in greater detail.

Statistical Analysis

Table 2 provides results from the three statistical analyses represented in Figure 1 applied to PFS. From the CEP analysis in Table 2, we see that patients in arm F are estimated to have a 32% lower hazard for PFS than patients in arm A (HR_C = 0.68, 95% confidence interval [CI] = 0.60 to 0.78), which is corroborated by the results from the separate univariate analyses: the HR_1* for tumor progression is estimated to be 0.67 (95% CI = 0.59 to 0.77) while the HR_2* is estimated to be 0.66 (95% CI = 0.58 to 0.75).

When the illness-death model is applied to PFS, we find rather striking effects of the informative role of death. In comparing arms A and F, the discrepancy between an HR_1* of 0.67 (95% CI = 0.59 to 0.77) for the univariate analysis of progression in Table 2 and an HR₁ of 0.49 (95% CI = 0.40 to 0.60) for progression in the illness-death model suggests that treating death as an independent censoring mechanism and/or introducing a frailty to account for between-patient variation substantially reduced the strength of the effect estimate. Such a reduction is also visible, although somewhat less dramatic, when comparing arms A and G.

Finally, the illness-death model also allows us to gather information about the hazard of the terminal event before and after the nonterminal event has occurred. In Table 2, for example, comparing arms A and F, the univariate HR_2* was reported to be 0.66 (95% CI = 0.58 to 0.75). Under the illness-death model, this is adjusted into an HR₂ of 0.60 (95% CI = 0.34 to 1.09) for death conditional on progression not having occurred and an HR₃ of 0.59 (95% CI = 0.48 to 0.72) for death given that progression has occurred, which are markedly lower than what we would have concluded from the univariate hazard ratio.

We have also performed analogous analyses on another CEP that could, in principle, have been an endpoint in the N9741 trial, combining grade 4 toxicity with the first of progression or death. These results provide a slightly different numerical perspective and can be found in the Supplementary Methods and Supplementary Table 3 (available online).

Simulation Study

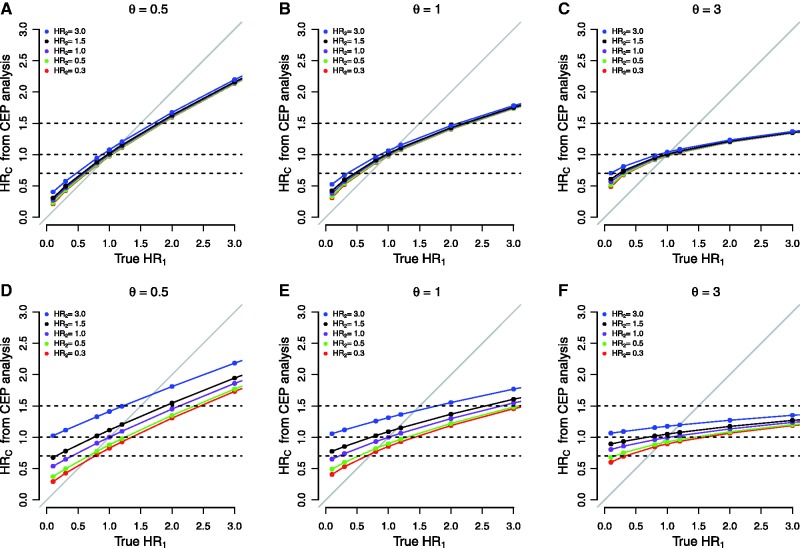
Figure 2 presents results for treatment F relative to treatment A for the simulations investigating CEP analyses. Figure 2, A through C, reports results when the 60-month death-without-progression event rate was set to 6%; Figure 2, D through F, reports results when the rate was set to 35%. Supplementary Figure 3 (available online) reports on parallel simulations regarding HR_1* in a univariate analysis of the nonterminal event.

Figure 2.

Graphical representation of the hazard ratio estimated in a composite endpoint analysis, denoted HR_C, under various hypothetical scenarios for the true values of the hazard ratio for progression (HR₁), the hazard ratio for death (HR₂), and θ from the illness-death model. In all cases, data were simulated to replicate the general structure of the progression-death data from the N9741 trial. In (A-C), the 60-month rate of death prior to progression was approximately 6%; in (D-F), the hazard was modified to increase this 60-month rate to approximately 35%.

From the results in Figure 2, we make a number of observations. First, as is well known, HR_C is generally a compromise between HR₁ and HR₂ and, for the most part, the numerical value of HR_C is attenuated relative to the “true” value of HR₁. Exceptions to this arise in Figure 2, D through F, when the true value of HR₁ is approximately 1.0 and the value of HR₂ is high. For example, in Figure 2D when HR₁ equals 1.0 and HR₂ equals 3.0, then HR_C equals 1.4.

Second, the impact of HR₂ on the compromise represented by HR_C depends heavily on the rate at which patients experience death events in the absence of progression. In Figure 2, A through C, HR₂ has little impact even when relatively large, whereas it plays a more prominent role in Figure 2, D through F. For example, focusing on Figure 2D, when HR₁ equals 0.8, the value of HR_C varies between 0.7 (ie, protective) and 1.3 (ie, detrimental), depending on the value of HR₂.

Third, examining the panels from left to right, we see that dependence between progression and death, as represented by θ, plays an important role in determining the value of HR_C. For example, in Figure 2, A through C, when HR₁ equals 2.0 and HR₂ equals 1.5, as θ increases from 0.5 to 3.0, the value of HR_C decreases from 1.59 to 1.22.

Finally, any given value of HR_C produced by a CEP analysis may be the result of a wide variety of configurations of the true HR₁ and HR₂. To highlight this, the dashed horizontal lines in each subfigure indicate HR_Cs of 0.7, 1.0, and 1.5. Consider, for example, an HR_C of 0.7 in Figure 2B for which θ equals 1.0 (the value closest to the observed θ = 0.85 in the N9741 data). The dashed line indicates that this “overall protective” effect can be produced if HR₁ equals 0.56 and HR₂ equals 0.30 (protective for both events), and also if HR₁ equals 0.33 and HR₂ equals 3.0 (protective for progression but harmful for death). Similarly, from Figure 2D, a null CEP hazard ratio HR_C of 1.0 can be produced if HR₁ equals 1.30 and HR₂ equals 0.50, if HR₁ equals 0.72 and HR₂ equals 1.50, and many other scenarios in between. Note that, in these cases, using a composite endpoint would lead to a substantial loss of power to detect a treatment effect.

Discussion

Although the term “semicompeting risks” is rarely used in the clinical/epidemiological literature, data following the semicompeting risks structure are ubiquitous in cancer research. The results we present based on the N9741 data demonstrate that reframing CEP analyses within the semicompeting risks framework makes full use of the available information and can provide key insights that cannot be obtained with more well-known frameworks, including traditional competing risks analysis (43,44). Moreover, by explicitly distinguishing the possible transitions that a patient can experience, treatment effects estimated via an illness-death model are more readily interpretable in the sense that they correspond to actual physical events. In contrast, the interpretation of treatment effects for a CEP is seldom straightforward, especially if the components vary greatly in clinical importance, which is particularly common for CEPs relating to toxicity or safety (3). Additionally complicating the matter is that the relative clinical importance of component events is often difficult to assign and can vary substantially across patients, researchers, and clinicians (48). Indeed, as shown in the simulation study, hazard ratios estimated via CEP analyses can be viewed as a complex mixture of component-specific hazard ratios influenced by dependence and component event rates that do not correspond to any actual physical event. In a semicompeting risks analysis, these difficulties are avoided altogether.

Throughout this study, we have focused on the illness-death model as a means to analyzing semicompeting risks data, in part because of its connection to standard methods for survival analysis but also because software is readily available; readers are referred to the freely available “frailtypack” (47) and “SemiCompRisks” (46) packages for the statistical programming language R (49). However, the illness-death model is not the only way to analyze semicompeting risks data (30,50); in this sense, this study is limited because we have not explored these other methods. It is also worth noting that our simulations are not exhaustive and the phenomena we describe may not appear in all settings.

Perhaps most importantly, we emphasize that the semicompeting risks framework broadens the range of scientific questions that researchers can address beyond those that can be addressed with a CEP. For example, in the case of PFS, although being both alive and progression-free is clearly an important clinical goal, by focusing the design and analysis on a CEP one loses the ability to distinguish treatment effects on different outcomes, as well as the ability to learn about how multiple outcomes covary across treatments. Additionally, by exploiting the full information in the data, one can investigate relatively complex phenomena, including the so-called rebound effect in which disease becomes more aggressive after progression (51,52), or the impact of different salvage treatments by incorporating additional covariates into the hazard for death after progression. Thus, embedding and analyzing component outcomes in the semicompeting risks framework as a supplement to CEP analyses, we believe, represents an important, underutilized, and feasible opportunity for cancer research.

Funding

This work was supported, in part, by the National Cancer Institute (NCI) at the National Institutes of Health (R01 CA181360-01 to SH, T32 CA009337-33 to IJ, K05 CA16938 to DS, and U10 CA180882 to DJS).

Notes

The sponsor was not directly involved in the preparation or submission of this manuscript. This manuscript does make use of data from the N9741 trial, an NCI-funded and -supported study conducted through the legacy NCI cooperative group program. N9741 did have supplemental support from Sanofi related to a US Food and Drug Administration filing. Sanofi had the opportunity to review the protocol and original manuscript (27) in order to provide input but did not have formal approval/disapproval authority. They had no role in data collection, analysis, or interpretation.