Abstract
Seasonal changes in environmental conditions are accompanied by significant adjustment of multiple biological processes. In temperate regions, the day fraction, or photoperiod, is a robust environmental cue that synchronizes seasonal variations in neuroendocrine and metabolic function. In this work, we propose a semimechanistic mathematical model that considers the influence of seasonal photoperiod changes as well as cellular and molecular adaptations to investigate the seasonality of immune function. Our model predicts that the circadian rhythms of cortisol, our proinflammatory mediator, and its receptor exhibit seasonal differences in amplitude and phase, oscillating at higher amplitudes in the winter season with peak times occurring later in the day. Furthermore, the reduced photoperiod of winter coupled with seasonal alterations in physiological activity induces a more exacerbated immune response to acute stress, simulated in our studies as the administration of an acute dose of endotoxin. Our findings are therefore in accordance with experimental data that reflect the predominance of a proinflammatory state during the winter months. These changes in circadian rhythm dynamics may play a significant role in the seasonality of disease incidence and regulate the diurnal and seasonal variation of disease symptom severity.
Keywords: cortisol, circadian, photoperiod, seasonal, immunity
for animals, physiological adjustments coincide with cyclical seasonal changes in the environment. During winter in temperate regions, these adaptations have evolved to favor animal survival throughout the pervasively harsh conditions. An increase in body fat by small birds, for instance, favors the higher thermoregulatory requirements of the winter season (151). These adaptations to seasonal changes develop progressively and organisms must be able to anticipate seasonal changes by relying on signals such as rainfall patterns, temperature, and duration of daily illumination. The latter, also known as the photoperiod, is considered the most pervasively used environmental cue that is capable of synchronizing seasonal changes in physiology (46). Apart from seasonal anatomical changes, physiological alterations in endocrine and metabolic function also occur. Glucocorticoids are a primary component of the stress response and studies have shown that cortisol (glucocorticoid in humans) levels exhibit seasonality, the general consensus being that cortisol levels are higher in winter than in summer (43, 97, 146).
Immune function varies significantly throughout the year in most vertebrates. It is commonly believed that enhanced immune responses and disease activity occur during the shorter winter days, with various aspects of the immune system being modified to adapt to the additional stresses associated with winter (87). The assumption is that the bolstering of immune function during the winter season is necessary for the organism to combat winter stressors such as lower temperatures. Lack of this seasonal-specific immunomodulation would otherwise compromise immune competence. While the patterns of seasonal variation in immune responses vary across species, cell type, and tissue analyzed, it has been shown that human serum concentrations of IL-6 and the soluble IL-6 receptor exhibit seasonality with higher expression during the winter months (74). A recent study on human mRNA and protein expression levels in peripheral blood mononuclear cells revealed that proinflammatory processes dominate during the winter season (28), when there are increased levels of IL-6R mRNA, soluble IL-6 receptors, and C-reactive proteins. These inflammatory components are considered risk biomarkers for cardiovascular and autoimmune diseases. Coronary heart disease (29) and inflammatory diseases such as rheumatoid arthritis (120) exhibit seasonality with higher prevalence and aggravated symptoms occurring during the winter and spring months. Apart from seasonal variations, rheumatoid arthritis (45) and coronary artery disease (108) exhibit diurnal activity fluctuations whereby symptom intensity is augmented in the late night and early morning. Cytokine production is normally under circadian control (55) and disrupted rhythms are associated with pathophysiological states. In rheumatoid arthritis patients, for example, the peak cytokine levels for serum IL-6 and TNF increase by a factor of 10 and the rhythms are phase shifted to a later time in the morning (23).
The underlying causes for the circadian perturbation and the seasonality associated with these inflammatory diseases remain to be elucidated. We aim to investigate seasonal immunological plasticity by considering the effect of seasonal changes on cortisol activity that influences the circadian rhythms of our downstream proinflammatory mediator. This mediator represents the combined effects of proinflammatory cytokines. Cortisol's role as a downstream regulator has been investigated earlier (116). External seasonal changes were modeled by varying the photoperiod for each respective season. Seasonality in adrenal function and glucocorticoid sensitivity at the peripheral level were also considered. In our model, cortisol was entrained to the external light schedule via the hypothalamic-pituitary-adrenal (HPA) axis. Within this axis, corticotropin-releasing hormone (CRH) secreted by the hypothalamus stimulates the production of adrenocorticotropic hormone (ACTH) from the anterior pituitary, which then drives the secretion of cortisol (FHPA) by the adrenal cortex. Our seasonal investigation here focuses on the circadian dynamics of HPA axis activity but there is considerable mathematical modeling work that quantifies both the circadian and ultradian dynamics of the axis activity (32, 33).
At the peripheral level, we assumed that cortisol entrains autonomous circadian oscillators known as peripheral clock genes (PCGs) to the external photoperiod and that it also influences the dynamics of our proinflammatory mediator and its receptor. Previously, we explored cortisol's entrainment of PCGs by employing a “two rates” cortisol production model (79) and by also considering the light-mediated regulation of cortisol activity by the external photoperiod (78). Also at the periphery, we considered both the immune permissive and suppressive effects of cortisol. We have previously hypothesized (77) that cortisol bestows its suppressive effects via its low-affinity glucocorticoid receptor (GR) and its permissive effects via the high-affinity mineralocorticoid receptor (MR). Again, we model these effects by simulating GR-mediated inhibition of transcription of the proinflammatory mediator and MR-mediated stimulation of transcription of the proinflammatory receptor. We also incorporated a mathematical model of human endotoxemia (35, 36, 115, 117) to assess the effect of seasonal changes on the systemic inflammatory response.
Experimental assessments of the role of the HPA axis in mediating photoperiod-induced seasonal immunological plasticity are lacking. Our goal in this work is to assess the influence of seasonally changing photoperiods on the neuroendocrine system and consider the role of cortisol, a peripheral entrainer, on modifying immune function activity. By understanding the dynamics of seasonal immunological function, we anticipate that our work may be used to predict the seasonality of disease and also to provide insight into the diurnal variation of cytokine levels associated with specific diseases. Knowledge of these rhythms and their seasonal modifications could be applied in the development of effective chronotherapeutic strategies for a variety of inflammatory diseases.
MATERIALS AND METHODS
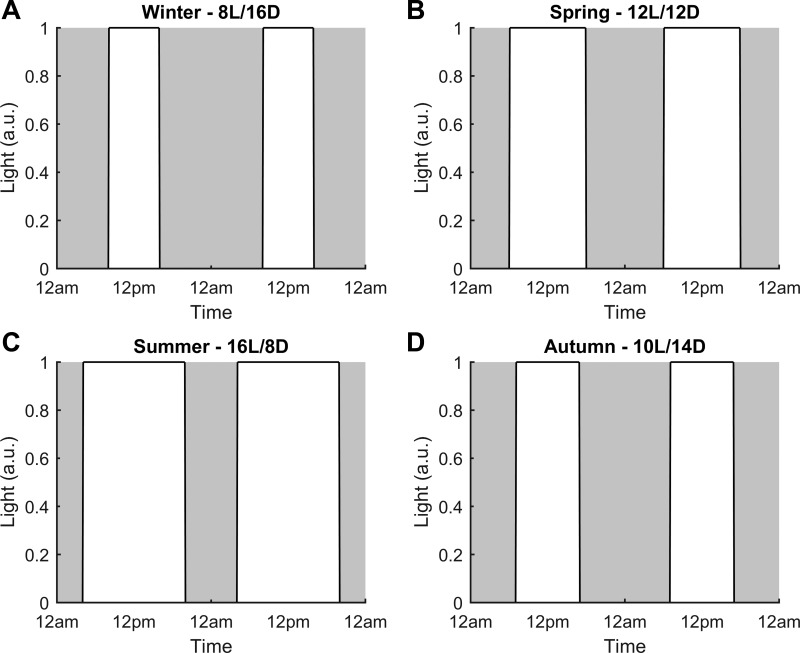
We consider the system as a two compartment model; namely central and peripheral. The central compartment comprises the HPA axis and its activity governs the release of CRH, ACTH, and cortisol (FHPA) while an immune subsystem constitutes the periphery. This subsystem is biologically comparable to an innate immune cell such as a neutrophil or macrophage. Reduced mathematical models describing simplified immune subsystems have been used to predict acute inflammatory responses to pathogenic insults (24, 106). Similarly, a simple three-equation model of an immune subsystem with an explicit spatial domain was employed to predict the effects of inflammatory stress on respiratory function (105). Immune activity involves a variety of components and encompasses a broad range of temporal and spatial scales. The main intent of our model is not to capture all the complexities of immune function and its elements. With this in mind, we use this generic immune compartment to focus on describing select mechanisms that we believe are imperative in linking external seasonal cues with changes in immune function biomarkers such as proinflammatory cytokines. The HPA axis is entrained to an external cue, the photoperiod. The summer light schedule was modeled with a photoperiod of 16 (16 h of light and 8 h of darkness) and winter with a photoperiod of 8 (8 h of light and 16 h of darkness); values obtained from (15). Also, spring was modeled with 12 h of light and darkness and autumn with 10 h of light and 14 h of darkness (99). Figure 1 depicts the light profile for each season. Light was modeled as a step function with an intensity of 1 during the light phase (L) and an intensity of 0 during the dark phase (D). The light profiles employed for the winter, spring, summer and autumn models are shown in Fig. 1, A, B, C, and D, respectively. Cortisol, synchronized with the light/dark cycles and output from the HPA axis, subsequently entrains clock genes at the peripheral level and modulates immune function dynamics (Fig. 2). Parameter values and their descriptions are included in Table A1 of the appendix.
Fig. 1.
The light profile for each season was modeled as a step function equal to 1 during the light phase (white area) and 0 during the dark phase (gray area). The photoperiod was varied for each seasonal model while keeping the light phase centered about 12 PM. Winter (A) was modeled with 8 h of light and 16 h of darkness (8L/16D), spring (B), with 12 h of light and darkness (12L/12D), summer (C) with 16 h of light and 8 h of darkness (16L/8D), and autumn (D) with 10 h of light and 14 h of darkness (10L/14D); a.u., arbitrary units.
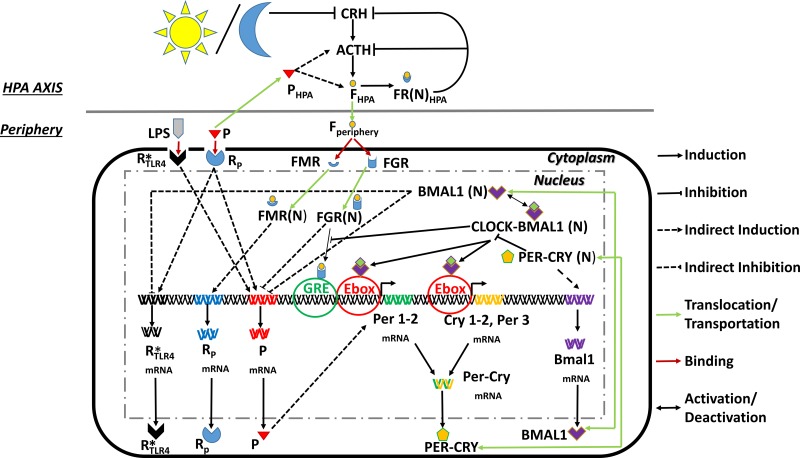
Fig. 2.
Schematic representation of our two compartment model. The hypothalamic-pituitary-adrenal (HPA) axis is entrained to the external light/dark cycle. Cortisol in the periphery entrains the peripheral clock genes (PCGs) and also regulates the proinflammatory mediator and receptor dynamics. See text for additional definitions.
Light entrainment and cortisol dynamics in the HPA axis.
The circadian profiles of CRH, ACTH, and FHPA were mathematically modeled using Eqs. 1–3. These core equations were adapted from our earlier work (78). We further optimized the parameters to improve the goodness of fit between cortisol's modeled circadian profile and normalized experimentally determined serum cortisol measurements taken throughout the day from healthy human subjects (47). We used outputs from our simulated spring season as baseline rhythms for validation with seasonally unspecified experimental data. All three equations are based on a variation of the Goodwin oscillator model that include Michaelis-Menten kinetics in both the production and degradation terms. The use of Michaelian kinetics here allows self-sustained oscillations that precludes the need to use impractically high Hill coefficient values (40). A variety of factors including neurotransmitters such as norepinephrine and acetylcholine, peptide hormones like angiotensin, and also CRH itself have been implicated in the positive regulation of CRH release (75). For simplification, we have assumed that this eclectic, extensive network of CRH secretagogues converges to yield a constant inducing input signal (InCRH), which triggers CRH production. The dynamics of CRH (Eq. 1) is characterized by production and degradation terms. Production depends on the production rate (kp1) and Michaelis constant for production (Kp1) while Vd1 and Kd1 represent the degradation rate and Michaelis constant for CRH degradation. Following production, CRH stimulates the anterior pituitary to release ACTH (Eq. 2). ACTH then triggers the release of FHPA from the adrenal cortex (Eq. 3). Similar to CRH, the temporal profiles of ACTH and FHPA depend on production and degradation where kp2 and kp3 are the production rates and Vd2 and Vd3 are the degradation rates for ACTH and FHPA, respectively. The Michaelis constants for production are Kp2 and Kp3 whereas Kd2 and Kd3 represent the Michaelis constants of degradation for ACTH and FHPA. Cortisol (FHPA) levels are regulated by a negative feedback mechanism whereby cortisol binds to its glucocorticoid receptors in the hypothalamus and anterior pituitary. The cytoplasmic cortisol receptor complex (FRHPA) translocates into the nucleus [FR(N)HPA] and inhibits production of both CRH and ACTH. This inhibition was mathematically modeled by incorporating FR(N)HPA in the denominator of the CRH and ACTH production terms. The signal transduction pathway involving the formation of the nuclear cortisol-receptor complex is described using Eqs. 4–7, derived from a corticosteroid pharmacodynamic model (103). These mechanistic equations and their related parameters are based on experimental data (plasma methylprednisolone, receptor mRNA, and cytosolic receptor measurements) following the continuous infusion of adrenalectomized rats with the methylprednisolone (MPL) corticosteroid. Receptor mRNA dynamics (mRNAR,HPA, Eq. 4) is described by a zero order synthesis/production rate (ksynRm) and a first order degradation rate kdgrRm. The experimentally observed downregulation of mRNAR,HPA by MPL was modeled via an indirect response model (IDR). IDRs are generally used to characterize pharmacokinetic/pharmacodynamic responses to factors via indirect, oftentimes unknown, mechanisms (121). The inhibition was modeled to occur via an indirect mechanism involving the cortisol-receptor nuclear complex [FR(N)HPA]. IC50Rm represents the concentration of FR(N)HPA at which the synthesis rate of mRNAR,HPA is reduced to half of its baseline value. The receptor protein (RHPA, Eq. 5) dynamic profile is dependent on the production rate of the receptor (ksynR), the degradation rate kdgrR, the binding rate between the glucocorticoid and its receptor (kon), the rate of receptor recycling from the nucleus to the cytoplasm (kre) and the fraction recycled Rf. Cortisol-receptor complex activity (FRHPA, Eq. 6) is characterized by the binding rate (kon) and the rate of receptor complex translocation into the nucleus (kT) while that of the nuclear activated complex [FR(N)HPA, Eq. 7] is contingent on the translocation rate (kT) and the rate of receptor recycling (kre). This activated complex induces its inhibitory effects on CRH and ACTH production via binding to its glucocorticoid-responsive element (GRE).
The master circadian clock resides in the suprachiasmatic nucleus (SCN) within the hypothalamus. This clock is entrained to external light cues via communication with retinal ganglion cells (RGCs) present within the eye (89). Findings indicate that the SCN regulates the circadian rhythm of cortisol (126) and a decrease in the SCN-mediated secretion of arginine vasopressin (AVP) increases cortisol levels (53). AVP, a hypothalamic hormone, stimulates both CRH and ACTH release (80). Given that acute bright light exposure downregulates cortisol levels (52) and assuming that this downregulation is mediated by AVP (under the entrainment of the SCN), we ultimately control cortisol production by regulating the degradation of CRH by light. The light response was modeled using Michaelis- Menten kinetics to reflect the response saturation of SCN-projecting RGCs (148).To investigate the influence of seasonal changes on immune function, we first made critical modifications to our core Goodwin oscillator model (Eqs. 1–3). Cortisol's activity, conferred via its glucocorticoid receptor, is considered immune suppressive and the HPA axis regulates rising proinflammatory cytokine levels by consequently increasing cortisol production (68, 98). While the HPA-activating effect of proinflammatory cytokines has been established, the mechanisms of cytokine action on HPA axis activity have not been entirely resolved. Various mechanisms have been proposed to describe cytokine regulation of axis activity. These processes include pathways that involve receptor binding and subsequent signal transduction and also the generation of intermediates such as neurotransmitters (139). Since cytokine effects may be arbitrated by confounding mechanisms, we have stimulated the ACTH and FHPA production terms with the proinflammatory mediator (P) using an IDR (Eqs. 2 and 3). The efficiency constant (kfp) describes the strength of stimulation by P. The SCN is a complex network of ∼20, 000 neurons. While rhythms of electrical activity for individual cells remain comparable across seasons (peak electrical activity between 4 and 5 h), the amplitude of activity at an ensemble level is dependent on the degree of synchronization among all neurons (15). Seasonal analysis on SCN neuronal activity measured from mice and rat hypothalamic slice explants have identified decompressed or less synchronized firing patterns among neurons during the longer summer days while winter days were more associated with compressed or synchronized activity (81, 109, 114, 142). The narrower phase distribution of electrical activity with decreasing photoperiod results in an increased ensemble amplitude as the season changes from summer to winter. Seasonal changes in SCN electrical activity were modeled by incorporating a multiplicative coefficient (Vseason) in the Michaelis-Menten, light-mediated, degradation term of CRH. This coefficient describes the maximum activity of the SCN. The Vseason parameter, related to the SCN ensemble amplitude, was set to decrease with photoperiod; based on rat neuronal electrophsyiological measurements from (114). Despite cortisol levels being higher, Walker et al. (146) concluded that the rate of cortisol production was actually reduced during the winter season. This decrease in production rate was attributed to a seasonal reduction in cortisol's clearance, a measure of cortisol's secretion rate (159). This seasonal variation of cortisol production rate was modeled by utilizing a seasonally varying Michaelis constant of cortisol production; cseason·Kp3 (Eq. 3). The cseason value for each season is numerically equal to Vseason and so increases with decreasing photoperiod. A higher Michaelis constant during the winter season reflects a lower substrate binding affinity and consequently results in the maximum rate of production being attained more slowly.
To account for the delay in transportation of the proinflammatory mediator and cortisol between the central and peripheral compartments, we applied a transit compartment model and employed a transient delay (τ) of 15 mins (Eqs. 8 and 9). A time delay in cortisol's production following ACTH stimulation is known (94) and so we theorized that a similar delay would exist for transport between the compartments. The numerical value of this delay term was chosen arbitrarily from a range of values previously explored in a numerical simulation study (147).
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Mineralocorticoid and glucocorticoid receptor dynamics in the periphery.
In the periphery, after diffusing into the cytoplasm, cortisol binds and activates its two receptors; the mineralocorticoid (MR) and the glucocorticoid (GR) receptors. Activation of these receptors involve the release of heat shock proteins, hyperphosphorylation, and receptor conformational changes (103). Here we consider hyperphosphorylation to be the rate-determining step (140) for both receptors (Eqs. 10 and 13). Assuming that the phosphorylation and degradation steps for both receptors exhibit saturation, we described these processes with Michaelis-Menten kinetics. Production of MR and GR is regulated by their base production rates (kMR, kGR), Michaelis constants for production (KF,MR, KF,GR) and the concentration of inactivated receptors, computed as the difference between the total receptor concentration (MRT, GRT) and the phosphorylated/activated receptor (MR, GR). Additionally, a cortisol mediated indirect mechanism of activation was used in lieu of modeling the multisite phosphorylation kinetics. The efficiency constants of stimulation are represented by the kF,MR and kF,GR parameters. Michaelis constants of cortisol induced activation are described by KF,MR and KF,GR. Clearance of the activated receptors depend on the degradation rates (kMR,deg, kGR,deg), and Michaelis constants of degradation (KMR,deg, KGR,deg). Apart from production/activation and degradation, the cytosolic availability of receptors is contingent upon the product of the fraction recycled and the recycling rate (kr,MR, kr,GR) as well as the rate of receptor removal due to binding (kb,MR, kb,GR). Similar reaction kinetics governing binding and translocation into the nucleus were assumed for both receptors. The cortisol-receptor complex rhythms (FMR, FGR, Eqs. 11 and 14) depend on the binding rates (kon,MR, kon,GR) and the rates of nuclear importation (kT,MR, kT,GR) whereas those of the nuclear activated complexes (Eqs. 12 and 15) depend on the importation rates and the rates of complex recycling from the nucleus into the cytoplasm (kre,MR, kre,GR). These nuclear complexes induce their effects via binding to their respective GREs. The variation in the binding affinities of cortisol to both receptors (113) was modeled by setting the Michaelis constant of the mineralocorticoid receptor (KMR) to a lower value than that of glucocorticoid receptor (KGR). Parameters used in the mineralocorticoid and glucocorticoid receptor equations were estimated previously (77) based on human cortisol and cytokine experimental data from Ref. 98.
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
Peripheral clock gene dynamics with cortisol entrainment.
Immunological activity such as cytokine production and lymphocyte proliferation oscillate with circadian rhythmicity (55). These diurnal variations in immune function are modulated by autonomous cellular oscillators known as peripheral clock genes (PCGs). Here, we have incorporated a network of transcriptional and translational feedback loops to describe the activity of these core diurnal regulators. These semimechanistic dynamic equations were developed previously and the predicted period of oscillations, relative phases between components and peak/trough ratios were validated against mRNA and protein concentrations from rodent data (11).
In this model, Per and Cry mRNAs and proteins were represented by the same variables since they exhibit synchronous nuclear accumulation (64), they form a nuclear complex together (104), and their regulation by CLOCK-BMAL1 and negative regulation of CLOCK-BMAL1 transactivational activity are comparable (50, 122). The transcription of Per-Cry genes is stimulated by the binding of the CLOCK-BMAL1 heterocomplex to an E-Box Enhancer (Eq. 16). The translated Per-Cry complex (Eq. 17) translocates to the nucleus (Eq. 18) and inhibits CLOCK-BMAL1 transcriptional stimulation of its own genes; consequently forming a negative feedback loop. The production term of Per-Cry mRNA was modeled to be linearly dependent on CLOCK-BMAL1 concentration and inversely dependent on Per-Cry(N) due to its self-inhibitory role. The rate of transcription is represented by v1b and the Michaelis constant for transcription by k1b and k1i is the inhibitory constant. The constant c is a constitutive activator Per-Cry transcription with p indicating a Hill function coefficient; used to model the switch-like behavior of the transcriptional response. The PCG dynamic equations have been revised to include the effects of seasonality and the proinflammatory cytokine influence. Treatment of human hepatoma cells with IL-6 has been found to induce Per1 expression (83). Moreover, TNF-α stimulation of human rheumatoid synovial and monocytic THP-1 cells enhances Cry1 and Cry2 mRNA expression (96, 155). We have therefore incorporated proinflammatory mediator (P) feedback into our Per-Cry transcription (Eq. 16) by applying an indirect stimulation term using the efficiency constant kf. Clearance of Per-CrymRNA is characterized by the degradation constant k1d.
Transcriptional oscillation of Per1, Per2, Per3, Cry1, Cry2, Bmal1, and other core clock components is regulated by glucocorticoid activity (128). The entraining effects of glucocorticoids on the phases of human peripheral clocks have been recently studied. It was determined that the oral administration of Cortef, a hydrocortisone, shifted the phases of Per2, Per3 and Bmal1 mRNA expression in peripheral blood mononuclear cells (PBMCs) by ∼9.5–11.5 h (20). We have accounted for cortisol's entrainment of PCG activity by including the FGR(N) additive term in Eq. 16 with the coupling strength between the HPA axis and periphery quantified by the parameter kc. The inclusion of CLOCK-BMAL1(N) in the denominator of this entrainment term reflects the complex's inhibitory role as transcriptional activity of the glucocorticoid receptor is suppressed via CLOCK-mediated acetylation (19).
While glucocorticoid sensitivity differs between individuals and tissues, more intense dermal blanching following topical glucocorticoid treatment (146) and increased number of glucocorticoid receptor binding sites (14) during the winter reveal a heightened glucocorticoid sensitivity in humans for this season. Seasonal alterations in glucocorticoid sensitivity were incorporated by modeling the FGR(N) entraining effects on Per-Cry transcription as a Hill response type function (158). The Hill coefficients (nseason) were kept the same as the Vseason (and cseason) coefficients explained previously. An increase in nseason with decreasing photoperiod yields an increase in the sensitivity of the response.
The PER-CRY oscillations (Eq. 17) are regulated by the complex formation rate (k2b). The formation reaction was described using bilinear kinetics, with a reaction order equal to the number of complex subunits (q = 2). The parameters k2t, k3t, and k2d signify the first order nuclear import rate, export rate, and degradation rate for the PER-CRY complex. Similarly, the dynamics of PER-CRY(N) (Eq. 18) rely on k2t, k3t, and a first order degradation rate (k3d). In addition to repressing their own transcription, PER-CRY(N) suppresses the CLOCK-BMAL1 promoted activation of Reν-Erbα transcription (30). REV-ERBα, a circadian clock protein, negatively regulates Bmal1mRNA transcription and so this double-negative feedback loop essentially represents a positive induction of Bmal1 transcription by PER-CRY(N). Bmal1mRNA (Eq. 19) production increases with increasing PER-CRY(N) and was modeled using a Hill equation with a coefficient r. The degradation of Bmal1mRNA is regulated by the first order degradation rate k4d. The circadian profile of BMAL1 (Eq. 20) is dependent on the translation rate k5b, the nuclear import k5t, export rate k6t, and the degradation rate k5d while the dynamics of the BMAL1(N) (Eq. 21) is characterized by the same nuclear and export rates as BMAL1 as well as the degradation rate k6d and activation/deactivation rates (k6a/k7a) of CLOCK-BMAL1 complex formation. CLOCK-BMAL1 activity (Eq. 22) is modulated by the same activation/deactivation rates (k6a/k7a) and a degradation rate k7d. The high Hill coefficients in Eqs. 16 and 19 were used to minimize the number of reaction steps while the dynamics of by PER-CRY(N), BMAL1, BMAL1(N), and CLOCK-BMAL1 were described using first order kinetics. In this model, CLOCK protein levels were assumed constant since Clock mRNA levels do not fluctuate diurnally (55).
For our description of the inducible effect of P on Per-Cry expression (Eq. 16) and in developing mathematical representations governing the dynamics of P (Eqs. 23 and 24), its receptor (RP, Eqs. 25 and 26), and the proinflammatory ligand-receptor complex (PR), we have consolidated the effects of numerous cytokines such as IL-6 and TNF-α into one representative proinflammatory mediator variable. Cytokine activity is considered to be both pleiotropic, exerting multiple actions, and also redundant whereby different cytokines can elicit overlapping responses. The pleiotropic actions can be explained by the presence of cytokine receptors on multiple lineages or by the activation of multiple signaling pathways that contribute to varied functions (93). The sharing of similar signaling pathways and comparable cellular distributions of receptors for different cytokines may account for the overlapping actions. Attributed to the pleiotropic nature of cytokine functionality, cytokines such as IL-6, TGF-β, and IL-10 exhibit both pro- and anti-inflammatory roles (112, 118). Of note, IL-6 can activate proinflammatory pathways via binding to its soluble receptor (sIL-6R) or mediate anti-inflammatory action via its membrane bound receptor (IL-6R) (118). The seasonal augmentation of sIL-6R expression in the winter (28), however, suggests an enhancement in the proinflammatory arm of IL-6 signaling. In conjunction with increased IL-6 levels, elevated serum sIL-6R concentrations are associated with numerous inflammatory conditions such as rheumatoid arthritis (57, 107, 141), ulcerative colitis, Crohn's disease (82), and allergic asthma (26). Considering that both TNF-α and IL-1β promote production of sIL-6R (37), we therefore assume that these cytokines operate as an ensemble with IL-6 to engender a proinflammatory state which may consequently account for disease seasonality.
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
Diurnal rhythm of the proinflammatory mediator and its receptor.
Equations 23–27 describe the dynamics associated with the proinflammatory mediator and its receptor. These equations, modified to include the influence of PCGs and seasonal sensitivity, were obtained from our group's previous work (77) whereby the regulatory processes were described using zero and first order kinetics. The dynamics of the proinflammatory mediator mRNA (mRNAP, Eq. 23) was modeled to be dependent on a base transcription rate () under the indirect influence of various factors. It is well established that cortisol functions as an immunomodulator that regulates proinflammatory cytokine activity (68). Due to the absence of GREs from the promoter regions of most proinflammatory genes, it is assumed that the cortisol-glucocorticoid receptor nuclear complex inhibits inflammatory gene expression indirectly (10). The indirect inhibition term in the transcription of the proinflammatory mediator's mRNA (Eq. 23), with an efficiency constant of kfr and Michaelis constant of cortisol induced inhibition Kfr, reflects cortisol's suppressive effects which occur via the cortisol-glucocorticoid receptor complex FGR(N). Similar to the glucocorticoid entrainment term regulating Per-Cry transcription (Eq. 16), we again use a Hill-type function to model seasonal glucocorticoid sensitivity changes. Proinflammatory cytokines exhibit diurnal rhythms (98) that are mediated by PCGs (55). In contrast to our previous model, we employ BMAL1 as the anti-inflammatory mediator of the immune system's circadian control. This anti-inflammatory role is supported by studies involving targeted deletion of BMAL1 mRNA in mice myeloid cells. When challenged with endotoxin or bacteria, these myeloid-specific BMAL1-deficient mice exhibit exacerbated immune responses which include heightened NF-κB activity and enhanced induction of cytokines such as IL-1β, INF-γ, and IL-6 (22, 39, 90). Putative BMAL 1 modulated anti-inflammatory mechanisms involve indirect inhibition of NF-κB activity by CLOCK sequestering and inhibition of IL-6 and Ccl2 expression by driving the expression of Nr1d1 (encoding REV-ERBα), an IL-6 and Ccl2 inhibitor (21). BMAL1(N) inhibition of P mRNA expression was therefore modeled using an IDR with an efficiency constant of kpc and Michaelis constant of induced inhibition Kpc. Cytokines such as IL-6, TNF-α, and IL-1 can induce their own production by autocrine effects (2). We simulated this autocatalytic role by indirectly stimulating the proinflammatory mediator's transcription via the proinflammatory ligand-receptor complex (PR) with an efficiency constant of 1. Following transcription, the proinflammatory mediator is then translated (Eq. 24). P dynamics is described using linear kinetics with first order production (kinp) and degradation koutp rates. In the periphery, basal glucocorticoid concentrations have immunopermissive effects (129). Assuming that lower cortisol levels would induce their effects via the high-affinity receptor, we modeled the upregulation of the proinflammatory receptor to occur via the mineralocorticoid receptor MR. Just as in Eq. 23, cortisol's effects were modeled via indirect stimulation of the proinflammatory receptor mRNA (, Eq. 25). This indirect regulation with an efficiency constant kfr2 and Michaelis constant of cortisol induced stimulation Kfr2 enhances the base transcription rate . Clearance of the receptor mRNA is characterized by the degradation rate . The prinflammatory receptor rhythm (RP, Eq. 26) is dependent on the first order translation rate , degradation rate , and binding rate kd whereas the proinflammatory ligand-receptor complex dynamics (PR, Eq. 27) is characterized by the binding rate kd and the degradation rate . The rate constants described in this section were independently estimated to yield a proinflammatory mediator diurnal profile that peaked in the early morning; as observed with proinflammatory cytokines in humans (98). We present here a simplified, semimechanistic mathematical depiction of the proinflammatory mediator, its receptor and the proinflammatory ligand-receptor complex dynamics (Eqs. 23–27). The mechanisms governing cytokine production and signaling is far more complex. The nuclear factor NF-κB pathway, for instance, has long been implicated in the proinflammatory signaling pathway and involves activation of the NF-κB transcription factor by microbial products or by cytokines such as IL-1 and TNF-α (66). NF-κB activation occurs by at least two separate pathways and involves either the phosphorylation, ubiquitination, and degradation of IκB (canonical pathway) or is IκB-α-degradation independent (alternative pathway) (150). Both pathways involve the activation of NF-κB containing complexes that translocate into the nucleus and regulate the expression of proinflammatory genes such as cytokines and chemokines. The released cytokines bind to and activate their receptors and further modulate immune function via additional mechanisms such as by activation of the JAK/STAT pathway (44). Extensive models describing these pathways can become computationally challenging. Recently, numerous groups have opted to utilize “minimal models,” applying the least number of equations to describe the inflammatory mechanisms (150). Our group previously incorporated a reduced NF-κB module in various inflammatory response models (34, 36, 115, 117). Here, we have modeled the rhythm of representative proinflammatory components with the use of limited equations, focusing on the major signaling effects and resultant diurnal rhythms. We consider the receptor (RP) as a generic single unit variable that facilitates the binding of the proinflammatory mediator (Eq. 27). Proinflammatory signaling via ligand-receptor binding is mediated by the proinflammatory ligand-receptor complex (PR) using an IDR (Eqs. 23 and 29).
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
Seasonality and innate immunity.
Human responses to acute treatment of an endotoxin [lipopolysaccharide (LPS)] provide a useful inflammation model for understanding disease mechanisms (72). To assess the innate immune response differences for the four seasons, we incorporated an endotoxemia model previously developed within our lab (Eqs. 28–31; Refs. 35, 36, 115, 117). This model, using an indirect response approach, was based on data acquired following the administration of endotoxin to human subjects. We refer the reader to Ref. 35 for a more detailed description of the model. The dynamics of LPS (Eq. 28) is described using a logistic type function with growth rate kLPS,1 and a first order elimination rate kLPS,2. The logistic function is typically used to model self-limiting growth of an entity, such as bacteria, and describes an initial exponential growth phase that eventually slows and stops as saturation occurs (160). As discussed in our previous work, these rate parameters were estimated such that the LPS profile decayed within 2 h posttreatment (35). The dynamics of the active form of the Toll-like 4 receptor mRNA () and of the receptor protein is expressed in Eqs. 29 and 30. Here, represents a receptor hetero-complex comprising TLR4, CD14, and MD-2. In Eq. 29, kLPS,3 represents the production rate while kLPS,4 describes the degradation rate of the receptor mRNA. LPS upregulates TLR4 mRNA expression in numerous cells types including mouse dendritic cells (4) and human monocytes (144). We have simulated this LPS-induced effect by indirectly stimulating transcription by PR, which increases following in silico LPS treatment, with an efficiency constant . Furthermore, we assumed indirect inhibition of transcription by BMAL1. This inhibitory function of BMAL1 is identical to its regulation of the mRNAP rhythm (Eq. 23). The dynamics of the receptor Eq. 30) depend on the translation of , association, and dissociation of the ligand-receptor complex and on receptor clearance. The translation rate is represented by ksyn and the degradation rate by kdeg. The association (k1) and dissociation rates (k2) were obtained from kinetic studies investigating the binding of LPS to mouse TLR4 protein (123). The equilibrium complex Eq. 31) activity is regulated by the association/dissociation rates and also the degradation rate k3. At a transcriptional level, we assume that the activated complex indirectly stimulates proinflammatory mediator mRNA production; due to increased cytokine secretion following LPS administration (144). Equation 32 shows the modified version of the proinflammatory mediator transcription equation which includes the inducible effect of
In Eq. 29, we have modeled to exhibit circadian rhythmicity as is entrained indirectly by BMAL1. While circadian rhythmicity of TLR4 expression has not been observed in mice macrophages (38, 55, 124) or in human monocytes and neutrophils (65), circadian control of components involved at all levels of the LPS-TLR4 response pathway exists (55). Within this signaling pathway, components under circadian regulation include those that regulate LPS binding to TLR4, are involved in the MAPK pathway (controlling transcription factor activation and cytokine protein processing), and are regulators of cytokine transcription, mRNA stability, and processing. CD14, a diurnally regulated member of this TLR4 signaling pathway, functions as a coreceptor (with TLR4 and MD2) to facilitate the detection of LPS and the LPS-mediated cell internalization of TLR4 (157). We therefore hypothesize that the active form of the TLR4 receptor complex is under circadian influence and the suppressive effects of BMAL1 (N) on the transcription of the receptor complex mRNA was included via the implementation of an indirect inhibition response model. Parameters used in Eq. 29, ksyn, kdeg, and k3 were estimated such that the components described by Eqs. 29–32 were restored to baseline values within 24 h following in silico LPS administration; based on human experimental endotoxemia data (17).
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
RESULTS
Our in silico experiments aimed to investigate the underlying relationships between photoperiod environmental cues, the adaptation of HPA axis activity and immune function to changing seasons. The data presented in this section are a result of numerical integration of the model equations (Eqs. 1–32).
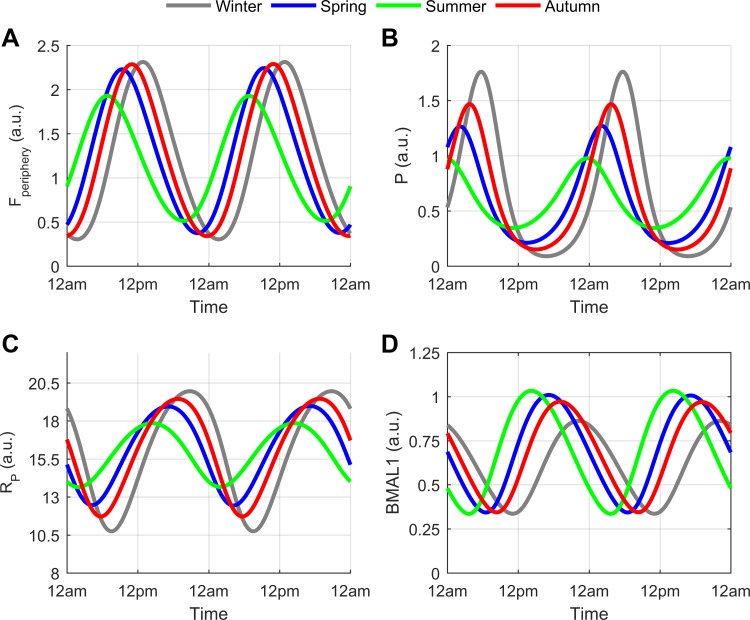
Figures 3 and 4 depict the circadian dynamics and amplitude/phase plots respectively for cortisol (Fperiphery), the proinflammatory mediator (P), proinflammatory receptor (RP), and BMAL1. The amplitudes of Fperiphery, P, and RP increased as the seasons progressed from summer through spring, autumn and winter. An opposite trend to the previous was found for BMAL1 as its circadian amplitude decreased from summer through winter. The higher cortisol amplitude predicted for the modeled winter season is in agreement with experimental findings (43, 97, 146). The winter increase in amplitude for our proinflammatory mediator (P) is comparable to the human IL-6 seasonal study by (74). Additionally, the results attained for RP and BMAL1 are in line with recent mRNA seasonal expression data (28). In this seasonal gene study, expression levels for immune system components were found to exhibit seasonality with increased expression of IL6-R mRNA, the soluble interleukin 6 receptor (sIL-6R), and C-reactive protein (an acute-phase inflammatory protein) during the winter months. The BMAL1 encoding gene Arnt1 was upregulated during the summer months. A winter increase in human serum concentrations of soluble IL-6 receptor has been previously reported (74).
Fig. 3.
Circadian rhythms for cortisol (Fperiphery), proinflammatory mediator (P), proinflammatory receptor (RP), and BMAL1 for winter (gray), spring (blue), summer (green), and autumn (red). The winter model predicted high amplitude oscillations for Fperiphery (A), P (B), and RP (C) with high amplitude BMAL1 rhythms predicted for the summer (D). The phases of the circadian rhythms were advanced for the summer and delayed in the winter model.
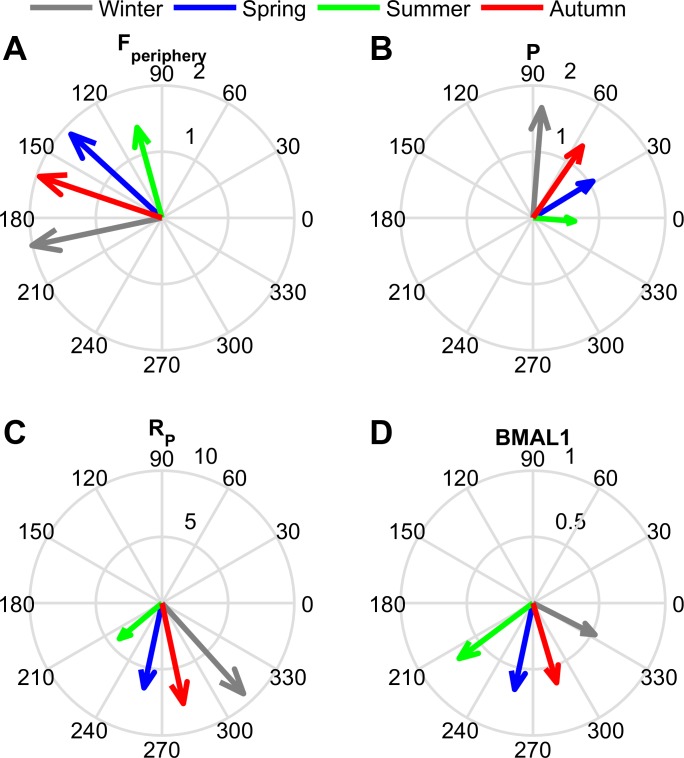
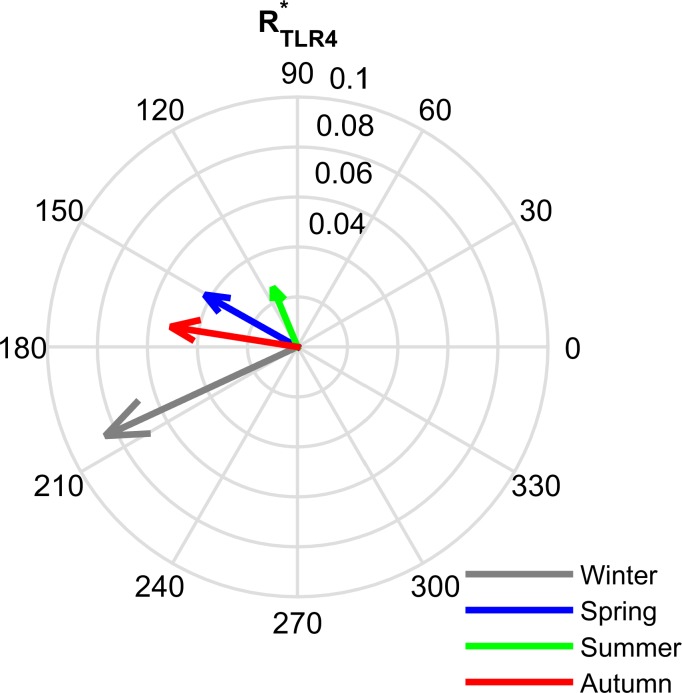
Fig. 4.
The amplitude (radial dimension) and phase (angular dimension) of the circadian rhythms for cortisol (Fperiphery), proinflammatory mediator (P), proinflammatory receptor (RP), and BMAL1 for each seasonal model. Amplitude was highest in the winter model for Fperiphery (A), P (B), and RP (C) while the BMAL1 (D) amplitude was highest in the summer. The summer circadian rhythms peaked earliest in the day (green arrow), followed by spring (blue arrow), autumn (red arrow), and then winter (gray arrow).
The peak time of all the circadian rhythms became more delayed with decreasing photoperiod. This delay is manifested as a phase shift to the right for the oscillations shown in Fig. 3 or a higher phase angle (angular displacement) for the vectors depicted in Fig. 4. The phase delay predicted by our model is comparable to the experimentally determined delay in cortisol's morning rise, which was found when comparing the winter to the summer rhythm (145).
We then explored the effect of seasonal changes on dynamics and the LPS-TLR4-mediated inflammatory response. Figure 5 illustrates the amplitude/phase plots for each season in the LPS-unchallenged (control) model. The seasonal variation is similar to that of the proinflammatory receptor (RP) with the highest amplitude and most delayed phase estimated for the winter model (gray vector). The rhythm for the summer model exhibited a phase advancement with a diminished oscillatory amplitude (green vector). To investigate both the circadian (time-of-day) and seasonal dependencies of the immune response, we modeled acute LPS dose administrations at each hour of the simulated day for all seasonal models. The inflammatory response was quantified for each treatment time by measuring the maximum proinflammatory mediator level (Pmax) that occurred as a result of in silico endotoxin treatment. Figure 6 illustrates the time of day variation of Pmax levels for all the modeled seasons after administration of a low dose of endotoxin [LPS = 0.5 arbitrary units (a.u.)]. The model predicts a sensitivity increase in the innate immunity response for winter vs. the other seasons; results similar to human ex vivo stimulation studies (58).
Fig. 5.
Compass plot showing the seasonal differences of the amplitude (radial dimension) and phase (angular dimension) of in the unchallenged model. The summer model (green arrow) produced the lowest circadian rhythm amplitude with the winter model (gray arrow) exhibiting the highest.
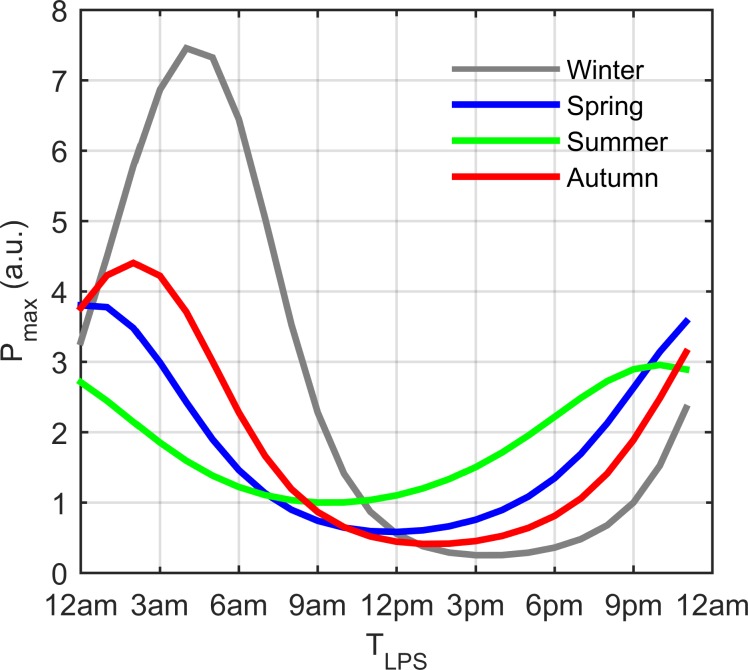
Fig. 6.
Seasonal variations in the inflammatory response following in silico administration of acute doses of endotoxin (LPS dose of 0.5 a.u.) at each hour of the simulated day. The maximum proinflammatory mediator level triggered by simulated LPS treatment (Pmax) is plotted vs. the time of LPS administration (TLPS). The winter model displayed the highest sensitivity to in silico LPS treatment and summer displayed the lowest. A time-of-day sensitivity was predicted for all seasons with the most intense response estimated following in silico LPS addition during the late night/early morning.
Figure 7 shows the seasonal Pmax profiles in conjunction with the cortisol circadian rhythms from the control model. The plots for each seasonal model reveal an interesting dynamical relationship between cortisol and the proinflammatory response. Inspecting at a superficial level, for a given season, we observe that in silico LPS administration at times near cortisol's nadir results in an intensified P response while treatment at times close to cortisol's zenith yields a suppressed response. These model findings are congruent with our laboratory's previous work (77). Upon closer inspection of the plots, we discover a more complex association. Apart from being sensitive to cortisol levels, the magnitude of the inflammatory response following simulated LPS addition depends on the phase of cortisol's diurnal profile; whether cortisol levels are increasing or decreasing. A more pronounced inflammatory response, measured as an increase in Pmax, occurs during cortisol's ascending vs. descending phase even at comparable cortisol levels. In our previous work, the time dependence of LPS sensitivity was attributed to the dual nature of cortisol's control on cytokine dynamics i.e., its permissive and suppressive effects. The permissive effects occur via the cortisol-mediated induction of the proinflammatory receptor while the suppressive effects result in cytokine transcription inhibition. It was determined that cortisol's permissive influence was more dominant near the nadir while the suppressive predominated near the zenith. Furthermore, the dominating effect at a given cortisol level was dependent on whether cortisol levels were ascending or descending. We expand on this investigation and consider the role of BMAL1, the anti-inflammatory circadian clock protein entrained by cortisol, in conferring circadian and seasonally sensitive immune responses. Figure 8 represents the seasonal circadian profiles for cortisol (Fperiphery) and BMAL1 in the unchallenged model for winter (A), spring (B), summer (C), and autumn (D). While the higher amplitude BMAL1 oscillations in the summer vs. the winter model predicts that the system is more anti-inflammatory during the summer season, phase also regulates the system's response. Considering BMAL1's rhythmic profile for the summer model (Fig. 8C), for instance, we see that BMAL1 peaks shortly after cortisol, during cortisol's descending phase. At this time the system is in a more enhanced anti-inflammatory state and so simulated LPS administration elicits a diminished immune response compared with the response provoked at similar cortisol levels during the ascending phase.
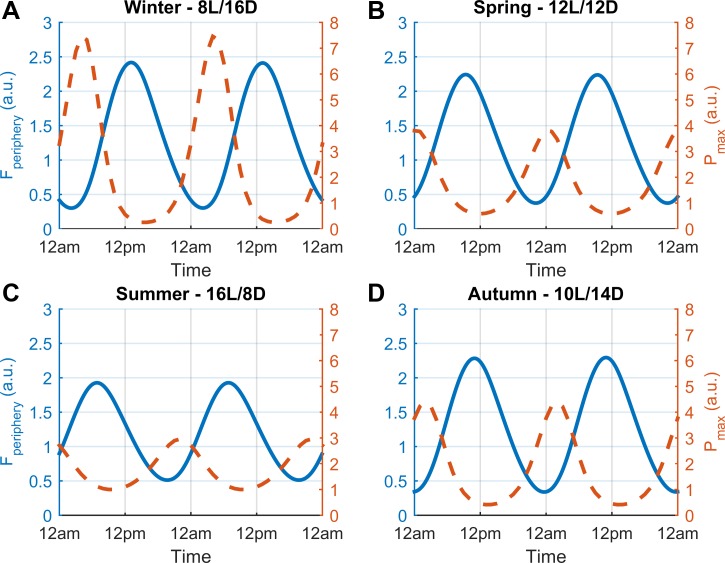
Fig. 7.
Diurnal profiles for cortisol and Pmax for each seasonal model. The circadian rhythm of cortisol (Fperiphery) for the LPS-unchallenged (control) model is represented by the blue plot and the maximum proinflammatory mediator level as a result of in silico LPS administration (Pmax) is shown by the red-dashed line. For the treated model, the x-axis represents time of LPS administration. The immune response to LPS, which reflects a time-of-day dependence, was predicted to be enhanced in the winter season (A). B, C, D: corresponding profiles for the spring, summer, and autumn models. The inflammatory response is maximized when simulated LPS is added at cortisol's nadir and during its ascending phase, namely during the late night/early morning.
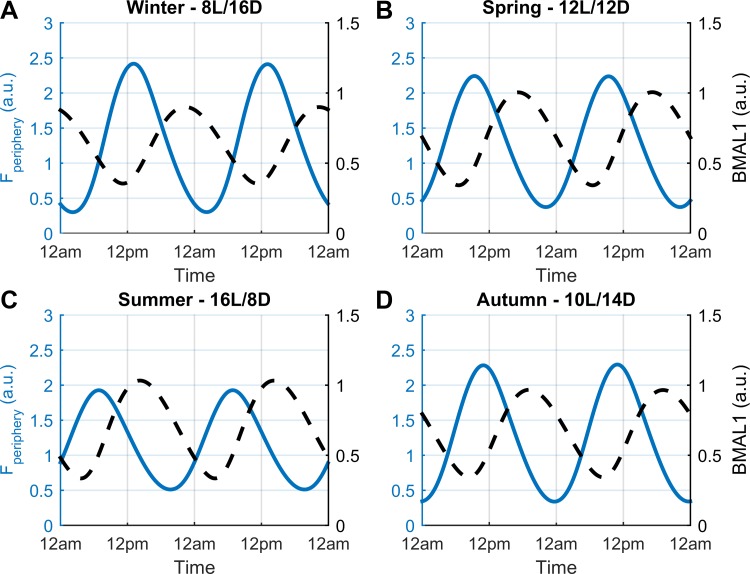
Fig. 8.
Circadian profiles of cortisol (Fperiphery) and BMAL1 for each season in the unchallenged model. The circadian rhythm of cortisol (Fperiphery) is represented by the blue plot and BMAL1 by the black dashed line. The relative phase between Fperiphery and BMAL1 oscillations results in BMAL1 levels peaking during the descending phase of cortisol's profile. At this time, the more pronounced “anti-inflammatory” state results in suppression of the immune response following in silico LPS administration. A, B, C, and D: corresponding rhythmic plots for winter, spring, summer, and autumn.
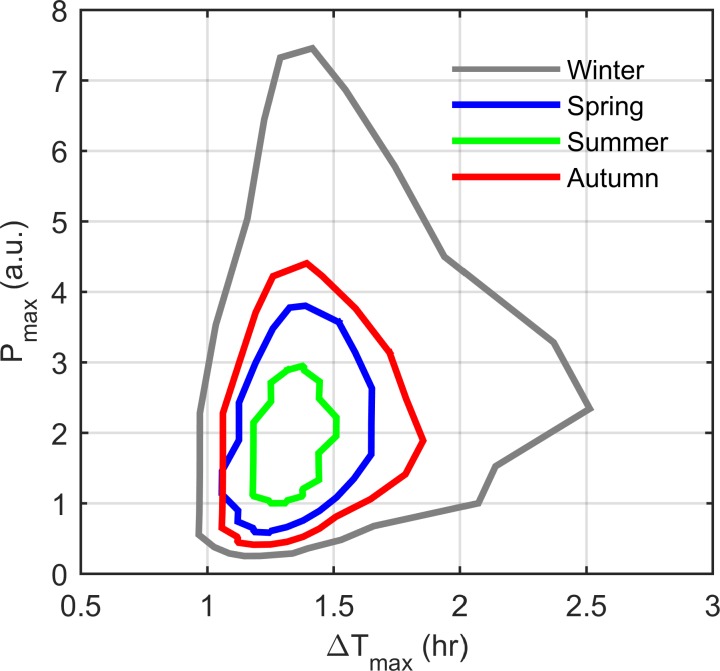
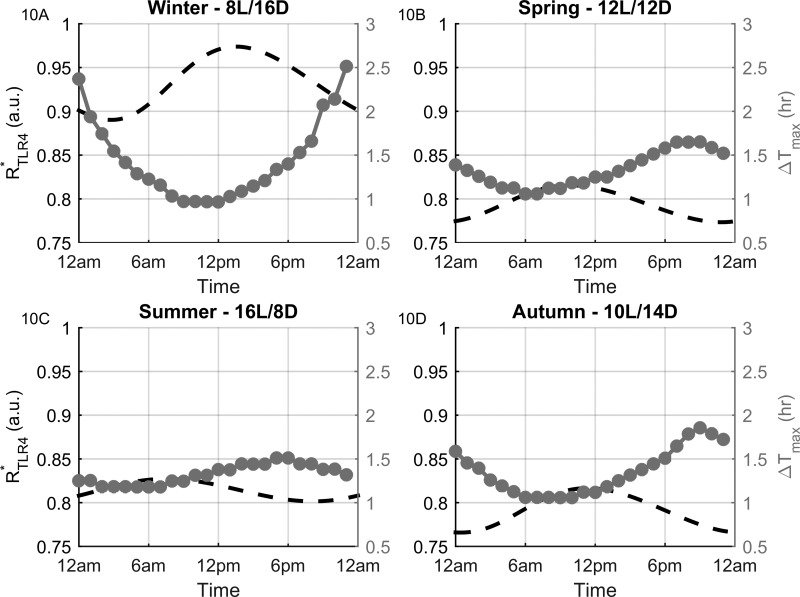
For each seasonal model, we then examined the temporal responsiveness (ΔTmax) of the system to modeled endotoxin treatment. ΔTmax was calculated as the difference between the time of LPS addition and the time-of-maximum proinflammatory mediator response. This parameter was measured for each of the 24 in silico treatment time points (every hour of the day). Figure 9 shows seasonal plots for Pmax vs. ΔTmax values. For all seasons, the magnitude of the inflammatory response appears to be somewhat independent of the time required to mount the response. The immune response magnitude to a given LPS dose is therefore associated with a dichotomy of response times, relatively rapid or slow. A critical contributing factor to the temporal responsiveness of the system to LPS administration is revealed when considering the diurnal profile of ΔTmax. Figure 10 shows the rhythms of of the control model and ΔTmax vs. the time of LPS treatment. This negatively correlated, anti-phasic relationship between the two profiles indicates the dependency of the system's immune response time on the circadian rhythm of the receptor complex. High levels increase the number of LPS-binding sites available which results in a rapid inflammatory response. Conversely, the proinflammatory response is more delayed when levels are low.
Fig. 9.
Maximum proinflammatory mediator level (Pmax) vs. the time delay between LPS addition and the time-of-maximum response (ΔTmax) for each simulated season. The lack of a unique relationship between Pmax and ΔTmax predicts that the intensity of the inflammatory response is independent of the temporal responsiveness of the system.
Fig. 10.
Profiles of for the unchallenged model and ΔTmax vs. the time of LPS administration for each season. The antiphasic relationship between the two profiles reveal the dependence of the system's temporal responsiveness. Higher levels result in a more rapid response as more of the receptor is available to bind with the added in silico LPS dose.
DISCUSSION
Our model predicts that the amplitude of oscillations of the proinflammatory mediator (P), proinflammatory receptor (RP), and cortisol (Fperiphery) increases as the seasons changed from summer through spring, autumn, and winter (Figs. 3, A–C, and 4, A–C). The opposite amplitude trend was estimated for BMAL1 as the summer model exhibited the highest amplitude (Figs. 3D and 4D). These results are in accordance with experimental findings whereby cortisol levels were found to be higher in winter (43, 97, 146). Additionally, the amplitudes of P, RP, and BMAL1 agree with human experimental studies (28, 54, 74).
In our model, cortisol's seasonal amplitude changes are attributed primarily to the Vseason and cseason coefficients, which are related to the seasonal plasticity of SCN activity and adrenal function, respectively. An increase in Vseason results in increased CRH degradation. Pronounced CRH degradation reduces FR(N) and consequently diminishes the inhibitory effect of FR(N) on CRH production. Increased CRH production then ensues, which results in higher cortisol production with increasing coefficient value. Secondly, a higher cseason value increases the Michaelis-Menten constant of cortisol production in the central compartment. As this constant increases from the summer to the winter model, the rate of cortisol production decreases. A slower production rate, however, results in the HPA axis producing a cortisol response that is both slow to turn on and off, yielding larger amplitude cortisol oscillations.
One would expect that increasing cortisol levels would suppress the proinflammatory oscillations. Contrarily, the opposite was predicted as the amplitude of the proinflammatory mediator was highest in the winter season when cortisol also oscillated with its highest amplitude. This result can be explained by considering both cortisol's rhythmic influences on immune function dynamics as well as the seasonal changes of glucocorticoid sensitivity; modeled via usage of the seasonally varying Hill coefficient (nseason). P is maximized at low cortisol levels and suppressed when cortisol is high. As the Hill coefficient increases, cortisol's inhibitory effect (at high levels) becomes more pronounced. At low cortisol levels, however, its inhibitory influence is diminished, which thus promotes higher P levels. BMAL1's oscillations were entrained to cortisol's minima. The decrease in cortisol's minima with increasing Hill coefficient towards winter results in a reduction of BMAL1's maxima.
For all the biochemical markers considered, decreasing photoperiod resulted in a phase delay of the circadian rhythms. This effect is related to the start of the light cycle. A decreasing photoperiod results in light presentation later in the day and since light promotes degradation in our model, CRH and cortisol rhythms peak later, manifested as a phase delay. Due to cortisol's entraining effects, phase delays were predicted for all our downstream entrained markers with decreasing photoperiod. The winter phase delay in cortisol's diurnal profile has been found experimentally (145).
The diversity of components within the immune system renders it difficult to collectively categorize the seasonal changes of all immune responses, which also vary between species. Field studies on mammalian rodents (69, 125) confirm the intra-annual variation in cell-mediated, innate, and humoral immunity; however, inconsistencies between immune responses and also between comparable seasons may arise due to differential regulation from environmental stressors. The general opinion, however, is that the rodent mammalian innate immune system is suppressed and the acquired immune system is enhanced during the winter (25). The effects of photoperiod in regulating these seasonal immunological changes have been investigated in laboratory settings following animal exposure to long (LD) or short day (SD) lengths. Administration of LPS to Siberian hamsters produces an attenuated sickness response and reduced expression of IL-1β and TNF-α in SD subjects (102) while T-lymphocyte counts are higher in rats exposed to SD lengths (101). Adding to the controversy in characterizing seasonal immunological plasticity, memory B-cell-mediated antibody responses are actually suppressed with the adaptation of Siberian hamsters to shorter winter photoperiods (133).
Limited studies are available that experimentally explore the seasonal adaptations of innate immune function in humans. An ex vivo study conducted on peripheral blood mononuclear cells isolated from 15 volunteers over the course of 1 yr and challenged with LPS showed an increase in the expression of IL-6, IL-1β, TNF, INF-γ, and IL- 10 in winter above all other seasons (58). Within this study, it was also found that the expressions of the Toll-like receptors 2 and 4 (TLR2 and TLR4) were reduced during the summer. As is illustrated in Fig. 5, the amplitude of simulated oscillations of was indeed diminished in the summer season. Furthermore, our endotoxemia model predicted an enhanced proinflammatory response during the winter season (Figs. 6 and 7). While Figs. 6 and 7 (also Figs. 9 and 10) are outputs generated from an in silico LPS dose of 0.5 a.u., we conducted similar analyses for LPS doses ranging from 0.1 to 1 a.u. Increasing the dose input intensified the resulting inflammatory response; however, the qualitative diurnal and seasonal differences (at a specific dose) remained unchanged.
Serum vitamin D3 levels were significantly higher in the summer and a strong negative correlation was established between its seasonal profile and the LPS response in the aforementioned ex vivo human study (58). The immunosuppressive effects of vitamin D3 was confirmed in vitro whereby addition of 1,25(OH)2D3, the biological active metabolite of vitamin D3, suppressed the LPS-mediated proinflammatory cytokine response. Most of the body's vitamin D3 is synthesized by the skin following exposure to UV-B radiation. In temperate regions, UV-B radiation varies seasonally such that exposure is reduced in the winter and peaks in the summer (16). This consequently results in a seasonal variation in serum vitamin D3 levels that correlate with the seasonal UV-radiation exposure. The vitamin D receptor (VDR), present on monocytes and activated T-helper cells (67), also displays peak expression during the summer (28). Apart from inhibiting human monocyte production of cytokines such as IL-1, IL-6, and TNF-α (3, 58), vitamin D3 inhibits both B cell and T-cell proliferation (7). While evidence suggests the involvement of vitamin D3 and its receptor in the regulation of seasonal immune function, human in vivo data are limited and contradictory. No correlation was found between vitamin D3 plasma levels and the LPS-induced cytokine response (61) and between the seasonal disease activity of rheumatoid arthritis (RA), ankylosing spondylitis (AS), and osteoarthritis (OA) and serum vitamin D (152) despite vitamin D insufficiency being regarded as a biomarker for RA and OA (41). Confounding factors such as sunscreen use, skin pigmentation, and dietary practice may complicate the establishment of a relationship between vitamin D status and immunological seasonality (85).
In Fig. 8, our model predicts both seasonal and time-of-day sensitivities of the inflammatory response. Higher amplitude BMAL1 oscillations in the summer model resulted in a diminished immune response. Alternatively, a more intense response was predicted in the winter model where the amplitude of BMAL1 oscillations was the lowest. From a diurnal perspective, the system was more immune sensitive in the ascending vs. the descending phase of cortisol's profile. Considering this, we note the importance of the phase of BMAL1 oscillations. Our model indicates that BMAL1 peaks in the afternoon to late night. Numerous studies investigating the circadian rhythms of human BMAL1 have emphasized the existence of circadian rhythmic interindividual variation amongst individuals (8, 20, 49, 137). Analysis of the phases of BMAL1 expression among human volunteers revealed the existence of two subgroups (137). One group exhibiting maximum expression during the mid-morning/early afternoon and the other at evening/late-night. In this regard, we can consider our modeled BMAL1 rhythms to be consistent with experimental data.
In our in silico investigation, we assumed that the autonomous P circadian rhythms were a consequence of BMAL1 entrainment (Eq. 23). The anti-inflammatory regulations by this PCG have been experimentally reported (21, 22, 39, 90) and were highlighted in materials and methods. Several other circadian clock proteins control fundamental aspects of immune function. CLOCK overexpression enhances transcriptional activity of NF-κB (130), REV-ERBα represses the LPS-mediated proinflammatory response (39), macrophages derived from Per2 mutant mice express reduced amounts of Tlr9 mRNA (124), and bone marrow-derived macrophages (BMDM) from Cry1 and Cry2 double knockout mice show an increased expression in baseline inflammatory cytokines such as IL-6 and Cxcl1 (86). The circadian regulation of immune function is complex with opposing functions of the core clock gene components. Models accounting for this diversity of circadian regulation on immune responses would indubitably provide more insightful and biologically-accurate circadian and seasonal dynamical predictions.
Time-course analysis of immunological mediator substances following endotoxin treatment can reveal the underlying mechanisms modulating immune function activity. Following LPS stimulation: the peak of serum levels of IL-6 30 min after TNF-α suggests the induction of IL-6 secretion by TNF-α (143). With our seasonal models, the temporal responsiveness of our system to in silico LPS administration also displayed a time-of-day sensitivity, oscillating between ∼1 to 3 h. The response times fall within the experimentally determined range found from human endotoxemia studies (56, 143). Figures 9 and 10 reveal that the rapidity of the LPS-induced response was seemingly independent of the magnitude of the response and primarily contingent upon the amplitude and phase of the seasonally varying circadian rhythm of the complex. Our model predicts that while regulates the response time of the system, the magnitude of the inflammatory response is heavily reliant on the circadian rhythms of Fperpihery and BMAL1 and to a lesser extent on the profile of It is recommended that studies assessing the inflammatory responses to endotoxin treatment consider these diurnal and seasonal fluctuations in activity. These variations may lead to the application of fluctuating and inconsistent baseline values or incorrect estimation of the proinflammatory response due to a poor time-window selection. Circadian rhythmic synchronization among subjects by exposure to common lighting conditions before the execution of a treatment protocol may be critical.
The kinetics and dynamics of our proinflammatory mediator (P) and its receptor (RP) were not modeled after unique biological entities and pathways. Immune function is orchestrated by a complex network of interconnecting intra- and extracellular pathways, which makes it extremely challenging to model all molecular species. While a large model will capture, in detail, the mechanisms of a system/subsystem and might provide accurate predictions, there is a tradeoff between reliability and feasibility. Complex models are computationally slow and suffer from parameter identification issues and the system's behavior is difficult to assess under varying conditions (6). Furthermore, validation of complex mathematical models is challenging when limited quantitative data are available. Circumventing the complications associated with complex systems, models describing immune function can be kept relatively simple, focusing on a subsystem and detailing select processes (138). Using a heuristic mathematical model that reduced the NF-κB regulatory network into a “NF-κB-like” circuit and describing a “cytokine-like” variable, Yde et al. (153) captured the characteristic dynamics of cytokine wave propagation that occurs following exposure to an inflammatory stimulus. A spatiotemporal mathematical model (PDE) using a minimal set of immune factors, including a “generic chemokine,” was developed to investigate fundamental aspects of tissue immune response to an antigen (134). This simple PDE model was able to describe antigen recognition, both the innate and adaptive immune responses, antigen clearance, and granuloma formation. Recently, a three-dimensional computational model capable of tracking the spatiotemporal evolution of necrotizing enterocolitis (NEC) and predicting the recovery-promoting, anti-inflammatory effects mediated by breast feeding was realized (9). In this NEC model, various components with similar characteristics were lumped/grouped together whereby the proinflammatory cytokines (IL-1, IL-6, IL-8, IL-12, IL-18, IFN-γ, and TNF-α) were represented by a single variable and anti-inflammatory cytokines (TGF-β1, IL-4, and IL-10) by another. Others have amalgamated the effects of cells and cytokines into one comprehensive term when predicting the dynamics of acute inflammatory responses to pathogenic insults (24, 63).
Limited availability of human experimental seasonal data and incomplete development of mechanistic pathways describing bidirectional relationships between unique PCGs and proinflammatory cytokines renders it difficult to mathematically model and assess the circadian seasonal variations of any one specific cytokine. We therefore opted to integrate the available experimental circadian and seasonal data into representative proinflammatory variable components that could be used as proxies to predict seasonal changes in immune function. As mentioned in materials and methods, we have consolidated the characteristics of cytokines such as IL-6, TNF-α, and IL-1β into our proinflammatory mediator (P). In contrast to TNF- α and IL-1β which are primarily classified as proinflammatory cytokines, IL-6 is pleiotropic with both pro- and anti-inflammatory roles. These contradictory roles are mediated via different IL-6 receptors. IL-6 activation of cells via the membrane bound IL-6 receptor (IL6-R) is referred to as classic signaling while activation via the soluble IL-6 receptor (sIL-6R) is known as trans-signaling (118). Classic signaling has been implicated in the anti-inflammatory effects of IL-6 and trans-signaling is assumed to arbitrate proinflammatory processes (73). Signal transduction for both the classic and transsignaling pathways is facilitated by the universal β-receptor subunit, glycoprotein 130 (gp130) (51, 118, 119). In both antigen- and collagen-induced mouse models of arthritis, it was determined that IL-6 knockout (KO) mice were protected against the disease (91, 92), indicating the proinflammatory function of IL- 6. Evidence supporting the immunosuppressive capabilities of IL-6 comes from another mice study that reported a higher inflammatory score for IL-6 KO mice following exposure to the irritant dextran sulfate sodium (42). In the antigen-induced arthritic mouse IL-6 KO model, administration of IL-6 in conjunction with sIL-6R and not IL-6 alone was able to restore disease activity (91), suggesting the involvement of trans-signaling in proinflammatory processes. Seasonally, human serum IL-6 and sIL-6R concentrations are higher in the winter than in the summer (28, 74), which conveys an augmentation in the proinflammatory signaling of IL-6. We believe that this seasonal revelation coupled with the increased levels of IL-6 and sIL-6R in various inflammatory diseases (26, 57, 82, 107, 141) renders our IL-6 proinflammatory assumptions, in the context of this seasonal model, to be valid. Just as one variable was used to represent the combined effects of proinflammatory cytokines (P), we considered P binding and signaling to be governed by a single unit generic receptor (RP). Arguably, these simplifications may limit our model in terms of its accuracy and scope of applicability. Our top down modeling approach, however, does provide a high-level description that considers the contributions of fundamental mechanisms in regulating seasonal variations of proinflammatory components. Our immune subsystem is intermediate in complexity and provides a useful framework that can either be simplified or further expanded, depending on the immune function of interest being explored.
Our seasonal model incorporates 32 differential equations from our group's previous work and from another modeling study (11). In addition to the previously measured and estimated parameters (from other models), we have implemented and optimized 12 new parameters, four of which were the seasonal coefficients. These parameters are emboldened in Table A1 of the appendix. As discussed within the relevant subcategories of materials and methods, the parameters used within this model were either acquired from experimental studies, independently estimated to describe profiles obtained from experimental data, or adapted from numerical simulation studies. For components without quantitative data, parameters were estimated so that their downstream effectors, of known profiles, were congruent with experimental measures. To describe unknown or complicated reaction processes, assumptions were made regarding the mechanism of interactions between components. Under such circumstances, we opted to use IDRs or simpler mathematical representations. Our aim was to investigate the potential pathways by which seasonal changes could modulate immune function and we sought to do so in a manner that reduced overfitting of data but could also yield a model that was relatable to established biological processes. It is possible, however, that the predictions made here could be estimated with the use of simpler models.
Model reduction techniques can be used to simplify complex biochemical reaction networks. The most common strategy employed is time scale decomposition. with the use of this approach, components or reactions that do not contribute significantly to the system's overall behavior are eliminated or reduced to simpler expressions if their reaction time scales are not in accordance with the time scale of interest. This method has been applied to reduce Wnt/beta-catenin (62), NF-κB (59), and glycolytic pathways (60, 136). Another common reduction technique involves sensitivity analysis, which ascertains how parameter variation affects the system's response (135). This knowledge can be used to either eliminate insignificant contributions or aid in redesigning the model structure. Variable lumping is an alternative technique, which transforms described species into a reduced set of pseudospecies, consequently minimizing the number of equations and parameters used (27) while optimization-based approaches can be used to determine the least number of reactions required to replicate the dynamics of the complex model for a given accuracy (5). The main focus of our investigation was to establish a simple yet comprehensive neuroendocrine-immune axis model and so reduction techniques were not implemented. In our future work, we do intend to utilize a model simplification strategy to aid in formally identifying the critical components of our model. We do believe, however, that the dynamics of cortisol (FHPA, Eq. 3 and Fperiphery, Eq. 9), BMAL1(N) (Eq. 21), the proinflammatory mediator (PHPA, Eq. 8 and P, Eq. 24), and LPS (Eq. 28) are central to our model's seasonal predictions. From a heuristic standpoint, and encompassing these variables, our model can be represented in a simpler form. Cortisol's circadian profile could be modeled using IDRs such as a single cosine function or a “two rates” production model (18), the PCG equations could potentially be replaced by a three-variable Goodwin model with dynamical variables BMAL1, PER-CRY, and REV-ERBα or by a set of reduced variable delay differential equations (127, 131) and the proinflammatory component dynamics could likely be characterized using a comprehensive proinflammatory response function (34–36). Similarly, an endotoxin (LPS)-mediated stimulus function (24) could potentially replace Eqs. 28–31. Although we have discussed a few speculative methodologies by which our model can be represented in a simpler manner, formal reduction techniques are needed to identify the significant components.
Our model does not provide a complete representation of all the underlying dynamics regulating seasonal changes in immunity. Seasonal variation in melatonin rhythms, for instance, has been associated with photoperiod-driven changes of immune and reproductive function (87, 88, 133). The role of melatonin in conferring immunological plasticity with changing photoperiods has been investigated in strains of inbred mice (154). C3H/HeN mice, which exhibit a robust melatonin rhythm, show augmented B-cell and T-cell counts when transferred from long to short days. Conversely, C57/BL6 mice, which do not display photoperiod induced melatonin rhythm changes, fail to display immunological photoperiodism (12). Assessing the febrile response to endotoxin challenges in Siberian hamsters, it was found that the reduction in fever duration and body temperature observed under SD conditions could be mimicked under long day light exposure with daily melatonin injections four h before darkness; simulating the SD melatonin signal (13). Further evidence corroborating melatonin's role in modulating photoperiod-driven immunological function arise from a study involving the surgical removal of the melatonin producing pineal gland [pinealectomy (PINx)] (149). SD PINx Siberian hamsters failed to exhibit increased leukocyte counts and did not attenuate their behavioral sickness response (anorexia, cachexia, nest building suppression) following an endotoxin challenge, as did the control SD group, while leukocyte counts and the sickness response were unaffected by PINx in the LD group. In addition to melatonin, gonadal and thyroid hormones have also been implicated in photoperiod-driven seasonal immunological changes (133). Gonadal regression and inhibition of testosterone secretion (a consequence of SD exposure in Siberian hamsters) is associated with a concurrent suppression of the sickness response (100). An increased localization of the thyroid hormone T3 in the cytoplasm of SD lymphocytes derived from Siberian hamsters has been observed (132). This shift in compartmentalization of T3, a potent immunomodulator, may regulate seasonal lymphocyte activity or differentiation. Other factors such as temperature and humidity may also contribute to seasonal immune plasticity. Cold temperature and low humidity, associated with winter conditions, are correlated with an increased occurrence of respiratory tract infections (RTIs) (31, 76, 84). It is postulated that winter conditions promote cooling of the respiratory epithelium, which inhibits mucociliary clearance (110) and the phagocytic activity of leukocytes (111), suppressing respiratory defenses against infection. Diminished barrier protection, crowding (70), and increased efficiency of respiratory droplet transmission (71) during the winter may contribute to enhanced RTI incidence. An association between compromised mucosal barrier function, due to a reduction in gastric mucosal factors, and the seasonal peak of peptic ulcer disease occurrence in winter has also been reported (156). Moreover, epidemiological studies on rheumatoid arthritis disease activity report that rainy and cold weather appear to increase joint pain and stiffness (1, 48, 95). In rheumatoid arthritis patients, colder temperatures may induce muscle stiffening around joints and contribute to exacerbated symptoms (1). Our mathematical model considers seasonal immunity adaptations from the perspective of photoperiod-driven seasonal changes in cortisol rhythms. Biologically, however, modulation is expected to involve an integration of numerous mechanisms including those previously discussed.
In summary, our model's seasonal predictions for circadian rhythm changes are in accordance with literature. Our model has predicted that seasonal changes due to varying photoperiod and the plasticities of SCN activity, adrenal function, and glucocorticoid sensitivity yield both amplitude changes and phase shifts of circadian profiles. The modification of these rhythms with seasons can result in the alignment or misalignment of rhythms, which can induce either the enhancement or suppression of the activity of biochemical markers existing in interconnecting pathways. Overall, our model results in the prediction of a proinflammatory “winter system.” There is the need to further investigate these circadian dynamics and to apply our work to a disease model, such as rheumatoid arthritis, so that a more profound understanding of these disease pathways from a seasonal context can be ascertained.
GRANTS
This work was supported by National Institute of General Medical Science Grant GM-24211 (to I. P. Androulakis and K. Pierre).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
K.P. performed experiments; K.P. and N.S. analyzed data; K.P. and I.P.A. interpreted results of experiments; K.P. prepared figures; K.P. drafted manuscript; N.S. and I.P.A. edited and revised manuscript; I.P.A. conception and design of research; I.P.A. approved final version of manuscript.
APPENDIX
Table A1 shows the parameter descriptions and their values.
Table A1.
Parameter descriptions and their values
| Parameter | Value | Units | Description/Reference |
|---|---|---|---|
| Vseason, cseason, nseason (winter) | 1.5 | Maximum SCN activity, seasonal coefficient for Michaelis constant of cortisol production, Hill coefficient/estimated | |
| Vseason, cseason, nseason (spring) | 1 | Maximum SCN activity, seasonal coefficient for Michaelis constant of cortisol production, Hill coefficient/estimated | |
| Vseason, cseason, nseason (summer) | 0.75 | Maximum SCN activity, seasonal coefficient for Michaelis constant of cortisol production, Hill coefficient/estimated | |
| Vseason, cseason, nseason (autumn) | 1.2 | Maximum SCN activity, seasonal coefficient for Michaelis constant of cortisol production, Hill coefficient/estimated | |
| kp1 | 0.7965 | μM/h | Rate constant of CRH production/(78) |
| InCRH | 1 | μM | Strength of input signals on CRH production/estimated |
| Kp1 | 1.0577 | μM | Dissociation constant for CRH production/(78) |
| Vd1 | 0.5084 | μM/h | Rate of CRH enzymatic degradation/(78) |
| Kd1 | 1.9627 | μM | Michaelis constant of CRH enzymatic degradation/(78) |
| kfp | 0.15 | μM −1 | Efficiency of P on ACTH and F stimulation/estimated |
| kp2 | 0.6857 | μM/h | Rate of ACTH production/(78) |
| Kp2 | 1.0577 | μM | Dissociation constant for ACTH production/(78) |
| Vd2 | 0.5129 | μM/h | Rate of ACTH enzymatic degradation/(78) |
| Kd2 | 0.3069 | μM | Michaelis constant of ACTH enzymatic degradation/(78) |
| kp3 | 1.0302 | μM/h | Rate of F central production/estimated |
| Kp3 | 0.9608 | μM | Michaelis constant of F central production/estimated |
| Vd3 | 0.3618 | μM/h | Rate of F central enzymatic degradation/(78) |
| Kd3 | 0.4695 | μM | Michaelis constant of F central enzymatic degradation/(78) |
| 2.9 | fmol·g−1··h−1 | Synthesis rate or glucocorticoid receptor mRNA/(103) | |
| 26.2 | nmol·l−1·mg protein−1 | Concentration of FR(N) at which mRNAR,HPA synthesis drops to its half/(103) | |
| R0 | 540.7 | nmol·l−1·mg protein−1 | Baseline value of free cytosolic glucocorticoid receptor/(103) |
| Rm0 | 25.8 | fmol/g | Baseline value of glucocorticoid receptor mRNA/(103) |
| /Rm0 | Degradation rate of glucocorticoid receptor mRNA/(103) | ||
| 0.0572 | h−1 | Degradation rate of cytosolic glucocorticoid receptor/(103) | |
| (R0/Rm0) × | Synthesis rate of free cytosolic receptor/(103) | ||
| Rf | 0.49 | Fraction of cortisol recycled/(103) | |
| kre | 0.57 | h−1 | Rate of receptor recycling from nucleus to cytoplasm/(103) |
| kon | 0.00329 | l·nmol−1·h−1 | Second order rate constant of glucocorticoid receptor binding/(103) |
| kt | 0.63 | h−1 | Rate of receptor translocation to the nucleus/(103) |
| kF,MR | 1.1011 | 1 | Maximum extent of Fperiphery-mediated activation of MR/(77) |
| KF,MR | 0.5 | nM | Michaelis constant for Fperiphery-mediated activation of MR/(77) |
| kF,GR | 15 | 1 | Maximum extent of Fperiphery-mediated activation of GR/(77) |
| KF,GR | 30 | nM | Michaelis constant for Fperiphery-mediated activation of GR/(77) |
| kMR | 0.34 | nM/h | Base production rate of MR/(77) |
| MRT | 1.45 | nM | Total MR concentration/(77) |
| KMR | 0.21 | nM | Michaelis constant for MR production/(77) |
| kMR,deg | 0.70 | nM/h | Degradation rate for MR/(77) |
| kb,MR | 0.00329 | nM−1/h | Rate of mineralocorticoid receptor removal due to binding/(77) |
| kr,MR | 0.001 | h−1 | Ratio of mineralocorticoid receptor recycled × rate of recycling/(77) |
| kb,GR | 0.00329 | nM−1/h | Rate of glucocorticoid receptor removal due to binding/(77) |
| kr,GR | 0.001 | h−1 | Ratio of glucocorticoid receptor recycled × rate of recycling/(77) |
| kon,MR/kon,GR | 1 | h−1 | Binding rate between cortisol and the MR/GR receptor/(77) |
| kT,MR/kT,GR | 1 | h−1 | Translocation rate of the activated cortisol-receptor complex/(77) |
| kre,MR/kre,MR | 1 | h−1 | Rate of receptor recycling from the nucleus to the cytoplasm/(77) |
| KMR,deg | 1.65 | nM | Michaelis constant for degradation of MR/(77) |
| kGR | 1.18 | nM/h | Base production rate of GR/(77) |
| GRT | 1.81 | nM | Total GR concentration/(77) |
| KGR | 0.74 | nM | Michaelis constant for GR production/(77) |
| kGR,deg | 1.52 | nM/h | Degradation rate for GR/(77) |
| KGR,deg | 1.05 | nM | Michaelis constant for degradation of GR/(77) |
| kf | 1.2 | nM−1 | Efficiency of P on transcription of Per-Cry/estimated |
| kc | 0.009 | nM/h | Coupling strength/estimated |
| v1b | 9 | nM/h | Maximal rate of Per-Cry transcription/(11) |
| k1b | 1 | nM | Michaelis constant of Per-Cry transcription/(11) |
| k1i | 0.56 | nM | Inhibition constant of Per-Cry transcription/(11) |
| c | 0.01 | nM | Concentration of constitutive activator/(11) |
| p | 8 | Hill coefficient of inhibition of Per-Cry transcription/(11) | |
| k1d | 0.12 | h−1 | Degradation rate of Per-Cry mRNA/(11) |
| k2b | 0.3 | nM−1/h | Complex formation rate of Per-Cry mRNA/(11) |
| q | 2 | No. of PER-CRY complex forming subunits/(11) | |
| k2d | 0.05 | h−1 | Degradation rate of cytoplasmic PER-CRY/(11) |
| k2t | 0.24 | h−1 | Nuclear import rate of the PER-CRY complex/(11) |
| k3t | 0.02 | h−1 | Nuclear export rate of PER-CRY complex/(11) |
| k3d | 0.12 | h−1 | Degradation rate of the nuclear PER-CRY complex/(11) |
| v4b | 3.6 | nM/h | Maximal rate of Bmal1 transcription/(11) |
| k4b | 2.16 | nM | Michaelis constant of Bmal1 transcription/(11) |
| r | 3 | Hill coefficient of activation of Bmal1 transcription/(11) | |
| k4d | 0.75 | h−1 | Degradation rate of Bmal1 mRNA/(11) |
| k5b | 0.24 | h−1 | Translation rate of BMAL1/(11) |
| k5d | 0.06 | h−1 | Degradation rate of cytoplasmic BMAL1/(11) |
| k5t | 0.45 | h−1 | Nuclear import rate of BMAL1/(11) |
| k6t | 0.06 | h−1 | Nuclear export rate of BMAL1/(11) |
| k6d | 0.12 | h−1 | Degradation rate of nuclear BMAL1/(11) |
| k6a | 0.09 | h−1 | Activation rate of nuclear CLOCK-BMAL1/(11) |
| k7a | 0.003 | h−1 | Deactivation rate of CLOCK-BMAL1/(11) |
| k7d | 0.09 | h−1 | Degradation rate of CLOCK-BMAL1/(11) |
| 7.3 | μM/h | Base transcription rate of mRNAP/(77) | |
| 59.81 | μM −1 | Efficiency of LPSR-mediated transcription of mRNAP/(77) | |
| kfr | 1.07 | 1 | Maximum extent of FGR(N)-mediated suppression of mRNAP/(77) |
| Kfr | 1 | μM | Michaelis constant for FGR(N)-mediated suppression of mRNAP/(77) |
| kpc | 0.3 | 1 | Maximum extent of BMAL1-mediated suppression of mRNAP and /estimated |
| Kpc | 25 | μM | Michaelis constant for BMAL1-mediated suppression of mRNAP and /estimated |
| 2.89 | h−1 | Degradation rate of mRNAP/(77) | |
| 0.29 | h−1 | Translation rate of P/(77) | |
| 1.06 | h−1 | Degradation rate of P/(77) | |
| 0.61 | μM/h | Base transcription rate of mRNARP/(77) | |
| kfr2 | 0.8 | 1 | Maximum extent of FMR(N)-mediated transcription of /(77) |
| Kfr2 | 0.5 | μM | Michaelis constant for FMR(N)-mediated transcription of /(77) |
| 0.19 | h−1 | Degradation rate of mRNARP/(77) | |
| 1.11 | h−1 | Translation rate of RP/(77) | |
| kd | 0.14 | μM−1/h | P-RP binding rate constant/(77) |
| 0.26 | h−1 | Degradation rate of RP/(77) | |
| 1.3 | h−1 | Degradation rate of PRP/(77) | |
| kLPS,1 | 4.5 | h−1 | Growth rate of LPS/(115) |
| kLPS,2 | 6.79 | h−1 | Clearance rate of LPS/(115) |
| kLPS,3 | 0.0914 | μM/h | Base transcription rate of mRNATLR4*/(115) |
| 1.74 | μM−1 | Efficiency of PRP-mediated transcription of /(115) | |
| kLPS,4 | 0.32 | h−1 | Decay rate of /(115) |
| ksyn | 0.02 | h−1 | Translation rate of /(115) |
| kdeg | 0.02 | h−1 | Degradation rate of /(115) |
| k2 | 0.04 | h−1 | Dissociation rate between LPS and of /(115) |
| k1 | 3 | μM−1/h | Binding rate between LPS and of /(115) |
| k3 | 5 | h−1 | Degradation rate of |
In addition to the previously measured and estimated parameters (from other models), we have implemented and optimized 12 new parameters, 4 of which were the seasonal coefficients, which are in bold. See text for additional definitions.
REFERENCES
- 1.Abasolo L, Tobias A, Leon L, Carmona L, Fernandez-Rueda JL, Rodriguez AB, Fernandez-Gutierrez B, Jover JA. Weather conditions may worsen symptoms in rheumatoid arthritis patients: the possible effect of temperature. Reumatol Clin 9: 226–228, 2013. [DOI] [PubMed] [Google Scholar]
- 2.Akira S, Hirano T, Taga T, Kishimoto T. Biology of multifunctional cytokines: IL 6 and related molecules (IL 1 and TNF). FASEB J 4: 2860–2867, 1990. [PubMed] [Google Scholar]
- 3.Almerighi C, Sinistro A, Cavazza A, Ciaprini C, Rocchi G, Bergamini A. 1Alpha,25-dihydroxyvitamin D3 inhibits CD40L induced proinflammatory and immunomodulatory activity in human monocytes. Cytokine 45: 190–197, 2009. [DOI] [PubMed] [Google Scholar]
- 4.An H, Yu Y, Zhang M, Xu H, Qi R, Yan X, Liu S, Wang W, Guo Z, Guo J, Qin Z, Cao X. Involvement of ERK, p38 and NF-kappaB signal transduction in regulation of TLR2, TLR4 and TLR9 gene expression induced by lipopolysaccharide in mouse dendritic cells. Immunology 106: 38–45, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Androulakis IP. Kinetic mechanism reduction based on an integer programming approach. AIChE J 46: 361–371, 2000. [Google Scholar]
- 6.Apri M, de Gee M, van Mourik S, Molenaar J. Identifying optimal models to represent biochemical systems. PLoS One 9: e83664, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Aranow C. Vitamin D and the immune system. J Investig Med 59: 881–886, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Archer SN, Viola AU, Kyriakopoulou V, von Schantz M, Dijk DJ. Inter-individual differences in habitual sleep timing and entrained phase of endogenous circadian rhythms of BMAL1, PER2 and PER3 mRNA in human leukocytes. Sleep 31: 608–617, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Barber J, Tronzo M, Harold Horvat C, Clermont G, Upperman J, Vodovotz Y, Yotov I. A three-dimensional mathematical and computational model of necrotizing enterocolitis. J Theor Biol 322: 17–32, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Barnes PJ. Anti-inflammatory actions of glucocorticoids: molecular mechanisms. Clin Sci (Lond) 94: 557–572, 1998. [DOI] [PubMed] [Google Scholar]
- 11.Becker-Weimann S, Wolf J, Herzel H, Kramer A. Modeling feedback loops of the Mammalian circadian oscillator. Biophys J 87: 3023–3034, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bhat GK, Hamm ML, Igietseme JU, Mann DR. Does leptin mediate the effect of photoperiod on immune function in mice? Biol Reprod 69: 30–36, 2003. [DOI] [PubMed] [Google Scholar]
- 13.Bilbo SD, Nelson RJ. Melatonin regulates energy balance and attenuates fever in Siberian hamsters. Endocrinology 143: 2527–2533, 2002. [DOI] [PubMed] [Google Scholar]
- 14.Blackhurst G, McElroy PK, Fraser R, Swan RL, Connell JM. Seasonal variation in glucocorticoid receptor binding characteristics in human mononuclear leucocytes. Clin Endocrinol (Oxf) 55: 683–688, 2001. [DOI] [PubMed] [Google Scholar]
- 15.Bodenstein C, Gosak M, Schuster S, Marhl M, Perc M. Modeling the seasonal adaptation of circadian clocks by changes in the network structure of the suprachiasmatic nucleus. PLoS Comput Biol 8: e1002697, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bolland MJ, Grey AB, Ames RW, Mason BH, Horne AM, Gamble GD, Reid IR. The effects of seasonal variation of 25-hydroxyvitamin D and fat mass on a diagnosis of vitamin D sufficiency. Am J Clin Nutr 86: 959–964, 2007. [DOI] [PubMed] [Google Scholar]
- 17.Calvano SE, Xiao W, Richards DR, Felciano RM, Baker HV, Cho RJ, Chen RO, Brownstein BH, Cobb JP, Tschoeke SK, Miller-Graziano C, Moldawer LL, Mindrinos MN, Davis RW, Tompkins RG, Lowry SF; Inflamm and Host Response to Injury Large Scale Collab Res Program. A network-based analysis of systemic inflammation in humans. Nature 437: 1032–1037, 2005. [DOI] [PubMed] [Google Scholar]
- 18.Chakraborty A, Krzyzanski W, Jusko WJ. Mathematical modeling of circadian cortisol concentrations using indirect response models: comparison of several methods. J Pharmacokinet Biopharm 27: 23–43, 1999. [DOI] [PubMed] [Google Scholar]
- 19.Charmandari E, Chrousos GP, Lambrou GI, Pavlaki A, Koide H, Ng SS, Kino T. Peripheral CLOCK regulates target-tissue glucocorticoid receptor transcriptional activity in a circadian fashion in man. PLoS One 6: e25612, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cuesta M, Cermakian N, Boivin DB. Glucocorticoids entrain molecular clock components in human peripheral cells. FASEB J 29: 1360–1370, 2015. [DOI] [PubMed] [Google Scholar]
- 21.Curtis AM, Bellet MM, Sassone-Corsi P, O'Neill LA. Circadian clock proteins and immunity. Immunity 40: 178–186, 2014. [DOI] [PubMed] [Google Scholar]
- 22.Curtis AM, Fagundes CT, Yang G, Palsson-McDermott EM, Wochal P, McGettrick AF, Foley NH, Early JO, Chen L, Zhang H, Xue C, Geiger SS, Hokamp K, Reilly MP, Coogan AN, Vigorito E, FitzGerald GA, O'Neill LA. Circadian control of innate immunity in macrophages by miR-155 targeting Bmal1. Proc Natl Acad Sci USA 112: 7231–7236, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cutolo M, Straub RH. Circadian rhythms in arthritis: hormonal effects on the immune/inflammatory reaction. Autoimmun Rev 7: 223–228, 2008. [DOI] [PubMed] [Google Scholar]
- 24.Day J, Rubin J, Vodovotz Y, Chow CC, Reynolds A, Clermont G. A reduced mathematical model of the acute inflammatory response. II. Capturing scenarios of repeated endotoxin administration. J Theor Biol 242: 237–256, 2006. [DOI] [PubMed] [Google Scholar]
- 25.Demas GE, Nelson RJ. Ecoimmunology. Oxford, UK: Oxford Univ Press, 2012. [Google Scholar]
- 26.Doganci A, Eigenbrod T, Krug N, De Sanctis GT, Hausding M, Erpenbeck VJ, Haddad el B, Lehr HA, Schmitt E, Bopp T, Kallen KJ, Herz U, Schmitt S, Luft C, Hecht O, Hohlfeld JM, Ito H, Nishimoto N, Yoshizaki K, Kishimoto T, Rose-John S, Renz H, Neurath MF, Galle PR, Finotto S. The IL-6R alpha chain controls lung CD4+CD25+ Treg development and function during allergic airway inflammation in vivo. J Clin Invest 115: 313–325, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dokoumetzidis A, Aarons L. Proper lumping in systems biology models. IET Syst Biol 3: 40–51, 2009. [DOI] [PubMed] [Google Scholar]
- 28.Dopico XC, Evangelou M, Ferreira RC, Guo H, Pekalski ML, Smyth DJ, Cooper N, Burren OS, Fulford AJ, Hennig BJ, Prentice AM, Ziegler AG, Bonifacio E, Wallace C, Todd JA. Widespread seasonal gene expression reveals annual differences in human immunity and physiology. Nat Commun 6: 7000, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Douglas AS, Dunnigan MG, Allan TM, Rawles JM. Seasonal variation in coronary heart disease in Scotland. J Epidemiol Community Health 49: 575–582, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Duez H, Staels B. Rev-erb-alpha: an integrator of circadian rhythms and metabolism. J Appl Physiol (1985) 107: 1972–1980, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Eccles R. An explanation for the seasonality of acute upper respiratory tract viral infections. Acta Otolaryngol 122: 183–191, 2002. [DOI] [PubMed] [Google Scholar]
- 32.Faghih RT, Dahleh MA, Adler GK, Klerman EB, Brown EN. Deconvolution of serum cortisol levels by using compressed sensing. PLoS One 9: e85204, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Faghih RT, Dahleh MA, Adler GK, Klerman EB, Brown EN. Quantifying pituitary-adrenal dynamics and deconvolution of concurrent cortisol and adrenocorticotropic hormone data by compressed sensing. IEEE Trans Biomed Eng 62: 2379–2388, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Foteinou PT, Calvano SE, Lowry SF, Androulakis IP. In silico simulation of corticosteroids effect on an NFkB-dependent physicochemical model of systemic inflammation. PLoS One 4: e4706, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Foteinou PT, Calvano SE, Lowry SF, Androulakis IP. Modeling endotoxin-induced systemic inflammation using an indirect response approach. Math Biosci 217: 27–42, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Foteinou PT, Calvano SE, Lowry SF, Androulakis IP. Multiscale model for the assessment of autonomic dysfunction in human endotoxemia. Physiol Genomics 42: 5–19, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Franchimont N, Lambert C, Huynen P, Ribbens C, Relic B, Chariot A, Bours V, Piette J, Merville MP, Malaise M. Interleukin-6 receptor shedding is enhanced by interleukin-1beta and tumor necrosis factor alpha and is partially mediated by tumor necrosis factor alpha-converting enzyme in osteoblast-like cells. Arthritis Rheum 52: 84–93, 2005. [DOI] [PubMed] [Google Scholar]
- 38.Gibbs J, Ince L, Matthews L, Mei J, Bell T, Yang N, Saer B, Begley N, Poolman T, Pariollaud M, Farrow S, DeMayo F, Hussell T, Worthen GS, Ray D, Loudon A. An epithelial circadian clock controls pulmonary inflammation and glucocorticoid action. Nat Med 20: 919–926, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gibbs JE, Blaikley J, Beesley S, Matthews L, Simpson KD, Boyce SH, Farrow SN, Else KJ, Singh D, Ray DW, Loudon AS. The nuclear receptor REV-ERBalpha mediates circadian regulation of innate immunity through selective regulation of inflammatory cytokines. Proc Natl Acad Sci USA 109: 582–587, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Gonze D, Bernard S, Waltermann C, Kramer A, Herzel H. Spontaneous synchronization of coupled circadian oscillators. Biophys J 89: 120–129, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Grazio S, Naglic DB, Anic B, Grubisic F, Bobek D, Bakula M, Kavanagh HS, Kuna AT, Cvijetic S. Vitamin D serum level, disease activity and functional ability in different rheumatic patients. Am J Med Sci 349: 46–49, 2015. [DOI] [PubMed] [Google Scholar]
- 42.Grivennikov S, Karin E, Terzic J, Mucida D, Yu GY, Vallabhapurapu S, Scheller J, Rose-John S, Cheroutre H, Eckmann L, Karin M. IL-6 and Stat3 are required for survival of intestinal epithelial cells and development of colitis-associated cancer. Cancer Cell 15: 103–113, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hadlow NC, Brown S, Wardrop R, Henley D. The effects of season, daylight saving and time of sunrise on serum cortisol in a large population. Chronobiol Int 31: 243–251, 2014. [DOI] [PubMed] [Google Scholar]
- 44.Hanada T, Yoshimura A. Regulation of cytokine signaling and inflammation. Cytokine Growth Factor Rev 13: 413–421, 2002. [DOI] [PubMed] [Google Scholar]
- 45.Haus E, Sackett-Lundeen L, Smolensky MH. Rheumatoid arthritis: circadian rhythms in disease activity, signs and symptoms, and rationale for chronotherapy with corticosteroids and other medications. Bull NYU Hosp Jt Dis 70: Suppl 1: 3–10, 2012. [PubMed] [Google Scholar]
- 46.Hazlerigg DG, Wagner GC. Seasonal photoperiodism in vertebrates: from coincidence to amplitude. Trends Endocrinol Metab 17: 83–91, 2006. [DOI] [PubMed] [Google Scholar]
- 47.Hermann C, von Aulock S, Dehus O, Keller M, Okigami H, Gantner F, Wendel A, Hartung T. Endogenous cortisol determines the circadian rhythm of lipopolysaccharide–but not lipoteichoic acid–inducible cytokine release. Eur J Immunol 36: 371–379, 2006. [DOI] [PubMed] [Google Scholar]
- 48.Iikuni N, Nakajima A, Inoue E, Tanaka E, Okamoto H, Hara M, Tomatsu T, Kamatani N, Yamanaka H. What's in season for rheumatoid arthritis patients? Seasonal fluctuations in disease activity. Rheumatology (Oxford) 46: 846–848, 2007. [DOI] [PubMed] [Google Scholar]
- 49.James FO, Cermakian N, Boivin DB. Circadian rhythms of melatonin, cortisol, and clock gene expression during simulated night shift work. Sleep 30: 1427–1436, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jin X, Shearman LP, Weaver DR, Zylka MJ, de Vries GJ, Reppert SM. A molecular mechanism regulating rhythmic output from the suprachiasmatic circadian clock. Cell 96: 57–68, 1999. [DOI] [PubMed] [Google Scholar]
- 51.Jones SA, Scheller J, Rose-John S. Therapeutic strategies for the clinical blockade of IL-6/gp130 signaling. J Clin Invest 121: 3375–3383, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Jung CM, Khalsa SB, Scheer FA, Cajochen C, Lockley SW, Czeisler CA, Wright KP Jr. Acute effects of bright light exposure on cortisol levels. J Biol Rhythms 25: 208–216, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kalsbeek A, van der Vliet J, Buijs RM. Decrease of endogenous vasopressin release necessary for expression of the circadian rise in plasma corticosterone: a reverse microdialysis study. J Neuroendocrinol 8: 299–307, 1996. [DOI] [PubMed] [Google Scholar]
- 54.Kanikowska D, Sugenoya J, Sato M, Shimizu Y, Inukai Y, Nishimura N, Iwase S. Seasonal variation in blood concentrations of interleukin-6, adrenocorticotrophic hormone, metabolites of catecholamine and cortisol in healthy volunteers. Int J Biometeorol 53: 479–485, 2009. [DOI] [PubMed] [Google Scholar]
- 55.Keller M, Mazuch J, Abraham U, Eom GD, Herzog ED, Volk HD, Kramer A, Maier B. A circadian clock in macrophages controls inflammatory immune responses. Proc Natl Acad Sci USA 106: 21407–21412, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Kemna E, Pickkers P, Nemeth E, van der Hoeven H, Swinkels D. Time-course analysis of hepcidin, serum iron, and plasma cytokine levels in humans injected with LPS. Blood 106: 1864–1866, 2005. [DOI] [PubMed] [Google Scholar]
- 57.Keul R, Heinrich PC, Muller-newen G, Muller K, Woo P. A possible role for soluble IL-6 receptor in the pathogenesis of systemic onset juvenile chronic arthritis. Cytokine 10: 729–734, 1998. [DOI] [PubMed] [Google Scholar]
- 58.Khoo AL, Chai LY, Koenen HJ, Sweep FC, Joosten I, Netea MG, van der Ven AJ. Regulation of cytokine responses by seasonality of vitamin D status in healthy individuals. Clin Exp Immunol 164: 72–79, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kourdis PD, Palasantza AG, Goussis DA. Algorithmic asymptotic analysis of the signaling system. Comput Math Appl 65: 1516–1534, 2013. [Google Scholar]
- 60.Kourdis PD, Steuer R, Goussis DA. Physical understanding of complex multiscale biochemical models via algorithmic simplification: glycolysis in Saccharomyces cerevisiae. Physica D Nonlinear Phenomena 239: 1798–1817, 2010. [Google Scholar]
- 61.Kox M, van den Berg MJ, van der Hoeven JG, Wielders JP, van der Ven AJ, Pickkers P. Vitamin D status is not associated with inflammatory cytokine levels during experimental human endotoxaemia. Clin Exp Immunol 171: 231–236, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Kruger R, Heinrich R. Model reduction and analysis of robustness for the Wnt/beta-catenin signal transduction pathway. Genome Inform 15: 138–148, 2004. [PubMed] [Google Scholar]
- 63.Kumar R, Clermont G, Vodovotz Y, Chow CC. The dynamics of acute inflammation. J Theor Biol 230: 145–155, 2004. [DOI] [PubMed] [Google Scholar]
- 64.Kume K, Zylka MJ, Sriram S, Shearman LP, Weaver DR, Jin X, Maywood ES, Hastings MH, Reppert SM. mCRY1 and mCRY2 are essential components of the negative limb of the circadian clock feedback loop. Cell 98: 193–205, 1999. [DOI] [PubMed] [Google Scholar]
- 65.Lancaster GI, Khan Q, Drysdale P, Wallace F, Jeukendrup AE, Drayson MT, Gleeson M. The physiological regulation of toll-like receptor expression and function in humans. J Physiol 563: 945–955, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Lawrence T. The nuclear factor NF-kappaB pathway in inflammation. Cold Spring Harb Perspect Biol 1: a001651, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Lemire JM. Immunomodulatory role of 1,25-dihydroxyvitamin D3. J Cell Biochem 49: 26–31, 1992. [DOI] [PubMed] [Google Scholar]
- 68.Leonard BE. HPA and immune axes in stress: involvement of the serotonergic system. Neuroimmunomodulation 13: 268–276, 2006. [DOI] [PubMed] [Google Scholar]
- 69.Lochmiller RL, Vestey MR, McMurry ST. Temporal variation in humoral and cell-mediated immune response in a sigmodon hispidus population. Ecology 75: 236–245, 1994. [Google Scholar]
- 70.Lofgren E, Fefferman NH, Naumov YN, Gorski J, Naumova EN. Influenza seasonality: underlying causes and modeling theories. J Virol 81: 5429–5436, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Lowen AC, Steel J. Roles of humidity and temperature in shaping influenza seasonality. J Virol 88: 7692–7695, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Lowry SF. Human endotoxemia: a model for mechanistic insight and therapeutic targeting. Shock 24, Suppl 1: 94–100, 2005. [DOI] [PubMed] [Google Scholar]
- 73.Maes M, Anderson G, Kubera M, Berk M. Targeting classical IL-6 signalling or IL-6 trans-signalling in depression? Expert Opin Ther Targets 18: 495–512, 2014. [DOI] [PubMed] [Google Scholar]
- 74.Maes M, Stevens W, Scharpe S, Bosmans E, De Meyer F, D'Hondt P, Peeters D, Thompson P, Cosyns P, De Clerck L, Bridts C, Neels H, Wauters A, Cooreman W. Seasonal variation in peripheral blood leukocyte subsets and in serum interleukin-6, and soluble interleukin-2 and -6 receptor concentrations in normal volunteers. Experientia 50: 821–829, 1994. [DOI] [PubMed] [Google Scholar]
- 75.Majzoub JA. Corticotropin-releasing hormone physiology. Eur J Endocrinol 155: S71–S76, 2006. [Google Scholar]
- 76.Makinen TM, Juvonen R, Jokelainen J, Harju TH, Peitso A, Bloigu A, Silvennoinen-Kassinen S, Leinonen M, Hassi J. Cold temperature and low humidity are associated with increased occurrence of respiratory tract infections. Respir Med 103: 456–462, 2009. [DOI] [PubMed] [Google Scholar]
- 77.Mavroudis PD, Corbett SA, Calvano SE, Androulakis IP. Circadian characteristics of permissive and suppressive effects of cortisol and their role in homeostasis and the acute inflammatory response. Math Biosci 260: 54–64, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Mavroudis PD, Corbett SA, Calvano SE, Androulakis IP. Mathematical modeling of light-mediated HPA axis activity and downstream implications on the entrainment of peripheral clock genes. Physiol Genomics 46: 766–778, 2014. [DOI] [PubMed] [Google Scholar]
- 79.Mavroudis PD, Scheff JD, Calvano SE, Lowry SF, Androulakis IP. Entrainment of peripheral clock genes by cortisol. Physiol Genomics 44: 607–621, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Mazzocchi G, Malendowicz LK, Rebuffat P, Tortorella C, Nussdorfer GG. Arginine-vasopressin stimulates CRH and ACTH release by rat adrenal medulla, acting via the V1 receptor subtype and a protein kinase C2197-dependent pathway. Peptides 18: 191–195, 1997. [DOI] [PubMed] [Google Scholar]
- 81.Meijer JH, Michel S, Vanderleest HT, Rohling JH. Daily and seasonal adaptation of the circadian clock requires plasticity of the SCN neuronal network. Eur J Neurosci 32: 2143–2151, 2010. [DOI] [PubMed] [Google Scholar]
- 82.Mitsuyama K, Toyonaga A, Sasaki E, Ishida O, Ikeda H, Tsuruta O, Harada K, Tateishi H, Nishiyama T, Tanikawa K. Soluble interleukin-6 receptors in inflammatory bowel disease: relation to circulating interleukin-6. Gut 36: 45–49, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Motzkus D, Albrecht U, Maronde E. The human PER1 gene is inducible by interleukin-6. J Mol Neurosci 18: 105–109, 2002. [DOI] [PubMed] [Google Scholar]
- 84.Mourtzoukou EG, Falagas ME. Exposure to cold and respiratory tract infections. Int J Tuberc Lung Dis 11: 938–943, 2007. [PubMed] [Google Scholar]
- 85.Nair R, Maseeh A. Vitamin D: The “sunshine” vitamin. J Pharm Pharmacol 3: 118–126, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Narasimamurthy R, Hatori M, Nayak SK, Liu F, Panda S, Verma IM. Circadian clock protein cryptochrome regulates the expression of proinflammatory cytokines. Proc Natl Acad Sci USA 109: 12662–12667, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Nelson RJ. Seasonal immune function and sickness responses. Trends Immunol 25: 187–192, 2004. [DOI] [PubMed] [Google Scholar]
- 88.Nelson RJ, Demas GE, Klein SL, Kriegsfeld LJ. The influence of season, photoperiod, and pineal melatonin on immune function. J Pineal Res 19: 149–165, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Newman LA, Walker MT, Brown RL, Cronin TW, Robinson PR. Melanopsin forms a functional short-wavelength photopigment. Biochemistry 42: 12734–12738, 2003. [DOI] [PubMed] [Google Scholar]
- 90.Nguyen KD, Fentress SJ, Qiu Y, Yun K, Cox JS, Chawla A. Circadian gene Bmal1 regulates diurnal oscillations of Ly6C(hi) inflammatory monocytes. Science 341: 1483–1488, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Nowell MA, Richards PJ, Horiuchi S, Yamamoto N, Rose-John S, Topley N, Williams AS, Jones SA. Soluble IL-6 receptor governs IL-6 activity in experimental arthritis: blockade of arthritis severity by soluble glycoprotein 130. J Immunol 171: 3202–3209, 2003. [DOI] [PubMed] [Google Scholar]
- 92.Nowell MA, Williams AS, Carty SA, Scheller J, Hayes AJ, Jones GW, Richards PJ, Slinn S, Ernst M, Jenkins BJ, Topley N, Rose-John S, Jones SA. Therapeutic targeting of IL-6 trans signaling counteracts STAT3 control of experimental inflammatory arthritis. J Immunol 182: 613–622, 2009. [DOI] [PubMed] [Google Scholar]
- 93.Ozaki K, Leonard WJ. Cytokine and cytokine receptor pleiotropy and redundancy. J Biol Chem 277: 29355–29358, 2002. [DOI] [PubMed] [Google Scholar]
- 94.Papaikonomou E. Rat adrenocortical dynamics. J Physiol 265: 119–131, 1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Patberg WR, Rasker JJ. Weather effects in rheumatoid arthritis: from controversy to consensus. A review. J Rheumatol 31: 1327–1334, 2004. [PubMed] [Google Scholar]
- 96.Perez-Aso M, Feig JL, Mediero A, Cronstein BN. Adenosine A2A receptor and TNF-alpha regulate the circadian machinery of the human monocytic THP-1 cells. Inflammation 36: 152–162, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Persson R, Garde AH, Hansen AM, Osterberg K, Larsson B, Orbaek P, Karlson B. Seasonal variation in human salivary cortisol concentration. Chronobiol Int 25: 923–937, 2008. [DOI] [PubMed] [Google Scholar]
- 98.Petrovsky N, McNair P, Harrison LC. Diurnal rhythms of proinflammatory cytokines: regulation by plasma cortisol and therapeutic implications. Cytokine 10: 307–312, 1998. [DOI] [PubMed] [Google Scholar]
- 99.Pidwirny M. Earth-sun relationships and insolation. In: Fundamentals of Physical Geography (2nd Ed.). Okanagan, Canada: University of British Columbia, 2006, http://www.physicalgeography.net/fundamentals/6i.html. [Google Scholar]
- 100.Prendergast BJ, Baillie SR, Dhabhar FS. Gonadal hormone-dependent and - independent regulation of immune function by photoperiod in Siberian hamsters. Am J Physiol Regul Integr Comp Physiol 294: R384–R392, 2008. [DOI] [PubMed] [Google Scholar]
- 101.Prendergast BJ, Kampf-Lassin A, Yee JR, Galang J, McMaster N, Kay LM. Winter day lengths enhance T lymphocyte phenotypes, inhibit cytokine responses, and attenuate behavioral symptoms of infection in laboratory rats. Brain Behav Immun 21: 1096–1108, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Pyter LM, Samuelsson AR, Quan N, Nelson RJ. Photoperiod alters hypothalamic cytokine gene expression and sickness responses following immune challenge in female Siberian hamsters (Phodopus sungorus). Neuroscience 131: 779–784, 2005. [DOI] [PubMed] [Google Scholar]
- 103.Ramakrishnan R, DuBois DC, Almon RR, Pyszczynski NA, Jusko WJ. Fifth-generation model for corticosteroid pharmacodynamics: application to steady-state receptor downregulation and enzyme induction patterns during seven-day continuous infusion of methylprednisolone in rats. J Pharmacokinet Pharmacodyn 29: 1–24, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Reppert SM, Weaver DR. Coordination of circadian timing in mammals. Nature 418: 935–941, 2002. [DOI] [PubMed] [Google Scholar]
- 105.Reynolds A, Bard Ermentrout G, Clermont G. A mathematical model of pulmonary gas exchange under inflammatory stress. J Theor Biol 264: 161–173, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Reynolds A, Rubin J, Clermont G, Day J, Vodovotz Y, Bard Ermentrout G. A reduced mathematical model of the acute inflammatory response: I. Derivation of model and analysis of anti-inflammation. J Theor Biol 242: 220–236, 2006. [DOI] [PubMed] [Google Scholar]
- 107.Robak T, Gladalska A, Stepien H, Robak E. Serum levels of interleukin-6 type cytokines and soluble interleukin-6 receptor in patients with rheumatoid arthritis. Mediators Inflamm 7: 347–353, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Rocco MB, Barry J, Campbell S, Nabel E, Cook EF, Goldman L, Selwyn AP. Circadian variation of transient myocardial ischemia in patients with coronary artery disease. Circulation 75: 395–400, 1987. [DOI] [PubMed] [Google Scholar]
- 109.Rohling J, Wolters L, Meijer JH. Simulation of day-length encoding in the SCN: from single-cell to tissue-level organization. J Biol Rhythms 21: 301–313, 2006. [DOI] [PubMed] [Google Scholar]
- 110.Salah B, Dinh Xuan AT, Fouilladieu JL, Lockhart A, Regnard J. Nasal mucociliary transport in healthy subjects is slower when breathing dry air. Eur Respir J 1: 852–855, 1988. [PubMed] [Google Scholar]
- 111.Salman H, Bergman M, Bessler H, Alexandrova S, Beilin B, Djaldetti M. Hypothermia affects the phagocytic activity of rat peritoneal macrophages. Acta Physiol Scand 168: 431–436, 2000. [DOI] [PubMed] [Google Scholar]
- 112.Sanjabi S, Zenewicz LA, Kamanaka M, Flavell RA. Anti-inflammatory and proinflammatory roles of TGF-beta, IL-10, and IL-22 in immunity and autoimmunity. Curr Opin Pharmacol 9: 447–453, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Sapolsky RM, Romero LM, Munck AU. How do glucocorticoids influence stress responses? Integrating permissive, suppressive, stimulatory, and preparative actions. Endocr Rev 21: 55–89, 2000. [DOI] [PubMed] [Google Scholar]
- 114.Schaap J, Albus H, VanderLeest HT, Eilers PH, Detari L, Meijer JH. Heterogeneity of rhythmic suprachiasmatic nucleus neurons: Implications for circadian waveform and photoperiodic encoding. Proc Natl Acad Sci USA 100: 15994–15999, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Scheff JD, Calvano SE, Lowry SF, Androulakis IP. Modeling the influence of circadian rhythms on the acute inflammatory response. J Theor Biol 264: 1068–1076, 2010. [DOI] [PubMed] [Google Scholar]
- 116.Scheff JD, Calvano SE, Lowry SF, Androulakis IP. Transcriptional implications of ultradian glucocorticoid secretion in homeostasis and in the acute stress response. Physiol Genomics 44: 121–129, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Scheff JD, Mavroudis PD, Calvano SE, Lowry SF, Androulakis IP. Modeling autonomic regulation of cardiac function and heart rate variability in human endotoxemia. Physiol Genomics 43: 951–964, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Scheller J, Chalaris A, Schmidt-Arras D, Rose-John S. The pro- and anti-inflammatory properties of the cytokine interleukin-6. Biochim Biophys Acta 1813: 878–888, 2011. [DOI] [PubMed] [Google Scholar]
- 119.Scheller J, Grötzinger J, Rose-John S. Updating interleukin-6 classic- and transsignaling. Signal Transduction 6: 240–259, 2006. [Google Scholar]
- 120.Schlesinger N, Schlesinger M. Seasonal variation of rheumatic diseases. Discov Med 5: 64–69, 2005. [PubMed] [Google Scholar]
- 121.Sharma A, Jusko WJ. Characteristics of indirect pharmacodynamic models and applications to clinical drug responses. Br J Clin Pharmacol 45: 229–239, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Shearman LP, Sriram S, Weaver DR, Maywood ES, Chaves I, Zheng B, Kume K, Lee CC, van der Horst GT, Hastings MH, Reppert SM. Interacting molecular loops in the mammalian circadian clock. Science 288: 1013–1019, 2000. [DOI] [PubMed] [Google Scholar]
- 123.Shin HJ, Lee H, Park JD, Hyun HC, Sohn HO, Lee DW, Kim YS. Kinetics of binding of LPS to recombinant CD14, TLR4, and MD-2 proteins. Mol Cells 24: 119–124, 2007. [PubMed] [Google Scholar]
- 124.Silver AC, Arjona A, Walker WE, Fikrig E. The circadian clock controls toll-like receptor 9-mediated innate and adaptive immunity. Immunity 36: 251–261, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Sinclair JA, Lochmiller RL. The winter immunoenhancement hypothesis: associations among immunity, density, and survival in prairie vole (Microtus ochrogaster) populations. Can J Zoology 78: 254–264, 2000. [Google Scholar]
- 126.Skene DJ, Lockley SW, James K, Arendt J. Correlation between urinary cortisol and 6-sulphatoxymelatonin rhythms in field studies of blind subjects. Clin Endocrinol (Oxf) 50: 715–719, 1999. [DOI] [PubMed] [Google Scholar]
- 127.Smolen P, Baxter DA, Byrne JH. A reduced model clarifies the role of feedback loops and time delays in the Drosophila circadian oscillator. Biophys J 83: 2349–2359, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.So AY, Bernal TU, Pillsbury ML, Yamamoto KR, Feldman BJ. Glucocorticoid regulation of the circadian clock modulates glucose homeostasis. Proc Natl Acad Sci USA 106: 17582–17587, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Sorrells SF, Sapolsky RM. An inflammatory review of glucocorticoid actions in the CNS. Brain Behav Immun 21: 259–272, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Spengler ML, Kuropatwinski KK, Comas M, Gasparian AV, Fedtsova N, Gleiberman AS, Gitlin II, Artemicheva NM, Deluca KA, Gudkov AV, Antoch MP. Core circadian protein CLOCK is a positive regulator of NF-kappa-mediated transcription. Proc Natl Acad Sci USA 109: E2457–2465, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Sriram K, Bernot G, Képès F. Discrete delay model for the mammalian circadian clock. Complexus 3: 185–199, 2006. [Google Scholar]
- 132.Stevenson TJ, Onishi KG, Bradley SP, Prendergast BJ. Cell-autonomous iodothyronine deiodinase expression mediates seasonal plasticity in immune function. Brain Behav Immun 36: 61–70, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Stevenson TJ, Prendergast BJ. Photoperiodic time measurement and seasonal immunological plasticity. Front Neuroendocrinol 37: 76–88, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Su B, Zhou W, Dorman KS, Jones DE. Mathematical modelling of immune response in tissues. Comput Math Methods Med 10: 9–38, 2009. [Google Scholar]
- 135.Surovtsova I, Sahle S, Pahle J, Kummer U. Approaches to complexity reduction in a systems biology research environment (SYCAMORE). In: Proceedings of the 2006 Winter Simulation Conference. Monterey, CA: WSC, 2006, p. 1683–1689. [Google Scholar]
- 136.Surovtsova I, Simus N, Hubner K, Sahle S, Kummer U. Simplification of biochemical models: a general approach based on the analysis of the impact of individual species and reactions on the systems dynamics. BMC Syst Biol 6: 14, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Teboul M, Barrat-Petit MA, Li XM, Claustrat B, Formento JL, Delaunay F, Levi F, Milano G. Atypical patterns of circadian clock gene expression in human peripheral blood mononuclear cells. J Mol Med (Berl) 83: 693–699, 2005. [DOI] [PubMed] [Google Scholar]
- 138.Thakar J, Poss M, Albert R, Long GH, Zhang R. Dynamic models of immune responses: what is the ideal level of detail? Theor Biol Med Model 7: 35, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Turnbull AV, Rivier CL. Regulation of the hypothalamic-pituitary-adrenal axis by cytokines: actions and mechanisms of action. Physiol Rev 79: 1–71, 1999. [DOI] [PubMed] [Google Scholar]
- 140.Tyson JJ, Chen KC, Novak B. Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr Opin Cell Biol 15: 221–231, 2003. [DOI] [PubMed] [Google Scholar]
- 141.Uson J, Balsa A, Pascual-Salcedo D, Cabezas JA, Gonzalez-Tarrio JM, Martin-Mola E, Fontan G. Soluble interleukin 6 (IL-6) receptor and IL-6 levels in serum and synovial fluid of patients with different arthropathies. J Rheumatol 24: 2069–2075, 1997. [PubMed] [Google Scholar]
- 142.VanderLeest HT, Houben T, Michel S, Deboer T, Albus H, Vansteensel MJ, Block GD, Meijer JH. Seasonal encoding by the circadian pacemaker of the SCN. Curr Biol 17: 468–473, 2007. [DOI] [PubMed] [Google Scholar]
- 143.Vedder H, Schreiber W, Yassouridis A, Gudewill S, Galanos C, Pollmacher T. Dose-dependence of bacterial lipopolysaccharide (LPS) effects on peak response and time course of the immune-endocrine host response in humans. Inflamm Res 48: 67–74, 1999. [DOI] [PubMed] [Google Scholar]
- 144.Visintin A, Mazzoni A, Spitzer JH, Wyllie DH, Dower SK, Segal DM. Regulation of Toll-like receptors in human monocytes and dendritic cells. J Immunol 166: 249–255, 2001. [DOI] [PubMed] [Google Scholar]
- 145.Vondrasova D, Hajek I, Illnerova H. Exposure to long summer days affects the human melatonin and cortisol rhythms. Brain Res 759: 166–170, 1997. [DOI] [PubMed] [Google Scholar]
- 146.Walker BR, Best R, Noon JP, Watt GC, Webb DJ. Seasonal variation in glucocorticoid activity in healthy men. J Clin Endocrinol Metab 82: 4015–4019, 1997. [DOI] [PubMed] [Google Scholar]
- 147.Walker JJ, Terry JR, Lightman SL. Origin of ultradian pulsatility in the hypothalamic-pituitary-adrenal axis. Proc Biol Sci 277: 1627–1633, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Warren EJ, Allen CN, Brown RL, Robinson DW. Intrinsic light responses of retinal ganglion cells projecting to the circadian system. Eur J Neurosci 17: 1727–1735, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Wen JC, Dhabhar FS, Prendergast BJ. Pineal-dependent and -independent effects of photoperiod on immune function in Siberian hamsters (Phodopus sungorus). Horm Behav 51: 31–39, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Williams R, Timmis J, Qwarnstrom E. Computational models of the NF-KB signalling pathway. Computation 2: 131, 2014. [Google Scholar]
- 151.Wu MX, Zhou LM, Zhao LD, Zhao ZJ, Zheng WH, Liu JS. Seasonal variation in body mass, body temperature and thermogenesis in the Hwamei, Garrulax canorus. Comp Biochem Physiol A Mol Integr Physiol 179: 113–119, 2015. [DOI] [PubMed] [Google Scholar]
- 152.Yazmalar L, Ediz L, Alpayci M, Hiz O, Toprak M, Tekeoglu I. Seasonal disease activity and serum vitamin D levels in rheumatoid arthritis, ankylosing spondylitis and osteoarthritis. Afr Health Sci 13: 47–55, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Yde P, Mengel B, Jensen MH, Krishna S, Trusina A. Modeling the NF-kappaB mediated inflammatory response predicts cytokine waves in tissue. BMC Syst Biol 5: 115, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Yellon SM, Tran LT. Photoperiod, reproduction, and immunity in select strains of inbred mice. J Biol Rhythms 17: 65–75, 2002. [DOI] [PubMed] [Google Scholar]
- 155.Yoshida K, Hashiramoto A, Okano T, Yamane T, Shibanuma N, Shiozawa S. TNF2547-alpha modulates expression of the circadian clock gene Per2 in rheumatoid synovial cells. Scand J Rheumatol 42: 276–280, 2013. [DOI] [PubMed] [Google Scholar]
- 156.Yuan XG, Xie C, Chen J, Xie Y, Zhang KH, Lu NH. Seasonal changes in gastric mucosal factors associated with peptic ulcer bleeding. Exp Ther Med 9: 125–130, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Zanoni I, Ostuni R, Marek LR, Barresi S, Barbalat R, Barton GM, Granucci F, Kagan JC. CD14 controls the LPS-induced endocytosis of Toll-like receptor 4. Cell 147: 868–880, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Zhang Q, Bhattacharya S, Andersen ME. Ultrasensitive response motifs: basic amplifiers in molecular signalling networks. Open Biol 3: 130031, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 159.Zumoff B, Fukushima DK, Hellman L. Intercomparison of four methods for measuring cortisol production. J Clin Endocrinol Metab 38: 169–175, 1974. [DOI] [PubMed] [Google Scholar]
- 160.Zwietering MH, Jongenburger I, Rombouts FM, van 't Riet K. Modeling of the bacterial growth curve. Appl Environ Microbiol 56: 1875–1881, 1990. [DOI] [PMC free article] [PubMed] [Google Scholar]