Finite-Element Modelling of the Acoustic Input Admittance of the Newborn Ear Canal and Middle Ear

Abstract

Admittance measurement is a promising tool for evaluating the status of the middle ear in newborns. However, the newborn ear is anatomically very different from the adult one, and the acoustic input admittance is different than in adults. To aid in understanding the differences, a finite-element model of the newborn ear canal and middle ear was developed and its behaviour was studied for frequencies up to 2000 Hz. Material properties were taken from previous measurements and estimates. The simulation results were within the range of clinical admittance measurements made in newborns. Sensitivity analyses of the material properties show that in the canal model, the maximum admittance and the frequency at which that maximum admittance occurs are affected mainly by the stiffness parameter; in the middle-ear model, the damping is as important as the stiffness in influencing the maximum admittance magnitude but its effect on the corresponding frequency is negligible. Scaling up the geometries increases the admittance magnitude and shifts the resonances to lower frequencies. The results suggest that admittance measurements can provide more information about the condition of the middle ear when made at multiple frequencies around its resonance.

INTRODUCTION

Hearing loss is one of the most common birth defects—about 3 in 1000 babies are born with some degree of hearing impairment (Kemper and Downs 2000; Harlor and Bower 2009). Early detection of hearing loss accompanied by appropriate early intervention is important in order to avoid problems associated with language development that affect daily communication, educational achievement, psychosocial development and later employment opportunities (e.g. Joint Committee on Infant Hearing 1994 Position Statement; American Academy of Pediatrics 2007). Hearing loss is either conductive, involving the outer and/or middle ear; or sensorineural, involving the inner ear, auditory nerve and/or brain; or mixed, with both conductive and sensorineural components. Most permanent newborn hearing loss is sensorineural (Marazita et al. 1993) but its detection and diagnosis are often affected by transient conductive losses (e.g. Chang et al. 1993; Couto and Carvallo 2009; Akinpelu et al. 2014).

Currently, otoacoustic emission (OAE) and/or auditory brainstem response (ABR) tests are employed as screening tools in newborn hearing screening programs. High false positive rates of screening tests are an important concern with universal newborn hearing screening (e.g. Nelson et al. 2008). Many false positives can be attributed to transient conditions in the external ear (e.g. collapse of the ear canal and the presence of debris) and middle ear (e.g. presence of amniotic fluid and mesenchyme) in the first 48 h postpartum, which conflicts with the desire for shorter hospital stays. It would thus be very valuable to be able to quickly assess the status of the outer and middle ear as part of the initial screening procedure, just after birth, and tympanometry is a promising tool for that purpose. In tympanometry, the acoustical input immittance of the outer and middle ear is measured in response to a probe tone, in the presence of a range of quasi-static air pressures in the ear canal. Immittance refers to either admittance Y, which is volume velocity divided by sound pressure, or impedance Z, the reciprocal of admittance. Both admittance and impedance are complex numbers, the former being composed of a real part G, conductance, and an imaginary part B, susceptance, and the latter being composed of a real part R, resistance, and an imaginary part X, reactance. Measurements of the separate real and imaginary parts (or, equivalently, of the magnitude and phase) contain more information about the middle ear than just the magnitude alone, but much remains to be understood about what they mean and how to interpret them.

Tympanometry is most often done with a 226-Hz probe tone. This frequency provides easy-to-interpret results for adult ears, but the results in newborns are very different from those in adults. The differences may be attributed to anatomical and physiological differences occurring during maturation (Saunders et al. 1983 pp.4–10; Eby and Nadol 1986; Qi et al. 2006, 2008). For example the newborn ear-canal wall is not ossified and is surrounded along most of its length by soft tissue (e.g. Standring 2008, chap. 36). This causes the newborn canal to be very compliant. In adults, only the most lateral third of the canal wall is composed of soft tissue, while the medial two thirds of the canal is encompassed by temporal bone (e.g. Anson and Donaldson 1992, p. 146). In addition, the orientation, shape and ultrastructure of the tympanic membrane (Ruah et al. 1991) and ear canal (e.g. Saunders et al. 1983, p. 4) undergo dramatic changes during growth, especially in the first months after birth. It has been known for some time that a 1-kHz tone provides better differentiation between normal- and liquid-filled newborn middle ears, but the differentiation is still far from perfect (e.g. Shahnaz et al. 2008). Furthermore, the fact that the main middle-ear resonance in newborns and infants is in the vicinity of 1.8 kHz (Keefe et al. 1993) suggests that the measurements may be quite sensitive to what frequency is used and where the resonance is in a given ear. More information can be obtained by using multiple frequencies (e.g. Alberti and Jerger 1974; Colletti 1975; Funasaka et al. 1984; Keefe and Levi 1996; Shahnaz et al. 2008). A number of groups have evaluated wideband measurements of immittance in newborns and infants, whether unpressurized (e.g. Keefe et al. 1993) or pressurized (e.g. Holte et al. 1991; Sanford and Feeney 2008).

In addition to immittance, it is also possible to characterize the ear in terms of energy reflectance (ER), the ratio of the reflected energy to the incoming energy, or absorbance (EA), equal to 1−ER. It has been assumed, at least for adults, that the ER measured in the ear canal represents the condition at the tympanic membrane (TM), independent of the location of the probe tip, based on the following approximations: (1) the energy loss of the sound wave in the enclosed air in the canal is negligible (e.g. Voss et al. 2008); (2) the ear canal acts like a transmission line with a smoothly varying cross-sectional area (i.e. no significant energy is reflected from abrupt changes in the canal cross section); and (3) the energy loss at the canal wall is negligible (e.g. Voss and Allen 1994). The first two assumptions are reasonable for both adults and newborns (e.g. Eby and Nadol 1986). The third assumption, however, is probably not valid for newborns and infants because, as stated above, the canal wall is composed of soft tissue, so sound energy is absorbed within it (e.g. Keefe and Levi 1996). Merchant et al. (2010) conducted a series of wideband energy measurements to define the normative energy response of the ear of newborns and infants.

The middle ear is a complex 3-D mechano-acoustical system containing many interconnected, highly irregular, asymmetrical and nonuniform components. There are many parameters that affect clinical measurements, and the contribution of each parameter to the output is difficult to identify (e.g. Sanford and Feeney 2008). The finite-element method can be utilized to provide a quantitative understanding of such a system. In this method, a complicated system is divided into a large number of relatively simple elements. A finite-element model is defined in terms of anatomical and biomechanical parameters that have very direct relationships to the structure and properties of the system (e.g. Funnell et al. 2013).

Funnell and Laszlo (1978) introduced the finite-element method to middle-ear modelling. Since then, this method has been widely used to investigate different aspects of both human and animal ears (e.g. Wada et al. 1992; Ladak and Funnell 1996; Koike et al. 2002; Gan et al. 2004; Motallebzadeh et al. 2013a). Qi et al. (2006, 2008) developed nonlinear finite-element models of the newborn ear canal and middle ear. They reported the displacements predicted by these models for static pressures in the range of those induced during tympanometry and calculated the ear-canal and middle-ear compliances.

In this study, we have developed linear finite-element models of the newborn ear canal and middle ear and analysed their responses to sound for frequencies up to 2000 Hz (preliminary versions of this model were described by Gariepy (2010) and Motallebzadeh et al. (2013b)). We set the upper limit of the frequency range to 2000 Hz because at higher frequencies, the input immittance is influenced by the spatial variation of sound pressure along the canal and the associated standing waves (e.g. Shanks and Lilly 1981; Stinson et al. 1982), so it becomes more sensitive to the position of the probe tip inside the ear canal (Keefe et al. 1993; Voss and Allen 1994). In addition, in this frequency range, the wavelength of sound is considerably greater than the dimensions of the ear components: in the newborn ear, for an average effective ear-canal length of 14 mm and a probe tip insertion depth of 5 mm (Keefe et al. 1993), the net length (the length of the canal that is exposed to the sound pressure) is 9 mm, which is only 5 % as long as the 171-mm wavelength of a 2 kHz sound in air. Stinson and Lawton (1989) used modified horn equations to take into account the effects of the cross-sectional area. They found that for adult canals, at frequencies below 1 kHz, since the wavelength of the acoustic waves are much larger than the canal dimensions, the longitudinal position and not the area variation affects the acoustic-pressure distribution along the canal. Farmer-Fedor and Rabbitt (2002) showed that for adult ear canals of 25 mm length, the pressure is distributed rather uniformly below 2 kHz. In addition, Ravicz et al. (2014) reported that the magnitude and phase of the acoustic pressure are approximately constant over the entire accessible TM surface, with a diameter of ∼10 mm, at frequencies below 6 kHz. Furthermore, Stinson and Daigle (2005) showed that the compliance of the boundary conditions (in adults, the TM) does not affect the pressure distribution at frequencies below 2 kHz. Gan et al. (2004, 2006) also showed that, in their finite-element models of the adult canal, at frequencies below 1 kHz, the pressure is almost uniform along the canal length. The dimensions in newborns are smaller than those in adults (cf. canal length of 15 mm in our newborn model compared with 25–35 mm in adults). In addition, the central axis of the canal is straighter in newborns than in adults (e.g. Eby and Nadol 1986) so less wall reflection is produced. The sound pressure along the canal and across the TM surfaces is therefore approximated here as being uniform in newborns for frequencies below 2 kHz. A second assumption that has been made in this work is that the border of the TM is clamped. This assumption has been used frequently in previous human middle-ear models (e.g. Rabbitt 1988; Gea et al. 2010; Aernouts et al. 2012). Based on these two assumptions, and the fact that the border of the TM is the only place where the canal and middle-ear models interact, the ear canal and middle ear can be modelled separately: they are exposed to the same sound pressure; the displacements of the canal wall in response to a given sound pressure are not affected by considering the TM to be rigid; and the displacements of the TM are not affected by considering the canal wall to be rigid. Thus, in this study, the admittances of the ear-canal wall and the middle ear were treated as parallel elements, which were previously also done by Keefe et al. (1993) for low frequencies. This permits us to compute the input admittances of the canal and middle ear separately and then combine them to give the overall admittance of the ear, similar to what is done when the canal and middle ear are treated as lumped acoustical elements (e.g. Shanks and Lilly 1981; Keefe et al. 1993). This approach, as discussed in the “Air in Middle-Ear Cavity and Ear Canal” and “Admittance Calculation” sections, makes it possible to investigate the individual contributions of the outer ear and middle ear to the overall response. The results are validated against previously reported clinical data. In addition, the effects of material property parameters are explored.

MATERIALS AND METHODS

3-D Geometry and Finite-Element Mesh

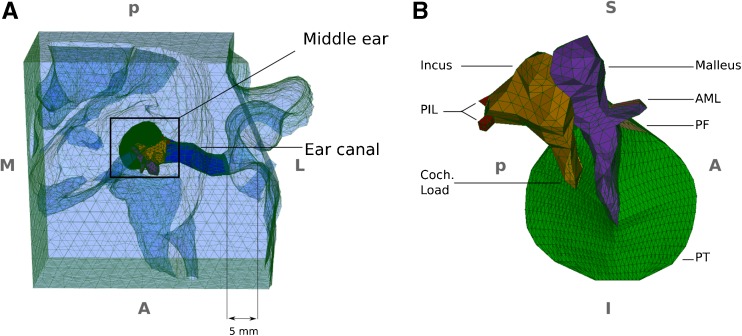
The 3-D geometries of the ear canal and middle ear are revised and refined versions of those of Qi et al. (2006, 2008). The geometries are based on a clinical X-ray CT scan (GE LightSpeed16, Montréal Children’s Hospital) of a 22-day-old newborn’s right ear. The scan had a pixel size of 0.187 mm and a slice thickness of 0.625 mm with a 0.125-mm overlap, resulting in a slice spacing of 0.5 mm. Three locally developed programs, Fie, Tr3 and Fad (http://www.audilab.bme.mcgill.ca/sw/), were used to generate a surface model. Gmsh (http://www.geuz.org/gmsh/) was then used to generate 3-D solid models with tetrahedral elements for each individual component of the ear-canal and middle-ear models. The solid models were then assembled in Fad (Fig. 1).

FIG. 1.

Meshed geometry of the finite-element model. A Superior-to-inferior view of the overall model including the ear canal, surrounding soft tissue and middle ear. The 5-mm distance indicates the estimated insertion depth of the probe tip into the canal in the clinical measurements. B Expanded medial-to-lateral view of the middle-ear model, with the TM annulus almost parallel to the page. PIL posterior incudal ligament, AML anterior mallear ligament, PT pars tensa, PF pars flaccida, S superior, I inferior, M medial, L lateral, A anterior, P posterior.

The canal model consists of the soft tissue surrounding the lumen of the ear canal. The interiors of bony structures in the region have not been included in the ear-canal model, but their surfaces are included and are considered as rigid boundary conditions for the model. In newborns, the connection between the superior wall of the canal and the TM forms a more obtuse angle than in adults (e.g. Eby and Nadol 1986). In our model, the tangential lines on the canal wall and the TM surface, at the most superior part of the TM, form an angle of ∼150 °, consistent with the report of Ikui et al. (1997). The diameter of the TM is ∼8 mm and the superior and inferior lengths of the canal (i.e. from the lateral opening of the canal to the superior and inferior boundaries of the TM) were ∼10 and 17 mm, respectively. The cross section of the canal is approximately elliptical and its major and minor diameters in the lateral portion are ∼4 and 3.6 mm, respectively. A probe tip is represented in the model by a small block located 5 mm inside the ear-canal entrance (Fig. 1, and also Qi et al. 2006, Fig. 2), based on the estimate of the clinical situation by Keefe et al. (1993, Table 1) and on our estimate of the situation for our own clinical data (see the “Clinical Data” section). The probe tip in the model was tightly connected with the surrounding tissue in order to simulate a hermetic seal.

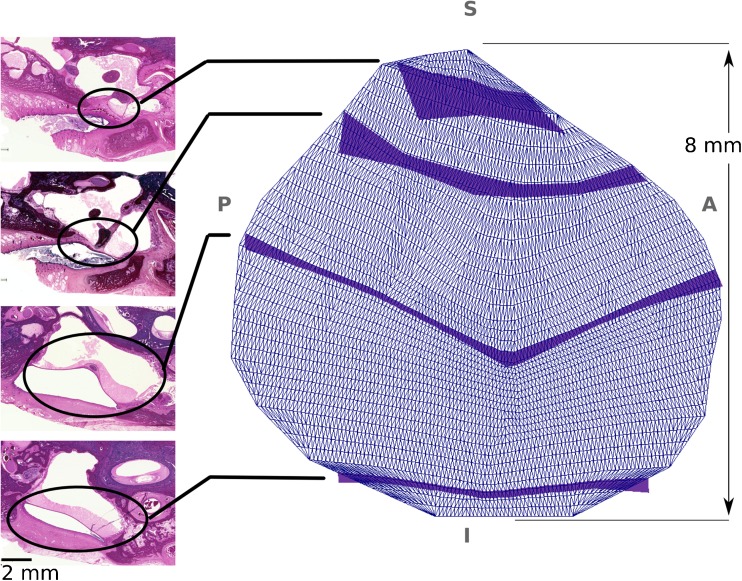
FIG. 2.

Lateral-to-medial view of the thickness map of the TM, with its annulus almost parallel to the page. On the left are four 20-μm-thick serial histological sections from a 3-week-old infant from which the thicknesses of the TM were derived for the finite-element model shown on the right. The positions of the TM in the histological images are indicated by ellipses, with lines connecting them to dark blue bands whose widths indicate the derived cross-sectional thicknesses of the TM model. The anatomical abbreviations are same as those of Figure 1. The cutting plane in the histological images are not in the thickness direction, but are oblique. The actual thickness of the TM was measured in the reconstructed geometry, perpendicular to the TM surface at multiple points.

TABLE 1.

Material properties

	Minimum	Baseline	Maximum
Young’s modulus (MPa)
Pars tensa (E pt)	2	6	10
Pars flaccida (E pf)	0.4	1.2	2
Soft tissue around canal (E st)	0.02	0.21	0.4
Ossicles (E os)	4000	10,000	16,000
Ligaments (E lig)	2	5	8
Poisson’s ratio
Soft tissues (around canal and in middle ear) (ν st)	0.485	0.49	0.495
Ossicles (ν os)	0.3
Density (kg/m3)
Soft tissues (ρ st)	1000	1100	1200
Ossicles (ρ os)	1600	1800	2000
Damping ratio (ζ)	0.1	0.25	0.4
Cochlear load
Spring (N/m) (K c)	200	600	1000
Dashpot (Ns/m) (C c)	0.2	0.45	0.7
Stapes mass (kg) (M s)	2 × 10−6	3 × 10−6	4 × 10−6
Cavity volume (m3) (V cav)	700 × 10−9	850 × 10−9	1000 × 10−9

The middle-ear model consists of the tympanic membrane (TM), the malleus and incus, the anterior mallear ligament (AML) and the two bundles of the posterior incudal ligament (PIL). The volumes of the malleus and incus models are 19 and 18 mm³, respectively. For a density of 1800 kg/m³ (the baseline density adopted for the ossicles in this study), their masses are 34.2 and 32.4 mg, respectively, which are within or slightly higher than the ranges of 17–28 (malleus) and 18–33 (incus) reported for dry ossicles (e.g. Wever and Lawrence 1954; Harneja and Chaturvedi 1973). The incudomallear joint is assumed to be fused, so there is no relative motion between the malleus and the incus. Andersen et al. (1962), Willi et al. (2002) and Decraemer and Khanna (2004) reported that sound transmission in the middle ear is rather insensitive to the fixation of the incudomallear joint, at least up to 2 kHz. This simplification was also used in the newborn middle-ear model of Qi et al. (2008) and in the adult human model of Eiber (1999).

The thickness of the TM was measured from a set of 26 20-μm-thick serial histological sections from a 3-week-old newborn. It is difficult to create a good ear model from the histological images because of misalignments and distortions, but we have reconstructed a rough model to compare the geometrical characteristics of the two ears. The orientations of the middle-ear components in the two models were similar. The CT-based model is about 10 % larger than the histology-based one. For example the TM diameters in the two models (in the anterior-posterior direction at the umbo) were 8.4 and 7.8 mm, respectively; the distances between the umbo and the end of the incudal long process were 2.8 and 2.5 mm; and the manubrium lengths were 4.6 and 4.2 mm. In our CT scan, there were 11 slices containing the TM, and 11 approximately corresponding histology images were selected. Fortunately, the histology images and the CT images had similar orientations, so the thicknesses that we measured on the histology images, at different locations on the TM, could be directly applied to the CT images in our segmentation software. These apparent thicknesses were measured at several points in each histological image using the Measure Tool in GIMP, a free (libre) and open-source image manipulation programme (http://www.gimp.org), and then a piecewise cubic Hermite interpolation algorithm (MATLAB, Release 2012b, The MathWorks, Inc., Natick, MA, USA) was used to determine a thickness distribution over the cross section of the TM surface at each slice. The thicknesses were applied manually in the segmentation software (Fie) to generate the 3-D geometry of the TM. Four of the 11 histological images, and corresponding cross-sectional thicknesses normal to the reconstructed 3-D TM surface, are presented in Figure 2. The measured thickness of the posterior-superior quadrant varies between 0.15 and 0.6 mm and that of the other three quadrants varies between 0.07 and 0.4 mm (the higher value in each quadrant corresponding to the TM annulus). The pars-flaccida thickness (0.5–2 mm) is significantly greater than that of the pars tensa. These thicknesses for the TM are consistent with the findings of Ruah et al. (1991).

Material Properties

Introduction

The probe tone in tympanometry typically has an amplitude of around 95 dB sound pressure level (SPL) (∼1.1 Pa) or less (e.g. Alberti and Jerger 1974), and tones of this amplitude cause deformations that are not large enough to push the system into its nonlinear range (e.g. Khanna and Tonndorf 1972). In fact, according to Rubinstein et al. (1966), the linearity of the response persists at least up to 104 dB SPL. Thus, in this study, all materials are assumed to be linearly elastic.

Since precise values for the material properties of newborn ear-canal and middle-ear components are not available, ranges of plausible values are used. For each material property, upper and lower limits were defined based on structural similarities between different tissues (e.g. skin and the pars flaccida) and/or on reported values for the adult ear. Each baseline material property is approximately the arithmetic mean of the upper and lower limits for that property. Thus, three models are each generated for the ear canal and the middle ear: (a) a low-impedance model (i.e. a model with the lowest stiffness, density and damping values for all components), (b) a baseline model (i.e. a model with baseline parameter values) and (c) a high-impedance model (i.e. a model with the highest stiffness, density and damping values for all components). Taking all possible combinations of the ear-canal and middle-ear models, nine scenarios were considered for the whole-ear response in this study.

Stiffness

Pars Tensa

Volandri et al. (2011) and Maftoon et al. (2015) recently reviewed the Young’s moduli that have been reported for the pars tensa in the literature. A Young’s modulus of 20 MPa has frequently been used for the pars tensa in numerical models (e.g. Funnell and Laszlo 1978; Gan and Sun 2002); Young’s moduli half as large and twice as large (i.e. 10 and 40 MPa) are still within the range of experimental measurements (e.g. Békésy 1949; Kirikae 1960 pp. 46–48; Decraemer et al. 1980; Cheng et al. 2007; Huang et al. 2008; Luo et al. 2009a; Zhang and Gan 2013).

Ruah et al. (1991) reported morphological changes of the TM during postnatal development and investigated the similarity between age-related ultra-structural changes of the TM and changes observed in human skin. Anthwal and Thompson (2016) reported that the maturation process of the lateral layer of the TM is similar to that of the skin and occurs with a similar time course. The age-related changes of human skin have been reported in several studies and have been attributed to the water content of the skin and to the orientation and density of the collagen fibres (e.g. Yamada and Evans 1970, p. 229; Rollhäuser 1950). Rollhäuser (1950) reported that the Young’s modulus for the skin of babies of less than 3 years old is 3–5 times smaller than that of adults. Based on these studies, we used Young’s moduli of 2, 6 and 10 MPa in our models. These values are approximately 3–5 times smaller than the lower, middle and upper values of the reported pars-tensa Young’s moduli mentioned above.

Qi et al. (2008) used Young’s moduli of 0.6, 1.2 and 2.4 MPa in their static model. Considering the report of Luo et al. (2009a, b), which states that the Young’s modulus of the normal TM in dynamic conditions is more than twice that in static ones, our values are consistent with those of Qi et al.

Pars Flaccida

The pars flaccida is considered to be the extension of the skin of the external ear canal (Lim 1970). Based on this observation, Maftoon et al. (2015) used a Young’s modulus of 2 MPa for the gerbil pars flaccida, in the range of the reported Young’s moduli of the human epidermis and stratum corneum (Geerligs et al. 2011). They also used a simplistic model of a circular plate to validate their value by comparing the results with their own experimental data from laser Doppler vibrometry. In this study, we used Young’s moduli of 0.4, 1.2 and 2 MPa for the pars flaccida. The 0.4 MPa value is approximately the Young’s modulus of the skin as reported by Agache et al. (1980), and it is approximately one fifth of the value used by Maftoon et al. (2015), consistent with the change of elastic modulus of the skin during maturation. The upper value was used in the model of Maftoon et al. (2015). The middle value is approximately one third of our baseline value of the pars-tensa Young’s modulus, a pars-flaccida/pars-tensa stiffness ratio that has been used in other modelling studies (e.g. Lesser and Williams 1988; Koike et al. 2002).

Ear Canal

In adults, the ear canal is mainly surrounded by bone, whereas in newborns the canal is surrounded almost entirely by soft tissue (e.g. McLellan and Webb 1950), including elastic cartilage, skin, glandular tissue and fat. Elastic cartilage is the least stiff type of cartilage in the human body (e.g. Kroemer and Kroemer 1997, p. 4). To the best of our knowledge, the stiffness of human elastic cartilage has never been reported in the literature. In this study, therefore, we based our estimate on previously reported Young’s moduli of adult human articular cartilage, adjusted to take maturation effects into account. Young’s moduli of 0.33–5.8 MPa have been reported for different adult human articular cartilages (e.g. Hayes and Mockros 1971). As a collagenous tissue, cartilage undergoes significant alterations from newborn to adult (e.g. Williamson et al. 2001), similar to the skin and pars tensa. Thus, the stiffness of the articular cartilage in newborns can be expected to be less than the values mentioned above by a factor of perhaps 3–5, giving a range of about 0.11–1.9 MPa. The stiffness of the elastic cartilage (the type of cartilage that surrounds the canal) would be expected to be less than these values.

Qi et al. (2006) used Young’s moduli of 30, 60 and 90 kPa for the soft tissue in their static model. In this study, we used Young’s moduli of 20, 210 and 400 kPa for the soft tissue (i.e. the complex of elastic cartilage, skin, glandular tissue and fat). The lowest value is approximately the mean of the Young’s moduli of fat and glandular tissue (Wellman et al. 1999), and the upper value corresponds to the Young’s modulus of skin in young adults (less than 30 years old) as reported by Agache et al. (1980).

Ossicles

Various values for the Young’s modulus of compact bone have been reported in the literature. Fung (1993, p. 511) reported a range of 17.6–18.9 GPa and stated that the mechanical properties of bone vary with age, sex, location in the body, orientation of the load and strain rate. Most recently, Soons et al. (2010) measured Young’s moduli of 16 ± 3 GPa for the rabbit incus and malleus. Qi et al. (2008) used Young’s moduli of 1, 3 and 5 GPa in their model. In this study, Young’s moduli of 4, 10 and 16 GPa were applied to the ossicles, where the lower value corresponds to the lowest Young’s moduli in the literature review of Funnell et al. (1992); the upper value corresponds to the average value in the measurements of Soons et al. (2010), and 10 GPa is the mean of these two values. It turned out that this parameter has very little effect on the behaviour of the model.

Ligaments

In previous adult models, Young’s moduli of 0.65 to 21 MPa have been used for middle-ear ligaments (e.g. Koike et al. 2002; Gan et al. 2004). Maftoon et al. (2015) used the same Young’s moduli for the ligaments as for the pars tensa, based on their structural similarities. Qi et al. (2008) used 1, 3 and 5 MPa in their newborn model. For the ligaments in this study, we applied the Young’s moduli of the pars tensa, namely, 2, 5 and 8 MPa.

It has been reported that at low frequencies (e.g. below 2 kHz), the stapes moves mainly in a “piston-like” or translational manner (e.g. Gundersen and Høgmoen 1976; Hato et al. 2003; Decraemer and Khanna 2004). Thus, although the stapedial annular ligament constrains the stapes motion in three directions, at low frequencies, the effective load is parallel to the translational motion of the stapes. Therefore, for simplicity, in this study, the effect of the stapedial annular ligament was represented by a single translational spring element, at the tip of the long process of the incus (i.e. where the incudostapedial joint would be). Gan et al. (2011, Fig. 6A) reported load-displacement curves for two adult human stapedial annular ligaments. In the linear region of their loading and unloading curves (i.e. for displacements <0.1 mm), we estimated that the stiffness was between 100 and 300 N/m. Cancura (1979) reported a stiffness of 182 N/m, and Lauxmann et al. (2014) reported this stiffness to be 1050 N/m based on load and displacement measurements. They also compared their result to the value of 182 and 940 N/m reported by Cancura (1979) and Waller and Amberg (2002), respectively. More recently, Kwacz et al. (2015) reported a mean value of about 120 N/m, with a range of about 68 to 198 N/m. Based on these values, we used stiffness parameters of 200, 600 and 1000 N/m in this study.

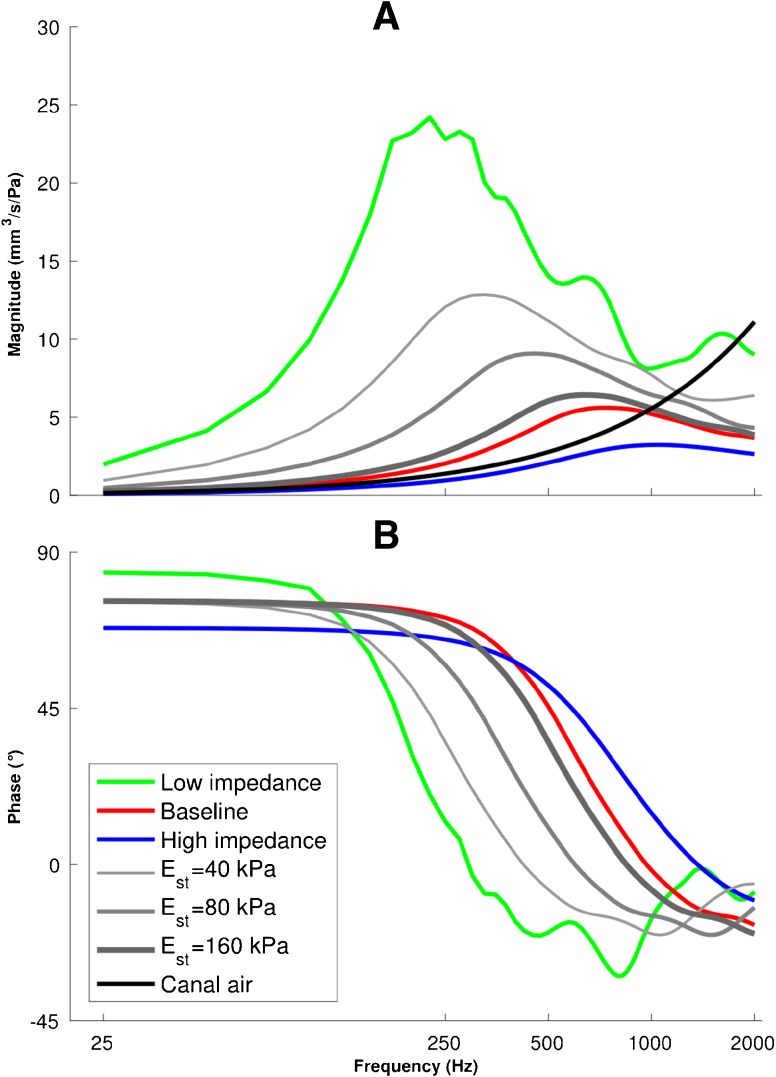
FIG. 6.

Admittance responses of the canal wall Y _wall and the air enclosed in the canal Y _can with a 25-Hz frequency resolution. Admittance magnitudes (A) and phases (B) of Y _wall are presented for low-impedance (green), baseline (red) and high-impedance (blue) parameters and for three intermediate cases (Young’s moduli of 40, 80 and 160 kPa for the canal soft tissue) to illustrate the smooth transition of the admittance response between the low-impedance and baseline models. The admittance magnitude and phase for the air enclosed in the canal Y _can presented as solid black lines; the phase is constant at 90 ° over the entire frequency range.

Poisson’s Ratio

Soft tissues are nearly incompressible, so values close to 0.5 are appropriate for their Poisson’s ratio (e.g. Decraemer and Funnell 2008). In this study, the value of 0.49 was used for the soft tissues to avoid numerical problems arising from full incompressibility. For bones, a Poisson’s ratio of 0.3 was used in this study, which is widely accepted (Cowin 2001, chap. 23.18) and has often been used in numerical models of the middle ear (e.g. Koike et al. 2002).

Density

The density of soft tissue is usually considered to be somewhere between that of water (1000 kg/m³) and that of dry collagen fibres (1200 kg/m³). In this model, densities of 1000, 1100 and 1200 kg/m⁻³ were used for the soft-tissue components. Fung (1993, p. 512) reported bone density as being between 1600 and 1950 kg/m³. Based on this, densities of 1600, 1800 and 2000 kg/m³ were used for the malleus and incus in this model. This is close to the range that Maftoon et al. (2015) used for the malleus, incus and stapes.

Wever and Lawrence (1954, p. 417) reported the mass of the stapes to be in the range of 2.0 to 4.3 mg (mean 2.86). Since our 3-D geometry did not include the stapes, its mass was represented by a discrete mass element of 2, 3 or 4 mg at the same location as the spring representing the stapedial annular ligament (at the tip of the long process of the incus).

Damping

The damping of a mechanical system is more difficult to understand than its mass or stiffness since it deals with internal friction and energy dissipation, processes that are difficult to isolate and measure. Several empirical models have been proposed for describing damping. One of the most common models is Rayleigh damping (e.g. Funnell et al. 1987). In this model, the damping matrix C is generated by

$$C=\alpha M+\beta K\text{,}$$ 1

where M and K are the mass and stiffness matrices, respectively, and α and β are the damping coefficients with units of s⁻¹ and s, respectively. The damping ratio ζ at each angular frequency ω = 2πf is related to the Rayleigh damping coefficients by

$$\zeta =\frac{1}{2}\left(\frac{\alpha }{\omega }+\beta \omega \right)\text{.}$$ 2

This implies that α corresponds to damping ratios that decrease with frequency, while β corresponds to damping ratios that increase with frequency.

Previously, used pairs of tympanic-membrane Rayleigh coefficients (α, β) include (0, 1.0 × 10⁻⁴), (260, 3.7 × 10⁻⁵) and (0, 0.75 × 10⁻⁴) (Volandri et al. 2011). For the frequency range of 50–2000 Hz that we use in our simulations, Eq. 2 gives values of ζ between 0.012 and 0.63 for these values of α and β. Wada et al. (1992) estimated a damping ratio of 0.126 for frequencies less than 3 kHz. Maftoon et al. (2015) assigned stiffness-proportional damping (i.e. α = 0) with β = 2 × 10⁻⁶, 3 × 10⁻⁵ and 2 × 10⁻⁷ s for the soft tissues with highly organized collagen fibres, the soft tissues with abundant elastic fibres and bones, respectively. These values result in damping ratios up to 0.001, 0.012 and 0.188, respectively, for frequencies up to 2 kHz. Keefe et al. (1993) used a quality factor ($Q=\frac{1}{2\zeta }$) of 2 as “typical of quality factors measured in mechanical impedance measurements on the human body”, corresponding to a damping ratio of 0.25. Assuming a damping ratio that is constant over the frequency range of interest and excluding the outliers of the damping ranges mentioned above, in this study, we used damping ratios of 0.1, 0.25 and 0.4. We used Rayleigh damping and calculate α and β at each frequency in order to obtain the desired damping ratio.

Cochlear Load

It has been reported that the cochlea influences the response of the ear mainly by damping, at least for the frequency range of interest here (e.g. Merchant et al. 1996; Aibara et al. 2001; both for human subjects). Since our model does not contain the stapes, we added a discrete dashpot (i.e. viscous damper) element to represent the damping effect, in the direction of stapedial piston-like motion, at the tip of the long process of the incus, where the discrete spring and mass were attached. The viscous damping coefficient (i.e. dashpot parameter) can be calculated by dividing the cochlear input impedance by the square of the footplate area of the stapes. Koike et al. (2002) calculated a coefficient of 0.89 Ns/m for their adult human model, for an impedance of 50 GΩ. For this impedance value, and a stapes footplate surface area of 2.3–3.75 mm² as reported by Wever and Lawrence (1954, p. 417) and Gan et al. (2011), we calculated a dashpot parameter of 0.2–0.7 Ns/m. We have not attempted to correct this for any possible differences between newborns and adults.

Air in Middle-Ear Cavity and Ear Canal

The Eustachian tube connects the middle-ear cavity to the nasopharynx and can be in either an open or a closed state. When the tube is closed (its normal state), a volume of air is trapped in the middle-ear cavity and it has been shown to have a large impact on the input admittance of the middle ear (e.g. Funnell and Laszlo 1982; Stepp and Voss 2005). A few finite-element models take this effect into account (e.g. Gan et al. 2004). According to the geometry reconstructed from our CT images, the volume of the middle-ear cavity was between 700 and 1000 mm³, and that of the air enclosed inside the ear canal, between the probe tip and the TM, was 128 mm³.

The compliance of an enclosed volume of air C _air (under adiabatic conditions) can be calculated by

$$C_{\mathrm{a}\mathrm{i}\mathrm{r}}=\frac{V}{\rho c^2},$$ 3

where V, ρ and c are the volume of the enclosed air (i.e. the volume of either the middle-ear cavity or the ear canal in our model), the density of air and the speed of sound in air, respectively. Neglecting the mass of the air, the enclosed air volumes inside the cavity and the canal were considered to be ideal stiffness elements. Thus, the cavity-air admittance Y _cav and canal air admittance Y _can are purely susceptance (i.e. imaginary) and were calculated at each angular frequency ω by

$$Y_{\mathrm{a}\mathrm{i}\mathrm{r}}=j\omega C_{\mathrm{a}\mathrm{i}\mathrm{r}}.$$ 4

where j = $\sqrt{-1}$.

The middle-ear input admittance Y _me is calculated based on a series combination of the cavity admittance Y _cav and the admittance of the TM, ossicles and cochlea Y _tm (e.g. Stepp and Voss 2005):

$$\frac{1}{Y_{\mathrm{m}\mathrm{e}}}=\frac{1}{Y_{\mathrm{t}\mathrm{m}}}+\frac{1}{Y_{\mathrm{c}\mathrm{a}\mathrm{v}}}.$$ 5

The air in the canal (the volume enclosed inside the undeformed canal) is assumed to act as a lumped admittance element Y _can in parallel with the ear-canal wall Y _wall and the middle ear Y _me (e.g. Keefe et al. 1993, Fig. 12), so the total admittance of the ear Y _ear is

$$Y_{\mathrm{e}\mathrm{a}\mathrm{r}}=Y_{\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}}+Y_{\mathrm{c}\mathrm{a}\mathrm{n}}+Y_{\mathrm{m}\mathrm{e}}.$$ 6

FIG. 12.

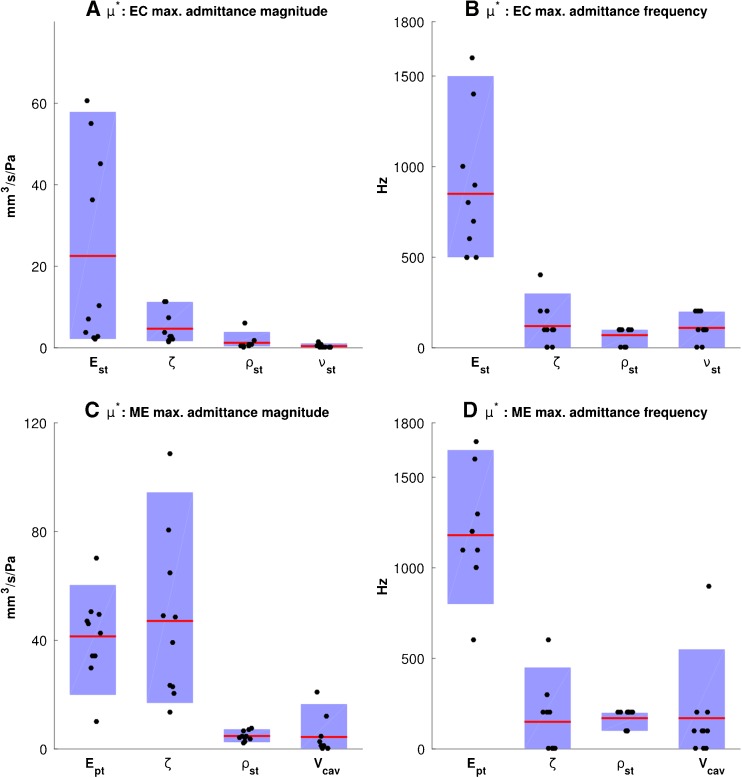
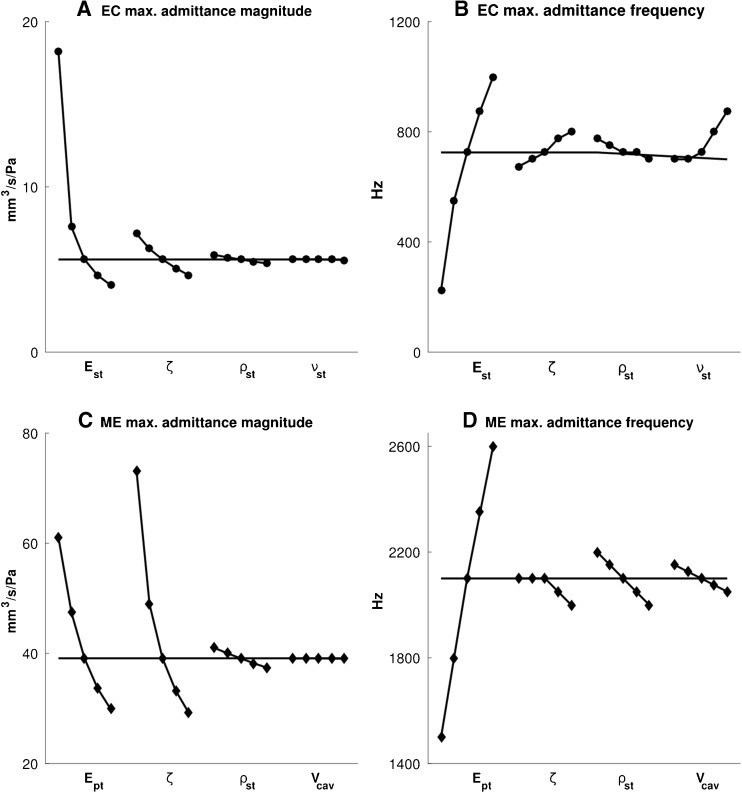
Sensitivity analysis using Morris method, showing the influence of the material parameters on the maximum admittance magnitudes (A, C) and the corresponding frequencies (B, D) for the ear-canal model (A, B) and the middle-ear model (C, D). The blue boxes indicate the 10th-to-90th-percentile ranges; each point represents a |d _i|, the absolute value of the partial difference of the output with respect to the change of each parameter (and not the absolute value of the deviation from the baseline values), and the red lines represent μ _i*, the average of the |d _i|’s. Please see the text for an explanation of how to interpret the results of the Morris method. Abbreviations for the material property parameters are the same as in Figure 11.

Boundary Conditions

The canal and middle ear were modelled separately, and their individual contributions to the total immittance response of the ear were investigated. This was made possible by clamping the border of the TM, which is the only place where the canal model and middle-ear model interact. This assumption has been used in previous human middle-ear models (e.g. Rabbitt 1988; Gea et al. 2010; Aernouts et al. 2012). In the ear-canal model, the TM was taken to be rigid and fixed and so were the probe tip (since it is assumed to be securely held in the canal) and the surfaces of the temporal bone. In our middle-ear model, the ends of the AML and PIL were fixed (clamped) where they are attached to the wall of the middle-ear cavity. The canal wall and probe tip were also fixed.

Loading Conditions

In this study, the sound pressures were applied as harmonic stimuli with an amplitude of 0.2 Pa root mean square (corresponding to 80 dB SPL) on the surfaces of the canal wall and the TM. For presentation, all displacements are normalized by the pressure. The frequency of the input pressure was varied between 25 and 2000 Hz in 25-Hz steps, and the input admittance of the model was calculated for each frequency.

Computational Methods

Finite-Element Solver

The finite-element solver was Code_Aster (http://www.code-aster.org) version 11.5, which is free (libre) and open-source software. Simulations were performed on the supercomputer Guillimin of McGill University. Guillimin is a part of the Compute Canada national high performance computing (HPC) platform. It is a cluster of Intel Westmere EP Xeon X5650 and Intel Sandy Bridge EP E5-2670 processors running under the CentOS 6 Linux distribution. We ran a maximum of 12 simulation scenarios at a time on nodes of 12 or 16 processors, each scenario on a single processor. Typical run times for the ear-canal and middle-ear models were 144 and 277 min, respectively.

The complex dynamic responses of the models were obtained using the dynamic linear harmonic (DYNA_LINE_HARM) module in Code_Aster. This module calculates the steady-state response of the models to the harmonic excitation.

Mesh Resolution

After the initial meshes were generated according to the procedure explained in the “3-D Geometry and Finite-Element Mesh” section, convergence tests were done to assess the adequacy of the mesh resolution for both the ear-canal and middle-ear models. Every element of each mesh was bisected three times. The admittance magnitudes at the resonance peaks for the meshes after the third bisection deviated by only 1.2 and 0.9 % from the results for the meshes after the second bisection for the ear-canal and middle-ear models, respectively. Thus, we used the mesh resulting from the second mesh bisection for all simulations reported below. The ear-canal mesh consisted of 45,086 second-order tetrahedral elements (17,544 and 27,542 elements for the ear-canal volume and the surrounding soft tissues, respectively). The middle-ear mesh consisted of 28,748 second-order tetrahedral elements (23,012, 6136 and 288 elements for the TM, ossicles and ligaments, respectively). The TM consisted of four layers of tetrahedral elements; because the newborn TM is relatively thick, thin-shell elements (as often used for the adult TM) are not appropriate.

Admittance Calculation

Gariepy (2010) calculated the volume displacement of each structure by Green’s theorem, by summing the scalar products of the displacement vectors and surface-normal vectors across the triangular boundary elements. As an alternative approach that is convenient for use with Code_Aster, in this study, we obtained the volume displacements of the TM surface and the canal wall by computing the volume displacement of a very-low-impedance pseudo-material mesh filling the canal and confined between the probe tip and the TM (the air actually filling the canal was treated separately as a lumped admittance as described in the “Air in Middle-Ear Cavity and Ear Canal” section). A Young’s modulus of 0.001 Pa, a density of 0.001 kg/m³ and a Poisson’s ratio of 0.01 were assigned to the pseudo-material mesh. We performed a series of sensitivity analyses on those parameters to confirm that the effects of this pseudo-material on the model responses were negligible: the maximum deviation of the admittance responses, for parameter values changed by a factor of 10, was less than 0.01 %. We also confirmed that our results were in agreement with those obtained by Gariepy (2010) using Green’s theorem for the same models. In the ear-canal model, since the probe tip was clamped at the lateral end of the canal and the TM was clamped at the medial end, the volume displacement of the pseudo-material reflects that of the canal wall alone. In the middle-ear model, since the canal wall and the probe tip were clamped, the volume displacement of the pseudo-material reflects that of the TM alone. Code_Aster calculated the real (ΔV _r) and imaginary (jΔV _i, j = $\sqrt{-1}$) volume displacements of the pseudo-material inside the canal. For harmonic motion, the real ($\stackrel{\cdot }{V_{\mathrm{r}}}$) and imaginary ($\stackrel{\cdot }{V_{\mathrm{i}}}$) parts of the volume velocity are obtained by

$$\begin{array}{c}\stackrel{\cdot }{V_{\mathrm{r}}}=j\omega \left(j\mathrm{\Delta }{V}_{\mathrm{i}}\right)=-\omega \mathrm{\Delta }{V}_{\mathrm{i}}\\ \stackrel{\cdot }{V_{\mathrm{i}}}=j\omega \left(\mathrm{\Delta }{V}_{\mathrm{r}}\right)=j\omega \mathrm{\Delta }{V}_{\mathrm{r}}.\end{array}$$ 7

The conductance G and susceptance B components of the admittance were calculated by

$$\begin{array}{c}\hfill G=\frac{\stackrel{\cdot }{V_r}}{P}\hfill \\ \hfill B=\frac{\stackrel{\cdot }{V_i}}{P}\text{,}\hfill \end{array}$$ 8

where P is the amplitude of the sound pressure. The admittance magnitude and phase were calculated as $\sqrt{G^2+B^2}$ and Tan^− 1(B/G), respectively.

Sensitivity Analysis

Introduction

A sensitivity analysis can lead to an improved understanding of the system and help establish how much the uncertainty in the parameters will affect the output. In this study, we performed three sensitivity analyses. To provide an estimate of the effects of anatomical variability, the geometry of the canal and middle-ear models was scaled by −10, −5, +5 and +10 % in the x, y and z directions simultaneously. In addition, the effects of the material parameters were investigated using (1) a traditional one-parameter-at-a-time method and (2) the method of Morris (1991), as described below. Two different criteria were used to evaluate the effects of each parameter on both the ear-canal and middle-ear models: (1) the maximum admittance and (2) the frequency at which the maximum admittance occurs. The range between the minimum and maximum values for each parameter (shown in Table 1) was divided into four intervals, so each parameter has p = 5 evenly spaced values.

One Parameter at a Time

In the one-parameter-at-a-time method, the effect of each parameter is studied individually by varying it while keeping all of the other parameters at their baseline values. This method provides a quantitative measure of the effect of each individual parameter on the output. Performing a linear regression analysis provides a measure of the size of the effect, given by the slope. The coefficient of determination R ², an indication of how well a straight line fits the outputs, can be used as a measure of the linearity or nonlinearity of the effect:

$$R^2=1-\frac{{\displaystyle {\sum }_{i=1}^m}{\left(y_i-g_i\right)}^2}{{\displaystyle {\sum }_{i=1}^m}{\left(y_i-\overline{y}\right)}^2}\text{,}$$ 9

where y _i (i = 1, 2, …, m) are the outputs at each of p simulations, $\overline{y}$ is the mean of the outputs and the g _i is the value in the fitted line corresponding to the y _i. R ² is a number between 0 and 1, and the larger it is, the more linear the parameter effect is.

Morris Method

The method of Morris (1991), on the other hand, is a qualitative screening method. The underlying intent of this method is to determine which input parameters may be considered to have effects that are (a) negligible, (b) linear and additive or (c) nonlinear and/or involved in interaction with other parameters. Assume that, for the model being studied, an output y is given by a function of a vector x of the inputs:

$$\begin{array}{c}y=f(\mathbf{x})\\ \mathbf{x}=\mathbf{x}(x_1,x_2,\dots x_i,\dots x_k),\end{array}$$ 10

where x ₁, x ₂, …, x _i, …, x _k are the parameters of the model. For this model, simulations are designed for n sets x ^j (j = 1, 2, 3, …, n). Each parameter x _i can take on p predefined values in the range [x _{i, min}, x _{i, max}]. At each x ^j+1, only one parameter x _i is given a value different from the value that it had in x ^j. Thus, for two consecutive simulations, we can define a simple partial difference of the output with respect to the change of x _i to x′ _i :

$$d_i\left({\mathbf{x}}^j\right)=\frac{f\left({\mathbf{x}}^{j+1}\right)-f\left({\mathbf{x}}^j\right)}{\Delta }=\frac{f\left(\mathbf{x}(x_1,x_2,x_3,\dots ,x_i^{\mathrm{\prime }},\dots x_k)\right)-f\left(\mathbf{x}(x_1,x_2,x_3,\dots ,x_i,\dots x_k)\right)}{\Delta },$$ 11

where Δ is a predetermined multiple of 1 / (p − 1). In our case, p = 5, and we took Δ = 1/4, so each parameter can take all five possible values in [x _{i, min}, x _{i, max}]. For the next simulation, the new value x _i′ is kept and some other parameter is also changed (in the one-parameter-at-a-time method, the changed parameter would be reset to its baseline value before another parameter was changed). Since for each simulation only one parameter changes, k + 1 simulations should be performed to obtain one d _i for each parameter, resulting in a total of n = r × (k + 1) simulations, r being the number of d _i’s desired for each parameter.

Morris (1991) introduced a method, which is used here, to randomly design each set of k + 1 simulations: in each of the r sets, for the first simulation, a random value is assigned to each parameter x _i within its specified range, then in the next simulation, one parameter changes while the others are kept constant and the procedure goes on until all k parameters have been changed once, so one d _i can be calculated for each x _i according to Eq. 11.

Once n simulations have been performed, then the effect of parameter x _i can be described using the following three measures:

$$\begin{array}{c}{\mu }_i=\frac{1}{r}{\displaystyle \sum _{j=1}^r}{d}_i\left({\mathbf{x}}^j\right)\\ {\mu }_i^{\ast }=\frac{1}{r}{\displaystyle \sum _{j=1}^r}\left|d_i\left({\mathbf{x}}^j\right)\right|\\ {\sigma }_i=\sqrt{\frac{1}{r-1}{\displaystyle \sum _{j=1}^r}{(d_i\left({\mathbf{x}}^j\right)-{\mu }_i)}^2}.\end{array}$$ 12

For each parameter x _i, the corresponding μ _i is the mean of the d _i’s across the r simulations and is thus a measure of the overall influence of that parameter on the output. μ _i ^* provides a more practical measure of overall influence of a parameter, in which oppositely signed values of the d _i do not cancel each other. σ _i is the standard deviation of the d _i’s for parameter x _i and is a measure of the interaction and nonlinear effects of x _i. If for parameter x _i we obtain a high value of σ _i (i.e. large deviations of d _i around its mean value), it means that the output is affected by the choice of the other parameters (i.e. there are parameter interactions) or that the parameter has a nonlinear effect in the range of [x _{i, min}, x _{i, max}], or both. In contrast, a low σ _i indicates that x _i has linear effects that are independent (or nearly so) of the values taken by the other parameters.

We set r = 10 as a trade-off between completeness and computation time. For the ear-canal model, the following four parameters were investigated (i.e. k = 4): Young’s modulus, density, Poisson’s ratio and damping ratio of the soft tissue. This resulted in 50 simulations for the ear-canal model. For the middle-ear model, the following 12 parameters were investigated (i.e. k = 12): Young’s moduli of the pars tensa, pars flaccida, ligaments and ossicles; densities of the soft tissue and ossicles; middle-ear cavity volume; Poisson’s ratio of the soft tissues; stapes mass; stiffness of the stapedial annular ligament; cochlear load (dashpot coefficient); and damping ratio (the Poisson’s ratio of the ossicles was not varied). This resulted in 130 simulations for the middle-ear model. Instead of just presenting the values for the σ _i’s, as done by Morris (1991), we present scatter plots and 10th-to-90th-percentile ranges of the d _i’s for each parameter.

Clinical Data

Three studies of immittance response have been reported in the literature for ages similar to the 22-day age of our model. Holte et al. (1991) reported pressurized admittance responses for infants in five age groups: 1–7, 11–22, 26–47, 51–66 and 103–133 days old. Their measurements were done from 250 to 1000 Hz. Keefe et al. (1993) reported impedance measurements performed under ambient pressure for age groups of 1, 3, 6, 12 and 24 months in addition to adults, for frequencies from 125 to 10,700 Hz with a one third octave resolution. The maturation effects were studied further by Keefe and Levi (1996) using the same data as in the 1993 study but expressed in terms of admittance, and inter-subject variations were reported in the 1996 paper. Sanford and Feeney (2008) measured pressurized admittance for infants at 1, 3 and 6 months and for adults, for frequencies from 250 to 8000 Hz with a one third octave resolution. Since our model represents unpressurized conditions, we used only the data of Keefe et al. (1993) and Keefe and Levi (1996) for comparison with our model to avoid the complications inherent in interpreting zero-pressure or peak-pressure data from pressure sweeps like those of Holte et al. (1991) and Sanford and Feeney (2008).

In addition, we used admittance measurements that we performed as part of another project on a group of 23 newborns with ages between 14 and 28 days old, for frequencies from 250 to 8000 Hz with a 1/12 octave resolution. That study was approved by the Institutional Review Board of the McGill University Health Centre. The measurements were made with a wideband tympanometry research system (WBTymp 3.2, Interacoustics Inc.). All measurements except one were performed in the otolaryngology outpatient clinic of the Montréal Children’s Hospital. More details about the measurement procedure can be found in Pitaro et al. (2016).

RESULTS

Displacement Patterns

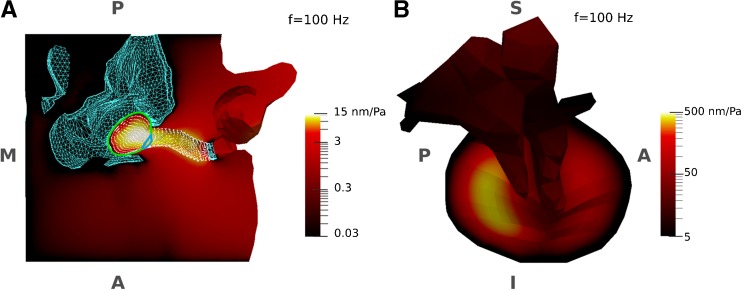
Displacement-magnitude maps of the ear-canal and middle-ear models at a low frequency (100 Hz), normalized with respect to the amplitude of the applied sound pressure (0.2 Pa), are presented in Figure 3 for the baseline parameter values. To present the small displacements of some components of the models (e.g. ossicles), the displacement maps are presented with logarithmic scales, with different ranges in the two panels (in the figure, the ear-canal model is sectioned in a horizontal plane to provide a superior-to-inferior direction of view of the temporal bone and the inferior wall of the ear canal). For the ear canal (with the canal terminated by a fixed probe tip laterally and a fixed TM medially), the greatest displacements (the brighter colours) occur at the medial and inferior portion of the canal, just inferior to the TM. This can be explained by the fact that there is temporal bone superior to the canal wall, and inferior to the TM the floor of the canal is broad and relatively flat. For the TM in the middle-ear model (with the canal wall being fixed), the maximum displacement occurs in the posterior region (where the TM is thinner and the distance from the manubrium to the TM boundary is greater) and a smaller local maximum occurs in the anterior region.

FIG. 3.

Displacement-magnitude maps of the models in response to sound pressures at a low frequency (100 Hz), normalized with respect to the amplitude of the applied sound pressure (0.2 Pa). Due to the small displacements of some components of the models (e.g. ossicles), the displacement maps are presented using logarithmic scales. The logarithmic colour scales represent displacements from zero (black) to a maximum (white) with monotonically increasing brightness. A Ear-canal model with TM fixed, sectioned in a horizontal plane to provide a superior-to-inferior view of the temporal bone and the internal surface of the ear canal. The TM has been removed to provide a more complete view of the canal and only the borders of the PT (green curve) and PF (blue curve) are presented. The surface of the canal wall is presented by its mesh nodes (white dots). The fixed surfaces of the temporal bone and the probe tip are shown with a blue mesh. The largest displacements are in the medial region of the canal. B Medial-to-lateral view of the middle-ear model with canal wall fixed. The largest displacements are in the posterior portion of the TM. The anatomical orientation and abbreviations are the same as for Figure 1.

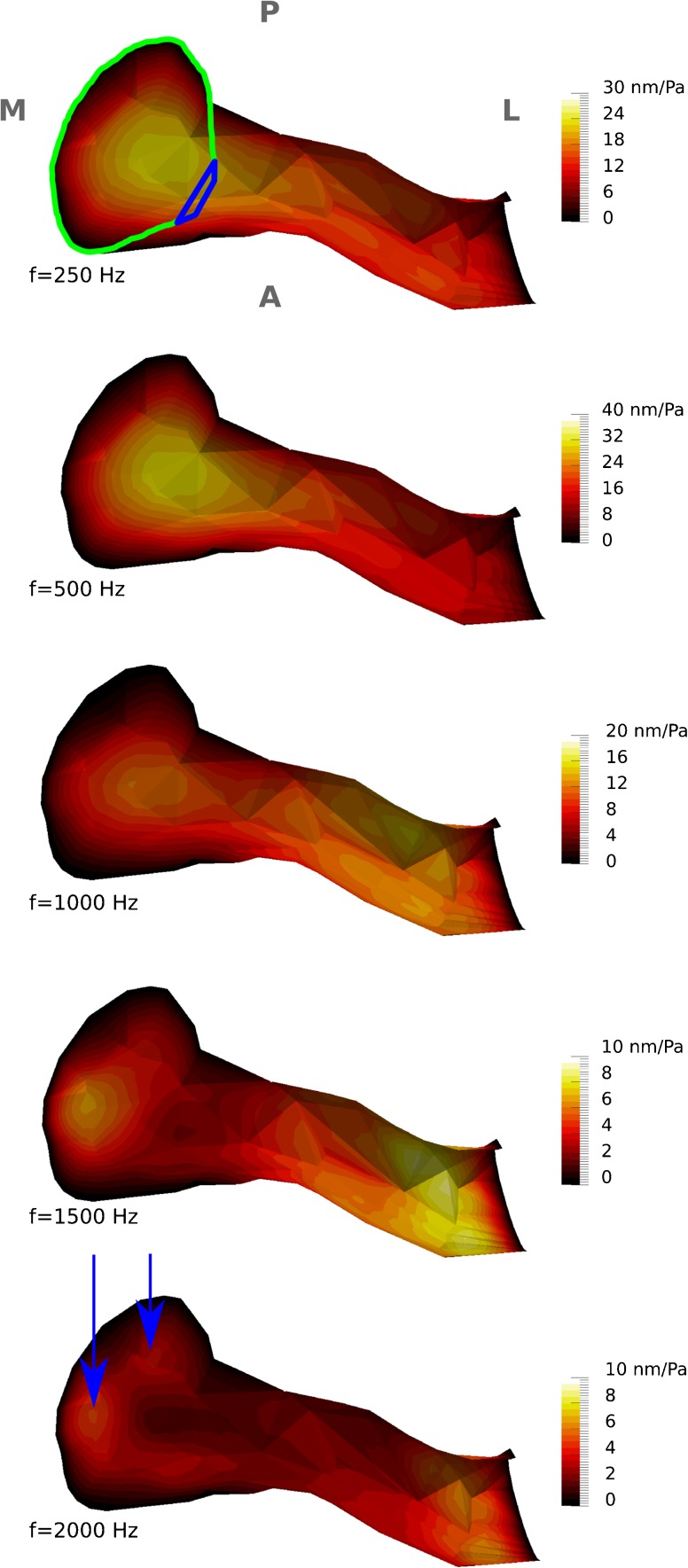
The vibration patterns of the ear-canal wall, for the baseline model, were computed in 25-Hz frequency steps. Since the vibration patterns change smoothly from one frequency to another, only the results for frequencies of 250, 500, 1000, 1500 and 2000 Hz are presented in Figure 4. Since the main displacements occur in the inferior portion of the canal at all frequencies, the canal model is sectioned horizontally as in Figure 3A and the viewing direction is again superior to inferior. Since the TM covers some of the medial portion of the canal, it was removed to provide an unobstructed view of the canal wall. As discussed in the next section, the first resonance of this model occurs at about 700 Hz. The initial vibration pattern (i.e. one maximal displacement region in the inferior medial portion of the canal) remains up to that frequency. The magnitude of the maximum displacement increases with frequency from 24 nm/Pa at 100 Hz to 32 nm/Pa at 700 Hz. In the frequency range of 700 to 1200 Hz, the region of maximal displacement moves towards the lateral portion of the canal and the magnitude of the maximum displacement decreases to 12 nm/Pa. At frequencies from ∼1200 up to ∼1500 Hz, two regions of maximal displacement are visible in the lateral and medial portions of the ear canal, and the magnitude of the maximum displacement decreases from 12 to 9 nm/Pa. As the frequency increases beyond 1500 Hz up to our upper limit of 2000 Hz, the region of maximal displacement in the medial portion splits into two regions (indicated by the arrows in Fig. 4) and the magnitude of the maximum displacement decreases from 9 to 6 nm/Pa.

FIG. 4.

Displacement-magnitude maps of vibration patterns, normalized with respect to the amplitude of the applied sound pressure (0.2 Pa), for the inferior wall of the ear-canal model at five different frequencies. The colour scales are linear, and their maximum values are different for different frequencies. As in Figure 3A, the TM has been removed. The borders of the PT (green curve) and PF (blue curve) are presented and the anatomical orientation, and abbreviations are the same as for Figure 1A. The arrows indicate the regions of maximal displacement in the medial portion.

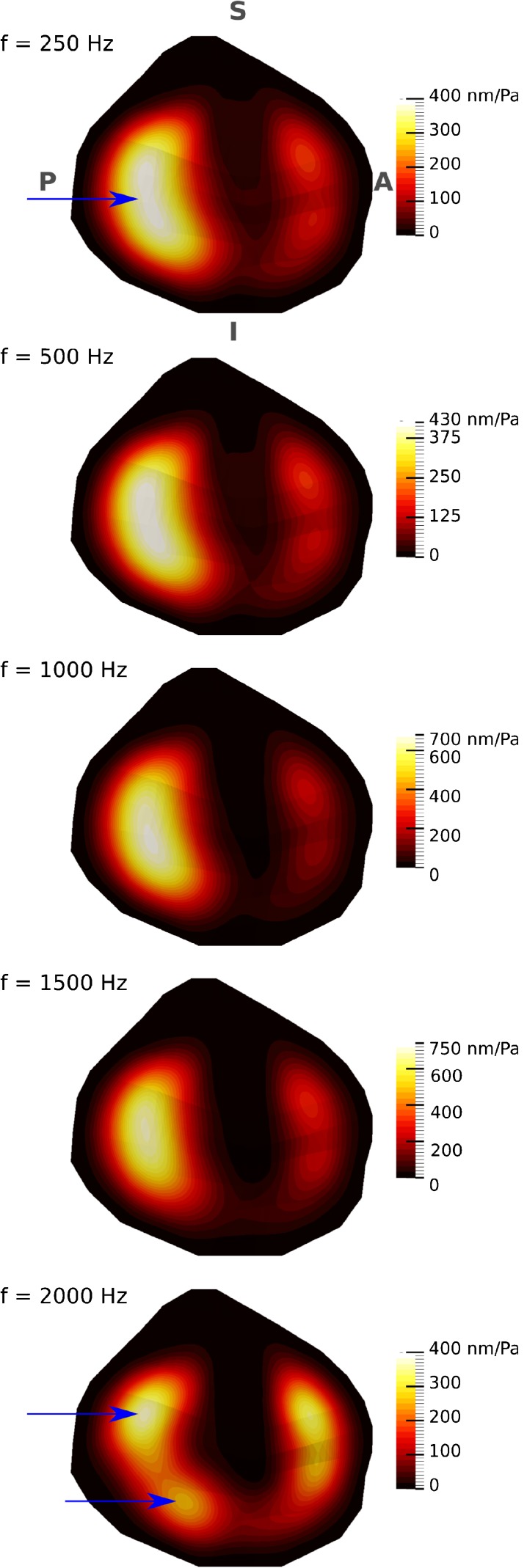
The vibration patterns of the TM, for the baseline model, were also computed in 25-Hz frequency steps. Since the vibration patterns again alter smoothly with frequency, only the results for frequencies of 250, 500, 1000, 1500 and 2000 Hz are presented in Figure 5. The initial vibration pattern (i.e. two maxima, in the posterior and anterior regions of the TM, with the maximal displacement in the posterior region) remains up to about 1800 Hz. The maximum displacement of the anterior region increases gradually from 180 nm/Pa at 250 Hz to 350 nm/Pa at 1800 Hz then drops to 330 nm/Pa at 2000 Hz. The magnitude of the maximum displacement in the posterior region increases from 390 nm/Pa at 250 Hz to 830 nm/Pa at 1200 Hz. Between 1200 and 1800 Hz, the posterior maximal-displacement region moves towards the superior quadrant. As the frequency increases beyond 1800 Hz, the posterior maximum splits into superior and inferior regions (indicated by arrows in Fig. 5) and the magnitude of the maximum displacement decreases to 370 nm/Pa.

FIG. 5.

Displacement-magnitude maps of vibration patterns, normalized with respect to the amplitude of the applied sound pressure (0.2 Pa) for the TM at five different frequencies. The colour scales are linear, and their maximum values are different for different frequencies. The figure presents a medial-to-lateral view of the TM, with the TM annulus almost parallel to the page, as in Figure 1B. The arrows indicate the regions of maximal displacement in the posterior portion.

Admittances of the Individual Models

As explained in the “Air in Middle-Ear Cavity and Ear Canal” and “Admittance Calculation” sections, the admittances of the ear-canal and middle-ear models were calculated separately; in the ear-canal model, the volume velocity of the canal wall alone was taken into account (the canal boundaries being fixed laterally and medially by the clamped probe tip and TM, respectively), and in the middle-ear model, the volume velocity of the lateral surface of the TM alone was taken into account (the canal wall and the probe tip being clamped). In all models, the frequency resolution was 25 Hz.

The input admittance magnitude and phase of the ear-canal wall Y _wall as functions of frequency for the low-impedance, baseline and high-impedance models (as described in the “Introduction” section) as well as for three intermediate cases, with Young’s moduli of 40, 80 and 160 kPa for the soft tissue (to fill the gap caused by the stiffness change by a factor of about ten between the baseline model and the low-impedance model) are presented in Figure 6. As the model becomes stiffer, the resonance peaks shift to higher frequencies, decrease in magnitude and become broader: the admittance magnitude peaks of 24.2, 5.6 and 3.2 mm³/s/Pa occur at 225, 700 and 1050 Hz, and the widths of the peaks (as defined by the frequencies at which the magnitudes are 90 % of the peak value) are 150, 500 and 850 Hz for the low-impedance, baseline and high-impedance models, respectively (we used a 90 % cutoff instead of the more common $1/2\mathrm{or}\sqrt{1/2}$ because in some cases, those values would lead to cutoff frequencies that were beyond the frequency range of interest or were beyond the minimum between one resonance and a neighbouring one, or both. The phases are constant at the lowest frequencies, as expected for a stiffness-dominated response. However, since the Rayleigh damping was set so as to provide a constant damping ratio, even at the lowest frequencies, the response is not purely stiffness dominated and the phase does not converge to 90 °. As the excitation frequency is increased, the mass contributes more to the response and the phases tend toward negative angles.

As explained in the “Air in Middle-Ear Cavity and Ear Canal” section, the admittance of the enclosed air in the canal Y _can is in parallel with the admittances of the ear canal and middle ear. Its admittance was calculated using Eqs. 3 and 4 and is presented in Figure 6A (black curve). It is a linear function of the excitation frequency and thus appears as an increasingly steep curve for the logarithmic frequency scale of the figure. The ratio between the static compliance of the enclosed air in the canal and that of the canal wall (for the adjusted model, their compliances are 0.9 and 3.1 mm³/Pa, respectively) is similar to the ratio between the corresponding compliances of 0.4 and 1.6 mm³/Pa, respectively, in Keefe et al. (1993). The low-frequency admittance of the wall (like the compliance) is thus somewhat higher than that of the enclosed air, and the ratio becomes even larger around the resonance of the wall. Since the canal air is modelled as a pure stiffness component, its phase is constant at 90 ° (black curve in Fig. 6B).

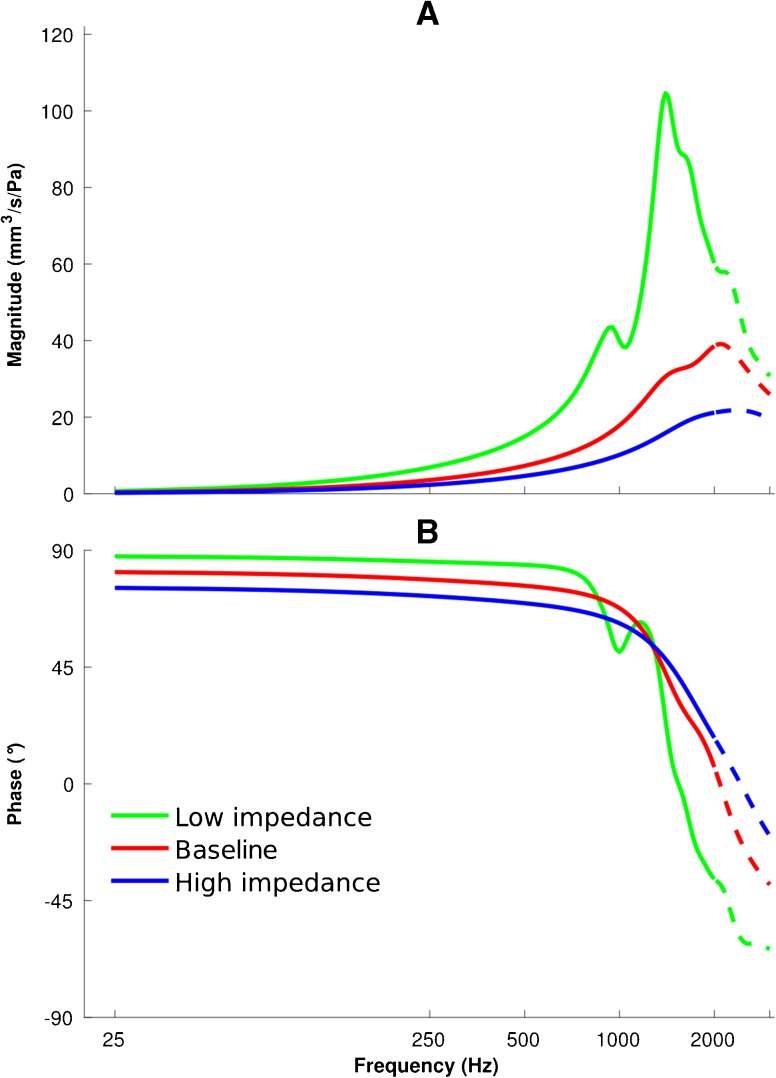
The input admittance magnitude and phase of the middle-ear model for three scenarios (i.e. the low-impedance, baseline and high-impedance models) are presented in Figure 7. As explained in the “Air in Middle-Ear Cavity And Ear Canal” section, the input admittance of the middle ear is a parallel combination of the admittances of the air enclosed in the middle-ear cavity (obtained from Eqs. 3 and 4) and of the middle ear (obtained from the volume velocity of the lateral surface of the TM in the middle-ear model). A larger middle-ear cavity results in a more mobile TM, so larger baseline and smaller middle-ear cavities are used in the low-impedance, baseline and high-impedance models, respectively, to calculate the total middle-ear admittances. As the model becomes stiffer, the resonance peaks shift to higher frequencies, decrease in magnitude and become broader, similar to what we see for the ear-canal model. The admittance magnitude peaks of 104.6, 39.1 and 21.8 mm³/s/Pa occur at 1400, 2100 and 2300 Hz, and the widths of the peaks (again defined by the frequencies at which the magnitudes are 90 % of the peak value) are 200, 900 and 1200 Hz for the low-impedance, baseline and high-impedance models, respectively. We extended the frequency range to 3000 Hz to provide an estimate of the resonance frequency of the middle ear. The parts above 2000 Hz are represented by dashed lines to emphasize that they are beyond our upper frequency limit of 2000 Hz. In the same way as for the canal model, the phases are constant at the lowest frequencies but do not quite reach 90 °. In the middle-ear model, the phase responses remain close to 90 ° over a larger range of frequencies than in the ear-canal model. For example in the low-impedance ear-canal and middle-ear models (green curves in Figs. 6 and 7), the phases drop from ∼90 to 45 ° at 200 and 1300 Hz, respectively, illustrating that the stiffness characteristics are dominant over a wider frequency range in the case of the middle ear.

FIG. 7.

Admittance responses of the middle-ear models with a 25-Hz frequency resolution. Admittance magnitudes (A) and phases (B) are presented for low-impedance (green), baseline (red) and high-impedance (blue) parameters. The dashed curves are the extensions of the solid curves for frequencies above 2000 Hz.

Admittance of the Combined Model

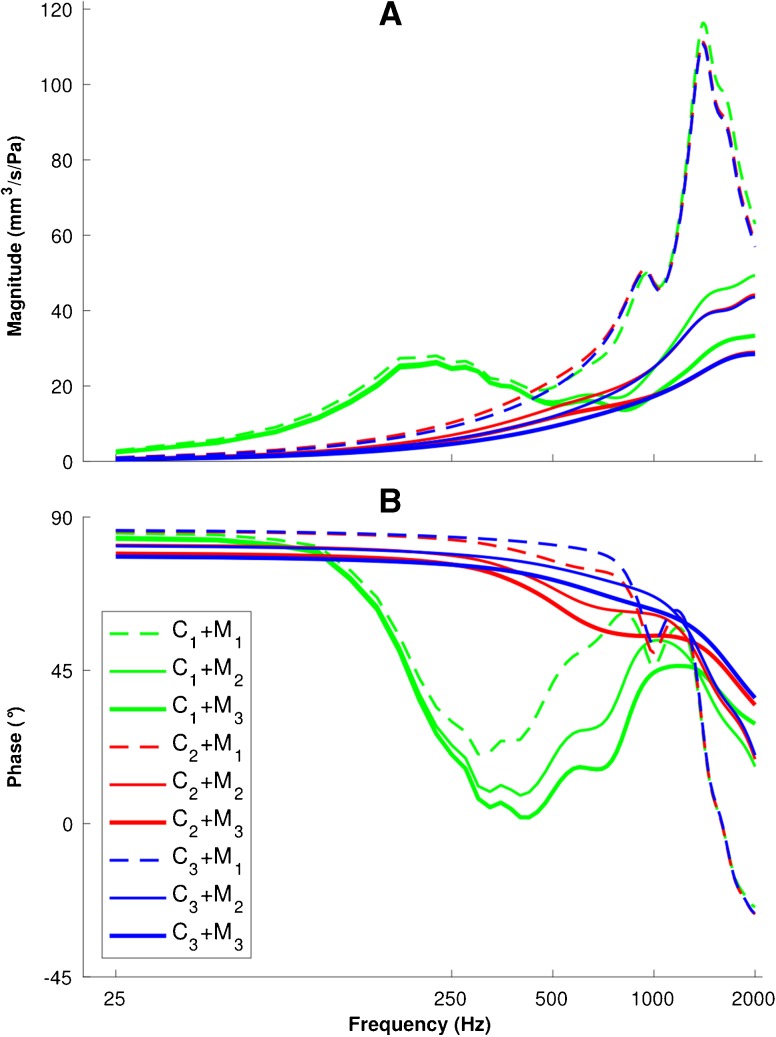
Based on the admittance responses of its components as shown in Figures 6 and 7, the combined input admittance response of the ear Y _ear was calculated using Eq. 6. All nine combinations of the three ear-canal scenarios and the three middle-ear scenarios are presented in Figure 8. In this figure, each pair C _i + M _j corresponds to the combination of the canal model i and the middle-ear model j, and the indices i = 1, 2 and 3 represent the low-impedance, baseline and high-impedance models, respectively.

FIG. 8.

Admittance responses of the combinations of three ear-canal and three middle-ear models with a 25-Hz frequency resolution. Admittance magnitudes (A) and phases (B) are presented for each pair C _i  + M _j corresponding to the combination of the canal model i and the middle-ear model j; the indices i,j = 1, 2 and 3 represent the low-impedance, baseline and high-impedance models, respectively.

In results with the low-impedance canal model (green curves), a local peak in the frequency range of 150–500 Hz is observed, along with a drop and subsequent rise of the phase response at frequencies below 1000 Hz, for all middle-ear models. Since the admittance of the ear is a combination of the admittances of the ear canal and middle ear, the magnitude at the main resonance is slightly higher than for those two individual components and its frequency lies between the two corresponding resonance frequencies. However, at higher frequencies, the magnitude and phase of the combined model are similar to that of the middle ear alone because the admittance of the canal is much smaller than that of the middle ear.

In all of the models with the most compliant canal wall (all green curves in Fig. 8), an admittance peak is observable around 200 Hz. This peak disappears in the baseline and high-impedance combined models (red and blue curves in Fig. 8). Since the resonances of the baseline and high-impedance canal wall models are at frequencies higher than 500 Hz (red and blue curves in Fig. 6), they have merged into the resonance of the middle ear in Figure 8 (red and blue curves). Furthermore, for all of the low-impedance canal wall models (green curves in Fig. 8), the phase stays close to 90 ° only up to about 100 Hz. In all of the combined models (Fig. 8), the main resonance magnitudes and frequencies are close to those of the middle-ear response (as shown in Fig. 7B) and all responses for a given middle-ear model (regardless of the canal wall model, i.e. different colours but same line style in Fig. 8) are similar above 1000 Hz, indicating that at higher frequencies, the middle-ear response is dominant.

Model Validation and Parameter Adjustments

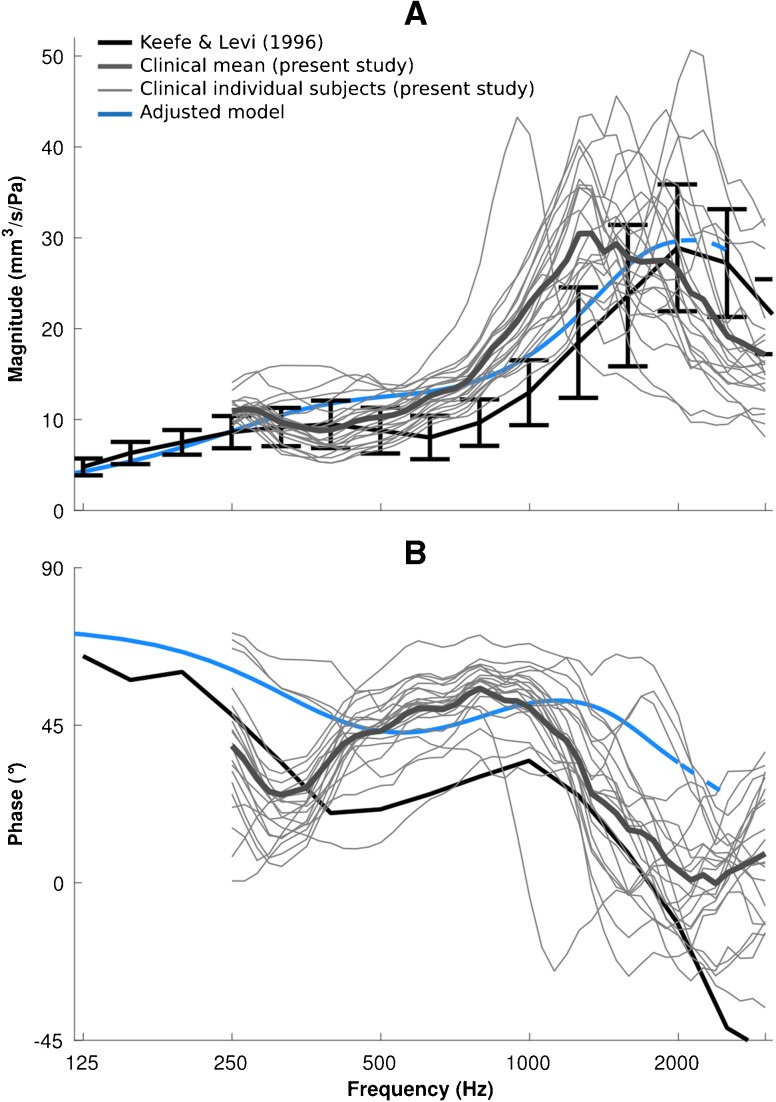
As explained in the previous section, the canal response has a strong effect on the total admittance of the ear at frequencies below 1000 Hz while the middle-ear response dominates at higher frequencies. A low-frequency resonance is observable in those combined models that have low-impedance canals, and in all of the combined models, the main resonance mainly reflects the resonance of the middle ear. Comparing the clinical data with the nine combinations of the canal and middle-ear models, it can be concluded that an intermediate-impedance canal model combined with a high-impedance middle-ear model can provide a reasonable match to the clinical data over the frequency range of interest. By assigning a high damping ratio of ζ = 0.4 and an intermediate stiffness of E = 80 kPa to the soft tissue surrounding the ear canal, we can adjust the admittance magnitude of the canal resonance and shift it to frequencies around 500 Hz to be more consistent with Keefe and Levi (1996, Fig. 1). Figure 9 shows the admittance for such an adjusted model of the ear, together with the two sets of clinical data, namely, the mean of Keefe and Levi (1996) and the curves for our individual subjects (thin grey curves) and their mean (thick grey curve). We extended the frequency range up to 3000 Hz (again with dashed lines) to provide insight into the admittance behaviour around the resonance peak at 2000 Hz. Some of our individual magnitude curves show much higher and sharper peaks than are seen in the mean curves, where sharp peaks at different frequencies are smeared out by the averaging. The features of our mean curve are somewhat sharper than those of Keefe and Levi because our frequency resolution was higher than theirs.

FIG. 9.

Results for model with adjusted parameters and comparison with two sets of clinical data. Admittance magnitudes (A) and phases (B) are presented for the data of Keefe and Levi (1996) (solid black lines and error bars) and for data from this study (thick grey lines for the mean, thin grey lines for the responses of individual subjects), compared with the output of the model with adjusted parameters (blue lines; see text for explanation of parameter adjustment).

The admittance magnitude response of the adjusted model is mostly within the variability of the clinical data of Keefe and Levi (1996), with values up to 30 % higher at frequencies between 500 and 1000 Hz (Fig. 9A). The model results are entirely within the range of the individual responses of our clinical data, where the resonance peaks of the admittances are in the range of 1000 to 2200 Hz and the peak values vary between 24 and 50 mm³/s/Pa; the admittance peak of the adjusted model (30 mm³/s/Pa at 2100 Hz) falls within this range.

Unfortunately the variability of the phase response were not reported in either Keefe et al. (1993) or Keefe and Levi (1996). The mean phase data of Keefe et al. (1993) show a minimum at 400 Hz, rise to a maximum at 1000 Hz and then drop at higher frequencies; in our mean clinical data, the minima and maxima are mostly at lower frequencies (about 300 and 800 Hz, respectively) and are somewhat sharper than those of Keefe et al. The shape of the model curve is similar to that of the mean curve of Keefe et al. but the minima and maxima are shifted to slightly higher frequencies and the phases are about 15 to 28 ° higher than those of Keefe et al., more like those of our clinical data.

Sensitivity Analysis

Geometrical Variations

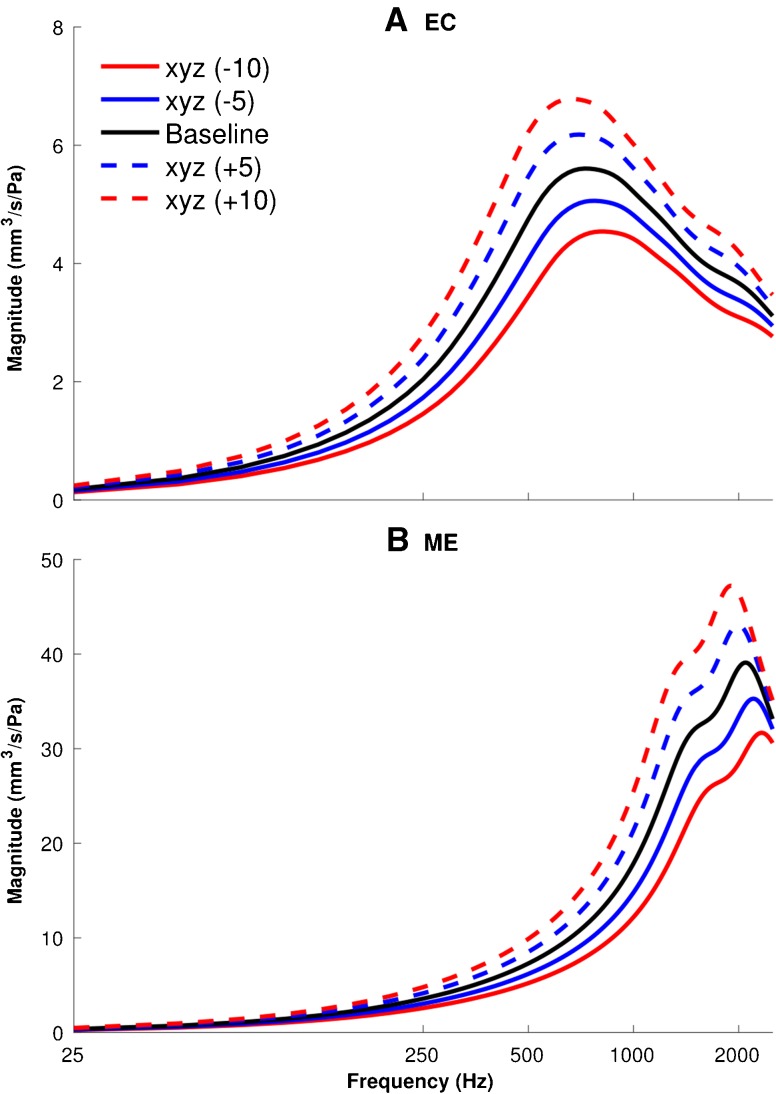
Figure 10 shows the effects of the geometry variation in the x, y and z directions simultaneously, for −10, −5, +5 and +10 % scaling of the baseline geometry of the ear-canal (upper panel) and middle-ear (lower panel) models. In both models, the larger geometries result in larger admittance magnitudes over the whole frequency range, especially around the resonance frequencies of 700 and 2000 Hz for the canal and middle-ear models, respectively. From −10 % scaling to +10 % scaling, the magnitude of the admittance resonance increases by 52 %, from 4.5 to 6.8 mm³ in the canal model; and by 50 %, from 31.7 to 47.2 mm³, in the middle-ear model. In both models, the resonance peaks also shift slightly to lower frequencies as the geometries become larger.

FIG. 10.

Geometrical variations sensitivity analyses, showing the effect of scaling the geometry of the models on the admittance responses of the models of the ear canal (A) and middle ear (B). The geometries of the models were scaled uniformly in all three directions (x, y and z) by –10, –5, +5 and +10 % and compared with the baseline models.

One Parameter at a Time

The results of the one-parameter-at-a-time sensitivity analysis are presented in Figure 11 for the two separate models (ear canal in the upper panels, middle ear in the lower panels) and for two features of the admittance (maximum magnitude in the left-hand panels and frequency of the maximum in the right-hand panels). All four parameters are shown in the figure for the canal model, and for the middle-ear model, only the four most influential parameters are shown.

FIG. 11.

One-parameter-at-a-time sensitivity analysis, showing the influence of the material parameters on the maximum admittance magnitudes (A, C) and the corresponding frequencies (B, D) for the ear-canal model (A, B) and the middle-ear model (C, D). The horizontal solid line indicates the corresponding values for the baseline model. E _st = Young’s modulus and ν _st = Poisson’s ratio of the soft tissue in the ear-canal model; E _pt = Young’s modulus of the pars tensa and V _cav = volume of the air cavity in the middle-ear model; ζ = damping ratio and ρ _st = density of soft tissue in both models.

Figure 11A shows the four parameters of the ear-canal model in order of decreasing influence on the maximum admittance magnitude: the Young’s modulus E _st, damping ratio ζ, density ρ _st and Poisson’s ratio ν of the soft tissue. The coefficients of determination R ² (i.e. the coefficients of determination of the linear regressions, as discussed in the “Sensitivity Analysis” section) for these parameters are 0.71, 0.95, 0.99 and 0.99, respectively, meaning that E _st has a quite nonlinear effect but that the others are practically linear. The same order of influence holds for the frequency of the maximum admittance magnitude (Fig. 11B), except that Poisson’s ratio plays an important role at its higher values. The R ² values for this criterion are 0.96, 0.99, 0.94 and 0.87 for E _st, ζ, ρ _st and ν, respectively, meaning that ν has a somewhat more nonlinear effect than the others do.

For the middle-ear model, panels c and d in Figure 11 show only the four parameters that have the greatest influence on the two admittance features being analysed. The damping ratio ζ affects the maximum admittance magnitudes more than does the pars-tensa Young’s modulus E _pt (Fig. 11C). The soft-tissue density ρ _st (i.e. the density of the components other than the ossicles) and the middle-ear cavity volume V _cav have much smaller effects. The R ² values for E _pt, ζ, ρ _st and V _cav are 0.94, 0.92, 0.99 and 0.98, respectively, reflecting the fact that E _pt and ζ have somewhat nonlinear effects. The frequency of the maximum admittance (Fig. 11D) is strongly affected by E _pt, and the order of the influence of the other parameters for this criterion is ρ _st, V _cav and ζ. The R ² values for E _pt, ζ, ρ _st and V _cav are 0.98, 0.75, 0.98 and 0.97, respectively, indicating that ζ is the only one with a notably nonlinear effect. The effects of the other parameters of the middle-ear model (i.e. the cochlear load, the stiffness of the ligaments, the pars flaccida, the ossicles, the mass of the ossicles, and the Poisson’s ratio) are less than 1 %, and they are not presented in this figure.

Morris Method

The results of the sensitivity analysis with the Morris method are presented in Figure 12, again for the maximum admittance and its corresponding frequency. Each point represents a |d _i|, the absolute value of the partial difference of the output with respect to the change of each parameter (and not the absolute value of the actual deviation from the baseline values), and the red lines represent μ _i*, the average of the |d _i|’s. The blue boxes indicate the 10th-to-90th-percentile ranges. The order of overall influence of the four ear-canal parameters (i.e. μ _i*) on the maximum admittance and its corresponding frequency (Fig. 12A and B) is the same as what the one-parameter-at-a-time analysis shows (Fig. 11A and B). The large 10th-to-90th-percentile ranges and the asymmetrical distributions of the |d _i|’s for the Young’s modulus E _st suggest possible nonlinear and/or interaction effects for both the admittance magnitude and the corresponding frequency.

For the middle-ear model, the four parameters having the greatest influence on the admittance features were the same as those that had the greatest influence according to the one-parameter-at-a-time analysis. The order, from most to least, of the overall influence of the middle-ear parameters (i.e. μ _i*) on the maximum admittance magnitude (Fig. 12C) is also the same as what the one-parameter-at-a-time analysis shows (Fig. 11C). However, the order of importance is slightly different for the corresponding frequency: as shown in Figure 11D, the mean sizes of the effects are similar for the damping ratio ζ, soft-tissue density ρ _st and middle-ear cavity volume V _cav, but the distributions around the means are different. For the cavity-volume effect, which is linear in Figure 11C, the wide (and asymmetrical) distribution of the deviations may be due to interactions with other parameters.

In both ear-canal and middle-ear models, the effects of the damping ratio are more complicated. Its broad distribution of |d _i|s in Figure 12D may be because of the strong nonlinearity seen in Figure 11D and that nonlinearity may be because the multiple peaks at low damping ratios (as can be seen in Figs. 6 and 7, green curves) are merged when the damping is higher (as mentioned in the “Introduction” section, the low-impedance models incorporate the lowest damping values as well as the lowest stiffness and density values). In addition, based on the definition of the Rayleigh model of damping, by which the damping is a function of stiffness and mass, these three parameters can be expected to interact with one another.

DISCUSSION

Displacement Patterns

To the best of our knowledge, no experimental data have been reported for vibration and displacement patterns of the newborn TM. However, there have been a few studies of the vibration patterns of the TM in adult humans and animals. Tonndorf and Khanna (1972), Rosowski et al. (2009) and Cheng et al. (2010) reported that the vibration patterns of the adult TM are simple at low frequencies, with larger displacements in the posterior region, and complex vibration patterns are observable at frequencies higher than 3000 Hz. Our model shows that the first, simple vibration pattern (i.e. two maxima, one posteriorly and one anteriorly), with maximum motion in the posterior half, remains only up to about 1800 Hz. Around this frequency, the patterns start to become more complex, as described in the “Displacement Patterns” section, and the posterior and anterior portions start to move out of phase with one another. The fact that the complex patterns begin at a lower frequency than in adults may be attributed to the lower stiffness of the TM in the newborn model.

Unlike the case for the TM, the vibration patterns of the ear canal cannot be readily observed in experimental measurements and no experimental data have been reported in the literature for either newborns or adults. As shown in the “Displacement Patterns” section, our model predicts three major displacement patterns of the canal: a single maximal-displacement region in the inferior medial region at low frequencies; a single maximal-displacement region in the lateral region at intermediate frequencies; and two maximal-displacement regions, in the lateral and medial regions, at high frequencies.

Admittance

Holte et al. (1991) and Keefe et al. (1993) found that an admittance maximum of the ear canal in infants less than 1 month old happens at frequencies around 450 Hz. With our adjusted parameters (see the “Model Validation and Parameter Adjustments” section), the resonance happens around 500 Hz in the model, similar to what was found in those studies. The canal resonances of the individual subjects in our clinical measurements occur in the range of 250 to 500 Hz, mostly close to 250 Hz.

Holte et al. (1991) did not measure to high enough frequencies to observe the middle-ear resonance, but they suggested that it is beyond 900 Hz. Keefe et al. (1993) reported that the overall ear resonance was in the vicinity of 1800 Hz. The ear resonances of the individual subjects in our clinical measurements are in the range of 1000 to 2500 Hz. In our models, the middle-ear resonances happen around 1400, 2000 and 2300 Hz for the low-impedance, baseline and high-impedance models (Fig. 7A), respectively, consistent with our clinical data.

As the frequency increases from 25 to 1000 Hz, the ratio of the admittance magnitude of the canal to that of the middle ear decreases from 0.6 to 0.3 for our baseline models. This ratio is larger (decreasing from 2.0 to 0.6 over the same frequency range) in the adjusted model. Thus, at frequencies below 1000 Hz, admittance measurements are highly affected by the canal response (Figs. 8 and 9) and they cannot satisfy their main goal of reporting the middle-ear response. The response of the ear canal becomes negligible at frequencies in the vicinity of the middle-ear resonance (i.e. between 1000 and 2000 Hz). This suggests that admittance measurements can provide more information about the condition of the middle ear when made at frequencies above 1000 Hz than when made at lower frequencies. However, since the resonance frequency may vary considerably due to inter-subject variability (as seen in the individual responses in Fig. 9), it may be important to measure at many frequencies over the range where the resonance may occur.

When comparing the model output with clinical data, one should keep several factors in mind. (1) Our model is reconstructed from one particular ear, whereas the clinical data of Keefe et al. (1993), for example are averaged over groups of infants with substantial inter-subject variability. Averaging across a group may cancel out fine features of the response. For example if different subjects have different resonance frequencies (as seen in the individual curves in Fig. 9), the average will display a flatter, smeared resonance, making it hard to compare the amplitude maximum and hard to draw conclusions about the resonance frequency. (2) There are substantial differences between our measurements and those of Keefe et al. (1993), which may be attributed to factors besides inter-subject variability, such as differences in the measurement devices, different screening of the subjects before inclusion in the study, etc. In addition, in the clinical measurements of Keefe et al. (1993), the earplugs were foam which may not provide a hermetic seal. This could explain the somewhat lower admittance response in their study in comparison with our clinical data, which were obtained with sealed earplugs. (3) During the first months after birth, the ear response is highly age dependent (e.g. Holte et al. 1991; Keefe et al. 1993), particularly for the first month of age. Hunter et al. (2010, Fig. 7) reported that within ∼100 h after birth, the reflectance response of the ear alters by more than 50 % at 2000 Hz. Our model is for a 22-day-old baby, while the data of Keefe et al. are for somewhat older babies, around 1 month old. A more compliant canal and TM in younger infants may increase the admittance magnitudes and shift the resonance to lower frequencies. (4) Biological tissues can be expected to have frequency-dependent behaviour (e.g. Cheng et al. 2007; Luo et al. 2009a, b; Motallebzadeh et al. 2013a, 2015), but in the models here, all material properties are assumed to be constant across frequencies. Such potential frequency dependence should be taken into account when the models are refined.

Sensitivity Analysis

In this study, the effects of geometrical variability were investigated by simple scaling of the x, y and z dimensions. However, other geometrical variations, such as the thickness of the TM, the shapes and sizes of the ossicles, the orientation of the canal and the cross-sectional dimensions of the canal, could be studied. Sensitivity analyses of such geometrical parameters would require more information about the inter-subject anatomical variations of newborn ears and also about maturation effects, particularly in the first months of life.

As stated in the “Introduction” section, the material properties of the ear undergo significant alterations with age, particularly in the first months of life, and their values are even less well known than for adults. We performed two sets of analyses to investigate the sensitivity of the model outputs (in particular, the maximum admittance values and corresponding frequencies) to the parameters.

The Morris method enables us to investigate the interaction and nonlinear effects of parameters as well as the overall importance of their effects on the output. Morris (1991) stated that “where important nonlinearity or interaction exists, an experiment of any design that is small relative to the number of inputs will generally not produce enough information to resolve the nature of these effects”. However, combined with information about the nonlinearities that we obtained from the one-parameter-at-a-time sensitivity analysis, the Morris method can provide preliminary suggestions about the nature of these effects, at least for some parameters. As stated in the “Sensitivity Analysis” section, for each parameter, we performed simulations for 10 randomly selected combinations of parameter values, as a trade-off between completeness and computation time. The conclusions could be strengthened by running more simulations.

The results of the sensitivity analysis provide information about the relative importance of different material parameters and which ones should be focused on to obtain more accurate values. In addition, the results provide insight into the sensitivity of the admittance data to possible pathologies or abnormal anatomical variations. For instance, a pathological condition that alters the stiffness and mass of the TM will result in significant changes in the admittance magnitude and resonance frequency. On the other hand, admittance data cannot provide accurate information about parameters or components that do not influence the admittance response significantly, such as the density of the ossicles.

Significance

The problems with immittance measurements in newborns and infants at low frequencies have been reported frequently in the literature (e.g. Paradise 1982; Holte et al. 1991), and they were attributed to the anatomical differences between adults and newborns, and especially to the contribution of the canal wall to the total input admittance response at low frequencies because of its compliant characteristics (e.g. Keefe et al. 1993). However, a quantitative understanding of the underlying mechanisms affecting the immittance data has been lacking. In this study, we performed numerical modelling of the input admittance response of a normal newborn ear up to 2 kHz. This frequency range is wide enough to allow investigation of the ear-canal and middle-ear resonances at the frequencies of traditional low-frequency tympanometry and more recent “high-frequency” (1-kHz) tympanometry (e.g. Margolis et al. 2003; Shahnaz et al. 2008).

Abnormalities in the ear canal and middle ear (e.g. the presence of debris, amniotic fluid and mesenchyme in the newborn canal and middle-ear cavity), as well as growth and development that result in differences in the geometrical and mechanical properties of the tissues, affect the input immittance response of the ear. In this study, we investigated the influence of the material properties, the volume of the middle-ear cavity and some geometrical variations. This provides a basis for future study of the effects of the presence of residual fluids and debris and of other geometrical variations such as the depth of the probe insertion and the degree of occlusion of the ear canal. In future modelling, it will be important to test the range of applicability of the approximations made here, especially in order to model the higher frequencies of wideband tympanometry, and the present linear dynamic modelling will need to be combined with our previous nonlinear static modelling of the canal wall and middle ear (Qi et al. 2006, 2008).

As stated in the “Introduction” section, energy absorbance and reflectance measurements in the newborn are dependent on the probe position in the canal, due to the compliant canal wall which absorbs some portion of the acoustic energy, unlike the situation in the adult ear. The characteristic admittance of the newborn ear canal is also frequency dependent (e.g. Keefe and Simmons 2003), and this should be taken into account in any further investigation of the energy response of the newborn ear. The admittance of the middle ear is dominant at frequencies around its resonance (Holte et al. 1991; Keefe et al. 1993) but, since this frequency may vary in different newborns, admittance measurements at multiple frequencies can provide more information about the middle-ear status.