Abstract
In Magnetic Resonance (MR), hardware limitation, scanning time, and patient comfort often result in the acquisition of anisotropic 3D MR images. Enhancing image resolution is desired but has been very challenging in medical image processing. Super resolution (SR) reconstruction based on sparse representation and over-complete dictionary has been lately employed to address this problem; however, these methods require extra training sets, which may not be always available. This paper proposes a novel single anisotropic 3D MR image upsampling method via sparse representation and over-complete dictionary that is trained from in-plane high resolution slices to upsample in the out-of-plane dimensions. The proposed method, therefore, does not require extra training sets. Abundant experiments, conducted on simulated and clinical brain MR images, show that the proposed method is more accurate than classical interpolation. When compared to a recent upsampling method based on the non-local means approach, the proposed method did not show improved results at low upsampling factors with simulated images, but generated comparable results with much better computational efficiency in clinical cases. Therefore, the proposed approach can be efficiently implemented and routinely used to upsample MR images in the out-of-planes views for radiologic assessment and post-acquisition processing.
Index Terms: Magnetic resonance imaging, Over-complete dictionary, Super resolution reconstruction, Sparse representation
I. Introduction
Spatial resolution in magnetic resonance imaging (MRI) depends on multiple factors, but is limited by the MRI hardware, tissue relaxation times and image contrast requirements, acquisition time, and patient comfort. In a trade-off to avoid prolonged scans to reduce the risk of subject motion and increase patient comfort, while maintaining high signal-to-noise ratio and contrast-to-noise ratio, many MRI scans are performed with relatively few slices but with rather large slice thickness. The acquired images often have higher in-plane resolution (i.e. in the phase-encoding and frequency-encoding dimensions) than the out-of-plane resolution (or the slice-select direction, also referred to as through-plane dimension), thus have anisotropic voxels (i.e. rectangular voxels with one direction longer than the other two) that are longer in the slice select direction. This results in significant partial voluming effect (PVE) in the out-of-plane views. Such low resolution (LR) images pose limitations on the performance of voxel-wise analysis, image segmentation, and other post-processing algorithms. Standard interpolation methods, such as nearest neighbor, bilinear, bicubic, and B-spline interpolations, may be used to scale up the LR images, but result in blocky edges.
Super-resolution (SR) techniques have emerged as efficient methods to improve the resolution of images. The idea behind SR is to reconstruct a high resolution (HR) image as accurately as possible based on single or multiple low-resolution images. In 2001 and 2002, initial attempts were made to adopt SR algorithms from the computer vision community to medical imaging with a focus on MRI [1]. The MRI framework is particularly well adapted to the application of SR techniques because of the control one has over the acquisition process [2]. The SR methods have shown to improve the trade-off between resolution, signal-to-noise ratio (SNR) and acquisition time of specific MR imaging sequences [3].
SR reconstruction can be performed both in the frequency domain and the spatial domain. The frequency-domain SR methods are simple, but the observation models are limited to global translation motion and linear space invariant blur. Besides, it is difficult to utilize the spatial prior information. On the other hand, in the spatial-domain SR methods, more comprehensive generative models, and spatial prior information may be used to achieve improved reconstruction accuracy. In the following discussion we focus on SR MRI methods in the spatial domain.
Previously in MRI multiple images of the same subject with small shifts were acquired to reconstruct the HR image aiming to improve both the in-plane and out-of-plane resolution. In [4] the authors tried to improve the in-plane resolution. This method was questioned by [5] since the in-plane images obtained by shifting the field-of-view (FOV) involved the acquisition of the same points in k-space (i.e. spatial frequency domain, where information about the frequency of a signal and where it comes from in the patient is stored), which means they contained the same information. In [6] variable demodulation frequency was used to obtain shifted sampling in the image space for in-plane SR. In [7] the authors compared the combination of images acquired at the same sample points in k-space but shifted afterwards, and the combination of the same number of images acquired at shifted positions through changes in demodulation frequency. They found that the HR images obtained by the latter method contained additional details in the form of image features, suggesting that new information was added through a denser sampling of the point-spread function (PSF). This study confirmed that the in-plane resolution in MRI was dependent on the effective width of the PSF and the extent of the k-space sampling.
Super-resolution in the out-of-plane directions of 2D MRI scans has been more promising as 2D MR acquisition is governed by slice-selective excitation in the image domain and Fourier encoding is only performed in the phase and frequency encoding directions. Shifted, rotated, or orthogonal anisotropic slice acquisitions therefore naturally contain additional information that can be used in SR reconstruction. Greenspan et al. [1] applied SR method to combine several orthogonal 2D MRI acquisitions to improve the out-of-plane resolution. The results were encouraging. Many methods from the SR reconstruction literature have been adopted to improve the out-of-plane resolution of MRI to generate isotropic (symmetrical) voxels. Typical reconstruction-based algorithms used for SR MRI are error back-projection [8], maximum a posteriori (MAP) estimation [9] and projection into convex sets [10]. Obviously, SR methods that combine multiple LR images for resolution enhancement rely on an exact correspondence between images. This may be achieved using image registration. The reconstruction results are highly dependent upon original alignment of images or the registration accuracy. These techniques have evolved into complex algorithms that correct for motion at the slice level and combine the image information in a robust fashion in an application like fetal MRI [11].
In another, more common scenario, improving resolution through upsampling is desired where no additional scans are available. The single-frame SR reconstruction has emerged to address this problem, with the specific aim of estimating the best possible HR image from only one single LR image. These techniques are naturally compared to interpolation algorithms that are routinely used for image upsampling (e.g. nearest neighbor, bilinear, bicubic, B-spline, and windowed Sinc interpolations). While high-order B-spline and windowed Sinc kernel functions provide good, practical estimations of the ideal Sinc interpolator, all these techniques are bounded by fundamental performance limits as they do not use any prior knowledge about image structure or appearance in upsampling.
A recent trend in SR reconstruction is learning-based methods which exploit the natural redundancy and self-similarity of images. These methods have shown competitive results compared to high order interpolation. The two most successful classes of techniques in this category use Non-local Means (NLM) and Sparse Representations. The NLM method was first proposed in [12] for image denoising. In [13], [14], the NLM approach was adopted to SR reconstruction in MRI. A feature-based multi-modality approach was proposed and generated better results in [15]. Sparse representation, which has shown great promise in processing natural images, has also been successfully applied to single-image SR [16], [17]. In [18], the algorithm from [16], [17] were applied to single anisotropic 3D brain MR image, with a knowledge-driven patch selection criteria based on brain tissue segmentation.
Despite the overall satisfactory performance of the learning-based single-image SR methods, they require extra HR reference images and training sets, and are typically demanding on computational resources. These will significantly reduce the applicability of these techniques in clinical practice. Based on the above analysis, and to mitigate the limitations of the current techniques, this paper proposes a new approach to upsample a single anisotropic 3D MR image without extra training sets based on sparse representation and over-complete dictionary. The proposed method is compared with classical interpolation and a state-of-the-art NLM-based SR approach [13], which also does not require an HR reference image but does not use the in-plane HR images either. Experiments were performed with both simulation and real clinical 3D brain MR images, showing that the proposed method achieves much better results than classical interpolation methods. In clinical MR images, this approach outperforms the NLM-based method both in terms of accuracy and the execution time and memory usage.
The rest of the paper is organized as follows. Section II provides a general formulation for SR reconstruction using sparse representation and over-complete dictionary. Section III describes the details of the proposed method. Extensive experimental results and analysis are presented in Section IV. Section V contains the concluding remarks.
II. FORMULATION
We begin our journey with a description of the theory behind SR reconstruction. The SR problem can be mathematically stated as:
| (1) |
Where Xh is the original HR image, D is the down-sampling operator, B is the blurring operator, G is geometric transformation, ν is an additive noise, Yl is the LR image. Equation (1) means the observed LR image Yl is the downsampled, blurred, transformed and noisy version of Xh. The goal of this problem is to recover Xh as accurately as possible based on the LR observation Yl. This is an ill-posed problem and has no unique solution, so we need regularizers to obtain a unique optimal solution for this problem. Since we perform the analysis at the level of small patches, ensuring to make use of the image redundancy, the formulation is rewritten in the following form:
| (2) |
Where and are patches respectively extracted from the LR and HR images at location k. is with size (n × s) × (n × s) and is with size n × n, s is the upsampling scale. νk is the noise on the patch k. Without loss of generality, (2) can be written as
| (3) |
The assumption of pattern redundancy of MR images means information can be sparsely coded. A patch can be sparsely represented by α over the dictionary A, namely:
| (4) |
| (5) |
and mean the number of non-zeros in vector or is much smaller than the sparsity sp, which is the number of the atoms of Ah and Al we use to represent the and .
According to (3) and (4), we can get , that is , where ε is related to noise νk. So which means can be represented by sparse representation over dictionary MkAh. So LR dictionary and HR dictionary can share the same sparse representation, i.e. . Both LR and HR dictionaries are over-complete, with more atoms than signal dimensions, allowing to represent a wide range of signal phenomena.
Supported by the above theory, the SR method based on sparse representation and over-complete dictionary is defined as follows: LR and HR dictionaries are trained from the training set. Then the observed LR image is sparsely represented over the trained LR dictionary. As assumed above, the sparse representations of the LR and HR image are the same, so based on the obtained sparse representation and trained HR dictionary, HR image is reconstructed. The above model based on sparse representation can also be referred as sparse land. This model constructs a connection between HR patches and the corresponding LR patches, which is exploited to recover the HR image.
III. Proposed Method
A. Motivations
For the SR reconstruction of single anisotropic 3D MR image based on over-complete dictionary, one key point is the construction of relevant learning database, i.e. the training set. But sometimes no extra training set is provided. To solve this problem, we should construct the training set from the anisotropic 3D MR image itself.
The more similar the observed LR image is to the training examples, the better reconstruction results we may obtain. Furthermore, the training set should include HR images and their corresponding LR images to learn the relationship between them. So the training examples should be HR and similar to the out-of-plane slices of anisotropic 3D MR image. It has been proven in [19] that the local self-similarity of anatomical features occurs both within the same plane and across the planes. That means the out-of-plane patches are similar to the in-plane patches. Meanwhile, the in-plane slices from anisotropic 3D MR image are HR. This is the rationale behind constructing the training set based on the in-plane patches.
Based on the above analysis, this paper utilizes in-plane HR patches from anisotropic 3D MR image to construct the training set for the over-complete dictionaries.
B. The Proposed Algorithm
The proposed SR method includes two main phases: training and reconstruction. The procedure is shown in Algorithm 1. The details are described in the following.
Algorithm 1.
The proposed Super-resolution approach.
| Input: |
|
Io: Single anisotropic 3D MR image with a slice dimension a × b and c slices. |
| s: In-plane to out-of-plane resolution ratio. |
| n: Size of patches extracted from LR images. |
| o: The overlap of LR patches. |
| Output: |
|
Iu: Upsampled isotropic 3D MR image with size a × b × (c × s). |
Step 1 Dictionary training
Step 1.1 Training set construction
Collect in-plane HR 2D slices , j = 1,2, …, c with size a × b from Io, where .
Produce the corresponding LR images , j = 1,2, …, c via averaging the near srows or columns.
-
Extract overlapped patches and , where k is the location of the patches, means extract the HR/LR patches from corresponding HR/LR slices at location k. is with size (n × s) × (n × s), is with size n × n, overlapped voxels number for and are respectively (o × s) and o.
The patch pairs construct the training set.
Step 1.2 Pre-processing
Remove the low-frequencies from , and extract features from , filters = {G,GT,L,LT}, where G = [1,0,−1], L = [1,0,−2,0,1]/2.
Perform dimensionality reduction by principal component analysis (PCA) over .
Step 1.3 Dictionary training
Based on the processed training set, train over-complete dictionary Al and sparse representation for by K singular value decomposition (K-SVD) algorithm companied with orthogonal matching pursuit (OMP) method, so that . Then obtain corresponding Ah for HR patches based on , to satisfy .
Step 2 Isotropic 3D MR image reconstruction Step
Step 2.1 Pre-processing
Interpolate each image of with a slice dimension a × c to the destination size using bicubic interpolation algorithm by factor s.
Cut every LR slice into patches with size n × n and overlapped voxels o.
Extract features from by the method used in the training phase.
Dimensionality reduction is performed again by PCA over .
Step 2.2 Reconstruction
For each , i = 1,2, …, b,
Sparse code by OMP method using the trained LR dictionary Al, and get the corresponding sparse representations .
Recover the HR patches by multiplying and HR dictionary Ah.
Add low frequency to HR patches.
Merge the HR patches by averaging the overlapped parts, and get the final reconstructed slice . Iu is the 2D slice stack of .
1) Dictionary Training Phasek
The dictionary training stage can be divided into three parts: training set construction, image pre-processing, sparse representation and dictionary training.
a. Training Set Construction
The training set is constructed by the HR in-plane slices. When constructing the training set, we obtain the corresponding LR images by averaging adjacent rows or columns. This simulates PVE (Partial Volume Effects) as a consequence of LR image acquisition. Besides, we cut the images into small patches to form the training set. This process is to utilize the redundancy of the images and reduce the computation time.
b. Image Pre-Processing
We subtract low frequency information from HR patches and extract the structure features for each patch, so that the dictionary represents image textures rather than absolute intensity. Here, the low frequency is the mean pixel value, which is the same with the LR patches. As mentioned before, the HR image loses its high-frequency information through the acquisition process, and our task is to recover the high-frequency information. That is why we use the high frequency features as the examples to train the dictionary. Another pre-processing operation is dimensionality reduction over the feature vectors by PCA. This simultaneously reduces computations and improves the reconstruction accuracy.
c. Dictionary Training and Sparse Representation
The dictionary and the corresponding sparse representation encode the connection between the LR patches and the corresponding HR patches. Based on this connection the HR patches can be reconstructed. The objective of this step is to express the LR patches by dictionary and sparse representation as accurately as possible based on the sparsity prior. This is an optimization problem which can be mathematically expressed in the following way:
| (6) |
An efficient algorithm is needed to obtain the best Al and . In this paper, we choose K-SVD [20] to train the dictionary for the sparse representation. The K-SVD algorithm is an efficient iterative method that alternates between sparse coding based on the current dictionary and updating the dictionary atoms to better fit the examples. This method is generalized from the K-means clustering process. It is flexible and can work with any pursuit method. In this paper, we use the OMP (orthogonal matching pursuit) [21] algorithm as it is simple and only involves the computation of inner products of matrices.
2) Up-sampling LR Anisotropic 3D MR Image
Based on the HR and LR dictionaries trained from the anisotropic 3D image itself, we up-sample the image through the following steps. Firstly, feature extraction and dimensionality reduction are performed again as in the dictionary training phase. The next step is reconstruction. For each , we get the sparse code for by OMP method using the trained LR dictionary Al based on (6). Because HR patches and corresponding LR patches share the same sparse representation, we can get the HR patches by multiplying and the trained HR dictionary Ah. In the training phase, we subtract low frequency from the HR patches. Therefore, the recovered HR patches so far do not contain the low frequency information. We should add the low frequency to the reconstructed HR patches. In this method, we process small patches not the whole image, so we should connect all the small patches into the whole image. The final HR image is constructed by solving the following minimization problem with respect to :
| (7) |
where Rk means an extractor to extract patches at location k from high frequency resulting image, . The extracted patches should be as close as possible to the reconstructed patches . This problem can be solved by the following equation:
| (8) |
It is equivalent to putting in their proper location, averaging the overlap regions, and adding the low frequency content of to generate the final image .
IV. Experiments
To demonstrate the advantages of the proposed approach, we conducted extensive experiments. This section has been divided into 4 parts. The first part describes implementation details including the selection of the parameters in the proposed SR reconstruction process. In the second part we introduce the experimental data sets. Then, in part 3, we talk about the quantitative and qualitative evaluation methods. Finally, in part 4 we have compared the proposed method with classical interpolation and a state-of-the-art upsampling method based on the Non-Local Means approach [13] to demonstrate the superiority and impact of the proposed method. Based on the results of experiments, we analyze how the slice thickness, noise, and pathology affect the accuracy of the proposed method.
A. Implementation Details
All algorithms were implemented in MATLAB R2014a, running on a Windows machine with 2 3.10 GHZ Intel Core i5 CPUs and 4.00GBytes of RAM. Since the proposed methodology may be implemented in a number of different manners, we clarify the following implementation details: K-SVD was chosen as the dictionary training method and OMP as the sparse representation method; Based on Table I and Table II, which present the reconstruction results of simulated axial T2W MR image with 2mm slice thickness, in a trade-off between accuracy and efficiency, we always used 3 × 3 LR patches with 1 pixel overlap between adjacent patches, corresponding to (3 × scale) × (3 × scale) patches with overlap of (1 × scale) for the HR patches. Feature extraction was done using gradient and Laplacian filters. For initial upsampling we used bicubic interpolation; for the dictionary training phase, 40 iterations was experimentally found to provide a good trade-off between the efficiency and accuracy; number of dictionary atoms and the maximum sparsity for the sparse representation were set to 512 and 3, respectively, following [16].
Table I.
Reconstruction results using the proposed method over different patch sizes
| Patch Size | 3×3 | 5×5 | 7×7 | 9×9 |
|---|---|---|---|---|
| PSNR(dB) | 31.5719 | 31.2039 | 30.8332 | 30.6010 |
| SSIM | 0.9845 | 0.9830 | 0.9802 | 0.9784 |
| Time(s) | 466.2860 | 142.3267 | 81.7516 | 57.4088 |
Table II.
Reconstruction results using the proposed method based on 3×3 patch over different overlap pixels
| overlap | 0 | 1 | 2 |
|---|---|---|---|
| PSNR(dB) | 31.1907 | 31.5719 | 31.7358 |
| SSIM | 0.9830 | 0.9845 | 0.9850 |
| Time(s) | 192.8939 | 466.2860 | 1701.6480 |
B. Brain MR Data Sets
To validate the proposed method, a synthetic dataset and several real MR images were used. Various simulated T2-weighted (T2W) brain MR images were obtained from the publicly available BrainWeb database [22], including normal and pathologic (multiple sclerosis) MR images, non-noisy and noisy ones. The HR T2W volumes had 181 × 217 × 181 voxels with a resolution of 1 mm × 1 mm × 1 mm. Different percentage noise (0%, 1%, 3%, 5%, 7% and 9%) levels were used to investigate the noise influence. The noise in the simulated images has Rayleigh statistics in the background and Rician statistics in the signal regions. The “percent noise” number represents the percent ratio of the standard deviation of the Gaussian white noise versus the signal for a reference tissue. For T2W images, the reference tissue is CSF (Cerebrospinal Fluid).
To test the proposed approach on real clinical data, three FSE (Fast Spin Echo) T2W brain MR images were collected, with different slice-selection directions but for the same subject. Those three-plane MR images all had a slice thickness of 2.0 mm, and a pixel size of 0.46875 mm × 0.46875 mm. The axial slice stacks had a slice dimension of 408 × 512 and 80 slices, the coronal scan had a slice dimension of 408 × 512 and 100 slices, while the sagittal scan had a slice dimension of 512 × 512 and 83 slices.
C. Evaluation Method
To quantitatively and qualitatively evaluate the performance of the proposed method over different brain data sets, we introduce four different methods in this section for two scenarios:
1) Images with ground truth
In the experiments, if we have an original HR image, considered as the ground truth, comparing the reconstruction with the original image is a good way to evaluate the results. The following two performance metrics are calculated when the ground truth is available:
Peak Signal-to-Noise Ratio (PSNR) is defined as:
| (9) |
Where MSE(Xo, Xh) stands for means square error, quantifies the pixel intensity difference between the original HR image Xo and the corresponding SR reconstruction Xh, using . and are the image intensity at location k, d is the dynamic range of the intensity value, i.e. d = max(Xo) − min(Xo). Typically, the PSNR values are between 25 dB and 50 dB. A higher value of PSNR indicates a better performance of the reconstruction method.
Structural Similarity Image Metric (SSIM) [23]
It measures the similarity between two images, with a definition that is more consistent with the human visual perception of image quality. Under the assumption that human visual perception is highly adapted to extracting structural information from a scene, SSIM is formulated as:
| (10) |
Where μo and μh are the mean intensity of images Xo and Xh, respectively; σo and σh are the standard deviation of images Xo and Xh, which are estimates of the signal contrast; σoh is the covariance of Xo and Xh, C1 = (K1L)2 and C2 = (K2L)2, K1 ≪ 1 and K2 ≪ 1 are small constants and L is the dynamic range of the intensity values. In this paper we use K1 = 0.01 and K2 = 0.03. SSIM values are between 0 and 1, where a higher value indicates the better reconstruction results.
2) Images without ground truth
In reality, for example in clinical data, no original HR reference image is available, so we cannot evaluate the reconstruction results by comparing the similarity with a ground truth image. Alternative methods to evaluate the results are as follows:
Visual inspection
visual assessment of images is also a precious method to compare and judge the benefit of proposed methods; however, it is obviously a subjective method, and also may not be easy when large datasets should be evaluated and compared. In this paper, we display several 2D reconstructed slices and evaluate the slices by viewing the image details.
Intensity profile
the intensity profile of an image is the set of intensity values taken from regularly spaced points along a line segment or multiline path in an image. The fundamental problem of SR reconstruction can be stated as restoring some high-frequency information (like edges) that has been lost during the acquisition process. An effective SR reconstruction technique should be able to recover these high-frequencies. Intensity profile can show intensity value changes at the interfaces between different tissues, thus may be used as a surrogate measure of how edge features appear and are distinguished in the image. We also evaluate the reconstruction results of our clinical MR experiments based on image intensity profiles in this paper.
D. Experimental Results and Analysis
In this part, we compare our proposed method with classical interpolation algorithms and a state-of-the-art single-image SR approach on both simulated database and real medical image. Furthermore, we analyze the influence of different factors to the proposed method based on the experiment results.
1) Comparison with Classical Interpolation Methods
To evaluate the efficacy of the proposed method, we perform comparisons with classical interpolation algorithms, including the nearest neighbor, bilinear, bicubic, B-spline interpolation. Different MR images have various features: different slice thickness, noise and lesions. So we compared the proposed method with the classical interpolation method on 3D T2W MR images with different features respectively.
Firstly, we constructed a down-sampled version of a normal non-noisy simulated HR T2w image. Axial slice stacks with different slice thickness (2 mm, 3 mm, 4 mm, 5 mm, 6 mm and 7 mm) were simulated. Adjacent slices were averaged to produce different slice thicknesses. This simulates the Partial Volume Effect (PVE). PVE increases as the slice thickness increases. For example, three adjacent slices along the Z direction were averaged into one slice to simulate an anisotropic acquisition at 1 mm × 1 mm × 3 mm resolution. The slice thickness became 3 mm and the matrix size was 180 × 216 × 60. The out-of-plane slices were reconstructed based on the dictionary trained from the in-plane slices in the axial direction. These simulated LR 3D MR images were upsampled to 1 mm × 1 mm × 1 mm. To see the relative degree of improvements, in this section we report the results of comparing the classic interpolation algorithm and the proposed method over normal non-noisy axial 2D slice stacks with slice thickness of 2 mm, 3 mm, 4 mm, 5 mm, 6 mm, 7 mm. Table III shows that the bicubic and B-spline interpolations generate very similar results and the proposed method generates the best results in terms of both PSNR and SSIM values. The improvements achieved in these metrics by using the proposed method are comparable to the amount of improvement obtained from higher-order interpolation methods (bicubic and B-spline) as compared to the nearest neighbor interpolation. This indicates major improvements. The PSNR/SSIM values obtained from the proposed method are 31.555 dB/0.9849 in 2 mm and 26.791 dB/0.9544 in 3 mm. The PSNR/SSIM values drop rapidly as the slice thickness increases from 2 mm to 3 mm. The reason for the influences is that the up-sampling scalar increases as the slice becomes thicker. The limitation of most SR algorithms is that their performance deteriorates quickly when the magnification factor is only moderately large.
Table III.
Reconstruction results using classical interpolation method and the proposed method over non-noisy MR images
| 2mm | 3mm | 4mm | 5mm | 6mm | 7mm | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Slice Thickness |
PSNR (dB) |
SSIM | PSNR (dB) |
SSIM | PSNR (dB) |
SSIM | PSNR (dB) |
SSIM | PSNR (dB) |
SSIM | PSNR (dB) |
SSIM |
| Nearest Neighbor | 27.105 | 0.9634 | 23.886 | 0.9178 | 22.098 | 0.8719 | 20.939 | 0.8305 | 20.142 | 0.7963 | 19.373 | 0.7576 |
| Bilinear | 28.254 | 0.9673 | 25.004 | 0.9287 | 22.859 | 0.8794 | 21.600 | 0.8385 | 20.639 | 0.7981 | 19.793 | 0.7575 |
| Bicubic | 29.613 | 0.9767 | 25.619 | 0.9388 | 23.418 | 0.8944 | 22.050 | 0.8527 | 21.033 | 0.8114 | 20.133 | 0.7700 |
| B-Spline | 30.008 | 0.9780 | 25.713 | 0.9389 | 23.460 | 0.8933 | 22.089 | 0.8509 | 21.027 | 0.8064 | 20.129 | 0.7638 |
| Proposed Method | 31.555 | 0.9849 | 26.791 | 0.9544 | 24.355 | 0.9174 | 22.803 | 0.8793 | 21.635 | 0.8382 | 20.635 | 0.7950 |
It is clear that the 0% noise case is an idealization of the real MR image acquisition. To compare the classic interpolation method and proposed method on noisy 3D MR images, another experiment was performed on T2W simulated MR images from BrainWeb with different noise levels (0%, 1%, 3%, 5%, 7% and 9%). Noisy axial MR images with voxel size 1 mm × 1 mm × 2 mm and matrix size 180 × 216 × 90 were simulated. The resolution in the slice-selected direction is improved based on the trained dictionary. The results are shown in Table IV. In addition, similar experiment is repeated using the MS (Multiple Sclerosis) T2W MR images, as shown in Table V. Again, the proposed method obtains the best results in all cases, including the noisy and pathological images. The PSNR/SSIM values drop as the noise level increases.
Table IV.
Reconstruction results using classical interpolation method and the proposed method over noisy MR images
| 0% | 1% | 3% | 5% | 7% | 9% | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Slice Thickness |
PSNR (dB) |
SSIM | PSNR (dB) |
SSIM | PSNR (dB) |
SSIM | PSNR (dB) |
SSIM | PSNR (dB) |
SSIM | PSNR (dB) |
SSIM |
| Nearest Neighbor | 27.257 | 0.9636 | 27.371 | 0.9531 | 27.436 | 0.9099 | 27.164 | 0.8719 | 26.658 | 0.8436 | 26.033 | 0.8217 |
| Bilinear | 28.422 | 0.9674 | 28.491 | 0.9554 | 28.281 | 0.9028 | 27.674 | 0.8541 | 26.893 | 0.8167 | 26.064 | 0.7871 |
| Bicubic | 29.794 | 0.9768 | 29.821 | 0.9651 | 29.371 | 0.9156 | 28.498 | 0.8708 | 27.520 | 0.8367 | 26.561 | 0.8098 |
| B-Spline | 30.200 | 0.9782 | 30.201 | 0.9660 | 29.619 | 0.9150 | 28.609 | 0.8691 | 27.539 | 0.8345 | 26.522 | 0.8071 |
| Proposed Method | 31.602 | 0.9846 | 31.537 | 0.9729 | 30.582 | 0.9251 | 29.271 | 0.8837 | 28.046 | 0.8535 | 26.941 | 0.8295 |
Table V.
Reconstruction results using classical interpolation method and the proposed method over pathologic MR images
| Nearest Neighbor |
Bilinear | Bicubic | B-Spline | Proposed Method |
|
|---|---|---|---|---|---|
| PSNR(dB) | 28.344 | 29.612 | 31.022 | 31.441 | 32.696 |
| SSIM | 0.9644 | 0.9687 | 0.9780 | 0.9793 | 0.9842 |
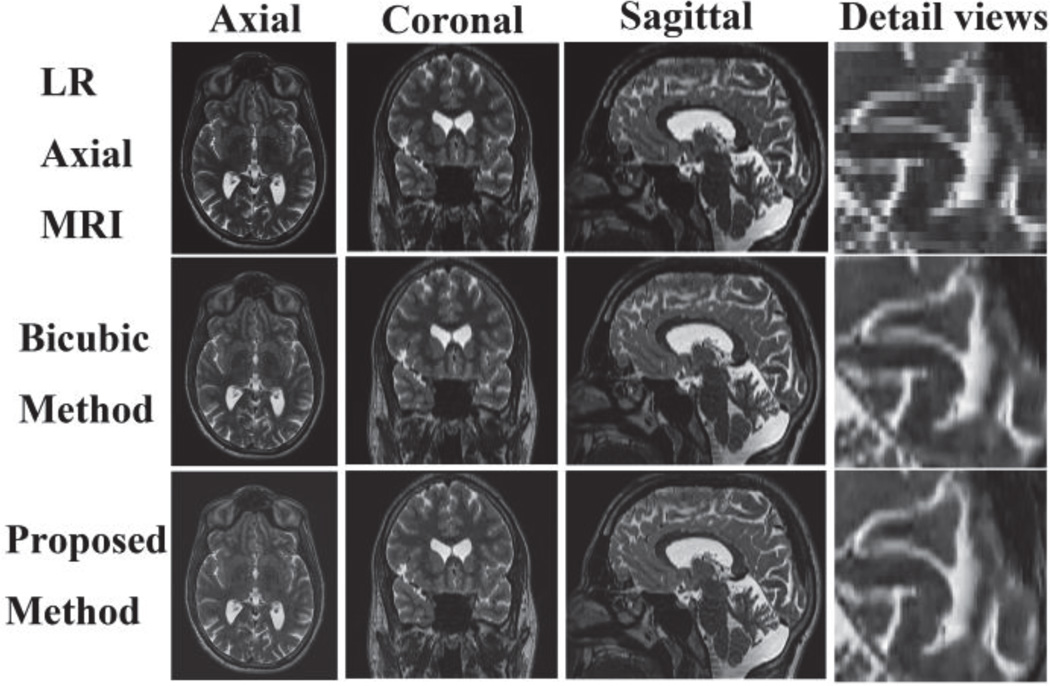
Experiments were also performed on real clinical data. Axial 2D slice stacks (voxel size: 0.46875 mm × 0.46875 mm × 2.0 mm) was up-sampled to 1 mm × 1 mm × 1 mm using bicubic interpolation and the proposed method. In Fig. 1, a visual comparison of the results is shown. One can see that the reconstruction using the proposed approach shows a better anatomical content. A close up of the image clearly shows the reconstruction using the proposed method is significantly less blocky and blurry. The proposed method is visually superior in particular near the image edges.
Fig. 1.
Clinical axial slice stacks reconstruction using bicubic interpolation and the proposed method
2) Comparison with Non-Local Means SR method
Furthermore, as mentioned before, we compared the proposed method with a recent SR method based on NLM (Non-local Means) without a reference image [13]. This technique was also shown to outperform the standard interpolation methods. First, simulated normal non-noisy axial 2D slice stacks, with 2 mm-7 mm slice thickness, were up-sampled by NLM and the proposed method. The results can be observed in Table VI. For slice thickness of 2 mm and 3 mm, the NLM method performs slightly better than the proposed approach. That is because the NLM algorithm optimizes the reconstruction results by mean preservation constraint, which has not been implemented in our proposed method. Although this step could have slightly improved the accuracy of our proposed method, it is time-consuming. Considering the trade-off between accuracy and computation cost, we omit this optimization step to make the proposed method more suitable for clinical applications. In addition, those two methods generate very similar results at higher upsampling factors (i.e. for slice thicknesses of 4 mm, 5 mm, 6 mm, and 7 mm). In general, the PSNR/SSIM values drop rapidly as the slice thickness increases.
Table VI.
Reconstruction results using the proposed method and NLM over non-noisy MR images
| Slice Thickness |
2 mm | 3 mm | ||
| PSNR | SSIM | PSNR | SSIM | |
| NLM | 33.2143 | 0.9899 | 27.7150 | 0.9629 |
| Proposed Method | 31.5550 | 0.9849 | 26.7908 | 0.9544 |
| Slice Thickness |
4 mm | 5 mm | ||
| PSNR | SSIM | PSNR | SSIM | |
| NLM | 24.8521 | 0.9239 | 22.9371 | 0.8768 |
| Proposed Method | 24.3551 | 0.9174 | 22.8025 | 0.8793 |
| Slice Thickness | 6 mm | 7 mm | ||
| PSNR | SSIM | PSNR | SSIM | |
| NLM | 21.7449 | 0.8333 | 20.6463 | 0.7852 |
| Proposed Method | 21.6345 | 0.8382 | 20.6349 | 0.7950 |
Next we reconstructed normal and noisy axial 2D slice stacks with 2 mm slice thickness by NLM and the proposed method. Table VII shows that the NLM method generates slightly better results when the simulated MR images have 0%, 1% and 3% noise. However, when the noise percentages are 5%, 7% and 9%, the proposed method generates comparable results as NLM does. Again, the PSNR/SSIM values drop as the noise level increases.
Table VII.
Reconstruction results using the proposed method and NLM over noisy MR images
| Noise Percentage |
0% | 1% | ||
| PSNR | SSIM | PSNR | SSIM | |
| NLM | 33.4947 | 0.9901 | 33.2515 | 0.9776 |
| Proposed Method | 31.6016 | 0.9846 | 31.5370 | 0.9729 |
| Noise Percentage |
3% | 5% | ||
| PSNR | SSIM | PSNR | SSIM | |
| NLM | 31.6812 | 0.9312 | 29.8899 | 0.8880 |
| Proposed Method | 30.5816 | 0.9251 | 29.2708 | 0.8837 |
| Noise Percentage |
7% | 9% | ||
| PSNR | SSIM | PSNR | SSIM | |
| NLM | 28.3897 | 0.8562 | 27.1382 | 0.8312 |
| Proposed Method | 28.0463 | 0.8535 | 26.9405 | 0.8295 |
Based on the above two experiments, we conclude that the proposed method generates results that are comparable to the NLM approach in clinical cases. In clinical applications, the in-plane and out-plane resolution ratio of FSE T2W images is often bigger than 3, which means that the anisotropic MR images should be upsampled into isotropic volumes by a factor of 3 or more. The noise percentage is also usually more than 3%. The proposed method is therefore, practically as effective as the NLM method, but is more efficient.
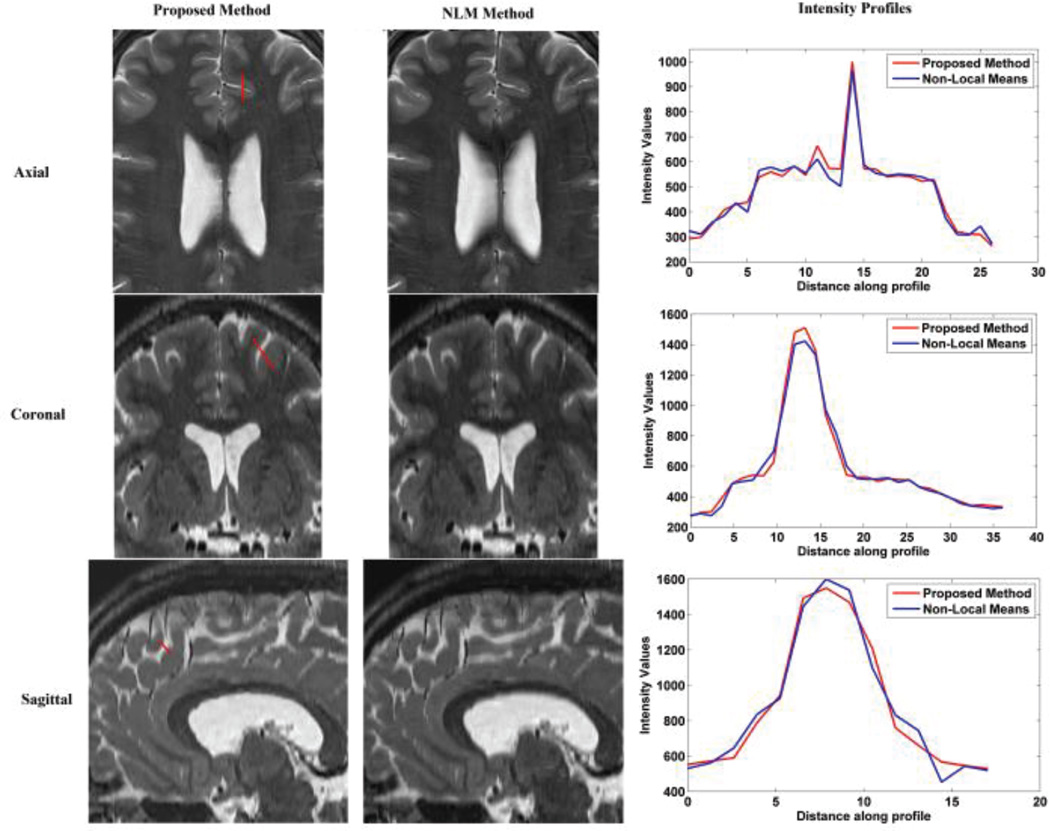
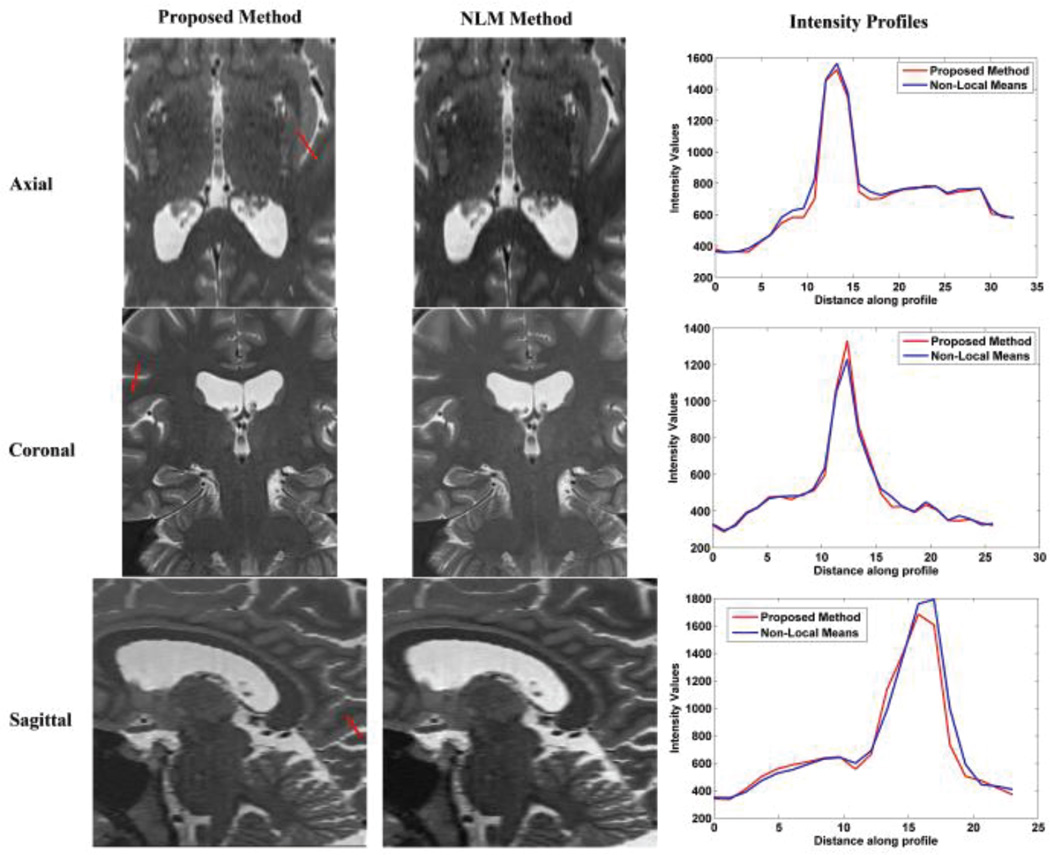
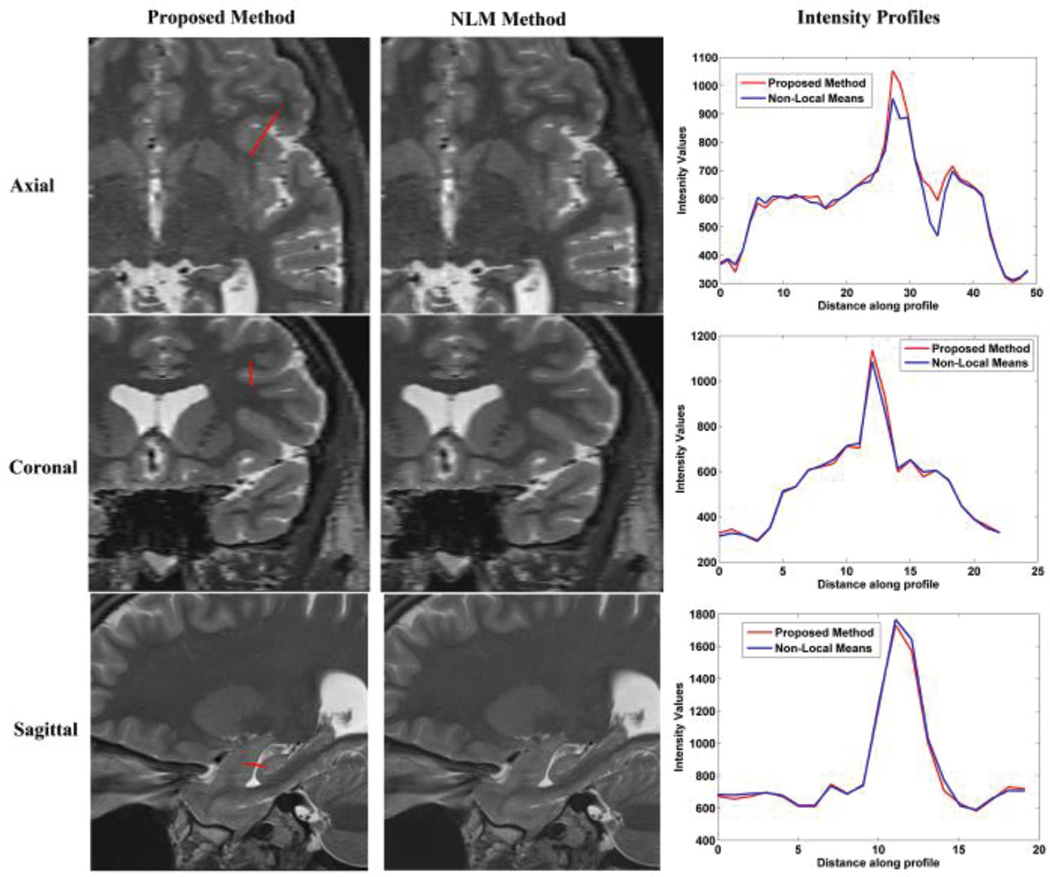
To verify our conclusion, the NLM and the proposed methods were respectively applied to clinical FSE T2W MR images, including axial, coronal and sagittal scans. The detail information of the clinical MR images were discussed in Section IV-B. The results are displayed in Fig. 2, 3, and 4. Visual comparison shows that these two methods generate similar results, and our proposed method generates slightly shaper intensity profiles which indicate better delineation of image edge features. Table VIII shows that our proposed method needs significantly less computation time and memory than the NLM method. Average computation time for the proposed method was about 2.9 minutes whereas the average computation time for NLM was 6 minutes. Moreover, average peak memory for the proposed method was about 107 Mb, while the average peak memory for the NLM was 245Mb in this experiment. Overall, we conclude that the proposed method outperforms NLM over the clinical MR images.
Fig. 2.
Reconstruction using NLM and the proposed method over axial slices stacks
Fig. 3.
Reconstruction using NLM and the proposed method over coronal slices stacks
Fig. 4.
Reconstruction using NLM and the proposed method over sagittal slices stacks
Table VIII.
Computation time and peak memory of NLM and the proposed method
| Axial | Coronal | Sagittal | Average | |||||
|---|---|---|---|---|---|---|---|---|
| Ta(s) | P.Mb (Mb) |
Ta(s) | P.Mb (Mb) |
Ta(s) | P.Mb (Mb) |
Ta(s) | P.Mb (Mb) |
|
| NLM | 345 | 179 | 352 | 179 | 394 | 377 | 364 | 245 |
| Proposed Method |
124c +41d =165 |
99 |
118c +37d =155 |
99 |
151c +47d =198 |
124 |
131c +42d =173 |
107 |
T means running time;
P.M means peak memory is used;
Training time;
reconstruction time.
3) Impact of the training set size
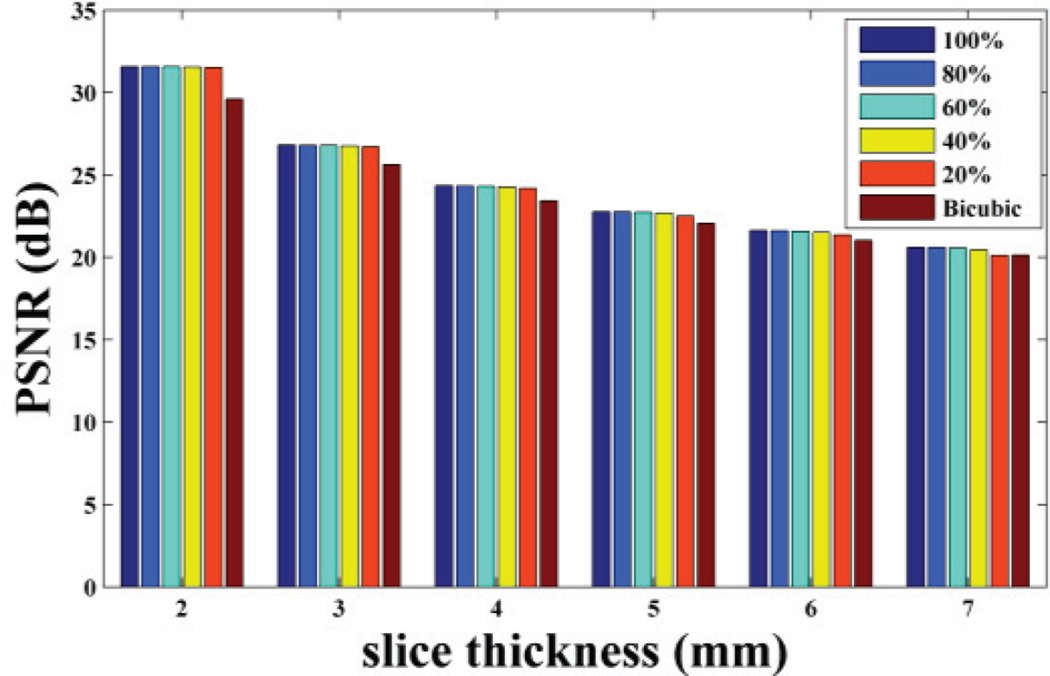
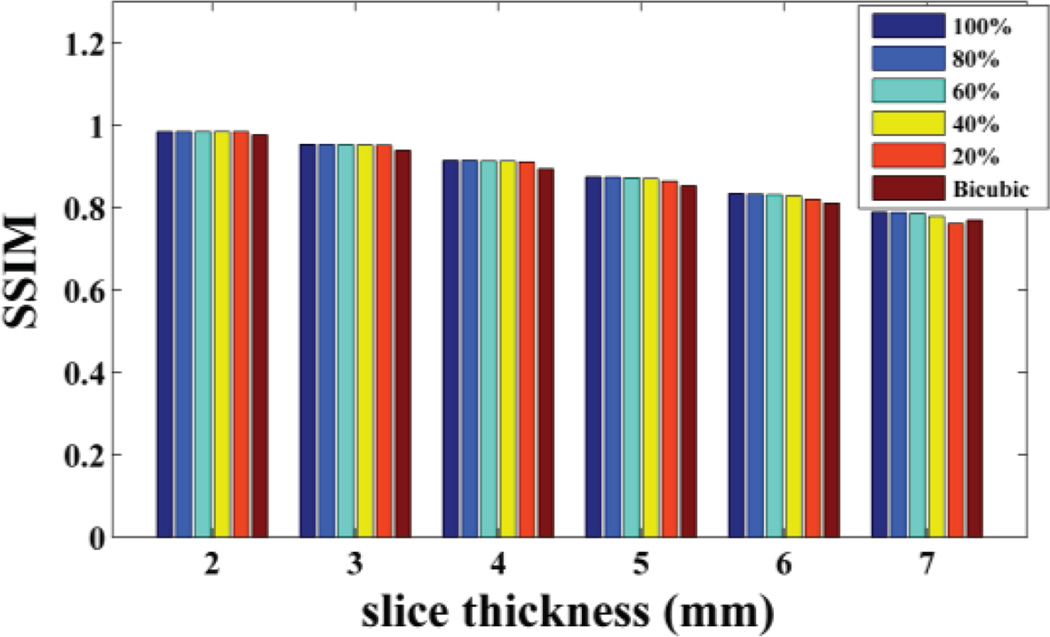
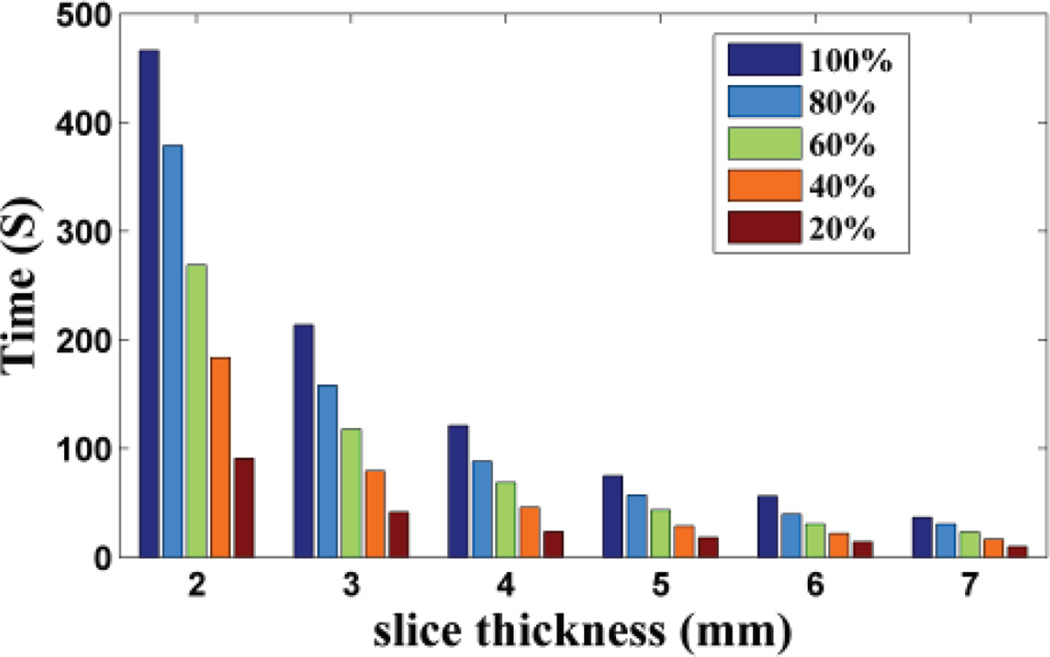
Based on the idea of the proposed method, the training set is extracted from the LR 3D MR image itself, i.e. from the HR in-plane slices. There are two choices to construct the training set: one is to select all the HR in-plane slices as the training examples, so the training set size is related to the number of slices; the other is to select only part of them to construct the training set. To test how the training set size impact the proposed method performance, we selected all the HR slices and randomly extracted part of the HR slices (including 80%, 60%, 40% and 20%) from the in-plane direction to construct the training set respectively. The reconstruction results of non-noisy axial 3D MR based on training sets of different size have been shown in Fig. 5, 6, 7. We repeated the experiments 10 times and calculated the average. Based on the results, we observed the PSNR and SSIM values decrease slightly as the training set size reduces, while the training time drops rapidly. This shows that the algorithm is robust to the training set size. But when the slice thickness is 7mm, if 20% of the available data were extracted, the proposed method is worse than the classic interpolation method (bicubic method). That is because while slice thickness increasing, the available data decreases rapidly. If part of the available data were extracted, the training set would be extremely small. That will affect the performance of the proposed method. Therefore in practice, to ensure the best performance, all available HR slices from the in-plane direction should be extracted to train the dictionary, which is already very efficient and fast than the state-of-art algorithm (NLM method).
Fig. 5.
PSNR value of the reconstruction results based on training set with different sizes
Fig. 6.
SSIM value of the reconstruction results based on training set with different sizes
Fig. 7.
Training time of training set with different sizes.
V. Conclusion
This paper presents a novel SR approach towards single anisotropic 3D MR image reconstruction based on sparse representation and over-complete dictionary without extra training sets. We train the dictionary from the in-plane HR slices. Our proposed method outperforms the classical interpolation algorithms. Furthermore, the proposed SR approach is compared with a recent single MR image SR method based on the NLM approach. Experiments show both methods can generate similar results in clinical applications, but our proposed algorithm is more efficient than the NLM-based method in terms of computation time and memory usage. The proposed approach may be used as an efficient method for upsampling anisotropic MR images in the out-of-plane dimensions.
Acknowledgments
This work was supported in part by the China Science and Technology Project of Ministry of Transport under Grant 2011318740240, by the Chongqing graduate education reformation research project under the No.yjg133005, by the Scientific and Technological Research Program of Chongqing Municipal Education Commission under Grant no. KJ1400409, and in part by the National Institutes of Health grant R01 EB018988, R01 EB013248, and R03 DE022109.
We are very thanks to the anonymous reviewers for their useful comments.
Contributor Information
Yuanyuan Jia, College of Computer Science, Chongqing University, Chongqing, China.
Zhongshi He, College of Computer Science, Chongqing University, Chongqing, China.
Ali Gholipour, Boston Children’s Hospital, Harvard Medical School, 300 Longwood Ave. Boston, MA 02115 USA.
Simon K. Warfield, Boston Children’s Hospital, Harvard Medical School, 300 Longwood Ave. Boston, MA 02115 USA
REFERENCES
- 1.Greenspan H, Oz G, Kiryati N, Peled S. MRI inter-slice reconstruction using super-resolution. Magn. Reson. Imaging. 2002 Jun.20(5):437–446. doi: 10.1016/s0730-725x(02)00511-8. [DOI] [PubMed] [Google Scholar]
- 2.Reeth EV, Tham IWK, Tan CH, Poh CL. Super-resolution in Magnetic Resonance Imaging: A review. Concept in Magn. Reson. 2012 Nov.40A(6):306–325. [Google Scholar]
- 3.Plenge E, Poot DHJ, Bernsen M, Kotek G, Houston G, Wielopolski P, Weerd LVD, Niessen WJ, Meijering E. Super-resolution methods in MRI: Can they improve the trade-off between resolution, signal-to-noise ratio, and acquisition time? Magn. Reson. Med. 2012 Nov.68(6):1983–1993. doi: 10.1002/mrm.24187. [DOI] [PubMed] [Google Scholar]
- 4.Peled S, Yeshurun Y. Superresolution in MRI: application to human white matter fiber tract visualization by diffusion tensor imaging. Magn. Reson. Med. 2001 Jan.45(1):29–35. doi: 10.1002/1522-2594(200101)45:1<29::aid-mrm1005>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 5.Scheffler K. Superresolution in MRI? Magn. Reson Med. 2002 Aug.48(2):408–408. doi: 10.1002/mrm.10203. [DOI] [PubMed] [Google Scholar]
- 6.Carmi E, Liu SY, Alon N, Fiat A, Fiat D. Resolution enhancement in MRI. Magn. Reson. Imaging. 2006 Feb.24(2):133–154. doi: 10.1016/j.mri.2005.09.011. [DOI] [PubMed] [Google Scholar]
- 7.Tieng QM, Cowin GJ, Reutens DC, Galloway GJ, Vegh V. MRI resolution enhancement: how useful are shifted images obtained by changing the demodulation frequency? Magn. Reson. Med. 2011 Mar.65(3):664–672. doi: 10.1002/mrm.22653. [DOI] [PubMed] [Google Scholar]
- 8.Ziye Y, Yao L. Super resolution of MRI using improved ibp. Int. Conf. on Computational Intelligence and Security (CIS); London, England. 2009. pp. 643–647. [Google Scholar]
- 9.Gholipour, Estroff JA, Sahin M, Prabhu SP, Warfield SK. Medical Image Computing and Computer-Assisted Intervention - MICCAI, Lecture Notes in Computer Science. Vol. 13. Beijing, China: 2010. Maximum A Posteriori estimation of isotropic high-resolution volumetric MRI from orthogonal thick-slice scans; pp. 109–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shilling RZ, Robbie TQ, Bailloeul T, Mewes K, Mersereau RM, Brummer ME. A super-resolution framework for 3-d high-resolution and high-contrast imaging using 2-d multislice MRI. IEEE Trans. Med. Imaging. 2009 May;28(5):633–644. doi: 10.1109/TMI.2008.2007348. [DOI] [PubMed] [Google Scholar]
- 11.Gholipour, Estroff JA, Warfield SK. Robust super-resolution volume reconstruction from slice acquisitions: application to fetal brain MRI. IEEE Trans. Med. Imaging. 2010 Oct.29(10):1739–1758. doi: 10.1109/TMI.2010.2051680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Buades, Coll B, Morel JM. A review of image denoising algorithms, with a new one. Multiscale Model. Sim. 2005;4(2):490–530. [Google Scholar]
- 13.Manjon JV, Coupe P, Buades A, Fonov V, Collins DL, Robles M. Non-Local MRI upsampling. Med. Image Anal. 2010 Dec.14(6):784–792. doi: 10.1016/j.media.2010.05.010. [DOI] [PubMed] [Google Scholar]
- 14.Rousseau F. A non-local approach for image super-resolution using intermodality priors. Med. Image Anal. 2010 Aug.14(4):594–605. doi: 10.1016/j.media.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jafari-Khouzani K. MRI upsampling using feature-based Non-local means approach. IEEE Trans. Med. Imaging. 2014 Jun.33(10):1969–1985. doi: 10.1109/TMI.2014.2329271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zeyde R, Eald M, Protter M. On single image scale-up using sparse-representations. Proc. Of the 7th Inter. Conf. Curves and Surfaces; Berlin, Heidelberg. 2012. pp. 711–730. [Google Scholar]
- 17.Yang JC, Wright J, Huang TS, Ma Y. Image super-resolution via sparse representation. IEEE Trans. Image. Process. 2010 May;19(11):2861–2873. doi: 10.1109/TIP.2010.2050625. [DOI] [PubMed] [Google Scholar]
- 18.Rueda, Malpica N, Romero E. Single-image super-resolution of brain MR images using overcomplete dictionaries. Med. Image Anal. 2013 Jan.17(1):113–132. doi: 10.1016/j.media.2012.09.003. [DOI] [PubMed] [Google Scholar]
- 19.Plenge E, Poot DHJ, Niessen WJ, Meijering E. Super-resolution reconstruction using cross-scale self-similarity in multi-slice MRI. 16th Intern. Conf. MICCAI; Nagoya, Japan. 2013. pp. 123–130. [DOI] [PubMed] [Google Scholar]
- 20.Aharon M, Elad M, Bruckstein A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006 Nov.54(11):4311–4322. [Google Scholar]
- 21.Tropp JA. Greed is good: Algorithmic results for sparse approximation. IEEE Trans. Inf. Theory. 2004 Oct.50(10):2231–2242. [Google Scholar]
- 22.Cocosco CA, Kollokian V, Kwan RK-S, Evans AC. Brain Web: online interface to a 3D MRI simulated brain database. Proc. of Third Intern. Conf. on Functional Mapping of the Human Brain. 1997;5(4) [Google Scholar]
- 23.Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004 Apr.13(4):600–612. doi: 10.1109/tip.2003.819861. [DOI] [PubMed] [Google Scholar]