Abstract
Clusters of transcription factor binding sites (TFBSs) which direct gene expression constitute cis-regulatory modules (CRMs). We present a novel algorithm, based on Gibbs sampling, which locates, de novo, the cis features of these CRMs, their component TFBSs, and the properties of their spatial distribution. The algorithm finds 69% of experimentally reported TFBSs and 85% of the CRMs in a reference data set of regions upstream of genes differentially expressed in skeletal muscle cells. A discriminant procedure based on the output of the model specifically discriminated regulatory sequences in muscle-specific genes in an independent test set. Application of the method to the analysis of 2710 10-kb fragments upstream of annotated human genes identified 17 novel candidate modules with a false discovery rate ≤0.05, demonstrating the applicability of the method to genome-scale data.
Technologies for large-scale assessment of gene expression have become a mainstay of the postgenome era. Such profiling studies in yeast have been analyzed to gain insights into the regulatory program of this organism (Segal et al. 2003). Unfortunately, however, application of profiling technologies in higher eukaryotes all too often yields little more than a laundry list of genes that are differentially expressed along with speculation about their potential common functions. A greater focus on mechanistic connections would be useful to address this deficiency, but the means to identify these are currently limited. Some progress towards this end has been achieved when prior models of the binding patterns of cognate transcription factors are known. Progress has been more limited when such patterns are not available. Here we describe a two-step procedure that identifies cis-regulatory modules (CRMs) de novo, and uses the resulting models as the basis of a discriminant procedure to identify additional genes in the regulon.
The CRM can be viewed as a circuit translating input signals from diverse pathways into an output, gene activity, through the binding of multiple transcription factors in a combinatorial fashion. Though regulatory circuits can be defined through extensive laboratory effort, most tissues and contexts are insufficiently characterized to allow such approaches. Although pattern discovery techniques have proven effective in the identification of transcription factor binding sites (TFBSs) for several single-celled organisms (McCue et al. 2000, 2002; Rajewsky et al. 2002a), successful applications in higher eukaryotes have been sparse and only partially effective (Aerts et al. 2003). Transcription factors can tolerate widely varying target sequences, resulting in computational binding profiles of low specificity. Such weak patterns become impossible to distinguish when regulatory regions are embedded within long candidate regions.
Cross-species comparison of sequences from orthologous genes, or phylogenetic footprinting, shortens the amount of sequence under consideration by focusing attention on conserved regions that are more likely to serve a biological function (Wasserman et al. 2000; Boffelli et al. 2003). Although such methods can increase binding-site densities by fivefold, only the strongest sites are detected at this level (Wasserman et al. 2000). Recently, based on the synergy arising from clusters of TFBSs with known binding patterns, a variety of computational methods have been created for the discrimination of CRMs. These include composite site models and statistical models of TFBSs (Wasserman and Krivan 2003). It is often the case that no prior information exists on binding patterns of any relevant transcription factors for sets of genes identified in large-scale expression studies. One approach is a method for identification of modules using known motifs, but it includes a preliminary step of motif identification using either a Gibbs sampling algorithm or an algorithm based on overrepresented oligonucleotide sequences (Rajewsky et al. 2002b). Another approach uses suffix-trees and a word consensus approach rather than a statistical model to locate ordered collections of motifs (Marsan and Sagot 2000). In this method, sites of each motif type are assumed to occur exactly once in each module. An expectation-maximization algorithm based on a discriminant model with multiple iterative optimization steps has also been described (Segal and Sharan 2004). Although these approaches are promising, computational identification of CRMs and TFBSs without prior knowledge of binding patterns remains elusive.
Protein interactions provide the mechanistic basis for much of gene regulation in all organisms (Wei et al. 2004). The activity of a particular transcription factor (TF) cannot be considered in isolation. Often, a particular TF can be stimulated either positively or negatively by its interaction with either cis-binding factors or coactivators (Latchman 1998). There is considerable evidence that cis-elements occur in clusters, in which the weak individual signals provide a collectively strong signal (Frith et al. 2002). For example, it has been shown that for proper spatial expression in the endoderm of the sea urchin, one particular pairing of Gata sites is essential and that these function synergistically with an adjacent Otx site (Yuh et al. 2004). To model modules of cis-elements, one must determine the essential spatial and ordering properties. Because synergy-based discrimination functions surpass the performance of models for individual TFBSs (Halfon and Michelson 2002), it is reasonable to expect that de novo pattern discovery methods based on regulatory modules will perform better than methods for detection of individual motifs.
In the present study, we developed a synergy-based de novo algorithm that models neighbor interactions among TFBSs. We also explored the utility of using aligned human-mouse sequences as an input data set for training the algorithm. We found that the use of aligned human-mouse sequences and the use of neighboring interactions both enhance the specificity of site and module predictions. We show that this model can be used to specifically discriminate regulatory sequences from control sequence in an independent test set, and we use the resulting discrimination procedure to predict additional genes that are likely to be regulated in a manner similar to those in the study set.
RESULTS
Positive Training Model
To explore the utility of human-rodent sequence comparison (an evolutionary distance of 50-100 million years) for locating CRMs, we selected a study set of 24 3-kb upstream regions of orthologous gene pairs specifically up-regulated in human skeletal muscle tissue. These genes were selected because they contain numerous reported TFBSs as determined from biochemical and genetic studies (Wasserman and Fickett 1998). Thus, each gene has at least one experimentally defined upstream TFBS that has a functional role in skeletal muscle-specific expression (Wasserman et al. 2000).
Within our study set, there are a total of 188 reported sites (94 mouse/human pairs). Because the regulatory mechanisms governing the expression of these genes have not been fully delineated, additional functional sites are likely to be present. After masking repetitive sequences in the human gene sequence with RepeatMasker (A.F.A. Smit and P. Green, unpubl.; http://www.repeatmasker.org/), using BLASTZ (Schwartz et al. 2003) to align the human-mouse pairs of sequences, and excluding all ungapped segments that were less than 65% identical, we reduced the searchable sequence to ∼41% of the original length. The aligned sequences, not surprisingly, contained aligned TFBSs, allowing the sampling of aligned pairs of sites. We present the algorithm's performance on the identification of each of the following: (1) sequence locations of the CRMs, (2) location of specific TFBSs within these modules, and (3) parameters of the derived motif models, the position weight matrices.
We defined a CRM to be a fragment of sequence in which there are at least two reported TF binding sites with intersite spaces ≤100 bp and similarly for predicted CRMs. In the 24 reference sequence pairs, there were a total of 20 sequence pairs containing experimentally reported modules, and four that did not. As reported in Table 1A, the algorithm predicts 85% (17/20) of these modules with at least 50% overlap of the reported module. The algorithm predicts a module in only one of the four sequences that does not have a reported module.
Table 1A.
Number of Modules Correctly Predicted by the Sampling Algorithm
| Reported modules | Predicted modules | Correctly predicted modules | Sequences with no predicted modules |
|---|---|---|---|
| 20 | 21 | 17 | 3 |
Three of the 24 pairs of sequences contained two distinct modules. The current algorithm can find at most one module per sequence, so in one execution of the algorithm, a maximum of 40 (20 pairs) modules and 96 reported Myf, Mef2, and SRF sites are identifiable. The three sequences with no predicted modules were not found to contain reported modules. A series of predicted motifs was considered as overlapping a reported module if they overlapped the reported module by at least half the length of the reported module as measured from start location of the reported TFBS proximal to the 5′ end of the gene to the end of the most distant TFBS.
Similar to the analysis by Wasserman et al. (2000), our analysis focuses on the well defined TFBSs for Myf, Mef2, and SRF. As shown in Table 1B, on average 69% of the reported Myf, Mef2, and SRF sites are correctly predicted. Mef2 shows the best correspondence, covering 87% of the reported sites and only four novel predictions. Because the laboratory characterization of these sequences is not complete, predictions of such nonannotated elements are ambiguous, representing either false positives or unreported sites.
Table 1B.
Predictions of the Module Sampler for the Sequence-Specific Mef2, Myf, and SRF Bindings Sites
| TF type | Reported sites | Predicted sites | Number overlapping reported sites | % of reported sites found | % of predicted overlapping reported sites | Additional predicted sites |
|---|---|---|---|---|---|---|
| Mef2 | 30 | 30 | 26 | 86.7 | 86.7 | 4 |
| Myf | 40 | 40 | 22 | 55.0 | 55 | 18 |
| SRF | 26 | 34 | 18 | 69.2 | 52.9 | 16 |
| Total | 96 | 104 | 66 | 68.75 | 63.4 | 38 |
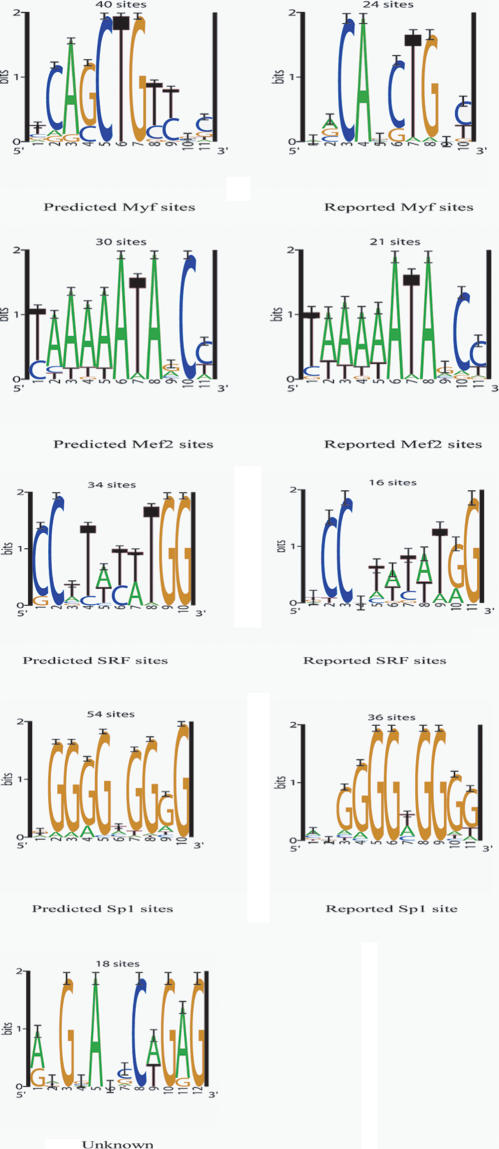
Sequence logos (Schneider and Stephens 1990) of four of the predicted motifs (Fig. 1) correspond well with motifs of the reported sites of the factors Mef2, Myf, SRF, and SP1 (Wasserman and Fickett 1998; see also weight matrices in the TRANSFAC database, http://www.gene-regulation.com; Matys et al. 2003). A fifth uncharacterized motif is also predicted. Mef2 and SRF are both members of the MADS-box family of transcription factors, and as such have binding patterns with an A-T rich core (Shore and Sharrocks 1995). We found that we could only separate these two related motifs with the use of a fragmentation algorithm (Liu et al. 1995). Information on frequencies of neighboring relationships is reported in the Supplemental material.
Figure 1.
Sequence logos (Schneider and Stephens 1990) of the motif models predicted by the module sampler for the 24 pairs of human-mouse sequences in the positive training set. The logos for the reported sites were produced by aligning the reported human sites for each motif type.
In order to examine the contributions of the various components of the algorithm, we compared its performance to two other modes of Gibbs sampling (Thompson et al. 2003). The first of these, the “Motif sampler,” looks for sites without additional restrictions, and the second includes the restriction that the sites must be ≤100 bp apart. As Table 2 shows, the most improvement in site identification emerges with phylogenic footprinting (the addition of the mouse sequences). Table 2 also shows that inferences of neighboring pair relationships that are unique to the module sampler also strongly improves site identification.
Table 2.
The Performance of the Various Sampling Modes in the Prediction of the Sequence-Specific Myf, Mef2, and SRF Sites
| Total no. of reported Mef2, Myf, and SRF sites | Total no. of predicted Mef2, Myf, and SRF sites | No. matching reported Myf, Mef2, and SRF sites | % of predicted sites overlapping reported sites | No. of sites predicted (includes predicted SP1 model and unknown model) | |
|---|---|---|---|---|---|
| Motif (no mouse)a | 48 | 123** | 13 | 27.1 | 369 |
| Motifb | 96 | 72 | 48 | 50 | 132 |
| Module (no mouse)c | 48 | 9* | 0 | 0 | 109 |
| Clustered sitesd | 96 | 112 | 52 | 54.2 | 222 |
| Modulee | 96 | 104 | 66 | 68.75 | 176 |
To examine the importance of the alignment of homologous sequences in finding regulatory modules and the role of clustering and neighboring interaction, we compared five versions of the algorithm: aRow 1: the motif sampler similar to the one used by Wasserman et al. (2000) (no restrictions on the clustering of sites and no neighboring effects) applied to the human sequences only; bRow 2: the motif sampler modified to sample simultaneously from aligned sequence pairs; cRow 3: the module sampler applied to the human sequences only; dRow 4: the module sampler applied to aligned human mouse sequence pairs but with the neighboring interaction component inactivated (thus, yielding a model that enforces clustering but has no neighboring effects); eRow 5: the full module sampler, including both clustering and neighboring applied to aligned human mouse sequence pairs. In all cases, we searched for five different models simultaneously. The * indicates that the algorithm did not predict a Mef2 or SRF-like model, but only a Myf-like model. ** indicates that two different weak Myf-like models were predicted.
To compare the module sampler results with predictions obtained when motif models were known a priori, we obtained the COMET software (Frith et al. 2002) from http://zlab.bu.edu/~mfrith/comet/ and applied it to the human sequences from our training set. Using the default parameters and matrices derived from the reported Myf, Mef-2, SRF, SP1, and Tef aligned pairs of sites, COMET, at an E-value cutoff of 1.0, correctly predicted 63% (30 of 48) reported Myf, Mef-2, and SRF TFBSs with 15 ambiguous predictions. It also correctly predicted 13 of the 20 reported modules and six modules that do not overlap a reported module (≥50% overlap). The module sampler correctly located 33 reported Myf, Mef-2, and SRF TFBSs with 19 ambiguous sites in the human sequences and 17 reported modules. (The human sequences represent half the totals in Table 2.) Thus, COMET predictions were somewhat more specific and slightly less sensitive than the module sampler's (see Table 2). These results demonstrate that the incorporation of aligned sequence pairs and neighbor interactions can circumvent the need for large reference collections.
In addition to the muscle-specific sequences, we collected a set of 10 human upstream sequences from genes expressed in liver tissue and their rodent orthologs (Krivan and Wasserman 2001). The sequences were aligned as described above, and the module sampler was applied to the aligned sequence pairs. The module sampler was run with four different motif models. One of the resulting predicted models strongly matched the pattern for the HNF-1 TFBS (Krivan and Wasserman 2001). Similar to the results described in Table 2, the module sampler in the absence of neighbor interactions produced similar models and a slightly higher maximum a posteriori probability (MAP) value (Liu et al. 1995) but yielded more ambiguous predictions. The motif sampler with no restriction on spacing or number of sites per sequence failed to find the HNF-1 model and did not produce any significant result.
Finding New Muscle-Specific Genes
One of the critical goals of the CRM discovery algorithm is the identification of additional genes that are likely to be regulated in a similar manner. To address this goal, we developed a discriminant method that uses for its positive control the CRM model derived above. To obtain negative data for training and cross-validation, we began with a set of 10-kb upstream regions from 2910 human genes labeled as “reviewed” or “provisional” in the RefSeq database (Pruitt and Maglott 2001) and the corresponding mouse orthologous sequences. The sequences were aligned and repeat-masked as described above. We randomly chose 100 pairs from this set as a negative training set and screened these against the literature to remove genes with any reports suggesting that they could be differentially expressed in muscle. Two sequences from the randomly selected set were eliminated by the literature review and subsequently replaced.
We found that models built with these data using uninformed prior models contained very few sites, and that the resulting models were so unlike those found in the muscle-specific set that they were of little value for discrimination. To force the negative model to focus on muscle-like features, we used the five predicted motif models shown in Figure 1 as very strongly informed prior motif models, and we set the distribution of the number of sites per sequence to that obtained from the original muscle-specific sequence pairs. Consequently, the discrimination of muscle-specific modules from negative controls stems primarily from the posterior differences in numbers of sites, the frequencies of each predicted type of site, and the neighboring relationships among them. Using these parameters, the algorithm predicted modules in 24 of the 100 negative training sequence pairs.
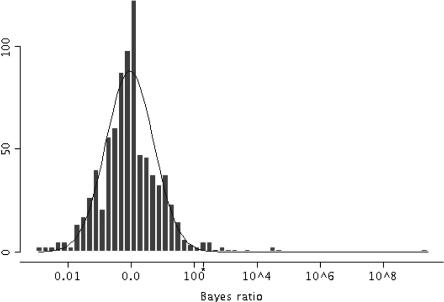
The ratio of the probability of a given sequence under the positive model to the probability under the negative model defines a Bayes factor ratio (Gelman et al. 1995), which gives the odds that the sequence is regulated in a manner similar to that of the muscle genes in our positive training set. Figure 2 illustrates the distribution of Bayes Factors. The Supplemental text gives details of the Bayes factor calculations.
Figure 2.
Histogram of the Bayes ratios for 688 intergenic pairs from the human and mouse genomes, that had predicted modules, plotted on a log base 10 scale. The asterisk at log10(194.5)∼2.3 indicates the position of the Bayes ratio cutoff. Sequences above this point have a q-value ≤ 0.05. The line shows the robust fit to the Bayes ratio distribution.
Validation
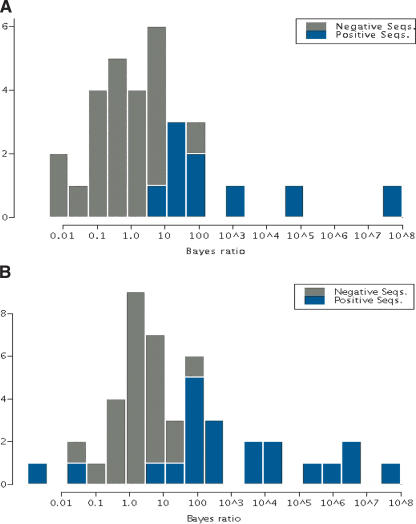
For direct validation, we performed an intensive search of the literature and found a set of 13 additional human genes with evidence of specific expression in muscle tissue and reported TFBSs. For each of these positive test sequences, we selected a 10-kb noncoding fragment that included the reported TFBS. We processed these and aligned them with mouse sequences as above. We randomly sampled another 100 from the remaining 2810 10-kb upstream regions as the negative test set. The module sampler was applied to both sets, using the parameters learned in training. Modules were found in nine of the 13 positive sequence pairs and in 22 of the 100 negative sequence pairs. Figure 3A shows a histogram of the Bayes ratios for these 31 positive and negative direct validation sequence pairs. The negative controls contained candidate CRMs with low Bayes ratios; the maximum Bayes ratio was only 90.0 with only two values greater than 10. Among the nine positive sequence pairs, five had ratios greater than 90 and three had ratios much above 90. A Kolmogorov-Smirnov test (Venables and Ripley 1999) of the difference between the distribution of the Bayes factor ratios of the sequence pairs for the positive sequences with predicted modules and those from the negative sample with predicted modules indicates that they are very unlikely to be drawn from the same distribution, with a P-value of ∼0.
Figure 3.
(A) Histogram of the Bayes ratio, on a log10 scale, for the positive and negative validation sequence pairs in which a module was predicted. There are nine positive sequences with a predicted module, and 22 negative sequence pairs. (B) The distribution of Bayes ratios, on a log10 scale, for positive and negative training sequences from cross-validation which contained a predicted module. A rebuild of the models was required for only the 24 negative pairs with predicted modules from the original negative training set, as the other sequences contributed nothing to the model.
To test the algorithm with a larger set of positive sequences, we used cross-validation. In this process one sequence pair at a time, the target pair, was removed from the data sets. For the 24 positive training-sequence pairs, the positive models were rebuilt, as necessary, with the remaining 23 sequence pairs. Bayes ratios for these are shown in Figure 3B. This cross-validation process was also applied to the 100 negative training sequences, and a module was identified in 24 of these. The Bayes ratio was below 10 for 21 of these negative pairs. The remaining three had ratios of 22.5, 35.8, and 130.8. Thirteen of the positive sequences had Bayes ratios above 130.8 and, as shown in Figure 3B, most of them had ratios several orders of magnitude higher.
Sequence Data Mining
To search for unreported modules and their associated genes, we searched for modules in and calculated the Bayes factor ratio for each of the remaining 2710 human-mouse sequence pairs described above. To test for modules, each sequence pair was sampled by the module sampler using the parameters learned from the positive model with the modification that the alignment and models were not updated. As above, we defined a predicted CRM to be a fragment of sequence in which there are at least two predicted sites with intersite spaces ≤100 bp. In this case, we reported the sequence pair as having a predicted module if sampling the sequences with the positive model predicted a CRM at least one time in 10 rounds of sampling. The probability of the sequence data was calculated using the positive and the negative model, and the Bayes factor ratio was calculated. Details of the procedure are given in the Supplemental text. No module was predicted in 2022 of the sequence pairs. Figure 2 shows a histogram of the log of the Bayes ratios for the candidate CRMs detected in the remaining 688 sequence pairs. To minimize the risk of erroneously recommending a negative gene for further study, we calculated the false discovery rate (FDR; Storey and Tibshirani 2003) as follows. The distribution of the log of the Bayes ratio of the 688 sequence pairs with predicted modules was fitted to a normal distribution by robust estimation of the distribution's location and scale (Venables and Ripley 1999). P-values were calculated using this normal distribution. The P-values were used to estimate q-values and the FDR (Storey 2002). Setting the FDR cutoff at 0.05 gives 17 predictions with q-values less than or equal to a critical Bayes ratio value of 194.5. Table 3 lists these 17 sequence pairs containing the candidate skeletal muscle CRMs. Eight of the candidate CRMs are supported by evidence in the literature indicating that the associated gene is either muscle-specific or displays selective elevation of expression in muscle. Our FDR cutoff indicates that ≤5% of observations above this critical value are expected to be negative; equating to ∼one false positive among these 17 pairs. The full results for all 2710 genes are available at http://bayesweb.wadsworth.org/gibbs/module/.
Table 3.
Sequence Pairs Having Both a Bayes Ratio Greater Than 194 and a Predicted Module
| Gene | Human RefSeq ID | Mouse RefSeqID | Bayes ratio |
|---|---|---|---|
| EGR1 (Aicher et al. 1999; Tsai et al. 2000) | NM_001964 | NM_007913 | 2.3854e+09 |
| CSNK1E | NM_001894 | NM_013767 | 4.5797e+04 |
| ACTG2 (Carson et al. 2000) | NM_001615 | NM_009610 | 3.9155e+04 |
| RXRG (Downes et al. 1994; Georgiades and Brickell 1997; Rebhan et al. 1997) | NM_006917 | NM_009107 | 2.9500e+04 |
| EEF1A2 (Bischoff et al. 2000; Knudsen et al. 1993; Rebhan et al. 1997) | NM_001958 | NM_007906 | 4.5916e+03 |
| STK23 (Brenner 1998) | NM_014370 | NM_019684 | 2.4573e+03 |
| IL 17B (Fohr et al. 1993; Hazama et al. 2002) | NM_014443 | NM_019508 | 1.4638e+03 |
| NGFB | NM_002506 | NM_013609 | 9.1709e+02 |
| KRT15 | NM_002275 | NM_008469 | 7.0175e+02 |
| PVALB | NM_002854 | NM_013645 | 5.4857e+02 |
| VAMP3 | NM_004781 | NM_009498 | 3.0971e+02 |
| RING1 | NM_002931 | NM_009066 | 2.9679e+02 |
| CYR61 | NM_001554 | NM_010516 | 2.8015e+02 |
| PPAP2B | NM_003713 | NM_080555 | 2.5995e+02 |
| TCAP (Rebhan et al. 1997; Valle et al. 1997) | NM_003673 | NM_011540 | 2.2401e+02 |
| LZTR1 | NM_006767 | NM_025808 | 2.0356e+02 |
| TRIM8 (Vincent et al. 2000) | NM_030912 | NM_053100 | 1.9458e+02 |
Referenced genes have literature evidence of being muscle-specific or of having emphasized expression in muscle tissue.
DISCUSSION
We introduce an algorithm, based on a generative statistical model, for finding CRMs in sequence data that requires only aligned human-mouse sequence pairs of likely coregulated genes, and does not require prior knowledge of motif models or other parameters. It makes only minimal assumptions about the sizes and numbers of differing kinds of binding sites. We also introduce a novel discriminant procedure for using the inferred models to search for other genes that might be specifically expressed in a manner similar to those in our study set. Our tests of this procedure, using both cross-validation and direct validation, indicate that a subset of muscle-specific genes can be discriminated from control sequences. Application of this procedure to 2710 upstream sequences from the human genome identifies 17 genes containing a module (q-values ≤ 5%).
The algorithm performs well on the positive training set data, a well studied collection of muscle-related genes with known regulatory sites. It locates ∼69% of the major reported TFBSs, and returns motif models matching the binding specificity of the four critical TFs—Mef2, Myf, SRF, and SP1 (Fig. 1). COMET, which requires prior weight matrices for the TFs, identified 63% of reported Mef2, Myf, and SRF sites. Thus, COMET was somewhat more specific but slightly less sensitive than the module sampler on these data. These results indicate that the use of aligned human and mouse data and the inclusion of additional features in the module sampler largely compensate for the absence of prior knowledge of motif binding patterns.
The predicted motif models were used to search the JASPAR database of transcription factor binding profiles (http://jaspar.cgb.ki.se; Sandelin et al. 2004). The predicted Mef2, MYF, SRF, and SP1 motif patterns each matched their respective binding patterns in the database as either the top or second hit, with P-values less than 0.012. Multiple runs of the program on the 24 muscle-specific sequence pairs produced similar models with similar MAP values (Liu et al. 1995) and small variations in the number of predicted sites and the number corresponding to reported sites. The results presented here are for the solution with the highest MAP value. The program had difficulty locating known binding sites for Tef, a TF linked to regulation in a subset of skeletal muscle fiber types. Although a fifth motif model was identified on most runs, the characteristics of the model were not consistent across the runs. The fifth model sometimes, but not always, contained reported Tef sites, but none of the associated motif models matched an entry in the JASPAR database.
The number of different motif models was initially set to five to facilitate the search for Mef-2, Myf, SRF, SP1, and Tef binding motifs, as suggested by others (Wasserman and Fickett 1998; Frith et al. 2002). We examined the effect of variations in the number of different models. With four models, we found that one of the motifs was a blend of two of the motifs found when using five different models, and thus we found a more specific result with five models. The blended motif typically contained a mixture of reported Mef-2 and SRF sites, which are both members of the MADS-box family of transcription factors. In our trials with six motif models, the sixth motif was often empty, or when not empty was a weak motif that was not reproducible for multiple runs, which indicated to us the presence of no more than five identifiable motif types.
Our model distinguishes itself from previous de novo models in four ways: it (1) incorporates terms that seek to capture interaction of neighboring TFs, (2) explores variations in the patterns of conserved base pairs in a binding motif via a fragmentation step, (3) searches for sites common to a pair of species, and (4) employs a generative statistical model. Our results show that the first three of these factors improved the performance of the algorithm. (1) The incorporation of neighbor interactions into the CRM pattern discovery process improves performance. In the absence of neighbor interactions, the module sampler produced a solution with a MAP value approximately equal to the MAP value produced by the full module sampler. However, in the absence of neighbor interactions, the number of reported sites correctly predicted for the solution with the highest MAP was lower (56% vs. 69%) and the total number of predicted sites was higher (222 vs. 176). An additional test with a liver-specific data set behaved similarly. Thus, these interactions seem to contribute significantly to specificity and sensitivity of the algorithm. (2) We found that use of the fragmentation algorithm was required to distinguish SRF sites from MEF sites. (3) The use of aligned sequence pairs greatly improved the Gibbs sampler's ability to detect TFBSs and CRMs, as shown in Table 2. In calculating the sampling distribution, we assumed that the individual sequences in the pairs were independent. Although this is almost certainly incorrect, we found that a down-weighting of the mouse sequences, to adjust for phylogenic correlation, adversely affected performance. We prefer the use of generative statistical models, because they provide a facile means for the future incorporation of additional models of biological processes such as selective evolutionary pressures. Our experiences with Gibbs sampling models from this class and the experiences of others with hidden Markov models from this class suggest that taking this path, though somewhat more demanding at the outset, will in the long run promote extensions that model emerging biological findings on the mechanisms of transcription regulation.
We examined three different prior distributions of the total number of sites per sequence. Both a prior that was equal to the reported number of sequences and a Poisson prior with λ = 3.5 produced very similar results (results from the former are shown in Table 1B). The latter yields very similar motif models for Myf, Mef2, SRF, and Sp1 with 184 total sites and correctly predicts 64.6% of the reported Myf, Mef2, and SRF sites. Uninformed prior models did not perform as well, correctly predicting a much lower proportion of the reported sites and making a larger nummaking a larger number of predictions.
The relatively small proportion of the total number of human genes represented by the orthologous gene pairs in our sequence mining set stems primarily from a requirement to identify unique mouse orthologs for each candidate human gene. We know of no reason why the resulting set should be biased, but we also have no good evidence that the set is not biased. However, it was the data set available from the human genome assembly at the time of the study. The latest revision of the human genome does not substantially increase this proportion of human genes with useful mouse orthologs.
We were somewhat surprised that the sampler failed to identify a CRM in three of the sequence pairs in the positive training set. However, this finding is consistent with the fact that the sequences making up the positive training set are regulatory regions of a heterogeneous mixture of regulatory mechanisms. This heterogeneity is further reflected by the findings from the test set, in which the sampler could not identify a module in four of the 13 positive control sequences. We thus suspect that the modules that we do detect are germane to some specifically regulated subset of muscle-specific genes.
The use of the FDR approach gave us a means by which to select a critical value cutoff that did not require input from our validation studies. The fact that this FDR-based critical Bayes ratio of 194.5 is somewhat greater than the highest ratio among the negative validations results supports its use. Throughout this study, our focus has been on producing CRM predictions that are unlikely to include false positives, that is, which have low q-values. We thus intentionally tipped the balance toward specificity with a concomitant loss of sensitivity. In our opinion, the confidence gained in the predicted set is well worth the tradeoff of missing some additional muscle-specific genes remaining in the data set that we mined.
Coexpression alone does not imply coregulation. Genes may be expressed within a given type of cell through multiple and cascading responses to a single stimulus, to say nothing of the complexity that exists in heterogeneous tissues containing multiple cell types. Thus, even though the module sampler has the capacity to ignore sequences that do not contain a cis module pattern common to the rest, we recommend that this approach be applied only to sets of genes that are likely to be coregulated, for example, to subsets from large-scale expression studies in cell cultures that follow a consistent and common time course. For such sets of coregulated genes, the present results indicate potential to unravel the mechanisms behind their coexpression patterns, through the identification of CRMs and specific TFBSs, and our findings also show that the resulting models may be employed to identify additional genes that are regulated in a similar manner.
METHODS
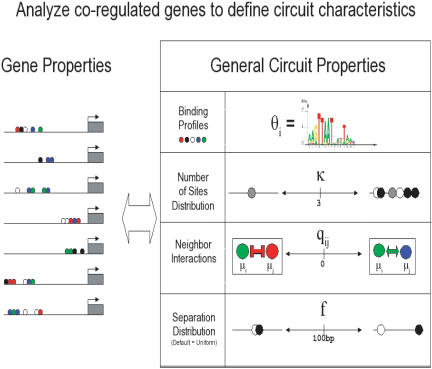
We adopted a procedure similar to that of Wasserman et al. (2000). First, we aligned orthologous sections of human and mouse sequence and identified conserved fragments. Next, we applied a new Gibbs sampling algorithm, the module sampler, which simultaneously identifies CRMs (clusters of regulatory sites), the binding patterns (motifs of unidentified transcription factors), specific binding sites for each motif, the neighboring relationship between sites, and site frequencies. Figure 4 illustrates the features of the algorithm.
Figure 4.
General parameters that the module sampler attempts to discover. A priori, motif binding models were modeled by uniform Dirichlet prior models. Nearest neighbor interactions were modeled as transition probabilities of a Markov chain. This allows us to calculate the posterior mean estimate of the transition probabilities based on the number of times that each specific type of binding site follows another and prior pseudocounts. A priori, we assume that all neighboring pairs also have uniform Dirichlet prior models. The algorithm also allows us to draw inferences regarding the number of sites per sequence. We chose a prior distribution on the number of sites per sequence based upon the distribution of reported sites. The separation distance was modeled as a flat function truncated at 100 bp.
Modules for different genes may vary in the total number of contributing transcription factors, and in both the number and order of binding sites for each type of factor. Some of the sequences in a data set may contain no sites at all, or no sites for one or more of the factors involved in regulating the rest. Because the algorithm is focused exclusively on cis-regulation, it makes no direct inferences regarding the trans components, the transcription factors. Rather, it infers the DNA binding patterns of unspecified transcription factors in the form of p different statistical models or motifs. The algorithm infers the total number, 0 ≤ k ≤ kmax, of TFBSs in each module, and the overall distribution of the number of sites per module. Because the order of the sites among the CRMs may vary but still reflect ordering preferences arising from protein-protein interactions, the algorithm also infers the frequencies of neighboring pairs of TFBSs. To address our key aim of finding modules without prior information on motif binding patterns, we employed uniform (i.e., uninformed) prior motif models. In addition, modules are kept compact by the requirement that no successive pair of TFBSs within a CRM be separated by more than 100 bp.
The algorithm has two phases. The forward phase, as described in the Supplemental material, uses recursive sums over all possible alignments of 0 ≤ kn ≤ kmax sites in the nth sequence, to obtain Bayesian inferences on the number of TFBSs in the nth sequence, and partial sums required for its back sampling phase. Although the algorithm is similar to a hidden Markov model, it is in fact a change-point algorithm (Liu et al. 2002). This recursion examines the simultaneous placements of all TFBS by summing over all possible combinations of the placement of p motifs in up to kmax sites per sequence. For each sequence, the algorithm infers the total number of sites, kn, the number of each of the p motifs, and the alignments and orderings of these sites in the nth sequence. In its back sampling step it simultaneously samples all kn sites in the nth sequence according to these inferences. As in previous Gibbs sampling algorithms, the widths of sites are inferred using a fragmentation algorithm (Liu et al. 1995). The sampling process iterates over the sequences one at a time, using currently sampled values from all other sequences, to guide the sampling process toward a converged result. The algorithm is an extension of the propagation Gibbs sampling algorithm (Liu et al. 1999) for the alignment of protein sequences. It is implemented in a manner similar to that of the Gibbs Recursive Sampler (Thompson et al. 2003) but differs from it in the inclusion of site spacing terms and neighboring interactions. For the purposes of sequence mining, sites were sampled in the sequences 10 times by the module sampler with the modification that the site alignment and models were not updated. If the Bayes factor ratio was much greater than the critical value associated with the prescribed FDR and the sampler predicted a module, the sequence pair was deemed likely to be regulated by a module similar to those found in the muscle-specific regulatory sequences. See the Supplemental material for details.
Acknowledgments
This work was supported by NIH grant R01HG01257, and NSF grant NSF-DMS 0204674, and a grant from the Canadian Institutes of Health Research (to W.W.W.).
Footnotes
[Supplemental material is available online at www.genome.org.]
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.2589004.
References
- Aerts, S., Van Loo, P., Thijs, G., Moreau, Y., and De Moor, B. 2003. Computational detection of cis-regulatory modules. Bioinformatics 19: 5ii-14ii. [DOI] [PubMed] [Google Scholar]
- Aicher, W.K., Sakamoto, K.M., Hack, A., and Eibel, H. 1999. Analysis of functional elements in the human Egr-1 gene promoter. Rheumatol. Int. 18: 207-214. [DOI] [PubMed] [Google Scholar]
- Bischoff, C., Kahns, S., Lund, A., Jorgensen, H.F., Praestegaard, M., Clark, B.F.C., and Leffers, H. 2000. The Human Elongation Factor 1 A-2 Gene (EEF1A2): Complete sequence and characterization of gene structure and promoter activity*1. Genomics 68: 63-70. [DOI] [PubMed] [Google Scholar]
- Boffelli, D., McAuliffe, J., Ovcharenko, D., Lewis, K.D., Ovcharenko, I., Pachter, L., and Rubin, E.M. 2003. Phylogenetic shadowing of primate sequences to find functional regions of the human genome. Science 299: 1391-1394. [DOI] [PubMed] [Google Scholar]
- Brenner, V. 1998. Von der Sequenz zur Funktion: Genomanalyse einer 102 KB-Region des humanen X-Chromosoms. Friedrich-Schiller University, Jena, Germany.
- Carson, J.A., Fillmore, R.A., Schwartz, R.J., and Zimmer, W.E. 2000. The smooth muscle γ-actin gene promoter is a molecular target for the mouse bagpipe homologue, mNkx3-1, and serum response factor. J. Biol. Chem. 275: 39061-39072. [DOI] [PubMed] [Google Scholar]
- Downes, M., Mynett-Johnson, L., and Muscat, G.E. 1994. The retinoic acid and retinoid X receptors are differentially expressed during myoblast differentiation. Endocrinology 134: 2658-2661. [DOI] [PubMed] [Google Scholar]
- Fohr, U.G., Weber, B.R., Muntener, M., Staudenmann, W., Hughes, G.J., Frutiger, S., Banville, D., Schafer, B.W., and Heizmann, C.W. 1993. Human α and β parvalbumins. Structure and tissue-specific expression. Eur. J. Biochem. 215: 719-727. [DOI] [PubMed] [Google Scholar]
- Frith, M.C., Spouge, J.L., Hansen, U., and Weng, Z. 2002. Statistical significance of clusters of motifs represented by position specific scoring matrices in nucleotide sequences. Nucleic Acids Res. 30: 3214-3224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman, A., Carlin, J.B., Stern, H.S., and Rubin, D.B. 1995. Bayesian Data Analysis. Chapman and Hall, London, UK.
- Georgiades, P. and Brickell, P.M. 1997. Differential expression of the rat retinoid X receptor γ gene during skeletal muscle differentiation suggests a role in myogenesis. Developmental Dynamics 210: 227-235. [DOI] [PubMed] [Google Scholar]
- Halfon, M.S. and Michelson, A.M. 2002. Exploring genetic regulatory networks in metazoan development: Methods and models. Physiol. Genomics 10: 131-143. [DOI] [PubMed] [Google Scholar]
- Hazama, M., Watanabe, D., Suzuki, M., Mizoguchi, A., Pastan, I., and Nakanishi, S. 2002. Different regulatory sequences are required for parvalbumin gene expression in skeletal muscles and neuronal cells of transgenic mice. Molecular Brain Research 100: 53-66. [DOI] [PubMed] [Google Scholar]
- Knudsen, S.M., Frydenberg, J., Clark, B.F., and Leffers, H. 1993. Tissue-dependent variation in the expression of elongation factor-1 α isoforms: Isolation and characterisation of a cDNA encoding a novel variant of human elongation-factor 1 α. Eur. J. Biochem. 215: 549-554. [DOI] [PubMed] [Google Scholar]
- Krivan, W. and Wasserman, W.W. 2001. A predictive model for regulatory sequences directing liver-specific transcription. Genome Res. 11: 1559-1566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latchman, D.S. 1998. Eukaryotic transcription factors. Academic Press, San Diego, CA.
- Liu, J., Neuwald, A., and Lawrence, C. 1995. Bayesian models for multiple local sequence alignment and Gibbs sampling strategies. J. Am. Stat. Assoc. 432: 1156-1170. [Google Scholar]
- Liu, J.S., Neuwald, A.F., and Lawrence, C.E. 1999. Markovian structures in biological sequence alignments. J. Amer. Stat. Assoc. 94: 1-15. [Google Scholar]
- Liu, J.S., Gupta, M., Liu, X., Mayerhofer, L., and Lawrence, C.E. 2002. Statistical models for biological sequence motif discovery. In Case studies in Bayesian statistics VI (eds. C. Gatsonis et al.), pp. 3-22. Springer-Verlag, New York.
- Marsan, L. and Sagot, M.F. 2000. Algorithms for extracting structured motifs using a suffix tree with an application to promoter and regulatory site consensus identification. J. Comput. Biol. 7: 345-362. [DOI] [PubMed] [Google Scholar]
- Matys, V., Fricke, E., Geffers, R., Gossling, E., Haubrock, M., Hehl, R., Hornischer, K., Karas, D., Kel, A.E., Kel-Margoulis, O.V., et al. 2003. TRANSFAC(R): Transcriptional regulation, from patterns to profiles. Nucleic Acids Res. 31: 374-378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCue, L.A., McDonough, K., and Lawrence, C.E. 2000. Functional classification of cNMP-binding proteins and nucleotide cyclases with implications for novel regulatory pathways in mycobacterium tuberculosis. Genome Res. 10: 204-219. [DOI] [PubMed] [Google Scholar]
- McCue, L.A., Thompson, W., Carmack, C.S., and Lawrence, C.E. 2002. Factors influencing the identification of transcription factor binding sites by cross-species comparison. Genome Res. 12: 1523-1532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruitt, K.D. and Maglott, D.R. 2001. RefSeq and LocusLink: NCBI gene-centered resources. Nucleic Acids Res. 29: 137-140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajewsky, N., Socci, N.D., Zapotocky, M., and Siggia, E.D. 2002a. The Evolution of DNA regulatory regions for proteo-γ bacteria by interspecies comparisons. Genome Res. 12: 298-308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajewsky, N., Vergassola, M., Gaul, U., and Siggia, E. 2002b. Computational detection of genomic cis-regulatory modules applied to body patterning in the early Drosophila embryo. BMC Bioinformatics 3: 30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rebhan, M., Chalifa-Caspi, V., Prilusky, J., and Lancet, D. 1997. GeneCards: Encyclopedia for genes, proteins and diseases. Weizmann Institute of Science, Bioinformatics Unit and Genome Center, Rehovot, Israel.
- Sandelin, A., Alkema, W., Engstrom, P., Wasserman, W.W., and Lenhard, B. 2004. JASPAR: An open-access database for eukaryotic transcription factor binding profiles. Nucleic Acids Res. 32: D91-94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider, T.D. and Stephens, R.M. 1990. Sequence logos: A new way to display consensus sequences. Nucleic Acids Res. 18: 6097-6100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz, S., Kent, W.J., Smit, A., Zhang, Z., Baertsch, R., Hardison, R.C., Haussler, D., and Miller, W. 2003. Human-mouse alignments with BLASTZ. Genome Res. 13: 103-107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segal, E. and Sharan, R. 2004. A discriminative model for identifying spatial cis-regulatory modules. In Proceedings of the 8th annual international conference on computational molecular biology, pp. 141-149. [DOI] [PubMed]
- Segal, E., Yelensky, R., and Koller, D. 2003. Genome-wide discovery of transcriptional modules from DNA sequence and gene expression. Bioinformatics 19: 273i-282. [DOI] [PubMed] [Google Scholar]
- Shore, P. and Sharrocks, A.D. 1995. THe MADS-box family of transcription factors. Eur. J. Biochem. 229: 1-13. [DOI] [PubMed] [Google Scholar]
- Storey, J.D. 2002. A direct approach to false discovery rates. J. Royal Stat. Soc. B 64: 479-498. [Google Scholar]
- Storey, J.D. and Tibshirani, R. 2003. Statistical significance for genomewide studies. PNAS 100: 9440-9445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson, W., Rouchka, E.C., and Lawrence, C.E. 2003. Gibbs recursive sampler: Finding transcription factor binding sites. Nucleic Acids Res. 31: 3580-3585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai, J.C., Liu, L., Cooley, B.C., Dichiara, M., Topper, J., and Aird, W.C. 2000. The Egr-1 promoter contains information for constitutive and inducible expression in transgenic mice. FASEB J. 14: 1870-1872. [DOI] [PubMed] [Google Scholar]
- Valle, G., Faulkner, G., De Antoni, A., Pacchioni, B., Pallavicini, A., Pandolfo, D., Tiso, N., Toppo, S., Trevisan, S., and Lanfranchi, G. 1997. Telethonin, a novel sarcomeric protein of heart and skeletal muscle. FEBS Lett. 415: 163-168. [DOI] [PubMed] [Google Scholar]
- Venables, W.N. and Ripley, B.D. 1999. Modern applied statistics with S-Plus. Springer, New York.
- Vincent, S.R., Kwasnicka, D.A., and Fretier, P. 2000. A Novel RING finger-b box-coiled-coil protein, GERP. Biochem. Biophys. Res. Comm. 279: 482-486. [DOI] [PubMed] [Google Scholar]
- Wasserman, W.W. and Fickett, J.W. 1998. Identification of regulatory regions which confer muscle-specific gene expression. J. Mol. Biol. 278: 167-181. [DOI] [PubMed] [Google Scholar]
- Wasserman, W.W. and Krivan, W. 2003. In silico identification of metazoan transcriptional regulatory regions. Naturwissenschaften 90: 156-166. [DOI] [PubMed] [Google Scholar]
- Wasserman, W.W., Palumbo, M., Thompson, W., Fickett, J.W., and Lawrence, C.E. 2000. Human-mouse genome comparisons to locate regulatory sites. Nat. Genet. 26: 225-228. [DOI] [PubMed] [Google Scholar]
- Wei, G.H., Liu, D.P., and Liang, C.C. 2004. Charting gene regulatory networks: Strategies, challenges and perspectives. Biochem. J. Epub ahead of print. [DOI] [PMC free article] [PubMed]
- Yuh, C.-H., Dorman, E.R., Howard, M.L., and Davidson, E.H. 2004. An otx cis-regulatory module: A key node in the sea urchin endomesoderm gene regulatory network. Dev. Biol. 269: 536-551. [DOI] [PubMed] [Google Scholar]
WEB SITE REFERENCES
- http://zlab.bu.edu/~mfrith/comet/; COMET.
- http://jaspar.cgb.ki.se; JASPAR database.
- http://bayesweb.wadsworth.org/gibbs/module; Module sampler results and data.
- http://www.repeatmasker.org/; RepeatMasker.
- http://www.gene-regulation.com; TRANSFAC.