Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2017 Jan 19;7:40862. doi: 10.1038/srep40862

Origins of Ripples in CVD-Grown Few-layered MoS2 Structures under Applied Strain at Atomic Scales

Jin Wang 1, Raju R Namburu 2, Madan Dubey 3, Avinash M Dongare 1,a
PMCID: PMC5244384  PMID: 28102351

Abstract

The potential of the applicability of two-dimensional molybdenum disulfide (MoS2) structures, in various electronics, optoelectronics, and flexible devices requires a fundamental understanding of the effects of strain on the electronic, magnetic and optical properties. Particularly important is the recent capability to grow large flakes of few-layered structures using chemical vapor deposition (CVD) wherein the top layers are relatively smaller in size than the bottom layers, resulting in the presence of edges/steps across adjacent layers. This paper investigates the strain response of such suspended few-layered structures at the atomic scales using classic molecular dynamics (MD) simulations. MD simulations suggest that the suspended CVD-grown structures are able to relax the applied in-plane strain through the nucleation of ripples under both tensile and compressive loading conditions. The presence of terraced edges in these structures is the cause for the nucleation of ripples at the edges that grow towards the center of the structure under applied in-plane strains. The peak amplitudes of ripples observed are in excellent agreement with the experimental observations. The study provides critical insights into the mechanisms of strain relaxation of suspended few-layered MoS2 structures that determine the interplay between the mechanical response and the electronic properties of CVD-grown structures.

The 2-dimensional (2D) structures of MoS2 exhibit significantly different electronic band structure from bulk MoS2 structures1,2 and therefore show significant promise for applications in field effect transistors3, optoelectronics4, photo transistors and detectors5, and chemical catalysts6,7. The variations in the electronic structure of 2D MoS2 structures under the application of external strain8,9,10,11 open up the possibility to tune the performance of the material for device applications. The optimization of the applicability of 2D MoS2 as a building block in future electronic devices hinges on a fundamental understanding of the stability and variations in the electronic properties of 2D MoS2 structures as well as the microstructural response of 2D MoS2 structures as a function of strain. As a result, a significant number of experimental12,13,14,15,16,17,18 and theoretical13,19,20,21,22 studies have investigated the strain response of mechanically exfoliated 2D MoS2 monolayer (ML) and few-layered (FL) structures.

The mechanical response of these 2D materials shows exceptionally high strengths under tension. For example, nanoindentation experiments using an atomic force microscope show that ultrathin free-standing MoS2 membranes have an effective Young’s modulus of 250 ± 150 GPa and may bear a large in-plane strain up to 11% before fracture, implying a broad operation range for strain engineering in 2D MoS2 materials23. In addition, structural ripples have been frequently observed as a strain relaxation mechanism in 2D materials, such as graphene24, ML and FL MoS225, and other van der Waals (vdW) layered materials26. The formation of ripples results in the degradation of mobility of the carrier mass and alteration of electronic structures in these 2D materials. Buckling and ripple formation has also been predicted using molecular dynamics (MD) simulations under uniaxial compression27. The size of the ripples generated during compression is observed to be associated with the strain rate and length of the sample28.

Recently, the capability to grow high quality and large areas of ML and FL MoS2 sheets for device applications has been made possible through chemical vapor deposition (CVD)29,30,31. These as-grown 2D terrace structures comprise of flakes of varying number of layers wherein the top layers are relatively smaller in size than the bottom layers, resulting in the formation of terrace regions and edges/steps across adjacent layers. The presence of these edges is likely to affect the observed strain-induced electronic and mechanical response of 2D MoS2 structures that do not include such edges. The strain response of such mechanically exfoliated FL-MoS2 structures with no edges is characterized by shifts in both the Raman in-plane mode and photoluminescence (PL) energy.

The strain response of the CVD-grown terraced MoS2 structures is determined by the presence of edges and also results in slippage between the layers32. Recent DFT simulations suggest that the response of such 2D structures (with unequal dimensions) is likely to create an inequality in the amounts of strain across the layers and hence exhibits inhomogeneous electronic properties33. In addition, ripples are observed near edge terminals in CVD-grown MoS2 structures using scanning tunneling microscopy (STM)34. These ripples, with a typical height of ~11 Å, are reported to be responsible for the reduction of band gap of the MoS2 sheets near edge terminals from 1.96 eV to 1.46 eV. A recent study35 suggests the formation of ripples in as-grown bilayer MoS2 structures that is induced by strong interlayer edge-to-basal plane coupling. In addition, the rippling instability is observed in the lower layer due to the interactions with the edges in the top layer.

Thus, while the strain response of MoS2 structures has been investigated extensively for the case of mechanically exfoliated flakes, the understanding of the effects of strain on the mechanical and electronic behavior of CVD-grown MoS2 structures is still in infancy. Although DFT simulations can provide insights in the effect of the presence of edges on the strain-induced variations in the local electronic structure of such multilayered structures, these simulations are limited to a system size on the order of a few nanometers. It is also likely that the effect of the presence of edges on the strain response observed at the nanoscale dimensions of the layers is significantly different at the micron scale dimensions of the layers as observed experimentally. Micron scale exceeds the capacity of DFT method, yet can be handled using classical MD. Moreover, the DFT simulations focused on the strain response of bilayer structures, hence, the effect of number of layers as well as the mechanism of strain relaxation at the atomic scale remain unknown.

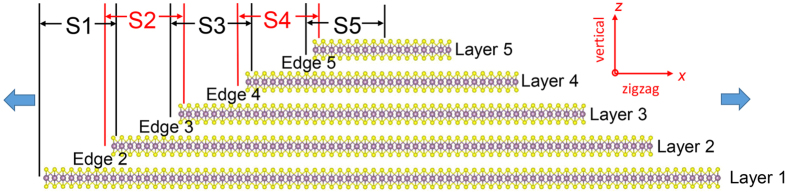
The current study investigates the effect of the size of the layers and mechanism of the strain relaxation of suspended CVD-grown multilayered MoS2 structures at the experimental length scales using classical MD simulations. The CVD-grown structures comprise of flakes of few layers wherein the top layers are relatively smaller in size than the bottom layers, resulting in the formation of edges/steps across adjacent layers. To model such a system, a simplified five-layered terraced MoS2 rectangular system in the basal plane with edges along X direction is created and shown in Fig. 1. All the layers have the same width in the Y direction (~11 nm), but have varying dimensions in the X direction. The CVD-grown terraced pyramid structure is created to have a 1/5 decrease in the length of each layer in the X direction as compared to the length of the layer below it. The X dimensions of the as-created pyramid system correspond to ~317 nm for the bottom-most layer (layer 1), ~254 nm for layer 2, ~203 nm for layer 3, ~164 nm for layer 4, and ~130 nm for layer 5. The thickness of each individual layer is 0.62 nm from our simulation, which leads to 3.1 nm for the five-layer system. The total dimensions of the representative system are 317 nm × 10.98 nm × 3.1 nm. Periodic boundaries are applied in X and Y directions, and a vacuum space of 20 nm is added in the vertical direction. Such a simplified system creates edges along the X direction, and allows the investigation of the strain response of a particular layer when the free edges may appear both above and below it. The interatomic interactions are defined by a combined reactive empirical bond-order (REBO)36 and Lennard Jones (LJ) potential. The strain response is investigated under the loading condition of uniaxial tensile strain (εx ≠ 0, εy = 0, σx ≠ 0, and σy ≠ 0,) where εx and εy (σx and σy) are the average strains (stresses) of the entire system along the X and Y directions.

Figure 1. Schematic of a model pyramid system used in the study.

Figure 1

Open in a new tab

Uniaxial strain is applied along the X direction as indicated by a blue arrow.

Results and Discussions

A uniaxial tensile strain is applied along the X direction in increments of 0.1% and the system is allowed to relax to minimize the total energy of the system at each increment. The straining is continued to reach a total tensile strain of 6% which is within the elastic region37 for the MoS2 system for the REBO potential. At each increment, a layer strain (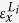Inline graphic) is calculated for each individual layer as

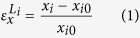graphic file with name srep40862-m2.jpg

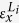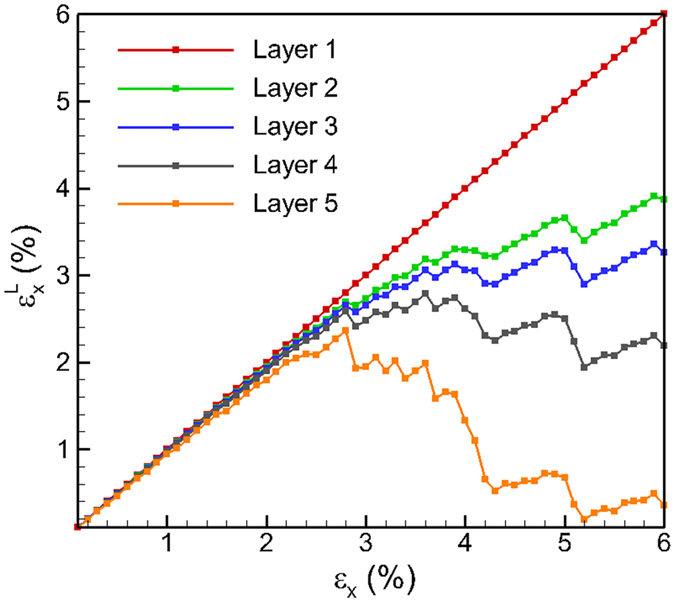
where i is the layer-id (1, 2, 3, 4, 5); xi and xi0 are final and initial layer length of ith layer in X direction, respectively. The analysis of the layer strain, Inline graphic, provides the strains of each individual layer and enables the investigation of the relaxation of each layer during the straining process. The variating of 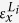Inline graphic is plotted as a function of the applied uniaxial tensile strain (εx) for each individual layer, from layer 1 to layer 5, in Fig. 2. It can be seen that the layer strain in the bottom layer varies as the applied external strain. No relaxation of the bottom layer is observed as there are no edges on the bottom layer. However, the variation in the layer strain for the upper layers i.e. layers 2 through 5, is observed to deviate from that observed for the bottom layer with the layer strains being lower than that for the bottom layer. The deviations are observed to be earlier and larger for the higher layers. Such a deviation suggests that the top layers start to relax first due to the presence of a free surface above the top layer, followed by the lower layers. The deviation in the layer strain, therefore, is larger for the upper layers where vertical relaxation is possible. The layer strain continues to increase with applied strain for each layer up to a certain value, after which a further increase in applied strain results in a drop in the local strain. These reductions in layer strain are observed to occur simultaneously for layer 2 through layer 5. Each reduction is then followed by a small increase in layer strain when strained further. Such increases and decreases in the applied strains continue to occur simultaneously as the applied strain increases, but the deviation in the magnitude of the layer strains is also observed to increase as the applied strain increases. For example, at an applied strain of εx = 4%, the layer strains, from layer 2, layer 3, layer 4 and layer 5 reduce to 3.29%, 3.06%, 2.62%, 1.33%, respectively. However, it is not clear if these simultaneous variations are related to the sliding between the layers or due to the slipping of the edges on top of the layers.

Figure 2. Variating of layer strain 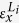Inline graphic for each layer as a function of applied strain εx for 317 nm MoS2 multilayered structure under uniaxial tension.

Figure 2

Open in a new tab

To investigate the strain relaxation mechanisms of the various layer strains, an out-of-plane vertical displacement is computed for each atom along the length of layers in the multilayered structure. This vertical displacement (δzi), at a certain atom i, is computed as δzi = zi−z0i, where zi and z0i are the instantaneous and initial Z-coordinate of atom i, respectively24,35,38. The vertical displacement will be expected to be uniform for the case of sliding between the layers as the strain relaxation mechanism. For the case of the slipping of the edges on the bottom layers, a vertical displacement profile will show high displacements at the edges of each layer. The visual analysis of these vertical displacements for the entire sample, however, become challenging due to the large X-to-Z ratio (2D structure) of the pyramid structure. As a result, the discussion is now focused on only the left half of the structure along the X direction as the structure is symmetric on both sides. The left half of the pyramid sheet is partitioned to five sections, S1 to S5, to visualize the local variations in vertical displacements at the atomic scale, as shown in Fig. 1. The five sections overlap with each other to include the terrace and an edge. A total number of four edges are investigated in this paper, noted as E2 to E5. Figure S3 shows the displacement map for sections S1 to S5 of the left half of the MoS2 pyramid at unstrained configuration. The atoms are colored by the displacement in the Z direction with the positive value (red color) corresponding to an upward displacement and a negative value (blue color) indicating a downward displacement as compared to the unstrained configuration. At strain-free configuration (εx = 0%), there is no displacement along vertical direction for all atoms. Therefore, δzi of all the atoms equals to zero and these atoms are colored in green, as shown in Figure S3.

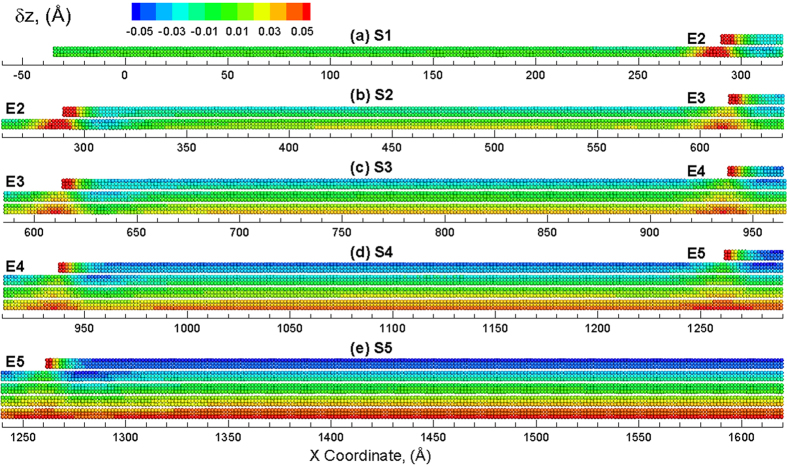
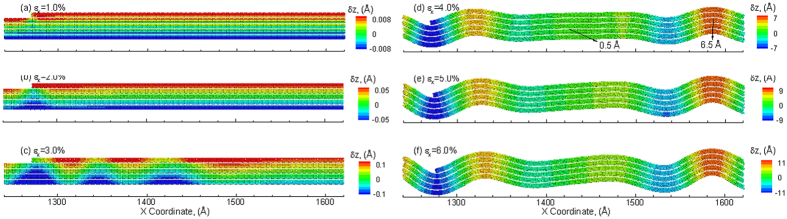
The vertical displacements can now be applied to investigate the response of the pyramid structure. The vertical displacements in the various sections of the pyramid structure at an applied strain of εx = 0.1% are shown in Figure S4. As can be seen in the snapshots, the top layer (sulfur atoms) of each section is displaced downwards (blue) and the bottom layer (sulfur atoms) is displaced upwards. It can be seen that the displacement is uniform along the length of each section and the maximal displacement is computed to be ~ 0.0005 Å at an applied strain of εx = 0.1%. The uniform straining of the layers continues to increase up to an applied strain of εx = 2%, wherein a deviation is observed in the layer strains in Fig. 2. The vertical displacements in the various sections of the pyramid structure at an applied strain of εx = 2% are shown in Fig. 3. It can be seen from the snapshots that a vertical displacement is observed at the edges in each of the sections. This vertical displacement of the edge also results in a vertical displacement of the layers below the edge region as suggested by the red colored atoms. This vertical displacement of the edge region is also compensated by having a slight downward displacement (as shown by blue color) in the region next to the edge region. This upward/downward displacement of the edges, as will be discussed later, results in the nucleation of ripples that result in the variations in the layer strains plotted in Fig. 2. The generated ripple can be observed at the right side of E2 as shown in Fig. 3(b). The ripple is more visible at the right side of E3 (Fig. 3(c)), E4 (Fig. 3(d)) and E5 (Fig. 3(e)). No ripple is nucleated in S1, as indicated by Fig. 3(a). This strain (~2%) coincides with the strain at which the local layer strain of top layers starts to deviate the applied strain (as discussed before). As a result, the relaxation of the top layers may be attributed to the ripples induced by the edge.

Figure 3.

Figure 3

Open in a new tab

Snapshots of different sections (a) S1, (b) S2, (c) S3, (d) S4 and (e) S5 of the multilayered structure at εx = 2% showing formation of ripples at the edge region. The atoms are colored by the displacement in the Z direction with the positive value (red color) corresponding to an upward displacement and a negative value (blue) indicating a downward displacement as compared to the unstrained configuration.

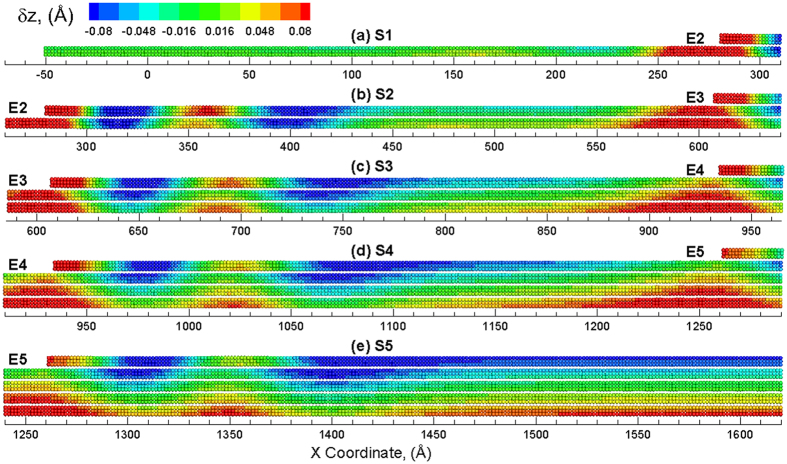
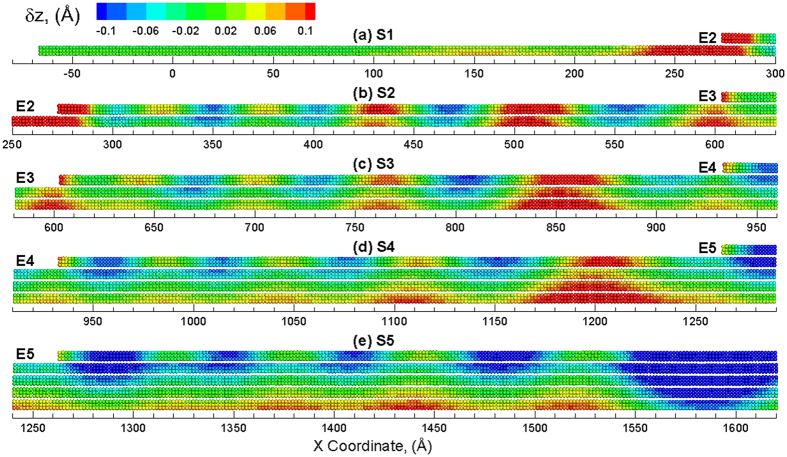
Further straining of the structure results in propagation of the nucleated ripples as well as nucleation of new ripples. The vertical displacements in the various sections of the pyramid structure at an applied strain of εx = 3% are shown in Fig. 4. As shown in Fig. 4(a), ripples are still not seen in section S1 as the strain increases to 3%. However, another ripple is nucleated at the edge region in other four sections (Fig. 4(b) to (e)). All of these ripples propagate from edge region towards the center of the structure, i.e., from left towards right. The number of ripples propagating in each section, i.e. 2 at εx = 3%, is the same. It should be noted that the top layers in each section show significant downward displacement (suggested from more blue atoms) as compared to the remaining layers in each section. This displacement attributed to the edges of the top layers results in the reduction in the layer strain for the top layers, as seen in Fig. 2. An applied strain of εx = 4% results in the propagation of ripples across the length of the sections as shown in Fig. 5. The number of ripples propagating in each section is the same except for that observed in section S1, where the ripples only propagate towards the half way for an applied strain of εx = 4%. However, five ripples are observed (indirectly implied by number of blue regions in the area) to be propagating in section S2. For sections S3, S4 and S5, five propagating ripples can be explicitly observed. It is also interesting to note that the ripples generated in section 4, propagate along the length of the section and interact with the edge (E5) in section 5 where ripples are nucleated in section 5. For the section S5 which belongs to the left half of the system, ripples are also generated in the right half of the system due to the edge that propagate towards the center of the multilayered structure i.e. from right to left. The ripples created meet and interact at the center of the system to create a large downward displacement (blue) region at the center of the multilayered system as shown in Figure S5(a). Further strain results in the propagation of this downward displacement region in the opposite direction of the ripples as shown in Figure S5(b). The application of more strain on the structure results in the nucleation of new ripples at the edges that propagate again towards the edges as shown in Figure S5(c).

Figure 4.

Figure 4

Open in a new tab

Snapshots of different sections (a) S1, (b) S2, (c) S3, (d) S4 and (e) S5 of the multilayered structure at εx = 3% showing propagation of ripples from edge towards center. The atoms are colored by the displacement in the Z direction with the positive value (red color) corresponding to an upward displacement and a negative value (blue) indicating a downward displacement as compared to the unstrained configuration.

Figure 5.

Figure 5

Open in a new tab

Snapshots of different sections (a) S1, (b) S2, (c) S3, (d) S4 and (e) S5 of the multilayered structure at εx = 4% showing ripples across the length of each section. The atoms are colored by the displacement in the Z direction with the positive value (red color) corresponding to an upward displacement and a negative value (blue) indicating a downward displacement as compared to the unstrained configuration.

The discussion so far has focused on the strain relaxation response under loading conditions of uniaxial tensile strain. The multilayered structure can also be subjected to compressive strains to investigate the strain response and ripple formation behavior. The variation of layer strain (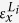Inline graphic) for each individual layer in multilayered structure as a function of applied uniaxial compressive strain (εx) is shown in Fig. 6. The variation of 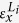Inline graphic is initially linear with εx. 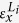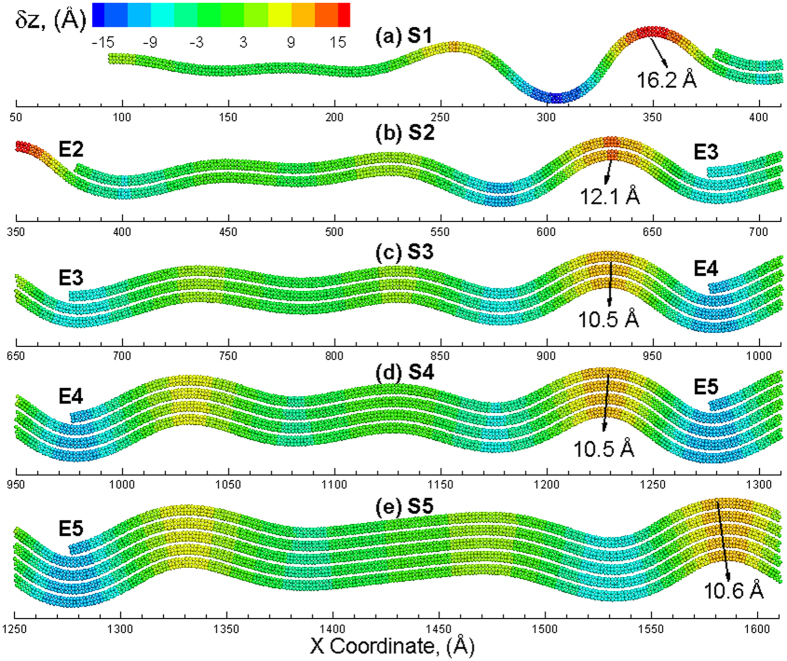Similar to that observed for tensile strains, Inline graphic is observed to relax at larger applied strains through the nucleation and propagation of ripples. However, there exist a few noticeable differences in the case of compressive loading. The amount of layer strain relaxation in top layers during compression is considerably larger than that observed during tension. As will be discussed later, the larger relaxation of strain is attributed to the larger amplitudes of the ripples under compression as compared to that under tension. In addition, as the applied compressive strain exceeds εx = 3.75%, 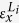Inline graphic increases consistently with the applied strain. Such a re-emerged increase in the layer strain indicates that no additional strain is relaxed through additional nucleation of ripples. Thus, there is a limit for the relaxation of the layers that can be attributed to the formation of ripples. The vertical displacements in the section S5 of the pyramid structure at various values of applied strain of are shown in Fig. 7. The vertical displacements are fairly uniform in the section at an applied compressive strain of εx = 1% as shown in Fig. 7(a). Continued strain results in the nucleation of ripples at the edge E5 as shown in Fig. 7(b). Further applied strain nucleates more ripples that propagate towards the center of the structure as shown in Fig. 7(c). The most significant difference under compressive loading is observed at an applied compressive strain of εx = 4%, wherein the amplitude of the ripples exceeds 8 Å (~8.6 Å) at the edge of section S5. The amplitude, however, reduces to 6.5 Å at the center of the pyramid (right side of S5 in Fig. 7(d)) where the ripple initiated from the right edge merges with the left one. The maximum number of ripples is observed at an applied compressive strain of εx = 4%. Application of additional compressive strain does not result in nucleation of additional ripples. This can be seen from vertical displacements in Fig. 7(f) at an applied compressive strain of εx = 6% wherein the number of ripples propagating across section S5 is the same as those observed at an applied compressive strain of εx = 4%. The only difference at the two strains, however, is the amplitude of the ripples, which is implied by the different legends of the two snapshots. The vertical displacements for sections S1 to S5 at an applied compressive strain of εx = 6%, are shown in Fig. 8. Ripples are observed to nucleate at the edges for all the sections and propagate towards the center of the multilayered structure. The peak amplitude of the ripples in sections S1, S2, S3, and S5 are calculated to be 16.2 Å, 12.1 Å, 10.5 Å, 10.5 Å, 10.6 Å, respectively. These amplitudes of the ripples are in excellent agreement with the amplitudes of the ripples observed experimentally34. Also, the amplitude for sections with lower number of layers is observed to be larger, especially when the number of layers is less than three. The slightly larger amplitude in S5 (5 layers) as compared to that observed for section S4 (4 layers) is attributed to the interaction and merger of two ripples in S5.

Figure 6. Variating of layer strain 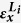Inline graphic for each layer as a function of applied strain εx for 317 nm MoS2 multilayered structure under uniaxial compression.

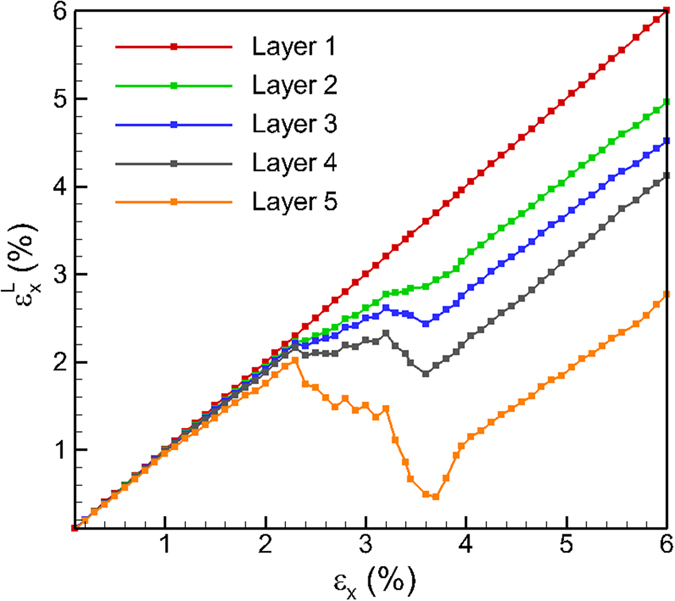
Figure 6

Open in a new tab

Figure 7.

Figure 7

Open in a new tab

Snapshots of S5 showing propagation of ripples at the edge region at applied compressive strains of (a) εx = 1%, (b) εx = 2%, (c) εx = 3%, (d) εx = 4%, (e) εx = 5% and (f) εx = 6%. The atoms are colored by the displacement in the Z direction with the positive value (red color) corresponding to an upward displacement and a negative value (blue) indicating a downward displacement as compared to the unstrained configuration.

Figure 8.

Figure 8

Open in a new tab

Snapshots of the sections (a) S1, (b) S2, (c) S3, (d) S4 and (e) S5 of 317 nm as-grown MoS2 structure at applied compressive strains of εx = 6%. The atoms are colored by the displacement in the Z direction with the positive value (red color) corresponding to an upward displacement and a negative value (blue) indicating a downward displacement as compared to the unstrained configuration.

While ripple formation has been reported using previous MD studies for the case of single layer MoS2 sheets27,28, the mechanism of ripple formation was attributed to buckling of the sheet under compression. The presence of edges in the multilayered structure considered here provides the necessary displacements to relax strain through the formation of ripples. The presence of terraced edges in these CVD-grown structures is observed to be the cause for the nucleation of ripples at the edges that grow towards the center of the structure under applied in-plane strains. To verify this, a five-layered MoS2 sheet with the same dimensions as section S5 of the multilayered structure is created with equal dimensions of all layers (i.e. no edges) and is subjected to uniaxial compression as discussed before. The multilayered MoS2 structure comprises of 317 nm in X direction and 10.98 nm in y direction, which is of same size as the bottom layer in 317 nm as-grown MoS2 multilayer. The top four layers are of the same dimensions as bottom layer in this multilayered MoS2 structure. The MD simulations of uniaxial tensile strain indicate that no strain relaxation is observed in the periodic sheet and the layer strain 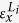Inline graphicfor each layer is observed to the be the same as the applied strain for all the layers up to an applied strain of εx = 4%. Thus, no ripples are generated without the presence of the edges, verifying the primary role of edges in ripple formation and strain relaxation of as-grown multilayered structures.

Another factor to consider in the role of edges on the formation of ripples is the size of the terrace structures between the edges. As a result, two multilayered MoS2 systems are created with the same ratio of the lengths of the layers, but with the dimensions of ~127 nm for the bottom layer (defined as the small system) and ~634 nm for the bottom layer (defined as the large system). Simultaneous relaxation is noticeably observed in 127 nm system and slightly in 634 nm system. For both cases, 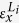Inline graphic in the bottom layer is identical to 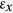Inline graphic, and top four layers relax to various extent. The relaxation strains of the top layer (fifth layer) are calculated to be 1.85%, 2.75% and 3.75% for the systems with dimensions of 127 nm, 317 nm and 634 nm, indicating the strains required to nucleate ripples increases for the larger dimensions of the terraces.

A terrace edge-to-bulk ratio (EBR) ratio can be defined for the layers in 2D MoS2 structure to describe the significance of edges in strain relaxation. For the multilayered structure considered here that is periodic in the Y direction, it is evident that a larger length in X direction will result in a smaller EBR, thus decreasing edge effect. It is revealed from Fig. 2 and Figure S6 that the values of the 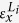Inline graphic decrease from bottom to the top layer, which is attributed to the diminishing EBR. The atoms in the top layers tend to relax to a larger extent due to more severe edge effect that results in vertical displacements and formation of ripples. Similarly, the layers in a larger sized pyramid have a smaller EBR, thus a smaller amount of strain reduction.

Conclusions

Molecular dynamics simulations are carried out to investigate the strain response of suspended CVD-grown MoS2 structures at the atomic scales. To investigate the strain response, a model multilayered system with terraces and edges is created to mimic the CVD-grown system. The MD simulations using a hybrid REBO/LJ potential suggest that the strain response of a suspended multilayered system is layer dependent and the relaxation of individual layers is attributed to nucleation, propagation and interaction of ripples. The ripples are observed to nucleate at the locations of the edges in the regions below the edge and propagate inward to the center of the multilayered structure. The ripples formed have vertical displacements of ~0.1 Å for loading under uniaxial tensile strain and ~10 Å for loading under uniaxial compressive strain. The strains required for the formation of ripples is observed to be dependent on the dimensions of the layers. It should be pointed out that current study is performed without a substrate so that the model is simplified enough to reveal the underlying origins of the ripples in suspended terraced MoS2 structures. As a result, the effects of substrate are not considered. For the case of MoS2 flakes or terraced few-layered MoS2 flakes on a substrate, the interaction between substrates and MoS2 layers will affect the rippling behavior significantly as the presence of a substrate limits the vertical displacements and the strain relaxation behavior will be determined by in-plane displacements. The formation of ripples in CVD-grown few-layered structures under strain need to be accounted for when analyzing strain effects on electronic properties of these as-grown structures materials using experimental methods or in continuum models. The strain response of suspended CVD-grown structures through ripple formation also shows promise for the use of strain engineering to generate inhomogeneous electronic properties for the design novel devices based on CVD-growth MoS2 structures.

Methods

Density Functional Theory

DFT calculations are carried out using projector augmented wave pseudo-potentials39 as implemented in the VASP code40. The cutoff energy is 500 eV for the plane-wave expansions and the Monkhorst–Pack k-point mesh is 17 × 17 × 1. The exchange-correlation functional is treated within the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximations (GGA)41. The conventional DFT energy is supplemented with a pairwise interatomic vdW potential which is determined by Tkatchenko and Scheffler (TS-vdW) from non-empirical mean-field electronic structure calculations42. The atomic positions of a unit cell (3 atoms) are optimized until all components of the forces on each atom are reduced to values below 0.01 eV/Å.

Molecular Dynamics

Large-scale MD simulations of model as-grown systems are carried out using LAMMPS43 with the interatomic interactions defined using the reactive empirical bond-order potential36 combined with a Lennard Jones potential. The time step for all simulations is defined to be 1 fs. All systems created are first equilibrated at 0 K for 10 ps at constant temperature and zero pressure (NPT ensemble using the Nose-Hoover algorithm), then the equilibrated structure is used as a strain free configuration for the following deformation simulations.

Interatomic Potentials

The reactive empirical bond-order (REBO) potential is chosen to describe in-plane covalent interaction of Mo-S system, because it is able to provide an accurate description of the structural energetics for bulk MoS2 (the in-plane lattice parameter a, the vertical S-S distance d, and the intra-layer lattice parameter c) as well as the bond breaking and formation processes at extreme tensile and compressive stresses44,45. The out-of-plane van der Waals (vdW) interaction between adjacent layers is described by pairwise Lennard Jones (LJ) potential. The energy for an atom in the REBO formulation is calculated as:

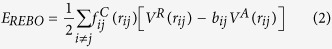graphic file with name srep40862-m13.jpg

where 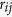Inline graphic is the distance between atoms i and j, 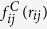Inline graphic is a cutoff function and smoothly switches REBO to LJ. VR(rij) and VA(rij) are repulsive and attractive portion, respectively.

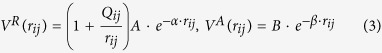graphic file with name srep40862-m16.jpg

The intralayer vdW interaction is described by the LJ potential:

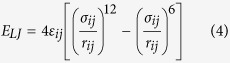graphic file with name srep40862-m17.jpg

To demonstrate the capability of the combined potential to model the strain response of the CVD-grown MoS2 structures, MD simulations are first carried out to reproduce the strain response of bilayer MoS2 structure with free edge as observed using DFT simulations33. The bilayer edge structure is shown in Figure S1. The system in the 2H stacking sequence is rectangular in the basal (XY) plane with the thickness of the two layers to be equal (Y direction), but relatively smaller along the X direction. Three dimensional periodic boundary conditions are applied in the calculations so that the bottom MoS2 layer is actually infinitely large along X and Y directions, whereas the top layer has a finite width in the X direction and infinitely long along the Y direction. A vacuum space of 20 Å thick is used along the vertical direction of the system to prevent unphysical interactions between adjacent images along this direction. The local strain maps33 under an applied uniaxial strain of εx = 4% as computed using DFT and MD simulations are shown in Figure S2. It can be seen that the MD simulations using the combined REBO-LJ potential are able to reproduce the strain variations in the two layers as predicted using DFT simulations33. The strain in the top layer is observed to be significantly lower as compared to the bottom layer that corresponds to the value of the applied strain (around 4%). Moreover, both methods show that the residual strain in the edge region of the top layer is smaller than the center region, while the opposite trend is observed for the bottom layer.

Additional Information

How to cite this article: Wang, J. et al. Origins of Ripples in CVD-Grown Few-layered MoS2 Structures under Applied Strain at Atomic Scales. Sci. Rep. 7, 40862; doi: 10.1038/srep40862 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Figures
srep40862-s1.pdf (641KB, pdf)

Acknowledgments

Research was sponsored by the Army Research Laboratory and was accomplished under Cooperative Agreement Number W911NF-14-2-0059. The authors R. R. Namburu and M. Dubey acknowledge the support of the US Army Research Laboratory (ARL) Director’s Strategic Initiative (DSI) program on interfaces in stacked 2D atomic layered materials. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory or the U.S. Government.

Footnotes

Author Contributions J. Wang and A.M. Dongare conceived and designed the simulations. J. Wang, A.M. Dongare, M. Dubey, and R.R. Namburu co-wrote the paper. All authors discussed the results and commented on the manuscript. Correspondence should be addressed to A.M. Dongare.

References

  1. Mak K. F., Lee C., Hone J., Shan J. & Heinz T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010). [DOI] [PubMed] [Google Scholar]
  2. Shi H. et al. Exciton dynamics in suspended monolayer and few-layer MoS2 2D crystals. ACS Nano 7, 1072 (2013). [DOI] [PubMed] [Google Scholar]
  3. Qiu H. et al. Electrical characterization of back-gated bi-layer MoS2 field-effect transistors and the effect of ambient on their performances. Appl. Phys. Lett. 100, 123104 (2012). [Google Scholar]
  4. Radisavljevic B., Radenovic A., Brivio J., Giacometti i. V. & Kis A. Single-layer MoS2 transistors. Nature Nanotechnol. 6, 147 (2011). [DOI] [PubMed] [Google Scholar]
  5. Wu S. et al. Vapor–solid growth of high optical quality MoS2 monolayers with near-unity valley polarization. ACS Nano 7, 2768 (2013). [DOI] [PubMed] [Google Scholar]
  6. Yin Z. et al. Single-layer MoS2 phototransistors. ACS Nano 6, 74 (2011). [DOI] [PubMed] [Google Scholar]
  7. Lauritsen J. V. et al. Chemistry of one-dimensional metallic edge states in MoS2 nanoclusters. Nanotechnology 14, 385 (2003). [Google Scholar]
  8. Butler S. Z. et al. Progress, challenges, and opportunities in two-dimensional materials beyond graphene. ACS Nano 7, 2898–2926 (2013). [DOI] [PubMed] [Google Scholar]
  9. Yun W. S., Han S., Hong S. C., Kim I. G. & Lee J. Thickness and strain effects on electronic structures of transition metal dichalcogenides: 2H-MX2 semiconductors (M = Mo, W; X = S, Se, Te). Phys. Rev. B 85, 033305 (2012). [Google Scholar]
  10. Xu M., Liang T., Shi M. & Chen H. Graphene-like two-dimensional materials. Chem. Rev. 113, 3766 (2013). [DOI] [PubMed] [Google Scholar]
  11. Lee G.-H. et al. Flexible and transparent MoS2 field-effect transistors on hexagonal boron nitride-graphene heterostructures. ACS Nano 7, 7931 (2013). [DOI] [PubMed] [Google Scholar]
  12. He K., Poole C., Mak K. F. & Shan J. Experimental demonstration of continuous electronic structure tuning via strain in atomically thin MoS2. Nano Lett. 13, 2931 (2013). [DOI] [PubMed] [Google Scholar]
  13. Conley H. J. et al. Bandgap engineering of strained monolayer and bilayer MoS2. Nano Lett. 13, 3626 (2013). [DOI] [PubMed] [Google Scholar]
  14. Zhu C. et al. Strain tuning of optical emission energy and polarization in monolayer and bilayer MoS2. Phys. Rev. B 88, 121301 (2013). [Google Scholar]
  15. Castellanos-Gomez A. et al. Local strain engineering in atomically thin MoS2. Nano Lett. 13, 5361 (2013). [DOI] [PubMed] [Google Scholar]
  16. Hui Y. Y. et al. Exceptional tunability of band energy in a compressively strained trilayer MoS2 sheet. ACS Nano 7, 7126 (2013). [DOI] [PubMed] [Google Scholar]
  17. Yang L. et al. Lattice strain effects on the optical properties of MoS2 nanosheets. Sci. Rep. 4, 5649 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Bertolazzi S., Brivio J. & Kis A. Stretching and breaking of ultrathin MoS2. ACS Nano 5, 9703 (2011). [DOI] [PubMed] [Google Scholar]
  19. Johari P. & Shenoy V. B. Tuning the electronic properties of semiconducting transition metal dichalcogenides by applying mechanical strains. ACS Nano 6, 5449 (2012). [DOI] [PubMed] [Google Scholar]
  20. Dong L., Dongare A. M., Namburu R. R., O’Regan T. P. & Dubey M. Theoretical study on strain induced variations in electronic properties of 2H-MoS2 bilayer sheets. Appl. Phys. Lett. 104, 053107 (2014). [Google Scholar]
  21. Bhattacharyya S. & Singh A. K. Semiconductor-metal transition in semiconducting bilayer sheets of transition-metal dichalcogenides. Phys. Rev. B 86, 075454 (2012). [Google Scholar]
  22. Lu P., Wu X., Guo W. & Zeng X. C. Strain-dependent electronic and magnetic properties of MoS2 monolayer, bilayer, nanoribbons and nanotubes. Phys. Chem. Chem. Phys. 14, 13035 (2012). [DOI] [PubMed] [Google Scholar]
  23. Scalise E., Houssa M., Pourtois G., Afanas’ev V. & Stesmans A. Strain-induced semiconductor to metal transition in the two-dimensional honeycomb structure of MoS2. Nano Res. 5, 43 (2012). [Google Scholar]
  24. Tapasztó L. et al. Breakdown of continuum mechanics for nanometre-wavelength rippling of graphene. Nature Phys. 8, 739 (2012). [Google Scholar]
  25. Brivio J., Alexander D. T. & Kis A. Ripples and layers in ultrathin MoS2 membranes. Nano Lett. 11, 5148 (2011). [DOI] [PubMed] [Google Scholar]
  26. Kushima A., Qian X., Zhao P., Zhang S. & Li J. Ripplocations in van der Waals layers. Nano Lett. 15, 1302 (2015). [DOI] [PubMed] [Google Scholar]
  27. Jiang J. W. The buckling of single-layer MoS2 under uniaxial compression. Nanotechnology 25, 355402 (2014). [DOI] [PubMed] [Google Scholar]
  28. Jiang J.-W. The Strain Rate Effect on the Buckling of Single-Layer MoS2. Sci. Rep. 5, 7814 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Liu Z. et al. Strain and structure heterogeneity in MoS2 atomic layers grown by chemical vapour deposition. Nature Commun. 5, 5246 (2014). [DOI] [PubMed] [Google Scholar]
  30. Zhan Y., Liu Z., Najmaei S., Ajayan P. M. & Lou J. Large‐area vapor‐phase growth and characterization of MoS2 atomic layers on a SiO2 substrate. Small 8, 966 (2012). [DOI] [PubMed] [Google Scholar]
  31. Jariwala D., Sangwan V. K., Lauhon L. J., Marks T. J. & Hersam M. C. Emerging device applications for semiconducting two-dimensional transition metal dichalcogenides. ACS Nano 8, 1102 (2014). [DOI] [PubMed] [Google Scholar]
  32. McCreary A. et al. Effects of Uniaxial and Biaxial Strain on Few-Layered Terrace Structures of MoS2 Grown by Vapor Transport. ACS Nano 10, 3186 (2016). [DOI] [PubMed] [Google Scholar]
  33. Dong L. et al. Edge effects on band gap energy in bilayer 2H-MoS2 under uniaxial strain. J. Appl. Phys. 117, 244303 (2015). [Google Scholar]
  34. Mills A. et al. Ripples near edge terminals in MoS2 few layers and pyramid nanostructures. Appl. Phys. Lett. 108, 081601 (2016). [Google Scholar]
  35. Zheng Y. et al. Quantum mechanical rippling of a MoS2 monolayer controlled by interlayer bilayer coupling. Phys. Rev. Lett. 114, 065501 (2015). [DOI] [PubMed] [Google Scholar]
  36. Liang T., Phillpot S. R. & Sinnott S. B. Parametrization of a reactive many-body potential for Mo–S systems. Phys. Rev. B 79, 245110 (2009). [Google Scholar]
  37. Xiong S. & Cao G. Molecular dynamics simulations of mechanical properties of monolayer MoS2. Nanotechnology 26, 185705 (2015). [DOI] [PubMed] [Google Scholar]
  38. Kumar H., Er D., Dong L., Li J. & Shenoy V. B. Elastic deformations in 2D van der Waals heterostructures and their impact on optoelectronic properties: predictions from a multiscale computational approach. Sci. Rep. 5 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994). [DOI] [PubMed] [Google Scholar]
  40. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996). [DOI] [PubMed] [Google Scholar]
  41. Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996). [DOI] [PubMed] [Google Scholar]
  42. Tkatchenko A. & Scheffler M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett. 102, 073005 (2009). [DOI] [PubMed] [Google Scholar]
  43. Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 117, 1 (1995). [Google Scholar]
  44. Dang K. Q. & Spearot D. E. Effect of point and grain boundary defects on the mechanical behavior of monolayer MoS2 under tension via atomistic simulations. J. Appl. Phys. 116, 013508 (2014). [Google Scholar]
  45. Stewart J. A. & Spearot D. Atomistic simulations of nanoindentation on the basal plane of crystalline molybdenum disulfide (MoS2). Model. Simul. Mater. Sci. Eng. 21, 045003 (2013). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Figures
srep40862-s1.pdf (641KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES