Chemical and electrical synapses perform complementary roles in the synchronization of interneuronal networks

Abstract

Electrical and chemical synapses exist within the same networks of inhibitory cells, and each kind of synapse is known to be able to foster synchrony among oscillating neurons. Using numerical and analytical techniques, we show here that the electrical and inhibitory coupling play different roles in the synchronization of rhythms in inhibitory networks. The parameter range chosen is motivated by gamma rhythms, in which the γ-aminobutyric acid type A (GABA_A)-mediated inhibition is relatively strong. Under this condition, addition of a small electrical conductance can increase the degree of synchronization far more than a much larger increase in inhibitory conductance. The inhibitory synapses act to eliminate the effects of different initial conditions, whereas the electrical synapses mitigate suppression of firing due to heterogeneity in the network. Analytical techniques include tracking trajectories of coupled cells between spikes; the analysis shows that, in networks in which the degree of excitability is heterogeneous, inhibition can increase the dispersion of the voltages between spikes, whereas electrical coupling reduces such dispersion.

It is known that electrical coupling between inhibitory cells exists in many parts of the nervous system (1-11). Inhibition (2, 12-19) and electrical coupling (8, 20-26) are each known to be able to foster synchrony among connected cells. However, it is not well understood what roles each of the two kinds of coupling current plays in the synchronization process.

Several groups (27-31) have investigated networks involving gap junctions with and without inhibitory coupling. In those articles dealing with spiking (not bursting) cells, the coupling is often taken to be weak. In the weak-coupling regime, the effects of inhibition and gap junctions sum linearly, and proportional increases in either have similar effects on synchrony. In the case of strong coupling, however, the effects do not sum linearly, and new effects are created.

Motivated by experimental and large scale modeling results on gamma rhythms in distributed networks (28), we consider here networks in which the chemical coupling is large but the electrical coupling is still weak. We use parameter values associated with gamma frequency rhythms, in which the period of the population rhythm is tightly tied to the decay time of the inhibition (16, 32, 33).

We find that, in the presence of heterogeneity of currents, the electrical coupling plays a role that is different from that of the inhibition, and a small amount of electrical coupling, added to already significant inhibitory coupling, can increase the synchronization more than a very large increase in the inhibitory coupling. This work helps explain the importance of gap junctions in spatially distributed networks (28) in which the coupling is heterogeneous, as well as in local networks in which the intrinsic currents are heterogeneous. However, gap junctions alone, unless very large, do not create the rapid synchrony associated with inhibitory coupling in a homogeneous network. Thus, the inhibition and electrical coupling play complementary roles in the coherence of rhythms in inhibitory networks.

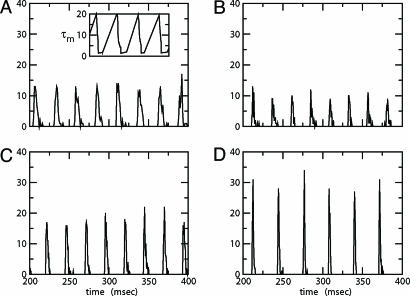
We start by showing the basic phenomena. In Fig. 1, we show histograms of a network of quadratic integrate-and-fire (QIF) neurons coupled with model γ-aminobutyric acid type A (GABA_A)-mediated inhibition and gap junctions. The cells are heterogeneous, with a range in natural frequency, and there is also noise (for details, see Methods; the Inset is discussed in Results). In Fig. 1, the cells are connected all-all. Note that there is essentially no increase in coherence by doubling the inhibitory coupling (A and B). If an electrical synapse whose conductance is 20% of the synaptic conductance is added (C and D), the coherence is sharply increased, more in D than in C. Addition of 10% electrical coupling also leads to a noticeable increase, but not as much (data not shown). In the noiseless, homogeneous network, synchrony is perfect within a cycle. The same phenomena occur when the 100 cells are arranged in a line, with each cell coupled with inhibition to 20 nearest neighbors on each side and to 10 on each side by means of electrical coupling (data not shown) so this is not just a consequence of the all-all connectivity. We have done the same calculations with biophysical models of interneurons (16), and the results are similar; in that case, setting the electrical coupling to be even 10% of the inhibitory coupling leads to very significant increases in coherence (data not shown; details of simulations in Appendix).

Fig. 1.

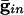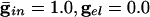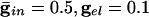Histograms for a network of 100 all-to-all-coupled QIF neurons after a long transient. (A) . (Inset) The effective membrane time constant for cell 4 in the network. (B) . (C) . (D) 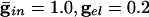. Spike counts are in 1-ms bins.

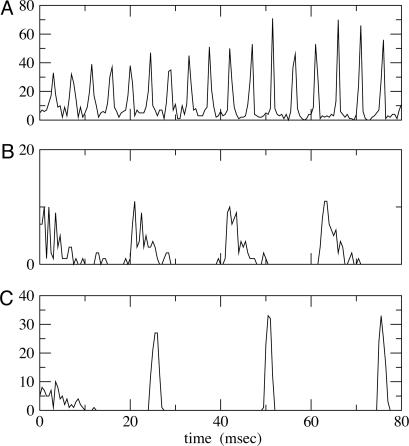
In Fig. 2 we show histograms of the onset of synchronization for different types and strengths of coupling. Fig. 2 A shows the slow development of coherence when there are only gap junctions. Fig. 2B shows that, with only inhibition, maximal coherence is reached in one cycle. Fig. 2C shows that a combination of gap junctions and inhibition leads to rapid coherence and a larger number of cells firing than in the case of pure inhibition.

Fig. 2.

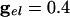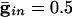Histograms for 100 QIF neurons with all-to-all coupling. At t = 0, coupling is turned on. (A) . (B) . (C) 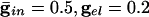.. With 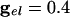, the peak coupling current has a magnitude of 28 μA/cm² whereas the peak current is 14 for 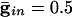. Note that maximal coherence takes many more cycles in A than in B, even though the peak coupling current is higher in A. (The frequency is higher in A because there is no inhibition.)

In the rest of this article, we explain the bases of the above phenomena. We show analytically that, with significant common inhibition to a population of cells, each cell displays a preferred trajectory that attracts all nearby trajectories (34, 35). The result is that there is an almost complete loss of memory of initial conditions within one cycle. If there were no heterogeneity, the synchrony would be almost total within one cycle. This result explains the behavior in Fig. 2B.

To understand the effects of the inhibitory and electrical coupling when there is heterogeneity, we analyze separately a subinterval of the cycle in which none of the cells fires and a complementary time interval in which all of the cells spike in a given cycle. We show that, if there is heterogeneity, the cells receiving common inhibition diverge in their voltages over the nonspiking epoch. Increasing the amount of the inhibition increases the attraction to the preferred trajectory, but actually increases the divergence of the voltages over the interval when no cells are spiking. We then show that similar effects hold for networks with mutual inhibition. Indeed, there is a limit to the amount of possible synchronization for a fixed amount of heterogeneity, no matter the size of the inhibition, with too large inhibitory conductances leading to suppression of some of the cells. Adding a relatively small amount of electrical coupling to the inhibitory coupling can make the voltages stay much closer during the nonspiking epoch.

During the epoch in which the cells spike, the main effect of the electrical coupling is to decrease the amount of suppression that would otherwise take place as the faster cells inhibit the slower ones.

Methods

The cells we are modeling are fast-spiking interneurons, whose behavior is well-described in Hodgkin-Huxley equations by using only standard spiking currents. Many model inhibitory neurons are so-called Class I excitable, including, for example, the Wang-Buszaki (WB) model (16) and a more recent model (30). These models are closely related to QIF neurons (36), which we use for our analysis. For each neuron, the basic equation is

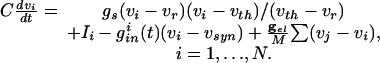[1]

Here, v_i is the voltage of the ith neuron, v_r is the rest potential, v_th is the threshold for spiking, and v_syn is the synaptic reversal potential. 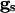is the resting conductance and 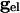is the strength of the electrical coupling. For γ-aminobutyric acid type A-mediated synapses, v_syn is set to a value near v_r. 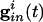is the total inhibitory conductance felt by cell i:

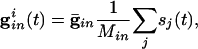where the sum is over all M_in cells inhibiting i and s_j is the synaptic gating variable (see Appendix for details.)

The parameter range for the model is what has been called (33) the “phasic” regime for an inhibitory network. This is a regime in which the natural drive to the cells is roughly tuned to the decay time of the inhibition; with too much drive, heterogeneity in drive or synaptic strength causes faster cells to precess one another, whereas too little drive makes the slower cells very susceptible to suppression. We use strong inhibition, so the drive is correspondingly strong: in the absence of inhibition, the natural rate of the cells is ≈100-125 Hz. In this regime, the period is proportional to the decay time of the inhibition (32); for a decay time associated with γ-aminobutyric acid type A, the frequency is in the gamma range (30-80 Hz). In this phasic regime, the network is least susceptible to suppression, i.e., can tolerate a wider range of heterogeneity for the same amount of suppression (see also ref. 19).

Parameters for the simulations of the QIF and the WB model (16) are found in Appendix. We attempted to choose parameters for the QIF so that the model produced a frequency-input curve quantitatively like the WB model (see also ref. 37). We assume that the spike occurs when the voltage reaches v_sp > v_th, and that the cell is then reset to v_reset < v_r. I_i is the drive to the cell, chosen to be large enough that the cell will fire periodically in the absence of inhibition. The inhibitory conductance is an exponentially decaying function of time after other cells spike, and depends on the subset of cells to which a given cell is connected. The last term is the electrical conductance, and the sum is done over the subset of M cells to which the ith cell is connected. (For all-all coupling, M = N.)

Results

Inhibition and Loss of History in Homogeneous Networks. The loss of effects of initial conditions is a direct consequence of the small effective membrane time constant when is large for all cells. Consider first a common inhibition 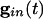. When 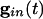is large, Eq. 1 has (at least) two time scales, that of the decay of inhibition and the effective membrane time scale. As seen in Fig. 1 A Inset, the effective membrane time constant is around 2 ms right after inhibition, over five times faster than the decay of inhibition. Such two-time-scale systems have been much studied (38), and it is well known that the voltage goes very quickly to the value (“quasi-steady state”) at which the dv/dt = 0. If there is no electrical coupling, the quasi-steady state of each cell is determined only by I_i and the connectivity, independent of the other cells and initial conditions, from the equation

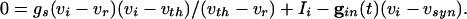[2]

That is, the voltage quickly goes to a value that is slaved to the inhibitory conductance. Thus, the dependence on initial conditions can be lost within one cycle. If 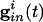and I_i are independent of i, the result is very fast synchronization, within one cycle.

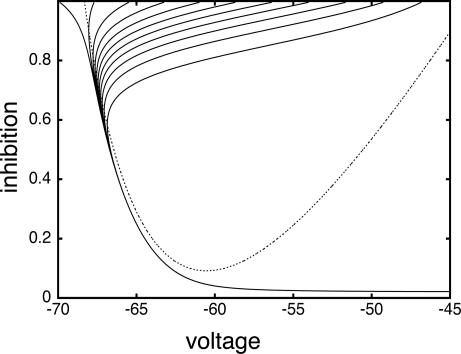
These dynamics are illustrated in the phase plane diagram in Fig. 3. Here, we show the trajectories of a single cell with inhibition that decays away with a time constant of τ_in = 12 ms:

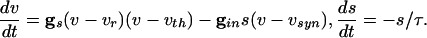We plot the voltage of a single cell vs. the inhibition with a set of different initial conditions for voltage when the inhibition begins (Fig. 3, top of box). Note that the trajectories are all drawn into a “river” (34). This observation implies that, for a set of cells that are homogeneous, when the inhibition has worn off enough for the cells to fire (the same level of inhibition for all cells), the voltages are almost identical. (See ref. 35 for a similar picture for a related set of equations.) The rivers exist even for a 5-fold decrease in the inhibition (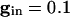, data not shown).

Fig. 3.

Phaseplane for a single QIF neuron subject to transient synaptic inhibition. Trajectories that start with the same inhibition (i.e., on same horizontal line of phaseplane) continue to have the same level of inhibition as time increases; the voltage values become closer together ()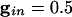

We now replace the common input with all-all mutual inhibition. Note that the common synaptic input is the sum of the decaying exponentials contributed by each cell, shifted in time from one another; thus, if the cells start with initial conditions distributed widely in phase, the common inhibition may have low amplitude (e.g., be almost constant) and need not create synchronization instantly. However, in all our simulations, synchronization was created quickly (within one cycle; see Fig. 2), and multiple clusters of cells were never observed.

If there is only electrical coupling, the coupling current becomes small as the v_i get closer to one another. Thus, the effective membrane constant is not so small, and there is no disparity in time scales to allow the network to behave as if dv_i/dt is ≈0. The synchronization thus can take multiple cycles as seen in Fig. 2 A, particularly if the coupling is not global, but rather along a line. Fig. 2 A also shows that, even with a large peak current, many cycles are required to achieve synchronization.

Dispersive Effects of Heterogeneity in an Uncoupled System. We show here that heterogeneity in uncoupled cells creates dispersion in the voltages before any of the cells fire.

For the uncoupled cells, 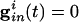and g_el = 0. Suppose these cells are started together, and we record the values of the voltages v_i at the time t_sp that the fastest cell reaches v_sp, the spike height. These values can be computed from Eq. 1), which can be integrated to t_sp to get an implicit formula for v_i. We get

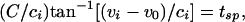[3]

where 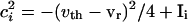and v₀ = (v_r + v_th)/2.

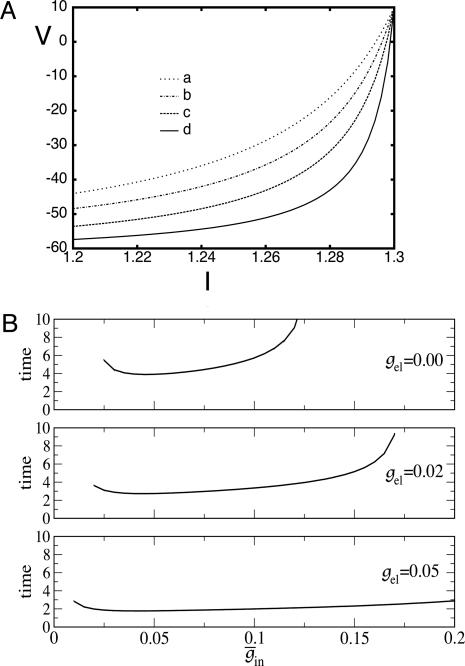
In Fig. 4A, curve c gives a numerical example of the spread in voltage at the time the most excited cell is ready to fire. Note that, for values of drive I near the maximum, the voltages are highly spread out. The reason for this spread can be seen from Eq. 2, using the shape of the arctangent near the horizontal asymptote: a small change in I_i, and hence in c_i, can make a large change in v_i. This spread is not dependent on the particular form of the QIF neuron: the same phenomena are displayed for the biophysical model (data not shown).

Fig. 4.

Effects of electrical coupling on dispersion of voltages. (A) Voltage spread due to current heterogeneity and common inhibition in the QIF. The horizontal axis is the drive, and the vertical axis is the potential of the neuron with the corresponding drive at the time that the fastest cell spikes (V = 10). The bottom curve shows that the maximal spread occurs when there is only inhibition (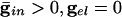), and the second curve from the bottom shows the uncoupled case. The top two curves show that electrical coupling reduces the spread in the potentials with or without inhibition. The values of (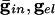) for curves a-d are, respectively, (0.0,0.05), (0.6,0.05), (0, 0), and (0.6,0). (B) Consequences of A for coupled cells. Time difference between the firing of two mutually coupled cells with slightly different drive. (Top) Nonmonotonic behavior of the spike time difference as a function of the strength of 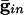. (Middle and Bottom) How gap junctions extend the range of 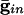, for which locking occurs, and reduce the time difference. Cell 1 has I = 1.3 and cell 2 has I = 1.36.

Inhibition Accentuates Dispersion in Voltage and Creates Suppression. We now show that, if the cells get common exponentially decaying inhibition, the dispersive effects are even larger. The cells get common input 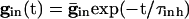, where 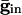is the maximal strength of the decaying inhibition. The cells are silent until the inhibition wears off enough; once some cell spikes, Eq. 2 is no longer valid. But we can compute the voltages of the other cells just before that time by using t = t_sp in Eq. 2. The bottom curve of Fig. 4A shows these voltages, again for the QIF. Similar curves are found for the WB model (data not shown). Note that the dispersion in voltages for those cells with drive near that of the fastest cell is larger when there is common inhibitory input.

If the cells are coupled mutually by inhibition, they behave like uncoupled cells with common inhibitory input between spikes, so increasing maximal conductance can lead to larger dispersion. This result is shown in Fig. 4B for a pair of QIF cells. For weak inhibition, the two cells cannot lock, but, at a critical value, locking occurs. However, due to the effects of common inhibition on the voltage spread, as 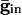increases beyond some optimal value (the minimum of the curves in Fig. 4B), the timing between the spikes of the two cells begins to diverge. At a second critical strength of 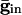, the slower cell is suppressed, and locking does not occur. Thus, no matter how strong the inhibition, it cannot lead to synchronization and, in fact, can actually make it worse. To explain this result, we use Eq. 2, with 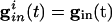independent of i. For large values of 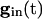, there are two quasi-steady states for each i. The lower one corresponds to an effective stable rest state, the upper one to an effective threshold. As 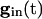decreases, these states come closer to one another and eventually annihilate one another. The most excited cell (say, cell 1) fires when it ceases to be held down by inhibition, i.e., when 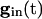reaches a sufficiently low value, depending on I₁, at which the two quasi-steady states for v₁ merge. From this description, we can see that increasing the strength of single inhibitory postsynaptic currents (IPSCs) does not decrease the heterogeneity in next spike time; it increases the time to the next spike, but not the dispersion of the voltages at that time, which is determined by Eq. 2 with 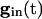set to the critical value for v₁.

Similarly, for a fixed sufficiently large level of inhibitory coupling, there is a maximal amount of heterogeneity for which there is locking; beyond this amount, there is suppression (data not shown). This analysis is for all-to-all coupling, but a similar analysis holds for networks with spatial structure.

Between Spikes, Gap Junctions Hold the Voltages Closer Together. We assume that the inhibition is sufficiently strong so that the initial-condition-removal is accomplished as in the first section of Results. Thus, we are concerned with how gap junctions deal with heterogeneity in the network. Formally, we consider the network all-all coupled, but some of the synapses may have zero strength.

As above, we consider here an interval of time in which no cell is spiking. Unlike the network with only chemical synapses, with electrical synapses, there is coupling whether or not there is a spike of some cell. The effect of the electrical coupling on the dispersion of the voltages when the leading cell is at its threshold is shown in Fig. 4 for the QIF model. The bottom curve in Fig. 4A shows the spread with 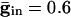, and the second from the top shows the spread with an added electrical conductance of 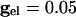. The spread is considerably lower. The consequence of this is shown in Fig. 4B for a pair of cells; gap junctions both improve the range in which locking occurs with inhibition and also decrease the time difference between a pair of cells.

To understand these effects, we use the full Eqs. 1, which we rewrite as

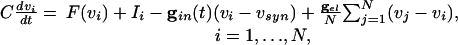[4]

where 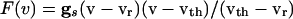. Using the differences in time scales of the voltage and decay of inhibition as before, we see that, when no cells are firing, the voltages are determined by

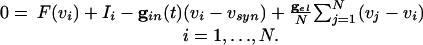[5]

These equations constitute the “slow manifold” associated with the changes in the voltages during the slow decay of the inhibition.

Suppose that I₁ is the largest of the drives. We now compute v₁ - v_i for i > 1, to see how this depends on the different kinds of coupling in the system. Using Eq. 5,

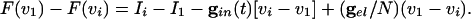[6]

We use the fact that F(v_i) = F(v_j) if v_i = v_j to factor the left hand side to

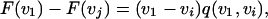[7]

where

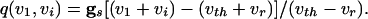[8]

Using Eqs. 6 and 7, we get

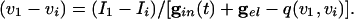[9]

The values of v_i stay close to those satisfying Eq. 9 provided that the slow manifold of Eq. 4 exists and remains attracting. As discussed above, for 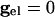, each equation has a pair of fixed points providing that 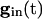is large enough. As 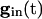decays, the fixed points coalesce to a saddle node and disappear. At this point, a spike occurs and Eq. 5 is no longer valid. Adding gap junctional currents couples the equations of Eq. 5, so it is not possible to solve each separately. However, it is still correct that, as 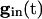declines, any of the 2^N fixed points may disappear only by coalescing with other fixed points. When 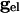is not zero, the value of 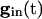at which this happens changes, but not the existence of such a value.

Note from Eq. 8 that, the larger v_i is (i.e., the closer it is to v₁), the more positive is q, and hence the smaller is the denominator of the right side of Eq. 9. The term 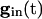decays exponentially and is at its smallest (between spikes) just when v₁ reaches v_th. Thus, during the last portions of the interval between spikes, the major force holding the voltages together is the conductance of the electric coupling.

Electrical Coupling Has Other Effects During Spiking Interval. At the time the first cell spikes, the voltages of the others are spread out, although less spread out than in the absence of the electrical coupling. We now consider the dynamics of the epoch during which there is firing of any of the cells that are not suppressed.

We first consider the case in which there are just two cells. Because both the QIF and the WB model have strong nonlinear regenerative currents (the sodium current for the WB and the quadratic nonlinearity for the QIF), there is a threshold or state such that the firing of a spike is inevitable (except for, perhaps, extremely strong inhibition). That is, even if the inhibition is abruptly increased, the postsynaptic cell will still fire. Suppose there is no electrical coupling and the faster cell fires. If the slower cell is sufficiently depolarized, the resulting inhibition will not stop it from firing. However, if the inhibition comes before the slow cell is depolarized enough to engage the regenerative currents, then the slow cell will be suppressed for this cycle.

Let V_slow be the potential of the slow cell at the point at which the fast cell begins its spike. (This is the point of inflection of the voltage of the fast cell, the voltage at which a spike is inevitable.) A short time later, the inhibition from the fast cell arrives and can either suppress the slow cell for this cycle or allow it to fire, but delay its firing. Let V^* denote the minimal voltage of the slow cell such that, if V_slow > V^* (respectively, V_slow < V^*), the slow cell will (resp., will not) fire. For example, in the WB model with 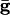, we find V^* = -57.3 mV when the fast cell reaches its inflection point at -55 mV. In the presence of electrical junctions, however, there are two competing influences during the spiking epoch. While the presynaptic spike is building up (before the inhibition is turned on), it is pulling up the slow cell closer to its threshold. Thus, electrical junctions could decrease the value of V^*, allowing for a greater voltage spread at the point of a spike. Indeed, for the WB, a small amount of electrical coupling (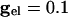) leads to a lowering of V^* to -60.5 mV. We can tease apart the contribution of the prespike and spiking epochs of the gap junctions by turning them off either during the spike or during the build-up. When the gap-junction contribution is removed for the spiking part, we find that V^* = -53 and when it is removed during the buildup, we find V^* = -60.5. Thus, the spike plays an important role in expanding the allowable spread in the potential of the slow neuron. This finding is consistent with results for large, biophysically detailed simulations that, in either the spiking or nonspiking epochs, the electrical coupling increases coherence (28).

The second possible effect of electrical coupling concerns the subinterval in which the spike of the fast cell is over and its voltage is below threshold. When the fast cell (presynaptic cell) repolarizes after a spike, this voltage change could pull the postsynaptic cell down and thus prevent it from firing. We have never observed this effect, most likely because (i) the after-hyperpolarization (AHP) of our cells is of much smaller magnitude than the reversal potential of a synapse (for QIF, reset is -67 mV and v_syn = -75 mV); and (ii) electrical coupling is considerably weaker than the synaptic coupling so that this small hyperpolarization is negligible compared with the synaptic inhibition.

Now, we suppose there are many cells, not just two. We consider the time between the spike of the most active cell and the spike of the last unsuppressed cell. All of the arguments above are still relevant. For spike widths that are not too narrow and after-hyperpolarizations that are not too deep, the major effect of the electrical coupling is to reduce suppression due to heterogeneity. It can have a small adverse effect on the spread of voltages right at the end of the last spike, but this effect is washed out by the stronger common inhibition.

Discussion

In this article, we have analyzed the different roles of inhibition and electrical coupling in the creation of synchronization of cells interacting through both types of coupling. The central result is that the two types of coupling are complementary in their effects. The inhibition is especially good at wiping out effects of initial conditions but cannot deal with significant heterogeneity (16, 33), no matter how strong the inhibitory coupling; indeed, stronger inhibitory coupling makes dispersion of the voltages worse and leads to suppression of cells. The electrical coupling acts to pull the voltages together during the intervals when no cells are spiking and to minimize suppression during the interval when spiking takes place. When the inhibition is sufficiently strong to quickly synchronize homogeneous networks, it takes only a small addition of electrical coupling to get similar results for a heterogeneous network.

The QIF model used in our analysis (36) is closely related to the “theta model” (39, 40), a one-dimensional but continuous differential equation. The effect of inhibition to erase initial conditions in those model neurons was analyzed in ref. 35. However, the QIF model allows the addition of electrical coupling in a straightforward way, whereas the theta model does not. Because of the ability of the QIF to produce a spike, we do not need to add a delta-function such as was used in ref. 29 with an integrate-and-fire-based model.

Some studies on electrical coupling and inhibitory cells (27, 31) deal with bursting neurons and address different issues. Here, we focus on the nonlinear effects in spiking neurons that come from adding electrical coupling to already strong inhibitory coupling. With weak coupling (25, 29, 30), one can get anti-phase locking that we do not see in our analysis, which focuses on strong inhibitory coupling. Indeed, it is known that weak gap junctional coupling alone can create stable anti-phase solutions for some frequencies and spike shapes (23). The nonlinear interaction of inhibition and electrical coupling allows electrical coupling that might, by itself, be desynchronizing to add to synchronization when there is strong inhibitory coupling.

The analysis in this article uses methods different from those of previous papers on electrical coupling, including averaging methods (24, 29, 30) or the spike-response method (23). The key idea in the current analysis is that the interacting voltages can be tracked between spikes, by using the fact that the strong inhibition creates a situation in which all of the cells are controlled by the state of the decaying inhibition. This fact allows us to see how the electrical coupling influences the voltages between spikes. Bem and Rinzel (31) also use differences in time scales to study the effects of gap junctions on coupled neurons. They show that gap junctions can stabilize the anti-phase state in reciprocally inhibiting cells whereas, without the gap junctions, the cells oscillate in a nearly synchronous state. Their model neurons are such that the recovery variable (for example, the delayed rectifier) is the slowest time scale, in contrast to the present results where the decay of inhibition dominates.

The analysis assumes that the period of the oscillation is related to the decay time of the inhibition. This assumption is motivated by the work of ref. 28 on gamma oscillations in a distributed network of fast-spiking interneurons; the gamma frequency in inhibitory networks is highly dependent on that decay time (32). The strong inhibition creates the period of the oscillation by enforcing an interval of silence until the inhibition wears off. These ideas are potentially relevant to other networks of interneurons as well. For example, the low-threshold spiking cells (1, 41, 42), known to have electrical coupling in addition to inhibitory coupling, produce rhythms at lower frequencies and also give rise to inhibitory postsynaptic potentials (IPSPs) in target cells that are considerably longer than those of fast-spiking interneurons. However, other classes of inhibitory cells, such as oriens-lacunosum moleculare cells of the hippocampus, display hyperpolarization-induced currents (43); these cells would not synchronize according to the scenario in this paper, because addition of hyperpolarization-activated currents changes the synchronization properties of cells (44, 45).

Appendix

The equations for the WB model are:

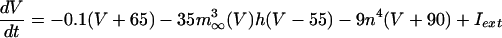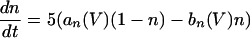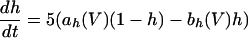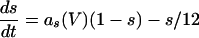where

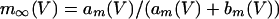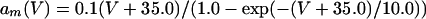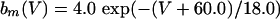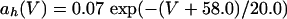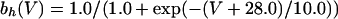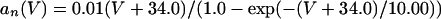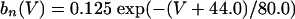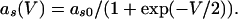The QIF model satisfies:

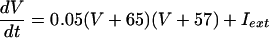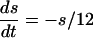with the condition that, when V = 30, s is incremented by 1 and V is reset to -67. The external current applied to each cell in each model was a combination of a fixed random bias current (between 1.3 and 1.6 for the QIF, and 2 and 2.5 for the WB), a normally distributed scaled random number (with variance 0.2√dt where dt is the time step), and the total synaptic current. The synaptic current was the sum of the electrical and chemical synapses. Electrical synapses from k to j have the form:

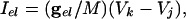where 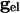is a parameter that we varied in the paper and M is the total number of cells to which a neuron is connected. For all-to-all, M = 101 whereas for the line of cells, M = 21 (10 neighbors to the right and left). Chemical synapses from k to j have the form:

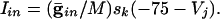For the linear array of cells, M = 41 with 20 cells to the left and right. Euler's method with a timestep of 0.05 ms was used to integrate the equations. All simulations were done by using xppaut, and the equations files are available upon request from B.E.