Multiple linear combination (MLC) regression tests for common variants adapted to linkage disequilibrium structure

ABSTRACT

By jointly analyzing multiple variants within a gene, instead of one at a time, gene‐based multiple regression can improve power, robustness, and interpretation in genetic association analysis. We investigate multiple linear combination (MLC) test statistics for analysis of common variants under realistic trait models with linkage disequilibrium (LD) based on HapMap Asian haplotypes. MLC is a directional test that exploits LD structure in a gene to construct clusters of closely correlated variants recoded such that the majority of pairwise correlations are positive. It combines variant effects within the same cluster linearly, and aggregates cluster‐specific effects in a quadratic sum of squares and cross‐products, producing a test statistic with reduced degrees of freedom (df) equal to the number of clusters. By simulation studies of 1000 genes from across the genome, we demonstrate that MLC is a well‐powered and robust choice among existing methods across a broad range of gene structures. Compared to minimum P‐value, variance‐component, and principal‐component methods, the mean power of MLC is never much lower than that of other methods, and can be higher, particularly with multiple causal variants. Moreover, the variation in gene‐specific MLC test size and power across 1000 genes is less than that of other methods, suggesting it is a complementary approach for discovery in genome‐wide analysis. The cluster construction of the MLC test statistics helps reveal within‐gene LD structure, allowing interpretation of clustered variants as haplotypic effects, while multiple regression helps to distinguish direct and indirect associations.

1. INTRODUCTION

In genome‐wide association studies (GWAS) and large‐scale candidate gene studies, researchers typically scan a large number of single nucleotide polymorphism (SNP) markers, one by one, to detect SNP‐trait association signals. This single‐SNP analysis strategy has been preferred as a simple and effective approach assuming the design and scale of the studies are sufficient to capture the marginal direct or indirect association of a SNP with complex disease traits (Kraft & Cox, 2008; Risch & Merikangas, 1996). As an alternative to single SNP test statistics, combined analysis of multiple SNPs within a gene (or a specified region) is a natural and interpretable analytic strategy at the gene level, and various methods have been advocated. A gene‐based approach offers other analytical merits—reduction of multiple testing burden, robustness to population differences regarding LD and allele frequency, and improved ability to replicate associations (Luo et al., 2010; Neale & Sham, 2004).

An established class of gene‐based methods applies multiple regression analysis in which each SNP is coded as a covariate (Chapman & Whittaker, 2008; Clayton, Chapman, & Cooper, 2004; Moskvina et al., 2012; Wason & Dudbridge, 2012). A multi‐SNP global statistic is constructed to represent a gene and test the global null hypothesis where the degrees of freedom (df) correspond to the number of SNPs. Alternatively, SNP genotypes can be represented by one or more principal components that explain their variability (Gauderman, Murcray, Gilliland, & Conti, 2007). Other reduced df global statistics have been constructed from single or multiple SNP analysis: the weighted sum method uses a linear combination of regression coefficients or their corresponding test statistics, but performance depends on the direction of the per‐SNP association, and how minor and major alleles are coded (Han & Pan, 2010; Madsen & Browning, 2009; Schaid, McDonnell, Hebbring, Cunningham, & Thibodeau, 2005; Wang & Elston, 2007). A weighted squared sum test of per‐SNP marginal effects avoids this problem, and is powerful for certain alternatives (Pan, 2009). Similar gene‐based tests include kernel regression and related variance component methods (Goeman, van de Geer, & van Houwelingen, 2005; Kwee, Liu, Lin, Ghosh, & Epstein, 2008; Schaid et al., 2005; Wu et al., 2010).

To improve power and robustness of genetic association analysis to gene structure and trait architecture, we proposed multiple linear combination (MLC) regression for regional testing (Bull, Yoo, & Sun, 2009; Yoo, Sun, & Bull, 2013). The MLC test adapts to the LD structure of SNPs in a gene by partitioning and recoding SNPs into bins of positively correlated SNPs, using only the pairwise SNP correlations. From a regression analysis of multiple SNPs in a gene, the individual SNP coefficients are combined linearly within each bin and then bin‐specific terms are combined in a weighted sum of squared and cross‐product (i.e., quadratic) terms. Trait association with the gene region is then represented by an overall global statistic with df equal to the number of bins. In this way, we improve robustness to the problem of opposing direction of effects and achieve some reduction in df while retaining the parsimony of a linear combination of multiple SNP effects within a bin.

In Yoo et al. (2013) and Yoo, Sun, Poirier, and Bull (2014), we constructed bins using LDSelect, an established method for tagSNP selection that lends itself to bin construction (Carlson et al., 2004). Initially, we examined trait model scenarios with one or two low frequency causal SNPs, analyzing only noncausal low‐frequency and/or common SNPs, and observed that reduced df MLC tests often showed better power than the full df Wald test. In further developments, we evaluated an alternative clustering method to construct bins for the MLC test by modeling SNPs as graphs and finding a substructure of the graph (Yoo, Kim, & Bull, 2015). Compared to LDSelect, this clustering algorithm tends to produce smaller clusters with stronger positive correlation, so the MLC test is less likely to be affected by the occurrence of opposing signs in the individual SNP effect coefficients.

The purpose of this report is to characterize conditions in which the clustering‐based MLC test performs better or worse than other gene‐based tests, limiting attention to non trait‐adaptive methods. Because MLC tests are based on multiple regression analysis, they are well‐designed for common variants. Their strength comes from incorporating the linkage disequilibrium (LD) structure among causal and neutral SNPs, which is expected to be more extensive for common SNPs. We illustrate application and interpretation of gene‐based analysis in candidate gene analysis of HDL cholesterol in participants of the Diabetes Control and Complications Trial. We investigate MLC test power in comparison with other gene‐based statistics for scenarios with multiple common causal variants (minor allele frequency (MAF) > 0.05) and conduct simulation studies under various genetic models where multi‐SNP regressions include all typed SNPs or exclude untyped causal SNPs. We consider realistic LD structure among causal and neutral SNPs based on SNP distributions and LD structures in HapMap Asian population data for 1,000 genes sampled from across the genome.

We propose two main applications of the MLC approach: (1) computationally efficient genome‐wide gene‐based gene discovery, as a complement to conventional single‐SNP analysis, and (2) large‐scale candidate gene studies or regional fine mapping of candidate regions; in both settings, we avoid the multiple testing cost associated with adaptive use of trait data in test construction. Although all gene‐based methods reduce the level of genome‐wide multiplicity by treating the gene as the unit of analysis, advantages of common‐variant multiple regression include computationally inexpensive use of asymptotic test distributions, variant prioritization and localization within a gene, ability to capture haplotype information at least approximately, and biological interpretability.

2. STATISTICAL METHODS

2.1. Estimation and hypothesis testing in multi‐SNP regression models

Denote the genotypes of K SNPs as $X=(X_1,X_2,\cdots ,X_K)$ and the trait variable as Y. Initially, we code the genotype values of 0, 1, and 2 as a count of the minor allele. Inference concerning overall association between the trait and the SNPs is obtained via a multi‐SNP regression model:

$$g^{-1}\left\{E\left(Y\right|X)\right\}={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots +{\beta }_K{X}_K,$$ (1)

where$E\left(Y\right|X)$is the expected value of $Y_i$ given X and $g^{-1}(·)$ is the link function. In this report, we focus on a quantitative trait, using the identity function for $g^{-1}(·)$, but analogous approaches can be applied to categorical traits, as typical in case‐control studies, or time‐to‐event traits in cohort studies.

Hypothesis tests for association in the joint multi‐SNP regression model are constructed using the parameter estimates $\widehat{\beta }={({\widehat{\beta }}_1,\cdots ,{\widehat{\beta }}_K)}^T$ and the corresponding estimated variance‐covariance matrix ${\mathrm{\Sigma }}_B$, obtained by least squares/maximum‐likelihood methods under large sample assumptions. In large samples, it is sufficient to assume that the regression coefficients $\widehat{\beta }$ follow a multivariate normal distribution with variance‐covariance matrix of rank K. In linear regression, $\mathrm{\Sigma }=\frac{{\sigma }^2}{n}{\left(S_X\right)}^{-1}$depends on a consistent error variance estimate and on SNP genotype variances/covariances in $S_X=X^{T}X$. A generalized, that is, multi‐df Wald test of the global null hypothesis of no association (${\beta }_j=0$ for all j) against the alternative that at least one ${\beta }_j\ne 0$ is defined as $G_W={\widehat{\beta }}^T{\mathrm{\Sigma }}_B^{-1}\widehat{\beta }$ which has a quadratic form. The asymptotic null distribution of this statistic is chi‐squared with K df, assuming the SNP design matrix is of full rank, that is, no linear dependency among SNPs. Single‐df tests of ${\beta }_j=0$ against the alternative that ${\beta }_j\ne 0$, taking into account other SNPs in the regression, correspond to $Z_j={\widehat{\beta }}_j/\sqrt{\mathrm{Var}\left({\widehat{\beta }}_j\right)}={\widehat{\beta }}_j/\sqrt{{\left({\mathrm{\Sigma }}_B\right)}_{jj}}$with large sample covariance ${\mathrm{\Sigma }}_Z$, which can be derived from ${\mathrm{\Sigma }}_B$ as the correlation matrix of $\widehat{\beta }={({\widehat{\beta }}_1,\cdots ,{\widehat{\beta }}_K)}^T$.

2.2. Multibin linear combination L df tests

Two versions of a multibin linear combination test $G_M={\left(C\widehat{\beta }\right)}^T{(C^T\sum C)}^{-1}\left(C\widehat{\beta }\right)$ can be constructed using $\widehat{\beta }$ estimates from the multi‐SNP regression model, and C, a K by L matrix of linear contrasts. One MLC test version combines parameter estimates (MLC‐B: $\widehat{\beta }={({\widehat{\beta }}_1,...,{\widehat{\beta }}_K)}^T$) and the other combines the corresponding test statistics (MLC‐Z: $Z={(Z_1,...,Z_K)}^T$). In our evaluations, they give similar results. Both versions incorporate predetermined bins into the construction of the test statistics; we discuss bin construction and allele coding in the following subsection. For now, suppose that L bins are formed from K SNPs (L≤K). Let J be a K by L matrix where the jth column represents assignment to jth bin, that is, $J_{ii}=1$ if the ith SNP belongs to the jth bin and $J_{ii}=0$ if not. We assume that the bins consist of mutually exclusive sets of SNPs. MLC tests of multiple bins are then defined as:

$$\mathrm{MLC}\text{-}\mathrm{B}=\left({\widehat{\beta }}^T{W}_B\right){\left(W_B^T{\mathrm{\Sigma }}_B{W}_B\right)}^{-1}\left(W_B^T\widehat{\beta }\right),$$

$$\mathrm{MLC}\text{-}\mathrm{Z}=\left({\widehat{\beta }}^T{W}_Z\right){\left(W_Z^T{\mathrm{\Sigma }}_Z{W}_Z\right)}^{-1}\left({W_Z}^T\widehat{\beta }\right)$$

with $W_B=\left({\mathrm{\Sigma }}_B^{-1}J\right){\left(J^T{\mathrm{\Sigma }}_B^{-1}J\right)}^{-1}$ and $W_Z=\left({\mathrm{\Sigma }}_Z^{-1}J\right){\left(J^T{\mathrm{\Sigma }}_Z^{-1}J\right)}^{-1}$, respectively. Assuming a fixed design matrix X and a prespecified bin definition algorithm, the matrix J is fixed and does not depend on the trait data; ${\mathrm{\Sigma }}_B$ estimation is carried out under the unrestricted linear regression model. The null distribution of MLC‐B (MLC‐Z) is approximately L df chi‐squared under the null hypothesis β = 0. MLC is a directional test with power oriented toward a restricted alternative specified by the matrix C (see Supplementary Methods B. for details). In the absence of knowledge about underlying genetic architecture, the added value of the proposed method is its ability to adapt to complex LD structure in constructing a reduced df test statistic, without incurring the price paid for examination of trait data.

The global regression Wald test is a special case in which each bin consists of one SNP, that is, J = diag(1, 1, …, 1), L = K. In this case, the test is fully quadratic with each regression coefficient entering the test statistic in squared and cross‐product terms. At the other extreme, 1 df linear combination tests (LC‐B, LC‐Z) can be constructed as special cases of MLC tests where J = (1, 1, ..., 1)^T, that is, all SNPs are in the same bin. LC‐B is a fully linear statistic in which the regression coefficients enter with sign corresponding to the direction of association with the trait. The gene‐based MLC test statistic with L df based on bins that reflect LD structure is a linear‐quadratic hybrid constructed from L bin‐specific linear combinations. The bin‐specific terms are aggregated in a sum of squared and cross‐product terms (Supplementary Methods B).

As we demonstrate in the application below, a bin‐specific statistic extracted from this sum can provide a refined localization compared to gene‐level and single SNP level analysis in that the global gene‐level test will usually represent a region too large for localization, while localization at the single‐SNP level can be misleading. Bin‐specific statistics can reveal association with a multilocus causal haplotype or multiple causal haplotypes for which single‐SNP signals would be weak.

The LC tests follow from early consideration of multiple outcomes in clinical trial data analysis (O'Brien, 1984; Pocock, Geller, & Tsiatis, 1987). We note that LC‐B is equivalent to the Wald‐type test statistic described by Stram, Wei, and Ware (1988) and the score test statistic proposed by Schaid et al. (2005). The LC test statistics asymptotically follow chi‐square distributions with 1 df, and therefore may be more powerful than the K df Wald test or the L df MLC test in certain conditions. However, such linear combinations are sensitive to the direction of alternatives in the parameter space. In particular, LC statistics are attenuated when multiple causal variants in a gene are coded such that the trait is affected both positively and negatively. This results in the occurrence of opposite signs among ${\widehat{\beta }}_1,...,{\widehat{\beta }}_K$ and possible cancellation of the effects in the linear combination, producing substantial loss of power. To reduce this problem, without introducing bias into the MLC test statistic from trait association evidence in ${\widehat{\beta }}_1,...,{\widehat{\beta }}_K$ we take an allele recoding and bin construction strategy that is independent of trait information.

2.3. Construction of SNP bins and allele coding

Our objective in bin construction is to cluster SNPs into subsets using within‐gene LD information such that correlation between additively coded SNPs within a bin is high and positive, while correlation between SNPs in different bins is low. To this end, we conduct bin selection based on a clique‐based clustering algorithm called CLQ developed in a previous study (Yoo et al., 2015). As a clustering criterion, CLQ uses the LD measure r, which is calculated as the Pearson correlation of a pair of additively coded SNPs, and can be positive or negative in sign. In this algorithm, we first model SNPs as a graph $G=(V,E)$ with a vertex set V of SNPs and an edge set E of which each edge denotes a pair of adjacent SNPs with |r| > c, a given threshold value. The CLQ algorithm partitions the graph G into cliques that are subsets such that all pairs of vertices of each clique are adjacent (see Yoo et al., 2015 for details). The size and number of clusters depends on the choice of the threshold value c. Based on simulations presented below, we recommend c = 0.5 for general use, and find that type 1 error and power are not sensitive to modest changes in this threshold value. When threshold choice is based only on LD structure, and not on results of genotype‐phenotype analysis using multiple threshold values, uncertainty in bin assignment does not need to be taken into account in the analysis.

In the multi‐SNP regression (1), the sign of the regression coefficients is determined by SNP coding of the minor and major alleles (usually coded as 1 and 0, respectively). Assuming an additive genotype score for an allele, switching the minor and major alleles changes the sign of the corresponding ${\widehat{\beta }}_i$ estimate and its covariance with other $\widehat{\beta }$ estimates. This affects the linear combination test statistics, but has no effect on the quadratic Wald statistic. A widely used allele coding method designates the minor allele as the “deleterious” allele under the presumption that this will be the case for most of the SNPs. If, however, the SNPs being tested are merely tagging a causal SNP or some of the causal effects are actually protective, the signs of the regression coefficients of these SNPs may be reversed.

To address potential inconsistencies in effect direction in the context of linear combination tests, we apply a coding correction method proposed by Wang and Elston (2007). Accordingly, the allele coding decision based on the genotype data is applied within each bin of the MLC test (or to the entire gene in the LC test) so that the number of positively correlated SNPs is maximized within a bin (or within a gene for the LC test). This approach first catalogues SNPs using the number of negative pairwise correlations with other SNPs for a given initial coding scheme (usually minor alleles coded as 1). Starting from the SNP with the largest number of negative pairwise correlations with others, the 1/0 coding is reversed. The correlation status between SNPs after recoding one SNP is reexamined and the procedure is repeated iteratively until the number of SNPs negatively correlated with one SNP is less than half of the number of SNPs. After applying this coding correction, the resulting matrix of pairwise LD measures r will have a minimized number of negative pairwise correlations between SNPs. However, we recognize that complete resolution can be difficult with linear combinations consisting of more than a few SNPs. Uncertainty in clique‐based clustering and recoding does not affect the validity of the asymptotic distribution of the MLC test, because the clustering and recoding that determine the direction of the test are based only on the genotype data, and variance estimation is carried out under the unrestricted linear regression model. Because this adaptive coding procedure ignores the direction of the trait association, it does not inflate the type I error of MLC and LC tests. We apply the recoding procedure in construction of the MLC and LC statistics throughout the subsequent application and evaluations.

2.4. Other gene‐based tests

We compare the performance of MLC tests against several popular gene‐based analysis methods (for details see Supplementary Methods A). One class of methods for gene‐based analysis derives a test of global association from multiple single‐SNP results, that is, from multiple marginal analyses (Pan, 2009). The sum of squared marginal beta coefficients (SSB) and sum of squared marginal beta coefficients with inverse variance weights (SSBw) statistics (Pan, 2009) are quadratic statistics obtained from the sum of squared beta coefficients with weights W = (1, 1, …, 1)^T and $W={(\mathrm{Var}{\left({\widehat{\beta }}_1^M\right)}^{-1},...,\mathrm{Var}{\left({\widehat{\beta }}_K^M\right)}^{-1})}^T$, respectively, where ${\widehat{\beta }}^M={({\widehat{\beta }}_1^M,...,{\widehat{\beta }}_K^M)}^T$ is the marginal regression coefficients vector. GWAS investigators performing single‐SNP‐based analysis effectively apply an intrinsic region‐based approach by using a maximum statistic (MinP‐M), which selects one SNP with the strongest association within a region (WTCCC, 2007). This practice implies that the biggest test score (or smallest P‐value) has been chosen as a global statistic for the region, but this approach can be insensitive when multiple independent moderate associations occur within a region. We consider a similar minimum P‐value test obtained from multi‐SNP regression (MinP‐J). The sequence kernel association test (SKAT) is derived from a variance‐component model in which beta parameters follow a random effects distribution (Ballard, Cho, & Zhao, 2010; Kwee et al., 2008). The SKAT‐O statistic is a combination of the quadratic SKAT statistic with a linear combination test statistic that aggregates minor allele variant counts (Lee et al., 2012; Wu et al., 2011). Finally, our comparisons include a gene‐based multi‐df statistic from multiple regression of principal components of multiple SNP genotypes (PC80) proposed by Gauderman et al. (2007) that performs well overall when there is more than one causal variant in the gene (Ballard et al., 2010; Petersen, Alvarez, DeClaire, & Tintle, 2013).

3. APPLICATION IN THE DCCT/EDIC CANDIDATE GENE STUDY

The Diabetes Control and Complications Trial/Epidemiology of Diabetes Interventions and Complications (DCCT/EDIC) study is a long‐term follow‐up study of randomized trial participants with type 1 diabetes (T1D; DCCT, 1993; EDIC, 1999). The DCCT/EDIC Genetics Study was designed to investigate the association of SNPs in a large set of candidate genes with complications of T1D. As detailed in the methods of Al‐Kateb et al. (2008), tagging SNPs within 5 kb flanking either side of each of 201 candidate genes were selected not to be in strong LD and to have MAF greater than 5% based on data from the HapMap Project. Study participants were genotyped by a custom Illumina GoldenGate Beadarray assay, and data were subjected to standard QC procedures. This set of candidate genes includes several recently reported by Teslovich et al. (2010) to be associated with high‐density lipoprotein (HDL) cholesterol in the general population: CETP, APOB, IRS1, LPL, ABCA1, APOA1, LIPC, LCAT, MC4R. It is of interest to assess these and other candidate genes for association in a population with T1D.

The dataset we analyzed for genetic associations with HDL consists of 1,362 white probands with genotyping data for 1,213 SNPs (MAF > 5%) in 183 candidate genes (with ≥2 SNPs per gene). The number of SNPs genotyped per gene ranges from 2 to 47, with a median value of 4. We applied the MLC tests and other gene‐based tests to the logged and centered HDL measures obtained at the DCCT baseline assessment. For each gene, we constructed clusters for the MLC tests using the threshold values in the range c = 0.1 ∼ 0.9 (see supplementary Table S1 with results for all 183 genes).

At c = 0.5, the recommended value from simulations, we obtained 1 to 30 clusters (median = 3) per gene. Out of 183 genes, 21 have at least one test that meets a liberal significance criterion of P‐value < 0.03, with 12 of these detected by the MLC method with c = 0.5 compared to 9 by the global Wald test, and 10 by MinP‐M (supplementary Table S2). As expected, there is strong concordance between MLC‐B and MLC‐Z, and between LC‐B and LC‐Z. With the exception of LC tests, which detected few genes, the various tests give similar signals for six of the genes, but otherwise there is little concordance among the tests. In this application, the Wald and MinP‐J tests perform relatively better than in the simulation studies below because the genotyped SNPs were selected to be in low LD.

The P values for the established HDL‐related gene CETP are genome‐wide significant for all the methods except MinP‐J, but for the remaining 182 genes, none of the methods reach a Bonferroni adjusted P‐value criterion of 3 × 10⁻⁴. For CETP, the PC80 test P‐value (4 df) is the smallest, although the MLC‐B (5 df) and SSBw tests yield similar small P values. The 10 SNPs in the CETP region cluster into five bins (Table 1 and Fig. 1). Two of the SNPs with strong marginal signals (SNP4, SNP5) are highly correlated (r = 0.68) and consequently the SNP5 signal disappears in joint regression of all 10 SNPs. SNP4 (rs12720922), with the strongest signal in the joint multi‐SNP regression, has been reported previously as associated with HDL (Asselbergs et al., 2012; Enquobahrie et al., 2008; Wu et al., 2013). SNP2, and SNP7 and SNP9 also have attenuated signals in the joint regression; the former possibly due to LD with SNP3 or SNP5, and the latter likely due to LD with SNP10 in the first cluster (see Fig. 1). Cluster‐specific statistics, constructed using SNP‐specific beta coefficients and the covariance matrix estimate from the joint regression analysis, also suggest haplotypes carrying the minor allele of SNP4 be given priority for further attention. In contrast, from the marginal analysis alone, the signals from SNP2, SNP5, SNP7, and SNP9 are difficult to differentiate from the SNP4 association without further analysis.

Table 1.

Application to DCCT/EDIC genetics study: Regression analysis and gene‐based analysis results for association of the HDL trait with 10 SNPS in the CETP gene

			Regression Analysis Results
			Joint Analysis						Marginal Analysis
SNP	rs ID	bp Position	Cluster Allocation	MAF	Beta	P‐Value	LC‐B per Cluster	Wald per Cluster	Beta	P‐Value
SNP1	rs17245715	56961078	1	0.082	–0.040	0.075	0.17	5.56	0.006	0.709
SNP8	rs12720898	56977331	1	0.068	0.048	0.058	(P = 0.682)	(P = 0.135)	0.037	0.043
SNP10	rs1801706	56983750	1	0.166	–0.018	0.556			0.014	0.262
SNP3	rs708273	56966037	2	0.299	0.001	0.985	0.372	0.482	–0.012	0.230
SNP6	rs289717	56975476	2	0.347	–0.011	0.497	(P = 0.542)	(P = 0.786)	–0.012	0.206
SNP4	rs12720922	56966973	3	0.173	–0.063	0.001	10.5	12.6	–0.080	4.33 × 10−11
SNP5	rs11076176	56973534	3	0.193	–0.008	0.767	(P = 0.001)	(P=5.00 × 10−8)	–0.067	5.34 × 10−9
SNP7	rs736274	56975857	4	0.109	0.011	0.690	0.789	0.813	0.045	0.002
SNP9	rs5882	56982180	4	0.304	0.003	0.893	(P = 0.374)	(P = 0.666)	0.032	0.001
SNP2	rs3816117	56962246	5	0.469	0.035	0.173	1.86	1.86	0.055	1.45 × 10−9
							(P = 0.172)	(P = 0.172)

Gene‐Based Analysis Results
	Joint Analysis							Marginal Analysis
	Walda	MLC‐B	MLC‐Z	MinP‐J	PC80	LC‐B	LC‐Z	SSB	SSBw	SKAT	SKAT‐O	MinP‐M
Stat	71.6	62.5	60.9	10.76	60.4	32.7	32.5	0.019	146.45	–	–	45.46
df	10	5	5	–	4	1	1	–	–	–	–	–
P	2.18 × 10−11	3.69 × 10−12	7.96 × 10−12	0.009	2.39 × 10−12	1.09 × 10−8	1.17 × 10−8	1.98 × 10−9	2.83 × 10−12	5.402 × 10−11	2.16 × 10−10	1.40 × 10−10

^aList of test statistics: Wald: generalized Wald test (10 df); MLC‐B: MLC test using beta coefficients; MLC‐Z: MLC test using Z statistics; LC‐B: linear combination test using beta coefficients; LC‐Z: linear combination test using Z statistics; MinP‐J: minimum P‐value test based on joint regression analysis; MinP‐M: minimum P‐value test based on marginal regression analysis; PC80: global test based on regression using the minimum number of principal components capturing 80% of variance (Gauderman et al., 2007); SSB: sum of squared marginal beta coefficients (Pan, 2009); SSBw: Sum of squared marginal beta coefficients with inverse variance weights (Pan, 2009); SKAT: SKAT for common variants with weights obtained from Beta(0.5,0.5) density function (Ionita‐Laza et al., 2013); SKAT‐O: Linear combination of SKAT and burden test with optimized mixing proportion (Lee et al., 2012).

Figure 1.

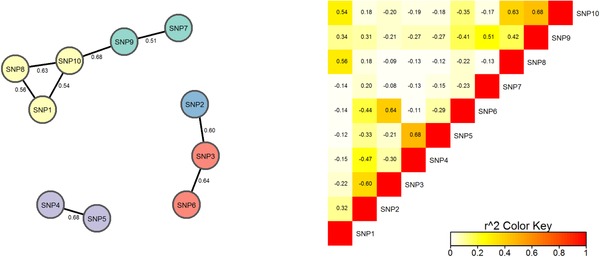
Clustering of SNPs in DCCT/EDIC CETP gene data by applying CLQ algorithm to linkage disequilibrium (r) pattern. Edges with |r| < 0.5 are removed. SNPs in the same cluster have the same color. The cluster construction threshold value for CLQ algorithm was set at c = 0.5

4. ANALYTIC POWER COMPARISONS

To gain insight into the relative performance of MinP and Wald, MLC‐B, and LC‐B tests, we analytically derived asymptotic distributions under simplified genetic models and LD structure (see supplementary Methods B). MinP‐M shows good performance for one causal SNP, but for two or more causal SNPs, the power depends on correlation between SNPs and can be low relative to the other statistics (see supplementary Methods and Figs. S1 and S2). Although less sensitive than LC‐B to the direction of the causal effects, the power of MLC‐B depends on within‐gene correlation and the underlying trait model.

The K‐df Wald test statistic can be partitioned into the sum of an L‐df MLC test statistic and an independent K‐L df statistic (Li & Lagakos, 2006). When the direction of the MLC test is well chosen, it will capture most of the information in the Wald test, but with fewer df and hence higher power. However, MLC test power will be affected adversely if the determined direction is not well chosen. The worst case for MLC occurs when opposing regression coefficients occur among correlated SNPs within a cluster. MLC performs best when high within‐cluster SNP correlation is combined with low variation in the within‐cluster variance‐standardized regression coefficients, such as would occur with multiple causal and/or indirect effects within a cluster. Thus in principle, the proposed MLC clustering approach can show substantial improved power compared to the Wald test, based on standard computationally efficient linear regression estimation, and requiring only straightforward preanalysis to cluster the SNP genotypes.

5. SIMULATION STUDIES

5.1. Design and methods

To better understand the data and model characteristics that influence the performance of the methods, we conducted a series of simulation studies based on observed human genotypes. As described below, trait data were simulated under null and various alternative models using genotype data derived from the HapMap Phase III Asian population (JPT and CHB). We selected 1,000 genes to compare the performance of gene‐based tests under various realistic gene structures.

A list of genes across 22 autosomes was obtained from the UCSC genome annotation database for NCBI hg18 Build 36.1 (http://hgdownload.soe.ucsc.edu/goldenPath/hg18/database/). Among 16,514 genes with at least one SNP present in the HapMap Asian data, there were 8883 genes consisting of 4 to 30 SNPs after excluding rare and low frequency SNPs (MAF < 0.05) and pruning SNPs in complete LD. From these, 1,000 genes were randomly selected for inclusion in the simulation studies (see supplementary Table S3 for a complete list).

For each gene, 1,000 replicated datasets, each consisting of genotypes and trait values for 1,000 individuals, were generated under each trait model scenario. To maintain the gene structure observed in the HapMap data, we generated genotype data for the 1,000 individuals using the method of randomly pairing haplotypes from the haplotype pool (for each gene) obtained from phased genotype data. The LD structure among the SNPs within a gene therefore arises entirely from the inherent structure in the HapMap haplotypes. Based on the genotypes for each individual, a quantitative trait Y was generated under an additive genetic model for a gene with C causal SNPs such that

$$Y=\sum _{j=1}^C{b}_j{G}_j+\epsilon ,$$

where $\epsilon \sim N\left(0,{\sigma }^2\right)$, b_j is the effect of jth causal SNP, and G_j is the number of minor alleles at the jth causal SNP, that is, G_j can be 0, 1, or 2.

We first considered five different quantitative trait models for each gene, including 0, 1, or 2 causal SNPs per gene (Table 2). In each of Models 1–5, causal SNPs were randomly selected from the set of SNPs for each gene, subject to the cluster structure. According to the analytic evaluations, Models 1–3, in which the signs of the effects are all positive for the causal SNPs, would be relatively favorable for LC compared to the Wald test, whereas Models 4 and 5 with opposite signs for the two causal SNP effects would be least favorable. Model 4 is expected to be least favorable to MLC and most favorable to MinP‐M when two positively correlated causal SNPs with opposite signs are in the same cluster, because there would be no recoding. On the other hand, MLC would be favored under Models 3 and 5 when causal SNPs are in different clusters, that is, are uncorrelated. In addition, we evaluated Model 6 in which each gene was assigned a random number of one to min(ns, 10) causal SNPs, where ns is the number of SNPs per gene, with each SNP equally likely to have a deleterious or protective allele regardless of the LD cluster structure.

Table 2.

Trait models for simulation study

Model	Description for Causal SNP Selection	No. of SNP	Effect Sizea	Correlationb	Error (σ)b	Allele Frequency
0	No SNP association	4∼30	All zero	HapMap	5	HapMap
1	One causal SNP within a gene	4∼30	b 1 > 0, randomc	HapMap	Adjusted	HapMap
2	Two causal SNPs in the same cluster, both deleterious	4∼30	b 1 > 0, b 2 > 0, random	HapMap	Adjusted	HapMap
3	Two causal SNPs in different clusters, both deleterious	4∼30	b 1 > 0, b 2 > 0, random	HapMap	Adjusted	HapMap
4	Two causal SNPs in the same cluster, one deleterious, and one protective	4∼30	b 1 > 0, b 2 < 0, random	HapMap	Adjusted	HapMap
5	Two causal SNPs in different clusters, one deleterious, and one protective	4∼30	b 1 > 0, b 2 < 0, random	HapMap	Adjusted	HapMap
6	Up to ten deleterious or protective causal SNPs, randomly assigned within a gene	4∼30	bj sign and magnitude, random	HapMap	Adjusted	HapMap

^aThe trait model is $Y={\sum }_{j=1}^C{b}_j{G}_j+\epsilon$, where $\epsilon \sim N(0,{\sigma }^2)$, C is the number of causal SNPs, b_j is the effect of jth causal SNP, and G_j is the number of causal alleles for the jth causal SNP. The jth SNP with j > C means neutral SNP.

^bHapMap: Based on the distribution and patterns of HapMap Asian gene panels. Adjusted: The error variance is adjusted to make the power of Wald test 60% for each gene.

^c  $|b_j|\sim U(0.01\times \mathrm{SD},0.05\times \mathrm{SD})$.

To estimate empirical type I error under the null hypothesis of no gene effect (Model 0), all b_j were specified to be equal to 0, and for each gene all SNPs were included in the regression analysis. Under alternatives with genetic association (Models 1–6), the causal SNP effect sizes (|b_j|) were randomly selected from a uniform distribution $U(0.01\times \mathrm{SD},0.05\times \mathrm{SD})$. Here, SD is the expected standard deviation of Y using the method for effect size estimation presented in Willer et al. (2013). The error variance σ² was adjusted separately for each gene and each trait model to obtain 60% Wald test power in a sample size n = 1,000, assuming the regression analysis includes causal SNPs. We estimated empirical power for each gene‐trait model combination under regression analyses that (1) included all SNPs, assuming the causal SNP(s) were typed and analyzed, and then (2) excluded the causal SNP(s), assuming they were untyped.

5.2. Comparison of threshold values for MLC cluster construction

In previous evaluations, we found a threshold value c of 0.4 or 0.5 for SNP clustering yielded generally better power for regression models including causal SNPs (Yoo et al., 2015). To re‐evaluate and extend these findings, we estimated MLC test size and power by simulation using threshold values from 0.1 to 0.9 with increments of 0.1. Under the null Model 0, type 1 error rates were robust to threshold value choice (supplementary Tables S4 and S5). For Models 1, 3, and 5 that specified only one causal SNP per cluster, average power was highest with threshold values of 0.4 or 0.5 including causal SNPs, but shifted to 0.5 or 0.6 excluding causal SNPs (Fig. 2, supplementary Tables S6 and S7). For Model 2 favoring the LC test, the best c value shifted toward few clusters, whereas in Model 4 the best c value shifted toward more clusters and greater similarly to global Wald test.

Figure 2.

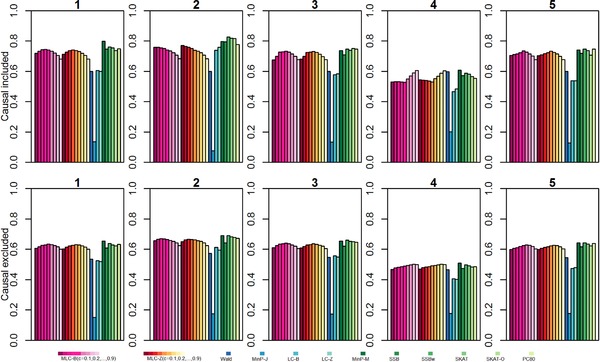
Simulation study results (Models 1–5): Average empirical power of MLC test statistics and other gene‐based statistics for 1,000 genes at nominal level α = 0.05 (N = 1,000 simulation replicates used to estimate power for each gene)

As a general rule for broad practical application, we conclude that a threshold value of c = 0.5 is a reasonable compromise because we found modest power differences at neighboring c values, particularly in analyses of SNP clusters not including the causal SNPs. Because clusters are constructed prior to regression analysis, it is valid to modify the threshold according to the LD structure of a specific gene, but postanalysis choice would need to account for multiple testing.

5.3. Type I error evaluation

The validity of MLC tests and other gene‐based tests was assessed for each of 1,000 genes at two nominal significance levels (α = 0.05 and 0.01). For the majority of the 1,000 genes, the estimated type I error rate (test size) of the MLC tests for a threshold c = {0.1, 0.2,..., 0.9} is within the nominal significance level range expected in 1,000 replicates (supplementary Tables S4 and S5); at c = 0.5, we observe 95% of 1,000 genes within 0.037∼0.064 and 0.005∼0.017 for α = 0.05 and 0.01, respectively. Under the null hypothesis, MLC test size SDs vary little across the threshold values suggesting that clustering and recoding do not affect standard error estimates. The average of the estimated Type I error rates over 1,000 genes is closest to nominal for the MLC (c = 0.5), LC, SKAT, and PC80 tests, while the average size of the generalized Wald, SSB, SSBw, and SKAT‐O tests tends to be inflated, MinP‐J is conservative, and the distribution for MinP‐M is skewed toward elevated values with higher variance. In particular, because MinP‐M gene‐specific type I error is elevated for many genes, we assessed average power differences both unadjusted and adjusted for Type I error differences (see supplementary Fig. S3 for details).

5.4. Power comparison between MLC tests and other gene‐based tests

For each of 1,000 genes, the power of each gene‐based test was estimated under nominal critical values for α = 0.05 from the asymptotic null distribution for the corresponding statistic. For Models 1–5, we calculate the average and SD of empirical power estimates across all 1,000 genes under each trait model (Fig. 2 and supplementary Tables S6 and S7); to directly compare test statistics at the gene level, we also plotted gene‐specific power differences (supplementary Figs. S4–S6). For Model 6, we constructed box plots of gene‐specific power stratified by the number of causal SNPs (Fig. 3).

Figure 3.

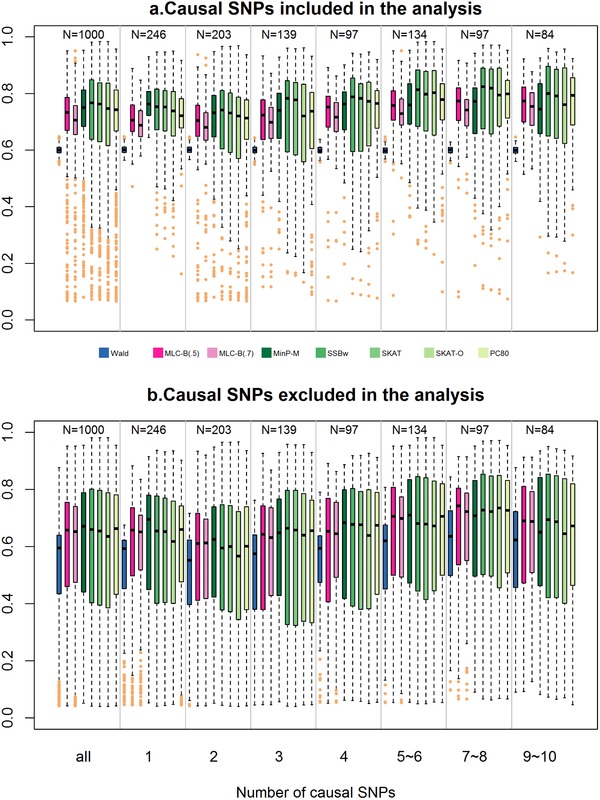
Simulation study results (Model 6): Distribution of gene‐specific empirical power of MLC‐B(c = 0.5 and 0.7) and other gene‐based statistics obtained for 1,000 genes at nominal level α = 0.05 stratified by the number of causal SNPs. The box plot shows five points: median, first, and third quartiles computed using Tukey's “hinges” and end points of whiskers. The whiskers extend to the most extreme values no more than 1.5 times the interquartile range. Outliers are shown in sand color. Note that the simulation error variance was adjusted separately for each gene to obtain 60% Wald test power in a sample size of n = 1,000 assuming the regression analysis includes causal SNPs. Upper panel (a) causal SNPs included in the regression analysis; lower panel (b) causal SNPs excluded from the regression analysis

Average MLC test power (both MLC‐B and MLC‐Z) is higher than global Wald test power whether or not the regression includes causal SNPs, with the exception of Model 4 in which the causal SNP effects have opposite directions and are located in the same cluster (Fig. 2). Under Model 4, average MLC test power is lower than average Wald test power for most cluster threshold values when causal SNPs are included in the regression, but is slightly higher than Wald when causal SNPs are excluded. For the vast majority of genes, MLC has higher power than the Wald test, except under the unfavorable Model 4 (supplementary Fig. S6). This suggests overall advantages of a reduced df MLC‐B statistic compared to the Wald statistic, while the low power exceptions may be due to difficulties in effective recoding within a particular gene cluster when positively correlated SNPs have opposing effects. On average, power of MinP‐J tests is quite low, and average LC power is lower than MLC for most CLQ cluster threshold values except under Model 2 with two deleterious causal SNPs in the same cluster, both typed. For a proportion of the genes, MLC exhibits a large power advantage over the LC test (i.e., when there are opposing effects); it is however worth noting that LC can be modestly more powerful than MLC (up to 0.20) for more than 50% of genes (supplementary Fig. S6).

For Models 1, 2, and 4, average MinP‐M power is 0.057–0.079 higher than average MLC‐B(c = 0.5) test power for regression including causal SNPs, but only 0.019–0.024 higher excluding causal SNPs (supplementary Table S8). For Models 3 and 5, average power differences are even less: 0.003–0.018 higher for MinP‐M compared to MLC‐B(0.5). Because type I error for MinP‐M tends to be elevated and overdispersed across genes, we also calculated adjusted power differences by regressing the gene‐specific power differences on the corresponding type I error differences in the 1,000 genes for each of the models. Although average differences are essentially unchanged by adjustment (supplementary Table S8), it is evident that gene‐specific power differences can be as large as ±0.4 and that MLC‐B power is higher than MinP‐M power for a substantial number of genes (supplementary Fig. S3). Although the MinP‐M test performs well overall under trait models with one or two causal variants, previous studies and our analytic results suggest that this may not be the case for trait models with multiple causal variants. In simulation studies under trait models with up to 10 causal variants (Model 6), we confirmed that MinP‐M becomes increasingly less competitive as the number of causal variants increases beyond 5 (Fig. 3, supplementary Table S9).

The MLC‐B, SSBw, SKAT, and PC80 tests perform well overall (Fig. 2). For all trait models, SSB has lower average power than SSBw, and SKAT usually has higher average power than SKAT‐O (except for Models 2 and 3 with typed causal SNPs that are favorable to a linear statistic). Average power of the MLC, PC80, SSBw, and SKAT gene‐based tests is remarkably similar for trait models with one or two causal SNPs (Models 1–5). For Models 2 and 4, average SSBw power is 0.059–0.115 higher than average MLC‐B(c = 0.5) power for regressions including causal SNPs, but only 0.011–0.021 higher for Models 1, 3, and 5 (supplementary Table S8). For regressions excluding causal SNPs, average power differences are even less: 0.004–0.021 higher for SSBw compared to MLC‐B(0.5) (supplementary Table S8). Moreover, the SD of MLC‐B gene‐specific empirical power among the 1,000 genes is generally smaller than those of the existing methods (supplementary Tables S7 and S8). Gene‐level comparisons between MLC‐B and the other tests also indicate that MLC‐B can be more powerful than SSBw, PC80, SKAT, or SKAT‐O tests, depending on the trait models, the gene structures, and whether the causal variant is typed (supplementary Figs. S4 and S5).

In contrast to MinP‐M, as the number of causal variants increases MLC‐B, SSBw and SKAT become more competitive (Fig. 3). This is particularly evident for MLC‐B in regressions excluding causal variants, which rely on indirect effects through LD to detect gene association. Quite remarkably MLC‐B has the narrowest interquartile range (IQR) of all the gene‐based tests regardless of the number of causal SNPs and whether they are included or excluded in the regression.

6. DISCUSSION

The MLC regression method differs from other gene‐based approaches designed to produce test statistics with fewer df, and is robust in the sense that it can be more powerful in some cases and has modest power deficits otherwise. Among test statistics evaluated asymptotically, we compared MLC to representatives of the main classes of gene‐based tests: linear combination, variance component, and minimum P‐value statistics. We observed that different methods can be more powerful than others under certain genetic structures, but genome‐wide, MLC test size and power are less variable compared to existing methods, and become increasingly competitive with increasing number of causal variants in a gene. This suggests the potential value of combining MLC with complementary methods for genome‐wide discovery analysis when the genetic architecture is unknown. MLC uniquely combines within‐ and between‐cluster signals in a global test statistic adapted to the gene LD structure, but is free of selection bias arising from trait‐based optimization. Because MLC derives from multiple regression, the coefficients are adjusted for all variants in the model, aiding in identification of independent associations within the gene. Moreover, cluster‐specific statistics can be extracted to assist in within‐gene localization.

In practical application of regression‐based tests, some computational issues need to be considered. First, depending on the LD structure in the dataset, the joint analysis model using multi‐SNP regression may encounter linear dependencies among the SNPs and near singularity in the variance‐covariance matrix. This can arise due to complete pairwise LD between SNPs or higher order multi‐SNP linear dependence; the latter is a particular concern for regressions that include SNPs imputed from genotyped SNPs. Most statistical software performing linear regression can deal with such singularities and automatically remove covariates to obtain a nonsingular matrix. By removing the SNPs that are redundant (in complete LD with some other SNP), possible singularity problems can often be resolved prior to analysis. Depending on sample size, regression analysis including low frequency SNPs may be underpowered and unstable. However, if a legitimate regression analysis can be performed for low‐frequency SNPs, the MLC tests can always be constructed.

MLC tests constructed from joint regression analysis and SNP‐specific beta coefficients thus account for direct and indirect association of all the SNPs in the regression. Clusters of SNPs in high correlation within a gene region represent haplotypes with relatively low diversity (Chapman & Whittaker, 2008; Wason & Dudbridge, 2012). The SNPs located at the extreme genomic positions of a cluster can be interpreted as the rough start and end points of the detected underlying haplotype. As illustrated in the detailed analysis of the DCCT/EDIC study CETP application (Fig. 1), MLC cluster construction by the CLQ algorithm is based on pairwise r values from (phased) genotype data, and SNPs within the clusters identified are not necessarily within physically consecutive blocks. Because the clique‐based clustering algorithm we incorporated in MLC testing can construct clusters of nonconsecutive SNPs, the spans of different haplotypes can overlap allowing for representation of a mosaic structure of haplotype intervals.

Cluster‐specific statistics can be constructed as shown in the CETP genotype analysis. To the extent that clusters associated with the trait correspond to possible causal haplotypes, cluster‐specific statistics can assist in potential cluster‐level localization. For example, once an associated gene region is identified by a MLC test, clusters of closely correlated SNPs may be examined to identify haplotypes that contribute to the overall gene region signal. In the CETP application, gene‐based statistics including MLC showed an overall strong signal, with a relatively strong cluster‐specific signal in the SNP4/SNP5 cluster. In the joint regression analysis, SNP4 is the only SNP with a P‐value as small as 0.001 (and large beta −0.063), consistent with previous reports of association between this SNP (rs12720922) and HDL (Asselbergs et al., 2012; Enquobahrie et al., 2008; Wu et al., 2013). We can conclude that the cluster including SNP4 represents a possible causal haplotype and is a candidate for dense fine‐mapping.

By means of evaluations performed under various trait models for each of 1,000 representative genes using HapMap Asian data, we determined the performance of the MLC test in two general situations. In one, the regression analysis excluded causal SNPs so as to imitate the complexity of conventional GWAS analysis consisting mainly of common tagging SNPs. In the second, to imitate the settings of GWAS imputation or dense genomic data such as exome array data, the regression analysis included both causal and noncausal SNPs. Our Asian HapMap gene panels included a large number of genes selected to represent the overall distribution of within‐gene LD structure across the genome; the number of SNPs per gene ranged from 4 to 30, and random assignment of causal variants and genetic associations under the alternative genetic models produced diverse genetic architectures, including variation in the number and proportion of causal variants per gene.

Based on the analytic and simulation results, we conclude that MLC tests can perform better than Wald, MinP‐J, LC, and SSB tests for genes with a complex LD structure. According to simulation results, MinP‐M, SSBw, and SKAT showed better performance on average than MLC‐B tests across five simple genetic models. In scenarios with multiple causal SNPs, however, MinP‐M, SSBw, and SKAT had larger IQR, and for untyped causal variants, they had lower median power than MLC tests. The Wald test is robust to the presence of multiple causal variants, but may not exploit LD information efficiently. MinP‐M does use LD information to adjust P values but can be prone to inflated type I error and is more suitable for situations with a single causal SNP. The SSBw statistic performs well with increasing numbers of causal SNPs, and incorporates LD through robust covariance estimation to provide an effective global gene‐based test. Here, however, the beta coefficients obtained are marginal and do not as easily lend themselves to localization of causal variants. The SKAT variance‐component method is also based on marginal beta coefficients, and furthermore does not incorporate SNP covariances directly into the test statistic. The linear burden test component of SKAT‐O also ignores SNP LD, whereas the LC test can benefit from positive SNP covariances. Our observation that power for SKAT is often greater than for SKAT‐O is consistent with rare variant study findings that the burden test is less powerful than the variance component test when many variants are noncausal (Lee, Abecasis, Boehnke, & Lin, 2014), which is predominantly the situation in our simulations. The principal component based method, PC80, also reduces the df based on the LD structure, and is close in spirit to the MLC method, yielding similar power for a majority of genes (supplementary Fig. S2); it showed overall good performance in this and previous studies. However, each principal component may not always have a ready biological interpretation, and some information may be lost by choosing a subset of the principal components. In contrast, each cluster in the MLC statistics maintains meaning as a small cluster of SNPs with high LD, and the df are effectively reduced using LD information while explicitly combining information from correlated SNPs. We therefore conclude that the MLC regression test has merits for gene‐based analysis of genetic association data as a robust, interpretable, and reasonably powerful multi‐SNP method.

The MLC methods have potential for application in large regional testing such as described by Paré, Asma, and Deng (2015) for analysis of common‐frequency whole genome scans not limited to prespecified SNP sets corresponding to genes. To proceed with regional analysis within a whole genome scan, genomic variants must be assigned to analysis units such as genes, haplotype blocks, or other biological regions (Wu et al., 2010). Kwee et al. (2008) suggest that only regions of modest size be examined; Petersen et al. (2013) suggest that only intergenic SNPs that are in high LD with intragenic SNPs be included in region‐based analysis. To limit the number of SNPs jointly analyzed in a multi‐SNP statistic, a sliding window approach can be useful to examine analytic units (Kwee et al., 2008; Paré et al., 2015; Petersen et al., 2013). Application of the MLC approach to dense genome‐wide data similarly requires partitioning of inter‐ and intragenic regions into workable analysis units prior to cluster construction. LD block regions consisting of consecutive SNPs can be determined using software such as Haploview (Barrett, Fry, Maller, & Daly, 2005). Although LD blocks could be used to identify haplotype blocks instead of clique clusters for the bin assignment for MLC, this precludes specification of multiple overlapping haplotypes. Furthermore, LD block sizes vary and large blocks with many SNPs may exacerbate problems of opposing effect directions. For MLC SNP clustering, it is undesirable to include SNPs that do not correlate well with their physical neighbors. Because MLC is focused on capturing within‐gene structure (and potentially, multiple causal associations), multiple clusters corresponding to different haplotypes are more likely to provide homogeneous within‐cluster effects suitable for combining statistically.

Multivariant methods designed for rare variants analysis are well‐developed (see Derkach, Lawless, & Sun, 2014, Lee et al., 2014; Pan, Kim, Zhang, Shen, & Wei, 2014; Wang & Biernacka, 2015 for recent reviews), and some methods can be applied to both rare and common variants (Ayers & Cordell, 2013; Ionita‐Laza, Lee, Makarov, Buxbaum, & Lin, 2013; Pan, Kwak, & Wei, 2015; Wang, Morris, Zhu, & Elston, 2013; Yoo et al., 2013). In gene‐based analysis, a high proportion of noncausal variants within a regional analytic unit reduces test effectiveness in rare variant analysis (Derkach et al., 2014; Lee et al., 2012), as well as in joint analysis of common SNPs (Petersen et al., 2013). Although test statistics that use trait association evidence can be more powerful, bias introduced by such adaptation needs to be taken into account, which can require adjustment to df or use of intensive computation (Bacanu, 2012; Derkach et al., 2014; Han & Pan, 2010; Pan et al., 2015). Furthermore, knowledge about relative test performance for rare variant analysis may not apply for common variant analysis, given that LD among common variants is stronger than among rare variants. Uniformly most powerful methods rarely exist for jointly evaluating multiple parameters, so no one method can be most powerful. Evaluations of methods for gene‐based analysis of typical GWAS data consisting mainly of genotyped common variants (with or without additional imputed SNPs) have largely concluded that without knowledge of underlying genetic architecture, it may be wise to apply complementary approaches (Asimit, Yoo, Waggott, Sun, & Bull, 2009; Bacanu, 2012; Ballard et al., 2010; Clayton et al., 2004; Gauderman et al., 2007; Han & Pan, 2010; Kwee et al., 2008; Pan, 2009; Petersen et al., 2013; Taub, Schwender, Youkin, Louis, & Ruczinski, 2013; Wason & Dudbridge, 2012; Yang et al., 2012).

We find MLC to be a well‐powered and robust choice among the existing methods across a broad range of complex genetic architectures. We are not aware of other studies that compare multiple methods in haplotypes drawn from 1,000 different genes. Compared to other methods, MLC test size and power are less variable, and mean power is never much lower, and can be higher, particularly with multiple causal variants. With accumulating evidence that LD structure influences the power of gene‐based tests, methods such as MLC specifically designed to utilize LD information are worthy of consideration as an alternative for analysis of dense genetic association data with correlated SNPs and complex LD structure.

Supporting information

Supplementary Information

Supplementary Figs S4–S6

Tables S1, S3, and S9