Identification of hair cycle-associated genes from time-course gene expression profile data by using replicate variance

Abstract

The hair-growth cycle is an example of a cyclic process that is well characterized morphologically but understood incompletely at the molecular level. As an initial step in discovering regulators in hair-follicle morphogenesis and cycling, we used DNA microarrays to profile mRNA expression in mouse back skin from eight representative time points. We developed a statistical algorithm to identify the set of genes expressed within skin that are associated specifically with the hair-growth cycle. The methodology takes advantage of higher replicate variance during asynchronous hair cycles in comparison with synchronous cycles. More than one-third of genes with detectable skin expression showed hair-cycle-related changes in expression, suggesting that many more genes may be associated with the hair-growth cycle than have been identified in the literature. By using a probabilistic clustering algorithm for replicated measurements, these genes were grouped into 30 time-course profile clusters, which fall into four major classes. Distinct genetic pathways were characteristic for the different time-course profile clusters, providing insights into the regulation of hair-follicle cycling and suggesting that this approach is useful for identifying hair follicle regulators. In addition to revealing known hair-related genes, we identified genes that were not previously known to be hair cycle-associated and confirmed their temporal and spatial expression patterns during the hair-growth cycle by quantitative real-time PCR and in situ hybridization. The same computational approach should be generally useful for identifying genes associated with cyclic processes from complex tissues.

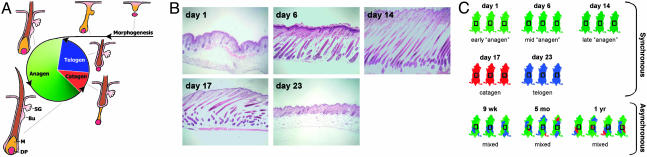
Hair-follicle morphogenesis starts late in embryogenesis and is completed on postnatal day (PN) ≈14 in mice (Fig. 1 A and B). After this period of growth, which is referred to as anagen, hair-follicle cycling is initiated with a regression phase called catagen, in which the lower two-thirds of the hair follicle undergoes apoptosis (1). Subsequently, the regressed follicle enters a resting phase known as telogen. After this period of quiescence, anagen is initiated with the start of a new hair-growth cycle (2). Cyclical growth of hair persists throughout postnatal life because of the regenerative capacity of hair-follicular stem cells (3, 4), which are believed to reside in the bulge region (Fig. 1 A) of the hair follicle. In mice, the first two hair-growth cycles occur in synchronized waves moving in an anterior-to-posterior direction. After the second cycle, synchronous hair growth occurs only in small patches (1), creating a mosaic pattern of hair follicles in different phases within the skin (Fig. 1C); overall, hair follicles are unsynchronized after the second cycle.

Fig. 1.

Design of microarray experiments on mouse skin. (A) Hair-follicle morphogenesis and cycling. Representative hair follicles for the embryonic morphogenesis and each phase of the postnatal hair cycle are shown. Bu, bulge; DP, dermal papilla; M, matrix; SG, sebaceous gland. (B) Histological sections of mouse back skin for the first five time points of the experiment, showing hair follicles at different phases of the hair-growth cycle. (C) Overview of experimental design, showing the number of mice that were independently analyzed for each time point. The progression of anagen is indicated by different shades of green. Catagen and telogen are indicated by red and blue, respectively. The back skins of 9-week-old, 5-month-old, and 1-year-old mice are asynchronously cycling, containing mosaic patches of different phases of the hair-growth cycle. The rectangular box indicates the region of the back skin that was excised from all mice.

Although a snapshot of gene expression in hair-follicle stem cells has been reported recently (5, 6), time-course profiling of all components of the skin is needed for comprehensive characterization of the complex molecular changes in hair-follicle development and cycling, which involves the epithelial and mesenchymal compartments. For example, similar to other regenerative organs such as the limb bud, tooth, and feather, the cycling hair follicle uses a combination of signaling systems, such as Sonic hedgehog, Wnt, transforming growth factor β (TGF-β), fibroblast growth factor (FGF), and Hox family members, which are known to be important for epithelial–mesenchymal interactions (1). For example, signaling by EDA/EDAR (ectodysplasin/ectodysplasin receptor) is required for induction of primary hair follicles, whereas proper activation of Wnt signaling pathway, by means of β-catenin and Lef1, is required for the initiation of hair-follicle morphogenesis and is sufficient to activate the anagen phase of subsequent hair-growth cycles (7–9). Identifying additional regulators in hair-follicle cycling is important because aberrant regulation of hair cycle control genes is responsible for several types of abnormal hair loss (10) and skin tumors (11–13).

To gain insights into hair-follicle morphogenesis and cycling, we used DNA microarrays to profile mRNA expression in mouse back skin over several time points when hair-follicle developmental phases are synchronized and asynchronized. Such a study is challenging because the skin is a complex tissue, in which multiple biological processes occur simultaneously, potentially masking each other at the level of gene expression. For example, during the initial morphogenesis of the hair, the rapidly expanding skin also undergoes noncyclic morphological changes, including dramatic thinning of the epidermis. Direct time-course profiling of gene expression data from whole skin and standard analysis based on differential expression could falsely identify many genes as being related to the hair-growth cycle. Therefore, methods are needed for distinguishing gene-expression changes that are associated specifically with the hair-growth cycle from noncyclic expression changes occurring simultaneously in the skin.

In this article, we describe computational approaches to identifying and classifying genes showing hair-cycle-associated changes in expression within the skin. We first identified hair-cycle-related genes based on the statistical difference in replicate variance between skin samples from synchronized and asynchronized time points. These hair-cycle-related genes were then classified into distinct time-course profile groups based on a multivariate probabilistic clustering algorithm. By using these approaches together, we identified pathways and genes that are likely to play roles in hair-follicle morphogenesis and cycling. These computational approaches should be generally applicable to the study of cyclic biological processes occurring within a complex tissue.

Materials and Methods

RNA Isolation and Microarray Experiments. Total RNA was isolated by using the TRIzol method (Invitrogen) from excised CB6F1 mouse back skin (2 × 2 cm), followed by purification, using RNeasy columns (Qiagen, Valencia, CA). Care was taken to remove skin from the same location in all mice to ensure that replicate skin samples represented comparable phases of the hair-growth cycle. Double-stranded cDNA was synthesized from the total RNA, and an in vitro transcription reaction was then performed on biotin-labeled RNA that was made from the cDNA. Labeled RNA was hybridized with MG-U74Av2 chips (Affymetrix, Santa Clara, CA) and washed according to the manufacturer's recommendations. The hybridized probe array was then stained with streptavidin-conjugated phycoerythrin, and each GeneChip was scanned twice in an HP GeneArray confocal laser scanner at 570 nm with a laser resolution of 3 mm by using mas 5.0 Microarray Suite software (Affymetrix) to produce a *.cel file for further data processing.

Transformation of Expression Data. We used a two-component noise model (TCM) to transform the raw expression data, resulting in uniform replicate variance and symmetric replicate residuals across the range of expression values (14). A log transformation of the intensities could be used if one assumed a multiplicative noise model on the measured intensities. However, although this transformation is appropriate at high-intensity values, it can amplify replicate variance artificially at lower-intensity values (15, 16) (see Fig. 6A, which is published as supporting information on the PNAS web site). In contrast, the TCM assumes an additive error model at lower-intensity values, a multiplicative error model at higher-intensity values, and a gradual shift from one to another, resulting in the following:

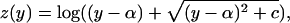where z is the transformed intensity and y is the original intensity. We estimated the two parameters {α, c} for this variance-stabilizing transformation by using the originally proposed algorithm (14) as follows. We assumed that the top 5% of the data have multiplicative noise and that the bottom 20% of the data have additive noise. Thus, we obtained transformed values characterized by nearly uniform replicate variance as a function of intensity (see Fig. 6B).

Statistical Test of Replicate Variance. The F test was used to identify genes with a significant difference in replicate variance between the synchronous and asynchronous periods. The F test estimates independently for each gene the probability of observing a particular set of replicate residuals (i.e., differences between individual replicates and the mean replicate value for a given gene and time point) under the null hypothesis of equal replicate variance in the synchronous and asynchronous periods: 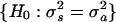. The F statistic was calculated by using the following equation:

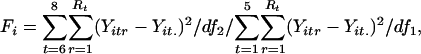where Y_itr is the transformed expression level for gene i, time point t, and replicate r; Y_it. is the mean transformed intensity for gene i and time point t; R_t is the number of replicates at time point t; and df₁ = 10 and df₂ = 7 are the degrees of freedom in the synchronous and asynchronous time periods (represented by 15 and 10 total replicates, respectively).

Probabilistic Clustering of Replicate Measurements. To determine distinct expression patterns during the hair-growth cycle, we clustered the profiles of selected genes into coherent groups. We formed the profiles by normalizing transformed replicates for each gene by subtracting the mean gene intensity and dividing by the standard deviation of the mean expression intensities of the gene. The model encodes the two key independent assumptions that (i) different time points are independent given the cluster variable, and (ii) different replicates are independent given the cluster and the true gene expression intensity per gene per time point. The likelihood of N independently and identically distributed observations under the proposed model with K components can be written as follows:

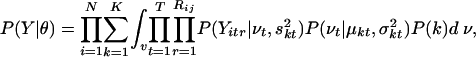where the cluster membership k and the true gene expression level v are unobserved (latent) variables that must be inferred for each gene. The complete set of model parameters θ = {P(k), μ, σ, s} includes the component probabilities P(1)... P(K), mean expression within the clusters μ_kt, intracluster variance σ_kt, and replicate variance s_kt (unpublished data).

A similar model based on an infinite-mixture model was proposed recently (17), treating the number of clusters as a random variable and estimating the model parameters by using Gibbs sampling. In contrast, here we assumed the number of clusters K to be fixed, allowing for a more computationally efficient and direct estimation procedure based on the expectation–maximization algorithm (18).

Validation of Expression Data by Quantitative Real-Time PCR (qr-PCR). As an independent experiment from the microarray studies, we isolated RNAs from the back skin of C57BL/6 mice covering the first two hair-growth cycles. RNA quality was checked by Northern blot analysis, and RNA was diluted to a concentration of 100 ng/μl before cDNA synthesis with the High-Capacity cDNA archive kit (Applied Biosystems). By following standard supplier protocol and thermal-cycler conditions, a 7900HT platform (384-well plate, Applied Biosystems) was used to detect the TaqMan Assays-on-Demand gene-expression products. Automatically detected threshold cycle (Ct) values were first normalized relative to an endogenous control, Pgk1, and the fold differences in expression were determined based on the cDNA standard dilution curve for each gene of interest. To facilitate comparison across time points for each gene, the lowest mean expression value was normalized to one, and the fold increase in expression of other time points was calculated relative to that normalization.

In Situ Hybridization. Back skin of PN 3 CB6F1 mice were excised and fixed in 4% paraformaldehyde at 4°C overnight before following the embedding procedure described in ref. 19. All procedures were performed according to the in situ hybridization protocol for detection of mRNA with digoxigenin (DIG)-labeled RNA probes (Roche Applied Science) with slight modifications for optimization.

Results and Discussion

Replicate Variance Analysis Identified a Large Portion of Skin-Expressed Genes as Hair Cycle-Associated. We used DNA microarrays to profile mRNA expression in mouse back skin from eight time points. The first five time points correspond to distinct phases of the first hair-growth cycle; the initial hair growth (anagen) is represented by PN 1, 6, and 14, and the first catagen and telogen by PN 17 and 23, respectively (Fig. 1B). The last three time points were sampled after the second hair-growth cycle (9-week-old, 5-month-old, and 1-year-old mice) (Fig. 1C). We refer to the first five time points as the “synchronous period” and to the last three time points as the “asynchronous period” throughout this article. Samples of the back skin from three or four littermates were used to generate replicated measurements for each of the eight time points.

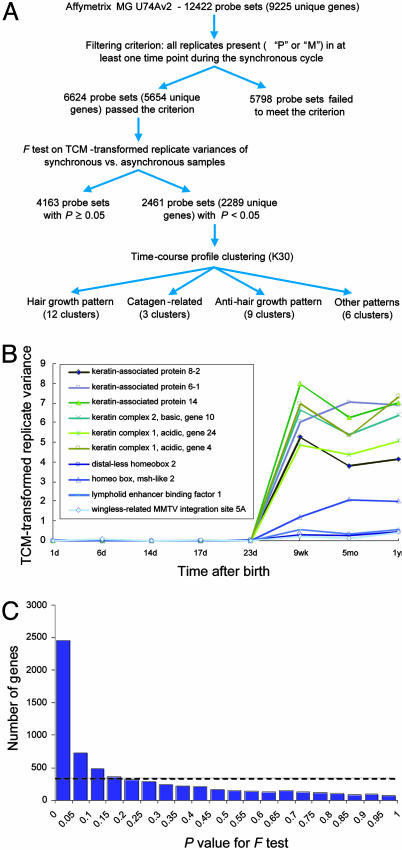
To identify genes showing expression changes related to the hair-growth cycle, we took advantage of the shift from synchronous hair growth over the entire mouse back skin during the first two cycles to the asynchronous growth during the later cycles (Fig. 2A). A key feature of this system is that the shift in hair-cycling pattern results in an additional source of variation that is present in the asynchronous replicates (tissue samples taken from different littermates of the same age) only. Whereas different replicates from the first hair-growth cycle represent the same phase of the cycle, the tissue samples from the later asynchronous time points are likely to contain varying proportions of follicles in different phases. Hence, we hypothesized that genes associated with the hair-growth cycle would have significantly higher replicate variance during the asynchronous period in comparison with the first hair-growth cycle. This hypothesis is supported by a plot of the replicate variance of 10 representative genes that are known to be associated with the hair-growth cycle (Fig. 2B). Consequently, we decided to take advantage of this feature to design computational approaches aimed at identifying genes showing hair-cycle-related changes in gene expression.

Fig. 2.

Identification of hair-cycle-associated genes. (A) Overview of data processing and results of profile clustering. (B) TCM-transformed replicate variance for 10 representative genes known to be associated with the hair-growth cycle. In comparison with the first five time points (synchronous), the last three time points (asynchronous) have significantly higher TCM-transformed replicate variances for all 10 genes (P < 0.0001). (C) Frequency distribution of P values for F test comparing replicate variance during the synchronous and asynchronous time points. The frequency distribution of the P values is plotted by using a bin increment of 0.05. Dashed line indicates the uniform distribution expected under the null hypothesis.

First, we excluded genes that are not expressed in the back skin by limiting the analysis to the 6,624 probe sets (corresponding to 5,654 unique genes) with either “present” or “marginally present” calls (based on mas 5.0) for all replicates in at least one time point during the synchronous period (Fig. 2 A). TCM was then used to transform the raw expression data in a manner that results in uniform replicate variance and symmetric replicate residuals across the range of expression values (14). Then, we used the F test to identify genes with a significant increase in replicate variance during the asynchronous period, compared with replicate variance during the first synchronous hair cycle (see Materials and Methods for details). The frequency distribution of P values for the F test shows a significant deviation from the uniform distribution that was expected under the null hypothesis (Fig. 2C).

We used the following two independent methods to assess different P-value cutoffs for identifying a gene as hair-cycle-associated: a literature-based validation (20) and a statistical analysis of the false discovery rate (FDR) (21) in the multiple-hypotheses testing scenario (in our case, 6,624 tests). For literature-based validation, we compiled a list of genes whose expression patterns have been shown to be hair-cycle-dependent, and we found that >80% of these genes have P < 0.05 (Table 1 and Fig. 7, which are published as supporting information on the PNAS web site). Independently, a statistical analysis (22) allowed us to estimate the FDR, which is the fraction of false positives among all tests determined to be significant for a given P-value cutoff. The analysis shows that the FDR associated with a P-value cutoff of 0.05 is <10% (Fig. 8, which is published as supporting information on the PNAS web site). Thus, a cutoff value of 0.05 allows us to identify a large fraction of known hair cycle-associated genes without including an excessive number of false positives.

This cutoff P value of 0.05 identified 2,461 probe sets (corresponding to 2,289 unique genes, Fig. 2 A and C), suggesting that many more genes may be associated, directly or indirectly, with the hair-growth cycle than identified previously in the literature. We identified genes expressed in all different compartments of the skin, which is consistent with the idea that hair-cycle-related changes in gene expression are not limited to the hair follicle proper. In addition to literature-based validation, we used qr-PCR in independent experiments to validate the expression pattern of selective genes covering both the first and second hair-growth cycles of mice (see below). Together, the literature-based and experimental validations support the approach of using statistical analysis of replicate variance between synchronized and asynchronized time points to identify hair-cycle-associated genes. The table of 2,289 hair-cycle-associated genes can be prioritized by P value (Table 2, which is published as supporting information on the PNAS web site); based on our validations, there is a strong indication that, the lower the P value, the more likely it is that a particular gene is associated with the hair-growth cycle.

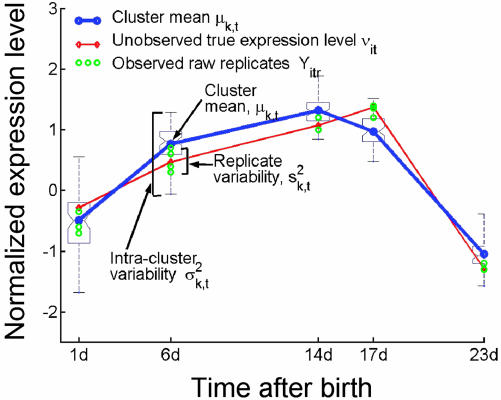
Hair Cycle-Associated Genes Belong to Clusters with Distinct Time-Course Profiles. To determine whether the 2,289 hair cycle-associated genes display distinct expression patterns during the hair-growth cycle, we clustered their profiles into coherent groups (Fig. 2 A). Conventional clustering algorithms, such as k means, agglomerative hierarchical, and model-based clustering (23–25), are traditionally applied to the mean profiles obtained by averaging the replicated measurements. However, the raw replicate data provide information about natural biological variation between similar tissues from different samples that is lost when the data are converted to mean expression profiles. Hence, we developed a probabilistic approach to cluster data with replicated measurements based on latent variable models. The proposed model captures intracluster variance and replicate variance by means of two independent terms (Fig. 3, see Materials and Methods for details), providing a more accurate representation of the expression profiles compared with modeling all variations with a single variance term (25). Based on two widely used statistical scores, the Bayesian information criterion score (26) and the cross-validated per-point log probability score (27), we selected K = 30 clusters as an appropriate number for characterizing this data set (Fig. 9, which is published as supporting information on the PNAS web site).

Fig. 3.

Probabilistic approach to clustering data with replicated measurements using mixture models. To incorporate input data in the form of replicated observations per gene per time point (green circles), we extended the standard mixture model by introducing an additional set of latent variables that encode unobserved true expression levels for a given gene per time point (red line). The resulting model allows decoupling of the intracluster variance and the replicate variance into two separate terms. The generative process is as follows. For each gene, sample its cluster k, and for each time point t, sample the unobserved true gene expression level v_it by using cluster mean value μ_kt and intracluster variability σ²_kt. Last, sample replicates by using the true gene-expression level v_it, and replicate variability s²_kt. All continuous-valued distributions are assumed to be Gaussian, and discrete distributions are multinomials.

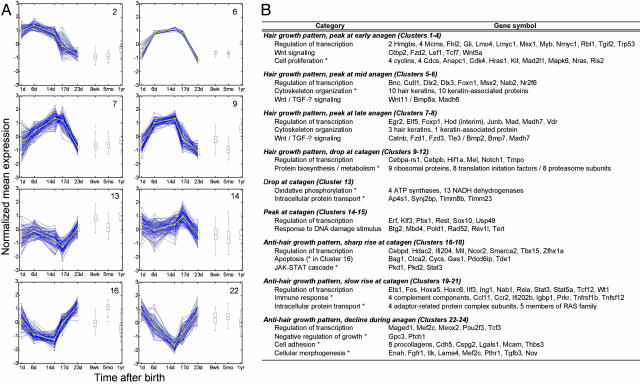
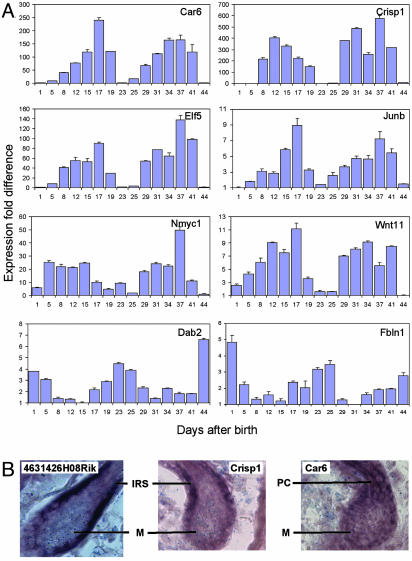
Interestingly, three general profile patterns emerge: 12 clusters (clusters 1–12) correlate with a hair growth pattern, three clusters (clusters 13–15) display catagen-related expression patterns, and nine clusters (clusters 16–24) follow an anti-hair-growth pattern. In addition, six clusters (clusters 25–30) contain genes whose expression profiles do not fit into any of the three general profile patterns (representative clusters in Fig. 4A and all clusters in Fig. 10, which is published as supporting information on the PNAS web site). To validate the time-course profile clustering, we used qr-PCR to examine the expression pattern over the first two synchronous hair cycles of a number of genes that were not previously known to be associated with the hair-growth cycle but were identified by using the statistical algorithms in our study (Car6, Crisp1, Elf5, Junb, Dab2, and Fbln1). We also profiled the previously unexamined expression pattern of Nmyc1 and Wnt11. Not only do the expression patterns from the qr-PCR match very well with the microarray data for the first hair-growth cycle (compare Fig. 5A with Table 3, which is published as supporting information on the PNAS web site), but the expression patterns are well preserved in the second cycle as well. However, it is crucial to note that there are key differences between the first and second hair-growth cycles. For example, epithelial–mesenchymal inductive processes unique to hair-follicle morphogenesis are taking place during the first hair-growth cycle. In addition, the adnexal structures of the hair follicle, such as the bulge region and sebaceous gland, are formed during the first cycle and become the permanent, noncycling portion of the hair follicle.

Fig. 4.

Representative time-course profile clusters and selected genes of interest within the clusters. (A) Representative examples of profile clusters. Clusters 2, 6, and 7 display hair growth patterns that peak at early, middle, and late anagen, respectively. Cluster 9 also displays a hair growth pattern but shows a sharp decline in expression level at catagen. Cluster 13 drops at catagen, whereas cluster 14 peaks at that phase of the hair-growth cycle. Clusters 16 and 22 display anti-hair-growth patterns that rise sharply at catagen and decline during anagen, respectively. For each time point, the standard deviation and the minimum and maximum values for each cluster are shown. Blue lines, expression profiles for individual genes. Yellow lines, mean expression profile for clusters. (B) Selective genes of interest within different clusters. ease (Expression Analysis Systematic Explorer, available at http://david.niaid.nih.gov/david/ease.htm) software was used to identify overrepresented gene categories. *, ease score of <0.05.

Fig. 5.

Experimental validation of statistical algorithms for identifying hair-cycle-associated genes from skin microarray data. (A) qr-PCR results of gene expression for time points covering the first two synchronous hair cycles. Representative time points for the first hair-growth cycle: PN 1, 5, 8, 12, and 15 (anagen); 17 and 19 (catagen); and 23 (telogen). Representative time points for the second hair-growth cycle: PN 25, 29, 31, and 34 (anagen); 37 and 41 (catagen); and 44 (telogen). Standard deviations and mean fold differences in expression for each time point were calculated by using three replicates. (B) In situ hybridization localizing 4631426H08Rik (homolog of a type I keratin expressed in the inner root sheath), Crisp1, and Car6 in PN 3 mouse back skin. IRS, inner root sheath; M, matrix; PC, precortex.

Of special interest was the identification of Crisp1 and Car6, which are two genes that were not previously known to be associated with the hair follicle. Both genes showed >100-fold changes in expression during the hair-growth cycle in the qr-PCR analyses. As predicted from their cluster membership (cluster 5), both genes were found by in situ hybridization to be expressed within the hair follicle proper (Fig. 5B). In mice, the androgen-regulated Crisp1 was detected mainly in the epididymis and, to a lesser extent, in the salivary and lacrimal glands (28). The Crisp1 protein is present on the sperm surface and mediates cell–cell interactions in the fusion of the sperm and egg plasma membranes (29). The hair-growth expression pattern and localization of Crisp1 transcripts to the inner root sheath suggest its possible involvement in cell–cell interactions during hair-follicle cycling. Car6 transcripts have been detected in isolated gland tissues as well as in mammalian saliva and milk, where it may participate in the maintenance of pH homeostasis (30). A CHOP (C/EBP homologous protein)-dependent, stress-inducible form of Car6, which has been implicated in apoptosis, has been identified (31). The expression of Car6 in the matrix and differentiating zone of the hair shaft, with highest levels at the beginning of catagen, suggests the possibility of its involvement in hair-follicle apoptosis.

Genes Participating in Distinct Genetic Pathways Are Enriched in Different Time-Course Profile Clusters. Having validated the profiling clustering, we next examined gene annotations within cluster groups to identify overrepresented gene categories (Fig. 4B). Clusters showing a hair-growth pattern can be classified further into the following four groups: genes whose expression profiles peak at early (clusters 1–4), middle (clusters 5 and 6), or late (clusters 7 and 8) anagen, as well as genes displaying a sharp decline in expression at catagen (clusters 9–12). Cell-proliferation-related genes such as Kit, Nras, and Ris2 are strikingly overrepresented in clusters peaking at early anagen. In contrast, genes encoding structural proteins, such as hair keratins and keratin-associated proteins, are found in clusters that peak at middle to late anagen (Fig. 4B). These findings are consistent with the idea that most active proliferative activities in the hair follicle occur before completion of the hair structure. A disproportionate number of genes involved in protein biosynthesis and metabolism are found in clusters that show a precipitous drop at catagen, indicating that these genes are crucial for cell proliferation and may be sensitive markers for apoptosis.

Clusters following an anti-hair-growth pattern can be divided into three groups: genes whose expression level rises sharply at catagen (clusters 16–18), rises slowly at catagen (clusters 19–21), or declines during anagen (clusters 22–24). As expected from the prevalent apoptosis during the catagen phase, a number of genes that display a sharp increase in expression at catagen are involved in the process of programmed cell death (particularly in cluster 16, Fig. 4B). Apoptosis-associated genes, such as genes responding to DNA damage stimuli, are found also in clusters showing a specific peak in expression at catagen (clusters 14 and 15). An inverse pattern, with a specific drop in expression at catagen, is found in cluster 13, which contains an overrepresentation of genes required for oxidative phosphorylation (e.g., ATP synthases and NADH dehydrogenases). In response to apoptotic events, genes that are responsible for proper immune responses must be precisely activated to maintain homeostasis (1), and we have identified many of these genes in anti-hair-growth clusters with a slow rise in expression at catagen (mostly in cluster 21). We found several genes encoding negative growth regulators in clusters with expression declining throughout anagen but increasing from catagen to telogen, suggesting that prevention of uncontrolled hair growth is an important function in hair-follicle cycling. In these clusters, we also found an overrepresented number of genes involved in cell adhesion and morphogenesis, suggesting the importance of these processes during hair-follicle regression and stabilization of surrounding connective tissues.

Clustering of genes associated with the hair-growth cycle is important because membership in distinct time-course profile clusters suggest potential biological roles. For example, many transcriptional regulators that have been genetically shown to be critical for hair-shaft formation (e.g., Catnb, Cutl1, Dlx2, Dlx3, Foxn1, Gata3, Gli, Lef1, Msx1, and Msx2) belong to the hair-growth clusters (Fig. 4B). Therefore, it is likely that other transcriptional regulators in the same clusters are also important for hair-follicle morphogenesis. These transcriptional regulators include the Ets factor Elf5, the homeodomain factor Hod, and the zinc finger factor Egr2, as well as its interacting protein Nab2. A list of all transcriptional regulators (178 probe sets and 167 unique genes) in our profile clusters is given in Table 4, which is published as supporting information on the PNAS web site.

In summary, we have developed a computational approach to identify hair cycle-associated genes successfully from a microarray data set of whole back-skin tissue samples. Genomic transcriptional profiling has been used recently to study the hair-growth cycle and other cyclic processes, including the circadian rhythm and cycles in the female reproductive system such as mammary gland regulation (32–37). We believe that our approach can be applied to time-course gene expression studies such as these to identify clusters of genes associated with a cyclic process of interest occurring in the context of a complex tissue. Furthermore, it is important to note that this time-course microarray data set, which is freely accessible at the National Center for Biotechnology Information (NCBI) Gene Expression Omnibus (www.ncbi.nlm.nih.gov/geo), may be useful for studies of other biological processes within the skin.