Automated Tilt Series Alignment and Tomographic Reconstruction in IMOD

Abstract

Automated tomographic reconstruction is now possible in the IMOD software package, including the merging of tomograms taken around two orthogonal axes. Several developments enable the production of high-quality tomograms. When using fiducial markers for alignment, the markers to be tracked through the series are chosen automatically; if there is an excess of markers available, a well-distributed subset is selected that is most likely to track well. Marker positions are refined by applying an edge-enhancing Sobel filter, which results in a 20% improvement in alignment error for plastic-embedded samples and 10% for frozen-hydrated samples. Robust fitting, in which outlying points are given less or no weight in computing the fitting error, is used to obtain an alignment solution, so that aberrant points from the automated tracking can have little effect on the alignment. When merging two dual-axis tomograms, the alignment between them is refined from correlations between local patches; a measure of structure was developed so that patches with insufficient structure to give accurate correlations can now be excluded automatically. We have also developed a script for running all steps in the reconstruction process with a flexible mechanism for setting parameters, and we have added a user interface for batch processing of tilt series to the Etomo program in IMOD. Batch processing is fully compatible with interactive processing and can increase efficiency even when the automation is not fully successful, because users can focus their effort on the steps that require manual intervention.

1. Introduction

Electron tomography has historically been time-consuming, both for acquisition and for alignment of images and reconstruction of a tomogram. Automating these processes and improving overall throughput has been a major goal since it became possible to acquire images with digital cameras (Fung et al., 1996; Koster et al., 1992). Improvements in microscope performance and development of automated acquisition (Mastronarde, 2005; Suloway et al., 2009; Zheng et al., 2004) have made it possible to acquire many gigabytes per day of tilt series data and thus to pursue research that requires large amounts of data. Tomography on frozen-hydrated samples (cryoET) is often destined for sub-volume averaging (for recent reviews, see (Asano et al., 2016; Briggs, 2013)), which has recently reached sub-nanometer resolution (Bharat et al., 2015; Pfeffer et al., 2015; Schur et al., 2013). Although various factors besides the number of particles limit the resolution of such averaging, such as the quality of the tilt series alignment, the efficiency of the camera in capturing high-resolution information, and the complexity and flexibility of the structure being averaged, having many particles from many tomograms was a key ingredient in the first of these studies (Schur et al., 2013). High-throughput tomography on plastic-embedded samples allows multiple strains or experimental conditions to be compared with a statistically meaningful number of samples (e.g., Nannas et al. (2014)); it also enables ambitious studies of very large volumes (~50 μm³ at 1.5 nm voxel, Hoog et al. (2007), ~200 μm³ at ~5 nm voxel, Noske et al. (2008), ~100 μm³ at 1.2 nm voxel, Redemann and Muller-Reichert (2013)). For either kind sample, high-throughput tomography at the cellular level enables informative comparative studies (Ding et al., 2015).

The IMOD software package (Kremer et al., 1996; Mastronarde, 1997) contains a comprehensive set of programs for tomographic reconstruction and a graphical user interface (Etomo) that manages the whole process, from removal of artifacts in the raw images to trimming and scaling of the final volume. It was developed in a national center for 3-D EM where tomography was done on a relatively diverse range of plastic-embedded and frozen-hydrated specimens. It has been widely used elsewhere with an even broader range of specimens and acquisition protocols. Problems have arisen in particular data sets, and the software has been improved either to handle more difficult sets as a matter of course, or to provide a special parameter or tool by which the user can resolve a problem. For any step that runs automatically, there is a fallback procedure so the user can get through the step if the automation fails. IMOD’s user interface provides access to those settings, tools, and procedures; although they are often hidden during ordinary use, they are available in its advanced display mode. The general approach has been to provide some way to rescue almost every data set. Although many cryo-ET projects can tolerate considerably less than 100% yield of usable tomograms, in some projects with plastic-embedded specimens there is a strong motivation to get a usable result from every data set, such as when serial sections are being reconstructed.

Every step in IMOD’s reconstruction process can now be run fully automatically to obtain a high-quality tomogram. This automation has been implemented within the existing processing framework and in a way that is compatible with interactive processing through Etomo. If there is a failure, users can resolve the problem interactively then resume automated processing. Thus, these capabilities can improve the efficiency of dealing with every tilt series, even the ones that require intervention. The flexibility of the user interface for batch processing makes computing tomographic reconstructions truly high-throughput.

This paper describes the key recent developments that have enabled this automation: 1) improvements in obtaining a model of fiducial marker positions and in solving for the tilt series alignment from those positions; 2) application of methods for determining the location of structure in a tomogram to several problems, including the accurate alignment of the two tomograms from dual-axis tilt series (Mastronarde, 1997; Penczek et al., 1995); and 3) the creation of tools that manage the automated processing. Because this paper covers a wide range of topics, there is an integrated presentation of motivation, methods, and relevant results for each topic in turn. Some of this work has been reported in abstract form (Mastronarde, 2013).

The software is freely available at http://bio3d.colorado.edu/imod. The improvements in fiducial alignment and a program to manage batch processing were available in the IMOD 4.7 stable release version. Beta releases since then have included significant refinements in the latter program plus the other features described here; for any batch processing, version 4.8.51 or higher should be used. Further details on the operations performed by programs described here can be found in the manual pages, accessible from http://bio3d.colorado.edu/imod/betaDoc/program_listing.html.

2. Methods and Results

2.1. Automatic generation of a seed model

The approach in IMOD for constructing a fiducial model has been to start with a “seed model” consisting of selected gold beads near 0° tilt and track those beads from one projection to the next with the program Beadtrack. An advantage of this method is that a faint or obscured bead can be detected using the a priori knowledge of where it should be, even if it would not meet some threshold for detection when attempting to find all beads on an image. IMOD already contained a program for automatically constructing the fiducial model, version 3.0 of RAPTOR (Amat et al., 2008), and some laboratories have relied on it extensively, particularly for cryoET. However, we and our colleagues have observed several deficiencies when using RAPTOR. It may fail to include beads that lie over darker areas; e.g., when isolated cells are surrounded by resin or empty ice, it may select almost exclusively beads over the empty areas. In fact, the opposite is often desired for reconstructions from plastic-embedded material because the empty resin changes under the beam in ways that differ from regions with cellular material. RAPTOR provides no way to limit the area from which beads are selected. At high tilt beads may be added that are far from the area being reconstructed. It fails with large areas, such as from montaged tilt series, whose significant nonlinear distortions must be fit with local alignments (Mastronarde, 2007), because it can only fit all points to a single, global alignment. It often does not behave well for the cryoET data available to us from our colleagues in Boulder (see section 2.3). Finally, its bead positions are significantly less accurate than those produced by Beadtrack, a point recently reported by Han et al. (2015) and on which we provide data in section 2.3.

We thus decided to build on the existing approach of seeding then tracking. To do so, it was necessary to develop a procedure for generating a seed model automatically. The overall goal was to generate a model at least as good as the one a user would choose manually: it should consist of beads that will track well and are well distributed both in the plane and between two sides of a section (when they have been deposited on both sides). There should also not be many more beads than the number needed to achieve a reconstruction of adequate quality for the scientific question being pursued, because having excessive beads creates extra labor if the manual procedures of filling in missing points and checking deviant positions are going to be used. The procedure followed by the script Autofidseed is as follows:

1. The program Imodfindbeads is run to detect all beads on 3–7 views near 0° tilt (Fig. 1A). This program first cross-correlates the images with a model bead of the specified size. It analyzes a smoothed histogram of correlation peak strengths to find a dip between two modes, first searching for this motif in a highly smoothed histogram (e.g., blue curves in Figs. 1C and 1A), then over a more restricted range in less smoothed histograms. The location of the dip in the least smoothed histogram examined (arrows and red curves, Figs. 1C and 1D) is considered the best threshold between beads and non-beads. A raw correlation score is used instead of the normalized cross-correlation coefficient (CCC) because the CCC loses the intensity information and does not discriminate well between beads and weaker features with the same shape. Points above the threshold, or above a conservative fallback threshold if the histogram analysis fails, are aligned and summed to get a reference for iterating the correlation, peak search, and histogram analysis. The final selection of beads is thus based on correlations with an averaged bead, not the model. To alleviate the bias caused by beads over low-density backgrounds having much stronger correlations, the correlation peaks are divided into 4 groups based on background density and the histogram for each group is analyzed separately. A relationship between threshold and background density is then derived from the thresholds found in the successful analyses, provided that at least two succeed. The criterion for deciding whether any given point is a bead can thus be based on its background density. When there are few beads, the number of projections analyzed is increased to 7 to make this analysis more robust. Figure 1A shows an example of beads selected by this process.

2. Three different seed models are extracted from the output of the first step, then Beadtrack is run with each of these seeds to track beads through the same set of 11 projections around 0° tilt. These numbers are used because they generally give adequate information on the consistency and quality of tracking and the locations of the beads in 3-D without excessive computation. Figure 1E shows a side view of such tracks, with beads tracked in only one or two of the three runs in green or magenta, respectively. Beadtrack can handle thousands of beads by working in a series of local areas, and it can do this job adequately even when there are beads in large clumps or some non-beads. It stores information about each bead tracked, including the 3-D coordinates and the mean error when fitting to 3-D alignment equations.

3. If beads are present on two surfaces, the program Sortbeadsurfs is used to assign the beads from each Beadtrack run to two surfaces based on the solved 3-D coordinates. A model file is produced with the points colored green or magenta (e.g., Fig. 1F).

4. The program Pickbestseed is given all of the information gathered so far. It matches up beads between the different tracking runs, then gives each bead a score that is an equally weighted sum of four measures of the consistency and quality of the tracking: the fraction of tracks the bead is missing from, the fraction of points missing in the tracks, the mean error from 3D alignments, and the mean distance between corresponding points in pairs of tracks. Each bead is also classified as clustered (i.e., expected to be too close to another bead at high tilt) or elongated, based on measures of elongation computed by Beadtrack. Elongation can represent either a single misshaped bead or two beads that are right on top of each other at some angles and are in slightly different projection positions at other angles; either way, the bead is undesirable. Clustered or elongated beads are excluded from consideration unless the user chooses to include them, in which case they are added only if necessary to reach the desired density of seed points. The program goes through several distinct phases of selecting beads, starting with the best-scoring ones and then dropping the criterion for acceptance to fill in areas of lower density. It progresses to later phases if the requested density has not been achieved yet. When beads are on two surfaces, density is evaluated separately for each surface to optimize the balance between the two sides.

Fig 1.

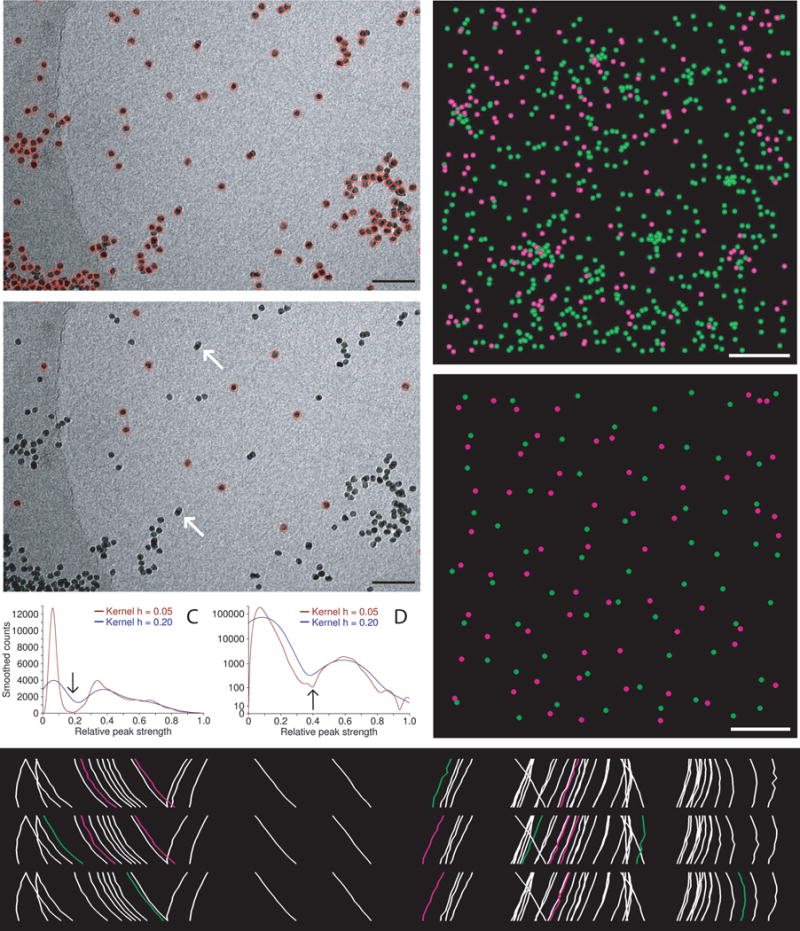
Automatic selection of seed points for fiducial tracking. (A, B) Subarea from 0° image of tilt series from frozen-hydrated cell infected with bovine papilloma virus, acquired by Mary Morphew. Scale bars are 100 nm. A shows all beads found in the first step of the procedure; B shows the ones selected for the seed model. Arrows mark some partially overlapping, paired beads that were not selected because of their elongated appearance. (C, D) Smoothed histograms of the distribution of correlation peak strengths when finding beads in the tilt series used for parts (A) and (E), respectively. Histograms are smoothed by convolving with a kernel (1 − (x/h)²)³/(0.9143 h), where h is the half-width of the kernel. A dip between two maxima is first sought in a histogram with an h of 0.2 (blue curves) then its final location (arrow) is picked in a less smoothed histogram with an h of 0.05 (red curves). The histograms in (C) are atypical in having comparable area in the two modes because of the large clumps of gold; the histograms in (D) are typical and require a logarithmic scaling to show the mode for true beads clearly. (E) Side view of bead positions tracked through the same set of 11 images, but starting with beads found at three different tilt angles. Beads present in only one or two of the tracks are shown in green and magenta, respectively. The cryo tilt series of a Giardia cell was acquired by Cindi Schwartz. (F, G) Identified beads (F) and ones selected for the seed model (G) from a 3 × 3 montaged tilt series of a high-pressure frozen, freeze-substituted SVG-A cell infected by JC polyomavirus, acquired by Kimberly Erickson. Fig. S1 shows these points overlaid on tilt series images. Scale bars are 1 μm. In (F), beads have been identified as being on the bottom (green) or top (magenta) of the section using the Z positions solved during tracking through 11 images. In (E), the selected beads are well-distributed on both surfaces.

Figure 1B shows that this procedure has avoided selecting both the beads in obvious clumps and also several overlapping paired beads that appear elongated at low tilt. The example in Figs. 1F, G is from a montaged tilt series with ~860 beads on two surfaces (see Fig S1 for tilt series images). The procedure selected 120 beads, as requested, with 60 on each surface; even the minority population (magenta) is well distributed in Fig. 1G except in the middle-right where there are simply none available.

Two other features of the automatic seeding are worth noting. First, it is possible to use model contours to define areas in which beads are selected. In ET of plastic-embedded cells, it is usually desirable to exclude beads over empty resin because those regions change under the beam in ways that differ from regions with cellular material. In cryoET, on the other hand, it may be desirable to exclude beads over the carbon film, which can behave differently from the ice. Second, the user interface in Etomo for automatic seeding gives access to several options for rerunning the final step with different parameters. The logic here is that for a user with a large area requiring over a hundred fiducials, it is still more efficient to experiment with some options than to make the seed model manually.

2.2. Robust fitting

To achieve an accurate alignment from a fiducial model produced automatically, it is important to protect against the deleterious effects of a small fraction of incorrectly placed points. The alignment program in IMOD, Tiltalign, is generally used with at least a 4-fold excess of measured values over parameters to be solved. This excess gives a solution that averages out some random errors, but it is not as effective at reducing the effects of outlying points, which tend to pull the solution away from nearby, correctly placed points. To handle outlying points, Tiltalign can now do robust fitting (Rousseeuw and Leroy, 2003; Wilcox, 2005), which involves giving less or no weight to the points with high deviations from the fit (residual errors). The procedure used is a form of iteratively reweighted least squares, similar to what was described for linear regression by Beaton and Tukey (1974) and Gross (1977). It starts with an ordinary fit to minimize a sum-squared error, and assigns weights to the points based upon their residual errors. The fitting is repeated with those weights applied when computing the sum squared error, new weights are assigned, and the process is iterated until changes in the weights become small enough.

Weights are assigned from a collection of errors by first computing the normalized median absolute deviation from the median (MADN), which is the median of the absolute value of deviations from the median error divided by 0.6745 (a factor that makes the MADN an estimate of sigma for a sample from a normal distribution (Wilcox, 2005)). Then for the i^th point with error e_i, the weight w_i is obtained from the Tukey bisquared expression by:

$$\begin{array}{l}{d}_i=(e_i/m_p-m_a)/(k\ast \text{MADN})\\ w_i={(1-{d_i}^2)}^2\text{for }0<=d_i<=1\\ 1\text{for}{d}_i<0\\ 0\text{for}{d}_i>1\end{array}$$ (1)

where m_p is an estimate of the median error for the projection p where point i is located, m_a is the median of the values of e_i/m_p being analyzed, and k is a factor that determines how extreme a point must be to receive a weight of zero. The value of m_p is obtained by finding the median error at each tilt angle and smoothing by three iterations of fitting a quadratic locally at each point. The default value of k is 4.685, a factor commonly used for robust fitting because, with normally distributed errors, it gives an asymptotic efficiency of 95% (i.e., it requires 1/0.95 more data points to reach the same reliability for estimates as a non-robust fit) (Holland and Welsch, 1977). Here, the factor is probably somewhat conservative because errors are all positive distances and outliers occur on only one side of the distribution. Users can enter a scaling for k of less or more than 1 to specify more or less aggressive down-weighting.

Figure 2 shows the progression of residual errors during the first three iterations of robust fitting for four different examples, starting with the error from non-robust fitting on the left. Each example shows a point with a particularly high residual that was given zero weight, and the points from the same fiducial at two adjacent tilt angles in each direction. In some cases one or two of those adjacent points also received zero weights. All of the points with zero weight showed an increase in residual error, which means that they are farther from the final solution than from the initial one. Some nearby points with weights near one show a reduction in residual, such as in the left two examples. Both of these trends are consistent with the notion that the aberrant points pull the initial solution away from other points while the robust solution fits other points better.

Fig 2.

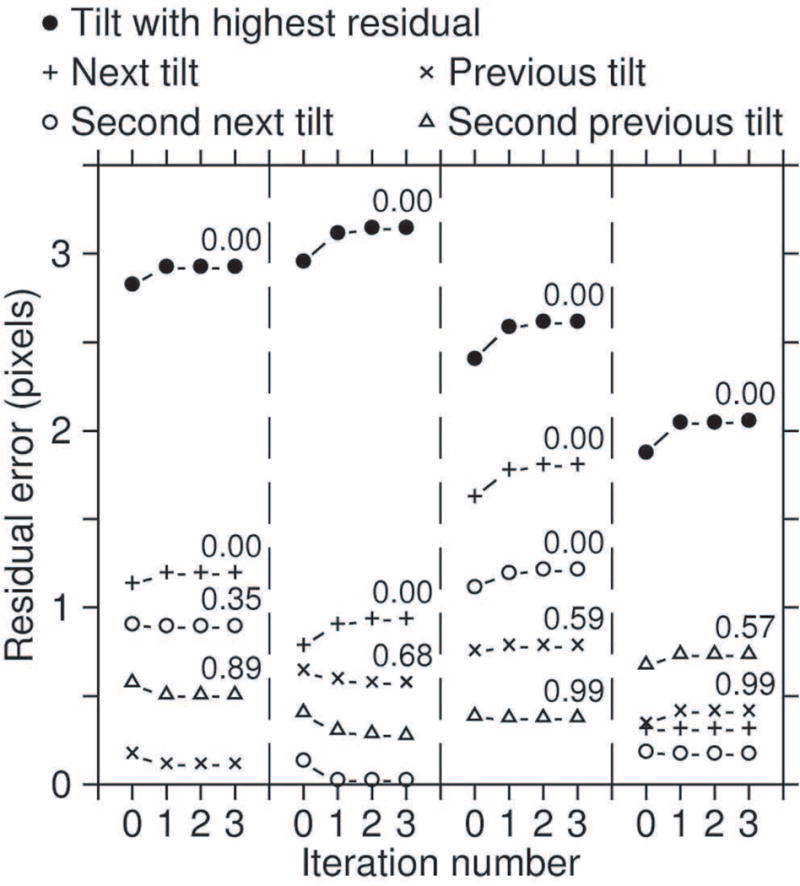
Progression of errors during the first 4 iterations of robust fitting for some incorrectly placed points in the IMOD tutorial data set. Filled circles are for points with high residual errors that were given a weight of zero in the robust fitting. Crosses and X’s are for the points from the same bead at the adjacent tilt angles; circles and triangles are from points two tilt increments away. The point at iteration 0 is the result from the non-robust fit. The number above the point at iteration 3 is the weight after that iteration, shown for all points with weights less than 1.

Tiltalign has several safeguards against inappropriate weights being assigned by this process. In a typical Tiltalign solution, residual errors increase systematically both with tilt angle and from the center outwards; the dependence on tilt angle is the reason for initial normalization of errors by the estimated projection median m_p in Eq. 1. For further protection against weights having similar systematic variations, points are divided into groups by tilt angle and then by distance from center, with the number of groups limited by a requirement for a minimum number of points in each group (e.g., 100). Medians, MADNs, and weights are computed separately for each group, thus keeping points at high angles from being assigned low weights simply because of their systematically larger errors. Moreover, since points in a group are from similar regions, the variability in their errors is less than that of the whole set of points, so it is easier for extreme errors to be detected as outliers. As another safeguard, the program applies several constraints on the number of points assigned low weights (e.g., no more than 25% of points in a group can have a weight less than 0.5). These constraints are important because most variables being solved for depend on a relatively small subset of the data, which must not be allowed to become too small. The typical robust fitting gives weights under 0.5 to about 5% of points.

Note that these robust procedures will identify points as “aberrant” only if they stand out from the rest statistically. If not all points fit the alignment model because of systematic deviations from the model, whether the worst fitting points are given low weights depends on their distribution and relative number. A few beads over empty resin that thins more than stained material under the beam may well be identified as outliers, but a ring of such beads around a cell will probably not. In cryoET, particles within the ice can rotate by different amounts and in different directions through a tilt series (Bharat et al., 2015); such changes might result from the doming of the ice in a carbon hole seen clearly with continuous exposure to higher doses (Brilot et al., 2012). In such a situation, if almost all fiducials lie near one surface of the ice and a few are at different heights, the alignment would be most accurate near that surface and worse elsewhere, and the robust fitting might give the latter beads low weights, thus increasing this bias. If beads are well-distributed in depth, robust fitting would primarily perform its proper role of identifying poorly centered points.

2.3. Sobel filtering to improve bead localization

In addition to a number of minor improvements to make the bead tracking program more likely to produce a model that gives a good automated alignment, one major enhancement has increased the accuracy of bead positions: the refinement of the bead position using a Sobel filter. This simple gradient-enhancing filter turns spheres into annuli (Fig 3 A, B). The motivation for using the Sobel filter was that both initial cross-correlation to find a bead and especially the refinement of the position with the centroid are thrown off by overlapping density. In the extreme case, when a bead on the opposite surface intersects the one being tracked, the centroid is placed in the middle of the two beads. Correlation of a Sobel-filtered image with a Sobel-filtered average or model bead should, however, tend to lock onto the edges of the beads and give a better center position, even when the annulus is incomplete because of overlapping density. In the case of two overlapping beads (arrow, Fig 3A, B), the annulus from Sobel-filtering should correlate better at the position of either bead than in the middle. However, because the standard Sobel filter operates over a block of 9 pixels, it is necessary to scale either the filter or the images so that the filter is tuned to enhance the strong edge of the bead. The optimal scaling is to bring the bead size to ~8 pixels after applying a Gaussian smoothing filter. Fig. 3D and E show an example of applying the Sobel filter to a cryoET image in Fig. 3C without and with such scaling. Although there is some recognizable signal in the unscaled image, the characteristic annuli are much more obvious in the scaled image, especially over the more dense background.

Fig 3.

Sobel filtering to enhance edges of gold particles and allow better localization. (A) Subarea with 15-nm gold from a tilt series of Chlamydomonas acquired by Eileen O’Toole. In both cases where two beads appear to touch (arrows), they are on opposite sides of the section and appear isolated at most tilt angles. Scale bar is 25 nm. (B) Sobel filter applied to image in (A). In (A) and (B), images were captured with a zoom of 4 and pixel interpolation; the beads are actually 5.3 pixels. (C) Subarea from a tilt series of frozen-hydrated Vibrio cholerae acquired by Yi-Wei Chang in Grant Jensen’s laboratory. Scale bar is 100 nm. (D) Sobel filtering of unscaled image fails shows weak signal from the beads. (E) Sobel filtering after scaling the image so that beads are 8 pixels gives a strong signal over the background and a recognizable annular signal even over the denser areas of the cell (arrows).

Use of the Sobel filter generally gives substantial improvements in the mean error of alignment for tilt series from plastic sections, and more modest benefits for cryo-specimens. This error is the mean distance between each fiducial point and the position predicted by the alignment solution. Figure 4 plots the improvement versus the mean error for a diverse collection of test sets. The mean reduction in error is 20% for the plastic sections (0.119 pixel, SD 0.089, n = 15) and 10.4% for the cryoET sets (0.076 pixel, SD 0.059, n = 15). However, such good results with cryoET sets are obtained only with a much higher sigma value for the Gaussian filter, typically 1.5 pixels instead of the 0.5 that is good for plastic section sets. The lower signal-to-noise ratio (SNR) in cryoET can explain both the need for a stronger filter and the lower effectiveness of Sobel filtering, because measurement based on edge enhancement rather than integration will be more sensitive to noise. The improved positioning with the Sobel filter contributes to automated processing in two respects: 1) a reduction in the random error of essentially correct points makes it easier to detect and apply less weight to outlying points; and 2) a general reduction in error increases the likelihood that the results from automated alignment will be considered acceptable.

Fig 4.

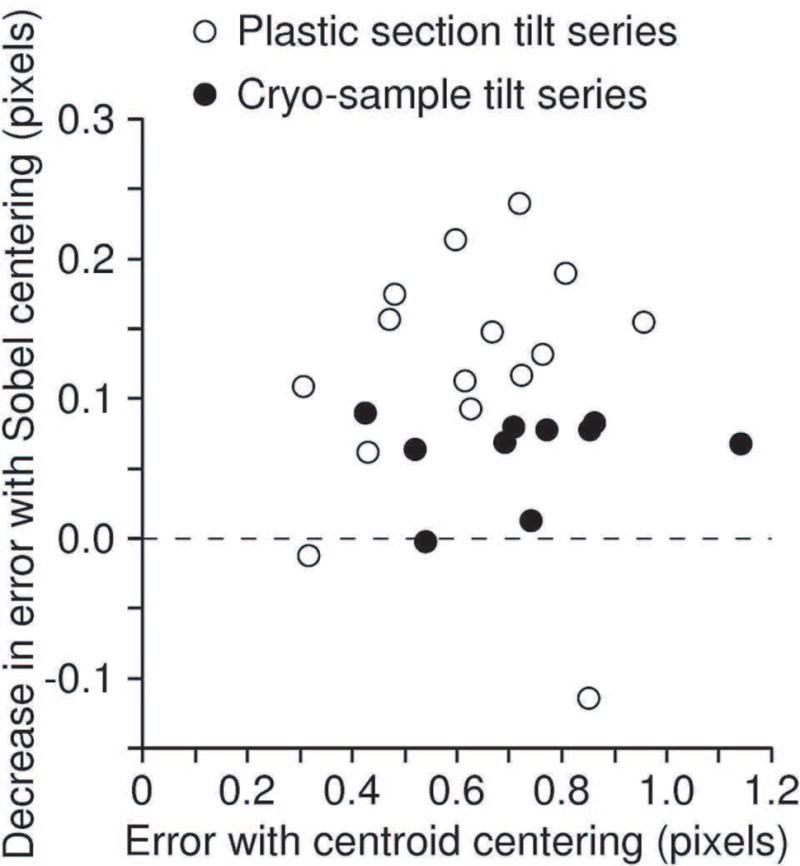
Reduction in mean residual error by refinement of positions with Sobel filtering, plotted against the mean residual of alignment solution, for tilt series from plastic sections (open circles) and frozen-hydrated samples (closed circles). The one poor result for a plastic section was observed recently and prompted a modification of Beadtrack so that it falls back to centering with the centroid when Sobel centering gives a worse mean residual.

For comparison, alignment with RAPTOR was attempted with 7 of these tilt series (2 plastic, 5 cryo). RAPTOR failed or behaved poorly in some respect for 4 of these sets, such as by giving a poor distribution across the field, tracking only half of the tilt series, picking ribosomes, or jumping from one bead to another in a track. For 5 sets where comparable residual errors could be obtained, the residual from RAPTOR was higher than that from Beadtrack by 0.17 pixel on average (range 0.04 to 0.28) with centroid centering and by 0.30 pixel (range 0.16 – 0.45) with Sobel centering. Thus the accuracy of bead positions was already higher from Beadtrack than from RAPTOR and this gap has widened with the new centering method.

2.4. Automatic alignment of dual-axis tomograms

Further developments were needed to automate the full processing of tilt series taken around two axes. In IMOD, such dual-axis tomograms are reconstructed separately, aligned with each other, then combined in Fourier space. The volumes are initially aligned with a linear transformation obtained from corresponding points; one volume is then transformed to match the other. Alignment is refined by cross-correlating an array of sub-volumes (patches) and fitting one linear transformation to the shifts between the patches; usually this fit is inadequate and a warping transformation is obtained by fitting a series of linear transformations to subsets of patch shifts. The initial alignment already worked automatically when there were fiducial markers but otherwise, the user was required to pick corresponding points manually. This step has been automated with a new script, Dualvolmatch, that reprojects each volume over a small range of tilt angles and finds the pair of reprojections that give the best alignment with a rotation within 20° of +90° or −90°. A 3-D linear transformation is derived from the two tilt angles and the 2-D linear transformation between the reprojections; if possible, it is refined by correlating large patches of the volumes. This initial transformation is good enough that the usual patch correlation for refinement proceeds without trouble.

The main problem in the second stage of alignment is that the correlations between patches become inaccurate in regions where there is not enough material. Users have been required to specify a range in Z that contains enough material for the patches, and to draw contours around the regions containing material to exclude empty areas laterally (Fig. 5A). Not only do these procedures become difficult when the section is arched or dome-shaped, but they are also incomplete because interior regions, such as vacuoles, may also have inadequate amounts of material. To automate this process, a measure of structure was developed that could be analyzed to determine which patches contained enough material for good correlations.

Fig 5.

Detection of structure to automate the alignment of tomograms from tilt series taken around two axes. (A) X/Y slice through tomogram for one axis, acquired by Mary Morphew from a high-pressure frozen, freeze substituted melanoma cell. The boundary contour was drawn to exclude regions without sufficient structure for correlations between the two tomograms. Density is shown as positive to match the polarity of the SD display in (B). (B) X/Z slice through the middle of a volume of local standard deviations, where each voxel has the SD of an 8 × 8 × 2 box of voxels after binning the tomogram isotropically by 4, and the boxes are spaced 4 × 4 × 1 voxels apart. The rectangle indicates the size of a patch that would be correlated in 3D between the two tomograms. (C) Corresponding X/Z slice through the tomogram. (D) Distribution of box SD values from the unbinned and binned tomograms, showing better separation between the modes representing background and structure with binning by 4. The arrow indicates the threshold that would be chosen between structure and background. (E, F) 3-D displays of the tomographic volume showing the vectors of local shifts between the two volumes; lengths are exaggerated by 5. (E) Shifts between patches when correlating with neither the boundary contour model nor limits in Z as constraints (F) Shifts when the correlation search program skips all patches with a structure score of less than 50%. All scale bars are 200 nm.

The local standard deviation (SD) can serve as a measure of structure, but only if it is taken at a scale where noise does not dominate. To find a good scale for distinguishing structure from background, a multi-scale computation of SD is done by applying different amounts of binning to the volume. Binning is always isotropic, but SD is generally computed in elongated boxes, such as 32 × 32 × 8 voxels, in order to have a higher resolution for detecting the abrupt change expected at a section surface and to ensure that some boxes are fully in the region outside the section, which may be relatively few pixels thick. Boxes at the different scales are based on the same number of unbinned voxels. The spacing between box centers is half the box size in each dimension. Volumes of box SD values are rapidly computed simultaneously for all selected binnings (such as 1, 2, 3, and 4) on one pass through the tomogram.

As seen in Fig. 5B, the local SD can give a sharp definition of the section surface, and it also allows regions within the section with little material to be detected easily. The X/Z slice of a box volume is shorter in X than the X/Z slice from the tomogram (Fig. 5B vs. C) because of the difference in box spacing in the X and Z directions. To pick a good binning, the median and MADN value of the box SDs is computed for boxes at the surfaces of the volume, and a histogram of all box SD values is analyzed to find a dip between two peaks. Figure 5D shows such histograms for binnings 1 and 4. It is evident even in such a histogram that the structure (in the peak to the right) is more distinguishable from background with binning 4. The number of MADN’s between the surface median and the peak of higher SD values generally increases with binning, and the binning above which these increases stop or become minimal is chosen. The dip between the peaks is used as a threshold between structure and background (arrow in Fig. 5D). Given this threshold, every candidate patch for correlation is given a structure score, the fraction of boxes in the patch above the threshold. For example, the rectangle in Fig. 5B represents a patch that would have a score of about 67%. These scores are used at two different steps: the program that does patch correlations skips patches with a score less than a criterion (typically 50%); and the program that finds the refining transformation can drop patches with progressively higher scores (up to 65%) to attempt to get an acceptable fit. For the example data set, Fig. 5E shows the vectors of correlation shifts throughout the volume when patch locations are not limited in Z or constrained by boundary contours. The first step alone is successful in eliminating the aberrant shifts (Fig. 5F). In more typical cases, there will be some incorrect shifts, but they will be few enough to be eliminated as outliers by the programs that analyze these shifts.

Avoiding patches with insufficient structure is necessary but does not solve two other problems in aligning the two volumes: often the patches are generally too small to give accurate enough correlations, and sometimes they are not spaced closely enough to allow good local fits with highly warped volumes. The new automatic patch fitting procedure in IMOD solves these problems with an iterative approach. If the initial patch size does not give good enough fits, the patch size is increased by 20% in each dimension and patch correlations and fitting are repeated. The size is increased one more time if necessary. If the fit is still not good enough, the patch density is increased for a final attempt, with twice as many patches in X and Y and up to 50% more in Z, and with a more generous criterion for an adequate fit allowed on that try. During development, this procedure was tuned to run successfully on 12 diverse data sets, including reconstructions from montages with up to 3 by 2 frames and from a set with very large warping between the two axes.

2.5. Finding the surfaces of the specimen

Several steps in tomogram processing require specimen boundaries to be determined: the “positioning” step to set optimal angles, thickness, and Z shift to make the specimen be level in a reconstruction of minimum size; final trimming of the tomogram; and flattening of curved sections so that they stack efficiently. The multi-scale analysis of local SD values was incorporated into a new program for finding specimen boundaries, Findsection. The main challenge is to avoid having the boundary determined by gold fiducials; this is particularly important for plastic sections where one layer of gold is on the other side of the support film. Robust methods are used to achieve this goal. Boundaries are found by analyzing how box SD changes through Z and taking points where it falls from its peak value to 25% above the background level. This analysis uses the median of a rectangle of at least 25 box SDs at each Z value; as long as the boxes themselves are sufficiently large, a single gold particle will affect the SD of at most 9 boxes in such a rectangle and thus not perturb the median. After an array of boundary points is found on each surface, it is smoothed by robust fitting of a 2-D polynomial, which will eliminate as outliers any remaining boundary points dominated by gold. Figure 6A shows an example of gold being avoided when marking section surfaces. This array of points is grouped into contours in X/Z planes and output directly when a model is required for tomogram flattening. The points are analyzed in other appropriate ways to produce the model with two-point lines required for positioning, or to provide Z limits suitable for patch correlations in tomogram combination and for final trimming.

Fig 6.

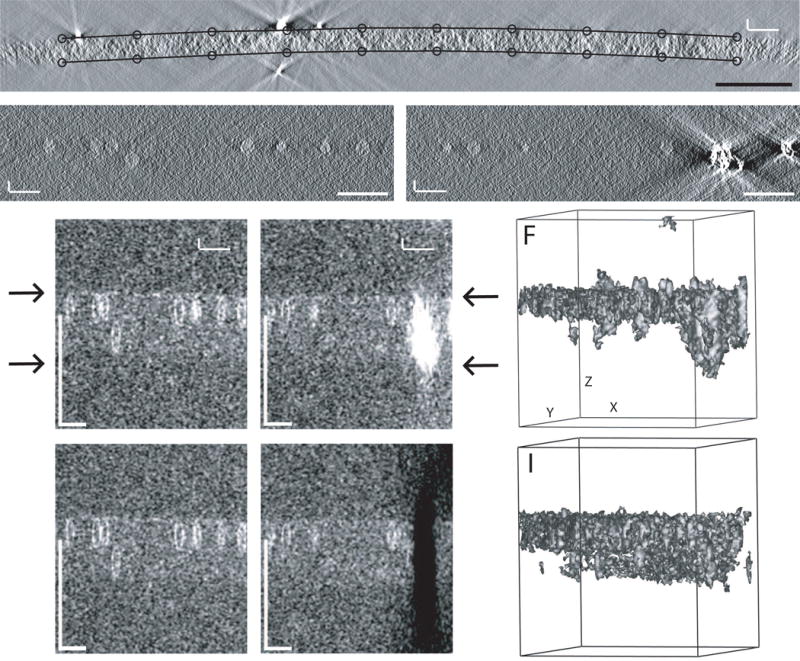
Structure detection for finding specimen surfaces. (A) Boundary points found by Findsection for an X/Z slice through a tomogram of a budding yeast mitotic cell acquired by Janet Meehl. The various robust procedures described in the text succeeded in excluding gold particles. A model like this is needed for flattening such a highly warped section, and starting with a model from Findsection greatly reduces the labor of preparing such a model. (B, C) X/Z slices through a tomogram of frozen-hydrated bovine papilloma virus, acquired by Mary Morphew. (D, E) Corresponding slices through a volume of box SDs. Arrows indicate the apparent surfaces of the ice. The virus particles show up clearly enough, but the ray artifacts extending outside the ice from the clump of gold in C have comparable strength and dominate the box SD values in (E). (F) Isosurface display of the box SD volume at a threshold that shows the virus particles. The volume has been rotated in X and Y to make the ice surfaces parallel to the direction of view. (G, H) Slices through a box SD volume from a tomogram generated after erasing gold and other high densities from the tilt series images. (I) Isosurface display of the erased volume, at a threshold that shows the surface of the ice. All scale bars are 200 nm.

The procedures just described are effective when working with plastic sections but fail with cryotomograms because of their lower contrast and SNR. Also, biological material is often more sparse in cryotomograms. Because of these factors, the procedures for finding the surfaces of the specimen are more complex and the goals more modest: to get the tomogram angles approximately correct and to determine a thickness that is sufficient but may be somewhat excessive. A primary impediment to the analysis of local SD values is that gold particles cast artifactual rays outside the specimen comparable in strength to the material of interest. For example, Figures 6B and D show an X/Z slice from a cryotomogram of bovine papilloma virus and the corresponding local SDs; in the latter, the upper surface of the ice is evident and the lower surface is also faintly visible. However, in a slice through a clump of gold particles (Figs. 6C and E), the shadows from the gold are much stronger than the signals from virus particles. The isosurface view of the volume of box SDs (Fig. 6F) also shows how high values extend beyond the specimen.

To overcome problems created by gold markers, the analysis is done on a tomogram built from projection images in which gold and other high densities have been removed. Yet another script, Cryoposition, makes such a tomogram in 10 steps, essentially by determining a threshold density for gold in a tomogram, finding features above that threshold and of a minimum size, and erasing pixels in the tilt series images to which those features project by setting them to the surrounding mean. After this procedure, the clump of gold that dominates the slice in Fig. 6E is gone in Fig. 6H. The isosurface view in Fig. 6I, even with a lower threshold than in Fig. 6F, has almost no features outside the ice layer and shows that simple thresholding of the SD values can give rich information about the location of both surfaces. To analyze erased tomograms, Findsection examines box SDs at each position in X and Y and takes the outermost Z values with an SD more than a criterion number of MADNs (5, by default) above the background median as potential lower and upper boundaries. If these X, Y, Z positions are rotated around the X and Y axes, the distribution of rotated lower or upper Z values will be sharpest when the specimen has been rotated parallel to the X/Y plane. The best rotation angles are thus found by searching for angles that minimize the MADNs of these two distributions. After that, the best lower and upper boundaries are found by analyzing the fall-off of each distribution away from the middle of the volume. The boundaries are spread apart by a small factor (10%, by default) to provide extra assurance that all material of interest is included. This procedure was evaluated on 13 cryoET sets and the modest goals given above were met. However, this is the least successful of the automated procedures described here. There are probably some kinds of specimens where it is unsuitable, such as ones where the biological material is particularly sparse, or where a large dense cell surrounded by ice has indistinct upper and lower surfaces.

2.6. A program and framework for automated processing

To connect all of these automated capabilities into a pipeline, the Batchruntomo script was developed for processing one or more tilt series. The program can run all of the required and optional steps (heavy and light boxes, respectively, in Fig. 7) in the IMOD tomography workflow. It allows one of four different alignment methods to be used: the automatic fiducial seeding and tracking described above; creation of a fiducial model with RAPTOR; use of the simple initial cross-correlation alignment to generate a rough tomogram; or patch tracking, which tracks image subareas between projections and creates a model of positions that can be used for alignment just like a true fiducial model. The processing operations are controlled with a text file containing keyword – value pairs referred to as “directives”. Other than this feature, processing is done within the same framework as when building a tomogram interactively in the Etomo graphical user interface.

Fig 7.

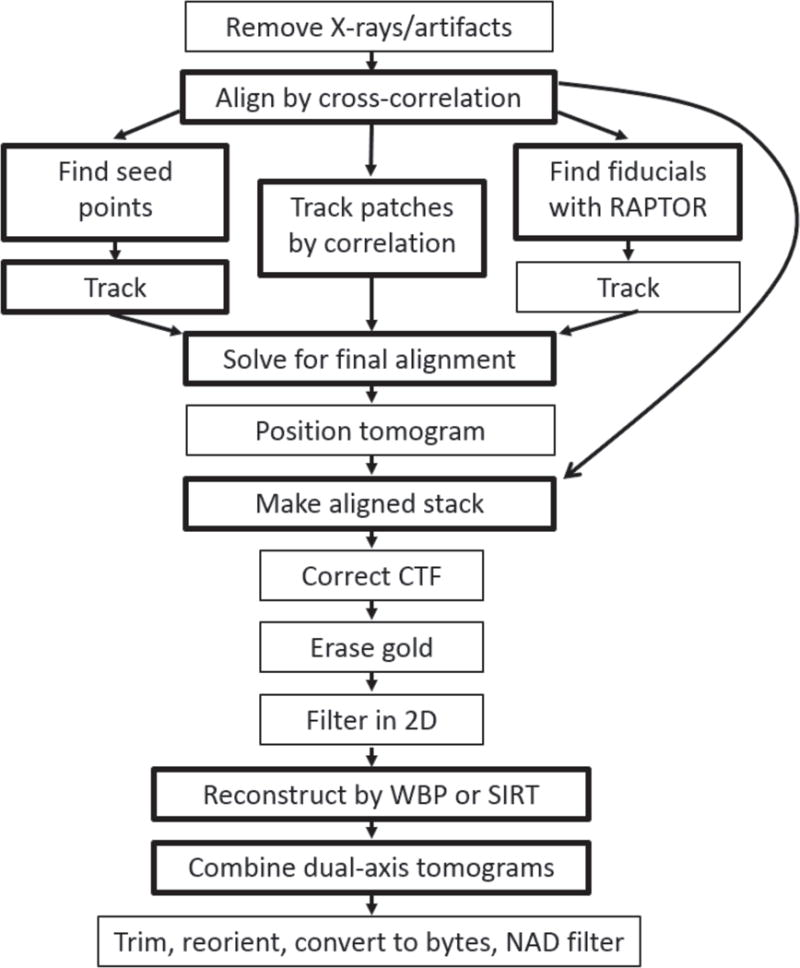
Steps in tilt series processing automated by the program Batchruntomo. The available alternative alignment pathways are shows. Boxes are drawn lighter for optional steps than for required ones. WBP is weighted back-projection, SIRT is Simultaneous Iterative Reconstruction Technique (Gilbert, 1972), NAD is nonlinear anisotropic diffusion (Frangakis and Hegerl, 2001), and CTF correction refers to measuring defocus and correcting the phases from the microscope contrast transfer function (Xiong et al., 2009).

For tilt series processing in IMOD, almost all operations are run via command files, which contain one or more lines to start a program, each followed by lines with parameter entries to that program. These files are converted to Python scripts and run with Python, simply as a means of running the programs with their parameters. Most command files are created with appropriate filename entries when a data set is started; some are created later when needed. The three programs that create command files can be given directive files and will process one form of directive generically. These directives start with “comparam.” followed by a command file name, a program name, an option to that program, and then the option value after an equals sign. For example, “comparam.track.beadtrack.KernelSigmaForSobel = 1.5” refers to the option KernelSigmaForSobel for the program Beadtrack in the file “track.com”. The program that makes track.com from a stock file will respond to the presence of this directive by adding the line “KernelSigmaForSobel 1.5” to the entries for Beadtrack, or modify the value to 1.5 if that option is already present. Any valid program option can be added, modified, or even deleted in this way (see also Fig. S2).

Directives serve a dual purpose because many can also be used to set parameters for interactive processing in Etomo. The “comparam” directives are supported simply by having Etomo pass the directive file to the programs that it runs to create command files. Other directives, which typically set processing choices and parameters that do not correspond to a command file option, have to be recognized and handled explicitly in the code. The subset of directives that can meaningfully be applied to multiple data sets can be placed into template files and supplied to either Etomo or Batchruntomo. We designed three levels of templates, called Scope, System, and User, where the Scope templates might have a few microscope-specific parameters, the System templates are distributed with IMOD or maintained for multiple users, and the User templates can be managed by individual users. These usages are not enforced, but there is a defined order of processing (Scope, System, User, and finally a batch file) so that later values can override earlier ones. Etomo has mechanisms for keeping track of which parameters have changed from their defaults and has a template editor that allows the user to save the changed parameters for a particular data set as a template.

2.7. An interface for batch processing

Most recently, we have added an interface in Etomo for setting up, running, and monitoring the batch processing of tilt series. Figure S2 presents the relationships between this interface and the other components just described: command files, directives, templates, and Batchruntomo. The interface consists of four tabs, three of them shown in Fig. 8.

Fig 8.

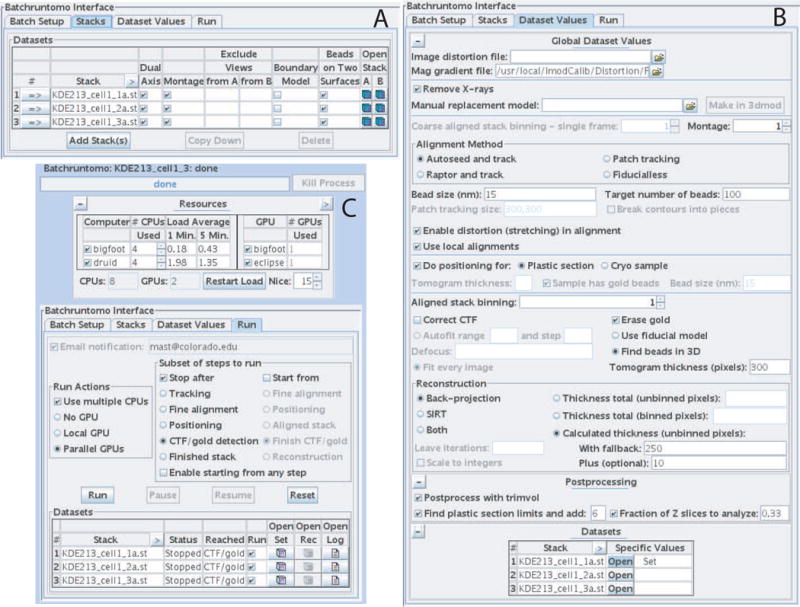
Three tabs of the batch interface in the Etomo program. (A) The Stacks tab allows one to enter the tilt series to process and set some basic properties of them. (B) The Dataset Values tab presents the choices and most commonly needed parameters for processing. (C) The Run tab has a Resources table at the top for selecting computer cores and graphics processors to use, choices for stopping and restarting all data sets at certain points, and a table showing the status of each data set.

Batch Parameters

This tab controls some features of the batch project. Templates can be selected here. A directive file can be entered from a previous batch run to set starting values for the processing parameters. Each data set will be processed in its own directory; this tab has an option for creating those directories in a specified location and moving the tilt series into those directories from one or more central locations.

Image Stacks

This tab has a table to which all of the tilt series are added by selecting in a file chooser (Fig. 8A). The table has entries that definitely would vary between data sets, namely as images to exclude and a boundary model, plus some other properties that we thought most likely to vary among sets, namely whether the set is dual axis, consists of montaged images, or has beads on two surfaces.

Dataset Values

The tab presents the processing parameters (Fig. 8B). Our goal was to keep these entries on a single screen, so only the commonly needed parameters are shown. We currently rely on other parameters to be entered through template or starting batch directive files, although we plan to make an advanced screen that would show all other entries that correspond to directives. This screen shows global values, but values can be set differently for any data set by pressing the Open button in the table at the bottom, which opens a screen just like the global one that applies to just one data set. The table will show which sets have individual values.

Run

This tab has several sections related to running the jobs (Fig. 8C). 1) If the buttons are selected to indicate the use of multiple CPUs (computer cores) or multiple GPUs (graphics processing units), then the Resources section at the top appears with available CPUs (either just in the local machine, or in multiple computers), or with available GPUs, or both. Multiple CPUs are used either by splitting a processing step (e.g, reconstruction) into multiple processes that are run in parallel, or by running an operation (e.g., image transformation) within one process in multiple threads with OpenMP. The GPU can be used for reconstruction, which is split into multiple processes to use multiple GPUs. 2) The buttons under “Subset of steps to run” allow one to run all jobs to a selected point, check some aspect of the processing, and resume at the logical next step, an earlier step, or even a later step. This is particularly useful for the contrast transfer function (CTF) correction and gold erasing steps, which may be the ones most likely to need attention. 3) The table at the bottom is updated as the jobs run to show what step has been reached and whether a set finished or failed. It is not necessary to leave Etomo open during the processing, however; if it is closed and reopened later, it will catch up on what has occurred in the interim and resume its monitoring. Each table line has buttons to open the data set in the interactive tomogram processing interface in Etomo, to open a reconstruction file for viewing, or to view the log file; these are enabled when appropriate. The checkbox in the Run column specifies that a set is to be processed in the current run and is turned off when the set finishes. With these features, one can restart a particular subset of the tilt series after attending to problems.

2.8. Results with batch processing

Users report generally good results with stained, embedded samples but more mixed results for cryo-samples. IMOD users were recently invited to answer a survey about the success of batch processing with IMOD, specifically, for what fraction of data sets it gave adequately aligned and positioned tomograms. When using fiducial markers, four respondents estimated success rates of 98, 95, 90, and 80% for non-montaged plastic section sets, three reported 90% for montaged tilt series, and five estimated that dual-axis data sets combined automatically 98, 85, 75, 70, and 5% of the time. One respondent using patch tracking reported 85% and 35% success in producing single-frame and montaged tomograms, respectively, with dual-axis tomogram combination succeeding 70% and 10% of the time in those two cases. For cryoET, one user estimated a 75% success rate and another reported 0% success. (Personal communications from Ori Avinoam, Mark Ladinsky, Eileen O’Toole, Helio Roque, Martin Schorb, Cindi Schwartz and two others.) In sum, the automated procedures are quite effective in many cases, but more work is needed to determine the causes of the lower success rates and to improve performance in those cases.

3. Discussion

The developments described above, chiefly the ones that enable automated fiducial alignment and registration of dual-axis tomograms, enable the automatic generation of high-quality tomograms in a range of situations; these were the impetus for providing tools to control automated reconstruction. Although it was previously possible to set up automated reconstruction with IMOD tools (e.g., the Caltech database originally used RAPTOR and scripts before adopting Batchruntomo (Ding et al., 2015)), the new features for such reconstruction are more flexible, comprehensive, reliable, and accessible to general users.

There are a number of benefits from the way that these tools have been implemented within IMOD. The automated processing is compatible with interactive processing in Etomo and can perform all of the steps that are available through that interface. These features should make it easier for users to adapt their workflow to the new tools, and also allow users to work through their data more efficiently even when the batch processing is not fully successful. Note that we have also made each of the key developments – Sobel centering, robust fitting, and automated seed model generation, registration of dual-axis volumes, and tomogram positioning – available in the interactive interface. Thus, benefits accrue from these developments in automated processing even for those who do not use the batch framework.

These automated procedures will be most effective and successful with fiducial markers. The approach of automatic seeding followed by bead tracking is clearly better than RAPTOR (Amat et al., 2008), the other automated procedure available in IMOD, both in terms of the range of data sets over which it is can be used successfully and the accuracy of fiducial positions. Accuracy is at least comparable to that for another fiducial marking method recently reported by Han et al. (2015). With the IMOD tutorial data set, Han et al. (2015) obtained a mean residual error in alignment of 0.57 pixel from automatic tracking with 38 fiducials, whereas the procedures described here result in an error of only 0.37 pixel with 38 fiducials. This difference (p < 0.000001) can be attributed to the better centering with the Sobel filter, without which 0.57 pixel is obtained.

Alignment without fiducials will be somewhat less effective. Markerless alignment methods fall into three categories: initial cross-correlation between successive tilt-series images with iterative refinement by correlation with reprojections from a tomogram (Owen and Landis, 1996; Winkler and Taylor, 2006); extraction of potential corresponding features from tilt series images and derivation of an alignment from their positions (Brandt et al., 2001; Han et al., 2014; Sorzano et al., 2009); and correlation between small image patches in successive images and fitting of positions to an alignment model (Castano-Diez et al., 2010; Castano-Diez et al., 2007). An approach very similar to that of Winkler and Taylor (2006) was attempted for IMOD, but the correlations with reprojections were incapable of removing long-range systematic misalignments introduced during the initial correlations. A patch-tracking approach similar to that of Castano-Diez et al. (2007) was implemented instead. Their method uses relatively small patches and can sort out good tracks from a large number of incorrect ones, whereas the IMOD patch tracking requires patches large enough to give generally accurate correlations, with robust fitting able to discard a small proportion of bad tracks. With the resulting model of patch positions, both the angle of the tilt axis and the rotations and size changes in the images can be solved and adjusted for. The tracks can be broken into overlapping segments to alleviate the problem that the same point in the volume may not stay centered in the patch from one end of the tilt series to the other. Although this approach may not give satisfactory alignment on all data sets, it has been surprisingly successful and can even be used with local alignments (Mastronarde, 2007) on large area tilt series and on cryoET used for subvolume averaging (Engel et al., 2015).

Noble and Stagg (2015) recently described a system for automated batch processing within the Appion framework (Lander et al., 2009), based on processing with Protomo (Winkler and Taylor, 2006). Some of the chief differences from IMOD processing are: it appears to work only with data acquired with Leginon (Suloway et al., 2009); it relies on one fiducial-less alignment method, which may well be better than our patch tracking for some tilt series, but would be unsuitable for large-area data requiring correction for nonlinear changes under the beam; and the alignment time is reported to be several hours. For comparison, the unbinned (1K × 1K) version of the IMOD dual-axis tutorial data set can be reconstructed in 4 minutes, including the optional steps of X-ray removal, positioning, gold erasing, and final trimming (CPU: Core i7-3930 at 3.2–3.8 GHz with 6 cores; GPU: GeForce GTX 580; using two RAID-0 7200-RPM hard drives).

Our automation framework does have some weaknesses. Because Batchruntomo handles many steps in the reconstruction process, there are many potential failure points, and the probability of all steps succeeding will be low if the probabilities of failure are not small enough for all of the steps. Our strategy for handling this difficulty is to collect failure cases from users and attempt to improve the performance of particular operations. This process has already occurred for some of the earlier steps but not yet for dual-axis tomogram combination, which is probably why users have thus far reported a lower success rate there. This situation is emblematic of a general challenge in making new methods work well on a wide range of data sets. Even when developed and tested on data from a laboratory engaged in diverse activity, plus data from some cooperative users, methods can easily not work as well in the hands of users with even more diverse specimens and practices, and less knowledge of the relevant parameter choices. Fortunately, in the case of IMOD, the community of users is large enough to help overcome this challenge.

Another limitation is that our automation framework works best if users select appropriate parameters that have been successful with similar tilt series and, in some cases, preview the data sets before reconstruction. The first requirement may be inevitable for a system designed to handle diverse data. It does not preclude automated reconstruction of data sets immediately after acquisition, provided users can set some basic parameters prior to acquisition, perhaps by selecting from some available directive files. The need to preview images, e.g., to exclude extracellular areas from fiducial tracking or to exclude bad images, does limit use of such an automated pipeline. Alleviating this constraint by automating such exclusions will be one focus of future work.

Supplementary Material

1

Fig. S1. Tilt series images at 0° for the example presented in Fig. 1E and F. (A) shows all gold beads detected on this image, as in Fig. 1E, except that the points are not colored by which section surface they are on, because that information is not present in the model of detected beads shown here. (B) shows the beads selected for the seed model, now colored by surface. Scale bars are 1 μm.

Fig. S2. An example of relationships between various programs, files, and option entries when batch processing through the Etomo interface. Boxes with yellow background represent initial input files for the processing. Defaults for Batch Run from Etomo is a file distributed with IMOD containing default values for directives that Etomo will include in any batch processing. It includes the directive to turn on robust fitting when running Tiltalign (red). User template is an optional file that the user has saved previously; the directive shown (blue) would appear if the user saved it after processing a data set with a non-default scaling factor for robust fitting of 0.9. Master align.com File is a file included in IMOD with the commands and default options for running Tiltalign. Boxes with blue background represent the batch processing user interface in Etomo and some of its output. Batch Interface lists the selections by the user that are relevant to the options followed through this example. The interface reads in the defaults and any selected template files and overlays the user’s choices on the values in those files. Batch Directive File is the output file from the interface for each data set. It includes the name of any template files rather than the directives contained in them (in reality, the full path would be shown for a user template). Also shown are the default directive for robust fitting and the alignment-related choices made by the user. Etomo also writes a command file for running Batchruntomo itself, which specifies the data sets, their batch directive files, computing resources, etc. Boxes with pink and peach backgrounds represent processing steps performed by Batchruntomo and the alignment command files that it operates with, respectively. In the Batchruntomo Setup Step, Batchruntomo runs Etomo in a setup-only mode, passing it the batch directive and template file. Etomo performs some setup actions and ultimately runs the Python script Copytomocoms, also passing it the batch and template files. Copytomocoms creates the Initial align.com File in the data set directory, adding the option RobustFitting (red) because of the directive in the batch file, and adjusting the setting for LocalAlignments and KFactorScaling (blue) based on directives in the batch and template file, respectively. In the Batchruntomo Alignment Step, Batchruntomo reads in the Initial align.com File and produces and runs the align.com for First Run, in which local alignments (green) have been turned off for this first run of Tiltalign. After evaluating whether there are enough fiducials on each surface to allow a reliable stretching solution, and enough to allow local alignments to be used, it turns on the two options for stretching and LocalAlignments (green) for the final run of Tiltalign. This example illustrates that “comparam” directives are incorporated when command files are first made, but the associated options may also be manipulated by Batchruntomo; whereas “runtime” directives are not incorporated directly into the command files but acted on by Batchruntomo at the appropriate point.

Abbreviations

CryoET

cryo-electron tomography

MADN

normalized median absolute deviation from median

SD

standard deviation

SNR

signal-to-noise ratio

CCC

cross-correlation coefficient

3-D

three-dimensional