Orbital angular momentum of photons and the entanglement of Laguerre–Gaussian modes

Abstract

The identification of orbital angular momentum (OAM) as a fundamental property of a beam of light nearly 25 years ago has led to an extensive body of research around this topic. The possibility that single photons can carry OAM has made this degree of freedom an ideal candidate for the investigation of complex quantum phenomena and their applications. Research in this direction has ranged from experiments on complex forms of quantum entanglement to the interaction between light and quantum states of matter. Furthermore, the use of OAM in quantum information has generated a lot of excitement, as it allows for encoding large amounts of information on a single photon. Here, we explain the intuition that led to the first quantum experiment with OAM 15 years ago. We continue by reviewing some key experiments investigating fundamental questions on photonic OAM and the first steps to applying these properties in novel quantum protocols. At the end, we identify several interesting open questions that could form the subject of future investigations with OAM.

This article is part of the themed issue ‘Optical orbital angular momentum’.

1. Introduction

The orbital angular momentum (OAM) of light emerges as a consequence of a spatially varying amplitude and phase distribution. Light beams with OAM have a ‘twisted’ or helical phase structure, where the phase winds azimuthally around the optical axis. The intensity distribution of such beams exhibits a characteristic intensity null at the centre due to destructive interference. In 1992, Allen et al. [1] showed that a single photon with such a spiral structure carries a well-defined value of OAM. While this was a significant development, it remained unclear whether photons can be entangled in their OAM degree of freedom [2]. Here, we explain the physical intuitions that led to the first OAM entanglement experiment [3], and then look into some of the developments since then.

2. Intuitions behind the first quantum orbital angular momentum experiment

From earlier experiments, it was known that linear momentum is conserved in spontaneous parametric down-conversion (SPDC) processes. As Laguerre–Gaussian modes can be decomposed in this basis, one would intuitively expect that OAM modes are also conserved. The measurement of the OAM of a photon is a projection into a superposition of k-states with a certain phase relation. This also projects its partner photon in the same k-state superposition but with inverse phase, as the sum of the phases of the down-converted pair corresponds to the phase of the pump photon. Obviously, this intuition needed to be verified experimentally.

While it was not known how to measure the OAM of light at the single-photon level, there were methods to create beams with OAM. For example, one could start with a Gaussian mode and send it through a hologram with a helical phase structure and thereby create a beam with OAM. The time-reversed scenario also works. A beam carrying a non-zero OAM incident on a helical phase hologram with opposite OAM can thus be transformed into a Gaussian mode and can then be coupled into a single-mode fibre and measured with a photon detector. In this manner, the combination of a hologram and a single-mode fibre could act as a mode filter for single photons carrying OAM (figure 1a,b).

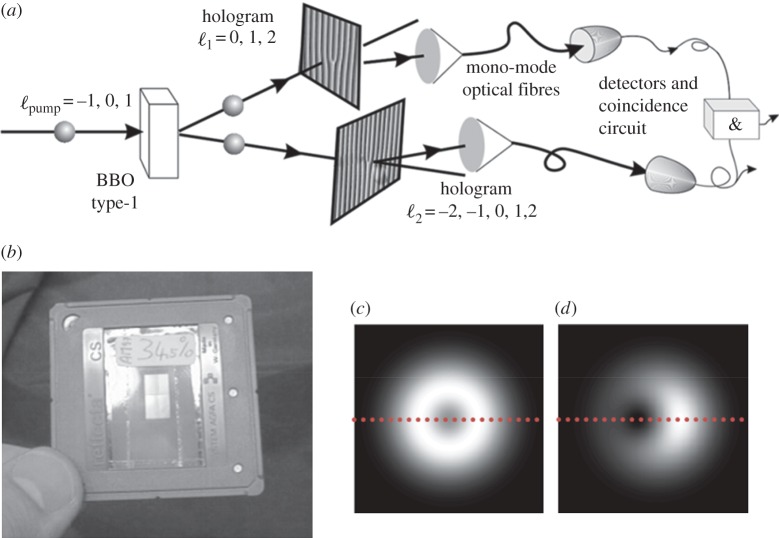
Figure 1.

(a) The experimental configuration of Mair et al. [3] consisted of an SPDC crystal (BBO), which produced photon pairs entangled in OAM. The entanglement was confirmed by using absorption grating holograms, which transform the OAM value of the mode. Using a single-mode fibre, only Gauss photons were detected, which allowed the OAM value of single photons to be determined (adapted from [3]). (b) Picture of the absorptive hologram used in the Mair experiment (adapted from [4]). (c) The incoherent mixture of a ℓ = 0 and ℓ = 1 mode (which is separable), while (d) shows coherent superpositions between those modes (adapted from [4]). This property can be used to verify entanglement, by measuring the intensity of one photon along the red dotted line, when its partner photon is projected into a superposition of ℓ = 0 and ℓ = 1. (Online version in colour.)

With this tool in hand, it could now be tested whether OAM is conserved in the SPDC process. By pumping the nonlinear crystal with a Gaussian mode ℓ = 0, it is expected to find the two down-converted photons having opposite OAM values ℓ₁= −ℓ₂. To show this, photon A was projected onto ℓ₁ and the OAM of the partner photon was measured. As expected, the partner photon always shows opposite OAM values. To show OAM conservation in general, different pump modes were used and the property ℓ_p= ℓ₁ + ℓ₂ was verified.

While this showed the conservation of OAM in the SPDC process, it did not demonstrate entanglement yet. To show that the photons did indeed exhibit entanglement in their OAM, one needs to show that they are in a coherent superposition 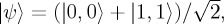as opposed to an incoherent mixture 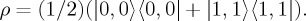The idea was to project one photon into a |0〉 + |1〉 superposition and observe the intensity structure of the partner photon. In an incoherent mixture, one would expect some intensity everywhere, because the Gaussian is uniformly non-zero in intensity. However, in stark contrast, a coherent superposition of |0〉 + |1〉 will have an intensity null that is shifted from the centre to a ring where the amplitudes of the |0〉 and |1〉 mode are equal to each other (figure 1c,d). The azimuthal orientation of the null is given by the relative phase between the modes.

The projection into the |0〉 + |1〉 superposition was performed with a +1 hologram shifted laterally from the centre of the optical axis. (Note that, in general, a coherent superposition of |0〉 + |ℓ〉 has ℓ intensity-nulls symmetrically arranged in a ring, thus shifted holograms can only be used to project into superpositions with ℓ = 1.) Scanning the transverse intensity profile of the triggered partner photon then showed the intensity null that was expected for a coherent superposition of |0〉 and |1〉 modes. In this manner, quantum entanglement of OAM was verified [3].

This work initiated a manifold of experiments investigating single and entangled photons carrying OAM. For example, the distribution of higher-order modes from down-conversion (called spiral bandwidth [5]) is not uniform, which means that higher-order modes have a lower probability of being generated in SPDC than Gaussian modes. In order to produce maximally entangled high-dimensional states, a filtering technique was developed that increased the amount of entanglement at the cost of reducing the total number of counts [6]. Another example of this procedure involved the generation of triggered qutrits for quantum communication [7]. Alternatively, others investigated the replacement of holograms by spiral phase plates [8] and sector plates [9–11] as a simple tool for analysing Laguerre--Gaussian modes. Spatial-mode entanglement was also investigated via Hong–Ou–Mandel interference [12,13].

A significant advance in OAM entanglement experiments was the replacement of static holograms by dynamic spatial light modulators (SLMs) [14]. With holograms, only one mode could be measured at a time, rendering many experiments infeasible. SLMs allow the projected mode to be dynamically changed without any realignment of the experiment. This enabled the quick and precise measurement of arbitrary superpositions [15] of OAM modes, which opened the door to many fundamental experiments with Laguerre–Gauss modes. For example, violations of Bell [16], Leggett [17] and Hardy [18] inequalities were demonstrated with the spatial degree of freedom. Bound states (curious states whose entanglement cannot be distilled) that can only exist in high-dimensional spaces have been created [19]. Furthermore, it allowed the investigation of entanglement in even more complex or exotic spatial-mode structures carrying OAM, such as Bessel modes [20,21], optical vortex links [22], and Ince–Gauss modes [23]. The application of this tool is now standard in entanglement experiments, and was necessary for the realization of many of the experiments discussed below.

3. High-dimensional entanglement

The creation of high-dimensional entanglement is a significant motivation for investigating Laguerre–Gauss modes in the quantum regime. The Mair experiment discussed above was the first to hint at the possibility of high-dimensional entanglement with OAM. In the years following it, several experiments were performed that quantified OAM entanglement in more concrete ways. Below, we discuss some of these experiments and the different methods they used for verifying high-dimensional entanglement.

In order to characterize correlations in higher dimensions and recognize their usefulness for potential applications and fundamental tests, it is important to distinguish between correlations in a high-dimensional space, entanglement in a high-dimensional space and genuine high-dimensional entanglement.

A classically correlated state in three dimensions can be written as

Such states can be produced by a classical source that produces two photons carrying ℓ = 0 sometimes, and ℓ = 1 or ℓ = 2 at other times, resulting in a completely incoherent mixture.

For example, two-dimensional entangled states can be written in the following way:

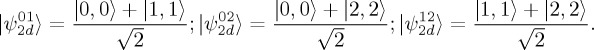An incoherent mixture of these three states,

has correlations in three dimensions; however, it is still only two-dimensional entangled, i.e. its Schmidt number is two. The important challenge is to distinguish it from genuine three-dimensional entangled states such as

One method of verifying that a quantum state is high-dimensionally entangled is to reconstruct it via quantum state tomography [24–26] and perform a numerical optimization for the most likely state that yields a physical density matrix (figure 2a). The resulting matrix can then be analysed with different entanglement measures. The largest two-photon reconstruction performed in this manner was with an eight-dimensionally entangled state [24], which required 14 400 measurements over a time of 40 h. The number of measurements grows rapidly for larger d-dimensional states (the number of measurements scales with O(d⁴) for a d-dimensional system) and quickly becomes infeasible, even with optimized versions of tomography [26]. Furthermore, the final state optimization step is computationally expensive and can almost take the same time as the measurements themselves. If prior knowledge is provided, the number of measurements can be vastly decreased. By using compressive sensing techniques, it became possible to reconstruct the quantum state of a 17-dimensional two-photon state [29].

Figure 2.

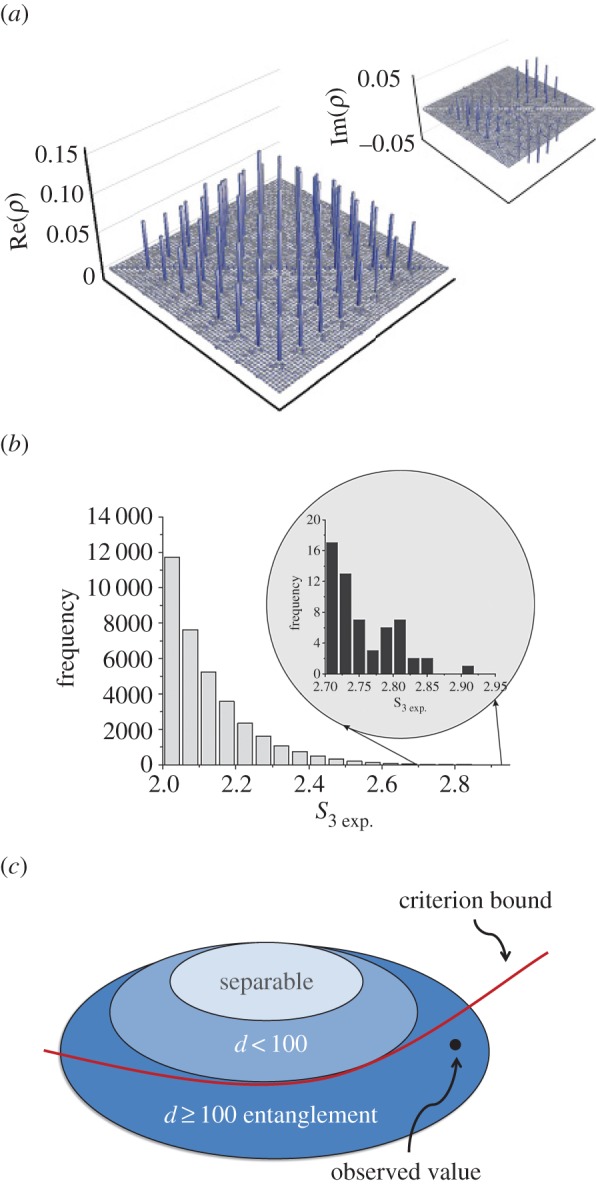
Three different methods to investigate high-dimensional entanglement. (a) Quantum state tomography, (b) violation of high-dimensional Bell inequalities, (c) entanglement dimensionality witnesses. (a) Quantum tomography, while experimentally and computationally expensive, gives the maximal possible information about the quantum state. The highest-dimensional two-photon state for which quantum tomography (without assumption of state properties) was reported is an eight-dimensionally entangled state. The figure shows the reconstructed density matrix (adapted from [24]). (b) Generalized Bell inequalities can also be used to verify high-dimensional entanglement. These values from [27] show the violation of a three-dimensional Bell inequality by exceeding the classical bound of S₃ = 2 for various settings in the experiment. (c) An entanglement dimensionality (Schmidt Number) witness gives a set of measurements and bounds that a state with entanglement dimension d can maximally reach. If an experiment exceeds this bound, the state was at least (d + 1)-dimensionally entangled. In this image, a situation is depicted where a measurement leads to an observed value exceeding the bound for d = 100-dimensional entanglement (adapted from [28]). (Online version in colour.)

The knowledge of the full state is not necessary for extracting information about high-dimensional entanglement (figure 2b). A different approach is to violate a high-dimensional generalization of Bell inequalities known as the Collins–Gisin–Linden–Massar–Popescu (CGLMP) inequality [30,31]. This was first demonstrated with fixed holograms in a follow-up of the Mair experiment [27], which for the first time verified that photons from SPDC are entangled in three dimensions of OAM. A much-improved version of this experiment using SLMs and deterministic measurements settings was performed in 2011, and it showed the violation of an 11-dimensional Bell-like inequality [32]. Tests of Bell inequalities are essential for showing a device-independent violation of local realism in high dimensions [27,33], and could be useful for performing high-dimensional quantum cryptography without the need for trusted devices.

If one is only interested in the entanglement dimensionality, the strong bounds posed by Bell-like inequalities on the required visibilities and the number of measurements can be significantly relaxed (figure 2c). The theoretical tools for doing so are called entanglement dimensionality (or Schmidt number) witnesses [34,35], which are generalizations of entanglement witnesses. In general, an entanglement witness is a function involving measurements performed on a given state, and is bounded by a value maximally reachable by a separable state. When the measurement outcomes exceed this bound, the state must have been non-separable and thus entangled. The premise of this is that the results of certain measurements for separable states (such as visibilities in different bases) are upper-bounded. If one exceeds this bound, the state was entangled [36]. This has been applied to many two-dimensional OAM subspaces [37]. Similarly, an entanglement dimensionality witness has bounds for a specific number of entangled dimensions. For example, an arbitrary two-dimensionally entangled state can only reach a certain maximum value of the witness for a set of measurement results. If the witness measurement exceeds this value, the state was at least three-dimensionally entangled. Such entanglement witnesses have been used to show up to 103-dimensional entanglement in a 168-dimensional two-photon system [28]. A particularly convenient version of a dimensional witness is one that is based on the fidelity of the quantum state. It is fully state-independent, can be generalized to multi-photon experiments (see below), and has recently been shown to be highly applicable to high-dimensional entanglement verification [38,39].

While the dimensionality of entanglement is an interesting fundamental property of the quantum state, it does not necessarily correspond to the usefulness of the state in quantum protocols. Consider the state 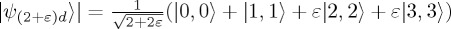, with small 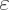. Such a state is four-dimensionally entangled, but the two photons barely share more than 1 bit of non-local information. The useful information is characterized by the ebits, or entangled bits, and is formally named entanglement-of-formation [40]. The distribution of modes in an OAM-entangled state can be optimized to increase this quantity, and several experiments have analysed [41,42] and demonstrated the shaping of the two-photon OAM spectrum [43]. Promising theoretical investigations of SPDC crystals show that the spectrum could be further increased significantly by applying chirped phase-matching [44]. In many cases, specific quantum states are required which need to be carefully engineered. One method to engineer specific antisymmetric high-dimensional entangled quantum states exploits Hong–Ou–Mandel interference for the precise quantum state filter [45].

4. High-orbital angular momentum, hybrid- and hyper-entanglement

The existence of quantum phenomena in large systems leads to apparent paradoxes first formulated in the form of Schrödinger's cat. While generally accepted definitions of macroscopic quantum superpositions and macroscopic entanglement are still missing, there has been much progress in creating quantum systems of larger and larger sizes [46,47], for example systems involving large masses or large spatial separation. A large difference in physical quantities or in quantum numbers has also been discussed as one potential route for creating macroscopic quantum superpositions [46]. The OAM degree of freedom offers the possibility for creating entanglement of arbitrarily large quanta in principle. This motivates the creation of two-photon states with very high-OAM entanglement [48]. The experimental idea is to create polarization-entangled photons and transfer their polarization information to OAM in an interferometric way. The OAM quantum number is then only limited by the quality of the hologram used. With SLMs, it was possible to create a two-dimensionally entangled state with an OAM quantum number difference of 600 ħ. In a follow-up experiment that replaced the SLM with spiral phase mirrors made of aluminium [49,50], it was possible to reach a quantum number difference of 10 000 ħ [51]. The coupling between polarization and OAM is not only possible in an interferometric scheme, but also with light–matter interaction in an anisotropic inhomogeneous medium. Such a device is called a q-plate [52,53] and has been used in several quantum experiments, such as a quantum random walk with up to five steps [54], non-contextuality tests with four-dimensional entangled quantum states [55], and quantum cloning [56,57].

Quantum states where the entanglement is distributed between different degrees of freedom are known as hybrid-entangled states. An example is the following state:

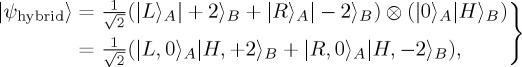where A and B stand for the first and second photon, R, L, H and V stand for the polarization, and ±2 and 0 stand for the OAM of the photon. While the state is only two-dimensionally entangled, the combination of two degrees of freedom allows for a large variety of complex entangled photon states. Such an entangled state was created using a q-plate, where the polarization of one photon was entangled with the OAM of the second photon [58]. Similarly, an interferometric method was used to create a quantum state with the polarization of one photon entangled with a complex polarization pattern (based on a combination of polarization and spatial modes) of the second photon [59]. These studies show the vast possibilities for quantum correlations encoded in complex ways and spread over several degrees of freedom. Note that while one can formally write single photons (and even classical Maxwell fields) with non-separable polarization-spatial wave functions, such systems cannot be considered entangled as they are missing the crucial property of quantum entanglement: spatial separation or non-locality (see [60] for an illuminating discussion). Modern ICCD cameras have the possibility to detect single photons, and can be triggered in the nanosecond regime. This allows their application in quantum experiments, and in particular in experiments involving the spatial modes of photons. Using hybrid entanglement, ICCD cameras have been used to image quantum entanglement in real time [61], as well as remote-state preparation with OAM-polarization hybrid states [62].

An interesting, complementary approach is hyper-entanglement. Such states are simultaneously entangled in their spatial-mode structure, as well as in other degrees of freedom. The first demonstration of such a state was one entangled in polarization, time and OAM [63], which is created as such directly in the SPDC process. The state can be written as

and contains 12-dimensional entanglement distributed over three degrees of freedom. Owing to the complex encoding of the entanglement, such states can be used for improved versions of quantum protocols. For example, in superdense coding, it allows one to go beyond the conventional linear-optics channel capacity limit and reach optimal performance [64]. Furthermore, hyper-entanglement has been used to implement resource-optimized versions of remote-state-preparation protocols with linear optics only [65].

5. Radial modes in quantum experiments

Radial modes are the second quantum number of Laguerre–Gaussian modes and correspond to a radial-momentum-like property of the photon. While they have not drawn as much attention as the OAM quantum number, they have seen an increased interest in recent years [66–68]. For example, several experiments have demonstrated the control of these modes and quantum correlations between them [28,42,69,70]. In particular, a recent experiment demonstrated Hong–Ou–Mandel interference between two photons carrying radial modes, clearly showing their quantum behaviour [71]. In this experiment, single photons were impressed with radial modes up to the ninth order and interfered at a beam splitter.

6. Measuring orbital angular momentum of single photons

The measurement technique used in most entanglement experiments using holograms or SLMs allowed one to determine the OAM content of a single photon. However, this method only allowed one to ask the following question: ‘Is the photon in a particular OAM mode (superposition)?’ In order to fully utilize the high-dimensional potential of the OAM degree of freedom, one would instead like to ask the following question: ‘What OAM quanta is the photon carrying?’ This would correspond to a measurement scheme that can distinguish among arbitrarily many OAM levels of a single photon with unit efficiency. This important question was first addressed in a 2002 experiment that used a modified Mach–Zehnder interferometer to separate even and odd quanta of OAM (figure 3a) [72]. Each arm of the interferometer contained a Dove prism that introduced a phase that depended on both the OAM value of the photon and the rotation angle of the prism. In this manner, a relative angle of α = π between the two Dove prisms resulted in constructive (destructive) interference for photons carrying even (odd) OAM quanta. At a different relative angle α = π/2, the interferometer sorted between even and odd OAM quanta in multiples of two. By cascading many such interferometer elements in a clever way, one was able to efficiently measure the entire spectrum of OAM modes carried by a single photon. A recent experiment used this device to split a high-dimensional two-photon entangled state into two lower-dimensional entangled states with opposite OAM parity, demonstrating a two-particle high-dimensional analogue of the Stern–Gerlach effect [39]. The device can also be used as a two-input, two-output device, in a manner analogous to a polarizing beam splitter that makes it particularly useful in quantum experiments. In that scenario, the Mach–Zehnder interferometer acts as a high-dimensional OAM-parity ‘beam splitter’, reflecting (transmitting) photons with odd (even) parity. That capability was significant for its utility in performing cyclic operations with OAM [74], as well as in multi-photon entanglement experiments with OAM [75], which are discussed later.

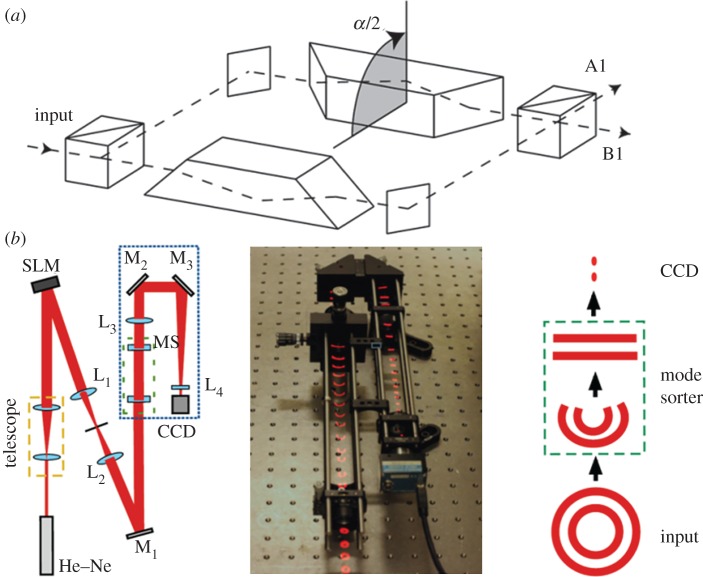
Figure 3.

The ability to measure the OAM of a single photon is very important for quantum experiments. (a) The idea of a non-destructive measurement of the parity of OAM in an interferometric way introduced in [72]. Owing to an OAM-dependent phase introduced by a Dove prism, even and odd modes exit from different output ports. This process can be cascaded for measuring arbitrarily large OAM spectra (adapted from [72]). (b) A refractive method for efficiently separating the OAM eigenstates of a single photon. A log-polar transformation is used to convert the helical phase profile of an OAM mode into a linear phase ramp with an OAM-dependent tilt. Such modes can then be spatially separated via a simple Fourier-transforming lens (adapted from [73]). (Online version in colour.)

In order to sort a large number of OAM quanta, the cascaded interferometer approach is technically demanding. In 2010, a significant experiment demonstrated a two-element refractive device that separates the OAM content of a photon into its components (figure 3b) [76]. The fundamental idea consists of using a transformation that unwraps the helical phase structure of an OAM mode into a plane wave with an OAM-dependent tilt. Thus, an ℓ = 2 mode would have twice the tilt of an ℓ = 1 mode, and so on. These tilted plane waves act similar to gratings and separate different OAM modes during propagation. In this manner, a superposition of many OAM modes can be transformed into spatially separated spots and detected individually. While the first version of this OAM sorter was realized on SLMs, a refractive version was subsequently developed that was used to sort up to 51 OAM modes [73,77].

The separation efficiency was later improved from 77.4% to a theoretical value of 97.3% by the addition of two diffractive elements that coherently copied the transformed plane-wave modes, thus reducing their overlap with neighbouring ones [78,79]. The improved OAM sorter also allowed the separation of modes in a basis mutually unbiased with respect to the OAM basis (also known as the angular basis). This enables the measurements in two mutual unbiased bases, thus its application in various quantum applications such as high-dimensional quantum key distribution (QKD) [80].

In the first entanglement experiment involving the OAM mode sorter, this device was used in reverse to convert a high-dimensionally entangled two-photon state encoded in the path degree of freedom to one entangled in the OAM degree of freedom [38]. It not only showed the reversibility of the sorter at the single-photon level, but also demonstrated its ability to act as a high-dimensional interface between the path and OAM degrees of freedom. The motivation is that in the path degree of freedom, it is known how to perform arbitrary unitary transformations [81–83]. The first experiment exploiting this feature has shown the multiplication of the OAM value by an arbitrary constant integer [84]. It is unknown whether such a transformation can be realized without leaving the OAM space.

7. Quantum cryptography with twisted photons

Photons carrying OAM have a natural application as carriers of quantum information, as they live in a discrete and theoretically unbounded state space. There are two primary advantages of using such a high-dimensional encoding scheme in quantum communication. First, the large state space offered by OAM allows one to send a vastly increased amount of information per photon when compared with other encoding schemes such as polarization. The second, slightly more subtle advantage is found in an increased resistance to errors in QKD [85]. The larger the dimension of the state space, the greater the probability that an eavesdropper will introduce errors in such a communication protocol [86]. Security against individual eavesdropping attacks is also increased slightly when using the full set of mutually unbiased bases (MUBs) available in a high-dimensional space [87], albeit at a reduced key rate. A recent study developed security proofs against coherent attacks on such protocols, taking into account finite-key effects [88].

Similar to polarization-based protocols, OAM-based QKD can be carried out as a prepare-and-measure [89] scheme, or an entanglement-based [90] scheme. The first proof-of-principle experiment demonstrating QKD with OAM was performed with OAM-entangled qutrits in 2006 [91]. Entangled photons were generated in a type-I BBO crystal and sent to two probabilistic mode analysers, which consisted of beam splitters, mode-selection holograms and single-mode fibres. A trinary key was generated by looking for coincident detections between the two analysers, while security was demonstrated by violating a three-dimensional Bell-like inequality [31]. A recent experiment used SLMs to extend this protocol up to d = 5, while also using the full set of d + 1 MUBs [92]. A key component of any practical QKD system is the ability to perform multi-outcome measurements, such as those performed by a polarizing beam splitter. The development of the OAM mode sorter [77,78] opened the door to such protocols, leading to a demonstration of an OAM-based BB84 protocol in 2015 (figure 4a) [80]. In addition to multi-outcome measurements, the experiment used a digital micro-mirror device to encode OAM modes at a rate of 4 kHz [94], which is two orders of magnitude higher than that possible with SLMs. An OAM-entanglement-based protocol with multi-outcome measurements is yet to be performed.

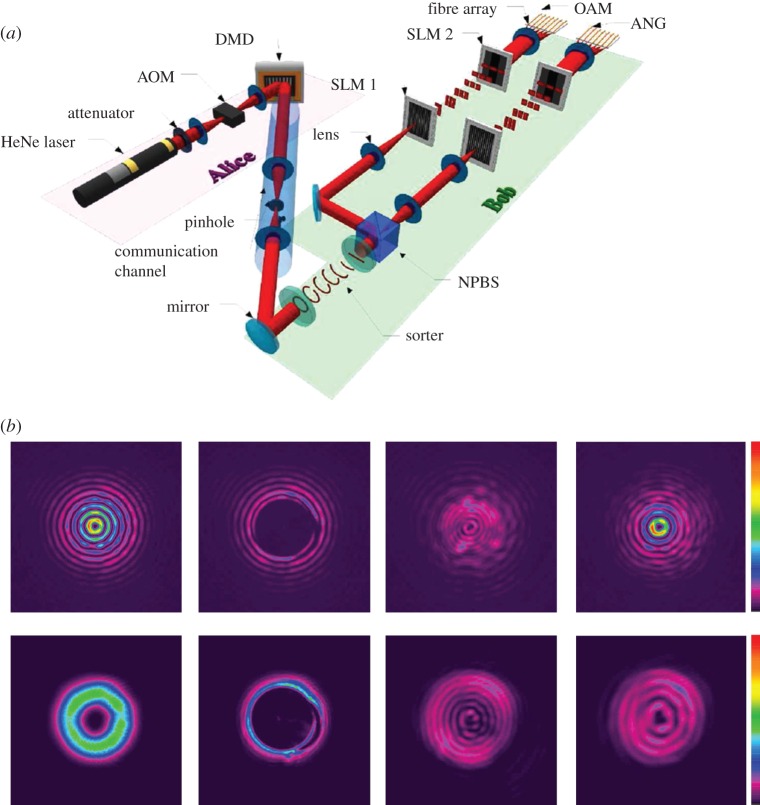
Figure 4.

(a) A high-dimensional BB84 QKD experiment has been implemented in [80]. It uses a digital micro-mirror device (DMD) for very fast encoding of spatial modes, and multi-outcome measurements in two mutual unbiased bases (OAM and angular modes) (adapted from [80]). (b) The self-healing character of Bessel modes, which might be useful for long-distance entanglement experiments and QKD. The upper row shows Bessel modes (with non-zero OAM), and the lower one Laguerre–Gauss modes. The second and third images show the beam after an obstruction and after 2 cm of propagation. Interestingly, in the last image after 5 cm of propagation, the Bessel mode reappears while the Laguerre–Gauss mode has not resumed its original structure. The self-healing property has been demonstrated for entanglement in [93] (adapted from [93]). (Online version in colour.)

8. Long-distance transmission of orbital angular momentum

In addition to efficient generation and detection, the transmission over large distances of photons carrying OAM is necessary for any practical OAM-based quantum communication protocol. This is also important for loophole-free demonstration of all-versus-nothing violations of local realism [95], which require large spatial separation of the photons. One can take two approaches to transmit photonic OAM over such macroscopic distances: in free space or through fibre. In a 2012 experiment, one photon from a pair of spatially entangled photons was transmitted through a 30 cm long hollow-core photonic crystal fibre. A Bell inequality was used to confirm two-dimensional spatial-mode entanglement after the transport (figure 5a) [96]. In a 2013 experiment, three lowest order OAM modes (−1, 0, and +1) carried by a laser beam were sent through 1.1 km of a specially designed fibre [98]. However, these types of fibres have not been exploited in quantum experiments yet.

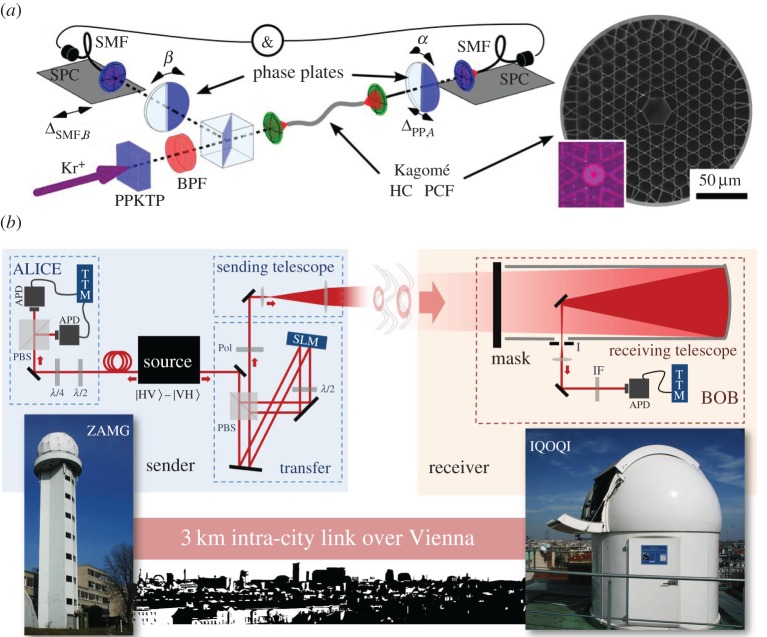
Figure 5.

Long-distance quantum communication can be done in two different ways. (a) An experiment which distributes OAM entanglement via a photonic crystal fibre [96], with subsequent measurement of a Bell inequality using sector plates. While the fibre was only 30 cm long, the experiment clearly shows that entanglement can in principle be coupled into and transported via fibres (adapted from [96]). An alternative method is the free-space transmission of OAM modes. A 3 km turbulent intra-city link has been shown to support the distribution of entanglement encoded in the first two higher-order modes [97]. In this experiment, a polarization-entangled pair of photons was created, where one of the photons was measured in polarization. The polarization information of the second photon was transferred to OAM and transmitted over 3 km, and measured using the infront of a telescope (adapted from [97]). (Online version in colour.)

Extensive research has been conducted on the topic of free-space transmission of OAM quanta and OAM entanglement through turbulence, including several theoretical [99–101] and laboratory-scale simulations [102–104]. These studies have predicted that the mode quality would deteriorate rapidly in turbulent atmosphere, leading to a drastic effect on OAM entanglement. Only two experiments involving single or entangled photons carrying OAM have been performed over large distances. The first experiment transmitted weak coherent laser pulses over a distance of 210 m, and used them to perform a two-dimensional BB84 quantum cryptography protocol [105]. That experiment was performed in a large hall in Padua in order to minimize the detrimental effect of atmospheric turbulence. A second experiment transmitted two-dimensional OAM entanglement over an outdoor intra-city environment of 3 km in Vienna (figure 5b) [97]. Because of sunlight and the necessity to identify individual photons, the experiment was performed during the night. An interesting method, which could improve long-distance distributions of OAM entanglement, is the application of self-healing Bessel beams. Entanglement directly after an obstruction has been shown to be destroyed; however, after some propagation distance, it is self-healed and can be detected again (figure 4b) [93].

9. Manipulating atoms with orbital angular momentum

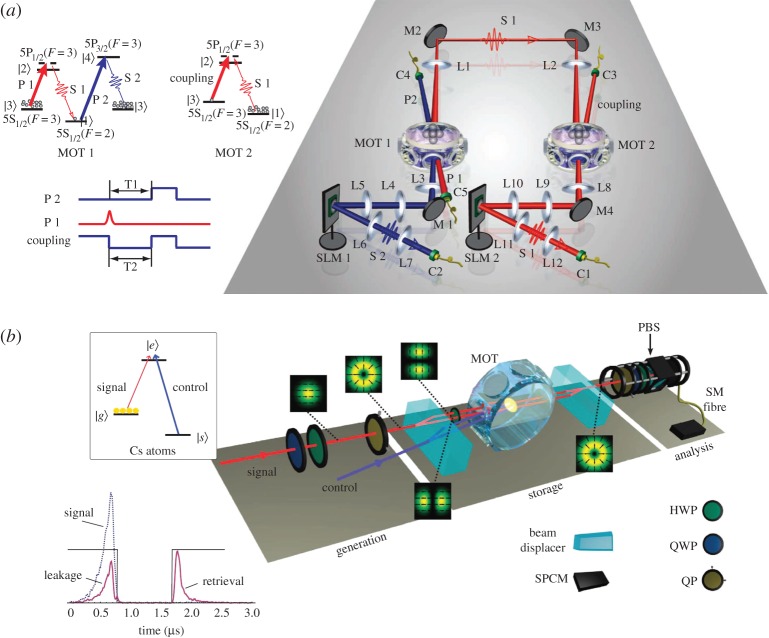
The prospect of coupling the OAM carried by single photons or pairs of OAM-entangled photons to quantum states of matter remains a tantalizing one. The first step in this direction was taken in 2006, when a laser beam carrying OAM was used to generate atomic vortex states in a sodium Bose–Einstein condensate (BEC) via the process of stimulated Raman scattering (SRS) [106]. Interference between the different resulting vortex states demonstrated the coherent superposition of OAM modes in the BEC. In the same year, an experiment demonstrated the creation of two-dimensional OAM entanglement between an ensemble of cold rubidium-87 atoms and a single photon [107]. A ‘write’ laser pulse excited an atomic transition in the cloud, emitting an anti-Stokes photon entangled with the atom cloud. After a storage time of 100 ns, a ‘read’ laser pulse mapped the atomic transition back into a Stokes photon, which was shown to be OAM-entangled with the anti-Stokes photon. This constituted the first demonstration of a read-only memory for OAM based on the SRS process, and was extended to three-dimensional atom--photon entanglement a few years later [108]. More recently, the same scheme was expanded upon to demonstrate the storage of high-dimensional OAM entanglement between two spatially separated atomic clouds (figure 6a) [109,111]. An alternative method involves the storage of high-dimensional quantum entanglement in a rare earth crystal [112]. A three-dimensional Bell inequality was violated after a storage time of 20 µs, with OAM values of up to ℓ = 25. Another recent experiment demonstrated the writing, storage, and read-out of single photons and weak coherent pulses carrying OAM modes via electromagnetically induced transparency in a cloud of cold rubidium with a storage time of approximately 400 ns [113] and caesium atoms with a storage time of approximately 1 µs [114]. The latter experiment has been extended in order to store both the polarization and OAM information of the photon (figure 6b) [110]. The photons were retrieved with a high fidelity, demonstrating this technique's potential in quantum information schemes. In addition to manipulating atomic excitations, there have been a series of theoretical proposals for exciting quadrupole transitions in ions with light carrying OAM [115,116], as well one recent experimental demonstration [117].

Figure 6.

Quantum memories for spatial modes. (a) A quantum memory for high-dimensional entangled states spatially separated by 1 m [109]. On the left side, one sees the energy-level diagram of ⁸⁵Rb, as well as the time sequence for creating and storing entanglement in it. On the right is a sketch of the experimental set-up with two distant magneto-optical traps (MOTs) between which entanglement is generated (adapted from [109]). (b) A quantum memory which can store both the polarization as well as the spatial-mode information of photons is shown. The photons are stored in a cloud of caesium atoms, and the storage time is roughly 1 µs (adapted from [110]). (Online version in colour.)

10. Multi-photon experiments with orbital angular momentum

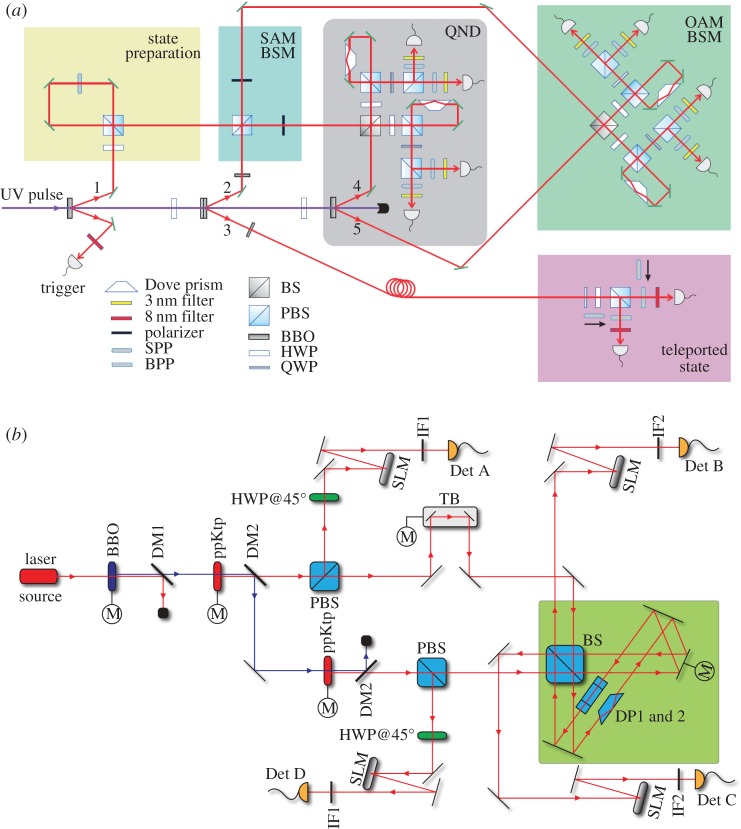
Over the last 2 years, experiments with OAM entanglement have ventured into the challenging multi-photon regime. The first such experiment teleported a photon in a hybrid four-dimensional OAM-polarization state space using three entangled photon pairs (figure 7a) [118]. In order to do so, the experiment implemented a unique feature—a quantum non-demolition (QND) measurement that heralded the presence of a photon without destroying it. In order to teleport a qubit, one needs to perform a so-called Bell-state measurement (BSM) on it, which involves projecting it into an entangled state with another qubit. In that experiment, two consecutive BSMs in the polarization and OAM state spaces were cascaded. However, for the second BSM to work, it was essential that each photon from the first BSM arrived in a different path. The QND measurement ensured that a photon was indeed on its way, and interestingly was itself implemented by quantum teleportation. In this manner, the authors were able to project into two hyper-entangled Bell states with an efficiency of 1/32, allowing them to teleport an OAM-polarization ququart with fidelities ranging from 0.57 to 0.68.

Figure 7.

Multi-photon quantum experiments involving OAM. In (a), an experiment is shown where two properties of a photon (the polarization and the parity of an ℓ = ±1 spatial mode) are teleported simultaneously. It is possible by a quantum non-demolition measurement, which curiously is implemented itself as a quantum teleportation scheme. For this, six photons are required to teleport the (2 × 2)-dimensional quantum state (adapted from [118]). In (b), an experiment is shown which creates a genuine multi-partite high-dimensional entangled state. Similarly to multi-photon polarization experiments, the which-crystal information is erased by an interferometer that sorts even and odd OAM modes. The resulting state has an asymmetric entanglement structure—a feature that can only exist when both the number of particles and the number of dimensions are larger than 2 (adapted from [75]). (Online version in colour.)

The next two experiments explored the creation of the first multi-photon entangled states of OAM. In one experiment, a nonlinear crystal was pumped with a strong laser in order to produce two OAM-entangled photon pairs. The four photons were then probabilistically split with beam splitters, which resulted in a four-photon Dicke state entangled in two dimensions [119]. In order to create specific multi-photon entangled states such as a Greenberger–Horne–Zeilinger state, one can combine two pairs of entangled photons in such a manner that the which-crystal information for one or more photons is erased, leading to a four-photon entangled state [120]. A recent experiment used the interferometric OAM beam splitter discussed above to combine OAM-entangled pairs from two different crystals in this manner (figure 7b) [75]. This device mixed the odd and even OAM components of the input photons, projecting them into a high-dimensional multi-photon OAM-entangled state given by 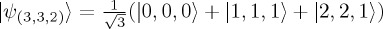. Interestingly, the state was asymmetrically entangled—two photons were in a three-dimensional OAM space and a third lived in two dimensions. This state is just one example out of a vast family of multi-partite entangled states that are only possible when both the dimension and the number of particles are greater than two [121]. Experimental methods for creating many of these states were recently found by using a computer algorithm that combined optical components and analysed the resulting state [122]. An interesting question that remains is how such novel types of entanglement can be used in quantum applications or fundamental tests.

11. Outlook

Many interesting questions on the OAM of photons are yet to be answered and several exciting avenues for future research can be identified.

One of them is whether high-dimensionally entangled states can be transmitted over large, multi-kilometre distances. This is necessary for any practical implementation of quantum communication protocols with OAM and could be useful in fundamental studies of local realism. While classical OAM beams have been transmitted over 1 km in fibre [98] and over 143 km in free space [123], similar distances are yet to be achieved at the quantum level.

One significant motivation to investigate photonic OAM is its potential advantage in quantum cryptography. An important step into that direction would be a full implementation of an entanglement-based QKD protocol, involving two parties separated by a large distance. These parties would share pairs of high-dimensionally entangled photons and perform multi-outcome measurements on them. A detailed analysis of QKD implemented with OAM of photons is necessary to understand how the high-dimensional alphabet can be fully exploited to finally outperform polarization-based QKD in terms of secure key-rate.

The investigation of the advantages offered by quantum computation with higher-level alphabets is another interesting avenue. A recent theoretical study has shown how to use ternary systems to employ the Shor algorithm, both by extending the algorithm to three dimensions, and by encoding two-dimensional quantum information in a three-dimensional system [124]. That study found several advantages compared with binary quantum architectures, such as more robust encoding of quantum information. Further analysis in high-dimensional quantum circuit designs, in particular the advantages and challenges compared with binary quantum circuits, would be desirable. We hope that the work reviewed here provides additional motivation for investigating possible applications of the high-dimensional degree of freedom in quantum computing.

Another intriguing question is how the non-local information encoded in photons (such as entanglement dimensionality and ebits) can be increased and verified in state-independent ways. Research in this direction might explore the combination of high-dimensional entanglement in frequency and spatial modes to use the full potential of space and time encoding. The investigation on whether a fundamental limit of non-locally shared information could exist would certainly be interesting. A related question is whether such a fundamental limit could exist for two-dimensionally entangled pairs with very high OAM values, and whether general relativistic effects would play a role in this scenario [125].

Quantum systems on a new level of complexity are accessible with multi-dimensional, multi-partite, multi-degree-of-freedom entangled states and could show interesting properties and possibilities not present in simpler systems. For that, both theoretical methods to quantify the complexity as well as experimentally feasible methods for generating such states will be necessary. In this respect, new types of transformations and interfaces between different degrees of freedom seem desirable for the implementation of various quantum protocols.

Coupling between high-dimensional entangled photons and matter could show interesting new physical insights. For example, the transfer or manipulation of photonic OAM to single quasi-particles such as polarons or plasmons would be intriguing. For this, nanophotonics and light–matter interactions with OAM of light [126,127] need further investigation at the quantum level.

While advances in technology, combined with important theoretical developments, have steadily pushed the limits of quantum optics research in the field of OAM, many striking directions remain to be explored. It is expected that research over the next few years will give new answers to several of the questions raised, and—hopefully—will ask new exciting ones on the physical and technical properties of individual photons carrying quanta of angular momentum.

Authors' contributions

All authors contributed to the work.

Competing interests

There are no competing interests.

Funding

This work was supported by the Austrian Academy of Sciences (ÖAW), by the European Research Council (SIQS grant no. 600645 EU-FP7-ICT) and the Austrian Science Fund (FWF) with SFB F40 (FOQUS).