Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2017 Jan 20;7:40985. doi: 10.1038/srep40985

Effect of myocyte-fibroblast coupling on the onset of pathological dynamics in a model of ventricular tissue

S Sridhar 1,a, Nele Vandersickel 1, Alexander V Panfilov 1,2,b
PMCID: PMC5247688  PMID: 28106124

Abstract

Managing lethal cardiac arrhythmias is one of the biggest challenges in modern cardiology, and hence it is very important to understand the factors underlying such arrhythmias. While early afterdepolarizations (EAD) of cardiac cells is known to be one such arrhythmogenic factor, the mechanisms underlying the emergence of tissue level arrhythmias from cellular level EADs is not fully understood. Another known arrhythmogenic condition is fibrosis of cardiac tissue that occurs both due to aging and in many types of heart diseases. In this paper we describe the results of a systematic in-silico study, using the TNNP model of human cardiac cells and MacCannell model for (myo)fibroblasts, on the possible effects of diffuse fibrosis on arrhythmias occurring via EADs. We find that depending on the resting potential of fibroblasts (VFR), M-F coupling can either increase or decrease the region of parameters showing EADs. Fibrosis increases the probability of occurrence of arrhythmias after a single focal stimulation and this effect increases with the strength of the M-F coupling. While in our simulations, arrhythmias occur due to fibrosis induced ectopic activity, we do not observe any specific fibrotic pattern that promotes the occurrence of these ectopic sources.

Mechanical contraction of the heart is preceded by the propagation of electrical waves of excitation. Under pathological conditions, regular wave propagation can breakdown creating reentrant or chaotic patterns of electrical activity1 known as arrhythmias. Such arrhythmias manifest as assynchronous or irregular contraction of the heart muscles which, if untreated, can result in the cessation of blood flow followed by sudden cardiac death2. In fact, cardiac arrhythmias are one of the leading killers in the industrialised world3. While our understanding of the mechanisms underlying the onset of arrhythmia remain incomplete, several physiological factors that increase the vulnerability of cardiac tissue to arrhythmia have been identified4,5. One of them is the presence of abnormal action potentials in cardiac cells called early afterdepolarizations (EADs)6, which is essentially the reversal of the action potential before complete cellular repolarization. EADs have been observed in cases of heart failure7, long QT syndrome8 and are also induced under the action of pharmacological drugs9 or conditions of oxidative stress10,11. Even though there has been significant improvement in our understanding since the earliest observations of EADs nearly half century ago12, there still remain several unanswered questions about the mechanisms linking EADs and arrhythmias. EADs occur in cells whose ability to completely repolarize is significantly reduced. This can happen when the net outward current required to repolarize the cardiac cell is not sufficient, either due to an excess of inward current or reduced outward current or both. Thus, at the level of the cell the occurrence of EAD is linked with ionic conductances and gating variables. At the tissue level, the generation of EADs has been shown to be a chaotic process that synchronizes spatially to produce waves that can overcome source-sink mismatches6.

Another well established arrhythmogenic condition is fibrosis of cardiac tissue that occurs as a result of proliferation of fibroblasts. Fibroblasts and myocytes are the two major cell types in mammalian heart muscle tissue, with the former outnumbering the latter even while occupying a much smaller volume of the heart13. While myocytes are functionally responsible for the cardiac electrical action, the role of fibroblasts pertain to maintaining the structural and electro-mechanical integrity of the heart13 and repair post-injury or disease14. In the normal heart, fibroblasts are much smaller than the myocytes and do not influence the electrophysiology of the myocytes. However, in aged hearts, and in many forms of heart diseases the number of fibroblasts can substantially increase (up to 40%)15. Further, in injured hearts fibroblasts may differentiate into much larger myofibroblasts. Fibrosis may substantially affect wave propagation in the heart and it is well established that fibrosis creates a substrate for the initiation of ventricular and atrial arrhythmias16,17. Several studies have reported the existence of heterocellular gap junctions between fibroblasts and myocytes18,19,20. Although the exact nature of myocyte-fibroblast coupling in vivo is still controversial14, there is substantial evidence for the existence of gap-junctional coupling between myocytes and fibroblasts in vitro under both physiological and pathological conditions21. Both experiments and simulation studies have shown that coupling between myocytes and fibroblasts significantly alter conduction properties of the cardiac tissue18,22 and myocyte excitability23, induce automaticity20, modify action potential duration (APD)24,25, and depolarize the resting membrane potential19,24 of myocytes.

Recently, there has been much interest in understanding the proarrhythmic tendencies of fibrosis, especially through its effect on afterdepolarization26. These afterpotentials can result in triggered activity causing fibrillation in both the atria27 and the ventricles28,29. Computational studies have shown that at intermediate ranges of coupling between myocytes and fibroblasts EADs can induce ectopic activity30 and the possibility of increased ectopic activity in fibrosis has been connected to source-sink mismatch31. EAD formation in rabbit myocytes was shown to be promoted by myocyte fibroblast coupling in a dynamic patch clamp experiment32. A recent paper33 studied the effect of regional heterogeneity and fibroblast-myocyte coupling on the onset of ectopic activity using a model of human heart tissue. The authors described the effect of fibroblast distribution and the coupling strength on ectopic activity for the case where fibroblasts are randomly attached to myocytes. All the papers referred to above provide excellent examples of research performed for particular physiological conditions and at the levels of organization such as a single cell, a small patch of cardiac tissue etc. Generally numerical studies are performed for limited parameter sets (usually two or more). Further, in most of the in-silico examples given above fibroblasts have been considered to be either an inexcitable obstacle or a “passive” RC circuit30,31,33. However, recent patch-clamp experiments have identified the presence of inward rectifying potassium (Kir), time and voltage gated potassium currents (Kiv) in ventricular fibroblasts34,35. The aim of our study is therefore to perform a detailed in-silico study of the effect of fibrosis on EAD related arrhythmias using a human ventricular cell model (TNNP-TP06)36,37 coupled with a state-of-the-art fibroblast model expressing Kir and Kiv currents, viz. MacCannell “active” fibroblasts25. While “active” fibroblast models have been used to study the onset of EADs in single cells32 and loading effect on myocytes24, to the best of our knowledge our work is the first to describe the effect of inserted “active” fibroblasts on the spatiotemporal dynamics in a 2D medium. In our system the “active” fibroblasts act as heterogeneities in the local ionic properties of the 2D tissue. While electrotonic interaction between myocytes and randomly inserted passive fibroblasts have been shown to increase the vulnerability for reentrant arrhythmia38,39, in our study we describe the effect of such M-F coupling on the onset of EAD induced focal arrhythmia. We perform a comprehensive study over a wide range of myocyte and fibroblast parameters and describe excitation patterns with EAD and fibrillatory wave dynamics similar to those identified in the absence of fibrosis by Vandersickel et al.40. We also study the effect of M-F coupling (by varying parameters such as coupling strength, fibroblast capacitance and resting membrane potential) on the excitation patterns and the likelihood of their occurrence. We find that depending on the value of the fibroblast resting potential, the coupling can have opposite effects on the myocyte dynamics: A less negative fibroblast resting membrane potential promotes EADs, while a more negative value of resting membrane potential suppresses such EADs. However it should be noted that the M-F coupling does not change the type of spatial EAD patterns. More importantly, irrespective of the parameter values M-F coupling always promotes the occurrence of pathological dynamics such as spiral wave fibrillation.

Methods

We will first describe the cell models and the parameter regimes that are considered in this paper. To describe the ionic activity of a myocyte we use the TNNP-TP06 model of human ventricular cell36,37. The time variation of the transmembrane voltage V for myocytes is given as,

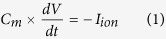graphic file with name srep40985-m1.jpg

Here Cm is the cell capacitance per unit surface area and Iion is the sum of all ionic currents:

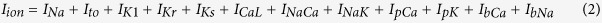graphic file with name srep40985-m2.jpg

where INa is the Sodium current, Ito is the transient outward current, IK1, IKr and IKs are the inward rectifier, delayed rectifier and slow delayed rectifier Potassium currents, ICaL is the L-type Ca2+ current, INaK is the Na+/K+ pump current, INaCa is the Na+/Ca2+ exchanger current, IpCa and IpK plateau Calcium and Potassium currents and IbCa and IbNa are the background Na+ and Ca2+ currents. To obtain EADs we have made a few modifications to the L-type Calcium current ICaL as suggested in literature40,41. Specifically, the time constant of the f-gate of the L-type Calcium current (τf) was reduced by half40,41, resulting in some shortening of the action potential. In order to compensate for this reduction, the value of conductance of the Calcium (GCaL) is increased by a factor of two40. In order to draw two-parameter phase portraits we vary ICaL and IKr in myocytes by changing the maximal conductances of GCaL and GKr respectively, since these currents are known to be responsible for the onset of EADs41,42. The electrophysiological properties for the fibroblasts are described using the MacCannell “active” fibroblast model25. The ionic currents in this model include the time- and voltage -dependent Potassium currents IfKv, inward rectifying Potassium current IfK1, IfNaK a Sodium-Potassium pump current and a background Sodium current IbNa+. The uncoupled resting membrane potential for this model is −49.6 mV. In our study we use two sets of values for the fibroblast properties to simulate “fibroblasts” and “myofibroblasts” respectively as suggested in literature25,32,34. For “fibroblasts”, we use a cell capacitance CF = 6.3 pF and for the larger myofibroblasts, we use a cell capacitance of CF = 50 pF. The values of fibroblast resting membrane potentials used are VFR = −49.7 mV and VFR = −24.5 mV. Different resting membrane potentials were obtained by shifting the gating variable voltage dependence of the time dependent Potassium current24. For the gap junctional coupling (Gs), we have chosen values falling in the range that are considered to be representative of the effect of fibroblasts in cell-cultures24. The values used for the simulations in the paper are listed in Table. 1.

Table 1. In this table, we list the values for the fibroblast parameters, viz., capacitance (C), resting membrane potential (V FR ) and coupling strength (Gs) used for the results described in the paper.

Dimension C (pF) VFR (mV) Gs (nS)
0D 6.3, 50.0 −49.7, −24.5 0–3
2D 6.3, 50.0 −49.7, −24.5 0.5, 2.0, 4.0
Open in a new tab

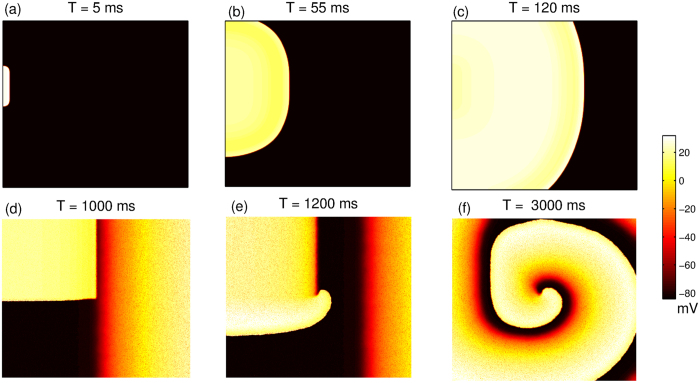
For the single cell simulations, the computation is performed using the forward Euler scheme with time- step 0.02 ms. The single cell is stimulated every 500 ms by a stimulus of strength 20 μA/mm2 applied for 2 ms. The 2D simulations have been carried out on a monodomain isotropic cardiac tissue with the systems discretized on a square lattice of size L × L where L = 1024. Each grid point corresponds to a group of myocytes or a cluster of N fibroblasts, where N = 5 for all results described here. In order to take into account the different sizes of the fibroblast and myocytes we assume that there is only a gap-junctional coupling and no diffusive coupling between myocytes and fibroblasts. Further, we assume that there is no gap-junctional coupling between fibroblasts. The differential equations are solved using the forward Euler scheme, the standard five-point stencil is used for the Laplacian and no-flux conditions are implemented at the edges of the system domain. The value of diffusion constant used is D = 0.00154 cm2/ms, and the space- and time- step are 0.25 mm and 0.02 ms respectively. The fibroblasts are distributed randomly as their locations are chosen from a uniform distribution (Supplementary Fig. S1). While most of the results shown here are for one particular distribution with 30% of the lattice points occupied by fibroblasts, we have verified that our results are qualitatively similar for different distributions of the same fraction of fibroblasts. We have also performed simulations where 10% and 20% of the lattice points are filled with fibroblasts. We have used two types of initial conditions generated by two different protocols as suggested in Vandersickel et al.40. For protocol P1, a stimulus of strength 20 μA/mm2 is applied for a period of 2 ms over a region of size 6 × 200 from a position slightly off center of the simulation domain. In Fig. 1(a–c) we describe this stimulation protocol using a system of size 512 × 512. This protocol mimics the condition that could lead to the origin of arrhythmia via the initial formation of a reentrant wave. Note that for the case of P1 stimulation, the initial condition for the myocytes is obtained by fixing xGKr = 1 and yGCaL = 1 and sending 50 waves at 1 Hz frequency in a 2D tissue without fibroblasts The results shown here are for the dynamics of the single wave in a medium where fibroblasts are interspersed with myocytes having this initial condition. For protocol P2, the initial condition is a spiral wave obtained by using S1−S2 stimulation as shown in Fig. 1(d–f). Stimulus S1 is used to set off a plane wave that propagates from one edge of the domain to the other. Once this wave has passed over the half of the domain, the second stimulus S2 is applied over the first quarter of the domain thereby producing a wavefront that evolves into a spiral. The aim of this protocol is to study the effect of M-F coupling on the transition from tachycardia (single spiral) to fibrillation (multiple spirals).

Figure 1.

Figure 1

Open in a new tab

Pseudocolor image of the transmembrane potential V for the two-dimensional system of size 512 × 512 describing protocols P1: Initiating a wavefront from a position slightly off the center of the simulation domain (a–c) and P2: Creating a spiral wave via S1–S2 stimulation (d–f). Once S1 wave propagates over half the domain, the first quarter of the domain is stimulated (d), creating a curved wavefront (e) that slowly evolves into a complete spiral wave of excitation (f).

Results

Single cell coupled to fibroblasts

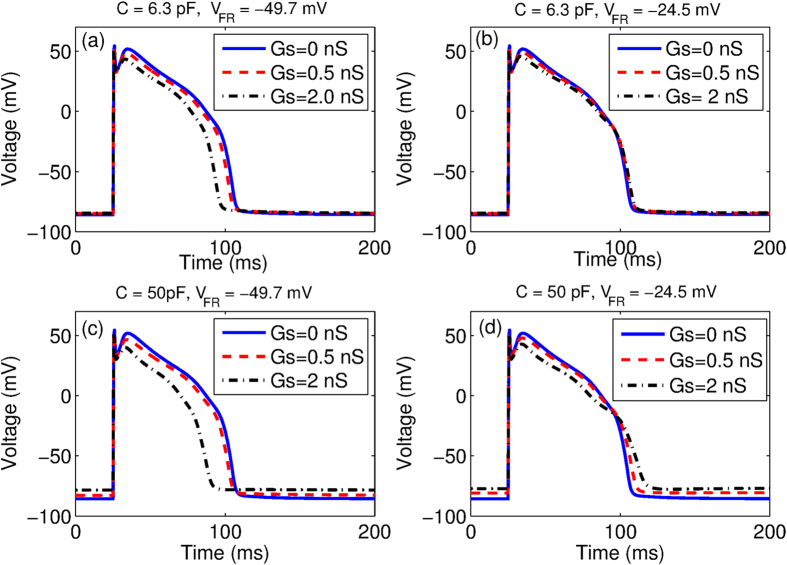
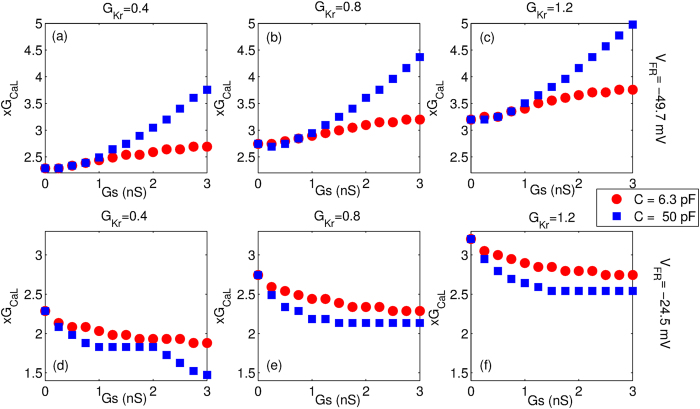
To understand the effect of M-F coupling on myocyte dynamics we first compare the single cell action potential in the presence and absence of coupling as shown in Fig. 2. The parameters are chosen so that in the absence of fibroblast coupling, no EADs are observed. We observe that for the case where VFR = −49.7 mV, the coupling leads to faster repolarization and hence reduction in action potential duration for both fibroblasts (Fig. 2(a)) and myofibroblasts (Fig. 2(c)). For VFR = −24.5 mV the M-F coupling leads to a larger increase in APD of the myocyte when coupled to “myofibroblasts” (Fig. 2(d)) than when coupled to “fibroblasts” (Fig. 2(b)). Further, coupling with “myofibroblasts” leads to a greater depolarization of the resting membrane potential especially at large values of Gs (Fig. 2(c and d)), than when connected with “fibroblasts” (Fig. 2(a and b)). Supplementary Fig. S2 shows the effect of MF coupling for the case of a myocyte that describes an EAD even in the absence of coupling. In Fig. 3, we plot the value of x GCaL at which the transition from the NO EAD to EAD state occurs as we vary the strength of the gap-junctional coupling (Gs) for yGKr = 0.4, 0.8 and 1.2 respectively. Note that x and y are the multiplicative factors of the maximal conductances for ICaL and IKr respectively. Depending on the resting membrane potential of the fibroblast (VFR), the transition boundary either shifts towards higher (Fig. 3(a–c)) or lower values of GCaL (Fig. 3(d–f)), with increase in the M-F coupling strength (Gs). For a given value VFR, the magnitude of the shift in boundary is larger for the case of coupling with “myofibroblasts” compared to coupling with “fibroblasts”. However the direction of the shift does not depend on whether the myocyte is coupled to “fibroblasts” or “myofibroblasts”. All the possible dynamical states that occur due to the M-F coupling are described using two-parameter phase portraits (see Supplementary Fig. S3).

Figure 2.

Figure 2

Open in a new tab

The effect of M-F coupling on single cell action potential, for Gs  = 0 nS (solid line), Gs  = 0.5 nS (broken line) and Gs  = 2.0 nS (dot-dash) for fibroblasts (a,b) and myofibroblasts(c,d) using resting membrane potentials VFR = −49.7 mV for (a and c) VFR = −24.5 mV for (b and d). Myocyte parameters used (xGCaL = 3 and yGKr = 0.75) do not produce EADs in the absence of coupling.

Figure 3.

Figure 3

Open in a new tab

The value of parameter xGCaL at which the transition from NO EAD to EAD state occurs is plotted as a function of the strength of M-F coupling for values of yGKr = 0.4 (a,d), 0.8 (b,e) and 1.2 (c,f) respectively for C = 6.3 pF (circles) and C = 50 pF (square). Panels (a–c) correspond to resting membrane potential VFR = −49.7 mV, while panels (d–f) correspond to the case when VFR = −24.5 mV.

Effect of fibroblasts in two-dimensional wave propagation

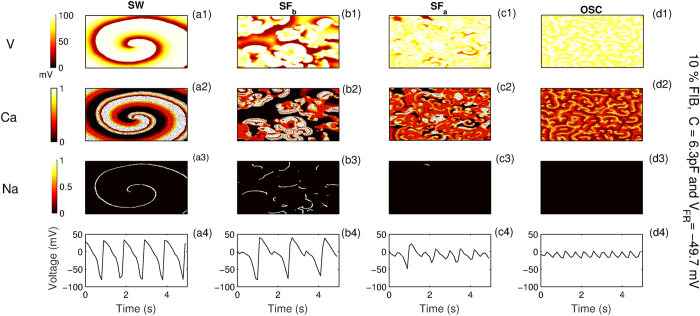
We next illustrate the effect of both “fibroblasts” and “myofibroblasts” on wave propagation in a 2D tissue. For this we consider two representative cases namely Fibroblast-1 (fibroblasts) with C = 6.3 pF and VFR = −49.7 mV and Fibroblast-2 (myofibroblasts) with C = 50 pF and VFR = −24.5 mV. Since the effect of coupling in single cells (Fig. 3) is observed to be more pronounced for the case of myofibroblasts (C = 50 pF) than for fibroblasts (C = 6.3 pF), we expect that the results for myofibroblasts (C = 50 pF) with VFR = −49.7 mV would be more pronounced than for the case with Fibroblast-1 (C = 6.3 pF and VFR = −49.7 mV). Similarly we expect that the results corresponding to the case of fibroblasts (C = 6.3 pF) with VFR = −24.5 mV would be less pronounced than the case of Fibroblast-2 (C = 50 pF and VFR = −24.5 mV). To study the spatial manifestation of the various dynamical states observed for a single cell, we use two different stimulation protocols. For protocol P1 a single wave is initiated from the boundary, while for the second case (P2) a spiral wave is created via the standard S1-S2 protocol. For both cases the dynamics of the wave interacting with fibroblasts is characterized by systematically varying the maximal conductances GKr and GCaL. In Fig. 4, we classify the different dynamical states obtained due to myocyte fibroblast interaction for stimulation protocol P2. These are spiral wave (SW), fibrillation mediated via Sodium waves (SFb), fibrillation via Calcium waves (SFa) and phase waves corresponding to the state where the cells continue to oscillate instead of repolarizing (OSC). The columns (a - d) in Fig. 4 correspond to the different dynamical states and rows (1−3) the pseudocolor plots for the voltage and the states of Calcium and Sodium channel gates respectively. The characteristic voltage time series for each dynamical state is shown in row (4).

Figure 4.

Figure 4

Open in a new tab

Characterizing the different possible dynamical states and their corresponding time series, due to M-F coupling for stimulation P2. The columns correspond to spiral wave (SW), spiral fibrillation (SFb and SFa) and oscillatory dynamics respectively. The rows correspond to voltage, state of L-type Ca gates (=dff2fCass) and Na gates (=m3hj) respectively. Fully open gates have a value of 1, while fully closed gates have value 0. Parameters used are yGKr = 0.2, Gs  = 0.5, with fibroblasts occupying 10% of the randomly chosen lattice points. The values of x (multiples of GCaL) are 2.25, 3.0, 3.5 and 4.75 for SW, SFa, SFb and OSC states respectively.

Below, we briefly describe the features of the dynamical patterns observed for the case of P2, namely SFa, SFb and OSC. While SFb and SFa are characterized by the existence of multiple spirals describing chaotic activity, the dominant ionic currents underlying the two are not the same. The patterns in the case of SFa are driven by L-type Calcium waves, while Sodium dominates the wave activity in SFb. This is evident from the spatial profile of the ionic gate dynamics and the time series in Fig. 4(b2-b4) (SFb) and Fig. 4(c2-c4) (SFa). For SFa we find that while there is significant Calcium gate dynamics (Fig. 4(c2)), there is hardly any Sodium gate activity (Fig. 4(c3)). Also the voltage time series (Fig. 4(c4)), shows that the cells do not repolarize completely, an indication that the activity is driven by by Calcium40,43. The patterns observed during SFb are driven by Sodium as observed from the spatial profile of the gate dynamics in Fig. 4(b3). Unlike in SFa, the cells repolarize completely (Fig. 4(b4)), indicating active Sodium channel dynamics. Finally, we also observe a state where all the cells are oscillating but because of synchronization seem to generate a wave like activity. Such waves have been identified to be a phase waves40, their dynamics being driven by Calcium. For protocol P1 instead of SW we have two other states (not explicitly shown) viz., NO EAD corresponding to the case where wave propagation occurs without oscillations in the action potential, and EAD, the state with the formation of an early afterdepolarization that propagates through the system but does not lead to any sustained electrical activity. For protocol P1, the state characterized by the existence of multiple spirals and excitation fragments (SF) includes both Sodium and Calcium mediated fibrillatory activity i.e., SFa and SFb. And finally as in protocol P2, OSC corresponds to the case where all cells are oscillating. Here the spatial activity observed is a phase wave and not a wave of excitation.

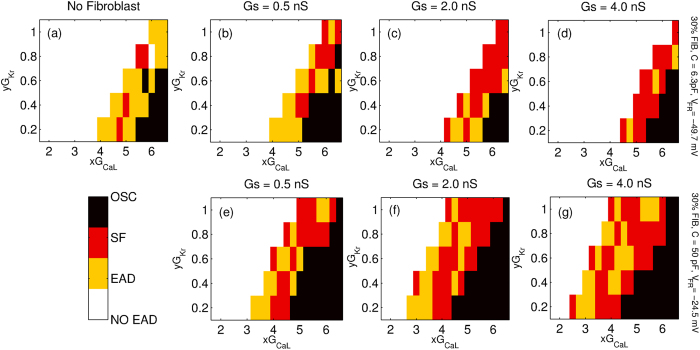
We first describe the effect of the strength of M-F coupling for protocol P2. In order to study the steady state dynamics we start with a spiral wave for the parameter xGCaL with x = 1.75 and slowly increase the value of x in steps of 0.25 every 4 s. Phase portrait Fig. 5 describes the various dynamical states obtained for different values of M-F coupling conductance (Gs = 0.5 nS, 2.0 nS and 4.0 nS) for both Fibroblast-1 (Fig. 5(b–d)) and Fibroblast-2 (Fig. 5(e–g)). For the sake of comparison, we have also plotted the case with no fibroblasts are present (Fig. 5(a)). The phase portrait in Fig. 5 shows that the type of fibroblast coupled to the myocyte determines the nature of the steady state dynamics. M-F coupling with Fibroblast-1 does not significantly change the region of the parameter observed with increasing coupling strength (see Supplementary Fig. S4(a)). On the other hand for the case of Fibroblast-2, we observe a significant shift of the spiral wave (SW) boundary to lower values of GCaL. We further observe that with increased coupling strength, more points turn SFa or oscillatory, while the region over which we get SFb dynamics shrinks (see Supplementary Fig. S4).

Figure 5. Two-parameter phase diagram of the steady state dynamics for a 2D system with 30% fibroblasts inserted randomly between myocytes and stimulated via protocol P2.

Figure 5

Open in a new tab

The x and y axis correspond to the factor by which GCaL and GKr are multiplied. The phase portraits are shown for three different coupling strengths Gs = 0.5 nS, 2.0 nS and 4.0 nS. While (a) corresponds to the case with no fibroblasts, (b–d) are portraits for Fibroblast-1(C = 6.3 pF, VFR = −49.7 mV) and (e–g) are phase diagrams for Fibroblast-2 (C = 50 pF and VFR = −24.5 mV). The colormap indicates the different dynamical states observed, viz. stable rotating spiral wave (SW), spiral fibrillation driven by sodium waves (SFb), spiral fibrillation driven by calcium waves (SFa) and fibrillation due to phase waves (OSC).

We next describe the effect of fibroblast coupling on the dynamics of the wave stimulated using protocol P1. Figure 6 describes the various dynamical states obtained for different values of M-F coupling conductance (Gs = 0.5 nS, 2.0 nS and 4.0 nS) for both Fibroblast-1 (Fig. 6(b–d)) and Fibroblast-2 (Fig. 6(e–g)). Again for the sake of comparison we have plotted the phase diagram for the case where no fibroblasts are present (Fig. 6(a)). Coupling with fibroblasts significantly alters wave propagation in the medium, the exact dynamics itself depending on the type of fibroblast. We observe that when compared to the case where there are no fibroblasts in the medium, coupling with Fibroblast-1 increases the parameter region over which no EADs or fibrillatory activity are observed. Further, with increase in coupling strength the number of cases that show early afterdepolarization but do not develop arrhythmic activity decreases (see Supplementary Fig. S5(a)). On the other hand, for the case of Fibroblast-2 we observe that the effect of the coupling is reversed, i.e., the M-F coupling promotes arrhythmic dynamics (Fig. 6(e–g)). The coupling induces EAD-mediated fibrillatory patterns even for values of GCaL and GKr that would not have displayed EADs in the absence of coupling.

Figure 6. Two-parameter phase diagram of the steady state dynamics for a 2D system with 30% fibroblasts inserted randomly between myocytes and stimulated via protocol P1.

Figure 6

Open in a new tab

The axes correspond to the factors by which GCaL and GKr are multiplied. The phase portraits are shown for three different coupling strengths Gs = 0.5 nS, 2.0 nS and 4.0 nS. While (a) corresponds to the case with no fibroblasts, (b–d) are portraits for Fibroblast-1(C  = 6.3 pF, VFR = −49.7 mV) while (e–g) are phase diagrams for Fibroblast-2 (C  = 50 pF and VFR = −24.5 mV). The colormap indicates the different dynamical states observed, viz. wave propagation without any oscillation in action potential (NO EAD), a propagating wave with oscillations in action potential but no persistent activity (EAD), spiral fibrillation consisting of many sources of activation (SF includes both SFb and SFa) and oscillatory fibrillation (OSC).

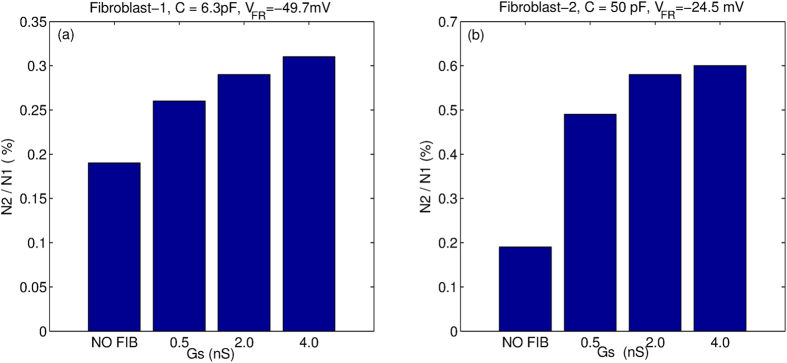
We next quantify the effect of M-F coupling in producing non-trivial pathological dynamical states such as spiral fibrillation (SFa and SFb) and oscillatory dynamics (OSC). For this we consider the ratio of the number of such states observed for both protocols (Fig. 7). N1 is the number of non-trivial pathological dynamical states obtained for stimulation protocol P2, while N2 is the number for protocol P1. We observe that while in general M-F coupling promotes the occurrence of spiral fibrillation or oscillatory dynamics (as measured by the ratio 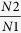Inline graphic), the effect for Fibroblast-2 (Fig. 7 (b)) is almost two times the effect of Fibroblast-1 (Fig. 7 (a)).

Figure 7. Effect of M-F coupling on the percentage of cases that result in non-trivial pathological dynamics (such as SFa or SFb or OSC) as a function of strength of coupling.

Figure 7

Open in a new tab

N1 and N2 are the number of non-trivial cases resulting from protocol P2 and P1 respectively. The results are shown for both Fibroblast-1 (a) and Fibroblast-2 (b).

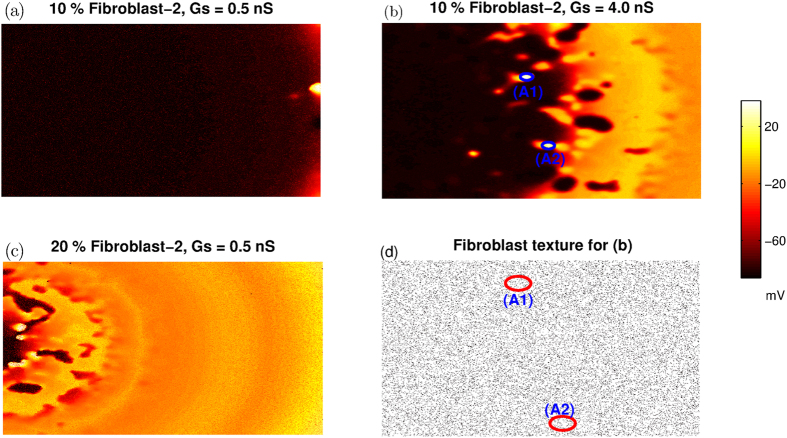
In order to confirm that the origin of fibrillation like patterns is indeed the effect of M-F coupling, we determine the location where additional waves are first induced for the case of protocol P1. We set yGKr = 0.4, and perform the simulations for 20 different values of xGCaL between 1.75 and 6.5. The results shown in Table. 2 are averaged over 40 simulation runs (two different realisations for each point) for the case of NO FIB. In the case of Fibroblast-1 inserted at 20% of the lattice points, the values shown are averaged over 80 simulation runs (i.e. over four different fibroblast distributions) for both Gs = 0.5 nS and Gs = 2 nS. For each of the three cases shown in Table. 2 we list the percentage of runs for which no additional depolarizing waves (other than P1) are formed in the medium (col-2), the fibrillatory pattern first occurs at the boundary (col-3) and ectopic activity is initiated away from the boundary (col-4). We observe that for the parameter value chosen here (xGKr = 0.4), the fibrillatory waves are mostly initiated at the boundary when fibroblasts are either absent or are weakly coupled (Gs = 0.5 nS) to the myocyte. However for larger coupling strengths, ectopic activity is mostly initiated at locations away from the boundary.Note that this table only lists the location of the first occurrence of ectopic activity for each simulation. The location of subsequent occurrences of ectopic activity are not considered. In Fig. 8 we show representative patterns of initiation of spiral wave activity in the presence of fibroblasts. For the case of 10% fibrosis with Fibroblast-2 (VFR = −24.5 mV and C = 50 pF), the reentrant activity (after the initial wave has passed through the medium) occurs at the boundary for small values of coupling (Gs  = 0.5 nS) (Fig. 8(a)). However for stronger coupling (Gs = 4 nS), fibrillatory activity is initiated in the middle of the simulation domain (Fig. 8(b)). We also observe that the location of the initiation of fibrillatory patterns depends on the fraction of fibroblasts present in the medium. While a lattice with 10% fibroblasts (Fibroblast-2) results in initiation at the boundary (Fig. 8 (a)), increasing the fraction to 20% leads to formation of wave activity away from the boundary (Fig. 8(c)). In order to associate the onset of ectopic activity to the underlying fibrotic texture, the spatial distribution of fibroblasts corresponding to Fig. 8(b) is plotted in Fig. 8(d). The circles are the locations in the tissue where ectopic beats first occurred for the case shown in Fig. 8(b). We observe that there is nothing specific about the distribution of fibroblasts at the location where the ectopic activity is initiated, implying that the onset of ectopic beats is not directly related to simple properties of fibrotic texture and needs to be studied further.

Table 2. In this table, we list the percentage of cases for the initial location at which additional waves first occur for the case of protocol P1.

Case No new waves (%) First new wave from boundary (%) First new wave from middle (%)
NO FIB 95 5 0
FIB-1, Gs = 0.5 nS 90 10 0
FIB-1, Gs = 2.0 nS 82.5 2.5 15
Open in a new tab

Rows correspond to different cases considered, viz., where there are no fibroblasts (row-1), for the case of 20% Fibroblast-1 (VFR = −49.7 mV and C = 6.3 pF) with Gs = 0.5 nS (row-2) and Gs = 2.0 nS (row-3). Simulations are performed by fixing yGKr = 0.4 and varying xGCaL values between 1.75 and 6.5 in steps of 0.25. The percentages are calculated over 40 (NO FIB) and 80 (Fibroblast-1) trials respectively.

Figure 8.

Figure 8

Open in a new tab

Pseudocolor images of transmembrane potential highlighting the location of initiation of reentrant activity for fibroblast fractions 10% (a,b) and 20% (c,d). For panels (a,b,d) Fibroblast-2 (C = 50 pF and VFR = −49.7 mV) is used, while for panel (c) Fibroblast-1 (C = 6.3 pF and VFR = −24.5 mV) is used.

Discussion

In this paper, we have presented results from our numerical study of the effect of gap-junctional coupling between myocytes and fibroblasts on both single cell dynamics and 2D wave patterns. Specifically, we have studied the effect of the fibroblast coupling on EADs and onset of fibrillation by inserting “active” fibroblasts25 in a 2D medium of human ventricular cells36,37. Although the presence of gap-junctional coupling between fibroblasts and myocytes in vivo is still debated14, there is substantial evidence for the existence of such a coupling in vitro18,19. Further, both cell-culture and simulation studies have shown that such a coupling could have arrhythmogenic effects32,33,44. While these studies have investigated the role of the M-F coupling, they have usually considered fibroblasts to be passive cells that do not express ionic currents. Recent studies have identified ionic currents in fibroblasts that could potentially affect the electrical activity of heart. The key motivation for this paper has been to combine a model of “active” fibroblasts that describes the experimentally observed ionic currents25 with a human ventricle model36,37. We consider two kinds of fibroblasts in our study, namely quiescent fibroblasts and myofibroblasts. Generally the term “fibroblasts” are used for cells in the normal heart, while “myofibroblasts” are used for those occurring in injured hearts44. Myofibroblasts are larger in size and have a larger membrane capacitance (C = 50 pF) than fibroblasts (C = 6.3 pF). We have used the fibroblast capacitance values as suggested in refs 25, 32 and 34. Recent experiments on human atrial fibroblasts suggest a capacitance value ~14.5 pF45. For our single cell studies we consider two different resting membrane potential for the fibroblasts (VFR = −49.7 mV and VFR = −24.5 mV) and study all four combinations of VFR and C. For the 2D studies we use two specific combinations of C and VFR, one mimicking a “quiescent fibroblast” (Fibroblast-1) and the other a “myofibroblast” (Fibroblast-2).

We observe in Fig. 2 that the most significant effect of coupling is on the APD and the myocyte resting membrane potential. While coupling with a more negative fibroblast resting membrane potential (VFR = −49.7 mV) reduces the myocyte APD (Fig. 2 (a and c)), coupling with a fibroblast with less negative resting membrane potential (VFR = −24.5 mV) increases APD (Fig. 2 (b and d)). On the other hand a larger fibroblast capacitance (C = 50 pF) leads to a larger depolarization of resting membrane compared to the case where C = 6.3 pF. The primary effect of the M-F coupling is to significantly shift the parameter boundary at which transition to EAD occurs (Fig. 3).We observe that while using a higher fibroblast capacitance of C = 14.5 pF as suggested in ref. 45 has a more pronounced effect than using C = 6.3 pF, there is no qualitative change in our results (see Supplementary Fig. S6).We observe that VFR is the critical parameter that determines whether M-F coupling promotes or suppresses EADs. The other parameters such as fibroblast capacitance and strength of the gap-junctional coupling do not critically modify myocyte dynamics but only affect the magnitude by which the transition boundary shifts. The crucial role of VFR in determining the myocyte dynamics is consistent with both experimental observations32 and simulations done using passive cells description of fibroblasts33. Supplementary Figs (S7 and S8) show the effect of MF coupling on the ionic currents. The effect of MF coupling is to essentially reactivate the L-type Calcium current. In Fig. S7(d) we observe that there is an increase in late ICaL similar to what was observed in MacCannell et al.25. When the resting membrane potential of the fibroblast VFR = −49.7 mV, this increase in ICaL is compensated by an increase in the gap-junctional current from myocyte to fibroblast (IMtoF) (Fig S7(c)), resulting in the shortening of the myocyte APD (Fig S7(a)). However when VFR = −24.5 mV, the increase in IMtoF is not sufficient to compensate the change in late ICaL, resulting in prolongation of the myocyte action potential (Fig S7(a)). Note that here we do not observe EADs both in the absence and presence of coupling. However, for the parameters considered in Supplementary Fig. S8, we observe that while there is no EAD in the absence of fibroblasts, MF coupling promotes EAD. As observed in Fig. S8(b), the main reason for the onset of EAD is the reactivation of ICaL around T = 300 ms. Although there is still an outward current from the myocyte to the fibroblast (IMtoF), it is not sufficient to exceed the value of the reactivated ICaL. This increase in the inward depolarizing current results in the formation of EAD.

We classify the different kinds of 2D patterns observed as a result of the M-F coupling and draw 2D phase portraits. Figures 5 and 6 suggest that the effect of M-F coupling on the promotion or inhibition of EADs and stabilisation or destabilisation of spiral waves depends on the properties of the fibroblast. Thus while coupling with Fibroblast-2 promotes propagating EAD waves (Fig. 6(e–g)) and destabilizes spiral waves (Fig. 5(e–g)), Fibroblast-1 suppresses EADs (Fig. 6(b–d)) and stabilizes spiral waves (Fig. 5(b–d)). However, irrespective of the type of fibroblast, M-F coupling promotes the occurrence of non-trivial pathological dynamics such as spiral fibrillation and oscillatory dynamics (Fig. 7). Thus while M-F coupling with Fibroblast-1 suppresses EAD and stabilizes spiral dynamics, it also gives rise to arrhythmic patterns (SF and OSC) for large values of GCaL. Note that these correspond to parameters that in the absence of fibroblast would have shown a propagating wave of EAD but no spiral fibrillation. Our results do not change qualitatively for other realisations of the fibroblast distribution (for the same number of fibroblasts), but do depend on the percentage of fibroblasts in the medium. For instance, we observe that the effect of the coupling is more pronounced for the medium with 30% fibroblasts than for a medium with 10% fibroblasts.

We find that the location of the initiation of arrhythmic activity depends on the strength of M-F coupling and the fraction of fibroblasts in the medium. For weak coupling (Gs = 0.5 nS) and/or small fraction of fibroblasts (10%), fibrillation is initiated at the boundary (Fig. 8(a). On the other hand for stronger coupling (Gs = 4.0 nS) and/or larger fraction of fibroblasts (20%), waves originate also from within the medium, away from the boundary (Fig. 8(b,c)). This suggests that the M-F coupling significantly modifies the wave dynamics in the medium, giving rise to new waves of electrical activity far away from the boundary.

The onset of ectopic activity in heterogeneous and fibrotic cardiac tissue was earlier studied in the ORd model for human ventricular cells33. However, there are some crucial differences between the earlier study and our work. In Zimik et al., the passive fibroblasts (modelled as RC circuits) were randomly attached to the myocytes. Such connections are classified as “single-sided coupling”14 where the fibroblasts act as a load that either drains or charges the myocyte. On the other hand, in our work we simulate ‘double-sided coupling’14 by inserting the “active” fibroblasts between myocytes in a 2D medium allowing coupling between the fibroblasts and all the non-fibroblast neighbours, thereby creating a heterogeneous medium with spatially varying ionic properties. Furthermore, the mechanisms of EAD generation in the ORd model is substantially different from that in the TNNP model. For example, while EADs are observed at very low pacing frequencies in ORd model, they occur at higher stimulation rates in the TNNP model. In spite of these differences both studies show similar effects for M-F coupling especially with respect to the onset of EADs and easier generation of ectopic beats in fibrotic tissue. Thus the results obtained in our paper are not model specific and are likely to occur in any cardiac cell model that can produce EADs, irrespective of the underlying mechanism.

One potential explanation for the occurrence of such ectopic activity would be to relate their onset to the underlying local fibrotic patterns. Such a pattern could initiate the ectopic activity by reducing the local current sink31. However we have not been able to identify any specific local fibrotic patterns that could drive such an ectopic foci, nor have we been able to predict the ectopic sites based on tissue texture (Fig. 7(b,d)). Identifying possible relationships between ectopic sites and the local texture of tissue is extremely important especially in the context of therapy. This is a line of study that needs to be pursued further using statistical approaches and machine learning algorithms46 In-silico studies have shown that the presence of EADs can substantially increase the defibrillation threshold in human ventricular tissue47. It has also been observed that conduction heterogeneities can help in tissue defibrillation48. Since fibrosis introduces spatial heterogeneities it would be interesting to study whether fibrosis can lead to a reduction in the defibrillation threshold in the presence of EADs. It would also be interesting to study the combined effect of fibrosis and heterogeneity as the latter can result in different types of spiral wave dynamics such as drift49,50. In addition, longer APD associated with EADs can facilitate meandering of the spirals51. To summarize, in this in silico study we characterize for the first time the different complex dynamics that occur due to gap junctional coupling between myocytes and “active fibroblasts” using models of single cell and 2D human heart tissue.

We conclude by stating the limitations of our study and the scope for future work. We have only studied dynamics in 2D isotropic systems. While fibroblasts themselves have been implicated in increasing anisotropy52, the tissue anisotropy itself can promote EADs especially for small values of gap-junctional conductances31. Incorporating 3D tissue structure and an anatomically correct description of wave propagation is crucial to understand arrhythmogenesis in the actual heart53. However in this paper we have only focussed on characterizing the effect of M-F coupling on the manifestaton of complex wave patterns in 2D domain by performing two-parameter studies for two kinds of fibroblasts. Studying the manifestation of EADs due to M-F coupling in 3D domains will be an area of future work. Experimental data suggest that fibroblasts may function as mechano-electric transducers54. In this context, it will be of interest to study the effect of mechano-sensitivity of fibrotic tissue on generation of EADs using methods suggested in Keldermann et al.55. Since the effect of fibroblast coupling is possibly dependent on the type of action potential24, it would be of interest to compare our results with other models of human heart tissue. Since the focus of our study was to showcase the different dynamical states that fibroblast-myocyte coupling can give rise to, we fixed the number of fibroblasts attached to a myocyte to be 5 in all our simulations. But the number of fibroblasts coupled to a myocyte is known to be an important factor that affects the action potential25 and can be systematically varied to investigate its effect of on wave propagation, a topic for future study.

Additional Information

How to cite this article: Sridhar, S. et al. Effect of myocyte-fibroblast coupling on the onset of pathological dynamics in a model of ventricular tissue. Sci. Rep. 7, 40985; doi: 10.1038/srep40985 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Material
srep40985-s1.pdf (180.2KB, pdf)

Acknowledgments

The authors would like to acknowledge Dr Ivan Kazbanov and Dr Rupamanjari Majumder for helpful discussions. S.Sridhar would like to acknowledge FWO Pegasus Marie Curie Fellowship for providing financial support. Research of A.V.P. was partially supported by the Interuniversity Attraction Poles Program (Belgian Science Policy) and FWO.

Footnotes

Author Contributions S.S., N.V. and A.V.P. conceived the in-silico experiments, S.S. conducted the experiments, S.S., N.V. and A.V.P. analysed the results. All authors have reviewed the manuscript.

References

  1. Sinha S. & Sridhar S. Patterns in Excitable Media: Genesis, Dynamics, and Control (CRC Press, 2014). [Google Scholar]
  2. Keener J. P. & Sneyd J. Mathematical physiology, vol. 1 (Springer, 1998). [Google Scholar]
  3. Heron M. Deaths: leading causes for 2010. National vital statistics reports: from the Centers for Disease Control and Prevention, National Center for Health Statistics, National Vital Statistics System 62(6), 1–96 (2013). [PubMed] [Google Scholar]
  4. Sridhar S., Sinha S. & Panfilov A. V. Anomalous drift of spiral waves in heterogeneous excitable media. Physical Review E 82(5), 051908 (2010). [DOI] [PubMed] [Google Scholar]
  5. Sridhar S., Ghosh A. & Sinha S. Critical role of pinning defects in scroll-wave breakup in active media. EPL (Europhysics Letters) 103(5), 50003 (2013). [Google Scholar]
  6. Weiss J. N., Garfinkel A., Karagueuzian H. S., Chen P. S. & Qu Z. Early afterdepolarizations and cardiac arrhythmias. Heart Rhythm 7(12), 1891–1899 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Nuss H. B., Kääb S., Kass D. A., Tomaselli G. F. & Marbán E. Cellular basis of ventricular arrhythmias and abnormal automaticity in heart failure. American Journal of Physiology-Heart and Circulatory Physiology 277(1), H80–H91 (1999). [DOI] [PubMed] [Google Scholar]
  8. Morita H., Wu J. & Zipes D. P. The qt syndromes: long and short. The Lancet 362(9640), 750–763 (2008). [DOI] [PubMed] [Google Scholar]
  9. Kannankeril P., Roden D. M. & Darbar D. Drug-induced long qt syndrome. Pharmacological Reviews 62(4), 760–781 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Xie L. H., Chen F., Karagueuzian H. S. & Weiss J. N. Oxidative stress–induced afterdepolarizations and calmodulin kinase ii signaling. Circulation Research 104(1), 79–86 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Karagueuzian H. S., Nguyen T. P., Qu Z., Weiss J. N., Karagueuzian Hrayr S. et al. “Oxidative stress, fibrosis, and early afterdepolarization-mediated cardiac arrhythmias. Frontiers in physiology 4, 1–14 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hauswirth O., Noble D. & Tsien R. W. The mechanism of oscillatory activity at low membrane potentials in cardiac purkinje fibres. Journal of Physiology 200(1), 255–265 (1969). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Camelliti P., Borg T. K. & Kohl P. Structural and functional characterisation of cardiac fibroblasts. Cardiovascular Research 65(1), 40–51 (2005). [DOI] [PubMed] [Google Scholar]
  14. Kohl P. & Gourdie R. G. Fibroblast–myocyte electrotonic coupling: Does it occur in native cardiac tissue? Journal of Molecular and Cellular Cardiology 70, 37–46 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kawara T. et al. Activation delay after premature stimulation in chronically diseased human myocardium relates to the architecture of interstitial fibrosis. Circulation 104(25), 3069–3075 (2001). [DOI] [PubMed] [Google Scholar]
  16. O’Hanlon R. et al. Prognostic significance of myocardial fibrosis in hypertrophic cardiomyopathy. Journal of the American College of Cardiology 56(11), 867–874 (2010). [DOI] [PubMed] [Google Scholar]
  17. de Jong S., van Veen T. A., van Rijen H. V. M. & de Bakker J. M. T. Fibrosis and cardiac arrhythmias. Journal of Cardiovascular Pharmacology 57(6), 630–638 (2011). [DOI] [PubMed] [Google Scholar]
  18. Gaudesius G., Miragoli M., Thomas S. P. & Rohr S. Coupling of cardiac electrical activity over extended distances by fibroblasts of cardiac origin. Circulation Research 93(5), 421–428 (2003). [DOI] [PubMed] [Google Scholar]
  19. Miragoli M., Gaudesius G. & Rohr S. Electrotonic modulation of cardiac impulse conduction by myofibroblasts. Circulation Research 98(6), 801–810 (2006). [DOI] [PubMed] [Google Scholar]
  20. Miragoli M., Salvarani N. & Rohr S. Myofibroblasts induce ectopic activity in cardiac tissue. Circulation Research 101, 755–758 (2007). [DOI] [PubMed] [Google Scholar]
  21. Camelliti P., Green C. R., LeGrice I. & Kohl P. Fibroblast network in rabbit sinoatrial node structural and functional identification of homogeneous and heterogeneous cell coupling. Circulation Research 94(6), 828–835 (2004). [DOI] [PubMed] [Google Scholar]
  22. Sachse F. B., Moreno A. P. & Abildskov J. A. Electrophysiological modeling of fibroblasts and their interaction with myocytes. Annals of Biomedical Engineering 36(1), 41–56 (2008). [DOI] [PubMed] [Google Scholar]
  23. Maleckar M. M., Greenstein J. L., Giles W. R. & Trayanova N. A. Electrotonic coupling between human atrial myocytes and fibroblasts alters myocyte excitability and repolarization. Biophysical Journal 97(8), 2179–2190 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Jacquemet V. & Henriquez C. S. Loading effect of fibroblast-myocyte coupling on resting potential, impulse propagation, and repolarization: insights from a microstructure model. American Journal of Physiology-Heart and Circulatory Physiology 294(5), H2040–H2052 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. MacCannell K. A. et al. A mathematical model of electrotonic interactions between ventricular myocytes and fibroblasts. Biophysical Journal 92(11), 4121–4132 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Morita N., Mandel W. J., Kobayashi Y. & Karagueuzian H. S. Cardiac fibrosis as a determinant of ventricular tachyarrhythmias. Journal of arrhythmia 30(6), 389–394 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Ono N. et al. Spontaneous atrial fibrillation initiated by triggered activity near the pulmonary veins in aged rats subjected to glycolytic inhibition. American Journal of Physiology-Heart and Circulatory Physiology 292(1), H639–H648 (2007). [DOI] [PubMed] [Google Scholar]
  28. Morita N. et al. Suppression of re-entrant and multifocal ventricular fibrillation by the late sodium current blocker ranolazine. Journal of the American College of Cardiology 57(3), 366–375 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Morita N. et al. Glycolytic inhibition causes spontaneous ventricular fibrillation in aged hearts. American Journal of Physiology-Heart and Circulatory Physiology 301(1), H180–H191 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Morita N. et al. Increased susceptibility of aged hearts to ventricular fibrillation during oxidative stress. American Journal of Physiology-Heart and Circulatory Physiology 297(5), H1594–H1605 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Xie Y., Sato D., Garfinkel A., Qu Z. & Weiss J. N. So little source, so much sink: requirements for afterdepolarizations to propagate in tissue. Biophysical Journal 99(5), 1408–1415 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Nguyen T. P., Xie Y., Garfinkel A., Qu Z. & Weiss J. N. Arrhythmogenic consequences of myofibroblast–myocyte coupling. Cardiovascular Research 93(2), 242–251 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Zimik S., Nayak A. R. & Pandit R. A computational study of the factors influencing the pvc-triggering ability of a cluster of early afterdepolarization-capable myocytes. PloS One 10(12), e0144979 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Chilton L. et al. K+ currents regulate the resting membrane potential, proliferation, and contractile responses in ventricular fibroblasts and myofibroblasts. American Journal of Physiology-Heart and Circulatory Physiology 288(6), H2931–H2939 (2005). [DOI] [PubMed] [Google Scholar]
  35. Shibukawa Y., Chilton E. L., MacCannell K. A., Clark R. B. & Giles W. R. K+ currents activated by depolarization in cardiac fibroblasts. Biophysical Journal 88(6), 3924–3935 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. ten Tusscher K. H. W. J., Noble D., Noble P. J. & Panfilov A. V. A model for human ventricular tissue. American Journal of Physiology-Heart and Circulatory Physiology 286(4), H1573–H1589 (2004). [DOI] [PubMed] [Google Scholar]
  37. ten Tusscher K. H. W. J. & Panfilov A. V. Alternans and spiral breakup in a human ventricular tissue model. American Journal of Physiology-Heart and Circulatory Physiology 291(3), H1088–H1100 (2006). [DOI] [PubMed] [Google Scholar]
  38. Xie Y. et al. Effects of fibroblast-myocyte coupling on cardiac conduction and vulnerability to reentry: a computational study. Heart Rhythm 6(11), 1641–1649 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Zlochiver S. et al. Electrotonic myofibroblast-to-myocyte coupling increases propensity to reentrant arrhythmias in two-dimensional cardiac monolayers. Biophysical journal 95(9), 4469–4480 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Vandersickel N. et al. A study of early afterdepolarizations in a model for human ventricular tissue. PloS One 9(1), e84595 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Zeng J. & Rudy Y. Early afterdepolarizations in cardiac myocytes: mechanism and rate dependence. Biophysical Journal 68(3), 949 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Asano Y., Davidenko J. M., Baxter W. T., Gray R. A. & Jalife J. Optical mapping of drug-induced polymorphic arrhythmias and torsade de pointes in the isolated rabbit heart. Journal of the American College of Cardiology 29(4), 831–842 (1997). [DOI] [PubMed] [Google Scholar]
  43. Chang M. G. et al. Bi-stable wave propagation and early afterdepolarization–mediated cardiac arrhythmias. Heart Rhythm 9(1), 115–122 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Nguyen T. P., Qu Z. & Weiss J. N. Cardiac fibrosis and arrhythmogenesis: the road to repair is paved with perils. Journal of Molecular and Cellular Cardiology 70, 83–91 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Poulet C. et al. Altered physiological functions and ion currents in atrial fibroblasts from patients with chronic atrial fibrillation. Physiological reports 4(2), e12681 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Zahid S. et al. Patient-derived models link re-entrant driver localization in atrial fibrillation to fibrosis spatial pattern. Cardiovascular research 110(3), 443–454 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Vandersickel N., Kazbanov I. V., Defauw A., Pijnappels D. A. & Panfilov A. V. Decreased repolarization reserve increases defibrillation threshold by favoring early afterdepolarizations in an in silico model of human ventricular tissue. Heart Rhythm 12(5), 1088–1096 (2015). [DOI] [PubMed] [Google Scholar]
  48. Keener J. P. & Panfilov A. V. A biophysical model for defibrillation of cardiac tissue. Biophysical Journal 71(3), 1335 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Rudenko A. N. & Panfilov A. V. Drift and interaction of vortices in two-dimensional heterogeneous active medium. Studia Biophysica 98(3), 183–188 (1983). [Google Scholar]
  50. Panfilov A. V. & Vasiev B. N. Vortex initiation in a heterogeneous excitable medium. Physica D 49(1), 107–113 (1991). [Google Scholar]
  51. Panfilov A. V. & Holden A. V. Computer simulation of re-entry sources in myocardium in two and three dimensions. Journal of Theoretical Biology 161(3), 271–285 (1993). [DOI] [PubMed] [Google Scholar]
  52. Ten Tusscher K. H. W. J. & Panfilov A. V. Influence of diffuse fibrosis on wave propagation in human ventricular tissue. Europace 9, vi38–vi45 (2007). [DOI] [PubMed] [Google Scholar]
  53. Ten Tusscher K. H. W. J. et al. Organization of ventricular fibrillation in the human heart: experiments and models. Experimental physiology 94(5), 553–562 (2009). [DOI] [PubMed] [Google Scholar]
  54. Kamkin A. et al. Cardiac fibroblasts and the mechano-electric feedback mechanism in healthy and diseased hearts. Progress in biophysics and molecular biology 82(1), 111–120 (2003). [DOI] [PubMed] [Google Scholar]
  55. Keldermann R. H., Nash M. P., Gelderblom H., Wang V. Y. & Panfilov A. V. Electromechanical wavebreak in a model of the human left ventricle. American Journal of Physiology-Heart and Circulatory Physiology 299(1), H134–H143 (2010). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Material
srep40985-s1.pdf (180.2KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES