Emergence of complex dynamics in a simple model of signaling networks

Abstract

Various physical, social, and biological systems generate complex fluctuations with correlations across multiple time scales. In physiologic systems, these long-range correlations are altered with disease and aging. Such correlated fluctuations in living systems have been attributed to the interaction of multiple control systems; however, the mechanisms underlying this behavior remain unknown. Here, we show that a number of distinct classes of dynamical behaviors, including correlated fluctuations characterized by 1/f scaling of their power spectra, can emerge in networks of simple signaling units. We found that, under general conditions, complex dynamics can be generated by systems fulfilling the following two requirements, (i) a “small-world” topology and (ii) the presence of noise. Our findings support two notable conclusions. First, complex physiologic-like signals can be modeled with a minimal set of components; and second, systems fulfilling conditions i and ii are robust to some degree of degradation (i.e., they will still be able to generate 1/f dynamics).

Complex systems are typically composed of interacting units that communicate information and are able to process and withstand a broad range of stresses (1–4). In physiology, free-running healthy systems typically generate complex output signals that have long-range correlations [i.e., a 1/f decay of the power spectra for low frequencies (**, 5–7)]. Deviations from the 1/f pattern have been associated with disease or aging in various contexts (3, 8).

Despite its practical and fundamental interest (9), the origin of such correlated dynamics remains an unsolved problem (4). Until recently, attention has focused primarily on the complexity of the specific physiologic subsystems or on the nature of the nonlinear interactions between them (10–12). In particular, Boolean variables (which can take one of two values, 0 or 1) and Boolean functions have been extensively used to model the state and dynamics of complex systems (see ref. 12 for an introduction). The reason such a “simplistic” description may be appropriate arises from the fact that Boolean variables provide good approximations to the nonlinear functions encountered in many control systems (10, 13–15). Random Boolean networks (RBNs) were proposed by Kauffman (10) as models of genetic regulatory networks, and they have also been studied in other contexts (13, 14). Wolfram (15), in contrast, proposed that cellular automata models, which are a class of ordered Boolean networks with identical units, may explain the real-word complexity. Neither of these two classes of models has been shown to generate the complex dynamics with 1/f fluctuations observed in healthy physiologic systems.

Here, we propose a modeling approach (Fig. 1a) that departs from traditional approaches in that we pay special attention to the topology of the network of interactions (4) and the role of noise (16). Our model is rooted in the following two considerations that are observed frequently in real-world systems. (i) The units in the system are connected mostly locally but also with some long-range connections, giving rise to so-called “small-world” topology (17, 18); and (ii) the interaction between the units is affected by “noisy” communication and/or by noisy stimuli (19–23). We demonstrate that simple rules, such as the majority rule, are able to generate signal with complex fluctuations under simple, but physiologically relevant, conditions.

Fig. 1.

Emergence of complex dynamics in simple signaling networks. (a) The units constituting the network, which are located on the nodes of a one-dimensional lattice, have bidirectional nearest-neighbor connections. (b) A number k_eN of additional unidirectional links is established between pairs of randomly selected units, where k_e is the mean excess connectivity and N is the number of units in the system. At time t = 0, we assign to each unit i = 1,...,N a state σ_i (0) randomly chosen from the set {0,1} and a Boolean function F_i; (Eq. 1). This Boolean function (or rule) determines the way in which the inputs are processed. Each unit effectively processes two inputs, one unit corresponding to the average state of its neighbors and one unit corresponding to its own state. With probability η, a unit “reads” a random Boolean variable instead of the state of a neighbor, where the parameter η quantifies the intensity of the noise. Note that the noise does not alter the state of the units but only the value read by its neighbor. At each subsequent time step, each unit updates its state synchronously according to its Boolean function. (c–e) Time evolution of systems comprising 512 units with F_i = 232 for all units, η = 0.1, and k_e = 0.15 (c), k_e = 0.45 (d), and k_e = 0.90 (e). Red indicates σ_i(t) = 1, and yellow indicates σ_i(t) = 0. The time evolution for systems starting from the same initial configuration and using the same sequence of random numbers is shown. Thus, the difference in the dynamics is uniquely due to the different number of long-distance links. For k_e = 0.15, the system quickly evolves toward a configuration with several clusters in which all of the units are in the same state. The boundaries of these clusters drift because of the noise, but the state of the system S(t) is quite stable, and the dynamics are close to Brownian noise. In contrast, for k_e = 0.90, a large stable cluster develops and the state of the system changes only when some units change state because of the effect of the noise. This process yields white-noise dynamics. For k_e = 0.45, clusters are formed, but they are no longer stable, in contrast to what happens for small k_e. In this case, information propagates through the random links, which can lead to a change in the state of one or more units inside a cluster. Our results suggest that because these long-range connections exist on all length scales, they lead to long-range correlations in the dynamics and the observed 1/f behavior (Fig. 3b).

Methods

The Model. We placed the Boolean units comprising the network on the nodes of a one-dimensional ring and established bidirectional nearest-neighbor connections (Fig. 1). Then, we added k_eN additional unidirectional links (where k_e is the mean excess connectivity and N is the number of units in the system) between pairs of randomly selected units. Hence, each unit had a set of links through which incoming signals arrive and that the unit then processes. During the system evolution, the state of each neighbor was replaced by a random value with probability η, which parameterizes the intensity of the noise.

We assigned to each unit i = 1,..., N a Boolean function F_i, which determined the way that the states of the neighbors and its own state were processed. We restricted our study to Boolean functions that had only the following two “effective” inputs: the state of the unit and the average state of all other neighbors. This restriction yielded 64 unique symmetric Boolean functions (see Figs. 2 and 7-11 and Supporting Methods, which are published as supporting information on the PNAS web site), and it had the advantage of permitting a topology-independent implementation of the Boolean functions, thus enabling a systematic study of the effect of different rules on the dynamics of the system.

Fig. 2.

Selection of Boolean rules for investigation. Our goal is to investigate Boolean functions that display nontrivial dynamics and can be generalized to any number of inputs. To this end, we start from 256 rules of three inputs but then restrict our attention to the ones that are symmetric under permutations of the external inputs. This selection results in 64 Boolean rules. However, each rule has another rule that is its complement (i.e., that displays the same dynamics when switching zeros and ones) or inverse (i.e., that displays the same dynamics when taken every other step). Because these pairs of rules have equivalent dynamics, we need to investigate only 32 independent rules. Of these rules, eight do not display fluctuations, even in the presence of noise, resulting in 24 independent rules that could present complex fluctuations. The phase spaces of each of these 24 rules are shown in Figs. 7, 8, 9, 10, 11.

Quantification of the Dynamical Behavior of the System. We started all of our numerical simulations with a random initial configuration and let the system evolve synchronously according to the rules of the model. We defined the state S(t) of the system as the sum of the states σ_i of all of the Boolean units as follows:

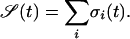[1]

We recorded S(t) during the course of the simulation (see Fig. 3 a–c) and quantified the complexity of the time series generated in terms of its autocorrelation function (3). We applied the detrended fluctuation-analysis method (5), which quantifies long-range time correlations in the dynamical output of a system by means of a single scaling exponent α (Fig. 3d). Brownian noise corresponds to α = 1.5, whereas uncorrelated white noise corresponds to α = 0.5. For many physiologic signals, one observes α ≈ 1, corresponding to 1/f behavior, which can be seen as a “trade off” between the two previous cases (3).

Fig. 3.

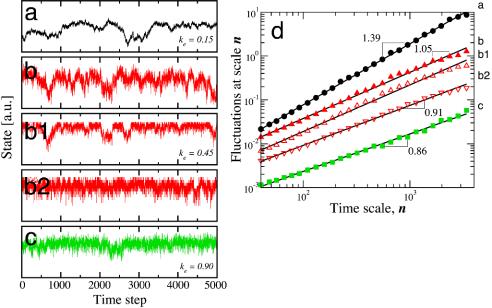
Quantification of the correlations in the state of Boolean signaling networks. As discussed, we define the state of the system as S(t) = Σ σ_i(t). We show S(t) for a system with n = 4,096 units; η = 0.1; F_i = 232; and k_e = 0.90, k_e = 0.45, and k_e = 0.15. The three values of k_e lead to quite different dynamics of the system. (a) For a small number of random links, the time correlations display trivial long-range correlations such as found for Brownian noise. (b) For an intermediate value of k_e, long-range correlations emerge and the power spectrum displays a power-law behavior, S(f) ∝ 1/f^β with β ≈ 1. b1 and b2 display the state of the system according to different definitions. In b1, the state of the system is defined as the sum of the states of a random sample comprising one-eighth of all units, whereas in b2, the state of the system is defined as the sum of the states of a block of contiguous units constituting one-eighth of the systems. Our results indicate that the evolution of a subset of the population is similar to the dynamics of the whole system. (c) For a large number of random links, k_e = 0.90, the dynamics are less correlated. (d) Estimation of temporal autocorrelations of the state of the system by the detrended fluctuation analysis method (5). We show the log–log plot of the fluctuations F(n) in the state of the system versus time scale n for the time series shown in a--c. In such a plot, a straight line indicates a power-law dependence F(n) ∝ n^α. The slope of the lines yields the scaling exponent α, which for a number of physiologic signals from free-running, healthy, and mature systems takes values close to 1 (3). The exponent α is related to the exponent β of the power spectrum of the fluctuations, S(f) ∝ 1/f^β, through the relation β = 2α - 1. The data sets have been shifted upward, and the different sets correspond (from top to bottom) to the time series shown in a–c.

Results

RBNs. The RBN model corresponds to a completely random network with randomly selected Boolean rules for the units. As shown in Fig. 4a, we find white-noise dynamics for essentially any pair of values of k_e and η within the ranges considered, suggesting that, even in the presence of noise, a system of random Boolean functions cannot generate 1/f dynamics. This result is not unexpected because the random collection of Boolean functions comprising the system prevents the development of any order or predictability in the dynamics.

Fig. 4.

Systematic evaluation of the correlations in the dynamics generated by different rules. We quantify the long-range correlations in the dynamics by means of the detrended fluctuation-analysis exponent α (5) systematically estimated for time scales 40 < n < 4,000. We show α for 3,721 pairs of values of k_e and the noise η in the communication between the units comprising the network. For all simulations, we follow the time evolution of systems comprising 4,096 units for a transient period lasting 8,192 time steps, and we then record the time evolution of the system for an additional 10,000 time steps. To avoid artifacts due to the fact that the units switch states with period 2 for some of the rules, we consider in our analysis the state of the systems at every other time step. (a) RBN as defined by Kauffman (10). Our results show that the dynamics generated by these systems are generally of the white-noise type, with a weak dependence on the noise intensity and no dependence on the number of long-distance links. (b) Rule 232, also known as the majority rule. This rule is representative of two other rules: rules 19 and 1. Rule 232 displays a very rich phase space with various dynamical behaviors all of the way from white noise (white and green) to Brownian noise (black). (c) Rule 50 is a threshold rule with refractory period. This rule is representative of eight other rules: rules 5, 36, 37, 73, 77, 94, 108, and 164. These rules display a relatively simple phase space with behaviors extending from white noise to 1/f noise. The 1/f behavior is restricted to very small noise intensities and there is a very weak dependence on k_e. (d) Rule 104. This rule is representative of 12 other rules (see Figs. 7, 8, 9, 10, 11). Their phase space is extremely simple because it displays only white-noise behavior.

Cellular-Automata Models with Small-World Topology and Noise. We systematically study the 64 symmetric rules (see Figs. 2 and 7-11 and Supporting Methods) for different pairs of values of k_e and η. Some of the rules have parallels to physiologically meaningful dynamics. Rule 232 is a majority rule; that is, each unit will be active at the next time step only if the majority of its neighbors is active presently. Rule 50 is a threshold rule with refractory time period; that is, whenever the inputs of the neighbors surpass a certain value, a unit becomes active in the next time step and then will be inactive for at least one time step. The 64 symmetric rules lead to three qualitatively distinct phase spaces (Fig. 4 b–d). Rule 232, the majority rule, which is representative of the first type of phase space, displays three distinct types of dynamical behavior (Fig. 4b). For small k_e, we find mostly Brownian-like scaling. For large k_e, we find mostly white-noise dynamics. Of greatest interest, for intermediate values of k_e and for a broad range of values of the intensity of the noise η, we find 1/f fluctuations.

Rule 50, which is representative of a second type of phase space, displays fewer types of dynamical behavior. In particular, we find only a narrow range of noise intensities (with a weak dependence on k_e) for which the dynamics display 1/f correlations. For η ≳ 0.1, the dynamics become uncorrelated (Fig. 4c). Rule 160, which is representative the third type of phase space, displays white-noise dynamics for all values of k_e and η (Fig. 4d).

Note that for k_e = 0 (i.e., when the network is a one-dimensional lattice), the model is not able to generate 1/f dynamics. This result implies that, in the context of the model, the existence of long-range connections (i.e., the small-world topology achieved by making k_e ≠ 0) is an essential ingredient for the emergence of 1/f dynamics.

Robustness of the Findings. To determine the generality of the results presented above, one needs to address the questions of how these findings are affected by (i) changes in the topology of the network and (ii) “errors” in the implementation of the rules by the units.

Concerning i, we note that the network topologies that have been considered span the cases of ordered one-dimensional lattices, small-world networks, and random graphs (24). However, all considered networks are composed of units with approximately the same degree, i.e., the same number of connections. To investigate the role of the distribution of number of connections, we also study networks that span the range of empirically observed degree distribution: a δ distribution, an exponential distribution, and a power law distribution. The last case corresponds to the so-called scale-free networks (18). Notably, we find that the picture of the phase space shown in Fig. 4b does not get altered by these changes in the degree distribution (see Figs. 7, 8, 9, 10, 11 and Supporting Methods).

To address ii, we systematically explore the dynamical behaviors in the phase space defined by (k_e,η) for systems composed of units operating according to either rule 232 or a randomly selected rule. Notably, we find that, with as many as one-fourth of all units operating according to random Boolean functions, the model still displays a rich phase space including white, 1/f, and Brownian noise (Fig. 5). This finding holds even if, instead of using random Boolean functions, we consider a single Boolean function (Fig. 6).

Fig. 5.

Phase space for signaling networks with mixing of Boolean rules. We systematically calculate the exponent α, by characterizing the correlations in the dynamics, for systems composed of units operating according to rule 232 but with some fixed fraction of units operating according to a randomly selected symmetric Boolean rule. Each value is an average over five independent runs. (a) One-sixteenth of the units operating according to a randomly selected rule. (b) One-eighth of the units operating according to a randomly selected rule. (c) One-fourth of the units operating according to a randomly selected rule. (d) One-half of the units operating according to a randomly selected rule. These figures suggest that the presence of random Boolean functions leads to a decrease in the richness of the phase space of the systems. Specifically, if more than one-fourth of all of the units operate according to randomly selected Boolean functions, then the phase space displays mostly white-noise dynamics.

Fig. 6.

Phase space for signaling networks with mixing of two Boolean rules. We systematically calculate the exponent α, characterizing the correlations in the dynamics, for systems composed of units operating according to either rule 232 or 50. Each value is an average over five independent runs. (a) One-sixteenth of the units operating according to rule 50 and 15/16ths of the units operating according to rule 232. (b) One-eighth of the units operating according to rule 50 and seven-eighths of the units operating according to rule 232. (c) One-fourth of the units operating according to rule 50 and three-fourths of the units operating according to rule 232. (d) One-half of the units operating according to rule 50 and one-half of the units operating according to rule 232. When both rules are present in the system, and at least 50% of the units operate according to rule 232, we still find several distinct classes of dynamical behaviors, including a wide range of parameter values that generate 1/f noise.

Discussion

Our results are notable for various reasons. First, they demonstrate that a model of signaling networks is able to generate a broad range of behaviors that are reminiscent of those observed in physiologic systems. Second, we show, for a rather general class of models, that various dynamical behaviors can emerge only under restrictive, but physiologically relevant, assumptions; namely, the system must have a small-world topology, and noise must be present.

An interesting aspect of our results is that some of the rules that we consider have plausible physiologic interpretations. For example, rule 232 is a rule in which a unit changes its state to that of the majority of the incoming inputs. A majority rule appears to be operative in the central nervous system, where multiple fibers (excitatory or inhibitory) converge onto a single neuron. Action potentials converging in a neuron summate to bring the neuron to the threshold for firing (25). A majority rule also appears to be operative in the baroreflex control of the cardiovascular system. The baroreflex is a feedback loop that controls heart rate continuously by modulating the degree of sympathetic and parasympathetic nervous system input to the sinus node of the heart. Changes in heart rate values are determined by whichever input is dominant at the moment (25).

Our results demonstrate that complex fluctuations are present even when a fraction of the units obeys randomly chosen Boolean functions, suggesting that systems composed of units operating according to the majority will be robust to the removal or failure of units. Also, because this complex dynamics does not depend on a scale-free topology, these systems do not necessarily display the vulnerability to targeted attack observed in scale-free networks (26). In biological systems, this robustness could support the “physiologic reserve” enabling an organism to overcome age- or disease-related loss of system components.

Additionally, our findings raise the intriguing possibility that the interactions within physiologic systems and their degradation with aging and pathology may be symbolically mapped as a “walk” on the phase space (k_e,η). According to this model, 1/f dynamics similar to that found for healthy physiology are generated when noise intensity and connectivity reside in a well defined range (27). A loss of complexity with a breakdown of long-range correlations would be anticipated when these parameters assume values outside this range (Fig. 4). Support for this formulation comes from analysis of heart rate dynamics with aging and disease, where connectivity or coupling among system components is likely to be degraded (3, 4, 8). Similarly, evidence suggests that decreased social connectedness and the corresponding decrease in noisy stimulation may be associated with increased cardiac mortality and decreased functional recovery from stroke or dementia (28, 29).

In a related way, the development of complex, adaptive dynamics during the maturation of the organism may be accounted for, at least in part, by the evolution of appropriate connections (see refs. 30 and 31 for empirical evidence). Our model predicts that the fraction of nonlocal connections has an optimal range of values; hence, an excessive number of certain types of inputs may also degrade functionality. Thus, our results are consistent with empirical evidence suggesting that development and maintenance of healthy function may require adjusting the number of connections. Last, the model may also provide a robust way to generate fluctuations that closely resemble physiologic signals, which could be implemented in medical devices, such as mechanical ventilators (32, 33) and hormone infusion pumps (34).