Convergence of excitatory and inhibitory hair cell transmitters shapes vestibular afferent responses

Abstract

The vestibular semicircular canals respond to angular acceleration that is integrated to angular velocity by the biofluid mechanics of the canals and is the primary origin of afferent responses encoding velocity. Surprisingly, some afferents actually report angular acceleration. Our data indicate that hair-cell/afferent synapses introduce a mathematical derivative in these afferents that partially cancels the biomechanical integration and results in discharge rates encoding angular acceleration. We examined the role of convergent synaptic inputs from hair cells to this mathematical differentiation. A significant reduction in the order of the differentiation was observed for low-frequency stimuli after γ-aminobutyric acid type B receptor antagonist administration. Results demonstrate that γ-aminobutyric acid participates in shaping the temporal dynamics of afferent responses.

Calculus has proven germane to our understanding of virtually all physical events. Because of the universal truth of mathematics and the success of manmade machines based on these truths, it is often assumed that the calculus discovered by Newton and developed by Leibniz is the same as that accomplished by the nervous system. However, the system-level connection between the two is often tenuous. The ability of the nervous system to effect integration is well established, as exemplified by the neural integrators of the vestibulo-ocular reflex (1–3). Input to this reflex originates in the vestibular semicircular canals, which respond to angular acceleration. The viscous drag of biofluid on the canal walls effectively achieves a mathematical integration of the angular acceleration stimulus to angular velocity and is the primary origin of the afferent signals transmitting velocity information to the brain (4, 5). However, simple integration at the vestibular periphery does not satisfactorily describe the broad repertoire of responses elicited from vestibular afferent fibers during head movements. Although hair cell receptor potentials primarily reflect the angular velocity input, a significant subset of the afferent fibers accomplish a differentiation of this signal and report angular acceleration (6). This incongruity suggests that additional signal processing occurs at the hair cell/afferent junction in a subset of afferent fibers.

Mathematically, the transformation from hair cell receptor potentials to afferent responses can be approximated as a fractional derivative, d^α/dt^α (7), with the fractional order (α) varying with stimulus frequency. For sinusoidal head rotations, the fractional derivative is perhaps better known as a fractional Laplace operator [s^α = (iω)^α, where s is the Laplace variable, ω is the frequency in rad per s, and 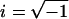]. The fractional power α provides the slope of the operator gain on a log-log scale (dB/dB) and the phase advance by θ = α × 90°. Afferents exclusively reporting velocity have order α = 0, whereas those exclusively reporting acceleration have order α = 1. In the present experimental model, toadfish afferents respond to canal stimulation with α values spanning a continuous spectrum from 0 to 1. The simplest empirical models describing canal afferent responses combine a fractional Laplace operator modeling neural adaptation with a wide band-pass filter modeling canal mechanics (8). This paper addresses the sensitivity of the fractional operator to γ-aminobutyric acid type B (GABA_B) receptor antagonists.

Regional variations in afferent responses have been demonstrated across the crista (8–12) and correlated with differences in structural attributes of the crista (13–15). In toadfish, responses form a continuum in which fibers with an α near 0 have few terminal endings and innervate the peripheral margins of the crista, whereas afferents with α values approaching 1 have greater numbers of terminal endings and innervate more central crista regions (13, 16). The biological origins of this diversity in afferent responses remain to be identified.

The principal transmitter used by crista hair cells is assumed to be a glutamate- or aspartate-like excitatory amino acid (for reviews cf. refs. 17–19). However, recent studies demonstrated that a population of hair cells in the toadfish are intensely GABA-immunoreactive, and ≈20% of these cells coexpress intense glutamate-like immunoreactivity (20). Whereas glutamatergic hair cells are present throughout the crista, GABAergic hair cells are found exclusively in the central region, precisely where the distal processes of afferents expressing high-order derivatives are distributed. The present study examined the putative role of GABAergic hair cell transmission in shaping diversity and mathematical differentiation in primary afferent responses.

Methods

Adult oyster toadfish of either sex, ≈500 g, obtained from the Marine Biological Laboratory were used and approved by the institutional animal care and use committees at the Marine Biological Laboratory, Washington University, University of Utah, National Aeronautics and Space Administration Ames Research Center, and/or Mount Sinai School of Medicine. Physiology preparation followed refs. 16 and 21. Fish were anesthetized by immersion in MS222 (25 mg/liter of sea water, 3-aminobenzoic acid ethyl ester, Sigma), partially immobilized (i.m. injection of pancuronium bromide; 0.05 mg/kg), and secured in a seawater-filled tank. A small craniotomy was made, allowing direct access to the horizontal canal nerve and canal duct. Fluorocarbon (FC75, 3M Co.) was injected to partially fill the cranial space. A layer of normal perilymph remained on the surface of the labyrinth, and a pool of perilymph bathed the canal nerve.

Glass microelectrodes were used for afferent nerve recordings. Conventional bridge amplification and external spike discrimination were used. Stimulation of the canal was by a piezoelectric microactuator (22–24). A curved forceps attached to an actuator (PZL 060-11, Burleigh Instruments, Fishers, NY) compressed the canal duct. The canal was preloaded with a step compression, and dynamic stimuli were applied about this steady indenter position only after the nerve had recovered its background discharge and the cupula had returned to its steady-state position. The endolymph volumetric displacement generated by this stimulus has been reported (22). Displacement of the forceps was continuously monitored with a linear variable differential transformer (Schaevitz DEC-050, Measurement Specialties, Fairfield, NJ) mounted in-line with the actuator. A waveform generator (Tektronix AFG 5102) and high-voltage amplifier (TrigTek 207A, Los Angeles) provided input to the microactuator to deliver sinusoidal and step stimuli. The rise time of the step stimulus was ≈8 ms (time constant ≈2.7 ms) with a holding time ranging from 2 to 150 s. The canal was patent and intact. A step compression of the canal generated a rapid step displacement of the cupula followed by a period of recovery when the cupula slowly returned to its undeformed configuration with an adaptive constant of ≈10 s (22).

Stimuli were restricted to magnitudes <10 μm (equivalent to ≈40° per s angular head rotation), a range over which afferents respond nearly linearly (16, 22). Digital data acquisition [Cambridge Electronic Design (Cambridge, U.K.) 1401Plus, Apple interface] recorded externally discriminated spike times, analog neural responses, and canal compression (by using a linear variable differential transformer). Analog signals were filtered below the Nyquist frequency and externally amplified to span the 16-bit range of the analog to digital converter.

For multiunit recording, a suction electrode (tip diameter ≈100 μm) was filled with artificial perilymph and applied to the intact canal nerve. A sum of 2- and 5-Hz sinusoidal signals was constructed, applied, and recorded as above. The suction electrode voltage was preamplified (10¹² Ω field-effect transistor, custom) and full-wave rectified. First harmonic responses of the rectified neural signal were measured in quadrature by using two lock-in amplifiers (SR830, Stanford Research, Sunnyvale, CA), one synchronized at the 2-Hz trigger and the other at the 5-Hz trigger. Complex-valued transfer functions were computed by relating the first harmonic response to the stimulus [T(ω) = (lock-in, V)/(stimulus, μm)], with gain 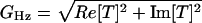(V/μm) and phase θ_Hz = Atan[Im(T)/Re(T)] (rad). For suction electrode data, the gain slope (m) for the two-component stimulus was determined by using m = [log(G_5Hz) - log(G_2Hz)]/[log(5) - log(2)] (Eq. 1), and the average phase was determined by using 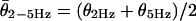(Eq. 2). Simultaneous single-unit recordings were compared to suction electrode results to validate this approach (data not shown).

Analysis was done off-line by using a custom interactive analysis procedure (igorpro, WaveMetrics, Lake Oswego, OR). For sinusoidal stimuli, the first harmonic gain and phase were computed for five or more consecutive stimulus cycles by manually selecting portions of the record and averaging the results. Spike times were averaged relative to the stimulus trigger by using 100 bins per cycle phase histograms. Results were inverted to yield the firing rate (spikes per s) as a function of phase in the cycle. Empty bins were ignored in the fitting procedure, and the average rate was constrained to be ≥0. The complex-valued first harmonic afferent response was then divided by the complex-valued first harmonic of the stimulus to determine the first harmonic gain (spikes per s per μm) and phase (degrees with respect to peak indentation). The relationship to gain and phase for compression stimuli with respect to angular head rotation has been reported (22–24). For step and square wave stimuli, afferent firing rates were fit by using both single- and double-exponent curves constrained to asymptote to the spontaneous discharge rate.

Changes in afferent gain and phase for sinusoidal stimuli were compared to predictions of a simple two-transmitter model of the form 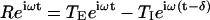(Eq. 3), where R(ω) is the complex-valued afferent response (spikes per s per degree per s), ω (rad per s) is the mechanical stimulus frequency, 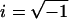, t is time (s), δ is the GABA_B receptor delay time (s), T_E(ω) is the frequency-dependent excitatory synaptic input (spikes per s per degree per s), and T_I(ω) is the frequency-dependent inhibitory GABAergic synaptic input (spikes per s per degree per s). In the simplest form of this model, the inhibitory input is proportional to the excitatory input so and 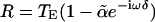(Eq. 4). This formula gives rise to response dynamics that closely resemble mathematical differentiation, at least for low frequencies of stimulation (ω < 1/δ). The parameter ã measures the strength of the inhibitory input relative to the excitatory input and is approximated by fractional differentiation of order α; the order α can be estimated from afferent responses in the control condition by using the slope of the gain or the phase advance (e.g., 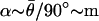with the range 0 ≤ α < 1).

Pharmacology. Initial setup was as above. A gill artery was cannulated with a tube filled with heparinized Ringer's solution for subsequent drug injections (all drugs were from Tocris Cookson, Bristol, U.K.). Drugs were dissolved in large volumes of Ringer's solution (≈50 mg/ml), and aliquots were taken for injection. CGP 55845 (2 mg) was dissolved in 50 μl of DMSO. For systemic injections for single afferent recordings, 250–400 μg of CGP 55845 (for example) were typically administered; doses of 100 μg or less were usually ineffective. Controls included saline, vehicle, and sham injections.

Morphology. Toadfish were anesthetized 20–30 min before perfusion. A catheter (18G) attached to a peristaltic pump was inserted into the cardiac conus, the atrium was cut, and ≈50 ml of heparinized (2 units/ml) room temperature (RT) PBS (0.01 M, pH 7.3) was infused over 2–3 min. Perfusion continued with delivery of 100 ml of RT fixative (4% paraformaldehyde/0.2% glutaraldehyde) in PBS for 5 min at 20 ml/min, then 400 ml of additional RT fixative at 13–15 ml/min. Ten milliliters of fixative was injected into the cranial cavity 5 min after perfusion onset. The labyrinths were harvested, placed in cold PBS, and further dissected to expose the sensory epithelia.

Endorgans were washed three times with PBS, treated with 0.2% NaBH₄ in water for 45 min at RT, and then washed five times in PBS. Samples were immersed in blocking buffer (5% normal goat serum in PBS with 0.05% Triton X-100 and 0.02% NaN₃) for 5–18 h at RT. After blocking, samples were incubated for 24 h at RT in fluorescent-tagged (Alexa dyes, Molecular Probes) monoclonal anti-GABA (GABA93 mAb) and anti-glutamate (mAb 21-5B2) antibodies, both produced in the Holstein laboratory (20), diluted in PBS with 5% normal goat serum, 0.01% Triton X-100, and 0.02% NaN₃ (incubation buffer). Specimens containing biocytin-injected afferents were immunoreacted with only one of these two fluorescent-tagged mAbs, and the biocytin was visualized by using a fluorescent-tagged streptavidin conjugate. Other samples were indirectly labeled with primary mouse monoclonals and fluorescent-tagged goat anti-mouse secondary reagents (Molecular Probes). After incubation in antibody, the specimens were rinsed in PBS and immobilized in Petri dishes thinly coated with 2% agarose. Controls included endorgans incubated in (i) GABA93 mAb that was preabsorbed with a GABA-glutaraldehyde-BSA conjugate and mAb 21-5B2 (anti-glutamate) that was preabsorbed with a glutamate-glutaraldehyde-BSA conjugate and then further processed as above, (ii) single-label GABA93 mAb and mAb 21-5B2 preabsorption controls, and (iii) incubation buffer with no primary antibodies (tissue autofluorescence control); none showed specific labeling. Specimens were examined with a Bio-Rad Radiance 2000 multiphoton laser scanning microscopy system equipped with an Olympus upright microscope and Mira 900F Ti:sapphire laser with Verdi 10 W pump (Coherent Radiation, Palo Alto, CA). Image stacks were compiled by using lasersharp 2000 (Bio-Rad), confocal assistant (Bio-Rad), quicktime (Apple), and iplab (Scanalytics, Billerica, MA). 3D opacity-rendered models were constructed by using volocity (Improvision, Lexington, MA). Publication images were prepared by using photoshop (Adobe Systems, San Jose, CA).

Results

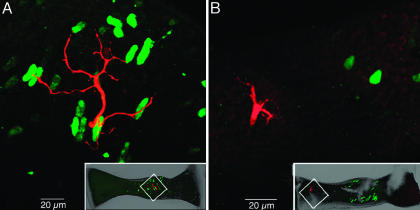
The regional localization of glutamatergic and GABAergic hair cells identified immunocytochemically was initially correlated with a map of distal neuritic endings of velocity- and acceleration-coding afferents (Fig. 1). Topological comparison suggests that GABA may influence only those afferents with α values above ≈0.5, because their dendritic fields are coextensive with the region of the crista containing GABAergic hair cells. In contrast, the distal neuritic processes of velocity afferents (α near 0) are far from the GABA-containing receptor cells and offer no possibility of synaptic contact. Direct support for this suggestion was obtained from double-labeling studies of physiologically typed, biocytin-injected afferents processed to visualize biocytin and GABA. High α (e.g., acceleration-coding) fibers received GABAergic hair cell innervation on their distal neurites, and unstained (presumed glutamatergic) hair cell input to the remainder of the dendritic tree (e.g., Fig. 2A; gain = 60.3 impulses/s-μm, θ = 76°, α ≈0.83 at 2.2 Hz). Low α (e.g., velocity-coding) afferent processes were distributed in the region containing only glutamatergic hair cells (e.g., Fig. 2B; gain = 7.9 impulses/s-μm, θ = 21°, α ≈0.2 at 3 Hz), demonstrating that GABAergic hair cells are positioned to modulate a subset of the synapses involving high α or acceleration-coding afferents.

Fig. 1.

Topography of GABAergic hair cells. (A) Low-magnification multiphoton laser scanning projected image showing the spatially restricted distribution of GABAergic hair cells (Alexa 488, green) in relation to the ubiquitous glutamatergic hair cells (Alexa 568, red) across an entire crista ampullaris of a double-labeled canal crista. Vertical dashed lines demarcate the central 60% of the crista. (B) Locations of dendritic fields of 38 physiologically characterized, labeled afferents. The relative center of each dendritic field for pure velocity-sensitive (V, red squares), mixed velocity/acceleration-sensitive (V/A, yellow circles), and acceleration-sensitive (A, green circles) afferents are plotted on a normalized crista (after ref. 13).

Fig. 2.

Multiphoton laser scanning images of physiologically characterized, biocytin-injected afferents. (A) Acceleration-sensitive afferent (red) contacts GABA-immunolabeled hair cells (green) in the central crista. (Inset) The location of the afferent dendritic field is shown in the low-magnification projected image. (B) Velocity-sensitive afferent (red) ramifying in the peripheral crista, far away from the GABAergic hair cells (green) of the central region. (Inset) Low-magnification contextual image is shown.

To investigate GABAergic action, GABA receptor antagonists were used while recording compound responses from a population of canal afferents (suction electrode). Responses were sampled during mechanical indentation or compression of the canal (24, 25). Stimulation was delivered as a sum of sinusoidal signals at 2 and 5 Hz; nerve responses were extracted and plotted as gain slope and phase advance versus time. Picrotoxin, a GABA_A receptor antagonist (i.v. injection; 20 mg/kg), had no effect on responses up to 45 min after administration (data not shown). Single-unit recordings from high α afferents obtained after i.v. picrotoxin injection replicated the suction electrode results, demonstrating that GABA_A receptors do not participate appreciably in shaping afferent temporal responses.

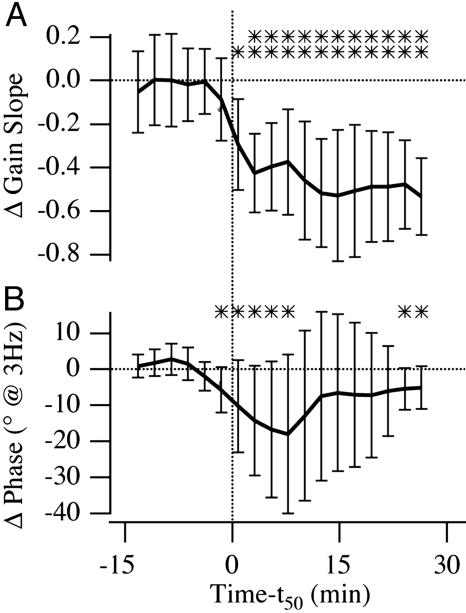
Compound responses were sampled by using lock-in amplification at 2 and 5 Hz before and after systemic injection of GABA_B receptor antagonists. The half-maximum drug effect occurred ≈15 min (±4.3 min) after injection. The afferent gain slope decreased and the phase became retarded with respect to the control condition (Fig. 3), both consistent with a reduction in the order of differentiation, α. Changes in the gain slope between 2 and 5 Hz were statistically significant at the P = 0.05 level with respect to the control condition and did not recover 30 min postinjection. Changes in the average phase at 2 and 5 Hz were not as large, but were significant at the P = 0.1 level 30 min postinjection. The relatively small changes in phase at these test frequencies is not surprising based on the time delay associated with the GABA_B receptors (see single-unit data below). These data establish the statistical significance of the CGP effect, indicating that GABA_B receptors are likely to participate in the mathematical differentiation observed in the responses of primary afferent fibers. In two experiments, nerves were cut proximal to the recording site before drug injection. Responses obtained after nerve section were indistinguishable from those of drug-treated, nerve-intact fish (data not shown), demonstrating that CNS efferent system feedback, which is interrupted by the nerve section, is not responsible for the changes in gain slope and phase observed after GABA_B receptor antagonist injections. Saline injections had no effect on the gain slope or phase.

Fig. 3.

Time course of change in gain slope and average phase in whole nerve, suction electrode recordings averaged over seven experiments before and after systemic injection of CGP 55845 (n = 2 at 1 mg), CGP 35348 (n = 2at 0.9 mg; n = 1 at 0.7 mg), and CGP 46381 (n = 2 at 0.5 mg). Data for individual fish are plotted vs. time relative to the time of half-maximal drug effect (vertical dashed line denotes t₅₀ = 15 ± 4.3 min). Error bars are interanimal standard deviations. ** indicates statistical significance at the 95% confidence level, and * indicate the 90% level with respect to preinjection control condition. (A) Gain slope calculated as the change in gain divided by change in frequency (log-log scale) by using lock-in suction electrode data at 5 and 2 Hz. (B) Phase is the average recorded at 5 and 2 Hz.

Although the changes in gain slope and phase advance obtained in the suction electrode experiments were statistically significant, considerable variability was observed. Undoubtedly, one source of this variability is the suction electrode sensitivity to signals from multiple units; it was not possible to control the relative mix of velocity-coding versus acceleration-coding afferents influencing the recording. To verify this interpretation, microelectrode recordings were obtained from representative single afferents during the injection of CGP 55845, a potent and specific GABA_B receptor antagonist (26), and were evaluated by using the Bode form of gain and phase. Fig. 4 illustrates a typical afferent exhibiting response dynamics falling between the extreme velocity- and acceleration-coding cases (control: α ≈ 0.47 at 0.2 Hz, and α ≈ 0.81 at 6 Hz). Within 15 min of injection (CGP 55845; 250 μg), the low-frequency gain (<2 Hz) increased whereas the high-frequency gain decreased, such that the average slope decreased from 1.0 in the control condition to 0.19 after the drug (Fig. 4A). Similar effects were obtained at doses of 250–1,000 μg. Phase changes observed in this particular unit were relatively small (Fig. 4B), consistent with predictions of the simple two-transmitter model presented in Methods. Acceleration-coding afferents exhibiting a higher phase in the control condition also showed an increase in low-frequency gain within 15 min of CGP 55845 injection (e.g., 400 μg; Fig. 5A). The retardation in low-frequency phase after the drug is particularly pronounced in this afferent (Fig. 5B). The response profile after CGP administration resembled a velocity-sensitive unit, rather than the acceleration-coding unit manifest in the control condition (single-unit recordings of this type; n = 5). The thin red curves in Figs. 4 and 5 show the two-transmitter model prediction for gain and phase of each unit after blocking the inhibitory component with CGP (block modeled by setting T_I = 0). To make these model predictions, we used a G protein delay of δ = 3 ms and estimated α based on the average phase recorded in the control 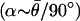. Although the model is extremely simple, predictions are in reasonable agreement with the data and support the hypothesis that the apparent mathematical differentiation that occurs at low frequencies in high-α afferents is caused by convergence of inhibitory and excitatory inputs. As expected, velocity-sensitive units (α = 0) were not affected by administration of GABA_B antagonists (data not shown). Figs. 4 and 5 provide single-unit examples that underlie the compound-unit suction electrode data (Fig. 3) and taken together indicate that the fractional derivative associated with acceleration-sensitive fibers is mediated by a GABA_B receptor mechanism, at least at low frequencies below the cut-off associated with the G protein receptor delay time.

Fig. 4.

Bode plots of log gain (A, spikes per s per μm of canal indentation) and phase (B, spikes per s with respect to peak amplitude of stimulation) versus log frequency of stimulation for a single mixed velocity/acceleration afferent before and after CGP 55845 injection at 250 μg. Different symbols correspond to measurements obtained 15, 30, and 67 min postinjection. Gain slopes are indicated for the linear fits of the data. Gain slope is plotted overlying that of the suction electrode experiments in A Inset. The two-transmitter convergence model (Methods) was used to predict how the unit in the control condition (thick black solid line) would be expected to respond after GABA_B receptor blockade (thin red curved lines). Note correspondence between the predicted response (red curved lines) and the postdrug data (dashed line curve fits).

Fig. 5.

Bode plots of log gain (A, spikes per s per μm of canal indentation) and phase (B, spikes per s re: peak amplitude of stimulation) versus log frequency of stimulation for a single high-α afferent before and after CGP 55845 injection at 400 μg. Different symbols correspond to measurements obtained 13 and 30 min postinjection. Gain slopes are indicated for the linear fits of the data. Gain slope is plotted overlying that of the suction electrode experiments in A Inset. The two-transmitter convergence model (Methods) was used to predict how the unit in the control condition (thick black solid line) would be expected to respond after GABA_B receptor blockade (thin red curved lines). Note correspondence between the predicted response (red curved lines) and the postdrug data (dashed line curve fits).

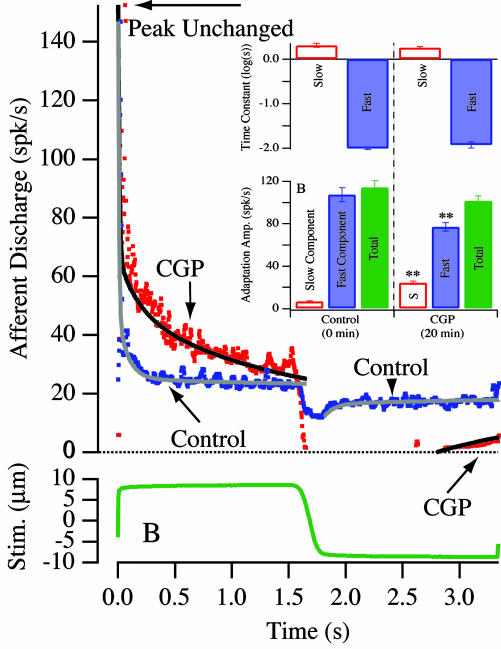
The time course of spike train adaptation to step displacement stimuli was recorded for high-α afferents (e.g., Fig. 6). Step indentation simulates angular acceleration during the rising phase and tonic velocity during the plateau (25). A velocity-encoding afferent (α = 0) would not adapt during maintained step cupular displacement; an acceleration-coding afferent (α = 1) would respond with an initial burst but then adapt almost immediately to the background discharge level (6). In Fig. 6, the control responded to step stimuli as an acceleration-coding unit with rapid adaptation, but shifted toward a velocity-encoding unit after administration of CGP 55845. By 20 min postinjection, the proportion of fast versus slow adaptation shifted toward the slow process, although neither the peak discharge during the step in the excitatory direction nor the time constants of the fast and slow processes changed. That the initial peak discharge did not change indicates that the antagonist did not influence the fast excitatory synaptic input driving the afferent. These data are summarized in Fig. 6 Inset. In general, after GABA_B antagonist administration, the time required for the high-α units to adapt back to their background discharge during step stimuli was increased significantly (n = 4), supporting the proposed role of a GABA_B receptor mechanism in expanding the temporal repertoire of afferent responses, namely by inducing an adaptive process effecting a mathematical differentiation at frequencies below ≈2 Hz.

Fig. 6.

Afferent adaptation to step excitatory and inhibitory stimuli (step amplitude indicated in B) of the mixed velocity/acceleration afferent illustrated in Fig. 4. Afferent discharge adaptation for excitatory stimuli was fit by using a double-exponential curve (slow and fast time constants t_s, t_f) and a single exponential for inhibitory stimuli (slow time t_s). (Inset) Summary statistics of afferent adaptation changes associated with GABA_B receptor administration. The data were fit as double exponentials by using: spikes/s = is the fast time constant, τ₂ is the slow time constant, A₁ is the fast component amplitude, A₂ is the slow component amplitude, and A₁+A₂ is the total adaptation amplitude. Error bars denote SEM. There was no statistically significant change in τ₁ or τ₂, but significant differences were observed in the relative proportions of A₁ and A₂ (** denotes 0.05 level) such that total time required to recovery lengthened after CGP administration.

The effects of CGP 55845 on spontaneous activity and the regularity of afferent fiber discharge rate, quantified as the coefficient of variation, were evaluated in single-unit recordings. Both the level of spontaneous activity and regularity of discharge were affected by GABA_B receptor antagonists within the same time frame as the changes in gain, phase, and adaptation. Spontaneous activity decreased (to zero in one case) while the discharge became more regular. In general, both spontaneous activity and coefficient of variation showed partial recovery within 1 h. Thus, for single units sensitive to CGP 55845: (i) the background discharge rate decreased and did not fully recover; (ii) the gain slope decreased and did not fully recover; (iii) individual fast and slow adaptation time constants did not change, but (iv) the contribution of fast adaptation was reduced such that recovery to background discharge was significantly slower. These data indicate that GABA_B receptors participate in shaping the spontaneous, as well as evoked, responses of some afferents. It is notable that changes in background discharge were contrary to that expected from a simple action on postsynaptic GABA_B receptors. The data suggest a dual action of GABA_B antagonists, one postsynaptic on the afferent terminal (present focus) and the other presynaptic, modulating the hair cells (18, 27).

Discussion

Our findings can be described in terms of a mathematical differentiation that is performed by convergence of excitatory and time-delayed inhibitory synaptic inputs. For control sinusoidal stimuli, the inhibitory input results in a phase advance toward acceleration and an increase in gain slope. For step stimuli, the inhibitory input results in responses that rapidly adapt to the spontaneous background discharge. Present results further show that the GABA_B-mediated dynamic is only part of the mathematical differentiation process in vestibular afferents, because (i) GABA antagonists did not decrease the mathematical differentiation present above ≈2 Hz or reduce the phase or order of differentiation completely to zero, and (ii) some afferents showed a phase advance and nonzero gain slope even in the absence of contacts with GABAergic hair cells. This partial effect is not surprising, given that GABA only, glutamate only, and GABA plus glutamate hair cells are all present in toadfish cristae, converge to varying degrees on individual postsynaptic fibers, and through that convergence activate different postsynaptic receptor arrays, thereby exerting a wide range of effects on innervated afferent processes. Moreover, three distinct effector mechanisms have been associated with the activation of mammalian neuronal GABA_B receptors: increased K⁺ conductance, decreased Ca²⁺ conductance, and modulation of the adenylate cyclase system (cf. ref. 26). In general, alterations in K⁺ conductance have been attributed to activation of postsynaptic GABA_B sites, whereas presynaptic GABA_B receptor activation impacts K⁺(A) currents (28), Ca²⁺ influx (29), and perhaps also protein kinase C activation. It is therefore likely that several GABA_B receptor-related mechanisms are present in the vestibular periphery and that our present results reflect a CGP effect on each.

In mammalian hair cells, GABA_B receptor activation results in a decrease in the Ca²⁺ concentration within the sensory cells (27). It follows that administration of GABA_B receptor antagonists in our study leads to an increase in presynaptic hair cell intracellular Ca²⁺ concentration, and thus to increased transmitter release and an increase in afferent gain. We hypothesize that the phase retardation associated with antagonist administration can be attributed to blockade of postsynaptic GABA_B receptors, which effectively differentiate the afferent response, generating gain slopes approximating 1. This hypothesis can also account for the effects of GABA_B receptor antagonists on afferent fiber adaptation to maintained velocity steps. The differential rates of recovery of these putative presynaptic and postsynaptic effects after antagonist administration suggest that the binding constants for these drugs vary at different sites. Finally, the regularity of interspike interval discharge is attributed to the activation of K⁺ conductances in postsynaptic elements (29). Because GABA_B receptor activation has been demonstrated to increase K⁺ conductance, it is not surprising that GABA_B receptor antagonism alters the discharge regularity of the afferents.

Results are also in concert with complex findings of GABA_B receptor-related mechanisms in various mammalian brain regions, in which evidence for both presynaptic and postsynaptic GABA_B receptors has been presented (cf. ref. 26). For example, in the hippocampus baclofen decreases mean quantal content and amplitude in transmission between dentate gyrus granule cells and CA3 pyramidal cells (30). Of note, the decrease in quantal amplitude displayed both presynaptic and postsynaptic components. Low doses of baclofen suppressed both the presynaptic and postsynaptic components almost equally, whereas high doses had a more profound presynaptic action (30). A similarly complex result has been reported in studies of the endbulb of Held (31).

Perforce, vestibular afferents in the present study achieve a mathematical differentiation presumably by convergence of excitatory and time-delayed inhibitory inputs on single afferents by using Eq. 4, a mechanism analogous to the definition of the derivative, i.e.

where α = 1 for the standard first-order derivative. In this simple conceptual model, the differentiation becomes ineffective as the frequency is increased because of the time delay (δ) inherent in G protein-coupled receptor signaling pathways and is imperfect because of the imbalance of the temporal waveforms of inhibitory and excitatory synaptic inputs (α ≠ 1).