Barrier-limited, microsecond folding of a stable protein measured with hydrogen exchange: Implications for downhill folding

Abstract

Folding experiments are conducted to test whether a covalently cross-linked coiled-coil folds so quickly that the process is no longer limited by a free-energy barrier. This protein is very stable and topologically simple, needing merely to “zipper up,” while having an extrapolated folding rate of k_f = 2 × 10⁵ s^-1. These properties make it likely to attain the elusive “downhill folding” limit, at which a series of intermediates can be characterized. To measure the ultra-fast kinetics in the absence of denaturant, we apply NMR and hydrogen-exchange methods. The stability and its denaturant dependence for the hydrogen bonds in the central part of protein equal the values calculated for whole-molecule unfolding. Like-wise, their closing and opening rates indicate that these hydrogen bonds are broken and reformed in a single cooperative event representing the folding transition from the fully unfolded state to the native state. Additionally, closing rates for these hydrogen bonds agree with the extrapolated barrier-limited folding rate observed near the melting transition. Therefore, even in the absence of denaturant, where ΔG_eq ≈ -6 kcal·mol^-1 (1 cal = 4.18 J) and τ_f ≈ 6 μs, folding remains cooperative and barrier-limited. Given that this prime candidate for downhill folding fails to do so, we propose that protein folding will remain barrier-limited for proteins that fold cooperatively.

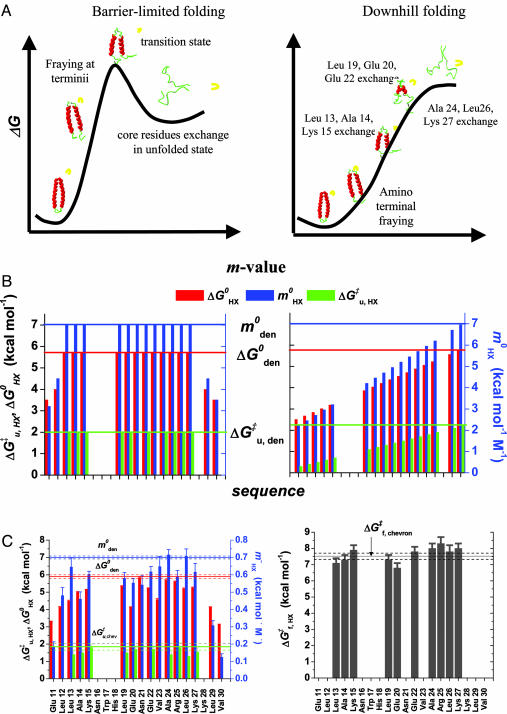
The two-state approximation of protein folding, in which the unfolded and native states are separated by a single free-energy barrier and no other species accumulate to a significant degree, appears to be adequate for most small proteins (1). Nevertheless, it is unsatisfying because it generally precludes identifying the individual steps involved in the folding process. To overcome this problem, experiments (2, 3, 4, 5, 6) have pursued the elusive theoretical prediction of “downhill folding” (7, 8, 9) (Fig. 1). If attainable, a downhill energy surface may allow the experimental identification of a series of intermediate states along the folding pathways that likely exists but largely has been observed only in computer simulations.

Fig. 1.

Barrier-limited vs. downhill folding. (A) For a two-state folding process, a free-energy barrier separates the folded and unfolded states (Left), whereas in downhill folding, no such barrier exists (Right). Native-state HX measures the free energy and surface area exposed in opening events in which hydrogen bonds are broken. (B) On a barrier-limited pathway (Left), positions on the native side of the barrier exchange at lower free energies and surface area exposure, but all other hydrogen bonds exchange from the unfolded state with the free energy (ΔG⁰_HX, red), surface area exposure (m⁰_den, blue), and rate of hydrogen bond breakage (unfolding free energies; ΔG^‡_u,HX, green) as global unfolding. In downhill folding for GCN4p2C (Right), a ladder of openings with increasing free energy, surface area exposure, and unfolding free energies starts at the N terminus, which is the last region of the protein to refold (11, 12). (C) HX data shown in Fig. 2 are replotted for comparison with the barrier-limited and downhill scenarios shown in B. For centrally located amide protons, ΔG⁰_HX = ΔG⁰_den, m⁰_HX = m⁰_den, ΔG_u,HX = ΔG^‡_u,chevron, and ΔG^‡_f,HX = ΔG^‡_f,chevron, demonstrating that these residues exchange concertedly in a global unfolding event. Cooperativity and agreement with measurements taken near the equilibrium midpoint, where folding is known to be barrier-limited, indicate that the folding remains barrier-limited even in the absence of denaturant. Dashed lines indicate one standard deviation from the mean.

Downhill-folding behavior is predicted to occur when folding rates approach the value of the attempt frequency of the barrier crossing process,

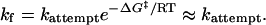Here, the barrier height does not contribute to the rate, and ΔG^‡ ≈0. This limit may be likened to extreme Hammond behavior (10) in which the folding transition state moves so far to the starting condition in response to heightened stability that the transition state coincides with the unfolded state.

A barrier-free reaction must be extremely rapid, but how fast is fast enough? Estimates from measured rates of helix, loop, and hairpin formation, reaction-rate and polymer-collapse theories, and folding simulations suggest that the minimum possible folding time constant is on the order of 1 μs (6). Because of the increased ruggedness of the energy landscape, downhill folders of high stability would have proportionally slower folding rates, as would those with longer sequences and greater β-sheet content. After correcting for length and stability, 12 proteins with predicted barrier-free time constants of <100 μs have been identified as potential downhill folders (6).

The folding speed and stability of the covalently cross-linked variant of the dimeric yeast transcription factor GCN4 coiledcoil places it with the top members of this group (11, 12). For the version GCN4p2C, with the Gly-Gly-Cys tether located at the C terminus, the extrapolated folding time constant is τ_f ≈ 10 μs and <1 μs when normalized for the high stability of the molecule (6). This fast folding rate may be due to a simple topology that requires that the helices only “zipper-up.” These qualities identify it among the most likely candidates for downhill folding. Here, we investigate whether this prime candidate does, in fact, exhibit such behavior. By combining traditional stopped-flow and denaturation experiments with native-state hydrogen exchange (HX) under EX1 and EX2 conditions (13, 14), we found that even in the absence of denaturant, where folding rates approach those predicted for downhill behavior and stability is -6 kcal·mol^-1 (1 cal = 4.18 J), folding remains cooperative and barrier-limited.

Materials and Methods

Peptides. GCN4p2C (Ac-RMKQLEGKVEELLAKNWHLENEVARLKKLVGERGGC) was synthesized as described in ref. 12. Bubbling of oxygen for 1 h at pH 9 in 20 mM borate buffer resulted in the formation disulfide bond between the terminal cysteines. To facilitate HX measurements, we inserted D7G and S14A substitutions, which accelerate unfolding and folding rates, respectively (11, 12). A Y17W substitution provides a fluorescent folding probe. Positions Leu-12, Leu-13, Ala-24, and Leu-26 were ¹⁵N-labeled to reduce NMR spectral overlap. Product identity and purity were confirmed by MS. Experiments were conducted in 0.2 M sodium chloride/10 mM phosphate/10 mM borate buffer at 40°C. Peptide concentrations were determined by using ε_280nm^1cm = 11,200 M^-1·cm^-1.

Equilibrium and Stopped-Flow Measurements. CD and fluorescence measurements were performed with a J715 spectropolarimeter (Jasco, Easton, MD) with a 1-cm path length. For rapid mixing fluorescence experiments, we used an SFM-400 stopped-flow apparatus (Biologic, Grenoble, France) connected by a fiberoptic cable to a A101 arc lamp (PTI, South Brunswick, NJ) with a 0.8-mm path length. For fluorescence spectroscopy, we used excitation and emission wavelengths of 280-290 nm and 300-400 nm, respectively.

Hydrogen-Exchange Theory. Spontaneous structural f luctuations break and reform hydrogen bonds at an unfolding rate, k_u, and a folding rate, k_f. When broken, and when amide proton is exposed to solvent of approximately pH >4, HX is base catalyzed and occurs according to the following (13, 15):

[1]

where k_int is the intrinsic exchange rate of an exposed amide proton, which depends on the identity of the amino acid, its N-terminal neighbor, and temperature, as calibrated in refs. 16 and 17, and is found to be accurate to within a factor of two. Provided that k_f and k_u are pH-independent, the observed exchange rate is given by the following expression:

[2]

For a stable protein in the EX1 limit where k_u < k_f << k_int[OH^-], every opening event leads to exchange, and the observed HX rate reduces to k_HX = k_u. In the EX2 limit where k_f >> k_int[OH^-], the protein establishes an equilibrium between the two states. The HX rate reduces to the fraction of time the protein is exchange competent multiplied by the rate of exchange in that state, k_HX = (k_u/k_f) k_int[OH^-] = K_eq k_int[OH^-]. Because K_eq equates to the unfolding equilibrium constant, the free energy required to break the hydrogen bond is accessible from measurements taken in the EX2 regime, ΔG_HX = -RT ln[(k_HX/(k_int[OH^-])].

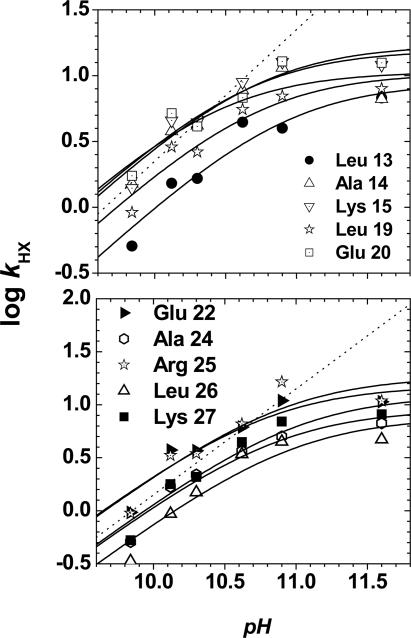
At lower pH, at which the EX2 condition occurs, k_int[OH^-] (and, therefore, k_HX) increases logarithmically with pH. At higher pH, at which exchange is governed by the EX1 mechanism, k_HX is independent of k_int[OH^-], and k_HX reaches a maximum equal to k_u. The measurement of the exchange rate over a pH range spanning the EX2 to EX1 behavior enables calculation of k_f, k_u, and K_eq, according to Eq. 2, provided that these parameters are pH-independent.

NMR Spectroscopy. Spectra were taken on a Unity Inova 600-MHz spectrometer (Varian) at a protein concentration of 0.5-2 mM. Amide proton resonances have been assigned (18) and were confirmed with 2D NOESY and total correlation spectroscopy (TOCSY) spectra. HX rates were determined with 1D spectra by using two sequences. At pH >9.5, at which exchange occurs faster than 0.5 s^-1, rates were measured by using the CLEANEX pulse sequence (19). This sequence acts by dephasing the protein NMR resonances while maintaining coherence of solvent protons. As exchange occurs, amide protein peaks reappear, and the heights of these peaks after exchange periods of different length are subjected to initial slope analysis to determine k_HX. Accuracy of the CLEANEX sequence is limited to rates of approximately >0.5 s^-1.

At pH <9.5, EX2 exchange often occurs more slowly, so these rates were measured by dephasing solvent protons and fitting the resulting exponential decrease in the amide peaks as they undergo chemical exchange with solvent proteins (16, 17). However, unlike the CLEANEX sequence, this method does not account for possible nuclear Overhauser effect (NOE) contributions to relaxation, which could result in a slight overestimate of k_HX for residues that have an NOE with a solvent molecule. Manipulation of the HSQC phase cycling in this second sequence allowed relaxation curves of ¹⁵N- and ¹⁴N-attached protons to be obtained independently.

Results and Discussion

Standard Equilibrium and Kinetic Measurements. A combination of equilibrium denaturation and chevron analysis identifies the folding of GCN4p2C as cooperative and barrier-limited under conditions near the denaturant melting transition at 40°C. The results of denaturation melts (Fig. 2) and standard (ms) stoppedflow experiments (Fig. 3) are analyzed according two-state folding transition, with ΔG_eq, ΔG^‡_f, and ΔG^‡_u depending linearly on denaturant concentration (20).

[3a]

[3b]

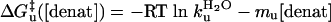[3c]

The slopes m⁰, m_f, and m_u represent the difference in the amount of denaturant-sensitive surface area buried between the initial and final states for the transition under consideration.

Fig. 2.

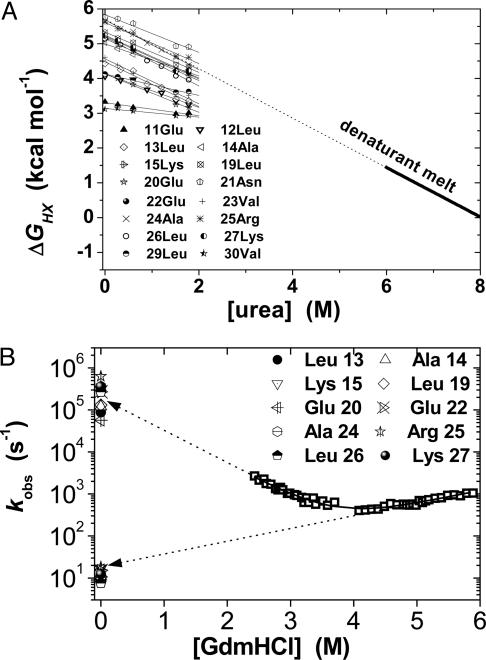
Denaturant dependence of equilibrium and kinetic parameters. (A) Stability monitored by HX under EX2 conditions (pH 9), for 16 amide protons in the center of GCN4p2C compared with the global stability measured by a denaturation profile (solid line). The exchange of most stable hydrogen bonds matches the (extrapolated) global stability of the protein (dotted line). (B) Denaturant dependence of folding and unfolding rates. The slopes of the chevron plot indicate the degree of surface area burial during the folding process. The rates of hydrogen bond formation and breakage for the 10 most stable amide protons (obtained from EX1/EX2 data shown in Fig. 3) equal the extrapolated folding and unfolding rates of the entire molecule. These data are also presented separately for each residue shown in Fig. 1C.

Fig. 3.

Native-state HX. The pH dependence of HX for the 10 resolvable protons is fit to Eq. 2 to determine the kinetics of hydrogen bond formation and breakage for each amide hydrogen. The resulting kinetic values are shown in Figs. 1C and 2B in and Table 1. The dotted diagonal line has a slope of 1, illustrating that at approximately pH <10, exchange occurs in the EX2 regime.

The observed kinetic rates, extrapolated to zero denaturant, are k_f = 1.7 ± 0.5 × 10⁵ s^-1 and k_u = 19 ± 6 s^-1. The equilibrium properties can be obtained from the kinetic parameters according to ΔG⁰_H2O = -RTlnk_f^H₂O /k_u^H₂O and m⁰ = m_u - m_f. These equilibrium values are in agreement with their kinetically determined counterparts (ΔG⁰_H2O = 5.91 ± 0.07 vs. 5.7 ± 0.2 kcal·mol^-1 and m⁰_GdmHCl = 1.57 ± 0.02 vs. 1.52 ± 0.05 kcal·mol^-1·M^-1, respectively). This result is widely accepted as a demonstration of a two-state, barrier-limited folding scenario (21).

Fluorescence measurements at six different pH values between 9.0 and 11.6 (see Fig. 4, which is published as supporting information on the PNAS web site) confirm that stability and surface burial do not vary significantly over this pH range. The insensitivity of ΔG_eq to pH simplifies the subsequent analysis of HX data taken over this pH range.

HX Measurements. The equilibrium and kinetic measurements described above indicate that the coiled-coil folds in a cooperative, two-state manner under conditions near the unfolding transition, ≈3 M GdmHCl. It is of central interest whether this barrier-limited behavior persists even in the absence of denaturant, where the extrapolated stability and folding rate are -5.7 kcal·mol^-1 and k_f = 1.7 × 10⁵ s^-1, respectively. These parameters, along with k_u, can be obtained under fully native conditions by monitoring HX rates in the EX2 and EX1 limits.

The ability to obtain this information under such highly stable conditions is generally unachievable with other rapid measurement techniques, such as pressure or T-jumps, where only a limited thermodynamic perturbation is obtainable. Furthermore, HX monitors multiple amide protons simultaneously, providing the stability and folding rates for ≈12 sites across the protein in which to test whether folding remains barrier-limited.

The linear pH dependence of log k_HX indicates that exchange is occurring in the EX2 regime at approximately pH <10 (data not shown). In this regime, the HX rate of an amide proton is proportion to K_eq of the associated hydrogen bond. For the 11 resolvable residues between positions 13 and 27, the HX-determined stability, ΔG_HX, equals the ΔG⁰ for whole-molecule unfolding (Fig. 2 A and Table 1). Furthermore, measurements taken across five to seven urea concentrations indicate that for these residues, m⁰_HX = m⁰. That is, these hydrogen bonds exchange in a reaction with the same free energy and surface exposure as the entire N↔U reaction. Therefore, the exchange of these amide protons monitors the global unfolding process.

Table 1. Equilibrium and kinetic parameters determined from HX.

Residue	ΔGeq,* kcal mol-1	m0,* kcal mol-1·M-1	kf,† × 105 s-1	ku,† s-1	P values§ for ΔG‡f (ΔG‡u)
Glu-11	3.30 ± 0.03	1.87 ± 0.26	ND	ND	NA
Leu-12	4.13 ± 0.05	4.80 ± 0.46	ND	ND	NA
Leu-13	4.48 ± 0.06	6.45 ± 0.53	0.88 ± 0.39	8.8 ± 2.7	0.20 (0.07)
			(7.1 ± 0.3)	(1.4 ± 0.2)
Ala-14	4.99 ± 0.05	4.60 ± 0.42	1.2 ± 0.7	10.7 ± 3.2	0.57 (0.16)
			(7.3 ± 0.3)	(1.5 ± 0.2)
Lys-15	5.14 ± 0.02	6.03 ± 0.18	3.1 ± 1.4	17.0 ± 4.9	0.27 (0.75)
			(7.9 ± 0.3)	(1.8 ± 0.2)
Leu-19	5.33 ± 0.04	5.80 ± 0.33	1.3 ± 0.5	10.4 ± 2.6	0.53 (0.12)
			(7.3 ± 0.2)	(1.5 ± 0.2)
Glu-20	4.13 ± 0.03	5.53 ± 0.25	0.57 ± 0.24	15.6 ± 4.0	0.03 (0.58)
			(6.8 ± 0.3)	(1.7 ± 0.2)
Asn-21	5.83 ± 0.06	5.41 ± 0.42	2.7 ± 1.4	15.1 ± 5.2	0.47 (0.58)
			(7.8 ± 0.3)	(1.7 ± 0.2)
Glu-22	5.22 ± 0.03	6.18 ± 0.30	ND	ND	NA
Val-23	4.57 ± 0.06	6.48 ± 0.58	ND	ND	NA
Ala-24	5.68 ± 0.03	7.15 ± 0.30	3.6 ± 1.5	9.0 ± 2.6	0.16 (0.07)
			(8.0 ± 0.3)	(1.4 ± 0.2)
Arg-25	5.61 ± 0.04	5.90 ± 0.35	6.3 ± 4.2	18.4 ± 8.7	0.08 (0.92)
			(8.3 ± 0.4)	(1.8 ± 0.3)
Leu-26	5.20 ± 0.05	7.06 ± 0.44	2.7 ± 1.5	7.6 ± 3.1	0.50 (0.07)
			(7.8 ± 0.4)	(1.3 ± 0.3)
Lys-27	5.24 ± 0.05	6.16 ± 0.50	3.6 ± 1.8	12.3 ± 4.3	0.20 (0.33)
			(8.0 ± 0.30)	(1.56 ± 0.22)
Leu-29	4.13 ± 0.03	3.08 ± 0.28	ND	ND	NA
Val-30	3.14 ± 0.02	1.24 ± 0.20	ND	ND	NA

Values given are at 40°C. ND, not determined; NA, not applicable.

^*From HX data under EX2 conditions (pH 9.2), as shown in Fig. 2A

^†Values in parentheses are ΔG^‡_f = RT In k_f or ΔG^‡_u = RT In k_u determined from the EX1/EX2 data shown in Fig. 3

^§The P values are 0.03-0.92 for ΔG^‡_f (ΔG^‡_u), obtained from HX data relative to that from the chevron data, indicating that there is no significant evidence that the HX and chevron data are not monitoring the same process. The P value is defined as the probability of getting observed values of ΔG^‡_f (ΔG^‡_u) from HX and chevron measurements with a greater difference than observed

A complete analysis of the pH dependence of HX rates provides the corresponding kinetic parameters (Table 1 and Figs. 1C, 3, and 5, which is published as supporting information on the PNAS web site). At pH ≈11, exchange shifts from the EX2 to the EX1 limit. Here, k_f is slower than the intrinsic HX rate in the exposed state, k_int, so that every opening results in exchange and k_HX = k_u. The transition from EX2 to EX1 occurs when k_f ≈ k_int, which is different for each amide proton because k_int depends on the amino acid sequence. Fitting the exchange data taken at pH 10-12 to Eq. 2 for the globally exchanging amide protons indicates that each of the associated hydrogen bonds breaks and reforms at the chevron-extrapolated unfolding and refolding rates for the entire molecule (Figs. 1C and 2B and Table 1).

Folding Remains Barrier-Limited. The HX measurements indicate that the folding behavior in the absence of denaturant is qualitatively the same as at the melting transition, where folding is barrier-limited. From the equilibrium perspective, the exchange of the centrally located amide protons occurs in the same, cooperative global unfolding process (Fig. 1 A and B). From the kinetic perspective, their closing and opening rates indicate that the most stable hydrogen bonds are broken and reformed in a single kinetic event representing the transition from N to U and back. In addition, k_f and k_u agree with the (extrapolated) barrier-limited rates within statistical error (Figs. 1C and 2B, and Table 1). Therefore, even in the absence of denaturant, where ΔG⁰ = -5.7 kcal·mol^-1 and τ_f = 6 μs, folding remains barrier-limited.

This conclusion is reinforced when the results for amide protons located at opposite ends of the protein are considered in light of the known folding pathway. Folding begins near the cross-linked C terminus and proceeds toward the N terminus (11, 12). Were folding to occur on a downhill landscape, hydrogen bonds toward the C terminus would unfold last and, thus, require the most energy and surface area exposure to exchange (Fig. 1B Right). Likewise, their opening rates would be slower than for bonds located at the N terminus. Neither of these two behaviors associated with downhill folding is observed, further amplifying the barrier-limited nature of the folding reaction.

It may be considered that the HX data could be fit by using a stretched exponential, which is a probable, but necessary, signature of downhill folding (7, 8, 9). Stretched exponential kinetics are appropriate for landscapes that are not dominated by a single kinetic barrier; for example, one of high dimensionality that is best described with a diffusion equation on a downhill landscape. Although the HX analysis is consistent with the folding process being limited by a single barrier, a more complex reaction scheme with additional parameters cannot be ruled out based on the fitting of the HX data alone.

However, this ambiguity can be circumvented by measuring k_f, k_u, K_eq, and their m values for multiple residues along the core of the protein (Fig. 1). In the situation in which the core residues have the same values for these parameters and they agree with their equilibrium counterparts, we are able to conclude that a cooperative, barrier-limited scenario is consistent with the measurements, whereas a downhill folding scenario is not.

This experimental strategy for distinguishing between the two major scenarios is superior to one that relies on a fit to a stretched exponential to argue for more complex behavior. True stretched exponential behavior may be hard to distinguish from barrier-limited behavior when there are additional phases associated with (i) heterogeneity in the unfolded state (e.g., cis/trans proline isomers), (ii) pathways with different kinetic barriers (multiple pathways), or (iii) experimental artifacts including aggregation, chromophore bleaching, temperature instability, and sample impurities, including posttranslational modifications.

Denaturant Does Not Alter Folding Behavior. Denaturants exert their destabilizing influence by interacting preferentially with the denatured state. Hence, even moderate concentrations of denaturant may stabilize the unfolded state such that it is more stable than an intermediate position, thereby creating an energetic barrier when one does not normally exist (3). However, HX data taken in the absence of denaturant identifies folding rates consistent with the chevron extrapolation. Because the extrapolation assumes barrier-limited behavior with the same denaturant dependence as observed near the melting transition, the values of m_f, m_u, and m⁰ measured in denaturant persist in its absence. Thus, not only is the barrier present in the absence of denaturant, but the surface burial in the unfolded and transition states is unchanged as well.

Cooperativity and Downhill Folding. Barrier-limited folding near the melting transition has been observed for many proteins. Barrier-limited behavior is associated with folding cooperativity. Whenever a system can be described with two thermodynamic states, a free-energy barrier, by necessity, must separate the two energy wells. Hence, a demonstration of cooperativity even in equilibrium mode is sufficient to preclude downhill folding. Munoz and coworkers (4) used this reasoning in reverse, arguing that the noncooperative equilibrium folding of the Escherichia coli BBL protein implies a downhill energy landscape.

Other ultra-fast folding proteins have been analyzed successfully in terms of a two-state process (22, 23), implying that barrier crossing reaction is an appropriate description for these systems as well. Generally, proteins fold cooperatively, either at the global, domain, or subglobal level (24, 25, 26). Therefore, downhill folding is likely to be limited to a few atypical systems, such as “molecular rheostats” (4) or, possibly, designed proteins with an unusually high hydrophobic content (27).

Early Folding Steps Are Uphill. Cooperative-folding behavior requires that early folding steps be uphill in free energy relative to the unfolded state. The unfolded state, however, can depend on the solvent condition (1, 28, 29, 30, 31). For example, changes in the CD signals observed upon a jump from high to low denaturant can be due to the average backbone conformation undergoing a minor population shift from a polyproline II geometry to a helical geometry (although not necessarily authentic helix formation, which requires a stretch of four residues) (31). This relaxation process is likely to be noncooperative across the chain and may appear to be downhill.

Downhill folding requires conditions in which initial chain-chain interactions are stronger than interactions between the chain and solvent. For two-state systems satisfying the chevron criteria m⁰ = m_u - m_f, no denaturant sensitive surface is buried before the kinetic barrier, implying that few, if any, additional protein-protein contacts are formed upon the jump to native conditions. Consistently, we found by using small-angle x-ray scattering that two small proteins, Ubiquitin and ctAcp, do not undergo any measurable collapse upon a jump to a low denaturant condition (31). This behavior is echoed in studies of nonfolding versions of lysozyme (32) and RNase A (J. Jacob and T.R.S., unpublished data), created by reduction of their four disulfide bonds. Therefore, protein-protein interactions are weak compared with those with solvent early in the folding process, even under aqueous conditions.

It is appreciated that hydrophobic interactions are enhanced upon the shift to aqueous conditions. However, such contacts are largely inhibited by the loss of conformational entropy (both backbone and side-chain) and the desolvation of the main chain. Empirically, water is a sufficiently good solvent that generic intra-chain contacts do not outweigh protein-solvent interactions. Certainly, these issues pointing to the uphill nature of early folding steps are only part of the origin of cooperativity, but they are the portions that pertain to the difficulty of encountering downhill folding.

Conclusion

With its simple topology, high stability, and extremely fast folding rate, GCN4p2C is a prime candidate for downhill folding. Nevertheless, even in the absence of denaturant, its folding behavior retains all of the barrier-limited characteristics observed under moderate denaturant concentrations. Although faster-folding proteins may possibly be found and would merit consideration as candidate downhill folders, the results given here suggest that the search may prove to be difficult in biologically relevant systems. Proteins that fold cooperatively cannot do so in a downhill manner. Nearly all single-domain proteins, as well as subunits of larger proteins, fold cooperatively and, therefore, are barrier limited. Downhill folding requires that initial protein-protein interactions be stable. With most naturally occurring proteins, sufficiently strong protein-protein interactions may be possible only in unusual solvent conditions, such as in sodium sulfate; however, such conditions also are likely to produce aggregation and nonnative species.