A biochemical oscillator explains several aspects of Myxococcus xanthus behavior during development

Abstract

During development, Myxococcus xanthus cells produce a series of spatial patterns by coordinating their motion through a contact-dependent signal, the C-signal. C-signaling modulates the frequency at which cells reverse their gliding direction. It does this by interacting with the Frz system (a homolog of the Escherichia coli chemosensory system) via a cascade of covalent modifications. Here we show that introducing a negative feedback into this cascade results in oscillatory behavior of the signaling circuit. The model explains several aspects of M. xanthus behavior during development, including the nonrandom distribution of reversal times, and the differences in response of the reversal frequency to both moderate and high levels of C-signaling at different developmental stages. We also propose experiments to test the model.

Myxobacteria are common soil bacteria that are often studied for their multicellular social behavior (1, 2). The life cycle of the myxobacterium Myxococcus xanthus resembles, in many respects, that of the well studied slime mold Dictyostelium discoideum. These rod-shaped cells propel themselves by a mechanism called “gliding” and, when food is scarce, aggregate into giant swarms, which then coalesce into giant streams that lead to fruiting bodies containing the spores that will seed the next generation. During this aggregation, they pass through a developmental stage called the “ripple phase” characterized by elaborate patterns of waves that propagate over the colony surface. These waves generate the same kinds of patterns observed in Dictyostelium aggregations, including wave, bulls-eye, and spiral patterns. However, these wave patterns are unlike those in D. discoideum in several crucial respects. First, they can persist for long periods in the absence of mass transport. Second, the spatial patterns in D. discoideum are organized by relaying diffusible morphogens, whereas myxobacteria communicate by direct cell contact only. Third, D. discoideum waves, like those in chemical wave systems, annihilate one another when they meet, whereas colliding waves of myxobacteria appear to “pass through” one another. This is an illusion: the waves actually reflect off one another, with every participating bacterium simply oscillating back and forth. A mathematical model for these waves and for the swirling aggregations that follow has been published (3, 4). Alternative models of rippling sharing similar ingredients have been developed (5–7).

When experiments are interpreted with the mathematical model, several important properties of the signaling system that control reversals of gliding direction stand out.

• The reversal time distribution is not random (i.e., not Poisson), and there are short pauses during reversals.

• There is a “refractory period” after each reversal during which the cell is not responsive to signaling.

• Signaling induces reversal during ripple stages of development but suppresses reversals during the streaming and aggregation stages of development.

These observations led us to hypothesize an internal biochemical cycle that acts as a “clock” to control reversals. Collisions between cells affect the speed of the clocks in both cells, leading to synchronization. With this assumption, the model successfully reproduces observed spatial patterns. However, the treatment of the reversal clock was abstract and did not involve any biochemical modeling (3, 4). Here we provide a biochemical model for this clock that explains both the cellular oscillations and the developmental progression of myxobacteria morphogenesis from vegetative swarming to the ripple phase and thence to the swirling aggregation phase that leads to fruiting body formation. The model is based on the components of the reversal regulating system in M. xanthus known from biochemical and mutational studies.

Biological Background

In the presence of nutrients, myxobacteria swarm outward and feed cooperatively by secreting digestive enzymes. When nutrients run low, they cease swarming and initiate a developmental program that culminates in the formation of fruiting bodies (1, 2, 8). This developmental switch requires the passage of at least two signals: the diffusible A signal and the cell surface-associated C-signal (2). C-signaling between cells requires direct end-to-end contact and influences the coordination of motion of individual cells, the shape of fruiting bodies, and the timing of sporulation (2, 9–17).

Individual myxobacteria are 5–7 μm long and ≈0.5 μm in diameter. Cells glide on surfaces by using two genetically distinct molecular motors, both of which are concentrated at the cell poles. It has been suggested that the Adventurous, or A-motility, motor generates propulsive force by extruding slime from nozzle-like organelles at the posterior pole (18). The pressure generated as the slime hydrates pushes the cell forward. The Social, or S-motility, system operates when the cells are in proximity to other cells. Type 4 pili extend from the forward pole, attach to fibrils secreted by nearby cells, and retract, pulling the cells together (19). Cells change direction not by making a U turn, but by reversing the polarity of their A and S motors. C-signaling coordinates the movements of individual cells by influencing the frequency of reversals, analogous to the run-tumble frequency of swimming Escherichia coli. C-signaling mutants are defective in aggregation and do not display developmental changes in reversal frequencies (12, 13, 16, 17). Mutational studies show that myxobacterial Frz (“frizzy”) proteins modulate reversal frequencies in growing cells and affect their aggregation abilities (20–23). Frz system components have many sequence homologies with those of the chemosensory signal transduction pathway (Che system) of E. coli (24).

Aggregation into fruiting bodies is often preceded by a pattern of traveling density waves (often referred to as ripples) that propagate over the surface of the bacterial culture (16, 25–27). Darker bands (crests) correspond to higher cell density, whereas lighter bands (troughs) are less dense. Counterpropagating crests appear to pass through one another unaffected, unlike developmental waves in Dictyostelium or Turing instability patterns in diffusion–reaction systems, which annihilate upon collision (28–31). A mathematical model of the myxobacteria traveling waves explains most of their characteristics (3, 4). In particular, the model shows that the waves do not pass through one another; rather, colliding waves reflect off one another, so that a crest oscillates back and forth between neighboring crests. Cell marking experiments show that each cell oscillates back and forth, reversing, on average, at the points of crest collisions. The model is based on the assumption that each cell has an internal biochemical cycle (“clock”) that controls the reversals. Head-to-head collisions between cells result in exchange of C-signal and speed up the reversal cycle; this initiates the events leading to synchronization of the cells' reversal cycle.

After ≈4–6 h of starvation, movement patterns begin to change. Cells commence organizing themselves into locally aligned streams and move with increased gliding speeds with longer intervals between reversals (13, 17). Eventually, transient “traffic jams” of cells form, and streams of cells become trapped in the circular orbits around the aggregates. Some of the aggregates break up, but others continue to grow and eventually form fruiting bodies. These developmental changes depend on C-signaling (13, 17). A mathematical model of the streaming and aggregation stages of development predicts all of these phenomena (3).

In this paper, we propose a cascade model that shows how the biochemical pathway that connects C-signal to the Frz proteins can transform into a sustained oscillator.

A Model for Oscillations in the C-Signal Transduction Circuit

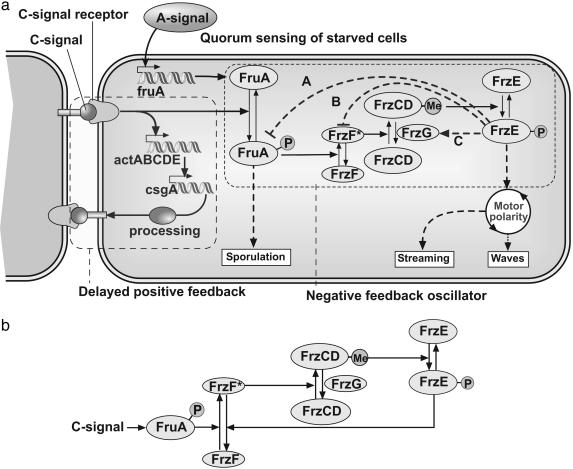
Fig. 1a summarizes the components of the reversal regulating system in M. xanthus known from biochemical and mutational studies on the Frz system, as well as the sequence homologies between the well characterized Che system of E. coli and Frz. The essential components of this signaling system and their supporting evidence can be summarized briefly.

Fig. 1.

Model for the signaling circuit in M. xanthus. (a) Schematic representation of signaling circuit of a myxobacterial cell (2). The delayed positive feedback circuit is shown by the dashed box on the left. As a result the number of C-signaling (csgA) molecules on the surface of the cell keeps increasing with every C-signaling event. The dotted box shows processing of C-signal through the cascade of covalent modifications. Several examples of hypothetical negative feedback loops that transform this circuit into an oscillator are shown by dashed lines. (b) Essential components of Frz system oscillator corresponding to feedback (B) in a. Phosphorylated FrzE deactivates methyltransferase FrzF.

Coordination of cell motion during rippling and aggregation depends on C-signaling. The C-signal is a 17-kDa cell surface-associated protein encoded by the csgA gene (2, 9, 14, 32–35). Transfer of C-signal requires direct cell–cell contact between motile cells (9, 14, 34). C-signaling could be restored to non-motile cells by mechanically aligning them end-to-end (14), suggesting that C-signaling protein is localized to cell poles or that cells exchange C-signal by end-to-end contacts (14, 16, 17).

Fig. 1a illustrates the sequence of events triggered by a signaling collision. The csgA gene expression is controlled by the C-signal itself in a positive feedback loop shown by the dashed box on the left side of Fig. 1a that includes act and csgA. Between 8 and 18 h of development, the number of C-signaling molecules on the cell surface rises steeply from a few to several hundred copies per cell (9, 36). This increase is a result of cell collisions, to which the proteins of the act operon respond by activating transcription of the csgA gene that encodes the C-signal. After enzymatic processing, the 17-kDa C-signal protein is found on the cell surface (35). Thus, signaling collisions beget an increasing amount of C-signal protein so that subsequent collisions transmit higher levels of signal.

Another response to C-signal is delimited by the dashed box on the right side of Fig. 1a. Transcription of the fruA gene is induced early (≈6 h) in development by the A-signal (15, 37). After C-signal transmission, FruA protein is activated by a posttranslational modification, most likely by phosphorylation of aspartate-59. The signal from phosphorylated FruA triggers aggregation by coordinating the cell motion. FruA-P interacts with Frz proteins related by sequence to those of the Che genes in enteric bacteria (24). As shown in Fig. 1a, the Frz system includes the cytoplasmic methyl-accepting protein, FrzCD; a methyltransferase, FrzF; a methylesterase, FrzG; and a protein kinase, FrzE (a fusion protein homolog of CheA/CheY). FrzCD is shown to be methylated in response to C-signal in a FruA-dependent manner (15, 38). Phosphorylated FruA (FruA-P) activates the methyltransferase FrzF (FrzF^* denotes the active form of FrzF). The phosphorylation of FrzE is induced by the methylated form of FrzCD. The active (phosphorylated) form of FrzE kinase induces reversals in M. xanthus (21).

Signal transduction cascades by covalent modification, such as methylation–demethylation or phosphorylation–dephosphorylation, are common in prokaryotic and eukaryotic signaling systems (39, 40). It is easy to transform these cascades into an oscillator by introducing a negative feedback between the down-stream and upstream ends of the cascade (41–43). Three hypothetical negative feedback loops that transform this circuit into an oscillator are shown by blue dashed lines. The phosphorylated form of FrzE either inhibits the phosphorylation or promotes the dephosphorylation of FruA-P (A in Fig. 1a), inhibits activation or deactivates FrzF (B in Fig. 1a), or activates FrzG by phosphorylation (C in Fig. 1a). We chose to investigate feedback (B), as shown in Fig. 1b. The rationale for this choice, as well as differences from and similarities to the other two feedbacks, are addressed in Discussion. For brevity, we shall refer to the scheme in Fig. 1b as the Frzilator (“frizzy-lator”).

Results

Here, we summarize the various dynamical behaviors exhibited by the biochemical circuit shown in Fig. 1b. The mathematical equations describing the system and the method of solution are presented in Appendix.

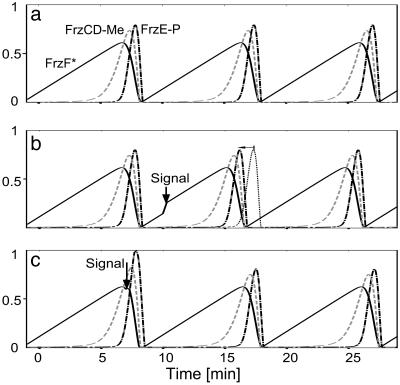
Oscillations. The covalent modification cascade with a feedback loop shown in Fig. 1b is modeled by solving the corresponding Michaelis–Menten kinetic equations (see Appendix for details). The system displays stable and robust oscillations over a wide range of parameters. The period of the oscillations can be tuned to coincide with a reversal period of isolated myxobacteria, ≈10 min (Fig. 2a).

Fig. 2.

Oscillations of Frz system components resulting from solving Michaelis–Menten kinetic equations for scheme shown in Fig. 1b. (See Appendix for details). Fractions of active FrzF, methylated FrzCD, and phosphorylated FrzE are shown by solid, dashed, and centered lines, respectively. (a) In the absence of signaling, the oscillation period can be tuned to ≈10 min, the reversal time of isolated myxobacteria cells. (b) A pulse of signaling (burst of the rate of FrzF activation) results in speeding up of the cycle, so that the maximum of FrzE-P occurs earlier (faster reversal). The dotted line shows unperturbed concentration of FrzE-P for comparison. The signaling event happens at t = 10 min, during the rising stage of active FrzF (sensitive period). (c) The pulse of the signaling does not affect the position of FrzE-P maximum. The signaling event happens at t = 7 min, during the decreasing stage of active FrzF. This stage corresponds to refractory period.

Signaling Speeds Up Reversal. When two cells collide end-to-end, their exchange of C-signal produces a pulse of downstream signal. This pulse results in a short burst in the rate of FrzF activation (see Appendix for details). This burst speeds up the oscillation cycle, as shown in Fig. 2b, so that the maximum of FrzE-P occurs earlier. This signaling pulse induces faster reversals. The mechanism by which FrzE-P induces reversal of both the A- and/or S-motility systems is unknown, and will not be addressed herein.

Refractory and Sensitive Periods. The pulse of signaling speeds up the oscillation cycle only if it occurs during the rising phase of FrzF^*. This phase corresponds to the sensitive period of the oscillator (Fig. 2b). On the other hand, the signaling pulse does not significantly shift the position of the FrzE-P maximum during the falling phase of FrzF^* (Fig. 2c). Therefore, the negative feedback oscillator has a built-in refractory period. The necessity of the refractory period is one of the main predictions of the mathematical models for rippling (3–5).

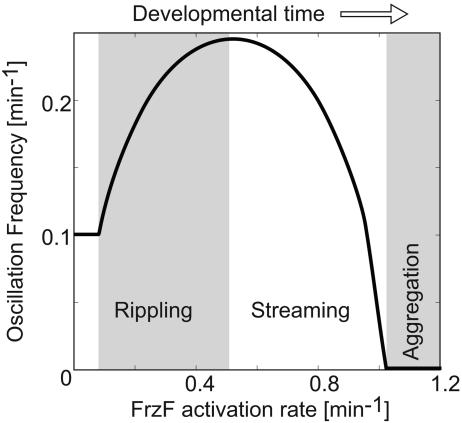
Oscillation Frequency vs. Signaling Strength. As a cell experiences more signaling events, the number of C-signal molecules on its surface rapidly increases as a result of the positive feedback loop (Fig. 1a). Therefore, as time passes, cells receive higher doses of the signal at each collision. During the streaming phase of development, cells appear to form long chains; in this configuration, each cell frequently signals the cells immediately in front and behind, suppressing their reversals (13, 17). Fig. 3 shows how the oscillation frequency is expected to vary with the increasing rate of FrzF activation that reflects the increasing signal strength. The nonmonotonic dependence of the frequency recapitulates the observed changes in reversal behavior. The frequency first rises, corresponding to the onset of the waves, then decreases, corresponding to the transition to streaming. Finally, the reversals are fully suppressed at some threshold value of the signaling rate, possibly corresponding to the later stage of aggregation at which sporulation is induced. The rationale for this nonmonotonic frequency response can be understood as follows. At low levels of signaling, the activation of FrzF is slow and deactivation of FrzF^* caused by feedback is fast (Fig. 2a). Therefore, FrzF activation is the rate-limiting process that determines the frequency. In this regime, increased signaling results in faster activation and higher oscillation frequency. At some point, rapid activation by FruA-P begins to compete with the negative feedback, and the deactivation of FrzF^* starts to slow down and becomes the rate-limiting step. At this point, the frequency is determined by the effective FrzF^* deactivation rate, and so it decreases with increasing signaling. Finally, a threshold is reached where the feedback cannot out-compete the signaling and oscillations are suppressed with nearly all FrzF activated.

Fig. 3.

Oscillation frequency of the Frzilator vs. signaling strength, defined as the maximum rate of FrzF activation, 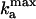(see Appendix for definitions). The nonmonotonic dependence of the oscillation frequency agrees with the nonmonotonic developmental history of reversal frequency of myxobacteria cells. The oscillations cease above a critical level of signaling.

Proposed Experimental Tests

Several experiments can be performed to test the model proposed here. One of the principal predictions of the model is that FrzE-P interacts, directly or indirectly, with FruA-P, FrzF^*, or FrzG. These interactions might be detected with yeast two-hybrid studies (44). Because FrzE receives input from FrzCD, negative feedback could be specifically targeted by using the output domain of FrzE as the bait.

A positive two-hybrid signal and all of the predicted interactions might be explored by genetic suppression. Missense mutations in the FrzE output domain that prevent regular oscillation of cell polarity could be sought from in vitro mutagenesis of that domain. Mutants are predicted to be defective in rippling and aggregation because they cannot oscillate regularly. Mutations that suppress the frzE defects and restore oscillation could be sought to pick up other relevant frz genes after chemical mutagenesis to induce point mutations in FruA, FrzF, FrzG, and the entire frizzy region.

Alternatively, once the FrzCD methylation assay is developed one can biochemically test how phosphorylated FrzE affects rates and equilibrium constants for FrzCD methylation. A long-term strategy for exploring the oscillator could include the engineering of a FrzE–GFP fusion that would emit light only when phosphorylated. The model predicts that fluorescence intensity within each cell would change periodically, correlating with the reversal of the cell.

The model also predicts that developmental changes of reversal frequencies correlate with the amount of C-signaling molecules on the surfaces of the surrounding cells. Thus, a few fluorescently labeled cells that are still early in their development could be transferred into a culture with older (longer starved) cells. These transplants should display reversal frequencies characteristic of the older cells.

An intermediate step between a C-signaling receptor and the Frz system involves the phosphorylation of FruA. Therefore, the rate of FruA dephosphorylation determines the time scale of the signaling memory, i.e., how long a cell “remembers” the signaling event. This time should be relatively short during the ripple stage, where quick responses to collisions are required for pattern formation (4). When C-signaling cells are removed from their high cell density environment and analyzed at a low cell density, they retain a high reversal frequency (12, 13, 17). This finding suggests that FruA-P is dephosphorylated fairly rapidly during aggregation.

Discussion

Most of the evidence for the circuitry shown in Fig. 1 comes from either mutation data or known homologies with the Che system of enteric bacteria. Because no quantitative measurements have been carried out to determine the kinetic parameters of the scheme, there is considerable freedom in choosing the parameters. However, numerical simulations show that the scheme in Fig. 1 is robust and its essential features depend on very few parameters. The frequency of the oscillations is mostly determined by the rate-limiting step: activation of FrzF. As long as other time constants are ≈1 order of magnitude faster than this rate, their exact values do not matter. Table 1 gives the values of the parameters used to compute Fig. 3. Because it was deduced mainly from genetic evidence, the scheme in Fig. 1b is probably oversimplified and misses some intermediate states. For example, there may be an intermediate step between FruA and FrzF activation; moreover, there is more than one methylated residue in Frz-CD (D. P. Astling, J. L. Lee, and D. R. Zusman, personal communication). The circuit shown in Fig. 1 comprises a negative feedback system with a delay resulting from the cascade of two (or possibly more) covalent modifications. It turns out that the qualitative predictions for such systems are relatively insensitive to parameter variations.

Table 1.

Parameters used in the simulations in Figs. 2 and 3

Parameter	Value
Ka	1 × 10-2
Kd	5 × 10-3
Km	5 × 10-3
Kdm	5 × 10-3
Kp	5 × 10-3
Kdp	5 × 10-3
k1a	0.08 min-1 (Fig. 2)
k2a	0 (Fig. 2a)
	0.5 min-1 (Fig. 2 b and c)
kdmax	1 min-1
kmmax	4 min-1
kdmmax	2 min-1
kpmax	4 min-1
kdpmax	2 min-1
Δt	0.5 min (Fig. 2 b and c)
t0	7 min (Fig. 2b)
	10 min (Fig. 2c)

The Frzilator model is based on the existence of a negative feedback from the downstream to the upstream ends of the covalent modification cascade. However, the robustness of this oscillator does not allow us to identify the exact place of the feedback, because all three options shown in Fig. 1a give the same qualitative results. Based on the genetic evidence, we chose the feedback denoted B in Fig. 1a. Null mutations of FrzF, FrzCD, and FrzE almost eliminate cell reversals, which is consistent with B in Fig. 1a. On the other hand, a null mutation of FrzG does not produce a nonreversing phenotype, and the mutants are still able to coordinate their motion to form fruiting bodies (20, 24); this observation excludes feedback (C in Fig. 1a). During vegetative growth, cells do not have FruA but still reverse. To account for this, one must either assume that the reversals in vegetative state are random or exclude feedback (A in Fig. 1a), and preliminary observations suggest that they are not random (D. P. Astling, J. L. Lee, and D. R. Zusman, personal communication).

The Frzilator is consistent with known and predicted properties of the C-signaling system. During the ripple phase, the pulses of signaling at collisions would speed up the oscillator. Immediately after a reversal, there is a short refractory period, during which cells are not sensitive to collisions. For certain values of the parameters (data not shown), there can be negative signaling during the refractory period, i.e., collisions slow down the oscillation, rather than speed it up. The model also explains the counterintuitive nonmonotonic developmental history of the changes in reversal frequencies shown in Fig. 3.

By adjusting the signaling strength during collisions, one can ensure that only a few signaling events are necessary for a cell to phosphorylate enough FruA to significantly affect the FrzF activation rate. In addition, a well known property of covalent modification cascades is its “zero-order ultrasensitivity” that produces a sharply sigmoidal stimulus-response behavior. This amounts to an effective cooperativity of signal processing (43, 45).

Note that, in order for a cell to reverse its direction, it must alternately activate the A (push) and S (pull) motility motors at opposite cell poles (18, 19, 46). Because the motors on both ends are presumed to be genetically and chemically identical, this process is likely controlled by a spatial chemical oscillator inside the cell, e.g., periodic assembly or disassembly of mesh-like structures at the cell poles. Similar structures are associated with the location of the division plane in enteric bacteria (the Min system oscillator) (47–52). Various models for these patterns have been constructed based on Turing instability reaction–diffusion patterns (48, 52). However, because little is known about the mechanism for coordinating the motors at opposite cell poles, we have modeled the circuit assuming spatially homogeneous distributions of the Frzilator components within a cell. This limitation can be removed once detailed experimental information is available.

Although the model presented here is unlikely to be correct in all its details, it provides a theoretical framework for understanding the biochemical circuitry underlying the reversal “clock” that has been shown to underlie the sequence of population-level patterns that myxobacteria exhibit on their way to fruiting body formation and sporulation.

Appendix: Model Equations and Parameters

To model the reaction scheme shown in Fig. 1b we follow Gonze and Goldbeter (43) and introduce the fractions of total protein concentrations corresponding to each component. The fraction of activated FrzF is given by

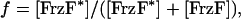[1]

the fraction of methylated FrzCD is given by

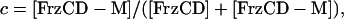[2]

and the fraction of phosphorylated FrzE is given by

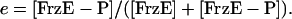[3]

By neglecting protein synthesis and degradation as well as concentrations of transient complexes with modifying enzymes, the equations for the fractions can be formulated as in ref. 43:

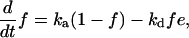[4]

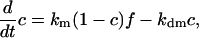[5]

and

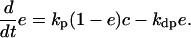[6]

The presence of e in the second term on the right hand side in Eq. 4 reflects the negative feedback exerted by FrzE-P on the accumulation of the active form FrzF. We suppose that each of the steps is an enzyme-controlled reaction described by Michaelis–Menten kinetics. Thus, the parameters for the FrzF activation–deactivation, FrzCD methylation–demethylation, and FrzE phosphorylation–dephosphorylation reactions in the above equations are given by

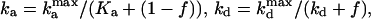[7]

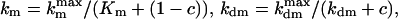[8]

and

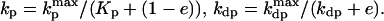[9]

When a cell collides with other cells, it receives a pulse of C-signaling that phosphorylates FruA. This, in turn, creates a burst in the activation rate of FrzF. For simplicity, we model a C-signal as a square pulse in ,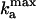

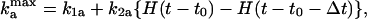[10]

where H(t) is a Heaviside function, H(t < 0) = 0, and H(t > 0) = 1, so that the expression in curly braces is a square pulse of unit amplitude. t₀ is the beginning of the signaling pulse, and Δt is its duration. The latter depends on the rate of FruA dephosphorylation. The parameters used to compute the results shown in Figs. 2 and 3 are collected in Table 1.