The solid mechanics of cancer and strategies for improved therapy

Abstract

Tumor progression and response to treatment is determined in large part by the generation of mechanical stresses that stem from both the solid and the fluid phase of the tumor. Furthermore, elevated solid stress levels can regulate fluid stresses by compressing intratumoral blood and lymphatic vessels. Blood vessel compression reduces tumor perfusion, while compression of lymphatic vessels hinders the ability of the tumor to drain excessive fluid from its interstitial space contributing to the uniform elevation of the interstitial fluid pressure. Hypo-perfusion and interstitial hypertension pose major barriers to the systemic administration of chemotherapeutic agents and nanomedicines to tumors, reducing treatment efficacies. Hypo-perfusion can also create a hypoxic and acidic tumor microenvironment that promotes tumor progression and metastasis. Hence, alleviation of intratumoral solid stress levels can decompress tumor vessels and restore perfusion and interstitial fluid pressure. In this review, three major types of tissue level solid stresses involved in tumor growth, namely stress exerted externally on the tumor by the host tissue, swelling stress and residual stress are discussed separately and details are provided regarding their causes, magnitudes and remedies. Subsequently, evidence of how stress-alleviating drugs could be used in combination with chemotherapy to improve treatment efficacy is presented, highlighting the potential of stress-alleviation strategies to enhance cancer therapy. Finally, a continuum-level, mathematical framework to incorporate these types of solid stress is outlined.

1. Introduction

Solid tumors consist of several structural components apart from cancer cells, such as blood and lymphatic vessels, the extracellular matrix (ECM) with most common constituents being the collagen and hyaluronan, and the stromal cells. Stromal cells can be further divided into three categories: a) angiogenic vascular cells, which include endothelial cells, and pericytes, b) infiltrating immune cells, which include platelets, mast cells, neutrophils, inflammatory monocytes, CD8⁺ T-cells, NK T-cells, and c) cancer-associated fibroblasts (CAFs) [1, 2]. The presence of these components in a solid tumor may vary depending on its type, location and stage of growth, and they can significantly affect the mechanical stresses exerted within as well as around the tumor.

Considering the fact that tumor progression is described by the growth of the tumor mass at the expense of the surrounding host tissue, the development of a tumor should be closely associated with the generation and accumulation of mechanical stresses. In this sense, solid tumors comprise an interesting and complex mechanical system that involves both solid and fluid mechanics, in which the stresses originating from the solid phase of a tumor determine, in large part, both the fluid stresses and cancer progression[3, 4]. Tissue-level solid stresses in tumors can be divided into three categories:

• A)stresses exerted on the tumor externally by the host tissue,
• B)swelling stresses, and
• C)residual stresses.

The reciprocal mechanical interactions between the tumor and the host tissue, as the one increases in volume at the expense of the other, give rise to externally applied stresses [5, 6]. Swelling solid stress can be a result of either the high negative charge density of hyaluronan that causes electrostatic repulsive forces among closely spaced hyaluronan chains or the swelling of cancer cells that modulate their tonicity in order to survive under compressive solid stresses [7, 8]. Finally, residual stresses are stresses remaining in the tumor when the tumor is excised and thus, any external loads from the host have been removed [9].

Solid stresses can affect cancer cell growth both directly, by compressing cancer cells, and indirectly by compressing blood and lymphatic vessels. On one hand, compression of cancer cells can hinder their proliferation rate, induce apoptosis and increase their invasive and metastatic potential [10–14]. On the other hand, compression of blood vessels causes hypo-perfusion and thus, hypoxia, whereas dysfunction of lymphatic vessels contributes to the elevation of the interstitial fluid pressure at the interior of the tumor. Interstitial hypertension creates a pressure gradient between the interior of the tumor and its periphery, which can promote tumor growth and metastasis by transferring growth factors and cancer cells from the tumor to the surrounding tissues[15]. Hypoxia fuels tumor progression and treatment resistance in multiple ways [16]; it might a) cause inflammation and immunosuppression by reducing the activity of immune cells [17, 18], b) induce a cancer stem cell-like phenotype making cancer cells more resistant to hypoxic conditions and cytotoxic drugs to drive selection of more malignant cells [19, 20], c) promote epithelial-mesenchymal transition and cancer metastasis [21], d) induce an angiogenic response causing the formation of a highly heterogeneous and abnormal vascular network [22], and e) reduce the efficacy of radiation therapy owing to insufficient oxygen supply [23]. Furthermore, hypo-perfusion and interstitial hypertension pose major barriers to drug delivery and can exclude large intratumoral areas from blood-borne therapeutic agents, which might lead to decreased efficacy of chemotherapy and nanomedicine [24, 25].

Despite the multiple origins of solid stress that evolve in tumors and their pleiotropic role in tumor progression and treatment, little work has been performed in the area of cancer biomechanics, compared to the biomechanics of other soft tissues such as blood vessels, heart valves and cartilage. In this article, the current knowledge in the tissue-level solid mechanics of cancer is reviewed and a mathematical framework for its computational description is outlined. Furthermore, strategies for alleviation of solid stresses in order to improve therapeutic outcomes in preclinical tumor models are presented and areas open for further research are discussed.

2. Solid Mechanics of Cancer

A. Externally applied solid stress

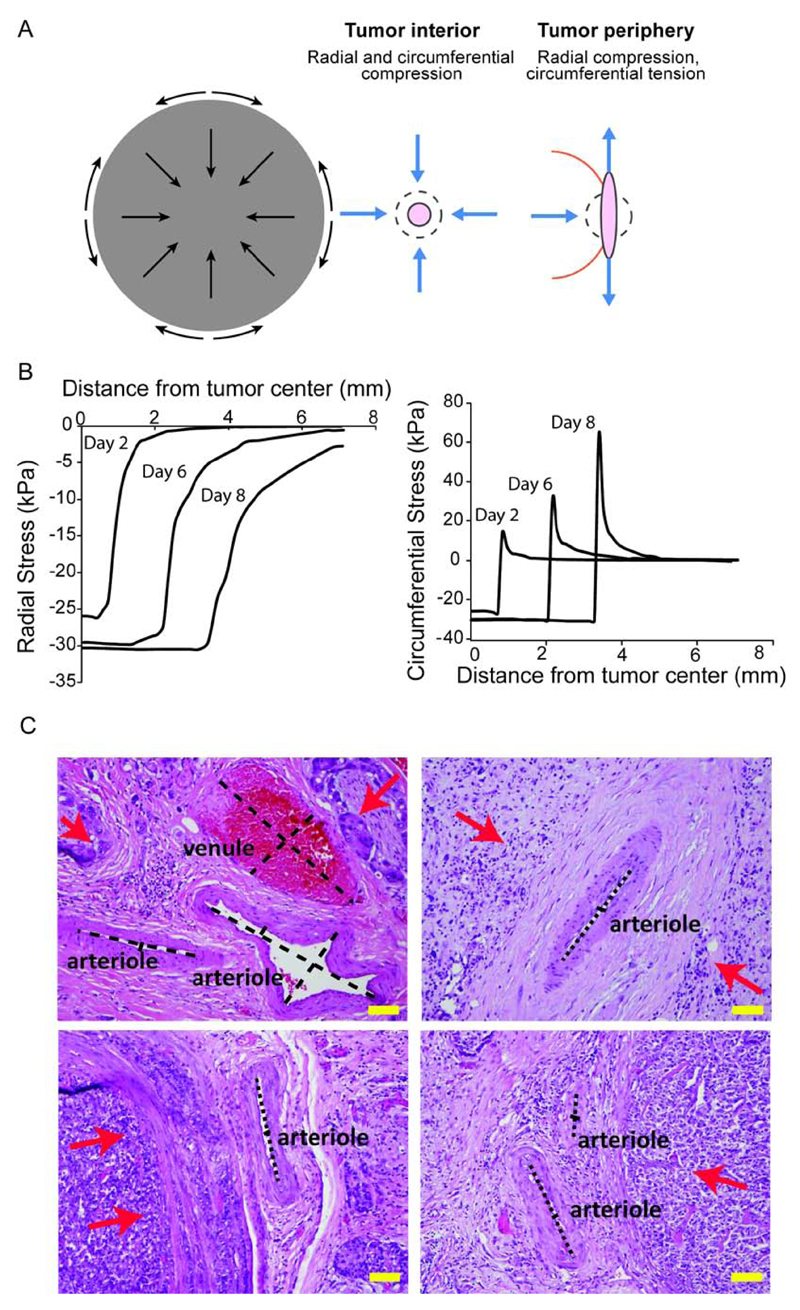
Uncontrolled cancer cell proliferation results in rapid and nonlinear tumor growth. Externally applied stress is generated as the growing tumor mass deforms the normal host tissue, which in turn resists tumor expansion. Solid tumors often stiffen as they grow in the host tissue, which is caused by the presence of increased amounts of structural components of the tumor, particularly the cancer cells and the ECM constituents. Tumor stiffening is the only mechanical aspect that patients and clinicians can feel as in many cases tumors become stiffer compared to the surrounding tissue. For example, typical elastic moduli of human breast cancer lesions have been measured in the range of 10.0-42.0 kPa (75.0-315.0 mmHg), one order of magnitude higher than the elastic modulus of normal breast (3.25 kPa/24.37 mmHg) [26]. For normal human brain tissue (gray and white matter) typical values of the elastic modulus are 2.0-6.0 kPa (15.0-45.0 mmHg) and for brain tumor tissue 35 kPa (262.5 mmHg) [27]. Tumor stiffening along with the continued accumulation of forces by the tumor constituents can displace the host tissue and allow the tumor to invade and grow in size. The mechanical properties of the host tissue play a central role in the magnitude of external solid stress in tumors [5]. Specifically, the state of stress in a tumor depends on the tumor-to-host relative stiffness; the stiffer the host tissue the higher the stress in the tumor becomes, up to a point where a plateau might be reached [5]. Given the lack of experimental methods to measure solid stress in vivo, it has been mathematically shown that the externally applied stress at the interior of the tumor can be as high as 40 kPa (300 mmHg) [5, 6]. Furthermore, both radial and circumferential components of solid stress are compressive at the tumor interior, while at the periphery of the tumor, radial stress diminishes and the circumferential stress turns rapidly to tensile (Fig. 1A&B) [6, 28–30]. These stresses are considered high enough to compress or eventually lead to the collapse of tumor vessels (Fig. 1C)[6, 31, 32]. Only recently, new experimental methods have been developed that confirmed the mathematical predictions for the contribution of the host tissue to the intratumoral solid stress and the spatial profile of the solid stress components [33].

Figure 1.

Externally applied solid stress. A) Schematic of externally applied stress at the tumor center and periphery. B) Mathematical model predictions of the spatial profile of radial and circumferential components of solid stress in tumors. C) Histological sections of human tumors show the deformation of tumor blood vessels. Top: salivary duct carcinoma (left), undifferentiated liposarcoma (right), Bottom: differentiated pancreatic neuroendocrine tumors. Red arrows show tumor location. (scale bar = 100 μm). [Adapted with permission from Reference [6]].

Contrary to most other soft biological tissues (e.g. tendons, ligaments, arteries, cartilage, heart valves etc.), little experimental work has been done on the constitutive modeling and the mechanical properties of solid tumors. In fact, there are only a few studies focusing on the mechanical response of tumors usually under confined or unconfined compression [5, 34] (Table 1). As shown in the Table, the elastic modulus of the tumors might change significantly among tumor types and it takes typical values for soft biological tissues, such as arterial walls but it is one to two orders of magnitude lower than the elastic modulus of articular cartilage and intervertebral disk [35, 36]. In these studies, tumors behave as viscoelastic solids and for their response linear elastic, hyperelastic or linear viscoelastic constitutive equations have been employed to predict their elastic/equilibrium or complete viscoelastic response [27, 34, 37–39]. Tumors, however, might have a highly non-linear stress-strain response and in these cases an exponential equation might be better suited to represent their bulk mechanical behavior [5]. Finally, it should be noted that due to the strong dependence of intratumoral stress on the mechanical properties of the host tissue, the choice of a constitutive equation appears to have small effect on the state of stress of the tumor [5].

Table 1.

Values of the elastic modulus (means and standard errors) of several tumor types. Tumors were grown in immunodeficient mice and the diameter of the tumors used for these measurements ranged from 7 to 10 mm (15-30 days post-implantation of cancer cells).

Tumor	Origin	Elastic Modulus [kPa]	Compression Experiment	Reference
MCaIV	murine mammary carcinoma	6.67±2.67	Confined	[34]
LS174T	human colon adenocarcinoma	4.00±1.33	Confined	[34]
U87	human glioblastoma	26.66±1.33	Confined	[34]
HSTS 26T	human soft tissue sarcoma	40.00±5.33	Confined	[34]
SW620	human colon adenocarcinoma	186.1±25.9	Unconfined	[5]
MCF10CA1a	human breast cancer	64.08±8.47	Unconfined	[77]
4T1	murine mammary carcinoma	64.83±7.15	Unconfined	[77]
MIA PaCa2	human pancreatic carcinoma	141.83±3.91	Unconfined	unpublished data

The effect of externally applied stress on tumor growth has been investigated in vitro with the formation of cancer cell aggregates (spheroids) grown within a three-dimensional collagen or agarose matrix of varying concentration to better mimic the host tissue. Increasing the concentration - and thus, the stiffness - of the surrounding matrix leads to decreased growth of spheroids, while their growth is completely inhibited in conditions of high concentration [10–12, 40]. Furthermore, anisotropic application of external loads can result in anisotropic spheroid growth towards the direction of lower stress levels [10, 12]. This inverse relation of tumor growth and compressive stress is attributed to an increase in cancer cell apoptosis and reduction in cell proliferation rate [12, 41].

B. Swelling solid stress

Similar to other tissues that are rich in hyaluronan, such as the articular cartilage, the interstitial space of many solid tumors has a high concentration of negative charges due to the negatively charged hyaluronan chains. This negative charge is known as the fixed charge density (FCD) of the tissue [42, 43]. Repulsive electrostatic forces among these closely spaced negative groups can cause the swelling of the tumor, which is referred to as chemical expansion and gives rise to swelling solid stress [43]. Additionally, in order for the electro-neutrality condition to be met in tumors, positively charged ions must be present within the tumor interstitial space. The latter can cause the transfer of fluid within the tumor interstitial space from the host to balance the ion concentration difference, creating a Donnan osmotic fluid pressure difference between the internal and external space of the tumor.

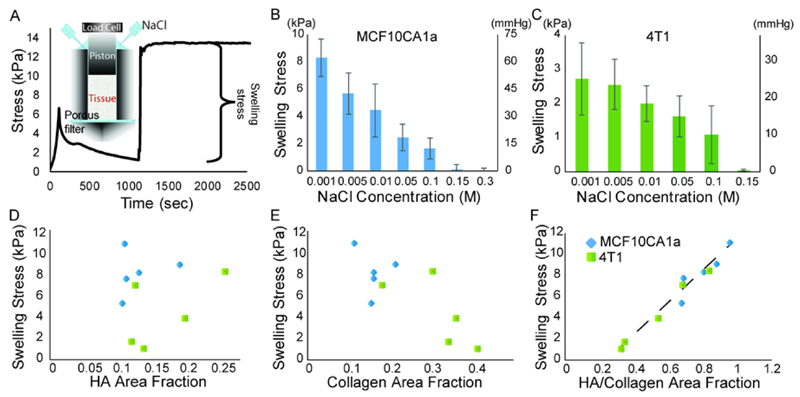
The range of electrostatic forces depends on the Debye length, a measure of the distance within which electrostatic interactions are important. The Debye length, in turn, is inversely related to the ionic strength of the fluid phase of the tumor and thus, the concentration of electrolytes within the tissue. To quantify swelling stress in tumors, an experimental set up that was initially developed for similar measurements in cartilage has been developed [8, 43]. Specifically, the confined compression experimental set up is employed. Tumor specimens are first compressed slightly to ~10% strain, so that they will start resist to deformations, followed by relaxation of the tissue (Fig. 2A). When tumors reach an equilibrium, NaCl solutions of specified concentrations are independently added to the confining chamber to create a hypotonic, isotonic or hypertonic environment, respectively. Addition of NaCl is followed by a rapid change of the recorded stress so that a new equilibrium stress is achieved. The difference between the two equilibrium stresses is the swelling stress required to keep the specimen in its initial length. The swelling stress values that have been measured are in the range of 0 kPa for isotonic and hypertonic tumor microenvironments to 10.0 kPa (75.0 mmHg) for hypo-tonic microenvironments [8]. Therefore, the magnitude of swelling stress can be within the same order as the magnitude of external stresses.

Figure 2.

Swelling solid stress. A) Schematic of the protocol for measuring swelling stress in tumors utilizing the confined compression experiment and modulated the electrolyte concentration of the tumor interstitial space. B) Swelling stress measurements as a function of NaCl concentration in two orthotopic breast tumor models (MCF10CA1a and 4T1). Swelling stress as a function of C) hyaluronan, D) collagen and E) hyaluronan to collagen content.

Interestingly, immunofluorescence analysis of tumor specimens has shown that although swelling stress is not correlated to the hyaluronan or collagen content alone, it is proportional to the ratio of hyaluronan to collagen area fraction. This indicates that the more the hyaluronan content in tumors, the larger the swelling stress will be. Similarly, the more the collagen content, the stiffer the tissue and the higher the resistance to swelling [8, 44]. Indeed, our laboratory has shown that enzymatic degradation of hyaluronan can completely eliminate tumor swelling, while collagen depletion has the opposite effect [8]. We have also shown the existence of an inverse relation between tumor perfusion and swelling, suggesting that reduction of tumor swelling can decompress tumor blood vessels.

Apart from hyaluronan, tumor swelling might also be caused by cancer cells [7]. Indeed, there is experimental evidence showing that cancer cell survival under solid stress requires osmotic regulation. Specifically, under compressive solid stress, cancer cells efflux sodium to decrease their intracellular tonicity, which in turn causes osmosis and cell swelling. The magnitude and contribution of cell-derived swelling stress has been found to be negligible compared to hyaluronan swelling [8] but further studies are required to elucidate the swelling behavior of cancer cells.

C. Residual solid stress

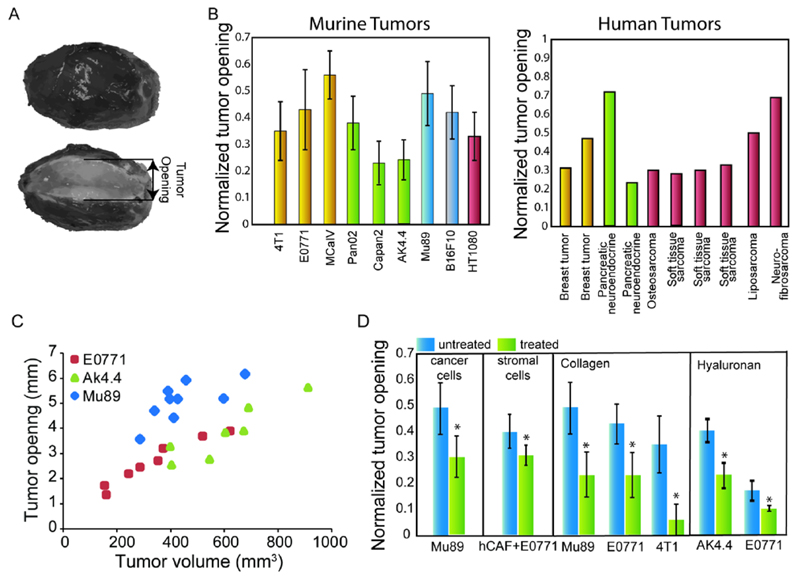
The presence of residual stresses in soft biological tissues has been known for more than three decades with the work of Professor Y. C. Fung on residual stresses in blood vessels to have influenced highly the field [45, 46]. Since then, residual stresses have been extensively analyzed both experimentally and mathematically including not only arterial but also cardiac, brain and other tissues [47–50]. In solid tumors, even though the presence of residual stresses was suspected more than two decades ago [10, 51], it was only recently that my coworkers and I systematically measured and quantified them in a large number of murine and human tumors [9]. Inspired by the work of Professor Fung, we found out that a partial cut through the center of the tumor would result in a measurable deformation, which was indicative of the presence of residual stresses (Fig. 3A,B). The mode of deformation involved bulging of the internal region of the tumor, which should be attributed to compressive residual stresses at the center and opening at the boundary, which is evidence of tensile stresses at the periphery that balance the compression at the center. Interestingly, we also found a positive correlation between the residual stress and the volume of the tumor, suggesting that residual stresses are accumulated into the tumor tissue during tumor progression (Fig. 3C) [6]. Using mathematical modeling and provided the material properties of the tumor are known, the measured deformations can be converted to solid stress. Therefore, residual stress levels have been calculated to range from 0.37 to 8.0 kPa (2.77 to 60.0 mmHg) for murine tumors and from 2.2 to 19.0 kPa (16.5 to 142.5 mmHg) for human tumors, comparable to the magnitudes of external and swelling stresses [9]. This range of residual stresses is on the same order of magnitude as residual stresses calculated in mouse cardiac tissue, the arterial wall and cancer cell spheroids and larger than the residual stresses calculated for the mouse brain [10, 50, 52, 53]. It should be further noted that residual stresses might include components of swelling stress because hyaluronan-derived tumor swelling does not vanish with tumor excision.

Figure 3.

Residual solid stress. A) Evidence of growth-induced, residual stress. A cut along the long axis of a tumor results in swelling of the interior and opening of the periphery of the tumor. B) Tumor opening measurements in murine and human tumors. Tumor opening is normalized by division with the diameter of the tumor [Reproduced with permission from Reference[9]]. C) Tumor opening increases with the volume of the tumor for three cancer cell lines, human melanoma Mu89, pancreatic adenocarcinoma AK4.4 and mammary adenocarcinoma 4T1 [Adapted with permission from Reference[6]]. D) Selective depletion of cancer cells, human CAFs (hCAFs), collagen or hyaluronan decreases significantly tumor opening in melanoma (Mu89), breast (4T1, E0771) and pancreatic (AK4.4) tumors, indicative of stress alleviation from [Adapted with permission from Reference [9]].

3. Stress-alleviation strategies to improve drug delivery and enhance cancer therapy

As mentioned in the Introduction, solid stresses affect tumor growth and treatment by compressing intratumoral blood and lymphatic vessels. Compression of the fragile intratumoral lymphatic vessels can cause their collapse, rendering the intratumoral lymphatic system dysfunctional [54]. As a result, drainage of interstitial fluid from the tumor cannot be performed efficiently, which contributes to the uniform elevation of the interstitial fluid pressure (IFP). Indeed, IFP can become as high as the microvascular pressure (typical range for many murine and human tumors, 0.5-5.0 kPa, 3.75-37.5 mmHg) and thus, there is a loss of pressure gradients across the tumor blood vessel wall [55, 56]. As a consequence, diffusion becomes the dominant transport mechanism of drugs through the vessel walls, which hinders transvascular transport of nanoparticles larger than 60 nm in size, as diffusion is a size-dependent and slow process for large particles [57–59]. At the periphery of the tumor, however, lymphatic vessels are hyper-plastic and still functional and thus, the IFP drops to normal values of zero pressure [54]. This creates a steep pressure drop at the periphery, which can cause a fluid flux from the tumor to the surrounding tissue [60, 61] and drive drugs outside the tumor [15].

Compression of tumor blood vessels can drastically reduce tumor perfusion, which can be seen by the fact that if an upstream vessel is hypo-perfused, it might exclude from blood supply a large number of downstream vessels. Preclinical studies in mice bearing breast and pancreatic tumors have shown that only a 20-40% of the tumor blood vessels are perfused with the rest of them being non-functional [9, 62]. Hypo-perfusion, in turn, hinders the transfer of immune cells and the systemic administration of any therapeutic agent to the tumor site and thus, immune cells and drugs can be heterogeneously distributed only to the adequately perfused regions of the tumor. Based on these observations, elevated solid stress levels in tumors could be also viewed as a mechanism for cancer cells to protect themselves from the immune system and the effect of drugs, sustaining tumor progression [63].

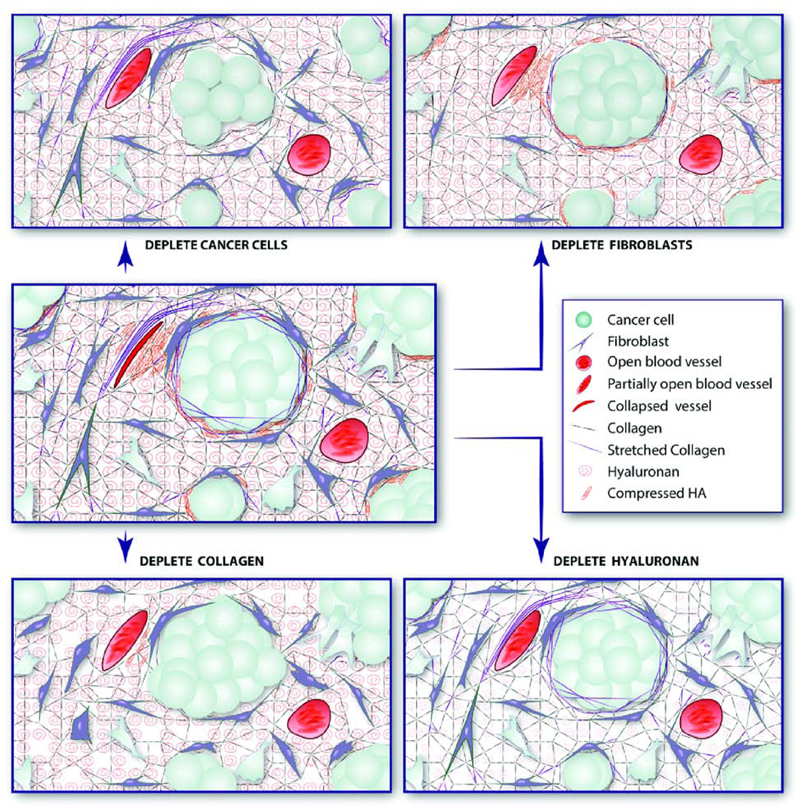
Taking all the above into account, alleviation of solid stresses to decompress tumor vessels could restore tumor perfusion and oxygenation, reduce IFP and thus, enhance drug efficacy [3, 64]. Prerequisite for the application of a stress alleviation strategy is the investigation of the tumor components that contribute to the accumulation of solid stress in tumors. To this end, a series of in vivo experiments targeting each time a specific component of the tumor microenvironment and measuring the resulting residual solid stress has been performed [9]. Depletion of cancer cells, CAFs, collagen or hyaluronan can significantly reduce residual stress levels as shown by the reduction in the tumor opening (Fig. 3D). Proliferating cancer cells can also exert forces on other cells and surrounding structures [31, 32]. These forces on nearby components cause them to deform, resulting in accumulation of solid stress. Additionally, CAFs and other stromal cells contract to remodel collagen fibers, which in turn can support high loads when in tension [65]. Finally, contrary to collagen, hyaluronan could resist to compressive loads owing to its ability to trap water molecules into its highly negative chains and thus, create gel-like regions within the tumor. Given the fact that the tumor interior is in compression, hyaluronan rich regions in the tumor would resist compression, owing to the incompressibility of the water and thus, could generate and store solid stress. Therefore, potential targets of the tumor microenvironment whose therapeutic depletion can alleviate solid stresses are CAFs, collagen and hyaluronan (Fig. 4).

Figure 4.

Schematic of stress alleviation treatments. Selective depletion of cancer cells, fibroblasts, collagen or hyaluronan can result in stress alleviation and blood vessel decompression improving vessel functionality [Reproduced with permission from Reference [9]].

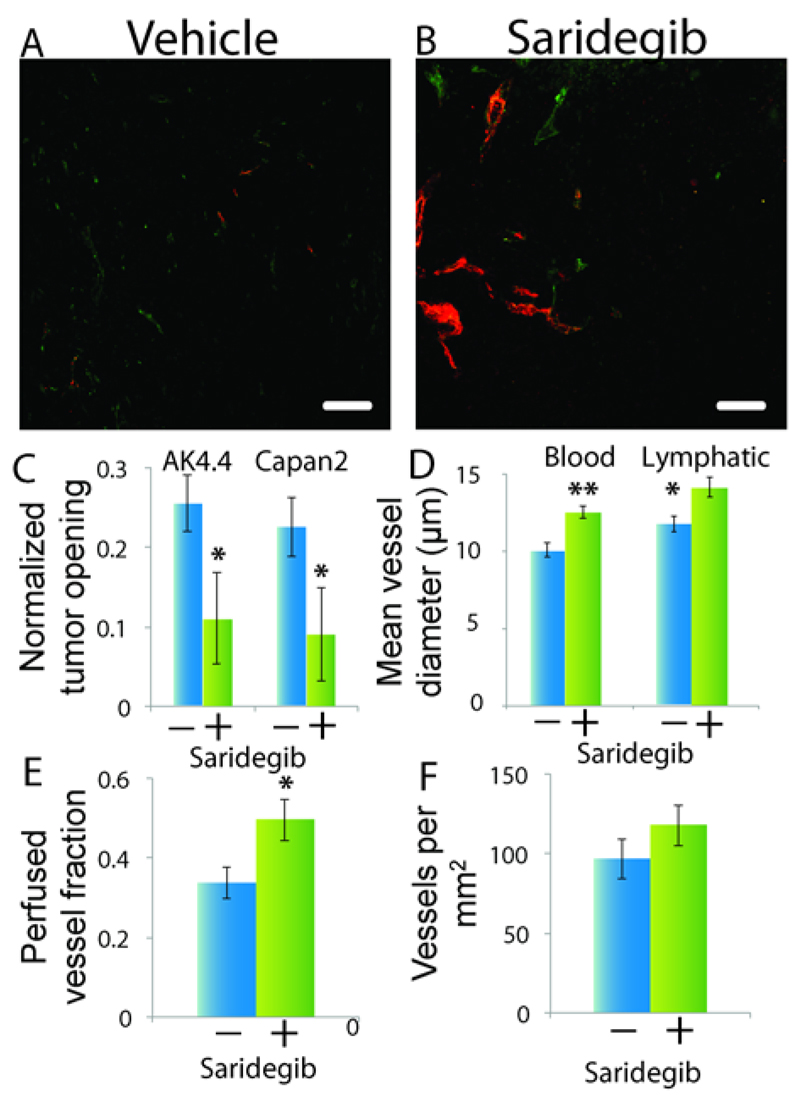
As a proof of concept of the stress alleviation strategy, we have shown in vivo that saridegib, an inhibitor of the sonic hedgehog pathway used to target CAFs in highly desmoplastic, hypovascular pancreatic tumors, alleviated solid stresses, decompressed blood and lymphatic vessels and improved the fraction of perfused vessels by 47%, without affecting total vascular density (Fig. 5) [9]. Saridegib has also shown to enhance delivery of chemotherapy and overall survival in a mouse model of pancreatic cancer [66] but failed in a phase II clinical trial when combined with gemcitabine for pancreatic cancer patients [67], presumably owing to tumors resistance to the cytotoxic drug. In another study, the angiotensin receptor blocker, losartan, was used to reduce collagen and hyaluronan content and improve perfusion and drug delivery in mice bearing skin, breast and pancreatic tumors [62, 68]. Losartan is an angiotensin receptor blocker, clinically approved as an anti-hypertensive drug and also an inhibitor of Transforming Growth Factor β (TGF-β), a growth factor implicated in tumor fibrosis. Combinatorial use of losartan with chemotherapy alleviated solid stresses, decompressed tumor blood vessels and significantly improved perfusion, drug delivery and treatment efficacy. Based on these preclinical findings, a phase II clinical trial with losartan and FOLFIRINOX in pancreatic ductal adenocarcinoma patients (clinicaltrials.gov identifier NCT01821729) has been underway at Massachusetts General Hospital to test the efficacy of the stress alleviation strategy in humans. Furthermore, retrospective analyses of clinical data has shown that patients with pancreatic ductal adenocarcinomas, lung or renal cancers exhibited increased survival when treated with angiotensin receptor blockers [69–72].

Figure 5.

Stress alleviation strategy improves perfusion in hypovascular orthotopic pancreatic AK4.4 and Capan2 tumors. A and B) Fluorescence images showing increased number of perfused vessels in saridegib treated tumors. Cd31 (green color) stains for all tumor vessels, while lectin (red color) stains only perfused vessels. C-F) Saridegib alleviates solid stress showed by the decrease in the tumor opening, decompresses both blood and lymphatic vessels, improves fraction of perfused vessels, without affected vascular density. +, saridegib; −, vehicle. The asterisks denote a statistically significant difference [Reproduced with permission from Reference [9]].

Other agents that have been employed as stress alleviating drugs include the PEGylated human recombinant hyaluronidase (PEGPH20), the TGF-β neutralizing antibody 1D11 and the antifibrosis drug Tranilast, which have been successfully used to deplete ECM components and improve the efficacy of chemotherapy [73–77]. However, it should be noted that, improved perfusion and oxygenation may also promote cancer cell proliferation and metastasis to distant organs through the tumor vasculature [78, 79]. Therefore, stress alleviating drugs should be considered only in combination with cytotoxic treatments, such as chemotherapy, radiation therapy, immune therapy, or another treatment that targets cancer cells.

4. Biomechanical Modeling of Solid Mechanics of Cancer

All components of solid stress discussed in this review as well as the coupling of solid stress with IFP and osmotic fluid pressure can be unified into a continuum-based biomechanical mathematical framework. This general framework involves the solid and fluid phase of the tumor as well as the ion transport and the fixed charge density integrated into a tumor growth theory.

Tumor growth theory

The most common methodology for modeling tumor growth is based on the multiplicative decomposition of the deformation gradient tensor. According to the work of Rodriguez et al.,[80] and of the late Professor R. Skalak [51] the deformation gradient tensor in tumors can be decomposed into three components: a tensor describing the (possibly geometrically incompatible) tumor growth, F_g, a tensor related to residual stresses, F_r, and a tensor for the elastic deformations that can restore compatibility, F_e, i.e,

$${\mathbf{\text{F}}=\mathbf{\text{F}}}_e{\mathbf{\text{F}}}_r{\mathbf{\text{F}}}_g.$$ (1)

Assuming isotropic built-up of residual stresses, phenomenological expressions for F_r fitting mathematical expressions to experimental data (Fig. 3C) [6] can be derived. Residual stresses can be also assumed to be part of F_g, breaking down the deformation gradient tensor into two components. In most models, tumor growth is assumed to be isotropic and the growth term, F_g, is usually given either by a phenomenological equation, such as the Gompertz law or as a function of oxygen and/or nutrients supply [28, 37–39, 81]. Finally, the term F_e is calculated algebraically by the expression F_e = F(F_rF_g)⁻¹.

Conservation of mass

Incorporation of the solid and fluid phase of a tumor as well as the ions involves the solution of the mass balance equations for the two phases and the transport equations for cations and anions. The mass balance equations can be written as

$$\frac{d{\phi }^s}{dt}+\nabla ·({\mathbf{\text{v}}}^s{\phi }^s)=S^s$$ (2)

$$\frac{d{\phi }^w}{dt}+\nabla ·({\mathbf{\text{v}}}^w{\phi }^w)=Q$$ (3)

where φ^s and φ^w are the volume fractions of the solid and fluid phase, respectively and v^s and v^w are the corresponding solid and fluid velocities. S^s is the creation/degradation of the solid phase and Q describes the fluid entering the tissue from the vasculature and exiting the tissue through the lymphatics. S^s is related to the growth term F_g and thus, it can be given either by a phenomenological expression or as a function of oxygen and/or nutrient concentration [37, 81]. The quantity Q in the fluid phase mass balance Eq. (3) can be calculated from Starling's approximation for semipermeable membranes[60]:

$$Q=\frac{L_{p}S}{V}(p_v-p)-\frac{L_{pl}{S}_l}{V_l}(p-p_l),$$ (4)

where p_v, L_p and (S/V) are the micro-vascular pressure, hydraulic conductivity and vascular density of the blood vessels, respectively, p_l, L_pl and (S/V)_l are the corresponding quantities for the lymphatic vessels and p is the IFP.

The transport equations for the cations, c⁺, and anions, c⁻, are written as [82]:

$$\frac{\partial ({\phi }^w{c}^{+})}{\partial t}+\nabla c^{+}·({\phi }^w{\mathbf{\text{v}}}^w)-\nabla ·[{\phi }^w{D}^{+}(\nabla c^{+}+\frac{F_c{c}^{+}}{RT}\nabla \Psi )]=0$$ (5.1)

$$\frac{\partial ({\phi }^w{c}^{-})}{\partial t}+\nabla c^{-}·({\phi }^w{\mathbf{\text{v}}}^w)-\nabla ·[{\phi }^w{D}^{-}(\nabla c^{-}-\frac{F_c{c}^{-}}{RT}\nabla \Psi )]=0$$ (5.2)

where D⁺ and D^- are the diffusion coefficients of the cations and anions, respectively and Ψ is the electric potential usually calculated by the Poisson-Boltzmann equation,

$${\nabla }^2\Psi =\frac{2F_c{c}_0}{\epsilon }\text{sinh}\left(\frac{F_c\Psi }{RT}\right)-\frac{F_c{c}_f}{\epsilon }$$ (6)

where ε is the dielectric permittivity, F_c is Faraday’s constant, c₀ is the ion concentration of the tumor and c^f is the concentration of the fixed ions.

Conservation of momentum

Finally the momentum balance equations have to be solved. The total stress, σ^total, of the tissue is given by the sum of the solid and fluid stresses [83]

$${\mathbf{\sigma }}^{total}={\mathbf{\sigma }}^s-T_c\mathbf{\text{I}}-p\mathbf{\text{I}}+p_{osm}\mathbf{\text{I}},$$ (7)

where σ^s is the elastic solid stress tensor, p is the IFP, T_c is the swelling solid stress, which can be derived by experimental data (Fig. 2) and p_osm is the Donnan osmotic fluid pressure. The linear momentum balance for quasi-static problems suggests that the divergence of the total stress tensor should equal zero

$$\nabla \cdot \left({\mathbf{\sigma }}^{total}\right)=\mathbf{0}.$$ (8)

Finally, taking the sum of the momentum balance equations for each phase, incorporating the corresponding constitutive equations and the mass balance equations (see Ref [82, 84] for a detailed derivation) yields:

$$-k{\nabla }^{2}p+\nabla \cdot {\mathbf{\text{v}}}^s=Q+S^s+k\left[F_c{c}^f{\nabla }^2\Psi +F_c\nabla c^f\nabla \Psi -RT\left(\varphi -1\right){\nabla }^2{c}^k\right]$$ (9)

where k is the hydraulic conductivity of the interstitial space, c^k is the sum of the free anions and cations within the tissue, and ϕ is the osmotic coefficient. Owing to the electro-neutrality condition, which suggests that the net electric charge at every point within the tumor and the host tissue must be zero, we have the equalities c^k = c⁺ + c⁻ and c^f = c⁺ − c⁻, whereas the osmotic pressure is defined as p_osm = ϕRTC^k, with R and T the gas constant and absolute temperature, respectively.

Constitutive modeling

It is common for the structural components of a tumor to be treated as a hyper-elastic material and models such as the neo-Hookean and Blatz-Ko material or exponential expressions have been used [5, 6, 37–39, 85]. If W is the strain energy density function of a hyper-elastic model, then the solid stress, σ^s, is given by [86]

$${\mathbf{\sigma }}^s=J_e^{-1}{\mathbf{\text{F}}}_e\frac{\partial W}{\partial {\mathbf{F}}_e^{\text{T}}},$$ (10)

where it should be noticed that F_e is the elastic part of the deformation gradient tensor, which as shown above it is calculated from the total deformation gradient tensor taking into account residual stresses and tumor growth. The constitutive equation for the solid phase can become more detailed to account for interactions at the microscale of the tissue. This involves the employment of continuum or multiscale mechanical models for soft tissues to represent intratumoral collagen mechanics and microscopic interactions among tumor components [87–89].

Model validation, extension and limitations

This mathematical framework has been validated against in vivo data and has been proved to be able to capture essential features of tumor's mechanopathology. Specifically, it can predict accurately the nonlinear growth pattern of solid tumors [5, 89] as well as the swelling stress, IFP and osmotic fluid pressure [6, 8, 82]. It can also provide qualitative predictions for the spatial distribution of the intratumoral solid stress components (Fig. 1B) [6, 33] and estimates of the residual stresses that agree with experimental observations [9]. The model has been further extended to predict tumor behavior in response to tissue oxygenation, delivery of anticancer drugs and radiation therapy [27, 81]. Additionally, similar models have been employed to model anisotropic tumor growth [38, 90].

The framework is limited in that it does not account explicitly for the tumor vascular network and its adaptation/remodeling during tumor progression. Models that integrate the existing framework with published models of tumor-induced angiogenesis can lead to the development of an even more sophisticated model of the tumor microenvironment and mechanics. The increase in sophistication, however, results in a larger number of model parameters whose values in many of them might be difficult to be measured experimentally. Furthermore these values might change among tumor types, between tumors of the same type, between a tumor and its metastases and in the same tumor during progression rendering their exact definition a challenging task. Therefore, model predictions would depend on the accuracy of the input parameters. Furthermore, the model does not account for biological parameters affecting tumor progression, such as the role of vascular endothelial growth factor (VEGF) and tumor growth factor beta (TGF-β) or changes in the amount of collagen and other extracellular proteins owing to a desmoplastic response often observed in tumors, which would change the mechanical properties of the tissue during growth [2]. Finally, the mathematical model does not account for the kinematic contribution of cell reorganization due to stress buildup. Such a contribution can be implemented by including an additional (plastic) part in the decomposition of the total deformation gradient tensor [85, 91].

5. Future perspectives

It has been well documented that mechanical stresses determine in large part the progression of solid tumors and that pharmacological alleviation of these stresses can result in better treatments. However, more work has to be done on the solid mechanics of cancer, opening novel avenues for future basic or translational research. As far as basic research is concerned, a more detailed mechanical characterization of solid tumors and the surrounding host tissues is necessary. Specifically, measurements of mechanical properties and development of specialized constitutive equations for primary tumors their metastases and host tissues as well as investigation of the relationship between the structure of tumor's microenvironment and its mechanical behavior should be among the first priorities. Furthermore, experimental and theoretical investigation of mechanical interactions among components of the tumor microenvironment such as collagen fibers, hyaluronan and CAFs and the contribution of these interactions to residual, swelling and external solid stress is another open area for future research. Given, on one hand, the differences in structure and mechanical function among tumor types, between tumors of the same type, in the same tumor at different stages and between the primary tumor and its metastases, and the very few published studies in the field on the other hand, biomechanical analysis of solid tumors is still at its infancy.

As for areas of translational research, first priority should be given to the establishment of specific rules for stress alleviation strategies. This involves the repurposing of clinically approved drugs or the development of new drugs that can be used as stress alleviating agents. Furthermore, the extent of depletion of components of the tumor microenvironment and thus, the degree of stress alleviation that can optimize the delivery and efficacy of chemotherapy, nanomedicine or radiotherapy should be also determined in more detail. This will lead to the derivation of specific dose protocols, which given the highly heterogeneous and dynamic nature of cancer might be different among tumors and give rise to patient specific protocols.

To conclude, better understanding and modulation of solid stresses in tumors is essential for the promise of stress alleviation strategies in patients to be realized.