Benthic and Pelagic Viral Decay Experiments: a Model-Based Analysis and Its Applicability

Abstract

The viral decay in sediments, that is, the decrease in benthic viral concentration over time, was recorded after inhibiting the production of new viruses. Assuming that the viral abundance in an aquatic system remains constant and that viruses from lysed bacterial cells replace viruses lost by decay, the decay of viral particles can be used as a measure of viral production. Decay experiments showed that this approach is a useful tool to assess benthic viral production. However, the time course pattern of the decay experiments makes their interpretation difficult, regardless of whether viral decay is determined in the water column or in sediments. Different curve-fitting approaches (logarithmic function, power function, and linear regression) to describe the time course of decay experiments found in the literature are used in the present study and compared to a proposed “exponential decay” model based on the assumption that at any moment the decay is proportional to the amount of viruses present. Thus, an equation of the form dVA/dt = −k × VA leading to the time-integrated form VA_t = VA₀ × e^{−k × t} was used, where k represents the viral decay rate (h⁻¹), VA_t is the viral abundance (viral particles ml⁻¹) at time t (h), and VA₀ is the initial viral abundance (viral particles ml⁻¹). This approach represents the best solution for an accurate curve fitting based on a mathematical model for a realistic description of viral decay occurring in aquatic systems. Decay rates ranged from 0.0282 to 0.0696 h⁻¹ (mean, 0.0464 h⁻¹). Additionally, a mathematical model is presented that enables the quantification of the viral control of bacterial production. The viral impact on bacteria based on decay rates calculated from the different mathematical approaches varied widely within one and the same decay experiment. A comparison of the viral control of bacterial production in different aquatic environments is, therefore, improper when different mathematical formulas are used to interpret viral decay experiments.

Over the past decade, viruses have been recognized to be the numerically dominant component in marine and freshwater environments (42), and most related studies have revealed that the viral infection of bacteria and subsequent lysis of cells account for a significant proportion of bacterial mortality (9, 40, 42). Through the control over bacterial populations, aquatic viruses can also play an important role in the biogeochemical cycling of nutrients (9).

Within marine and freshwater sediments, viral abundance is 10- to 1,000-fold higher than in the overlying water column (6, 8, 15, 16, 17, 21, 22, 24, 32), and a limited number of recent studies revealed bacterial mortality rates of 4 to 14% h⁻¹ (17) and a control of bacterial production from 12 to 57% (mean, 28%) (24) in marine sediments. In freshwater systems, viruses controlled 0 to 25% (mean, 7%) of benthic bacterial production in an oxbow lake (8) and some 18% in river sediments (24). Consequently, evaluation procedures leading to the determination of decay and production rates of viruses are essential prerequisites to describe and quantify biogeochemical relationships between benthic organisms. One of the generally accepted approaches for the determination of viral production and decay was introduced by Heldal and Bratbak (14), who recorded the decrease in viral concentration after inhibiting the production of new viruses by the addition of cyanide. For this approach, one has to assume that the viral abundance in a system remains constant through time and that viruses from lysed bacterial cells replace viruses lost by decay. Therefore, this method can also be used to assess viral production. However, the time course pattern obtained during decay experiments from both the water column and sediments allows a number of different mathematical interpretations, which raises the question of the proper choice of the mathematical model to be used.

Another problem is the choice of the representative time period for the appropriate fitting of the data obtained during a 24-h experiment and its ecological meaning. Different scientists have used different time periods, which leads to a heterogeneous flow of information with respect to viral decay rates (VDR). Therefore, comparing trends deduced from the different systems is misleading. Within the frame of an investigation of viral decay in oxygenated freshwater sediments, where the cyanide method was adapted to determine viral production, the comparison of the available mathematical approaches to interpret viral decay experiments was appropriate. A literature screen revealed that the extent to which the use of different mathematical methods influences the calculation of VDR and the subsequent determination of the viral control of bacteria has never been tested. In the present study, a mathematical model for the quantification of viral decay is proposed, which leads to the best curve fitting on the data set and provides a realistic description of viral decay occurring in aquatic systems. Furthermore, it is shown that this method allows a direct estimation of the impact of viruses on bacterial production.

MATERIALS AND METHODS

Study site and sample collection.

Sediment samples were taken in August and September 2000, January 2001, and April and May 2001 at 9 to 10 a.m. from different shallow (1- to 3.5-m) backwater systems of the River Danube, Austria, which are characterized by silty sediments with a water content of 73 to 86%, a porosity of 0.77 to 0.87, and an organic matter content of 16.7 to 21.8 mg ml⁻¹ fresh weight.

After water temperature was measured at about 5 cm above the sediment surface, five replicate sediment samples were collected by hand coring by using Plexiglas tubes (inner diameter, 5.8 cm; penetration depth, 15 to 20 cm). The sediment cores were brought to the laboratory within 30 min, and the experiments were started immediately after the arrival at the laboratory. The overlying water was removed carefully, and the top 0.5 cm of each core was extruded. We sampled the uppermost-oxygenated zone, indicated by its being light brown in contrast to the dark brown layer below. The sediment of the five cores was pooled by gentle mixing with a stirring magnet. Sediment parameters (bulk density, water content, and organic matter content) were determined as described in Kirschner and Velimirov (19). Porosity was calculated from the bulk density and water content of the sediment.

Viral decay experiments.

The decay, that is, the decrease in viral concentration over time, was recorded after inhibiting the production of new viruses by the addition of potassium cyanide (KCN; final concentration, 2 mM) to 40 g of sediment slurry in autoclaved 100-ml glass bottles. The pH of the KCN stock solution was adjusted to the in situ pH. The bottles were incubated at in situ temperature and under constant light conditions (with respect to the wavelength spectrum of in situ conditions and to average in situ light intensity of 50 W m⁻²) in a glass container filled with a sediment layer of 10 cm and an overlying water column of 30 cm (8). To ensure that the concentration of KCN usually used for water column experiments (2 mM) (14) is also sufficient to inhibit the metabolism of the high number of benthic bacteria, we counted bacterial abundance during two of the decay experiments. Moreover, we measured bacterial secondary production (BSP) after the addition of KCN during one of the experiments. In order to get information about the long-term effect of the added KCN concentration, we observed viral abundance during three of the experiments for 3 days.

In the experiments lasting for 24 h, samples (1-g) were taken at intervals of 30 min to 9 h, diluted, and fixed with electron microscopy grade glutaraldehyde (final concentration, 3%). Prior to the removal of samples, the sediment was gently mixed with a stirring magnet. After treatment with 0.02-μm-pore-size filtered sodium tetrapyrophosphate (5, 6, 23, 31) (final concentration, 5 mM) for at least 20 min, sonication three times for 20 s at 70 W with a Sonifier 450 (Branson Ultrasonics Corporation, Danbury, Conn.) (5, 22), and appropriate dilution (100×) with Milli-Q water, aliquots (1-ml) were filtered through 0.02-μm-pore-size Al₂O₃ Anodisc membrane filters backed by a 0.2-μm-pore-size cellulose nitrate filter at approximately 20 kPa vacuum. The filters were stained with SYBR Gold (a 2.5 × 10⁻³ final dilution of the stock solution; Molecular Probes, Eugene, Oreg.) for 15 min in the dark (3, 26, 28) and then mounted on a glass slide with a drop of Citifluor (glycerol-phosphate-buffered saline solution-AF1; Agar Scientific Ltd., Stansted, United Kingdom) (B. Luef, personal communication). All preparations were done under subdued light. Filters were examined at a magnification of ×1,250 with a Leitz-Diaplan microscope (Leica, Wetzlar, Germany) equipped with an HBO 50 W mercury lamp (excitation wavelength, 450 to 490 nm; cutoff filter, 515 nm). Total counts of 30 to 50 randomly selected fields usually exceeded 200 viruses per subsample. The inventory of viruses from bulk sediment included particle-adsorbed viruses as well as viruses in pore water. Viral numbers are expressed as particles ml⁻¹ of wet sediment.

The mathematical model.

The following model used for the interpretation of the experiments proved to be compatible with the measured data. Under the assumption that the viral production and decay over time only depend on the actual bacterial and viral abundances, respectively, the change in viral abundance can be written as:

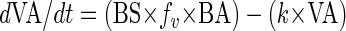(1)

where the first term describes the production and the second one the decay of viruses. BS is the burst size of infected bacterial cells (viruses bacteria⁻¹), f_v is the rate of successful viral infection of bacterial cells (i.e., infection actually leading to proliferation of new viruses) (h⁻¹), BA is the bacterial abundance (cells ml⁻¹), k is the VDR (h⁻¹), and VA is the viral abundance (viral particles ml⁻¹).

Assuming steady-state conditions in the oxygenated sediment layer over long time periods (thus neglecting short-term variations), the viral abundance is maintained and viruses from lysed bacterial cells replace viruses lost by decay, then the change in viral concentration over time is given by

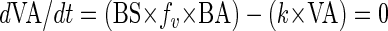(2)

In the present study, the production of new viruses was artificially stopped, thus ending the steady-state conditions and leading to

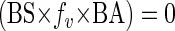(3)

which inserted into equation 1 gives the decay function

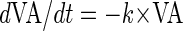(4)

or in its integrated exponential decay form

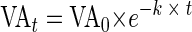(5)

where VA_t is the viral abundance (viral particles ml⁻¹) at time t (h) and VA₀ is the initial viral abundance (viral particles ml⁻¹).

Fitting the above curve to the experimental data, k can be computed. Taking this result of the laboratory investigation into equation 2, which holds in nature, the rate of successful viral infection of bacterial cells can be derived as:

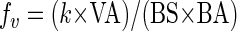(6)

Since bacterial production is given by

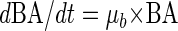(7)

where μ_b is the bacterial growth rate (h⁻¹), the viral control, VC (%), of BSP can be calculated as follows:

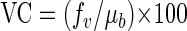(8)

DNase test.

In order to eliminate uncertainties in virus counting due to extracellular DNA interference, we tested the effect of DNase treatment on sediment samples. Samples (1-g) of the sediment slurry were diluted, treated with sodium tetrapyrophosphate, and sonicated. A total of 250 Kunitz units of DNase I from bovine pancreas were added to 1-ml aliquots and incubated for 30 min at room temperature (33). Additional aliquots (1-ml) without DNase were incubated under the same conditions and served as controls. After fixation with glutaraldehyde and further dilution, the viruses in triplicate samples containing DNase and in untreated samples were counted by epifluorescence microscopy. Viral numbers obtained from DNase-treated samples did not differ significantly from those in untreated samples (Mann-Whitney U test, P > 0.60; n = 12) (data not shown).

Virus extraction efficiency.

A known amount of viruses concentrated from the water column of the study site by ultrafiltration (34) was added to samples (1-g) of the sediment slurry, mixed, and incubated for 30 min at room temperature in order to allow the adsorption of viruses to sediment particles (20). After fixation with glutaraldehyde, treatment with sodium tetrapyrophosphate, sonication, and further dilution, the viruses were counted by epifluorescence microscopy. Extraction efficiency was determined by dividing virus counts in virus-amended sediment by the sum of counts in nonamended sediment samples plus counts of the known concentration of viruses, and multiplying this ratio by 100. The mean efficiency of virus extraction was 88.8% (standard deviation, 11.9%). Viral numbers obtained in virus-amended sediment samples did not differ significantly from the sum of counts in untreated sediment samples plus counts of the known concentration of viruses (Mann-Whitney U test, P > 0.10; n = 6) (data not shown).

Bacterial parameters.

Bacterial numbers were determined from the same filters as viral counts were made and are expressed as cells ml⁻¹ of wet sediment. BSP was measured by the incorporation of [³H]thymidine, following the protocol of Kirschner and Velimirov (19), with modifications after Wieltschnig et al. (39).

Statistical analysis.

Data were analyzed according to Zar (43). A probability of ≤0.05 was considered significant in all statistical analyses. We used SPSS version 10.0 (SPSS, Inc., Chicago, Ill.) software.

RESULTS AND DISCUSSION

Time course of viral decay experiments.

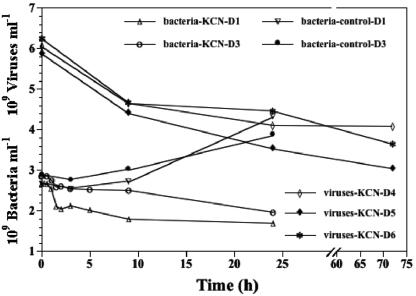
To ensure that the concentration of KCN usually used for water column experiments (2 mM) is also sufficient to inhibit the metabolism of the high number of benthic bacteria, we counted bacterial abundance during the decay experiments D1 and D3 over a period of 24 h (Fig. 1). The concentration of bacteria slightly decreased in both cases and was approximately only half the abundance of untreated control samples after 24 h, indicating that production of new cells was inhibited by the addition of KCN. Bacterial production, measured in the course of experiment D2, was below the detection limit (data not shown). In order to get information about the long-term effect of the added KCN concentration, we observed viral abundance during experiments D4, D5, and D6 for 3 days (Fig. 1). Viral numbers decreased over the entire observation period. The result of this experiment as well as the results of the foregoing approaches (bacterial counts and bacterial production measurement) all indicated that the KCN concentration used in water column experiments is also applicable for sediment experiments lasting for 24 h.

FIG. 1.

Changes in benthic bacterial and viral counts as a function of time after inhibiting production of new viruses by the addition of KCN and in untreated samples (control).

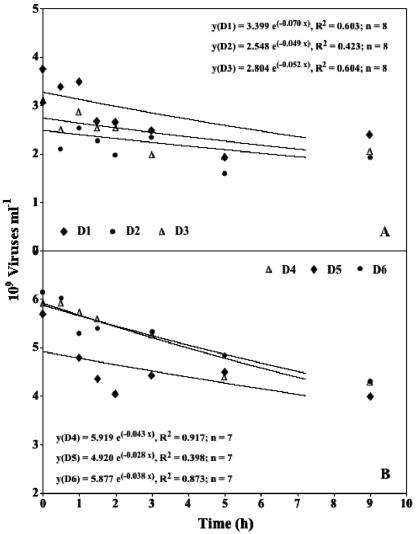
The time courses of the viral decay experiments are shown in Fig. 2. All experiments exhibited a similar pattern of viral abundance over time. Since the concentration of viruses dropped off rapidly at first (<9 h) and afterwards either decreased more slowly or remained constant, only data of the initial 9-h period are shown. A similar time course of viral decay has been observed in the water column of marine and freshwater environments (7, 11, 14, 23).

FIG. 2.

Changes in benthic viral counts as a function of time after inhibiting production of new viruses by the addition of KCN.

However, the KCN-decay method raises several problems: it has been suggested that the rate of pelagic as well as benthic viral production and decay may follow a diel periodicity (2, 8, 14, 18, 35, 38, 41). Since the decay experiments in the present study were made on sediment samples taken in the morning, the assumption that the viral decay measurements are representative of the daily average may be rather conservative. Also, one has to consider that the addition of KCN inactivates both the protozoan and bacterial metabolisms, thus inhibiting the production of new bacterial enzymes (14, 23). Potential viral loss factors such as degradation by enzymes and ingestion by protozoa are reduced and eliminated, respectively. Grazing by protozoa seems to be of negligible importance as a loss process for the virioplankton community (10, 35), but it is not known yet to what extent bacteria in in situ conditions produce enzymes capable of contributing to the degradation of viral protein capsids. There is a high probability, therefore, that the VDR are underestimates, and a definite judgment concerning the importance of the above mentioned processes in viral decay cannot be drawn with the experimental setup used in the present study.

Interpretation of viral decay experiments.

The data obtained during viral decay experiments were analyzed according to different mathematical functions proposed in the literature (7, 8, 13, 14, 23). Guixa-Boixereu et al. (13) suggested that there are three options to interpret the time course of decay experiments.

(i) Linear regression.

The first option is to calculate VDR from the log-linear part of the curves by using linear regression, as proposed by Heldal and Bratbak (14) and as used by numerous authors (2, 7, 11, 23), and to consider the first rate (the first 3 to 8 h), where viruses decay rapidly, as valid (13). However, the time period used for the calculation of the VDR depends on the time course of each single experiment and is, therefore, to a certain extent subject to individual interpretation. In the present study, the VDR was calculated for the period 0 to 5 h (VDR_0-5) in experiments D1, D2, D3, and D4, for 0 to 3 h in D5 (VDR_0-3), and for 0 to 9 h (VDR_0-9) in D6 (Table 1). The VDR ranged from 0.0369 to 0.1312 h⁻¹ (mean, 0.0839 h⁻¹). It was on average four times higher than the VDR calculated by using other mathematical approaches (logarithmic function, power function, and exponential decay function), and seven times higher than the VDR calculated for the second period of the experiments (i.e., after 3 to 9 h until the end of the experiment) by linear regression. A Mann-Whitney U test revealed that these differences were statistically significant (P < 0.03, n = 6), with the only exception being the VDR calculated with data from the period 0 to 9 h with an exponential decay function (see below). We suggest that the fast VDR observed at the initial period (first 2 to 3 h) may partly be caused by the handling of the samples at the beginning of the experiments (pooling of replicate water samples and preparing the sediment slurry of replicate cores and the addition of KCN and subsequent mixing) and not by occupation of all the possible sites for virus adsorption (one of the factors assumed to be responsible for viral disappearance) as the experiment proceeds (13). The handling of samples may enhance the encounter probability between enzymes and viruses, leading to enzymatic degradation of the viral particles. Proteases and nucleases have been reported to be important contributors to viral breakdown (27, 29, 35). We therefore do not consider the very first rate (first 2 to 3 h), where viruses decay very rapidly, as valid for the description of viral decay naturally occurring in the water column and sediments of aquatic systems.

TABLE 1.

Viral decay rate (h⁻¹) calculated by using different mathematical approaches and different periods of time

Expt	Time period (h)	Linear regression (y = a + b × x)	Power function (y = a × xb)	Logarithmic function [y = a + b × ln(x)]	Exponential decay function (y = a × e−b × x)
D1	0-3 (A), 0-5 (B), 0-9 (c)	0.1312B		0.0527C	0.0696C
D1	0-24		0.0247	0.0223	0.0181
D1	3-24 (A), 5-24 (B), 9-24 (C)	0.0000B			0.0000C
D2	0-3 (A), 0-5 (B), 0-9 (C)	0.0922B		0.0554C	0.0490C
D2	0-24		0.0238	0.0243	0.0183
D2	3-24 (A), 5-24 (B), 9-24 (C)	0.0000B			0.0065C
D3	0-3 (A), 0-5 (B), 0-9 (C)	0.0895B		0.0438C	0.0515C
D3	0-24		0.0268	0.0224	0.0286
D3	3-24 (A), 5-24 (B), 9-24 (C)	0.0139B			0.0189C
D4	0-3 (A), 0-5 (B), 0-9 (C)	0.0604B		0.0234C	0.0426C
D4	0-24		0.0196	0.0136	0.0235
D4	3-24 (A), 5-24 (B), 9-24 (C)	0.0102B			0.0110C
D5	0-3 (A), 0-5 (B), 0-9 (C)	0.0931A		0.0376C	0.0282C
D5	0-24		0.0219	0.0195	0.0221
D5	3-24 (A), 5-24 (B), 9-24 (C)	0.0200A			0.0200C
D6	0-3 (A), 0-5 (B), 0-9 (C)	0.0369C		0.0275C	0.0377C
D6	0-24		0.0174	0.0138	0.0179
D6	3-24 (A), 5-24 (B), 9-24 (C)	0.0033C			0.0037C

The second option of Guixa-Boixereu et al. (13) is to calculate VDR from the log-linear part of the curves by using linear regression and to consider the second rate (after 3 to 8 h until the end of the experiment), where viruses decay slowly, as valid. They argued that the natural decay rate is restored only a few hours after the beginning of the experiment and that the decrease of viruses in the first 3 to 8 h is an artifact of enclosing samples in bottles. However, Noble and Fuhrman (27) suppose that certain viruses may be more resistant to degradation than others. This has partly been evidenced by the observation of a faster degradation of viral particles of <60 nm compared to larger ones in the water column of different backwater systems of the River Danube, Austria (7, 23). Losses decreased with the relative increase of viral size, with no detectable losses occurring in the size class of >150 nm. Since bacteriophages show a mean capsid size of 70 nm (1), while the average head diameter for viruses of eukaryotic algae was reported to be 152 nm (37), we speculate that the second decay rate (9 to 24 h) might mainly be caused by viruses other than bacteriophages. This rate, which ranged from 0 to 0.02 h⁻¹ (mean, 0.0079 h⁻¹) in the present study (Table 1), is therefore considered as not important for the assessment of viral control of the bacterial community.

(ii) Power function.

The last approach of Guixa-Boixereu et al. (13) is to fit a power function to the whole data set in order to calculate losses for a given period of time. They calculated the total number of viruses after 24 h by using the power function fitted for each experiment. Then they subtracted from this the number of viruses that were present at the first hour of the experiment, calculated by the same power function. The resultant viral concentration would be the number of viruses produced during a period of 24 h. VDR calculated by using a power function varied from 5.7 × 10⁷ to 10.6 × 10⁷ particles ml⁻¹ (mean, 8.4 × 10⁷ particles ml⁻¹), corresponding to 0.0174 to 0.0268 h⁻¹ (mean, 0.0224 h⁻¹) in the present study (Table 1). VDR calculated by means of the power function were not significantly different from the corresponding VDR_0-24 calculated with another mathematical approach used to interpret viral decay experiments, namely, the logarithmic function (23) (Mann-Whitney U test, P > 0.26; n = 6).

(iii) Logarithmic function.

Mathias et al. (23) and Fischer and Velimirov (7) calculated VDR by a similar method but by using a logarithmic curve instead of a power function. They calculated the total number of viruses after 24 h by using the logarithmic function fitted for each experiment. Subsequently, the number of viruses counted at the beginning of the experiment was subtracted. The resultant viral concentration would be the number of viruses produced during a period of 24 h. In the study of Fischer and Velimirov (7), the VDR was calculated only with data from the initial 9-h period of the experiments (VDR_0-9), because a negligible loss of viruses occurred afterwards. The VDR calculated for the entire period of the decay experiments (VDR_0-24) was similar to that calculated for the same period by using a power function (Mann-Whitney U test, P > 0.26; n = 6). It ranged from 5.4 × 10⁷ to 8.8 × 10⁷ particles ml⁻¹ (mean, 6.7 × 10⁷ particles ml⁻¹), corresponding to 0.0136 to 0.0243 h⁻¹ (mean, 0.0193 h⁻¹) (Table 1). In contrast, VDR_0-9 was on average twice the VDR_0-24, varying between 11.3 × 10⁷ to 18.1 × 10⁷ particles ml⁻¹ (mean, 14.3 × 10⁷ particles ml⁻¹), corresponding to 0.0243 and 0.0554 h⁻¹ (mean, 0.0401 h⁻¹) (Table 1). The difference between VDR_0-9 and VDR_0-24 was statistically significant (Mann-Whitney U test, P < 0.01; n = 6).

(iv) Exponential decay function.

In the present study, we applied the mathematical model described earlier in Material and Methods by using the “exponential decay” function to describe viral decay. The software Delta Graph version 4.0.1 (DeltaPoint Inc., Monterey, Calif.) provides two numerical approaches for fitting the function curve to the experimental data. The first one is the “intrinsic exponential” fitting, which transforms the equation y = a × e^b×x into its mathematically equivalent form ln(y) = ln(a) + b × x. Then, it uses a linear square fit to optimize b and ln(a), not a directly. The other method is to use an iterative optimization of a user-defined function (exponential decay function, y = a ×e^b×x), that, in this case, directly computes the optimal values for b and a. The latter method requires more computing resources, but since it optimizes a directly and not ln(a), which gives smaller values a higher weight, thus biasing the overall trend, we used the results computed by this second method.

In order to compare VDR calculated by using the exponential decay function with the other mathematical approaches and time periods previously used in studies concerning viral decay, VDR was calculated in three different ways: (i) with data from the initial 9-h period of the experiments (VDR_0-9), (ii) with data from the entire observation period (VDR_0-24), and (iii) with data from the period 9 to 24 h (VDR_9-24). VDR_0-9 ranged from 0.0282 to 0.0696 h⁻¹ (mean, 0.0464 h⁻¹), VDR_0-24 ranged from 0.0179 to 0.0286 h⁻¹ (mean, 0.0214 h⁻¹), and VDR_9-24 ranged from 0 to 0.02 h⁻¹ (mean, 0.01 h⁻¹). VDR_0-9 as well as VDR_9-24 were not significantly different from the corresponding VDR calculated with the linear regression of log-transformed data (Mann-Whitney U test, P > 0.05; n = 6) (Table 1). Nevertheless, we favor the exponential decay function because it is derived from the realistic assumption that the decay is proportional to the viral population (see Materials and Methods). Table 1 also shows the VDR calculated with a logarithmic and a power function. No statistically significant differences between the VDR of the logarithmic and the corresponding VDR of the exponential decay function were found (Mann-Whitney U test, P > 0.50; n = 6). The same result was obtained when the power function and the exponential decay function were compared (Mann-Whitney U test, P > 0.60, n = 6). One may argue that the use of a logarithmic or a power function would result in an even more precise curve fitting. But since one speculates that the decay of the initial period of the experiments (first 2 to 3 h) is mainly an artificially triggered process (see above), a perfect curve fitting on the data set is not the main objective. The exponential decay function in combination with using only data from the period 0 h to approximately 9 h weakens this rapid artificial decay at the beginning of the experiment. It therefore represents the best compromise between an accurate curve fitting and a realistic description of viral decay occurring in aquatic systems. An additional major advantage of the exponential decay function is that the parameter k of the curve's equation represents the VDR and can directly be used for the determination of the viral impact on the bacterial community (see Materials and Methods). The period that should be used to calculate VDR strongly depends on the time course of viral decrease during the different experiments. The time course pattern of over 60 decay experiments (34 water column experiments and 33 experiments in sediments) (7, 8, 11, 12, 13, 14, 23, 36; Fischer et al., unpublished data) were screened in order to detect the time period for the transition of the rapid decay to the asymptotic phase. With the exception of 10 experiments (4 for the water column and 6 from sediments), all experiments revealed a passage into the asymptotic phase after approximately 9 h. Even though each experiment needs individual interpretation by the investigator, published evidence on decay experiments indicates that it is advisable to propose a time period of approximately 9 h for the determination of VDR. In the present study, no statistically significant difference between VDR_0-24 and VDR_9-24 could be obtained for the exponential decay function (Mann-Whitney U test, P > 0.05; n = 6). In contrast, VDR_0-9 was significantly higher than VDR_0-24 as well as VDR_9-24 (Mann-Whitney U test, P < 0.007; n = 6), no matter which mathematical approach was used for the calculation. As mentioned above, viruses other than bacteriophages might mainly cause the decay obtained during the second part of the decay experiments (i.e., 9 to 24 h). Hence, if the VDR is used for the assessment of viral control on the bacterial community, the asymptotic part of the curve should not be included in the calculations of VDR. Therefore, we only plotted the data obtained during the initial 9-h period in the present study.

Viral control of BSP.

A burst size of 25 and 40 (minimum and maximum burst size of pelagic bacteria in the investigated backwater systems of the River Danube, respectively [7, 23]) was used to calculate the viral control of BSP. The problem arising from use of a burst size from pelagic bacteria was extensively discussed and justified in Fischer et al. (8). However, we wish to emphasize that the magnitude of the burst size does not affect the comparison of different mathematical approaches to assess VDR used to calculate viral control of bacterial production or the recommended choice for a defined time period of the experiment to evaluate decay rates.

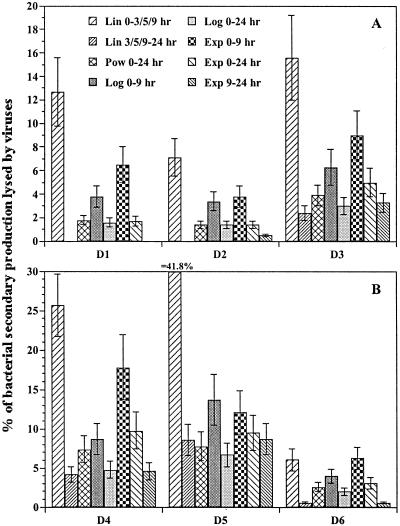
Due to the differences in VDR calculated by using different mathematical approaches as well as different time periods of the decay experiments, the viral control of BSP varied widely within one and the same decay experiment, as can be seen in Fig. 3. These results clearly show that it is improper to compare the impact of viruses on bacteria in different aquatic environments when different mathematical approaches are used to interpret viral decay experiments.

FIG. 3.

Viral control of benthic BSP. Calculation is based on VDR determined by using different mathematical approaches and different time periods of the decay experiments as follows: by linear regression and data from the period 0 to 3 h (D5), 0 to 5 h (D1, D2, D3, and D4), and 0 to 9 h (D6) (all, Lin 0-3/5/9 h); by linear regression and data from the period 3 to 24 h (D5), 5 to 24 h (D1, D2, D3, and D4), and 9 to 24 h (D6) (all, Lin 3/5/9-24 h); by power function and data from the entire period (Pow 0-24 h); by logarithmic function and data from the initial 9-h period (Log 0-9 h) and data from the entire period (Log 0-24 h); and by exponential decay function and data from the initial 9-h period (Exp 0-9 h), data from the entire period (Exp 0-24 h), and data from the period 9 to 24 h (Exp 9-24 h). Error bars indicate the range of values calculated by using a burst size of 25 and 40.

The origin of benthic viruses.

When using the decay approach to assess viral production in sediments, one has to consider that it still remains unclear whether viruses found in sediments are actually produced in this environment or originate from the overlying water column. No routine techniques exist to distinguish between viruses that are locally produced in the sediments and those that have accumulated after sedimentation out of the water column. Since the investigated backwater systems are shallow, with an average depth of only 1 and 3.5 m, it seems reasonable to propose that viral abundance in the sediment is, at least partially, supplied by particle fluxes. One may thus argue that the measurement of viral decay in the sediment to assess viral production is not a reliable approach. But, due to the small size and weight of viral particles, it seems unrealistic to suppose that there is a pronounced sinking of free viral particles from the water column down to the sediment. The settling of viruses might contribute to the benthic viral pool only when virus is attached to aggregates. In fact, correlations of viral abundance and solids suggest that viruses adsorb to suspended material in the water column and may settle out to contribute to the benthic viral population (15). In contrast, Simon et al. (31) reported that viruses are readily decomposed in aggregates, possibly as the results of destruction of the protein capsid by bacterial enzymes. The authors further suggested that aggregates are, thus, presumably not a vehicle for viruses to deep-water layers and the bottom sediment. Recently, Hewson and Fuhrman (17) measured the adsorption of viruses to suspended sediment particles and combined the virioplankton scavenging rates with published sedimentation rates within shallow areas of the Los Angeles harbor. They demonstrated that this mechanism of virus arrival could only account for 0.01% of daily benthic virus production. Moreover, significant positive correlations between viral abundance and bacterial numbers (4, 25) as well as between viral numbers and bacterial activity in deep-sea sediments of the Mediterranean Sea and coastal sediments of Denmark (5, 25) strongly suggest that the abundance of benthic viruses is closely coupled to the activity of benthic bacteria and that viruses are produced by bacteria within the sediment. Other evidence for production of viruses by benthic bacteria was recently presented by Hewson and Fuhrman (17) as well as Mei and Danovaro (24). They diluted sediment samples with sterilized sediment and virus-free seawater, respectively, in order to terminate viral infection of bacteria, and then observed the time course increase in virus abundance caused by the lysis of already infected benthic bacteria during incubation (dilution technique). Benthic viral production ranged from 2.8 × 10⁸ to 5.0 × 10⁸ viruses cm⁻³ h⁻¹ (17) and from 0.13 × 10⁸ to 1.6 × 10⁸ viruses ml⁻¹ h⁻¹ in different marine sediment systems (24), suggesting viral turnover rates of 1 to 5 h (17) and 10 to 44 h (24), respectively. In river sediments, the dilution technique revealed that some 0.77 × 10⁸ viruses were produced ml⁻¹ h⁻¹, with a turnover rate of approximately 13 h (24).

We therefore suppose that sedimentation of viruses in the freshwater systems investigated is of minor importance and that the rate of benthic viral decay measured in the present study is a reliable assessment of viral production in sediments. The decay method, which is well established to measure the pelagic proliferation of viruses, is thus also a useful tool to assess viral production in sediments. The possibility of estimating this parameter is a crucial step in the investigation of the ecological role of viruses in this environment.