Abstract
Particle swarm optimization (PSO) has gained widespread use as a general mathematical programming paradigm and seen use in a wide variety of optimization and machine learning problems. In this work, we introduce a new variant on the PSO social network and apply this method to the inverse problem of input parameter selection from recorded auditory neuron tuning curves. The topology of a PSO social network is a major contributor to optimization success. Here we propose a new social network which draws influence from winner-take-all coding found in visual cortical neurons. We show that the winner-take-all network performs exceptionally well on optimization problems with greater than 5 dimensions and runs at a lower iteration count as compared to other PSO topologies. Finally we show that this variant of PSO is able to recreate auditory frequency tuning curves and modulation transfer functions, making it a potentially useful tool for computational neuroscience models.
Keywords: Biological Neural Networks, Evolutionary Computation, Model Optimization, Particle Swarm Optimization
1 Introduction
Computational modeling at all levels of abstraction can be a powerful tool to make experimentally falsifiable hypotheses and guide experimental design. Furthermore, network models can make inferences about neural circuits that are difficult or impossible to test in physiology. However, one of the major issues incurred in modeling is the tuning and fitting of model parameters to physiological data. Typically, models fit general classes of physiological observations rather than having the ability to fit individual or small sets of observations.
In order to capture biophysically relevant neural behaviors, models often have to encapsulate a wide variety of parameters or include computationally costly Hodgkin-Huxley modeling. Particle swarm optimization (PSO) is a swarm intelligence optimization paradigm that models the schooling of fish or flocking of birds to solve complex problems.19 PSO was initially developed by Kennedy and Eberhart19 as a nonlinear optimization scheme which models the emergent solving problem capabilities of swarms of relatively simple agents. As its operation is independent of the mathematical program cost function, it has found applications in far reaching fields such as the design of optimal power systems22 or the training of neural networks.33, 46 PSO has also been extended to solving multi-objective optimization problems.7, 14
Particle swarm optimization is a derivative-free meta-heuristic which does not require explicit knowledge of underlying system dynamics to solve mathematical programming problems. Classical optimization methods, such as gradient descent and linear programming, utilize problem derivatives to quickly converge to minima or maxima. However, if this information is not easily available or is too computationally costly to calculate iteratively, such as those found in Hodgkin-Huxely based neural models, these classical models fail. PSO can be applied to problems where no explicit derivative exists. PSO is also advantageous to other meta-heuristics such as genetic algorithms (GA) when calculation of the mathematical problem is computationally expensive because PSOs generally converge in fewer iterations than GAs.11 GAs also require the problem to be recast into a binary optimization problem, while PSO in general does not require modification of the problem. Finally, each iteration of PSO is computationally cheap, only requiring vector addition and scalar multiplication to update its parameters, easing the computational load of optimization.
The power of PSO arises from the emergence of intelligent problem solving behavior in the interactions of simple agents in social networks. Adjustments to the PSO algorithm typically arise in the mathematical representation of agent interactions or social network topologies, such as inertial weight constraints.29, 37 Metaheuristics, PSO specifically, have an inherent trade-off between swarming and convergence behaviors.4, 20 As these are population metrics, they are largely controlled by the architecture of the social network. Too little swarming may lead to the swarm prematurely converging to an incorrect local minimum, while too much may become computationally burdensome and may prevent convergence on the optimal solution.18 Therefore, the study and design of social networks is of prime importance to PSO.
Swarm social networks can largely be thought of as a continuum across two fundamental swarm types: the fully connected and ring topologies. The ring topology (Fig. 1 right) only transmits information between its nearest neighbors. Information therefore takes a relatively long time to traverse across all agents of the network.18 This may allow for a more thorough searching of the solution space. Conversely, the fully connected topology can be thought of as a fully connected graph in which every agent has instantaneous access to information from every other agent (Fig. 1 left). This offers quick convergence but may cause the swarm to become trapped in local minima. Most other social networks draw from aspects from the two extremes. The four-corners network, for example, (Fig. 1 bottom) is fully connected locally but information is bottle-necked by sparse connectivity of the four networks.
Fig. 1.
The continuum of social networks. Top left: The fully-connected topology is a fully-connected graph where each agent is directly connected to every other agent. Top right: The ring topology slows down information transfer by only allowing connections between an agents nearest neighbors. Bottom: Many social networks draw from aspects of both fully-connected and ring topologies. The four corners social network is fully-connected locally but sparsely connected between neighborhoods.
Models of central nervous system neurons and networks often run into the ”curse of dimensionality”, in which even relatively simple optimization problems become difficult to solve when the number of input variables is high. Furthermore, in most models, general classes of response profiles are modeled, rather than being able to model individual response profiles. Particle swarm optimization has been used in many computational biology models, including fitting somatosensory responses to chirp functions43 and training recurrent neural networks which model gene regulatory networks.21 Van Geit et al41 developed an optimization program which allows for the optimization of neuron model parameters to fit time dependent traces. While this is advantageous for tuning models to fit single neuron spike trains, it does not lend itself to the fitting of tuning where model response is dependent on frequency or another non-time based measure.
In this work we present a new particle swarm social network which draws influence from small world networks found in the visual cortex of the central nervous system.23, 28, 40 Specifically, winner-take-all particle swarm optimization (WTAPSO) is a dynamic, hierarchical topology that utilizes winner-take-all coding strategies found in the visual system which shows improved performance on high-dimensional problems as compared to traditional particle swarm networks (Fig 2.). We begin with a derivation of WTAPSO. We demonstrate that WTAPSO is able to fit a wide variety of neural models by showing fits of physiological data from a biophysically accurate computational model of an inferior colliculus (IC) neuron.
Fig. 2.
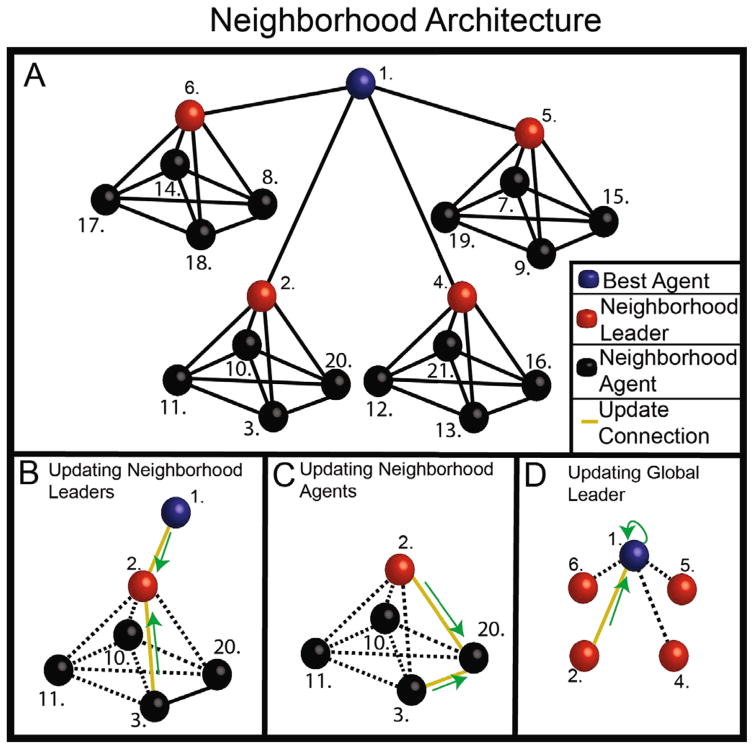
Hierarchical architecture for the winner-take-all particle swarm social network. A.) The overall topology of the WTAPSO social network. The global leader is shown as a blue sphere, while local neighborhood leaders and agents are shown as red and black spheres respectively. Numbers near agents represent a sample of agent placement in the swarm. By definition, the global leader is always 1, while local leaders represent the best performing agents of a given neighborhood. Once the best performing local agent is determined, update connections are broken, represented by dotted black lines, so that only good influences are updating the target agent. B.) A sample of updating a neighborhood leader. The neighborhoods are disconnected at update and only the best two performing agents are allowed to update the neighborhood leader. By its rank, the global leader always updates the neighborhood leader. C.) Updating a neighborhood agent is very similar to updating a neighborhood leader. Only the best two best performing agents are allowed to update the target agent. By virtue of its position, the local leader will always update the target agent, while the next best performing local agent acts as the other update agent. D.) The global leader receives update information from its own previous best performance and the best performing local leader.
2 Methods
Particle swarm optimization is a metaheuristic, derivative free optimization paradigm which models flocks of birds or the schooling of fish to solve mathematical problems.4, 19 Individual agents are relatively simple with complex behavior emerging from carefully designed social networks. We begin with a treatment of agent interactions in canonical PSO.
2.1 Canonical Particle Swarm Optimization
While many updates schemes have been derived for PSO, for this work we will utilize the constriction coefficient method presented by Clerc and Kennedy6, 29, 42 as it is a widely used update method and insures swarm stability with appropriate parameters selected. In short, updates for the ring topology are calculated as follows:
| (1) |
| (2) |
where v corresponds to an agents velocity, x to its position, U is a uniform random number drawn between 0 and ϕ1,2. For this application, ϕ1 = ϕ2. The constriction coefficient χ is defined as29
| (3) |
where ϕ = ϕ1 + ϕ2 = 4.1. In the case of the ring social network, pi is the current agent’s best position, pg is the best position of the best agent in the neighborhood, and xi is the agent’s current position.
The fully-informed PSO can be formulated by allowing each agent to provide the agent under update with its best past performance.25
| (4) |
| (5) |
Here pbn is the best position of the nth neighbor. Sociometrically, this network draws influence from each of its neighbors irrespective of neighbor performance. This network has shown good performance in some cases, but may suffer from premature convergence to local minima.
Many other social networks have been developed to compromise between the two extremes of social network design, namely the ring and fully connected social networks. Here we develop a biophysically inspired network which maintains the relative simplicity of static social networks while performing well on benchmark optimization problems.
2.2 Winner-Take-All Particle Swarm Optimization
Social networks presented for particle swarm optimization are not often biophysically inspired. Here we present a new social network which takes inspiration from winner-take-all (WTA) neural coding in visual cortex. Seminal work in graph theory has shown that small world, high information throughput networks emerge from normal ring topologies after a relatively small number of non-neighbor connections are made.8, 44 These small world networks are of particular interest in the central nervous system. Specifically, previous studies have shown the emergence of hierarchical structures and points of influence in connection heavy areas of the human connectome.40 In the realm of PSO, Kennedy has shown that PSO problem solving behavior is topology dependent and exhibits small world dependence.18 Interestingly, full small world inclusion does not necessarily facilitate more robust problem solving behavior, and may even be detrimental in comparison to a more sparsely connected network.25 Indeed, our preliminary studies have indicated that simply creating a fully informed network typically exhibited weaker problem solving ability than a ring social network (data not shown). Therefore, inclusion of small world shortcuts into swarm topologies must be carefully designed and evaluated.
Drawing from biological neural networks, we propose a new social network for particle swarm optimization. Figure 2 displays the overall social network architecture. The social network is built around a dynamic hierarchical structure that allows for performance based promotion among agents. A number of networks in visual and parietal cortex exploit winner-take-all (WTA) coding schemes.23, 28 In WTA coding, input neurons compete for output neuron activation, with the response of the output cell most closely resembling the firing rate and tuning characteristics of the strongest input. Physiologically, WTA rules are thought to be involved in visual attention and saliency detection throughout the visual system, including object orientation and direction.15, 34 Visual cortical regions also exhibits small world connectivity.36 Figure 2 displays the overall social network architecture. The social network is built around a dynamic hierarchical structure that allows for performance based promotion among agents. First, a global leader is selected by polling the swarm for the agent who is performing best on the fitness function. Agents are then grouped into a lower tier of local neighborhoods. From the neighborhoods, local leaders are selected based upon which agent is performing best on the fitness function from the neighborhood. The hierarchical structure shares characteristics of information transmission seen in ring networks by limiting the speed of update influence between any two agents. The graph analysis software Gelphi2 was used to derive relevant static graph measures for each social network structure (Table 1). Interestingly, the average path length, a measure of the distance information travels along a graph, is shorter in WTAPSO than the ring or dynamic ring topologies, but longer than that in the four corners social network. The cluster coefficient, a measure of the amount of grouping, displays the same characteristic, with WTAPSO being more clustered than the ring networks, but less so than the four-corners network. These however, while true in the static sense, will be fundamentally altered in dynamic networks when parameters change during updates as connections are dynamically broken and reassembled. In WTAPSO, updates between any two agents follow a modified winner-take-all rule where agents compete for influence on the agent under update. To update a neighborhood agent (Fig. 2C) the neighborhood is polled for the two best performing agents with the agent under update excluded from the poll. Since the neighborhood leader is by definition the best performer of the neighborhood, it is included as one of the updating agents. The other updater is then the local agent who is currently performing the best on the fitness function. At this point, the neighborhood becomes temporarily disconnected and the agent under update is only updated by the two best performing agents. This works to remove any bad influence from updating a target agent. Quantitatively, updates for neighborhood agents are as follows:29
Table 1.
Social Network Parameters
| Network | Ave. Path Length | Diameter | Modularity | Ave. Clustering Coefficient |
|---|---|---|---|---|
| WTAPSO | 2.971 | 4 | 0.664 | 0.584 |
| Ring | 5.5 | 10 | 0.56 | 0 |
| Dynamic Ring | 5.5 | 10 | 0.56 | 0 |
| Four | 2.263 | 3 | 0.62 | 0.76 |
| (6) |
| (7) |
where pn,pl correspond to the best neighbor position and best neighborhood leader positions respectively. Updates of neighborhood leaders draw influence from their local neighborhood as well as the global leader (Fig. 2B). Like the agent update, the neighborhood leaders neighborhood is polled for the best performing agent, excluding the neighborhood leader. Neighborhood leaders will always draw influence from the global leader as the global leader by definition is the best performing agent of the swarm. Similar to neighborhood agents, updates are made as follows:
| (8) |
| (9) |
where pn corresponds to the best performing neighborhood agent and pg corresponds to the global leader. Finally, the global leader draws influence from the best performing of the local leaders as well as its past best performance (Fig. 2D). This is to ensure that if the swarm is traveling down a good path that this influence continues. Updates are given by:
| (10) |
| (11) |
where pg corresponds to the global leader’s best past performance and pl corresponds to the best performing local leader. After updates are complete, agents are re-evaluated against the fitness function and positions within the swarm are updated. If at any point an agent, irrespective of its place in the social network, performs better than the global leader on the fitness function, it is promoted to the global leader position. Neighborhoods are then reformed and local leaders elected.
2.3 Methods of Testing Optimization Algorithms
In practical optimization, metrics such as algorithm performance and time costs are very important. For example, algorithms that have better problem solving ability may not be useful if run times are exceptionally long. For this study, we tested WTAPSOs ability to solve high dimensional problems, its problem solving ability across a variety of problems, and its runtime and compared these against commonly used social networks designed in-house and in software toolboxes.
In this study, we utilize the common ring network, a dynamic variant of the ring network which reshuffles agent positions in the ring after each update, and the four corners social network (Fig. 1). Updates for these networks followed a static constriction coefficient method discussed above. We also utilized the Common and Trelea type 2 networks found in a pre-designed Matlab Particle Swarm Optimization toolbox.3
Next, we aim to test WTAPSO performance across dimensions compared to other social networks. For this experiment, the classic test optimization Rosenbrocks function31 was utilized and spanned across 2 to 10 dimensions. Rosenbrocks function in arbitrary dimension is given by:31, 35
| (12) |
and has a minimal value of 0 when all inputs are identically 1. Significance was assessed via a multi-way ANOVA followed by post hoc Tukey Honest Significant Difference (HSD) tests between groups. Points were deemed significant for p ≤ 0.05. Groups were across social network type and problem dimension. Each optimization problem was repeated 500 times.
To see how WTAPSO performs against a diversity of problems, we ran each social network against a conglomerate of test optimization functions. Their known global minimums are shown in Table 2. In this test, we used 10 dimensional Ackley, Griewank, Rastrigin, Sphere, and Styblinsky-Tang problems, 30 and 100 dimensional Rosenbrock function, 2 dimensional Schaffer N.2 and N.4 functions, and 10 and 20 dimensional Styblinksy-Tang functions. These functions represent a wide variety of classical test optimization functions at many different dimensions and degrees of difficulty. The less common Styblinsky-Tang function is used to demonstrate that the solutions were not preprogrammed into the algorithm, as its global minimum is a function of problem dimension. A subset of these functions was tested with the Common and Trelea networks found in the Matlab Particle Swarm Optimization Toolbox. These were the functions pre-built into the toolbox. Again, each problem was run 500 times. Initial conditions were set such that initial position was set as a uniform random variable between the function domain and velocities set to 0 as previous studies have shown better swarm solutions in this condition.42
Table 2.
Frequency Tuning Optimization Parameters
| Frequency | AM Tuning |
|---|---|
| AMPA Conductance (%) | AMPA Conductance (%) |
| NMDA Conductance (%) | NMDA Conductance (%) |
| GABAA Conductance (%) | GABAA Conductance (%) |
| Membrane Potential (mV) | Membrane Potential (mV) |
| Excitatory input Q10 factor | EX Rate Beta params |
| Excitatory input firing rate | IN Rate Beta params |
| Inhibitory input Q10 factor | EX VS Beta params |
| Inhibitory input firing rate | IN VS Beta params |
| Inhibitory input CF (Hz) | EX,IN total rate |
| Inhibitory Lag | EX,IN total VS |
| Excitatory input PSTH factors | |
| Inhibitory input PSTH factors |
To test the speed of algorithm completion, we utilize the Rosenbrock function across 2, 5, 8, 10, and 30 dimensions. The swarm was allowed to run until a function value of 100 or less was reached, which is considered a good fit for the Rosenbrock function.25 However, if the swarm reaches 10000 iterations, the solution is coded as not found and the program stopped. After the 10000 iteration mark, it is unlikely the swarm will find the target solution in a reasonable time frame. For this study, only the ring, dynamic ring, and four corners social network were used. As the PSO toolbox was self-contained, we could not test run time in this manner. Tests were repeated 500 times for each problem. All graphs are plotted as means with standard deviations.
2.4 Neuron Model tests
To test the ability of WTAPSO to fit neural models, a previously published biophysical model of an inferior colliculus neuron with NEURON software5 was modified and utilized.30 The inferior colliculus is a major point of convergence of the central auditory system, integrating excitatory inputs from dorsal and ventral cochlear nucleus and lateral and medial superior olive and inhibitory inputs from dorsal and ventral nucleus of the lateral lemniscus and superior paraolivary complex.17, 32 It is not well understood, however, how the confluence of these diverse inputs form neural responses to simple and complex stimuli. Computational models are a useful tool for explore integration patterns of the IC. We demonstrate in this work how physiological recordings and computational models can be used to solve the inherent inverse problem of input parameters to response generation.
Briefly, this biophysical conductance based neuron model was constructed using NEURON software,5 modified from a previous IC modeling study.30 First, models of spiking activity are recreated using WTAPSO. Real physiological spiking data were evoked via presentation of tonal and amplitude-modulated stimuli. To demonstrate the diverse range of neural problems WTAPSO can solve, frequency tuning curves (FTC) and temporal modulation transfer functions (tMTF) from pure sinusoidal and sinusoidal amplitude modulated tones respectively were modeled. In each case, five repetitions of each stimuli were modeled.
Inputs in the frequency tuning models consisted of peri-stimulus time histograms whose input shapes were allowed to dynamically vary according to swarm updates. Once input PSTHs were formed, a curve-fit was made to approximate an input probability density function. Cumulative density functions were then formed. Input spike times were drawn from excitatory and inhibitory input CDFs via an inverse transform sampling method.10 Briefly, a value U was generated from a uniform distribution. Then, a random variable X was found satisfying:
| (13) |
with F(*) denoting the CDF which a sample is to be drawn from. The random variable X is then a sample from CDF F(*). It should be noted that while this is a traditional method of sampling from an arbitrary probability distribution, slight aliasing is inherent in the method. The model feature space can be defined as necessary to capture relevant aspects of the model. Table 3 displays features for model reconstruction in AM and frequency tuning models. Finally, as PSO performance modulates across fitness functions(Table 3), careful selection of an appropriate function is important to algorithm performance. In order to preserve shape and absolute rates endemic to frequency tuning curves, a fitness function which accounts for both the correlation between experimental and model curves as well as their relative distance was used39 as shown:
| (14) |
where RMSE corresponds to the root mean square error, r is the correlation coefficient, and xc and xm are the experimental and model curves respectively. This function is bounded between 0 and 1, with values closer to zero corresponding to a better fit. For AM rate tuning, inputs consisted of two-parameter Beta-functions which approximate all-pass, band-pass, and low-pass inputs dependent on parameter value. A mean-square error metric was utilized for AM tuning responses. Spontaneous rates were modeled by an Ornstein-Uhlenbeck process9 with mean rates modeled from spontaneous activity recordings in young and aged rats.
Table 3.
Social Network Performance on Test Optimization Functions
| Problem | WTAPSO | Dynamic Ring | Ring | Four |
|---|---|---|---|---|
| Ackley10 | 0.15(±0.33) | 1.68(±0.64) | 1.92(±0.66) | 2.81(±0.53) |
| Griewank10 | 0.03(±0.09) | 1.99(±1.53) | 2.61(±2.02) | 6.66(±3.41) |
| Rastrigin10 | 0.90(±4.40) | 28.67(±8.19) | 38.09(±10.48) | 32.98(±6.85) |
| Rosenbrock30 | 0.03(±0.08) | 5.85E5(±3.89E5) | 8.23E5(±5.52E5) | 1.3E6(±7.98E5) |
| Rosenbrock100 | 0.10(±0.25) | 4.77E6(±1.56E6) | 6.21E6(±2.06E6) | 8.2E6(±2.65E8) |
| Schaffer’s F 2 | 8.98E−13(±1.78E−12) | 6.25E−6(±1.4E−4) | 0(±0) | 0.01(±0.02) |
| Schaffer’s F 4 | 0.29(±2.20E−6) | 0.29(±4.98E−16) | 0.29(±4.98E−16) | 0.30(±0.01) |
| Sphere10 | 0.004(±0.005) | 167.12(±197.12) | 189.97(193.97) | 683.56(±416.84) |
| Styb10 | −365.55(±34.07) | −316.65(±19.77) | −322.35(±20.61) | −260.91(±20.31) |
| Styb20 | −757.48(±70.44) | −530.73(±31.60) | −542.26(±33.72) | −446.43(±32.02) |
Responses were recorded from Fischer-344 rats, similar to Rabang et al30 and Herrmann et al.13 Briefly, all surgical procedures used were approved by the Purdue University animal care and use committee (PACUC 06-106). Auditory brainstem responses were recorded from these animals a few days preceding surgery to ensure all animals had hearing thresholds typical for their age and to ensure there were no abnormal auditory pathologies. Surgeries and recordings were performed in a 9′x 9′ double-walled acoustic chamber (Industrial Acoustics Corporation). Anesthesia was induced in the animals using a mixture of ketamine (VetaKet, 80mg/kg for young animals and 60 mg/kg for aged) and medetomidine (Dexdomitor, 0.2 mg/kg for young and 0.1 mg/kg for aged animals) administered intra-muscularly via injection. The animals were maintained on oxygen through a manifold. The pulse rate and oxygen saturation were maintained using a pulse-oximeter to ensure normal range. Supplementary doses of anesthesia (20 mg/kg of ketamine, 0.05 mg/kg of medetomidine) were administered intra-muscularly as required to maintain areflexia and a surgical plane of anesthesia. An initial dose of dexamethasone and atropine were administered to reduce swelling. Constant body temperature was maintained via a heating pad (Gaymar) set at 37 degrees C. A central incision was made along midline and calvaria was exposed. A stainless steel headpost was cemented anterior to bregma and secured via bonescrews and a headcap constructed with dental cement. Cranioectomy was performed posterior to lambda and 1 mm lateral from midline. The dura matter was kept intact and target structure location was estimated via stereotaxic coordinates and physiological measurements in response to auditory stimuli. Recordings were typically made from the right IC.
2.5 Neural Stimuli
Once the inferior colliculus was located, stimuli were presented free-field, azimuth 0° elevation 0°. Stimuli were generated via Tucker-Davis Technology (TDT) Sig Gen RP. Stimuli were sampled at 97.64kHz and presented through custom written interface in Open-Ex software. For frequency tuning curves, sinusoidal stimuli were 200 ms in length and presented at five repetitions in logarithmic steps between 500 and 40000 Hz presented in random order for each trial. Sound level was set as the minimum sound level that produced a maximum response, typically corresponding to 60–70dB SPL in young animals. Sinusoidal amplitude modulated stimuli were 750 long with modulation frequencies in logarithmic steps between 8 and 1024 Hz.
3 Results
Here we display our results of WTAPSO performance across three separate tests and against previously defined social networks and PSO toolboxes. We will then discuss these results.
3.1 WTAPSO Behavior
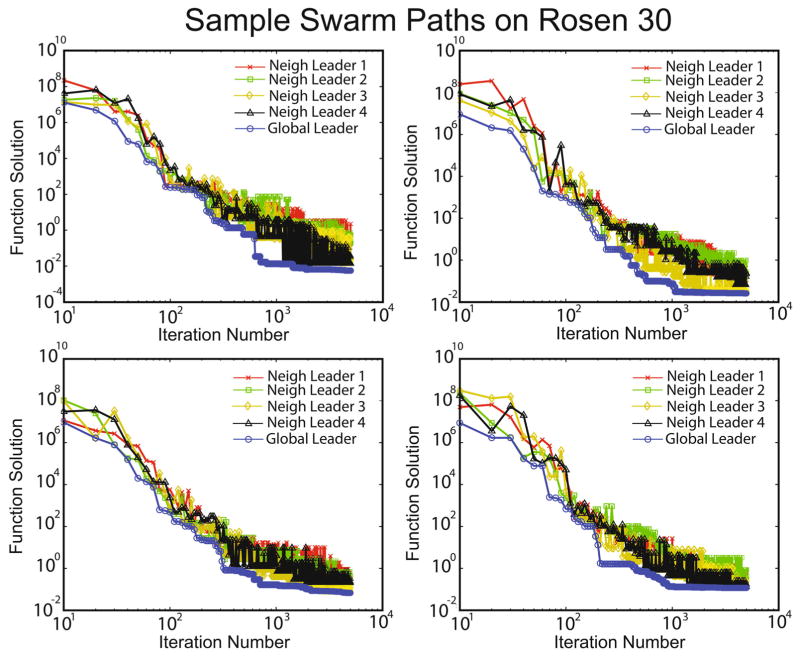
To begin, we demonstrate local and global neighborhood behavior of the WTAPSO algorithm. Figure 3 displays 4 sample paths of WTAPSO solving the 30 dimensional Rosenbrock function. This figure only represents values for the individual neighborhood leaders and does not indicate when leadership changes. Neighborhood leader dynamics show highly oscillatory behavior as the iteration count increases, indicative of the fact that minor changes in input variables from update changes can cause relatively significant changes in the output of the Rosenbrock function. Oscillation behavior might also be due to agents changing rank in the social network. However, we cannot say this for certain as leadership changes were not tracked for this test. Irrespective, the overall trend for each neighborhood leader is towards the minimum. The global leader is always monotonically decreasing towards the minimum value. Notably, there are areas in which the global leader seems to get stuck in local minimums, but network dynamics push it out of these minimums (Fig. 3 Upper and Lower Right).
Fig. 3.
Sample paths for WTAPSO on the Rosenbrock 30 problem. The global leader shows monotonically decreasing function values while the local leaders demonstrate decreasing trends with oscillations about error values, most likely due to the rearranging of the swarm networks. This also demonstrates WTAPSOs ability to move out of local minima until convergence at higher iteration values.
3.2 WTAPSO is able to solve high dimensional problems
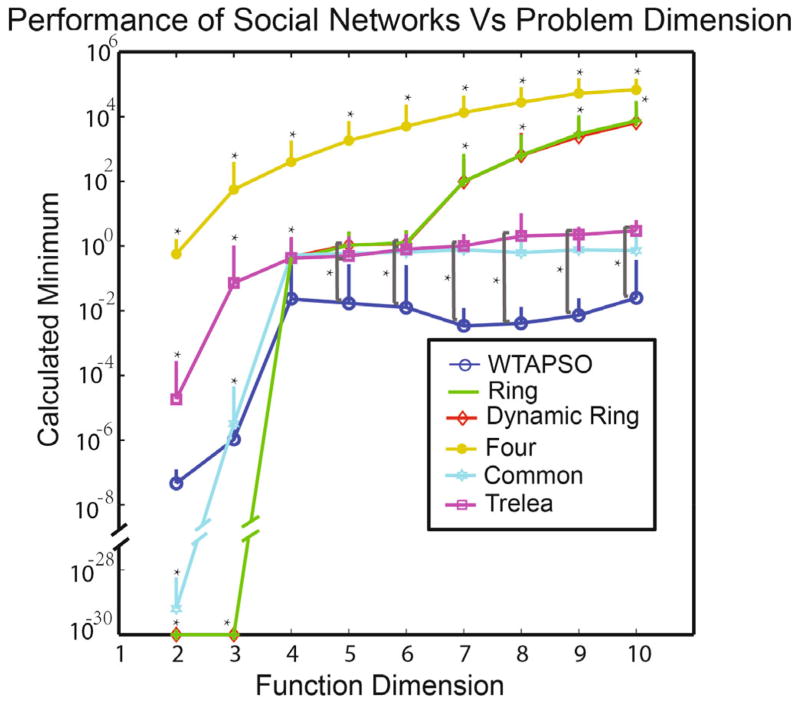
Our first test compared the performance of WTAPSO on high dimensional problems compared to other social networks. Figure 4 displays the performance of all social networks on the Rosenbrock optimization problem between 2 and 10 dimensions. Significance was assessed by a two-way ANOVA with Tukey Honestly-Significant-Difference (HSD) post tests between groups. Data was log transformed before analysis. Minimal value was truncated at 10−30 in order to represent data on a log plot.
Fig. 4.
Social network performance versus dimensionality on the Rosenbrock function. While Canonical ring, dynamic ring, Common and Trelea social networks perform best in low dimensions, the winner take all social network performs on par with the toolbox Matlab toolbox Common network and better than all others. Significance was assessed by a two-way ANOVA with Tukey honestly-significant-difference post tests. * indicates a significant difference between WTAPSO and social network under test.
In lower dimensions (less than 5), traditional social networks can perform better than WTAPSO. This is not to say, however, that the WTAPSO performs poorly. According to a metric presented by Mendes et al,25 WTAPSO is performing well. As higher order dimensions are introduced, performance of every social network decreases as expected. After 4 dimensions, WTA PSO starts to perform as well as Matlab PSO tool-box Common network and outperforms every other network. It is interesting to note that many of the social networks grow worse in problem solving ability as dimensionality increases, but WTAPSO (and the tool-box networks) seem to plateau and maintain a stable ability to solve problems. Subsequent experiments show that even in extremely high dimensional problems (30–100 dimensions), WTAPSOs problem solving ability does decrease somewhat, but remains much more robust than the other social networks (Tables 3 and 4).
Table 4.
WTAPSO vs. Toolbox Networks
| Problem | WTA | Common | Trelea |
|---|---|---|---|
| Ackley10 | 0.14(±0.33) | 17.20(±6.79) | 16.16(±7.77) |
| Griewank10 | 0.031(±0.092) | 2.77(±2.34) | 3.03(±2.41) |
| Rastrigin10 | 0.90(±4.40) | 9.67(±5.54) | 10.52(±6.10) |
| Rosenbrock30 | 0.03(±0.08) | 37.02(±39.67) | 12.03(±15.84) |
| Rosenbrock100 | 0.10(±0.25) | 203.79(±56.29) | 714.27(±4.5E3) |
| Sphere10 | 0.004(±0.01) | 9.49E−40(±1.02E−38) | 1.12E−36(±3.96E−36) |
3.3 WTAPSO successfully solves a wide variety of problems
The no-free-lunch theorem (NFL)45 states that given the set of all possible optimization problems, on average no optimization paradigm will perform better than any other paradigm on all possible problems. In other words, there are some problems that will be more difficult for an optimization paradigm to solve. With that in mind, we will show that WTAPSO can solve a wide variety of nonlinear problems that will be of interest to real systems analysis. Table 3 shows the results of WTAPSO, ring, dynamic ring, and four social networks against the 10 dimensional Ackley function, 10 dimensional Griewank problem, 10 dimensional Rastrigin problem, 30 and 100 dimensional Rosenbrock programs, 2 dimensional Schaffer F 2 and F 4 functions, 10 dimensional sphere function, and 10 and 20 dimensional Styblinsky-Tang function. Inputs to each function leading to global minimums can be found in Table 2 and problem formulations are found in the appendix. On the Ackley and Griewank 10 dimensional problems, all social networks got relatively good results, but WTAPSO in both cases averaged closer to the global minimum of 0 on both problems. The 10 dimensional Rastrigin problem proved difficult to solve for the three test social networks to solve, but WTAPSO was able to find values closer to the global minimum of 0. To test the ability of WTAPSO to solve very high dimensional problems, the 30 and 100 dimensional Rosenbrock problems were used. Due to the nonlinear nature of the Rosenbrock problem, even slight variations in the input can cause explosion of the output. The ring and four corners social networks fail to find satisfactory answers in all both dimensional cases. WTAPSO was able to find satisfactory answers even in the very difficult 100 dimensional case. In the two dimensional Schaffer problems, all social networks performed roughly the same, with the dynamics ring social network finding the exact minimum of 0 on the Schaffer N.2 problem and smaller standard deviations in the Schaffer N.4 problem.
To show that WTAPSO is able to track changing global minimums, the Styblinksy-Tang function was used, which has a global minimum that changes with problem dimension, defined by:
| (15) |
In both the 10 and 20 dimensional variants, WTAPSO performed better than the other social networks, demonstrating the ability to track changing global minimums on a problem definition. It should be noted that these topologies used in Mendes et al25 do provide better results. However, the update functions and use of information were fundamentally different, owing to the difference in observations and further proving the importance of all aspects of the design of a swarm.
Next we compared the performance of WTAPSO against a previously established Matlab PSO toolbox. Only the subset of test functions available within the toolbox were used for this analysis. Results in Table 4 demonstrate that WTAPSO performs better on most test functions, with the exception of the 10 dimensional sphere problem. This helps to illustrate the no-free-lunch theorem and that there are problems that are easier for some social networks to solve.
3.4 WTAPSO takes fewer iterations to solve problems
Our final test was to determine whether WTAPSO was able to solve problems faster that other social networks. For this test, to account for differences in CPU time and processing, we utilized iteration count as our time metric. To standardize against problem type, we used only the Rosenbrock problem at 2, 5, 8, 10 and 30 dimensions. Following the convention of Mendes et al,25 swarms were allowed to run until a function value of 100, corresponding to an acceptable solution, was reached or the number of iterations exceeded 10, 000, at which point it is assumed that the swarm would not converge onto an adequate solution. Figure 6 demonstrates that on the 2 dimensional Rosenbrock problem, every swarm was able to reach an adequate solution at a reasonable number of iterations. In 5 dimensions, the ring social networks are able to solve the problem in an adequate time, but the four corners social network can no longer find a solution. As dimensionality increases, only the WTAPSO is able to solve the problem and does so in a remarkably low number of iterations ( 100 iterations). This test shows that, independent of CPU processing power, WTAPSO is able to find solutions in a lower iteration count than the test social networks which in most cases will translate to lower run times.
Fig. 6.
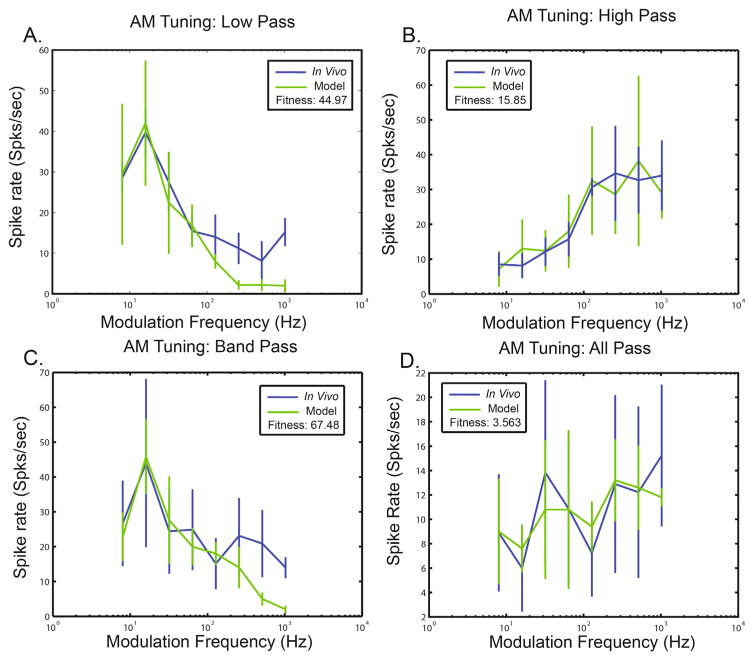
Example rMTFs. Functions were optimized around synaptic conductance values and input beta distribution priors. WTAPSO is able to recreate a wide variety of response classes including low-pass, high-pass, band-pass, and all-pass shapes.
3.5 Inferior Colliculus Measurements
To demonstrate the viability of WTAPSO to solve biophysical neuron model inverse problems, we show response generation from three different auditory feature representations in the IC.
3.5.1 Frequency Tuning Curve Fitting
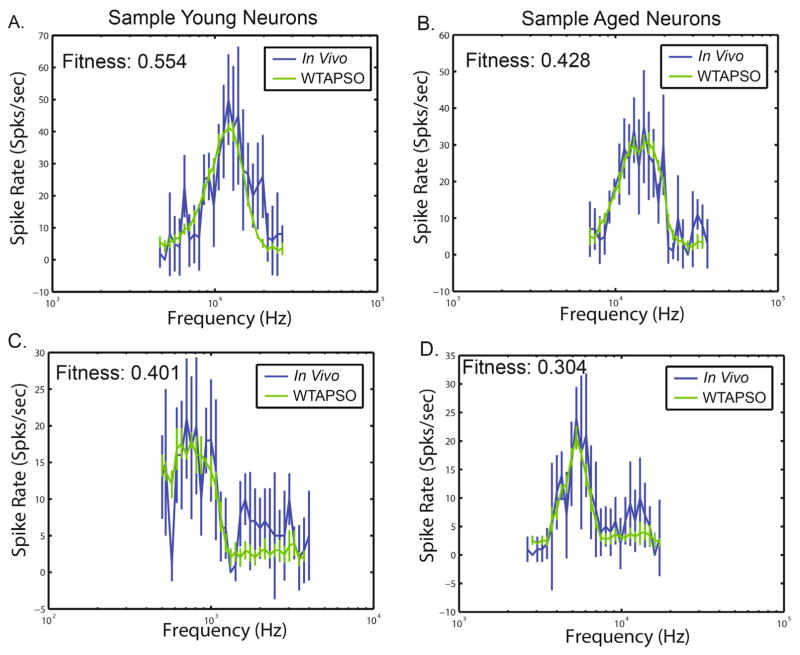
Neurons throughout the auditory pathway exhibit tonotopic frequency mappings with different spatial regions of auditory regions characterized by neurons exhibiting maximal firing at a specific frequency, known as the characteristic frequency. We demonstrate WTAPSO systematically fitting input parameters and distributions to recreate FTCs recorded in vivo (Fig. 5). Figure 5A,D demonstrates reconstruction of typical FTC curves with maximum mean rate at its center frequency. WTAPSO is also able to recreate more challenging tuning curve, such as those with two disjoint peaks in the mean (Fig. 5B). Finally, WTAPSO is able to recreate tuning curves with less well defined shapes, such as in Fig 5C. While the driven region of the curve is well fit, there is some error at the non-driven region, as spontaneous rate is a fixed parameter not subject to optimization in this version of the model. Table 4 shows the reconstructed parameters for the fits in Figure 5. Several constraints were put in place to ensure operation in a biophysically relevant region, such as resting membrane potential set between −80 and −50 mV and fully positive conductance values. For the purpose of this work, parameters governing input PSTH values were not constrained. However, careful attention to these should be paid when drawing physiological relevance from fits.
Fig. 5.
Recreation of in vivo FTCs using a biophysical neuron IC model using WTAPSO. Responses were illicited from sinusoid tones of varying frequencies. The fitness function varies between 0 and 1 with 1 being a better fit. Spontaneous responses were not fit, but set to rates typically seen in recordings (data not shown). WTAPSO is able to recreate a wide variety of responses types and shapes seen in vivo.
3.5.2 AM-Tuning Fits
Utilizing the same biophysical IC neuron model, responses to sinusoid-amplitude modulated tones were reconstructed. Figure 6 demonstrates reconstructed modulation transfer functions (MTFs). For these examples, inputs were derived from a beta prior and demonstrate that incomplete knowledge of input parameters can still lead to good fits. Importantly we are able to fit a wide variety of IC neural response classes seen in the IC.30 For these fits, we utilized a mean-square error metric which measures relative distance between the mean of the experimental and model rMTFs, with lower values representing better fits. Sources of error most likely arise due to the choice of the beta function prior which may not fully encompass input distributions. With naive assumptions about the underlying input distribution, WTAPSO was able to recreate the rMTFs of individual IC neurons that were representative of the most common rMTF classes, demonstrating the ability to draw inference even in situations with incomplete information.
4 Discussion
4.1 WTAPSO performs best in high dimensional problems
In optimization, many solvers suffer from the curse of dimensionality, where higher dimensional problems become overly difficult to solve. This necessitates the need for specialized high dimensional solvers. Further complicating these issues is the fact that many experimental paradigms may not provide access to explicit derivatives, meaning that classical optimization methods cannot be utilized. Furthermore, computational neuroscience models are often high dimensional in nature. In this work we present a new social network for particle swarm optimization which mimics winner-take-all connectivity found in visual cortex neural networks. We have demonstrated that WTAPSO is able to solve very high dimensional problems, outperforming traditional social networks and publicly available particle swarm toolboxes. In this study, we used a relatively simple static constrained coefficient method. It is predicted that allowing for a dynamic constriction coefficient will yield better results as step size can be modified based on distance from a solution. It was also seen that individual agents in WTAPSO can get stuck in local minima and cannot be drawn out even with well behaving influences. Depending on problem complexity, there is some wasted processing spent on agents which are no longer able to find solutions. A way to mitigate this may be the inclusion of a grim-reaper routine, which searches for agents that are both far away from the best performing agent and no longer making significant advances in fitness function. This routine will then remove the agents from the swarm, and thus reduce computational load, or reinitialize the agent based on best performing network and global leaders. The latter may also provide the algorithm better influences as one more agent will now be searching a space that is more likely to contain the local minimum than its previous location, but this is remains to be tested.
4.2 WTAPSO is relatively simple to implement
Some swarm intelligence methodologies seek to address the problem of dimensionality by subdividing the swarms into many sub-swarms to search problem sub-spaces and then pool what was learned to find an optimum solution.42 However, many problems, such as biophysical neural models which require the simultaneous tuning of many model parameters, are computationally demanding. and subdividing swarms into miniswarms would unacceptably blow up computation time. WTAPSO may provide a viable framework for modeling problems such as these because its construction is as simple as defining a new social network and does not require any more computation time than a swarm with comparable number of agents. Furthermore, it is able to find solutions in a fewer number of iterations in comparison with other PSO methods, meaning that complex models may run in faster time. Toolboxes adopting this method may then use ring topologies to solve low dimensional problems and an option for WTAPSO for high dimensional problems. While other particle swarm paradigms, such as comprehensive learning PSO,24 attempt to mitigate the amount of bad influences updating an individual agent, WTAPSO does so in a more deterministic fashion and allows for systematic testing of various particle hypotheses. For example, each neighborhood can be initialized to different regions of the solution space.
4.3 Fitting of Physiological Response Curves
We have shown the ability of WTAPSO to solve the inverse problem of retrieving physiological inputs from neural response tuning curves. While general input distributions can be utilized, as in the Beta distribution in the AM tuning model, physiologic inputs will most likely give rise to more accurate fits. Thus, when making inferences regarding neural function, one must pay special attention to the region of feasible physiologic inputs, both in feature selection and constraints. While this method does fit individual tuning curves, synaptic inputs are almost certainly not unique mappings, i.e., each response curve could be generated by different sets of inputs. However, this method generates inputs which serve as a basis for parameters which can empirically tested in electrophysiolgy experiments. This method is also problem independent: as long as there is a mathematical model of the neuron under test, WTAPSO can be used to fit physiological responses.
4.4 Further Considerations
One consequence of the No Free Lunch theorem is that there can be no guarantees on optimal performance on every problem an optimization paradigm might encounter. However, in line with Mendes et al25 assertion that the NFL theorem does not negate the need to find better PSO social networks, there is a large subset of interesting problems that are high dimensional. As our data have shown, traditional particle swarm social networks and toolboxes often fail at finding adequate solutions to high dimensional problems. The WTAPSO social network shows improved performance on high dimensional problems. Furthermore, our preliminary studies in using this social network on real-world system models has shown excellent performance in parameter tuning in high dimensional problems with run times that are reasonable on a personal PC. The WTAPSO social network also offers unique abilities to explore solutions spaces of real world problems. For example, the four social networks can be started at vastly different initial conditions that test potential biophysical mechanism hypotheses. The networks swarms can be allowed to run independently to find local optimum solutions then connected to see which physical parameter dominates in a certain operating zone. Finally, the swarm can be recursively defined, incorporating more neighborhoods extending below the lower agents which might contribute to better problem solving behavior.
5 Conclusion
Here we present a new hierarchical particle swarm optimization social network which draws influence from winner-take-all coding found in visual cortical neurons. WTAPSO shows improved performance in high dimensional test optimization problems and may be valuable in parameter tuning problems of physical models. While many PSO social networks are not biophysically inspired, we hope to show that power of drawing influence from real world networks as a way to inspire better problem solving behavior in artificial social networks. Futhermore, WTAPSO serves as a potentially powerful tool for fitting complex neural responses across sensory modalities.
Table 5.
Frequency Tuning Synaptic Recreations
| Parameter | 13 Y2 | 14 Y10 | 13 A3 | 13 A6 |
|---|---|---|---|---|
| AMPA Conductance(%) | 257.79 | 95.76 | 183.33 | 149.90 |
| NMDA Conductance(%) | 192.26 | 280.95 | 159.54 | 150 |
| GABAA Conductance(%) | 182.35 | 217.78 | 170.45 | 150 |
| Membrane Potential (mV) | −57.37 | −57.88 | −50.86 | −53 |
| EX Q10 Factor | 3.13 | 2.12 | 4.76 | 2.91 |
| EX Firing Rate (spks/sec) | 129.31 | 60.60 | 80.46 | 115.89 |
| IN Q10 Factor | 3.70 | 3.36 | 7.1 | 5.2 |
| IN Firing Rate (spks/sec) | 71.98 | 71.57 | 84.40 | 119.8 |
| Inhibitory CF (kHz) | 12.13 | .71 | 5.28 | 14.93 |
Acknowledgments
This work was supported by the National Institutes of Health under grant DC-011580
6 Appendix
The following test optimization functions were used in accessing WTAPSO performance.
| (16) |
Minimum: 0 at X = (1, 1, ..., 1)
Sphere Function26
| (17) |
Griewank’s Function12
| (18) |
Rastrigin’s Function27
| (19) |
Ackley’s Function1
| (20) |
Schaffer’s F216
| (21) |
Schaffer’s F416
| (22) |
Styblinsky-Tang38
| (23) |
Contributor Information
Brandon S. Coventry, Weldon School of Biomedical Engineering, Purdue University
Aravindakshan Parthasarathy, Weldon School of Biomedical Engineering, Purdue University.
Alexandra L. Sommer, Weldon School of Biomedical Engineering, Purdue University
Edward L. Bartlett, Weldon School of Biomedical Engineering and the Department of Biological Sciences, Purdue University
References
- 1.Ackley DH. A Connectionist Machine for Genetic Hill-climbing. 1. Kluwer Academic Publishers; Boston: 1987. [Google Scholar]
- 2.Bastian M, Heymann S, Jacomy M. Gephi: An Open Source Software for Exploring and Manipulating Networks. International AAAI Conference on Weblogs and Social Media. 2009:1–2. [Google Scholar]
- 3.Birge B. Particle Swarm Optimization Toolbox. 2006. [Google Scholar]
- 4.Blum C, Roli A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Computing Surveys. 2003 Sep;35(3):268–308. [Google Scholar]
- 5.Carnevale NT, Hines ML. The NEURON Book. Vol. 30. Cambridge University Press; 2006. [Google Scholar]
- 6.Clerc M, Kennedy J. The particle swarm - explosion, stability, and convergence in a multidimensional complex space. IEEE Transactions on Evolutionary Computation. 2002;6(1):58–73. [Google Scholar]
- 7.Coello Coello C, Lechuga M. MOPSO: a proposal for multiple objective particle swarm optimization. Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02 (Cat. No.02TH8600); IEEE; 2002. pp. 1051–1056. [Google Scholar]
- 8.Collins JJ, Chow CC. It’s a small world. Nature. 1998 Jun;393(6684):409–10. doi: 10.1038/30835. [DOI] [PubMed] [Google Scholar]
- 9.Destexhe A, Rudolph M, Fellous JM, Sejnowski TJ. Fluctuating synaptic conductances recreate in vivo-like activity in neocortical neurons. Neuroscience. 2001 Jan;107(1):13–24. doi: 10.1016/s0306-4522(01)00344-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Devroye L. Non-Uniform Random Variate Generation. 1. Springer; New York: 1986. [Google Scholar]
- 11.Elbeltagi E, Hegazy T, Grierson D. Comparison among five evolutionary-based optimization algorithms. Advanced Engineering Informatics. 2005;19(1):43–53. [Google Scholar]
- 12.Griewank AO. Generalized descent for global optimization. Journal of Optimization Theory and Applications. 1981 May;34(1):11–39. [Google Scholar]
- 13.Herrmann B, Parthasarathy A, Han EX, Obleser J, Bartlett EL. Sensitivity of rat inferior colliculus neurons to frequency distributions. Journal of neurophysiology. 2015;114(5):2941–54. doi: 10.1152/jn.00555.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hu X, Eberhart R. Multiobjective optimization using dynamic neighborhood particle swarm optimization. Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02 (Cat. No.02TH8600); IEEE; 2002. pp. 1677–1681. [Google Scholar]
- 15.Itti L, Koch C. Computational modelling of visual attention. Nature reviews. Neuroscience. 2001;2(3):194–203. doi: 10.1038/35058500. [DOI] [PubMed] [Google Scholar]
- 16.Jamil M, Yang XS. A literature survey of benchmark functions for global optimisation problems. International Journal of Mathematical Modelling and Numerical Optimisation. 2013;4(2):150. [Google Scholar]
- 17.Kelly JB, Caspary DM. Pharmacology of the Inferior Colliculus. In: Winer JA, Schreiner CE, editors. The Inferior Colliculus. Springer; New York: 2005. pp. 248–281. [Google Scholar]
- 18.Kennedy J. Small worlds and mega-minds: effects of neighborhood topology on particle swarm performance. Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406); IEEE; 1999. pp. 1931–1938. [Google Scholar]
- 19.Kennedy J, Eberhart R. Particle swarm optimization. Proceedings of ICNN’95 - International Conference on Neural Networks. 1998;4:1942–1948. [Google Scholar]
- 20.Kennedy J, Mendes R. Population structure and particle swarm performance. Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02 (Cat. No.02TH8600); IEEE; 2002. pp. 1671–1676. [Google Scholar]
- 21.Kentzoglanakis K, Poole M. A swarm intelligence framework for reconstructing gene networks: Searching for biologically plausible architectures. IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2012;9(2):358–371. doi: 10.1109/TCBB.2011.87. [DOI] [PubMed] [Google Scholar]
- 22.Kim J-Y, Mun K-J, Kim H-S, Park JH. Optimal power system operation using parallel processing system and PSO algorithm. International Journal of Electrical Power & Energy Systems. 2011 Oct;33(8):1457–1461. [Google Scholar]
- 23.Lampl I, Ferster D, Poggio T, Riesenhuber M. Intracellular measurements of spatial integration and the MAX operation in complex cells of the cat primary visual cortex. Journal of neurophysiology. 2004;92(5):2704–2713. doi: 10.1152/jn.00060.2004. [DOI] [PubMed] [Google Scholar]
- 24.Liang JJ, Qin AK, Suganthan PN, Baskar S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Transactions on Evolutionary Computation. 2006;10(3):281–295. [Google Scholar]
- 25.Mendes R, Kennedy J, Neves J. The Fully Informed Particle Swarm: Simpler, Maybe Better. IEEE Transactions on Evolutionary Computation. 2004 Jun;8(3):204–210. [Google Scholar]
- 26.Mikki SM, Kishk AA. Particle Swarm Optimization: A Physics-Based Approach. Synthesis Lectures on Computational Electromagnetics. 2008 Jan;3(1):1–103. [Google Scholar]
- 27.Mühlenbein H, Schomisch M, Born J. The parallel genetic algorithm as function optimizer. Parallel Computing. 1991 Sep;17(6–7):619–632. [Google Scholar]
- 28.Oleksiak A, Klink PC, Postma A, van der Ham IJM, Lankheet MJ, van Wezel RJa. Spatial summation in macaque parietal area 7a follows a winner-take-all rule. Journal of neurophysiology. 2011;105(3):1150–1158. doi: 10.1152/jn.00907.2010. [DOI] [PubMed] [Google Scholar]
- 29.Poli R, Kennedy J, Blackwell T. Particle swarm optimization. Swarm Intelligence. 2007 Aug;1(1):33–57. [Google Scholar]
- 30.Rabang CF, Parthasarathy A, Venkataraman Y, Fisher ZL, Gardner SM, Bartlett EL. A computational model of inferior colliculus responses to amplitude modulated sounds in young and aged rats. Frontiers in neural circuits. 2012 Jan;6(November):77. doi: 10.3389/fncir.2012.00077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rosenbrock HH. An Automatic Method for Finding the Greatest or Least Value of a Function. The Computer Journal. 1960 Mar;3(3):175–184. [Google Scholar]
- 32.Saldaña E, Aparicio MA, Fuentes-Santamaría V, Berrebi AS. Connections of the superior paraolivary nucleus of the rat: projections to the inferior colliculus. Neuroscience. 2009;163(1):372–387. doi: 10.1016/j.neuroscience.2009.06.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Salerno J. Using the particle swarm optimization technique to train a recurrent neural model. IEEE Comput Soc; Proceedings Ninth IEEE International Conference on Tools with Artificial Intelligence; 1997. pp. 45–49. [Google Scholar]
- 34.Salzman C, Newsome W. Neural mechanisms for forming a perceptual decision. Science. 1994 Apr;264(5156):231–237. doi: 10.1126/science.8146653. [DOI] [PubMed] [Google Scholar]
- 35.Shang Y-W, Qiu Y-H. A Note on the Extended Rosenbrock Function. Evoluationary Computation. 2006;14(1):119–126. doi: 10.1162/evco.2006.14.1.119. [DOI] [PubMed] [Google Scholar]
- 36.Shi L, Niu X, Wan H. Effect of the small-world structure on encoding performance in the primary visual cortex: an electrophysiological and modeling analysis. Journal of Comparative Physiology A. 2015;201(5):471–483. doi: 10.1007/s00359-015-0996-5. [DOI] [PubMed] [Google Scholar]
- 37.Shi Y, Eberhart R. A modified particle swarm optimizer. 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98TH8360); 1998. pp. 69–73. [Google Scholar]
- 38.Styblinski M, Tang T-S. Experiments in noncon-vex optimization: Stochastic approximation with function smoothing and simulated annealing. Neural Networks. 1990 Jan;3(4):467–483. [Google Scholar]
- 39.Tiilikainen J, Bosund V, Mattila M, Hakkarainen T, Sormunen J, Lipsanen H. Fitness function and nonunique solutions in x-ray reflectivity curve fitting: crosserror between surface roughness and mass density. Journal of Physics D: Applied Physics. 2007;40(14):4259–4263. [Google Scholar]
- 40.van den Heuvel MP, Sporns O. Rich-Club Organization of the Human Connectome. Journal of Neuroscience. 2011 Nov;31(44):15775–15786. doi: 10.1523/JNEUROSCI.3539-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Van Geit W, Achard P, De Schutter E. Neurofitter: a parameter tuning package for a wide range of electrophysiological neuron models. Frontiers in neuroinformatics. 2007;1(November):1. doi: 10.3389/neuro.11.001.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.VandenBergh F, Engelbrecht A. A Cooperative Approach to Particle Swarm Optimization. IEEE Transactions on Evolutionary Computation. 2004 Jun;8(3):225–239. [Google Scholar]
- 43.Vayrynen E, Noponen K, Vipin A, Yuan TX, Al-Nashash H, Kortelainen J, All A. Automatic parametrization of somatosensory evoked potentials with chirp modeling. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2016;4320(c):1–1. doi: 10.1109/TNSRE.2016.2525829. [DOI] [PubMed] [Google Scholar]
- 44.Watts DJ, Strogatz SH. Collective dynamics of ’small-world’ networks. Nature. 1998 Jun;393(6684):440–2. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 45.Wolpert D, Macready W. No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation. 1997 Apr;1(1):67–82. [Google Scholar]
- 46.Zhang C, Shao H. Particle swarm optimisation for evolving artificial neural network. SMC 2000 Conference Proceedings. 2000 IEEE International Conference on Systems, Man and Cybernetics. ’Cybernetics Evolving to Systems, Humans, Organizations, and their Complex Interactions’ (Cat. No.00CH37166); 2000. pp. 2487–2490. [Google Scholar]