A novel algorithm for network-based prediction of cancer recurrence

Abstract

To develop accurate prognostic models is one of the biggest challenges in ”omics”-based cancer research. Here, we propose a novel computational method for identifying dysregulated gene subnetworks as biomarkers to predict cancer recurrence. Applying our method to the DNA methylome of endometrial cancer patients, we identified a subnetwork consisting of differentially methylated (DM) genes, and non-differentially methylated genes, termed Epigenetic Connectors (EC), that are topologically important for connecting the DM genes in a protein-protein interaction network. The ECs are statistically significantly enriched in well-known tumorgenensis and metastasis pathways, and include known epigenetic regulators. Importantly, combining the DMs and ECs as features using a novel random walk procedure, we constructed a support vector machine classifier that significantly improved the prediction accuracy of cancer recurrence and outperformed several alternative methods, demonstrating the effectiveness of our network-based approach.

1 Introduction

High-throughput profiling techniques such as DNA microarray and next-generation DNA sequencing have enabled systematic screening of genomic, epigenomic, and transcriptomic changes associated with cancer, and rational design of more accurate and non-invasive cancer diagnosis and prognosis tools based on whole omics analysis (e.g. [1, 2, 3]). In particular, increasing evidence shows that DNA methylation plays significant roles in cancer, from the silencing of tumor suppressors to the activation of oncogenes and the promotion of metastasis, as well as the development of drug resistance [4, 5]. Though not altering DNA sequence itself, DNA methylation may change chromatin structure that renders the accessibility of promoters to transcriptional machinery and regulate gene expression [4, 5]. As DNA methylation changes are usually more stable than transcriptional changes, but are reversible (unlike DNA changes), they are promising biomarkers for accurate cancer diagnosis and prognosis [4, 6, 7].

Several large-scale profiling studies have revealed that the number of cancer-associated changes are tremendous and that very large number of patients are needed to isolate the few true “driver” changes from the vast number of sporadic “passenger” changes [8, 9]. In addition, common cancer-associated changes are often stable only on the level of functional pathways but not on individual loci [10, 11, 12, 13, 14, 15]. As the number of pathways is much smaller than the number of genes, pathway-based analysis can significantly reduce the number of variables and improve the stability of cancer prognostic models. Furthermore, most pathways have relatively well defined functions, which can possibly enable a better mechanistic understanding of obtained prognostic models, and provide a basis for the development of more effective intervention strategies.

A major hurdle of the pathway-based approach is that the majority of human genes have not been assigned to definitive pathways. To circumvent this limitation, one idea is to identify gene/protein subnetworks that are significantly altered in certain phenotypes as candidate pathway markers. The main rationale is that genes located closely in a gene/protein network are likely involved in similar functions, and that a group of genes with high connectivities among themselves and relatively fewer edges to the other genes are likely representing functional pathways. Indeed, screening of transcriptomic changes within the context of protein-protein interaction subnetworks has enabled systematic discovery of novel disease-associated pathways and development of more stable classification models [16, 17, 18, 14, 19, 20, 21, 22, 23, 24, 25].

Ideally, another advantage of the network-based approach over the pathway-based approach is that gene/protein networks provide an explicit wiring of genes among all genes, which can be utilized to characterize the “information flow” within the cell and pinpoint critical functional links between different pathways; in contrast, the existing pathways available in databases do not provide sufficient connectivity among different pathways. However, this theoretical advantage has not yet been fully exploited. In the existing subnetwork-based cancer classification models, subnetworks are usually treated as meta-genes, whose activity levels are defined as the mean activity levels of its member nodes [16, 21, 11, 24, 25]. This “averaged” view may provide statistical robustness by reducing noise; on the other hand, it will likely cause loss of information. Importantly, the internal structure within and between subnetworks are completely ignored. In addition, these subnetworks often have a high level of overlap, which introduces redundancy among features and reduces classification performance.

In this study, we propose a novel computational method to perform subnetwork-based cancer classi-fication. Our algorithm includes two important steps: (1) to identify a single subnetwork that connects important cancer-associated genes such as genes that are dysregulated, genes that are in the same pathways as the dysregulated ones, as well as key genes connecting these pathways; and (2) to compare cancer patients based on systems-level similarity by considering both the activities of individual genes and their connections embedded in the subnetwork identified from step 1.

The method is implemented and applied to analyze whole-genome DNA methylation data within the context of protein-protein interaction (PPI) network to identify subnetworks as potential biomarkers for predicting tumor recurrence in endometrial cancer, which affects the internal lining of the uterus. It is estimated that about 60,000 women will be diagnosed with endometrial cancer in the United States in 2016, making it the third leading cancer in new cases in women (Cancer facts and Figures, 2016, American Cancer Society). Although therapeutic intervention includes the removal of the uterus, hysterectomy, about 20% of endometrial cancer cases recur due to regrowth of occult disease and/or metastasis [26].

Using the network-based approach, we identified differentially methylated (DM) genes and additionally non-differentially methylated, termed epigenetic connectors (ECs), whose combination can significantly improve the prediction of three-year tumor recurrence as compared to using the DMs alone and two competing methods. Furthermore, while the DCs are not enriched in any cancer-related KEGG pathways, the ECs are significantly enriched in pathways well-known to be involved in tumorgenesis and metastasis, and include several known epigenetic regulators, signifying the effectiveness of our approach.

2 Methods

2.1 Method overview

In this study, we developed a novel computational method to analyze whole-genome DNA methylation data within a protein-protein interaction (PPI) network, and to identify epigenetically regulated functional pathways / subnetworks as potential biomarkers for predicting recurrent cancer. Our method consists of the following steps. First, the global DNA methylation patterns in primary endometrial tumors and normal control samples were determined by methyl-CpG binding domain-based capture coupled with massively parallel sequencing (MBDCap-seq). Second, the so-called DM genes, whose CpG islands exhibited statistically significant differential DNA methylation levels between recurrent and non-recurrent patients, were identified and mapped onto a human PPI network. Then, using the DM genes as seeds and an in-house graph algorithm for finding Steiner trees, we identified genes (termed epigenetic connectors, ECs for short) that were topologically important for connecting the DM genes on the PPI network. Finally, a random-walk based machine learning method was developed to propagate the DNA methylation scores from the DM genes to ECs, and the derived scores for the EC genes were used to construct a support vector machine for classifying tumor recurrence.

2.2 Raw data collection and processing

Endometrial tissue specimens were obtained as part of our ongoing work on characterizing molecular alterations in endometrioid endometrial carcinomas and were described in a previous report [27]. Global DNA methylation pattern of the 60 tumors and 12 controls were surveyed using methyl-CpG binding domain-based capture [28] coupled with massively parallel sequencing (MBDCap-seq; [7]). Briefly, methylated DNA was eluted by the MethylMiner Methylated DNA Enrichment Kit (Invitrogen) according to the manufacturer’s instructions. Eluted DNA was used to generate libraries for sequencing following the standard protocols from Illumina. MBDCap-seq libraries were sequenced using the Illumina Genome Analyzer II as per manufacturer’s instructions. Image analysis and base calling were performed with the standard Illumina pipeline. Sequencing reads were mapped by ELAND algorithm. Unique reads up to 36 base pairs were mapped to the human reference genome (hg18), with up to two mismatches. Reads in satellite regions were excluded due to the large number of amplifications. Biological reproducibility, technical repeat, and validation analysis were conducted, and the results suggest that MBDCap-seq can reliably identify differentially methylated regions in the genome. The methylation level was normalized based on the unique read numbers for each sample by a linear method.

The tumor differential methylation (TDM) score was calculated for each of the known promoter CpG islands for each cancer patient by comparing the average methylation level in a 8-kb window covering the CpG island in the tumor relative to normal controls using one-sample t-test. Let p be the p-value resulted from the t-test, for a CpG island significantly hypermethylated (over-methylated) in tumor, a positive TDM score was calculated as −log₁₀(p); similarly, for a hypomethylated (under-methylated) CpG island, a negative TDM score was calculated as log₁₀(p). In both cases, p-values greater than 0.01 were converted to 1 and as a result the corresponding TDM scores became zero. These CpG island level TDM scores were then mapped to gene-level scores, by assigning to each gene the highest TDM score among the CpG islands associated with the gene. This resulted in 4214 genes that had non-zero TDM scores for at least one patient. A detailed description and analysis of the complete DNA methylome for these patients has been published elsewhere [29].

2.3 Epigenetic marker and epigenetic connector subnetwork selection

Among the 60 patients available for analysis, 16 had recurrence within 3 years and were designated as recurrent, and the remaining were designated as non-recurrent. Because our objective is to classify tumor recurrence, patients that had persistent tumors or had non-recurrent tumor but last follow-ups were within three years after surgery were pre-excluded. In order to identify potential epigenetic markers for recurrence, we compared the TDM score of each gene between the recurrent tumors and the non-recurrent ones using two-sample t-test. Genes with a p-value < 0.02 were termed differentially methylated (DM) genes. Next, we mapped the DM genes to the human protein-protein interaction network obtained from HPRD (Release 9) [30]. We used the largest connected component of the network, which contained 9,205 unique genes (official gene symbols) and 36,720 interactions.

We then used these DM genes as seeds to identify the connector genes to link the seed genes into a singly connected subnetwork of the PPI. The rationale is that, if the seed genes are in the same pathway, the connectors should also have a high chance of being in the same pathway. On the other hand, if the seed genes belong to multiple pathways, the identified genes should contain both the in-pathway connectors and between-pathway connectors, and the latter can possibly contain the critical genes for cross-talks between pathways. By the Occam’s razor principle, we are interested in the most parsimonious solution, i.e., a spanning tree that connected the seed genes with the fewest additional genes. In graph theory, this mapped to the well-known Steiner tree problem. Formally, the Steiner tree for an edge-weighted graph G = (V, E, w) and a subset of vertices S⊆V is a minimum-weight connected tree T, with vertices U⊆V and edges D⊆E that spans all vertices in S. Here the vertices in S were known as terminal vertices and U-S as Steiner vertices. For an unweighted graph G, the problem then became finding the minimum number of vertices to connect all the vertices in S through a tree in G. The Steiner tree problem is NP-hard [31]. We implemented a polynomial-time shortest path heuristic algorithm of the Steiner tree problem [32].

To deal with noise and to increase the chance of covering all core members in the pathways and alternative functional links between pathways, we designed a simple randomized algorithm to obtain multiple Steiner trees with similar quality. To achieve this, we assigned to each edge of the PPI network a random weight between 0.99 and 1, and run the Steiner tree algorithm. These random weights effectively broke ties, so that if there were two paths with the same weight in the original network, one path would be chosen randomly. This procedure was repeated multiple times with different random weights, until the total number of unique Steiner vertices converged approximately. In this work, the rate of new coming Steiner vertices reduced significantly after 200–300 iterations. We pooled the Steiner vertices in the 300 Steiner trees to obtain a set of unique genes, which we termed epigenetic connectors (ECs), as they had important roles in forming connections among the differentially methylated epigenetic markers.

2.4 Using EC genes to predict recurrent tumors

As the ECs are not differentially methylated between recurrent and non-recurrent tumors, they are not expected to be very useful in predicting tumor recurrence when used alone. As a reminder, the ECs are either neighbors of many DMs or bottleneck nodes that are topologically important for connecting the DMs in different subregions of the PPI network, they may be functionally important for the integrity of the DM subnetwork.

To utilize the ECs as biomarkers, we propose a novel machine learning algorithm to derive a score for each EC gene from the methylation changes of its neighbors, while taking into consideration its topological property in the network. The method is adapted from the random walk with restart (RWR) algorithm [33] popular in machine learning and works as follows.

We first retrieved the PPI subnetwork consisting of the DM and EC genes, and then made it a directed network by adding arrows from the DM genes to EC genes. Therefore, the DM genes can only “pump” their TDM scores into the subnetwork but do not receive any scores. The ECs on the other hand have edges in both directions so they can act as both a donor and a receiver of TDM scores. We then used random walk to calculate the influence of each node on other nodes.

Formally, let A be the adjacency matrix of an unweighted, directed graph, where A_ij = 1 if there is an edge from node i to node j and 0 otherwise, and P be the row normalized adjacency matrix (i.e. the transition probability matrix) defined on the graph, where $p_{ij}=\frac{A_{ij}}{{\sum }_j{A}_{ij}}$ is the transition probability from node i to node j. Assume that a random walker starts from a node v, with a uniform probability to visit each of its neighboring nodes, and with a fixed probability c to revisit the starting node v at any time point during the walk. The probability for the random walker started at node v to be present at any node j, at a discrete time point k, is $f_{vj}^k=(1-c){\sum }_i{f}_{vi}^{k-1}{p}_{ij}+c{\delta }_{jv}$ , where δ_jv = 1 if j = v, and 0 otherwise. In our experiment c is set to 0.5 by default, while the performance of the algorithm is almost invariant with c between 0.3 and 0.7. This random walk procedure is guaranteed to converge, as shown previously [33]. The stationary probability vector $F_v^{inf}$, or simply denoted as F_v, is the influence of node v on any node in the network. Evidently, if v has no incoming edges, then f_vv = c and F_jv = 0 for any j ≠ v. The vector F_v is pre-computed for every v, using the matrix form F = (1 − c)FP + cI, where F is a square matrix and I is an identity matrix.

Finally, we derived a score for each gene based on its own TDM score and the influence it received from other nodes. Let s_i(t) be the TDM score of the i-th gene on the DM-EC subnetwork for patient t. The network-based methylation (NBM) score of gene i for t is calculated as: r_i(t) = Σ_v sv(t)Fi(v). It can be seen that for nodes with no incoming edges, r_i(t) = cs_i(t). In other words, the effect of this random walk procedure to the DM genes is simply multiplying their TDM scores by a constant factor c. Therefore at the end we multiply all the NBM scores by 1/c so that the TDM scores and NBM scores for the DM genes are equivalent.

2.5 Classification methods and performance evaluation

Support vector machine (SVM) classifiers were built using the SMO implementation in WEKA 3.6.6 [34]. Default settings were used for all parameters, with a linear kernel, and complexity parameter C = 1. Classification performance was estimated 100 times using 10-fold cross-validation. Classification accuracy is defined as the percent of patients classified correctly. As the dataset has much more non-recurrent patients than recurrent patients, “accuracy” can be misleading (for example, if a dataset has 90% negative and 10% positive instances simply predicting all cases to be negative would result in 90% accuracy.). Therefore, we also computed kappa statistic, κ, which measures the agreement between the class labels and the predictions made by the classifier, corrected by the amount of agreement that may be achieved by chance [35]. Formally, let TP, TN, FP, and FN be the numbers of true positive, true negative, false positive and false negative predictions made by a binary classifier, respectively, and N = TP + TN + FP + FN. The kappa statistic κ of the classifier is defined as $\kappa =\frac{A-C}{1-C}$, where $A=\frac{TP+TN}{N}$ is the fraction of correctly predicted instances and C is the expected percentage of instances that a classifier can predict correctly by chance, defined as $C=\frac{TP+FP}{N}\times \frac{TP+FN}{N}+\frac{TN+FN}{N}\times \frac{TN+FP}{N}$. Conventionally a kappa value over 0.75 is considered as excellent, 0.40 to 0.75 as good, and below 0.40 as poor. Additional evaluation metrics include the Area Under ROC Curve (AUC), sensitivity, as well as specificity. Sensitivity is defined as $\frac{TP}{TP+FN}$ and specificity is defined as $\frac{TP}{TP+FP}$.

3 Results and Discussion

3.1 EC-subnetwork is enriched in cancer-related pathways

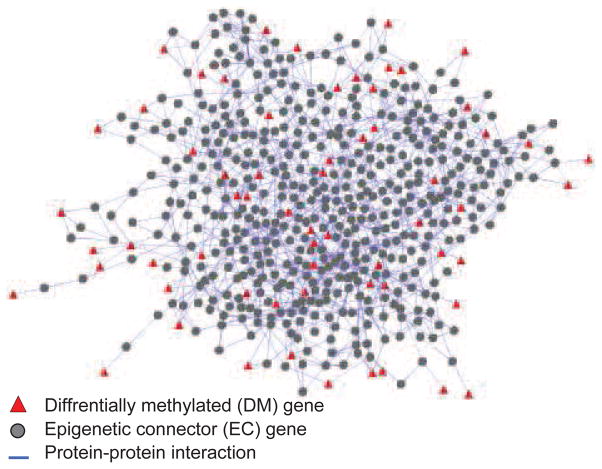
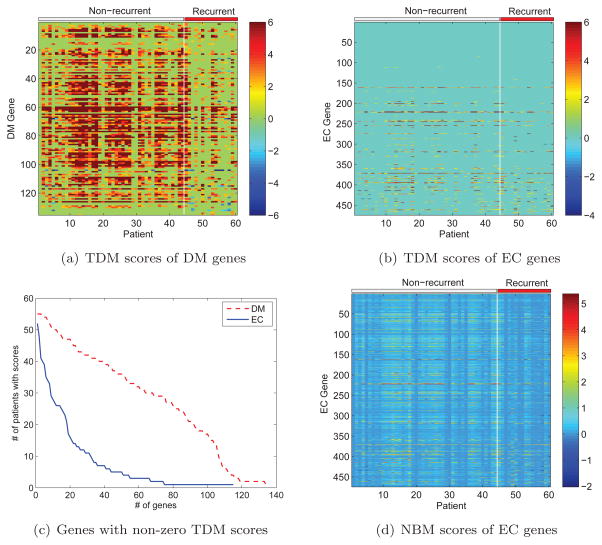
We identified 135 DM genes (p < 0.02, see Methods) connected by 474 EC genes (Figure 1). Interestingly, most of the DM genes are hyper-methylated in non-recurrent tumors, while only a small number of DM genes are hypo-methylated in recurrent cancers (Figure 2a). Unlike the DM genes, the EC genes are not differentially methylated between recurrent and non-recurrent tumors. Furthermore, many of the ECs have no non-zero TDM scores or have scores in only a few patients (Figure 2b), suggesting that DNA methylation change is not a main regulatory mechanism for them. For example, among the 474 EC genes, only 115 have a non-zero TDM score for at least one patient, and a mere of 8 have non-zero TMD scores for at least half of the patients (Figure 2c). In contrast, 68 of the 135 DM genes have TDM scores for at least half of the patients.

Figure 1.

A PPI subnetwork of DM and EC genes.

Figure 2.

Comparison between DM and EC genes.

The DM and EC genes were then used for KEGG pathway enrichment analysis by the Fisher’s exact test, using the size of the PPI network as background for the ECs and the number of genes with nonzero TDM scores for the DMs. Remarkably, while the DM genes are not significantly enriched with any known KEGG pathways, the EC genes are significantly enriched with many KEGG pathways that are well known to be involved in tumorgenesis and metastasis, such as GnRH signaling pathway (p < 1E-14), ErbB signaling pathway (p < 1E-12), gap junction (p < 1E-12), Wnt signaling pathway (p < 1E-8) and TGF-β (p < 1E-6), among others (Table 1). Many of these pathways are interrelated. For example, ErbB tyrosine kinase receptor family activates many MAPK factors during transmission of extracellular signals to induce cancer cell growth and invasion [36]. Induction of ErbB signaling has been associated with poor prognosis in several malignancies including gynecologic cancers [37]. Cellular proliferation is mediated by cell cycle factors, which are downstream of MAPK and VEGF. VEGF pathway is involved in angiogenesis, which is a hallmark of cancer progression due to generation of new vasculature, giving tumor cells a growth advantage [38]. The enrichment of these pathways is consistent with aggressive growth and metastasis associated with endometrial cancer recurrence.

Table 1.

Enriched KEGG pathways in EC genes. Enrichment score is calculated as −log10(p-value).

KEGG Pathway	Score
hsa05200 Pathways in cancer	19.5
hsa04722 Neurotrophin signaling pathway	14.8
hsa04912 GnRH signaling pathway	14.0
hsa04020 Calcium signaling pathway	13.6
hsa04080 Neuroactive ligand-receptor interaction	13.1
hsa04012 ErbB signaling pathway	12.8
hsa04540 Gap junction	12.8
hsa04520 Adherens junction	12.4
hsa04062 Chemokine signaling pathway	11.3
hsa04510 Focal adhesion	10.5
hsa04010 MAPK signaling pathway	10.4
hsa04360 Axon guidance	10.1
hsa04144 Endocytosis	9.0
hsa04310 Wnt signaling pathway	8.6
hsa04530 Tight junction	8.1
hsa04110 Cell cycle	8.0
hsa04350 TGF-beta signaling pathway	6.4
hsa04270 Vascular smooth muscle contraction	6.2
hsa04920 Adipocytokine signaling pathway	6.2
hsa04620 Toll-like receptor signaling pathway	5.0
hsa04370 VEGF signaling pathway	4.8
hsa04810 Regulation of actin cytoskeleton	4.3
hsa04630 Jak-STAT signaling pathway	3.9
hsa04910 Insulin signaling pathway	3.4
hsa04621 NOD-like receptor signaling pathway	3.0
hsa04115 p53 signaling pathway	2.4

3.2 Classification results

3.2.1 EC genes significantly improve classification accuracy

The ECs alone are not able to predict recurrence (Table 2, AUC ≈ 0.5, Kappa ≈ 0). This is understandable as they are not differentially methylated, and many ECs have TDM scores only for a few patients (Figure 2d). Nevertheless, the combination of ECs and DMs (DM+EC, Table 2) improved the classification accuracy significantly compared to that of DMs alone (0.453 vs. 0.300, kappa statistic, corresponding to 81.2% and 73.4% accuracy, respectively). Note that this improvement cannot be explained by the increased number of features, since expanding the DM feature set size to 609 (=135+474) by using a less stringent p-value cutoff for differential methylation (DM+), or by combining DMs with 474 randomly selected genes (DM+rand) only resulted in small improvement of classification performance (Table 2). Therefore, the improvement of classification accuracy is likely due to the combinatorial effect of DM and EC genes. One possible explanation is that while the methylation changes for some ECs are patient specific and have weaker statistical significance in terms of differential methylation, the combination of multiple weakly differentiated methylated ECs within the same pathway as the DMs can be complement to the DM genes and improve classification performance.

Table 2.

Classification performance obtained with various features.

	AUC	Kappa	Accuracy	Sensitivity	Specificity
DM	0.646 ± 0.034	0.300 ± 0.071	0.734 ± 0.031	0.458 ± 0.056	0.834 ± 0.036
EC	0.464 ± 0.026	−0.089 ± 0.063	0.653 ± 0.028	0.059 ± 0.042	0.868 ± 0.037
EC*	0.629 ± 0.039	0.301 ± 0.087	0.767 ± 0.029	0.333 ± 0.076	0.924 ± 0.032
EC#	0.516 ± 0.037	0.035 ± 0.082	0.660 ± 0.033	0.207 ± 0.061	0.825 ± 0.036
DM+EC	0.700 ± 0.044	0.453 ± 0.096	0.812 ± 0.033	0.459 ± 0.075	0.940 ± 0.027
DM+	0.662 ± 0.038	0.358 ± 0.082	0.773 ± 0.029	0.424 ± 0.069	0.900 ± 0.030
DM+rand	0.658 ± 0.039	0.326 ± 0.079	0.744 ± 0.030	0.474 ± 0.070	0.840 ± 0.034
DM+EC*	0.731 ± 0.038	0.513 ± 0.078	0.829 ± 0.026	0.522 ± 0.070	0.941 ± 0.019
DM+EC#	0.698 ± 0.036	0.442 ± 0.078	0.805 ± 0.028	0.468 ± 0.063	0.927 ± 0.026
KEGG	0.548 ± 0.018	0.116 ± 0.046	0.713 ± 0.023	0.194 ± 0.020	0.902 ± 0.031
DS	0.486 ± 0.040	−0.028 ± 0.078	0.596 ± 0.038	0.249 ± 0.060	0.723 ± 0.045
DS*	0.656 ± 0.033	0.307 ± 0.063	0.725 ± 0.026	0.507 ± 0.059	0.805 ± 0.030
DM+DS	0.671 ± 0.042	0.369 ± 0.089	0.772 ± 0.032	0.457 ± 0.073	0.886 ± 0.030
DM+DS*	0.710 ± 0.035	0.426 ± 0.073	0.777 ± 0.030	0.568 ± 0.053	0.854 ± 0.032

Values shown are mean and standard deviation across 100 runs. The two best values from each column are highlighted. EC*: EC with NBM score. EC^#: Similar to EC*, but using a randomized PPI network. DM+: DM genes selected with a less stringent p-value cutoff. rand: randomly selected genes. KEGG: KEGG pathways as metagenes. DS: Non-DM genes from discriminative subnetworks. DS*: discriminative subnetworks as metagenes.

3.2.2 Network based methylation (NBM) score of EC gene further improves classification accuracy

Since many ECs do not show methylation changes between the recurrent and non-recurrent tumors, they may have played a role through their interactions with the DMs, for example, DNA methylation changes of the DM genes may affect the functions of the ECs via protein-protein interactions. To measure the relevance between the DMs and ECs based on the network topology, we used a well-established random walk procedure to compute the probability for a random walker starting at a DM gene to reach any EC genes. The TDM score of a DM gene is then distributed to the EC genes according to these probabilities. As some of the ECs may also have TDM scores, probabilities were also calculated for a random walker starting at an EC gene to reach other EC genes and the ECs may both distribute its TDM scores to other ECs and receive distributions from other DMs and ECs. These are combined together to derive the NBM scores for all the ECs (see Methods).

Figure 2(d) shows the NBM scores for the ECs. Interestingly, while none of the ECs were differentially methylated at p-value < 0.02 according to the TDM scores, 203 (43%) of the 474 ECs show statistically significant difference between recurrent and non-recurrent tumors (p < 0.02, student’s t-test) according to the NBM scores, confirming that the ECs may indeed have functions related to the DMs in cancer metastasis.

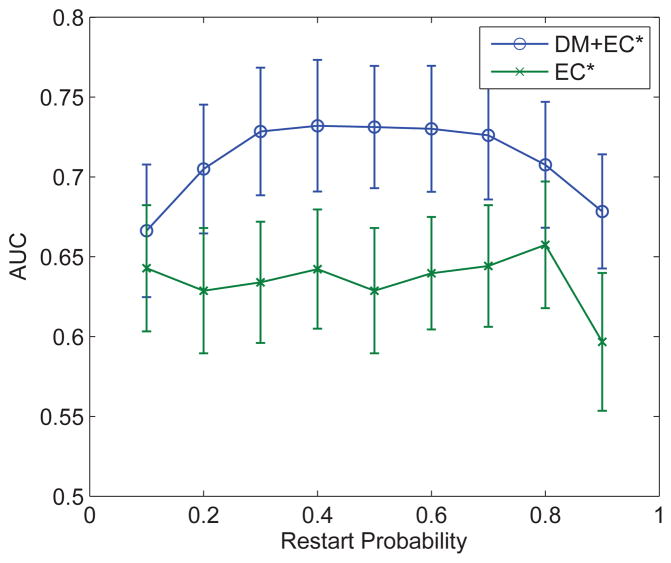
These NBM scores of ECs are then used, either alone or in combination with the TDM scores of the DM genes, to construct a support vector machine (SVM) classifier to separate recurrent and non-recurrent tumors. As shown in Table 2, the performance of the classifier constructed with the NBM scores of the ECs (EC*) is significantly higher than that with the original TDM scores of the ECs, and even slightly better than that of the DM genes. This is to some extent not surprising, as the NBM scores of the ECs are derived from the TDM scores of the DMs. To see if indeed the ECs provide any additional information other than approximating the DM genes, we combined the TDM scores of the DMs and the NBM scores of the ECs (DM+EC*, Table 2). As shown, this resulted in the highest classification accuracy (kappa statistic 0.513 and accuracy 82.9%), suggesting that the topologically derived scores for the ECs provide non-redundant, orthogonal information than the TDM scores of the DM genes. In addition, when the PPI network is randomly rewired, the benefit of the EC genes vanishes¹ (Table 2, EC^# and DM+EC^#). Finally, it is worth noting that the performance of the algorithm is relatively robust with respect to the parameter (restart probability) of the random walk procedure (Figure 3).

Figure 3.

AUC for DM+EC* and EC*-based classifiers as a function of RWR restart probability.

3.2.3 Comparison with existing methods

We compared the performance of our algorithm with two alternative methods. First, we implemented a simple pathway-based approach by using each KEGG pathway as a metagene. Briefly, for each KEGG pathway and each patient, we counted the number of genes in that pathway that had a positive TDM score, as well as the number of genes that had a negative score. Therefore, each pathway will result in two features: one for positive scores and one for negative scores. (This strategy has the best clas-sification performance among multiple variations of pathway-based models.) We used all 208 KEGG pathways, resulting in 516 features for each patient. Second, we downloaded the program from [25] for identifying discriminative subnetworks, i.e., subnetworks whose average node activity can discriminate the two classes of samples. Following the suggestions from the authors, we limited the subnetwork size to five, and obtained the top 100 subnetworks with the highest discriminative power. These discriminative subnetworks (DS) are then used in two ways (denoted DS and DS*, respectively): (1) the genes in the subnetworks were pooled, and these individual genes were used as features, either independently or combined with the DMs; (2) each subnetwork is used as a metagene by averaging the TDM scores for genes in the same subnetwork.

As shown in Table 2, our network topology-based classifier, DM+EC*, resulted in the highest AUC, kappa, specificity, and accuracy. Although DM+DS* has higher sensitivity, that was achieved with the price of a much lower specificity. In addition, DS genes alone resulted in very low accuracy, similar to the EC genes. Furthermore, DS*, by treating each subnetwork as a metagene, had an accuracy similar to EC*. KEGG pathways resulted in much lower accuracy than DS*, which shows the advantage of using subnetworks rather than known pathways as metagenes. Finally, while combining the DM and DS genes only resulted in marginal improvement over DM alone, combining DM and DS* significantly improved the performance. Further analysis showed that our EC and DM genes contain 77 and 38 of 252 DS genes, respectively. This supports our notion that the ECs contain not only genes in differentially methylated pathways (hence the overlap with DS genes), where individual genes are only weakly differentially methylated, but also genes that are not part of differentially methylated pathways but are important for cross-talks between the pathways. The method by [25] directly targets the first type of genes, while ignoring the second type of genes. As a result, their method may identify more genes of the first type than our method. As both types of genes may be important for classification, it may be beneficial to combine the two methods for a better model in future work.

3.3 Analysis and literature validation of significant DM and EC markers

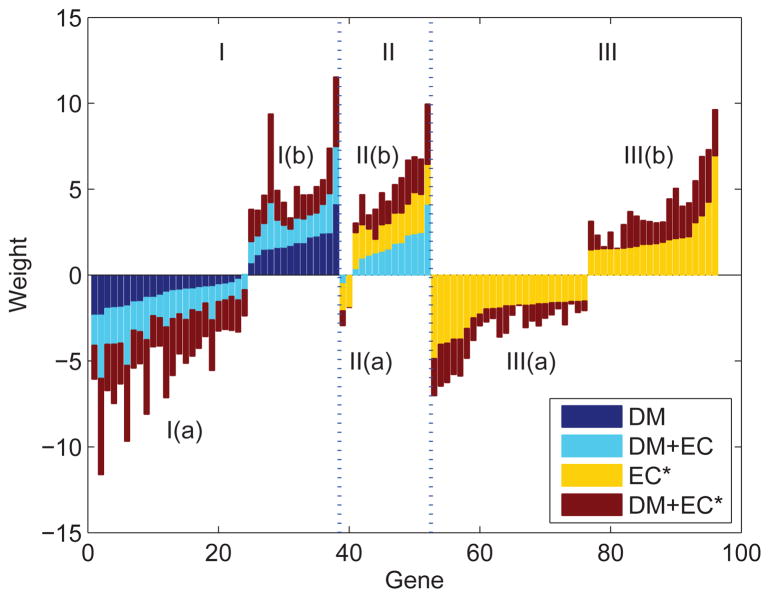
To further investigate the role of DM and EC genes as potential biomarkers, we analyzed the normalized feature weights (z-scores) for each of the genes used by the four SVM classifiers based on DM, DM + EC, EC*, and DM + EC*, respectively, where EC* means that the NBM scores rather than the TDM scores are used for the ECs. A larger feature weight indicates that the gene is more important for classifying recurrence. For genes with positive weights, their hyper-methylation is contributing towards recurrence, and for genes with negative weights their hyper-methylation is contributing towards non-recurrence.

Figure 4 shows the weights for the genes with a normalized weight ≥ 1.5 or ≤ −1.5 in at least one classifier. Region I contains DM genes, which may represent universal epigenetic markers. Region II contains EC genes that had non-zero TDM scores in some patients and contributed to the DM + EC classifier; these are EC markers that are epigenetically reprogrammed in specific patients. Finally, region III contains EC genes that were not used by the DM+EC classifier but had important contributions in the EC* or DM+EC* classifiers. These EC genes themselves are not epigenetically affected; however they are either regulating or regulated by the universal or patient-specific epigenetic markers. As shown in Figure 4, whenever a feature appears in multiple classifiers, the weights in different classifiers usually have similar sign and magnitude, confirming that the feature weight in support vector machine is a robust measure for the importance of the feature.

Figure 4.

Feature weights in four SVM-based classifiers for selected genes. Colors depict the classifier from which the weight is obtained. Genes in Region I are DM genes and are sorted by their weights in DM-based SVM classifier; genes in Region II are ECs and are sorted by their weights in DM+EC based classifier; genes in Region III are ECs and are sorted by their weights in EC* based classifier.

Table 3 lists the top ten positively weighted or negatively weighted genes from each of the three regions described above, and validation of their relevance to recurrence using literature mining. While the role of the DM genes in metastasis is unclear, many of the ECs in regions II and III are well known to have important functions in cancer progression and metastasis, such as BRCA1, EPHB2, ID2, ID3, SSTR2, SSTR3, SST, MYOD1, PAX3, HOXD10, and SCT, as shown by the results of literature mining. Interestingly, two genes in region III(a), TLE1 and PARP1, are known as epigenetic regulators [39, 40, 41].

Table 3.

Top markers and literature validation. Markers are categorized as shown in Figure 4. Numbers represent number of PUBMED abstracts retrieved using the combination of the gene name and the term “metastasis or metastatic” (M), and “epigenetic or methylation” (E).

I(a)	M	E	II(a)	M	E	III(a)	M	E
GALNTL6	0	0	SCT	77	14	PARP1	31	27
FTHL17	0	2	CAMKK1	0	0	TXNDC17	0	0
ZFP3	0	0				AVPR1A	7	12
SIX6	1	0				SPHK1	12	3
SPHKAP	0	0				TLE1	4	8
POLA1	0	0				AES	?	5
NPY1R	0	1				CORT	0	6
EPHA5	4	3				PAX6	4	51
C19orf34	0	0				NFIC	0	2
GABRA2	0	3				AVPR2	0	0
I(b)	M	E	II(b)	M	E	III(b)	M	E
DYNC1I1	0	0	SMC1A	0	1	EPHB2	18	12
CYP26C1	0	2	UCN	9	2	COIL	209	65
NCRNA00087	0	0	SST	84	11	STAU1	1	1
ACSS1	1	0	MYOD1	28	63	GSK3B	2	3
TSC22D3	0	0	PAX3	47	26	ID3	13	8
KLHL13	0	0	KCNA4	0	1	ID2	23	16
NXPH2	0	0	SNCA	0	9	MCM6	1	1
ELK1	11	9	TRPC3	2	1	BRCA1	297	356
TOP3A	0	1	HOXD10	11	4	SSTR2	28	1
ADRA1A	4	14	EFNA5	1	4	SSTR3	8	0

4 Conclusions

In this paper we have presented a novel network-based algorithm for identifying biomarkers to predict tumor recurrence from high-throughput DNA methylation data. Our network-based algorithm goes beyond the conventional differential analysis and finds (1) genes with insufficient statistical significance of differential methylation but are within the local neighborhood of the significantly differentially methylated genes, and (2) genes that are not differentially methylated but play important topological roles in connecting the epigenetic markers in the protein-protein interaction networks and therefore are assumed to have functional significance in epigenetic regulations. Our results show that the network-based markers are significantly enriched in many KEGG pathways well-known to be involved in tumorgenesis and metastasis, and can be used to significantly improve the accuracy in predicting recurrence. A unique contribution of this work is that we showed even for the genes without any DNA methylation changes, which therefore cannot be considered as biomarkers in conventional analysis, can be utilized to improve the classification performance, suggesting that their functions may have been functionally disturbed by the epigenetic changes of their protein-protein interaction partners.

Our method can be extended in several directions. First, for the EC genes, currently we do not differentiate whether they are regulated by the DM genes or are regulating the methylation changes of the DMs. This may be partially addressed by including protein-DNA interaction networks where the directions between some nodes can be determined. Second, it is known that markers selected from different datasets for the same cancer are usually not comparable. Although our recent results on gene expression data showed that the connectors selected based on Steiner trees are much more stable than the genes selected based on differentially expression [42], it seems that the classification accuracy based on the connectors alone can be further improved. We therefore would like to develop a general classification method that does not depend on the DM genes. For example, after obtaining the EC subnetwork, we may extend the subnetwork to include all genes that are within a certain distance to the ECs or satisfy some additional topological requirements. Finally, it may be interesting to combine computationally derived subnetworks with curated pathways that are known to play important roles in cancer.

Highlights.

• An algorithm to identify and utilize protein-protein interaction subnetworks as biomarkers for cancer prognosis

• Application of our algorithm to endometrial cancer DNA methylation data identified many cancer-related genes an pathways that were otherwise not identifiable

• Significantly outperformed existing methods in predicting endometrial cancer recurrence