A Most Odd Ratio

Abstract

Introduction

The OR is one of the most commonly used measures of association in preventive medicine, and yet it is unintuitive and easily misinterpreted by journal authors and readers.

Methods

This article describes correct interpretations of ORs, explains how ORs are different from risk ratios (RRs), and notes potential supplements and alternatives to the presentation of ORs that may help readers avoid confusion about the strength of associations.

Results

ORs are often interpreted as though they have the same meaning as RRs (i.e., ratios of probabilities rather than ratios of odds), an interpretation that is incorrect in cross-sectional and longitudinal analyses. Without knowing the base rate of the outcome event in such analyses, it is impossible to evaluate the size of the absolute or relative change in risk associated with an OR, and misinterpreting the OR as an RR leads to the overestimation of the effect size when the outcome event is common rather than rare in the study sample. In case-control analyses, whether an OR can be interpreted as an RR depends on how the controls were selected.

Conclusions

Education, peer reviewer vigilance, and journal reporting standards concerning ORs may improve the clarity and accuracy with which this common measure of association is described and understood in preventive medicine and public health research.

Introduction: A Tale of Three ORs

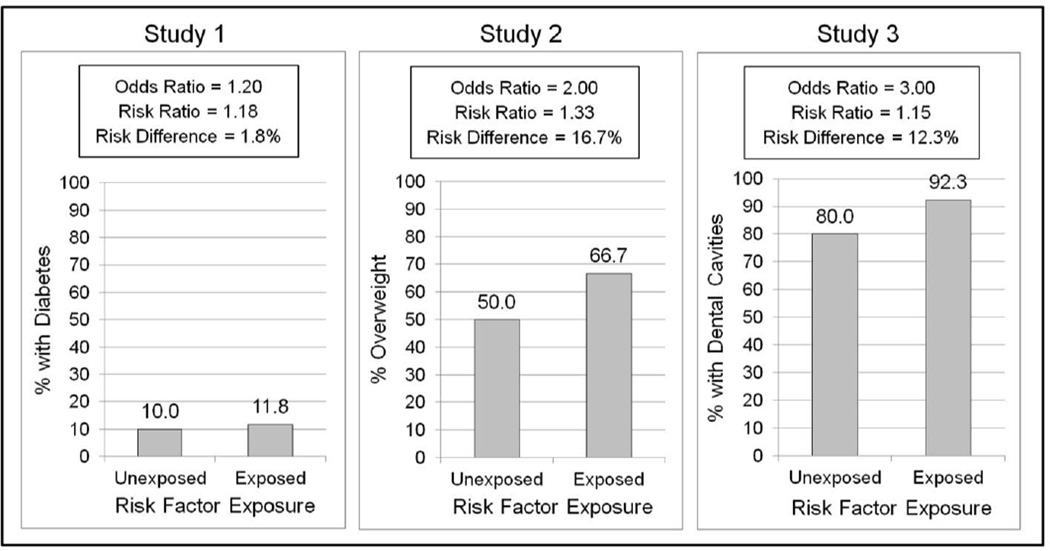
Imagine the results of three hypothetical, cross-sectional studies on a risk factor for various health problems. The risk factor was associated with increased odds of being diagnosed with diabetes in Study 1 (OR=1.2), increased odds of being overweight in Study 2 (OR=2.0), and increased odds of having dental cavities in Study 3 (OR=3.0). Of these, which outcome has the greatest association with the risk factor? Some readers may be tempted to say that the risk factor increases risk for dental cavities the most, compared with diabetes or being overweight, believing that an OR of 3.0 means that exposed participants were 3.0 times more likely than other participants to have cavities, and that ORs of 1.2 and 2.0 reflect 20% and 100% increases in risk, respectively. These interpretations of ORs are incorrect.

In fact, the increase in risk associated with each OR depends on the rate of the outcome in the study sample. Figure 1 shows hypothetical results of each study. As shown, in Study 1, if only 10% of the participants unexposed to the risk factor had diabetes, then an OR of 1.2 would reflect an increase in risk from 10% to 11.8% (an 18% increase). In Study 2, if 50% of the participants unexposed to the risk factor were overweight, then an OR of 2.0 would reflect an increase in risk from 50% to 66.7% (a 33% increase). Finally, in Study 3, if 80% of the participants unexposed to the risk factor had cavities (e.g., if the study was conducted in a very high-risk population), then an OR of 3.0 would reflect an increase in risk from 80% to 92.3% (a 15% increase). Thus, based on these hypothetical outcome rates, Study 2 would have shown the largest increase in risk in both relative and absolute terms, even though the OR from the study was much smaller than the OR from Study 3 (i.e., 2.0 vs 3.0). Moreover, Study 3 would have shown the smallest relative risk (a 15% increase in risk), despite having the largest OR.

Figure 1.

Hypothetical results of three cross-sectional risk factor studies showing that the increase in risk associated with a given OR depends on the rate of the outcome variable in the study sample. Study 3 found the largest OR (3.0) but the smallest risk ratio (15% increase in risk) and the second largest risk difference (increase in risk from 80% to 92.3%).

Distinguishing Between ORs and Risk Ratios

Because ORs are ratios of odds rather than probabilities, they are unintuitive. A probability is an easy-to-understand concept that refers to the number of times an event is expected to occur divided by the number of chances for it to occur (frequentist interpretation) or the degree of belief that an event will occur (Bayesian interpretation). For instance, in ten fair coin flips, the probability of “heads” is 5 divided by 10, or 0.5. By contrast, odds refer to the number of times an event is expected to occur divided by the number of times it is expected to not occur. In ten fair coin flips, the odds of “heads” are 5 divided by 5. In daily life, risk is rarely described in terms of odds, as odds have “no clear conceptual meaning (outside of horse racing circles),”¹ and many consumers of public health research may be unaware that odds are defined differently from probabilities.

As shown in Table 1, ORs are defined in terms of odds, whereas risk ratios (RRs) are defined in terms of probabilities. For instance, in a hypothetical study of the cross-sectional association between sitting time and obesity in which 450 of 1,000 sedentary participants were obese, compared with 300 of 1,000 non-sedentary participants, the OR for obesity would be 1.9 (i.e., [450/550] / [300/700]). However, sedentariness would be associated with only a 50% increase in the risk of obesity (i.e., RR=[450/1,000] / [300/1,000]=1.5). The practical meaning of the results based on the OR (i.e., 1.9 times higher odds of obesity among sedentary individuals) may be unclear to readers, and misinterpreting the OR as an RR would overestimate the size of the association.

Table 1.

Terms of Interest

Term	Definition
Risk ratio (RR)	the probability of an outcome event in one group divided by the probability of the event in another group
OR	the odds of an outcome event in one group divided by the odds of the event in another group
Risk difference	the probability of an outcome event in one group minus the probability of the event in another group

Confusion about the meaning of odds leads many authors and readers of scientific articles to misinterpret ORs from cross-sectional and longitudinal studies to mean the same thing as RRs.² For instance, a report may incorrectly conclude that a risk factor “doubled the risk (OR=2.0)” for an adverse outcome, or that people in one group were “over three times as likely (OR=3.2)” or “75% more likely (OR=1.75)” than those in another group to engage in a risk behavior. Such incorrect interpretations of ORs have been flagged in medicine and public health for decades,^2–10 and yet they proliferate.

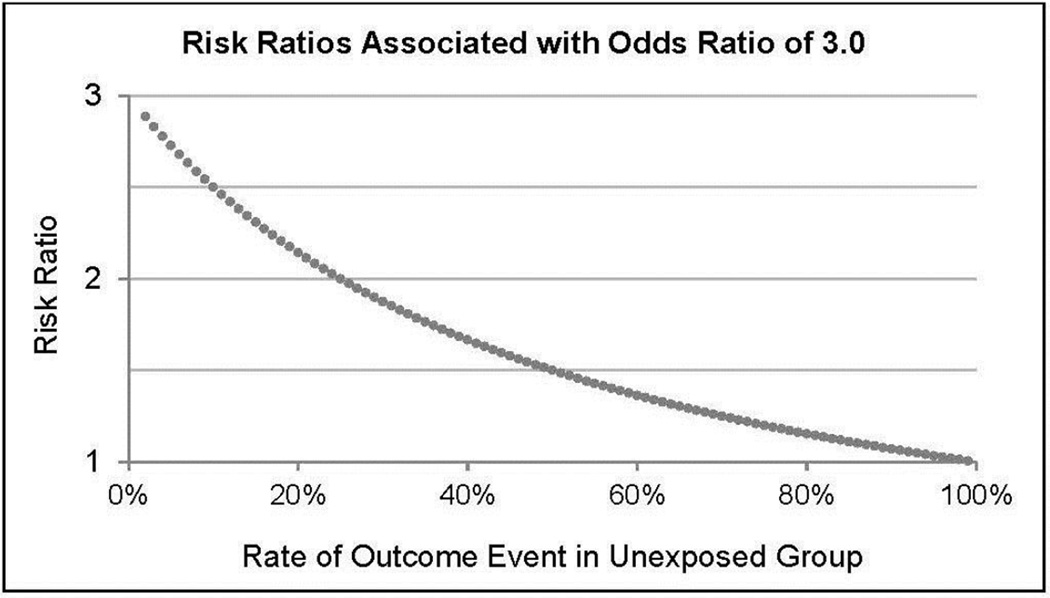
In cross-sectional and longitudinal analyses, misinterpreting an OR as an RR leads to inflating the size of an association. The extent of overestimation depends on the base rate of the outcome variable in the study sample. If the outcome has a very low base rate in the sample (i.e., if it is very uncommon among people unexposed to the risk factor), the OR may give a rough approximation of the RR (e.g., Study 1, Figure 1). This is referred to as the “rare disease assumption” in epidemiology.¹¹ However, as the base rate of the outcome variable increases, the OR and RR deviate, because the OR increases while the RR does not. Thus, when outcomes are common, the OR can severely exceed the RR. Figure 2 provides an example, showing that an OR of 3.0 does not indicate a tripling of risk and, in fact, corresponds to a shrinking RR as the base rate of the outcome in the sample increases.

Figure 2.

Risk ratios associated with an OR of 3.0, depending on the rate of the outcome event among participants unexposed to the risk factor, in cross-sectional and longitudinal analyses.

In case-control analyses, ORs can be used to estimate RRs without the need for the rare disease assumption, but this depends on how the controls are selected.^1,12 To understand the logic behind this approach, it should be noted that ORs have a statistical property whereby the OR for an outcome based on an exposure is mathematically equivalent to the OR for the exposure based on the outcome.¹³ Because of this property, in case-control analyses, the OR for an outcome based on an exposure can be calculated by selecting cases and controls and comparing their odds of exposure. Furthermore, if the controls are selected without regard to their status on the outcome variable (i.e., if controls may or may not have experienced the outcome event), the controls will provide information about the odds of exposure among the overall sample including cases and non-cases, and the OR from such case-control analyses will be equivalent to the RR regardless of the base rate of the outcome event in the study sample (i.e., no rare disease assumption needed).¹²

Understanding the difference between ORs and RRs in cross-sectional and longitudinal analyses is critical because researchers in the field of preventive medicine often deal with highly common outcomes (e.g., obesity, adverse outcomes in high-risk populations), which causes the two measures of association (RR and OR) to diverge. In cases where the RR is small but the outcome event is common, a large OR may lead to unwarranted attention or conclusions among those who interpret and apply results. Such misinterpretations may be particularly common among those who disseminate or apply (rather than conduct) research—such as the media, policymakers, or clinicians—if they are not familiar with the statistical calculations underlying ORs and RRs. Moreover, misinterpretations of ORs may also have implications for meta-analytic syntheses of research results, as statistical recommendations for converting ORs to effect sizes for metaanalyses do not require incorporation of the likelihood of the outcome.¹⁴

Improving Communication About Relative and Absolute Risk

Although unintuitive, the OR remains a very commonly used measure in public health research because of its statistical properties. In cross-sectional and longitudinal analyses, the frequent use of ORs likely owes to the fact that the statistic is easy to compute in logistic regression models using commonly available statistical software.⁶ In particular, AORs can easily be computed to describe associations after controlling for one or more potentially confounding variables.⁶ As mentioned above, the OR also has statistical properties that make it an ideal statistic for use in case-control analyses.¹³

The popularity of ORs, combined with their unintuitive nature, means that researchers need to be better educated to make proper use of ORs. As with other concepts in the increasingly complex field of medical statistics, this requires a foundational understanding of probability.¹⁵ Moreover, given the interest of non-researchers (e.g., policymakers and the media) in scientific research,^16,17 future papers in which ORs are presented might take steps to help readers understand the sizes of the relative and absolute risks being described.

One potential method of clarifying the sizes of relative and absolute risk is to calculate and present the predicted probability of the outcome at various levels of the predictor variable (e.g., exposed versus unexposed). This can be done using standard output from a logistic regression.¹⁸ When a logistic regression model includes covariates, the predicted probabilities can be calculated based on specific values of the covariates (e.g., their average values, modal values, or reference levels), but it should be noted that the resulting predicted probabilities will allow inference only to the stratum specified by the values of the covariates in the calculations.¹⁹

Predicted probabilities can also be averaged across values of the covariates (incorporating weights that reflect the distribution of the covariates in the population of interest) to yield predicted probabilities for the overall population.¹⁹ These predicted probabilities can be used to compare the risk of exposed versus unexposed individuals using an RR.^19,20

Additionally, predicted probabilities from logistic regression can be compared using a risk difference by subtracting the predicted probability among unexposed individuals from that among exposed individuals. When the risk factor is causal, the difference between exposed and unexposed individuals is termed the attributable risk,²¹ a statistic that can be helpful in describing the potential benefits of risk mitigation efforts. Presenting the absolute risk among exposed and unexposed individuals is consistent with expert recommendations on communicating research findings to the public, which point out that it is inadequate to describe relative risk (e.g., “twice the risk”) without describing the absolute levels of the risks involved.²² After all, a doubling of risk may reflect an increase from 0.001% to 0.002% or from 10% to 20%, which have much different implications and importance.²²

Alternatives to logistic regression are also available to calculate and present relative risk information without the need for ORs, as described in a recent paper.⁷ Simulations revealed that Poisson regression, log-binomial regression, and a “doubling of cases” method (i.e., in which the data are manipulated such that a logistic regression can produce an RR) can yield correct RRs and CIs.⁷ Each of these methods has unique limitations that should be considered in relation to a data set, researchers’ programming expertise, and the goals of the analysis (e.g., log-binomial regression models may fail to converge in some cases).⁷ Also, although presenting RRs rather than ORs can help clarify the size of the relative risk being reported, it does not clarify the absolute levels of risk involved. Thus, providing information about the base rate of the risk is still useful for interpretation.

Of note, clearly and accurately presenting measures of association also involves other considerations such as avoiding misleading readers about causality. As noted in a seminal discussion of the population attributable fraction, policymakers and others have an inherent interest in “how much of the disease burden in a population could be eliminated…”²³ Thus, statistically intuitive measures of relative and absolute risk are most useful “when the factor of interest is clearly causally related to the end point and when there is consensus that the exposure is amenable to intervention.”²³ When these conditions are not met, authors should note this and explain the limitations concerning what can be learned from the particular measure of association. When part or all of an association may be caused by another variable, even a statistically accurate presentation of an OR or RR may generate unwarranted attention concerning a risk factor among researchers, the public, or those interested in mitigating risk.

Ensuring clear and accurate effect size presentation is critical to scientific advancement in preventive medicine, as reflected in policy statements from professional organizations²⁴ and discussions of “the importance of meaning” in public health research.^25,26 Making progress toward this goal may require a multipronged approach. Raising awareness among researchers and authors about the meaning of ORs is one strategy, including the present article, which can contribute to this effort. Vigilance is also required on the part of journal reviewers during the peer review process to ensure accurate interpretation of ORs and to suggest alternatives or complements to the presentation of ORs to clearly describe relative and absolute risk. Finally, a parsimonious way of reaching the research community, including all authors—and, by extension, an entire journal readership—may be to include standards for the presentation of relative risk information directly in the journal’s instructions for authors. Instructions may include a warning against misinterpreting ORs as RRs and potential supplements and alternatives to the presentation of ORs to clearly describe levels of relative and absolute risk.