Individual differences in implicit motor learning: task specificity in sensorimotor adaptation and sequence learning

We investigated individual differences in the ability to implicitly learn motor skills. As a prerequisite, we assessed whether individual differences were reliable across test sessions. We found that two commonly used tasks of implicit learning, visuomotor adaptation and the alternating serial reaction time task, exhibited good test-retest reliability in measures of learning and performance. However, the learning measures did not correlate between the two tasks, arguing against a shared process for implicit motor learning.

Abstract

In standard taxonomies, motor skills are typically treated as representative of implicit or procedural memory. We examined two emblematic tasks of implicit motor learning, sensorimotor adaptation and sequence learning, asking whether individual differences in learning are correlated between these tasks, as well as how individual differences within each task are related to different performance variables. As a prerequisite, it was essential to establish the reliability of learning measures for each task. Participants were tested twice on a visuomotor adaptation task and on a sequence learning task, either the serial reaction time task or the alternating reaction time task. Learning was evident in all tasks at the group level and reliable at the individual level in visuomotor adaptation and the alternating reaction time task but not in the serial reaction time task. Performance variability was predictive of learning in both domains, yet the relationship was in the opposite direction for adaptation and sequence learning. For the former, faster learning was associated with lower variability, consistent with models of sensorimotor adaptation in which learning rates are sensitive to noise. For the latter, greater learning was associated with higher variability and slower reaction times, factors that may facilitate the spread of activation required to form predictive, sequential associations. Interestingly, learning measures of the different tasks were not correlated. Together, these results oppose a shared process for implicit learning in sensorimotor adaptation and sequence learning and provide insight into the factors that account for individual differences in learning within each task domain.

NEW & NOTEWORTHY We investigated individual differences in the ability to implicitly learn motor skills. As a prerequisite, we assessed whether individual differences were reliable across test sessions. We found that two commonly used tasks of implicit learning, visuomotor adaptation and the alternating serial reaction time task, exhibited good test-retest reliability in measures of learning and performance. However, the learning measures did not correlate between the two tasks, arguing against a shared process for implicit motor learning.

studies of motor learning and performance tend to focus on group-level measures, characterizing the behavior of the “average” person (Kanai and Rees 2011; King et al. 2012). Interindividual differences are typically ignored, treated as one source of “noise” that can be averaged out across the group or factored out by random group assignments. However, daily life experience makes it evident that people vary considerably in their abilities to learn new skills or modify the way in which they perform a learned skill. Whereas historically the study of individual differences in skilled performance has been of considerable interest in the field of human factors (Keele and Hawkins 1982; Seashore and Tiffin 1930), recent work in motor learning has tended to ignore this topic. Identifying the underlying sources of individual differences and the extent to which they generalize across tasks is critical to the development of a comprehensive account of motor learning.

In this report, we take an individual differences approach to examine implicit motor learning. We focus on two task domains that have been hypothesized to be emblematic of procedural motor learning, sensorimotor adaptation and sequence learning. In adaptation studies, the environment is perturbed in some novel way and the participants learn to adjust their behavior to minimize the consequences of that perturbation. For example, in visuomotor rotation tasks, an angular displacement is introduced between movements of the hand and a cursor and successful performance requires moving the hand in the opposite direction to counter the perturbation. Sequence learning has been studied with a range of tasks in which a series of stimulus-response pairs form a sequence that is either deterministic (for example, Nissen and Bullemer 1987) or probabilistic (for example, Howard and Howard 1997), with learning defined as the difference in reaction time (RT) between predictable and nonpredictable events.

As suggested by their taxonomic linkage with procedural learning, adaptation and sequence learning can occur implicitly. For example, the perturbation in adaptation studies might be small and/or introduced in a gradual manner, conditions in which the participants are unaware of the perturbation (Criscimagna-Hemminger et al. 2010; Kagerer et al. 1997; Michel et al. 2007; Schlerf et al. 2013; Taylor and Ivry 2012). Similarly, various manipulations have been devised to reduce or eliminate awareness during sequence learning, including the use of long (Pascual-Leone et al. 1993; Sanchez and Reber 2012) or probabilistic (Howard and Howard 1997; Nemeth et al. 2010) sequences or the use of a dual-task procedure (Gheysen et al. 2009; Hazeltine et al. 1997; Sanchez et al. 2010). While the magnitude of learning is reduced under such conditions (Rüsseler and Rösler 2000; Spencer et al. 2006), robust learning is still observed (Reber and Squire 1994).

Here we examine three issues regarding individual differences across these two implicit motor learning domains. First, how do individual differences in motor learning generalize across tasks? The earliest studies of individual differences tended to focus on stable or trait-based variability, asking, for example, whether the abilities of an individual across a wide range of tasks were related to single construct such as intelligence (for example, Spearman's “g factor”; Spearman 1904). Motivated by models of cognition, studies of human performance have identified individual differences in the operation of core components that generalize across task domains (Henry 1968). For example, Keele et al. (1985) showed that individual differences in temporal precision account for performance differences across motor and perceptual timing tasks. In a related vein, sensorimotor adaptation and sequence learning might entail overlapping processes, because learning in both tasks entails predictions of spatial events (Keele et al. 1985; Sanchez et al. 2010; Seidler et al. 2012; Spencer and Ivry 2009) and both have been associated with cerebellar function (Ferrucci et al. 2013; Galea et al. 2011; Seidler 2006). On the other hand, there are good reasons to expect that learning in these two task domains might entail very different processes. Computationally, adaptation is assumed to depend on mechanisms designed to reduce sensory prediction errors (Shadmehr et al. 2010), whereas sequence learning is hypothesized to depend on associative processes (Kinder et al. 2008; Spencer and Ivry 2009). Even in terms of the cerebellum, adaptation and sequence learning may be associated with different cortico-cerebellar loops (Kelly and Strick 2003; Krienen and Buckner 2009) and cerebellar regions (Bernard and Seidler 2013; Burciu et al. 2014; Hazeltine et al. 1997; Rabe et al. 2009; Ramnani et al. 2000; Seidler et al. 2002).

Second, we ask whether individual differences in implicit motor learning are stable. At the heart of studies of individual differences is an interest in understanding sources of variability. Variability is observed at all levels, be it the expression of proteins, the firing of neurons, or movements of the body (Faisal et al. 2008). There is also measurement noise, reflecting the fact that our measurement tools are imprecise. An important distinction can be made between stable and unstable sources of variability in performance. The latter emerges from the specific conditions at the time of measurement (for example, random noise, fatigue, attentiveness), which tend to average out with repetitions. The former, on the other hand, refers to stable characteristics of the system, and measurements of these sources of variability should be relatively consistent over test sessions. The reliability of our measurements (namely, consistency over repeated tests) limits the ability to infer the relationships between variables, because the size of the correlation between two variables is limited by the reliability of either (or both) of the variables (Gulliksen 2013).

Surprisingly, we are not aware of any studies that have examined the reliability of measures of implicit motor learning. Studies that tested people over multiple days have focused on consolidation (off-line learning), using the same task and stimulus parameters to look at retention of learning from one session to the next (Doyon et al. 2009; Krakauer 2009; Meier and Cock 2014; Nemeth et al. 2010; Spencer et al. 2006; Zarahn et al. 2008). Not only do these studies rarely discuss the reliability of individual differences across days, but also the consolidation design limits the ability to draw inferences about reliability (namely, individual differences in off-line consolidation will introduce variation in the estimates of learning across sessions). Given these concerns, we designed our study such that each participant was tested twice on each task, employing variants that should minimize any contribution (savings or interference) from the initial test session to the second test session. We employed conditions in which awareness was absent or minimized, ensuring that learning was entirely implicit. In this manner, we can ask if individual differences in each task are stable or unstable across repeated measurements, a prerequisite for examining factors that account for individual differences in performance.

Third, we used an individual differences approach to examine how variability contributes to, and constrains, skill acquisition. We often think of variability as an unwanted feature that interferes with learning and performance (Faisal et al. 2008; Wu et al. 2014). This perspective is formally captured in models such as the one offered by a Kalman filter within the framework of Bayesian estimation. For example, as sensory noise increases (e.g., when the position of a cursor indicating hand position is artificially blurred), the learning rate decreases (Burge et al. 2008; Wei and Körding 2010). Theories of optimal control posit that actions are planned to minimize the impact of variability on performance (Kording et al. 2007; Körding and Wolpert 2004). In this framework, part of skill acquisition entails a reduction in variability. Alternatively, movement variability can also be seen as a signature of exploration, allowing the system to gather knowledge concerning new or unstable environments (Ishii et al. 2002; Sutton and Barto 1998). In this view, an increase in variability might come about from a propensity to explore. It is also possible that causation is reversed, such that high variability increases the likelihood that the system will explore new associations. We sought to identify factors that might account for individual differences in learning on these two tasks, focusing on measures of performance variability that were obtained outside the learning context or early during learning, asking how differences in variability might impede or enhance learning (Wu et al. 2014).

METHODS

Participants

A total of 123 neurologically healthy young adults were recruited through the Research Participant Pool at the University of California, Berkeley (63% women; age 21.2 ± 2.4 yr). All were right-handed as assessed by the Edinburgh Handedness Inventory (0.83 ± 0.19, where −1 is strictly left-handed and 1 is strictly right-handed). Participants received course credit for completing the study. The protocol was approved by the University of California, Berkeley institutional review board.

Experimental Tasks

There were three experimental tasks, one used as a measure of sensorimotor adaptation and the other two measured sequence learning. Participants were tested twice on each task, in two runs. Runs were completed either in separate sessions (at least 2 days apart) or during the same session [serial reaction time (SRT) task only; after a 10- to 15-min break].

Visuomotor adaptation task.

Participants made center-out reaching movements to visually displayed targets, sliding a digitizing stylus with their right hand across a digitizing tablet (33 cm × 20 cm; Wacom Technology Corporation). Movement trajectories were recorded by sampling the stylus tip at 100 Hz with customized software, written in Python (www.python.org). The visual stimuli were displayed on a 15-in. monitor oriented in the normal upright position. The tablet was oriented horizontally and positioned below a wooden box that occluded vision of the arm. To provide feedback, a small white cursor (4-mm diameter) was displayed on the screen to indicate the position of the stylus. The system was calibrated such that there was a 1:1 correspondence between the movement distance of the stylus and the displacement distance of the feedback cursor on the screen.

To begin each trial, a circle (5-mm diameter) appeared at the center of the monitor, indicating the start position. Participants moved the stylus to center the feedback cursor within the start position. After participants held this position for 500 ms, four circles appeared. The radial distance from the start circle to each of the four circles was 8 cm. The circles were separated by 30°, forming a virtual arc on the upper part of the monitor (locations 45°, 75°, 105°, and 135°, where 90° is directly above the starting position). Three of the circles were colored blue (5-mm diameter), and one, the target, was colored white and was slightly larger (8 mm).

Participants were instructed to reach to the target “as fast and as accurate” as possible. The start circle disappeared when the movement amplitude exceeded 1 cm. Online visual feedback, by means of the feedback cursor, was presented while the participant reached outward toward the target. The trial ended when the participant intersected the target. At that moment, the target turned green and auditory feedback was provided, based on movement speed. If the movement time (MT) was <500 ms, a pleasant high-pitch “ding” sound was played. If MT exceeded this time criterion, an unpleasant low-pitch “buzz” sound was played. Notably, RT was not emphasized; the auditory feedback was based solely on MT. The cursor end-point position, defined at the point where the reach amplitude crossed 8 cm, was displayed for 500 ms.

At the end of the feedback interval, the cursor and four circles disappeared and the start circle reappeared. The participant was visually guided back to the starting location with radial feedback, a white circle with a diameter that corresponded to the distance of the hand from the starting position (namely, providing no information on hand angle). The participant was instructed to move so as to reduce the diameter of this circle. When the hand was within 1 cm of the start position, the circle changed to a cursor and the participant moved the cursor into the start location. When this position was maintained for 500 ms, the next target appeared.

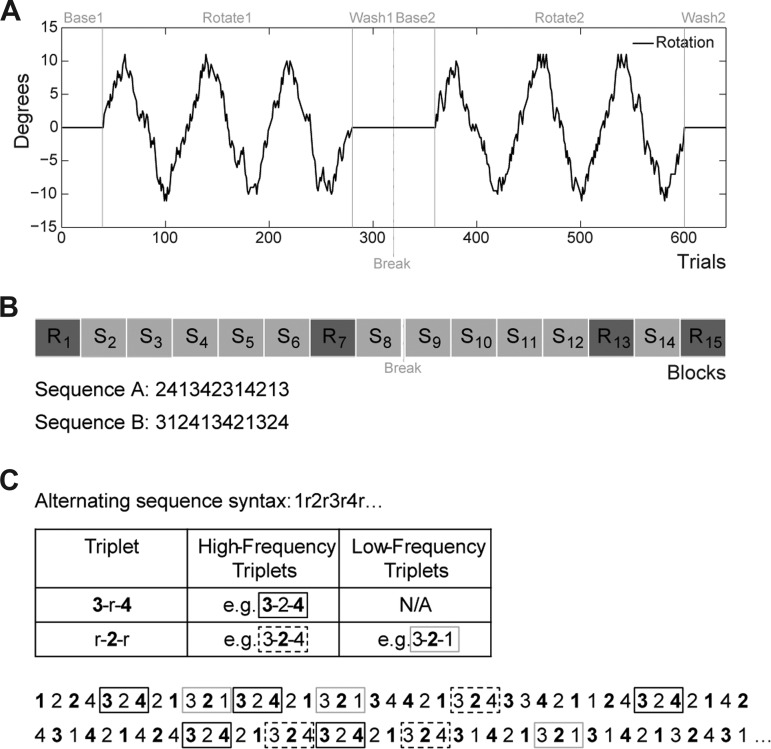
Participants were briefly introduced to the task with a short training block of 24 trials, six reaches to each of the four possible target locations. The experimental session consisted of 640 trials, divided into six blocks (Fig. 1A). The first block (Baseline1) consisted of 40 trials in which the mapping between hand position and cursor position was veridical. In the second block (240 trials, Rotate1) a pseudorandom walk visuomotor perturbation was imposed by rotating the position of the feedback cursor with respect to the true position of the hand (see below). After the end of the rotation block, the participant completed a third block consisting of 40 trials with veridical feedback (Wash1). The participant was then given a short break before repeating each of the three blocks for the second time (Baseline2, Rotate2, Wash2). The task transitioned smoothly between blocks without indicating the change between blocks to the participants. The order of target locations was pseudorandom, such that each target location was used twice every eight trials, avoiding successive repetitions of each location. The 640-trial run took ∼35 min to complete.

Fig. 1.

Experimental tasks. A: visuomotor adaptation (VMA) task. The perturbation followed a pseudorandom walk of a global sinusoidal pattern. B: serial reaction time (SRT) task. On Random blocks (R) the stimulus positions were selected randomly, and on Sequence blocks (S) the stimulus positions followed a repeating 12-element sequence. C: alternating serial reaction time (ASRT) task. Odd-numbered elements follow a fixed sequence, and even-numbered elements are selected at random (r). This creates high- and low-frequency triplets (see text).

During the rotation blocks, the perturbation of the visual feedback followed a global sinusoidal pattern with local jitter (modified from Cheng and Sabes 2006), increasing or decreasing by 1–2° on each trial. The maximum rotation was 12° in either the clockwise or counterclockwise direction, with the cycle spanning 80 trials (Fig. 1A). In terms of actual distance on the screen, a displacement of 1° corresponded to 0.14 cm. We chose to use small trial-to-trial changes in the size of the rotation along with a maximum rotation size of only 12° (corresponding to 1.67-cm displacement) to minimize awareness of the perturbation (Cheng and Sabes 2007; Schlerf et al. 2013).

Participants completed the visuomotor adaptation (VMA) task twice, with each run performed on different days. Two different versions of the task were created by varying the local jitter of the perturbation and the order of the target locations. A different version was used for each of the two runs.

Serial reaction time task.

We employed a version of the SRT task that is designed to minimize the contribution of explicit learning (for example, Robertson 2007; Spencer and Ivry 2009). Four horizontal lines (3.5 cm, with 1.5-cm edge-to-edge spacing) were continuously displayed on the monitor throughout the experiment. At the start of each trial, an “X” symbol (1.8 × 2 cm) appeared above one of the lines. Participants were instructed to press the spatially compatible key as fast as possible. Responses were made with one of four fingers of the right hand, with the fingers positioned on the V, B, N, and M keys on a standard computer keyboard. The target stimulus disappeared 100 ms after the participant pressed a key (either the correct key or a wrong key), or after an interval of 2,000 ms if no key press was detected. Once the target disappeared, a 100-ms intertrial interval was initiated, followed by the presentation of the next stimulus.

The experimental run consisted of 1,260 trials, organized into 15 blocks of 84 trials each. The task transitioned smoothly between blocks without indicating the change between blocks to the participants. There were two types of blocks, Random or Sequence. On Random blocks, the stimuli were selected randomly with the constraints that the stimulus did not appear at the same location on successive trials (for example, 2-2 or 4-4) and did not form three-element trills (for example, 1-3-1 or 2-4-2) or three-element runs (for example, 1-2-3 or 4-3-2) and that each stimulus appeared three times every 12 trials. On Sequence blocks, the stimuli followed a repeating 12-element deterministic sequence (repeating 7 times/block). Two sequences were created (SeqA: 241342314213, SeqB: 312413421324). The second sequence was created by shifting each element of the first by one position, with position 4 becoming position 1. On the basis of past work, we expected that a 12-element sequence would minimize awareness (Pascual-Leone et al. 1993; Spencer and Ivry 2009). We opted not to use a dual-task procedure as a way to minimize awareness because participants vary in how they allocate attention between the sequence learning and secondary tasks, making it difficult to associate individual differences to sequence learning per se. Blocks 1, 7, 13, and 15 were Random blocks, and the other 11 blocks were Sequence blocks (Fig. 1B). Overall, it took ∼15 min to complete the 1,260 trials, including a short break provided after block 8. Participants completed two 1,260-trial runs, with different sequences (SeqA or SeqB) used in each run.

Alternating serial reaction time task.

As described in results, the SRT task proved to be problematic for a study of individual differences given that within-subject measures of learning showed low reliability. As such, we switched to a different assay of implicit sequence learning, the alternating serial reaction time (ASRT) task (Howard and Howard 1997; Janacsek et al. 2012; Remillard 2008). Unlike the deterministic SRT task, the ASRT task involves a probabilistic second-order grammar in which odd-numbered elements follow a fixed sequence and even-numbered elements are selected at random.

The ASRT task used stimulus-response mapping similar to the SRT task (Howard and Howard 1997; Janacsek et al. 2012; Nemeth et al. 2010). Four empty circles (1.5-cm diameter, with 2.5-cm edge-to-edge spacing) were continuously displayed on the computer monitor throughout the experiment. The stimulus on each trial was a dog's head that appeared over one of the circles (2-cm diameter; Nemeth et al. 2010). Participants had to press the spatially compatible response key as fast as possible. Responses were made with the four fingers of the right hand, with each finger mapped to one key on a keyboard (keys V, B, N, and M). The trial ended after the correct key was pressed; thus if the wrong key was pressed, the stimulus remained presented until its associated key was pressed. The target stimulus disappeared immediately after the correct key was pressed, replaced by an empty circle. This initiated a 120-ms intertrial interval before the onset of the next stimulus.

The stimuli followed an eight-element sequence of the structure 1r2r3r4r where the four odd-numbered elements follow a fixed sequence (1-2-3-4 in this example) and the even-numbered elements (indicated by r in this example) were selected at random (Fig. 1C). For each participant, the four fixed elements were randomly mapped to the four stimulus locations, and the only constraint on the random elements was that they were chosen with equal probabilities (allowing successive elements, trills, and runs). The experimental session consisted of 45 blocks of 85 trials each (3,825 trials in total). The first five stimuli in each block were selected at random and were not included in the analysis. The eight-element sequence was then repeated 10 times for each block. At the end of each block, the participant received feedback on the screen, indicating mean RT and overall accuracy. The task took ∼60 min to complete.

Procedure

We present the results in terms of four groups, based on the tasks that the participants completed. Group 1 (n = 38) were tested on the VMA task twice, with a break of 2–5 days between the sessions. These participants were also tested on a reaching version of the SRT task (Spencer and Ivry 2009). However, we did not observe consistent sequence learning with this task, either at the group level or at the individual level, and thus we do not report these data here. This led us to switch to the keyboard variants of the SRT tasks (as described above). Group 2 (n = 23) were tested only on the keyboard SRT task, with the task repeated twice within a single session. Groups 3 and 4 completed both a sensorimotor adaptation task and a sequence-learning task. Group 3 (n = 37) were tested on the VMA and SRT tasks, with 17 participants starting with the VMA task and 20 participants starting with the SRT task. The two tasks were repeated in a separate session with the same order used for each participant. Group 4 (n = 25) were tested on both the VMA and ASRT tasks, with all participants first tested on the VMA task. This 2-h session (given the length of time required for each task) was repeated a second time, again with a 2- to 5-day break between sessions.

For all groups, the first and second runs with a given task used a different stimulus pattern. For the VMA task, this meant that the order of targets and perturbation function differed in the two runs; for the SRT task, different sequences were used in the two runs. The order of the two versions of each task was counterbalanced across participants and days. As noted above, the same grammar was used for all participants on the ASRT task, although the mapping of the grammar elements to stimuli/responses was randomly set for each participant, with the constraint that different mappings were used in the two runs.

At the end of the second run, a questionnaire was administered to assess the participants' awareness of the task manipulations, with separate sets of items used to probe awareness of the VMA and sequencing tasks. The first question was whether the participant had noticed any changes over the course of the specified task. For the second question, the participants were told that there were two groups and that they should report, using a 7-point Likert scale, which group they thought they belonged to. For the VMA task, the choices were between a group for whom the feedback matched the position of the hand and a group for whom the feedback and hand did not match. For the sequencing tasks, the choices were between a group for whom the stimuli were selected at random and a group for whom the stimuli followed a pattern. The third question tested the participants' knowledge of the manipulations in the last run (regardless of their response to the preceding question). For the VMA task, the participants were “forced” to judge whether the feedback cursor had been shifted, relative to hand position, to the left, to the right, or to both directions. For the sequence learning tasks, the participants were informed of the length of the sequence (12 for SRT; 8 for ASRT) and asked to generate, as best as they could, the repeating sequence.

We recognize that there are limitations to the use of postexperimental questionnaires as probes of probe awareness (Howard and Howard 1997; Perruchet and Amorim 1992). On the basis of previous research, we were confident that awareness would be low in the VMA task given the subtle changes in the size and direction of the perturbation from trial to trial, as well as the limited size of the maximum perturbation (Cheng and Sabes 2007; Schlerf et al. 2013). Similarly, awareness has been shown to be very low or nonexistent in the ASRT task because of the insertion of the random elements (Howard and Howard 1997; Janacsek and Nemeth 2012). In terms of awareness, the SRT task is more problematic, with performance measures sometimes providing results that are at odds with postexperimental subjective reports (for example, Perruchet and Amorim 1992; Shanks et al. 2005). Given this, we also examined performance measures as possible indicators of awareness in the analysis of the data.

Data Analysis

For each task, we calculated measures of performance, variability, and learning. The measures were calculated separately for each run, allowing tests of reliability. When appropriate, we averaged the data over the two runs to facilitate comparisons between tasks. All data were analyzed with MATLAB (MathWorks, Natick, MA).

Correlational analyses were performed to evaluate reliability (comparing the same measure from 2 different runs) and to compare different performance measures (comparing 2 measures, each averaged over the 2 runs). Pearson correlation coefficients represent the strength of the linear dependence between the variables of interest. We also employed orthogonal (Deming) regression to evaluate the relationship between variables of interest (Cornbleet and Gochman 1979; Linnet 1993, 1998). Regular least-squares regression assumes that the x-axis variable is noise free and that all of the variance is confined to the y-axis variable. In contrast, the Deming method is symmetrical with respect to the two variables, making no assumptions regarding their dependence or independence, and does not assume the lack of variance of the variable plotted on the x-axis. This method is appropriate for the present study because we make no assumptions about dependence (for example, second run performance is not influenced by first run performance). Thus Deming regression provides the best estimate of the slope of the relationship between the x and y variables, based on estimates of noise in both variables.

Visuomotor adaptation task.

Using the output from the stylus, movement trajectories were reconstructed off-line. To minimize the contribution of online corrections, the initial heading angle was used as the primary dependent variable. It was calculated as the angle between a line connecting the center of the start circle and the center of the target and a line connecting the center of the start circle and the hand position midway to the target (4 cm from start position). We also calculated RT and MT. The former was measured as duration from target onset until the time at which the hand crossed a 1-cm ring around the center of the starting circle. The latter was measured as the duration between the reaction time and the time at which the cursor intersected the target circle.

Trials were discarded when the heading angle was more than ±3 SD from the mean heading angle or when MT was more than 3 standard deviations (SDs) longer than the mean MT (calculated per participant and run). Two percent of the trials were removed on the basis of these criteria (2.0 ± 0.68%, ranging from 0.2% to 4.4% over participants). We did not exclude data based on the RT data because the instructions did not emphasize RT. All 100 participants who were tested on VMA were included in the analysis.

Learning in visuomotor rotation tasks is manifest by changes in heading angle that counter the direction of the perturbation. As a global measure of learning, we calculated the cross-correlation between the sequence of heading angles and the sequence of perturbations across all rotation trials (Rotate1 and Rotate2). We repeated this calculation by shifting the heading angle time series up to a quarter of a cycle to identify the lag at which the correlation was largest (based on goodness of fit).

Our main analysis of the learning data focused on the participants' learning rate, measured by the trial-by-trial response to the evolving rotation. We employed a standard state-space model of adaptation (Cheng and Sabes 2007; Thoroughman and Shadmehr 2000), in which the internal model (x) of the motor system (in this case heading angle) is updated at each trial (n + 1) according to a learning rule:

$$e_n=x_n+r_n$$ (1)

$$x_{n+1}=x_n-B\times e_n$$ (2)

The error (e_n) experienced at trial n is given by the difference between the hand heading angle (x) and the rotation (r). The hand heading angle for the next trial (x_n+1) is updated based on the weighted (B) error on the current trial. Effectively, B is a learning rate, reflecting the percentage of error that is corrected from trial to trial. As such, large values of B indicate faster learning. This model was fit to estimate each participant's learning rate (B) by minimizing the root-mean-square (RMS) error between the actual time series of heading angles and the model output (Eq. 1) with the fminsearch function in MATLAB. We obtained a single measure of learning for each session by fitting the data from both the Rotate1 and Rotate2 blocks.

A main question of interest in the present experiment was to assess individual differences in sensorimotor adaptation and to ask if these individual differences are related to movement variability. To measure performance variability that was not contaminated by learning, we focused on the data from the Baseline1 block. Spatial variability (sSD), defined as the SD of the heading angles across the Baseline1 block, served as our measure of performance variability for the VMA task. MT was also taken from the Baseline1 block.

Serial reaction time task.

The median RT was calculated for each block. We used the median rather than mean RT to minimize the effect of outliers, although the results are similar with either measure. Only correct trials were used in the analysis. Learning in the SRT task is defined as the increase in RT on Random blocks following training with Sequence blocks.

It is important to note that the learning measure for the SRT task is not based on a trial-by-trial measure but rather involves a comparison across blocks in which the stimuli are predictable or selected at random. Our initial plan was to focus on the contrast of learning at the end of the task (as done in previous SRT studies such as Spencer and Ivry 2009), comparing the final two Random blocks (blocks 13 and 15) and the final two Sequence blocks (blocks 12 and 14). After finding that the learning measure defined on the final Random blocks showed poor reliability (see below), we also defined a second learning measure (initial learning) based on the Random block included in the middle of the task, or what we refer to as the midtask probe. Here we compared the median RT on this Random block (block 7) and the two adjacent blocks (blocks 6 and 8).

In our analysis of individual differences, we sought to find out whether variation in SRT learning was related to any performance variables. To this end, we used measures of RT from blocks 2–4. At this point in training, we expected learning to be modest. The means of these RT data were used to estimate basic motor speed and temporal variability (tSD). For the latter, we took the SD of the RT data and normalized this by dividing by the mean RT for these blocks.

We did not have data for both runs for 4 of the 60 participants from the SRT task (1 participant was accidentally tested twice on the same sequence; the program did not run properly on the second session for 3 participants). In addition, two participants were excluded from the final analysis because their RTs increased by >200 ms on the final Random blocks compared with the neighboring Sequence blocks (and, correspondingly, their learning scores were >3 SDs above the group mean learning score). We interpreted this as a performance-based indicator that these participants had developed explicit knowledge of the sequence during at least one of the testing sessions. Finally, from the questionnaire data, one participant was fully aware of the sequence, recalling the entire sequence, and we thus excluded this participant from the analysis. In total, the data from 53 participants were included in the final analysis.

As described above in Procedure, the third questionnaire question required participants to generate a 12-element pattern, attempting to produce the sequence employed in the second run. From these data, we calculated a match index (MI) based on the generation of three or more successive elements that corresponded to the actual sequence (Bo et al. 2011; Martini et al. 2013; Reber and Squire 1998; Wilkinson and Shanks 2004). This composite score MI served as a proxy of awareness, with scores ranging from 0 (no match) to 1 (full recall). We calculated the probability of recalling triplets, quartets, and quintets from the original sequence (for example, SeqA includes triplets of 241, 413, 134, etc., quartets of 2413, 4134, 1342, etc., and quintets of 24134, 41342, etc.), comparing this to the probability of randomly recalling matches (avoiding repetitions). For the latter, the probabilities of reporting, by chance, a triplet, a quart, and a quint given 12-element sequences are 0.33, 0.11, and 0.037, respectively. We gave larger weight to longer sequences, using weights equal to the length of minisequences. Thus by chance the MI score would be 0.316 (3 × 0.33 + 4 × 0.11 + 5 × 0.037). We did not look for matches longer than five elements because these matches have minimal impact on the expected value by chance. The MI scores were calculated for the second sequence because we assumed that this information, if available, would be most active at the time of the questionnaire. This analysis was limited to 52 participants because questionnaire data were missing from 1 participant.

Alternating serial reaction time task.

RTs from correct trials were grouped over triplets of three sequential trials. Two types of triplets were created from the data: high-frequency triplets, in which the first and third elements are sequential elements of the basic sequence, and low-frequency triplets, in which the first and third elements do not follow the basic sequence. In the 1r2r3r4r example above (r indicating random elements), triplets of 1x2, 2x3, 3x4, and 4x1 (x indicating any possible element, either random or sequence) would occur more often, either from including two consecutive stimuli of the repeating sequence (for example, 132 created from 1r2) or from two consecutive random elements that, by chance, follow the basic sequence (for example, the same 132 for a triplet of r3r). By contrast, triplets of 1x3 or 4x2 (for example, 123) would occur less frequently because they could never be obtained from two consecutive sequence elements. Rather, they would only occur when an r2r triplet results in a specific random selection (when the initial and final r are chosen to be 1 and 3, in the above mentioned example). Overall, there were 68% high-frequency triplets and 32% low-frequency triplets in the experiments (as in Nemeth et al. 2013).

Following the criterion used in previous studies (Howard and Howard 1997; Janacsek et al. 2012; Nemeth et al. 2010), and similar to the restrictions imposed in the SRT task, two kinds of low-frequency triplets were excluded from our analyses: repetitions and trills. Elimination of these special triplets assured us that differences between high- and low-frequency triplets were not confounded by response patterns that might produce fast RTs.

Sequence learning in the ASRT is calculated by comparing RT for high-frequency and low-frequency triplets (Janacsek et al. 2012; Nemeth et al. 2010). The difference between the two types of triplets was calculated separately for each block by subtracting the median RT of the high-frequency triplets from the median of the low-frequency triplets (Nemeth et al. 2010). Note that, unlike the SRT task, learning in the ASRT is based on a within-block, trial-by-trial measure. To test for reliability between sessions, we calculated an average learning value over the entire session (from blocks 4–45).

To relate learning to performance measures, the overall mean and SD of the RT data were calculated from blocks 2 and 3, again choosing an early time point where learning should be minimal. We did not include the block 1 data, given the assumption that the participants are becoming familiar with the task during this block. As with the SRT data, we created a normalized measure of temporal variability (tSD) by dividing the SD of RT during blocks 2 and 3 by the mean RT of these blocks.

Four of the 25 participants in group 4 were excluded from the final analysis. The mean RTs for two participants were >3 SDs from the group mean, and the temporal variability of the other two participants was >3 SDs from the group mean. In total, data obtained from 21 participants were included in the final analysis.

RESULTS

Individual Differences in Visuomotor Adaptation

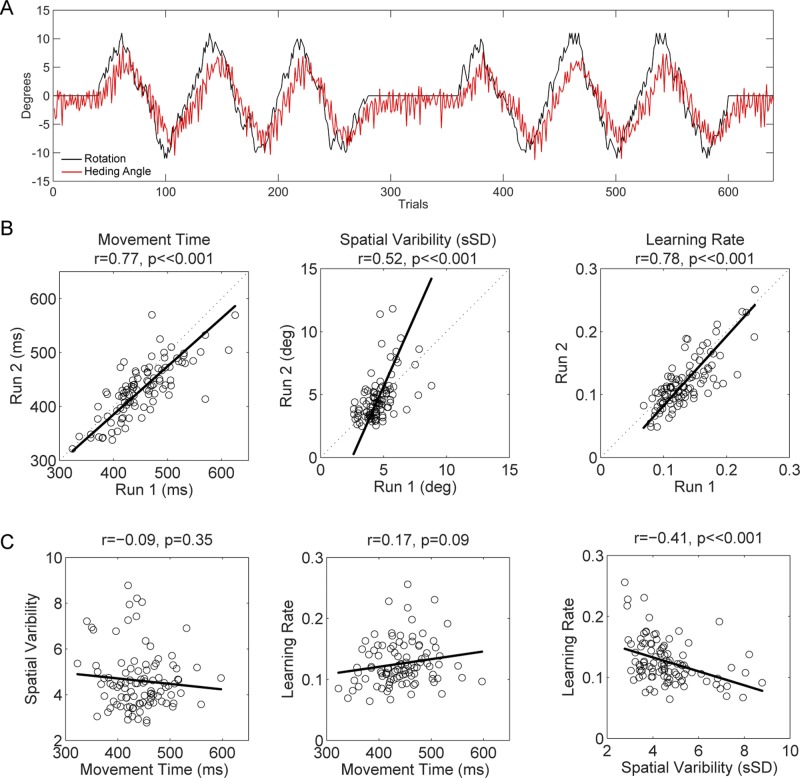
To look at implicit sensorimotor adaptation, we used a pseudorandom perturbation of visual feedback cycling, every 80 trials, between 12° clockwise rotation and 12° counterclockwise rotation. Overall, there was a group bias as participants tended to reach in a slightly counterclockwise direction of the targets in the absence of any perturbation (baseline block), a pattern that was evident throughout the task. The participants adapted to the perturbation, modifying their initial heading angle in a direction opposite the perturbation (Fig. 2A shows the group average over both runs). In terms of our global measures of learning (over all participants and runs), the mean correlation between the perturbation and initial heading was 0.66 ± 0.13, and the best fit was obtained when the heading angle function lagged the perturbation function by 4.9 ± 1.5 trials. Note that despite the similar low frequency of the perturbation and behavior, the high-frequency local jitters reduced the overall correlation between the graphs. The mean learning rate, calculated by the state-space model, was 0.13 ± 0.04.

Fig. 2.

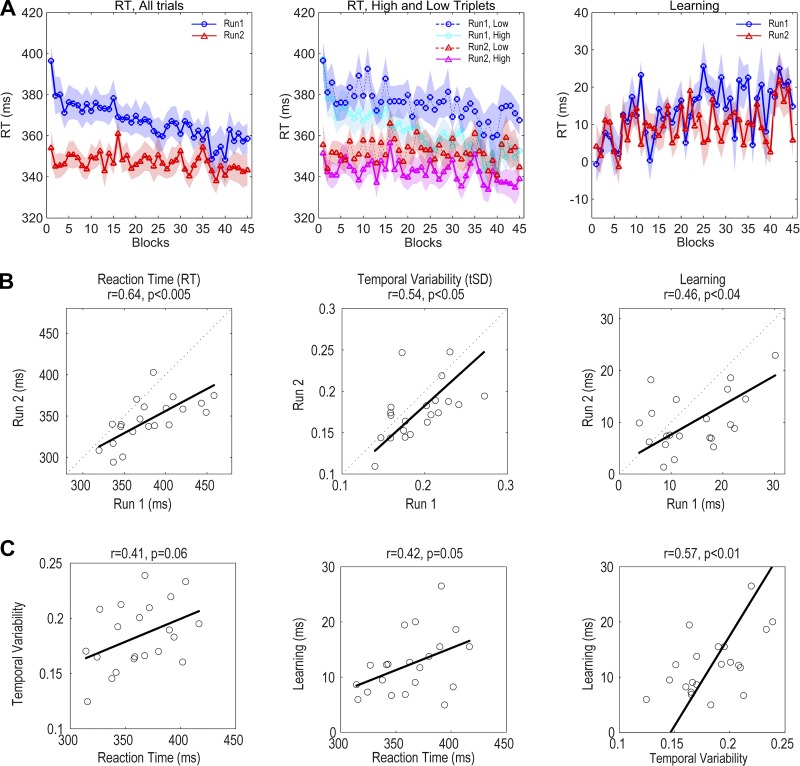
VMA results (n = 100). A: group average response (red, shaded region is group SE) to a gradual perturbation (black). For visualization purposes, the response function has been flipped, although the actual changes in movement heading were in the opposite direction of the perturbation. B: reliability of movement time, spatial variability, and learning rate between run 1 and run 2 (circles correspond to individual participants). Baseline movement time and spatial variability measures are taken from the baseline block. Learning rate is estimated from the model fit of the data from the perturbation blocks. C: correlations between different measures of performance. In all figures, r and P values represent the strength and significance of the Pearson correlation coefficients of the linear dependence between the variables of interest. Orthogonal (Deming) regression lines evaluate the relationship between variables of interest, without making assumptions concerning their dependence or independence.

Three different groups were tested on the VMA task, differing in whether they performed this task alone or in combination with either the SRT or ASRT task. For all three groups, the VMA task was repeated in two separate runs (on separate days), with different orders of target locations and perturbations for the two runs. We first assessed whether there were any differences between groups on our three primary dependent variables: MT and spatial variability (both calculated from Baseline1 trials before the visuomotor perturbation was introduced) and learning rate (estimated from the Rotate1 and Rotate2 trials with the state-space model). For this analysis, we conducted mixed ANOVAs with the between-subject factor Group and the within-subject factor Run. In all of the ANOVAs, there was no effect of Group or Group × Run interaction (P > 0.1). In a secondary analysis limited to group 3, where some participants completed the VMA task before the SRT task and vice versa for others, we confirmed that there was no effect of order (P > 0.15), indicating that performance of the VMA task was unaffected by whether the participants had first completed the SRT task. Over the three groups, there was a significant effect of Run on MT (run 1 = 451.9 ± 55.1 ms, run 2 = 431.6 ± 50.5 ms; P < <0.001) and learning rate (run 1 = 0.133 ± 0.037; run 2 = 0.120 ± 0.040; P < <0.001), indicating that participants reached faster and learned slower during the second run. There was no change in spatial variability across runs (run 1 = 4.6 ± 1.1°, run 2 = 4.6 ± 1.8°; P = 0.46).

Our main interest in this study was to explore individual differences in implicit motor learning. Such questions are only sensible if our individual measures are reliable over time. Importantly, even though there was a significant change in the group means between runs, measures can be reliable if the rank order of the samples remains approximately constant. Given that there was no effect of Group, we can look at this question in a large sample by combining the 100 participants into one group and comparing performance on the VMA task between the two runs (with minimum separation of 2 days). As shown in Fig. 2B, reliability was high for MT (r = 0.77; 95% CI = [0.68, 0.84]), spatial variability (r = 0.52; 95% CI= [0.36, 0.65]), and learning rate (r = 0.78; 95% CI = [0.69, 0.85]) (all P < <0.001). These data demonstrate that there is some stable factor or set of factors that underlie individual differences in terms of how the participants reached, as well as in terms of their ability to respond to a visuomotor perturbation. Note that while MT was constrained experimentally, there remained considerable variability in how fast the participants moved and this remained consistent over runs.

We next looked at the relationship between these three variables, averaging the scores for the two runs for each individual (Fig. 2C). There was a trend for MT and learning rate to be positively correlated (Fig. 2C, center; r = 0.17, P = 0.09, 95% CI = [−0.03, 0.36]), with faster learning associated with slower movements. However, MT and spatial variability were not correlated (Fig. 2C, left; r = −0.09, P = 0.35, 95% CI = [−0.28, 0.10]), indicating, that at least in terms of initial heading, there was no speed-accuracy trade-off. Importantly, there was a significant negative relationship between spatial variability and learning rate (Fig. 2C, right; r = −0.41, P < <0.001, 95% CI = [−0.55, −0.22]): Participants who exhibited higher reaching variability during baseline blocks adapted to the visuomotor rotation at a slower rate.

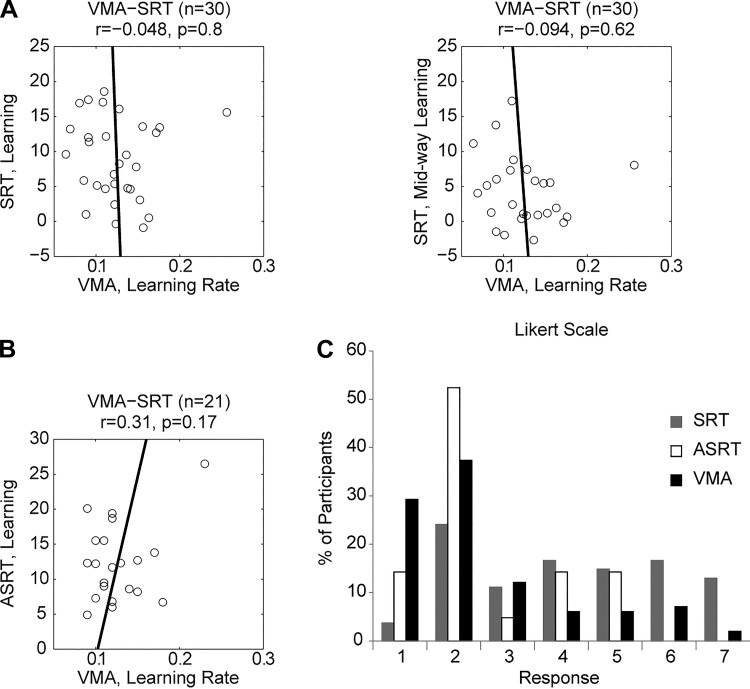
To examine the influence of awareness on learning, we looked at the questionnaire data. Because we did not want to bias participants to expect a perturbation, the questionnaire was administered only at the end of the second run. The data indicated that participants had no or minimal awareness of the visuomotor perturbation. Only a third (38%) of the participants reported that they “experienced any change in apparatus during the test session.” When pressed to explain the change, none described a mismatch of the visual feedback; rather, the participants offered a large variety of explanations (for example, “I became better with practice” or “the distance between the starting point and end point is becoming longer”). When asked if they belonged to a no-perturbation (match) or perturbation (no match) group with a 7-point Likert scale, the mean rating was 2.5 ± 1.6, falling between the “2: Somewhat confident in match group” and “3: Minimal confidence but expect in match group” categories (see Fig. 5C). When pressed to indicate the direction of a “mismatch,” the majority (57.7%) selected the answer that there was a unidirectional mismatch, whereas the actual perturbation included both clockwise and counterclockwise rotations.

Fig. 5.

Between-task correlations of learning scores. A: correlation between learning measures of visuomotor adaptation SRT using the final probe of SRT learning (left) and midway SRT learning (right). B: correlation between learning measures on visuomotor adaptation and ASRT. Note that the positive correlation is largely influenced by the participant who had the fastest rate of adaptation and exhibited the largest amount of sequence learning. When the correlation is recalculated without this individual, there is no correlation between the learning measures for the 2 tasks (r = −0.17, P = 0.48). C: histogram of responses on Likert scale to survey question probing awareness of the perturbation (VMA) or sequence (SRT and ASRT). Low values correspond to low awareness; high values correspond to high awareness. Although all of the scores are toward the lower end, there is a rightward shift of the distribution for the SRT task, indicative of higher awareness of the presence of a sequence.

To summarize, we observed impressive reliability in measures of performance and learning on a visuomotor rotation task. Adaptation to the pseudorandom perturbation was implicit for all participants and faster for those with lower baseline variability.

Individual Differences in Sequence Learning

Serial reaction time task.

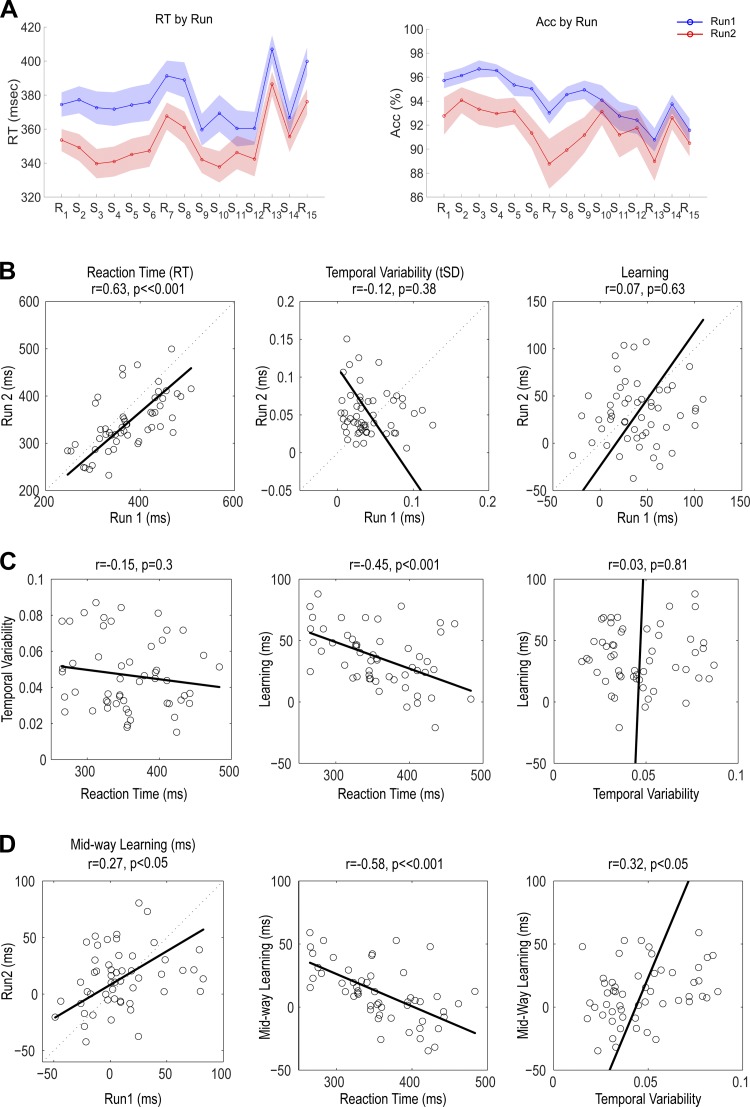
To study implicit sequence learning, we used a 12-element version of the SRT task in which participants responded to the location of visual stimuli by pressing spatially compatible keys on a computer keyboard. Accuracy was relatively high (93% ± 7% across participants, over all blocks). Over all participants and the two runs, there was a significant increase in RT on the final two Random blocks, indicative of sequence learning [Fig. 3A, left: 36.1 ± 23.6 ms; t-test vs. 0, t(52) = 11.1, P < <0.001]. There was also an increase in RT for the midtask probe, although to a smaller extent [11.2 ± 22.5 ms; t(52) = 3.6, P < 0.005]. A similar pattern was evident in the accuracy data (Fig. 3A, right), with mean increases in error rates of 2.2 ± 3.3% and 1.8 ± 4.9% in the late and midtask probes, respectively [t(52) = 4.8, P < <0.001 and t(52) = 2.7, P < 0.01, respectively]. We note that these learning costs were evident despite the fact that RT showed only a modest decrease over the course of the Sequence blocks.

Fig. 3.

SRT results (n = 53). A: group average of median RT (left) and accuracy (Acc; right) for run 1 (blue) and run 2 (red). Shaded areas represent group SE. B: reliability of RT, temporal variability, and learning between the run 1 and run 2 scores. Baseline metrics of RT and the SD of RT are taken from blocks 2–4 (early in training). Learning is calculated from the last 4 blocks (Random blocks 13 and 15 minus Sequence blocks 12 and 14). C: correlation between different measures of performance. D: reliability of learning (left) and correlation of learning and baseline metrics of learning at the midway probe (Random block 7 minus Sequence blocks 6 and 8) (center and right).

Two groups were tested on the SRT task. One group (group 2) were tested in a single session, completing two runs with different sequences. The other group (group 3) were tested over two separate sessions, with each session also including VMA testing. As with the VMA analysis, we first assessed whether there were any differences between groups on our three primary dependent variables: two performance variables, RT and temporal variability, calculated from the early stages of the task (blocks 2–4) where we assume learning is relatively modest, and learning, calculated from the final-task random probes. These data were analyzed with a set of mixed-design ANOVAs with the between-subject factor Group and the within-subject factor Run. In all of the ANOVAs, there was no effect of Group or Group × Run interaction (P > 0.34). In an analysis limited to group 3, there was also no effect of order (P > 0.15), indicating that SRT performance was unaffected by whether the participants had first completed the VMA task.

There was a significant Run effect on RT. Participants responded faster in the early baseline blocks of run 2 compared with run 1 (run 1 = 373 ± 65 ms, run 2 = 343 ± 59 ms; P < <0.001). The reduction in RT came at a modest, nonsignificant cost in accuracy (run 1 = 96.5 ± 4.1%, run 2 = 93.5 ± 8.1%; P = 0.11) and an increase in variability, operationalized as the SD of these baseline RTs (divided by the mean RT), (run 1 = 0.041 ± 0.029, run 2 = 0.052 ± 0.031; P < 0.05). Learning was comparable for the two runs (run 1 = 10.1 ± 8.3, run 2 = 8.9 ± 8.6; P = 0.43). In terms of sequence-specific learning, participants exhibited faster RTs for SeqA than for SeqB (SeqA: 44.8 ± 33.8 ms, SeqB: 27.3.0 ± 28.4 ms, P < 0.005).

In the absence of Group effects, we combined the data from the 53 participants to assess reliability on the SRT task. Baseline RTs were reliable across runs (Fig. 3B, left; r = 0.63, P < <0.001, 95% CI = [0.43, 0.77]). In contrast, our measure of variability, the SD of these baseline RTs, was not reliable (Fig. 3B, center; r = −0.12, P = 0.38, 95% CI=[−0.38, 0.15]). Even more striking, the measures of sequence learning were not reliable when taken at the end of the runs (Fig. 3B, right; r = 0.07, P = 0.63, 95% CI = [−0.21, 0.33]). Thus, although we observed consistent learning on this task in the group analysis, the degree of learning in run 1 was not predictive of the degree of learning in run 2 on an individual basis. We also looked at reliability by correlating learning scores between the sequences, correlating SeqA with learning scores on SeqB. Here, too, we failed to observe consistency in terms of individual differences (r = 0.14, P = 0.3, 95% CI = [−0.14, 0.39]).

There are several reasons why reliability might be poor for our measure of sequence learning. First, whereas learning in the VMA task is based on trial-to-trial adjustments, learning in the SRT task is based on a comparison across blocks. The latter might be more susceptible to contamination from other factors (for example, fluctuations across blocks in motivation or fatigue). We return to this issue below when addressing performance on the ASRT task, where learning is based on trial-to-trial measures.

Second, a subset of participants may have developed some degree of awareness in one of the sessions. The cost observed on Random blocks is much larger when participants are aware of the sequence, in large part because they can anticipate the stimulus (as reflected in RTs < 200 ms and/or in learning scores > 200 ms). As such, we would expect a poor correlation if some participants were aware of the sequence in one run and unaware in the other. As noted in methods, we purged participants with high levels of sequence awareness by excluding the data from the two participants who had learning scores > 3 SDs of the mean score and the one participant who recalled the full sequence.

Nonetheless, there may be some graded level of contamination from awareness. Indeed, the questionnaire data indicated that participants might have had some awareness of the repeating sequence, with more than a third (40%) of the participants agreeing with the statement that they had “experienced any change in the experiment during the test session.” When asked to mark their confidence in being assigned to a random group or a sequence group on a 7-level Likert-scale (Fig. 5C), the mean rating was 4.17 ± 1.85, not significantly different from “4: Not sure which group” (P = 0.51). We also asked the participants to recall or make their best guess of the repeating sequence on run 2. The extent of recall was measured by MI, ranging from 0 (no match to actual sequence) to 1 (perfect match), with random guessing expected to produce a value of 0.136. The mean MI value over all participants was 0.21 ± 0.15, significantly above chance (2-tailed t-test: P < 0.001), suggesting that the participants had partial awareness of some segments of the sequence.

The absence of reliable individual differences in SRT learning, in conjunction with the awareness concern, led us to examine an alternative measure of learning. In particular, we reasoned that awareness (as well as factors such as fatigue) would be less problematic during the initial stages of the experimental run. As such, we performed a post hoc analysis of learning using the midtask random probes (see Fig. 1B). As expected, learning was lower at this initial probe compared with the late probe [t(52) = 7.74, P < <0.001, between the 2 probes; Fig. 3D]. Interestingly, these initial learning scores showed modest reliability across runs, despite having a more restricted range than that observed for the late learning scores (Fig. 3D, left; learning: r = 0.27, P < 0.05, 95% CI = [0.00, 0.50]). We also observed reliability between the initial and late stages of learning (r = 0.49, P < 0.005, 95% CI = [0.25, 0.67]), suggesting that despite the possible contamination of explicit factors on the late learning measure, some aspect of implicit learning was maintained over the course of the experimental task.

Last, we looked at the relationship between our dependent variables, averaging the scores for the two runs for each individual (Fig. 3, C and D). There was no correlation between RT and temporal variability (Fig. 3C, left; r = −0.15, P = 0.3, 95% CI = [−0.4, 0.13]). Participants who responded faster during the baseline blocks exhibited greater learning, as indicated by significant negative relationships between the baseline RT and learning, during both late (Fig. 3C, center; r = −0.45, P < 0.01, 95% CI = [−0.64, −0.20]) and initial (Fig. 3D, center; r = −0.58, P < <0.001, 95% CI = [−0.73, −0.36]) stages of the task. There was no correlation between learning and baseline variability for the late learning probe (Fig. 3C, right; r = 0.04, P = 0.79, 95% CI = [−0.24, 0.30]), whereas there was a weak correlation with the initial learning (Fig. 3D, right; r = 0.31, P < 0.05, 95% CI = [0.05, 0.54]).

In summary, we observed robust learning on the SRT task. However, when we focused on the traditional measure used in SRT studies, namely, RT differences between the final Sequence and Random blocks, we failed to observe reliable individual differences: Learning in one run was not predictive of learning in a second run. This lack of reliability in the learning scores contrasts with the reliable individual differences in mean RT. We suspect that two factors contribute to the lack of reliability. First, SRT learning is based on comparing RTs across blocks, and various factors can produce considerable variation in RT across blocks. Second, the late probes might be contaminated by awareness. Consistent with these explanations, we did observe a modest degree of reliability when the analysis was limited to the initial probe. Moreover, the extent of learning at this earlier probe was higher for participants who responded more slowly and exhibited larger variability in the early stages of the task.

Alternating serial reaction time task.

Given the concerns with the SRT task, we opted to use the ASRT task as a different way to assay sequence learning. One major advantage of the ASRT is that learning is calculated continuously from each triplet of trials (see methods). Moreover, as reported in previous studies, learning in the ASRT task appears to be completely implicit (for example, Howard and Howard 1997; Janacsek et al. 2012; Nemeth et al. 2010). Only a single group was tested on the ASRT task, with each participant performing the task on two separate sessions. Accuracy was reasonably high in this task (90 ± 3% across participants).

We observed robust improvements in performance on the ASRT task (Fig. 4A). Overall, RTs became faster over the successive blocks, and there was a substantial overall reduction in RT on run 2 compared with run 1. In terms of sequence learning, we focus on the comparison of RTs to high- and low-frequency triplets. Sequence learning was evident in both runs. In separate repeated-measures ANOVAs, the effect of Triplet Type (high vs. low) was significant for both run 1 (P < <0.001) and run 2 (P < <0.001). The effect of Block was only significant for the run 1 data (run 1: P < <0.001; run 2: P = 0.28). However, the Triplet Type × Block interaction was significant on both runs (run 1: P < 0.001; run 2: P < 0.05), reflective of the fact that the difference between the high- and low-frequency triplets increased over the test session, indicative of learning.

Fig. 4.

ASRT results (n = 25). A: group average of median RT for run 1 and run 2 (left), divided into low- and high-frequency triplets (center), and as difference scores (right). B: reliability of RT, temporal variability, and learning between run 1 and run 2 scores. Baseline metrics of RT and the SD of RT are based on data from blocks 2 and 3 (early in training); learning is averaged over blocks 4–45. C: correlations between different measures of performance.

As can be seen in Fig. 4, the participants were much faster in the second run. This performance difference was evident in blocks 2 and 3, which serve as our proxy for baseline performance where sequence learning is assumed to be low. Not only were RTs faster in run 2 compared with run 1 (run 1 = 379.7 ± 40.0 ms, run 2 = 345.3 ± 26.4 ms; P < <0.001) but variability was also lower in these blocks (run 1 = 0.192 ± 0.034, run 2 = 0.174 ± 0.034 ms; P < 0.001). Mean sequence learning across the run (see methods) was also lower in run 2 (run 1 = 14.4 ± 7.3, run 2 = 10.1 ± 5.5; P < 0.01).

We next turned to our assessment of reliability (Fig. 4B). In terms of baseline measures of performance, individual differences in mean RT and temporal variability were reliable across runs (RT: r = 0.64, P < 0.005, 95% CI = [0.29, 0.84]; tSD: r = 0.51, P < 0.02, 95% CI = [0.096, 0.77]). Learning on the ASRT was also reliable (RT: r = 0.46, P < 0.04, 95% CI = [0.04, 0.74]). As can be seen in Fig. 4B, right, most of the data points fall below the unity line, reflective of the fact that learning was lower on run 2 compared with run 1. Nonetheless, participants who showed higher levels of learning on run 1 tended to show higher levels of learning on run 2. This correlation is especially impressive given the very modest level of learning (and thus restricted range) on the ASRT.

Given that individual differences in probabilistic sequence learning are reliable, we can ask whether these differences are related to baseline performance measures (Fig. 4C). First, we observed a trend for a positive correlation between RTs and temporal variability, a pattern that is in the opposite direction to that observed for the SRT task (Fig. 3C, left; RT: r = 0.41, P = 0.06, 95% CI = [−0.03, 0.72]). Also in contrast to the SRT task, we observed a trend for a positive correlation between RT and learning with the ASRT task: Better learning was associated with slower RTs (Fig. 4C, center; RT: r = 0.42, P = 0.05, 95% CI = [−0.01, 0.72]). There was also a positive correlation between sequence learning and temporal variability: Better learning was associated with higher variability (Fig. 4C, right; RT: r = 0.56, P < 0.01, 95% CI = [0.17, 0.80]), a result consistent with that observed in the initial probe data for the SRT task. We note that in the ASRT task high temporal variability could reflect a difference in RT between high- and low-frequency triplets, a difference that is accentuated in good learners. However, the positive correlation is also observed when the analysis is performed separately for the high and low triplets (high: r = 0.52, P < 0.05; low: r = 0.57, P < 0.01).

Analysis of questionnaire data (Fig. 5C) indicated that participants were not aware of the presence of a repeating probabilistic sequence. Only a third (33%) of the participants reported that they “experienced any change in the experiment during the test session.” From the Likert scale, participants were more likely to judge that they had been in the random (no sequence) group (2.62 ± 1.32).

To summarize, we observed impressive reliability in measures of performance and learning on probabilistic sequence learning. Learning the probabilistic sequence was implicit for all participants and higher for those with slower baseline RTs and higher baseline variability.

Individual Differences Across Tasks

The participants in groups 3 and 4 completed two implicit motor learning tasks, the VMA and the SRT tasks (group 3) or the VMA and ASRT tasks (group 4). We compared performance across tasks, asking whether there are consistent individual differences in implicit learning in two distinct task domains. Within each task, we averaged performance across the two runs. Note that given the lack of reliable learning in the late probe for the SRT task, the data from this task should be viewed cautiously.

Tables 1 and 2 present the correlation matrix and Fig. 5 depicts correlations between the different measures for each task. Overall, there was little correlation between the rate of adaptation and the magnitude of sequence learning, the key measures of implicit learning. There was essentially no correlation between VMA adaptation and SRT learning (Fig. 5A), measured either at the end of training or at the midpoint of the task (where learning is likely implicit and the measure was reliable). Regarding ASRT, there was a positive correlation, albeit nonsignificant, between VMA adaptation and ASRT learning over all participants (Fig. 5B; r = 0.38, P = 0.17, 95% CI = [−0.14, 0.65]). However, this correlation is largely driven by one participant who showed faster adaptation and higher sequence learning. We consider the effects of this outlier in two ways. First, when we simply removed this data point, not only did the correlation coefficient become much weaker but the direction actually reversed (r = −0.17, P = 0.48, 95% CI = [−0.57, 0.3]). Second, we used a more conservative winzoring procedure, replacing the values of the outlier with the SRT/VMA values from the closest neighbors. This procedure also indicated that there was no correlation between the two learning scores (r = 0.03, P = 0.87, 95% CI = [−0.4, 0.46]). In sum, both trimming methods indicate that there is no relationship between learning on the ASRT and VMA tasks. Thus the correlational data fail to support the hypothesis that there is some common process that contributes to implicit motor learning across task domains.

Table 1.

Correlation matrices of key performance and learning variables for VMA and SRT tests

	SRT			VMA
	tSD	Learning	Initial Learning	MT	sSD	LR
SRT
RT	0.02	−0.31*	−0.58***	0.08	0.37*	0.08
tSD		−0.06	0.28	−0.05	−0.02	0.04
Learning			0.54**	0	−0.04	−0.06
Initial learning				−0.27	−0.22	−0.07
VMA
MT					−0.08	0.21
sSD						−0.4*

Subsets of participants who completed both visuomotor adaptation and sequence learning.

^*P < 0.05,

^**P < 0.005,

^***P < 0.001.

Table 2.

Correlation matrices of key performance and learning variables for VMA and ASRT tests

	ASRT		VMA
	tSD	Learning	MT	sSD	LR
ASRT
RT	0.44*	0.42	0.30	−0.17	0.14
tSD		0.57**	−0.02	−0.06	0.11
Learning			−0.04	−0.19	0.31
VMA
MT				−0.20	0.04
sSD					−0.45*

Subsets of participants who completed both visuomotor adaptation and sequence learning.

^*P < 0.05,

^**P < 0.005.

The correlation matrix does highlight one other important result. Learning was correlated with motor variability for both the adaptation and sequence learning tasks. However, the direction of the correlation was the opposite. For adaptation, the correlation was negative, suggesting that participants with high spatial variability adapt at a slower rate. For sequence learning, the correlation was positive, suggesting that participants with high temporal variability learn sequential associations at a faster rate. This effect was only significant for the ASRT task; nonetheless, a similar pattern was observed in the late phase of the SRT task.

DISCUSSION

Motor skills occupy a prominent place as representative of implicit or procedural memory in standard memory taxonomies (Squire and Zola 1996; Sun et al. 2007). We used an individual differences approach to examine the relationship between two classes of tasks commonly used to study implicit motor learning, sensorimotor adaptation and sequence learning. Participants were tested in two separate runs, allowing us to first examine whether measures of learning and performance were reliable—a prerequisite for evaluating individual differences. We then examined factors that might account for individual differences within each task, as well as the relationship in learning between the two task domains.

Reliability of Implicit Learning

Surprisingly, we were unable to find any previous work examining the reliability of individual differences in implicit motor learning. Studies that tested people over multiple days have generally focused on consolidation and thus repeated the exact same task over successive days to look at variables such as forgetting or off-line learning (for example, Doyon et al. 2009; Krakauer 2009; Meier and Cock 2014; Nemeth et al. 2010). These consolidation factors limit our ability to draw inferences about reliability because there might be individual differences in consolidation and other memory processes. Savings, the phenomenon in which people show faster relearning of a previously forgotten memory, has been observed in visuomotor adaptation tasks, but these studies have not reported individual differences and have used conditions in which participants are likely aware of the perturbation (Morehead et al. 2015; Zarahn et al. 2008).

In the present study, we observed reliable individual differences in core performance measures. Focusing just on the data from the baseline phase of the tasks, MT was highly correlated across runs in the VMA task and RT was reliable in both the SRT and ASRT tasks. We do not consider these differences as indicative of some sort of individual limit in performance. Rather, they may be best viewed as a “signature” of a consistent individual style, perhaps reflecting an idiosyncratic criterion for how people choose to trade off speed and accuracy in the context of each task. During the second exposure to the tasks, participants reached faster in the VMA task and had faster RTs in the sequence learning tasks, suggesting that familiarity with the tasks led to similar improvements (broadly speaking) across participants.

Our main interest was to ascertain the reliability of measures of implicit learning. The rate of trial-by-trial adaptation exhibited reasonable reliability across runs on the VMA task with trial-by-trial adjustments that, on average, corrected for ∼10% of the error. Similarly, learning, measured by the difference in RT to high- and low-predictability stimuli, was reliable in the ASRT task with a mean overall difference of 12 ms between the high- and low-frequency elements. Post-experiment questionnaires confirmed that learning in the VMA and ASRT tasks was implicit. We employed a very gradual perturbation in the VMA task and never allowed the perturbation to exceed 12°. For the ASRT task, various lines of evidence suggest that the presence of random elements for 50% of the trials completely disrupts awareness of the repeating elements (for example, Howard and Howard 1997; Nemeth et al. 2010). The modest learning scores are also consistent with the hypothesis that learning was implicit.

Whereas we found consistent group-level learning on the SRT task, the standard probes of learning were not reliable across runs: On both runs there was a marked increase in RT on the final Random blocks relative to surrounding Sequence blocks, but the magnitude of this increase was inconsistent between the two runs at the individual level. We are of the opinion that at least two factors account for the lack of reliability on the SRT task. First, learning on the form of the SRT task used here is based on a measure that requires averaging data across all of the trials within a block and then comparing means across blocks. Variables that might introduce block-by-block variation or low-frequency changes in performance can have a large impact on such measures. For example, the motivation level or idiosyncratic speed-accuracy criterion might fluctuate from one block to the next. The VMA and ASRT tasks are not impacted by such factors given that their learning measures are continuously based on trial-to-trial performance.

Second, the lack of reliable SRT learning could be related to awareness. There is an extensive literature concerning the role of awareness in the SRT task, as well as the methodological challenges for assessing or eliminating/minimizing awareness (for example, by adding a concurrently secondary task: Gheysen et al. 2009; Grafton et al. 1998; Hazeltine et al. 1997; Sanchez et al. 2010; or by using long sequences: Pascual-Leone et al. 1993; Sanchez and Reber 2012; Spencer and Ivry 2009). Empirically, a number of the participants exhibited a large increase in RT on the Random blocks in the late learning probe (for example, 30% had an increase >50 ms), a difference that, in conjunction with fast RTs on the Sequence blocks, is suggestive of awareness. Moreover, while we recognize the limits in drawing comparisons between the tasks on the questionnaire data, it is noteworthy that the participants' confidence in the presence of a repeating pattern was higher in the SRT task compared with the ASRT task and higher than participants' confidence in the presence of a perturbation in the VMA task. Awareness would contaminate our measure of implicit learning (Reber and Squire 1998; Willingham et al. 1989) and impact assessments of reliability. Consistent with this hypothesis, we observed a modest correlation of the learning scores at the midtask probe, a time point at which we expect awareness to be lower.

Note that the contamination from awareness could either increase or decrease reliability. If a subset of the participants were aware (and thus had larger learning scores) on both run 1 and run 2, the correlation would be inflated. On the other hand, awareness could decrease reliability if different subgroups of participants became aware in run 1 and run 2. The reported results suggest that the latter is more likely to have occurred here. We do not claim that explicit learning is unreliable. Had we used a completely explicit sequence-learning task, reliability might have been high. The problem, though, is when a measure of learning is a composite of multiple processes and that the weight given to those processes varies across measurements.

In summary, the present results indicate that implicit measures of learning were reliable at the individual level in response to a pseudorandom visuomotor rotation and in becoming sensitized to the predictability of sequential elements. The lack of reliability in the SRT task presents a challenge for studies that have used this task to explore individual differences (Noohi et al. 2014; Norman et al. 2007; Unsworth and Engle 2005), and the presence of awareness also compromises the utility of this task for studying implicit learning (Grafton et al. 1998; Hazeltine et al. 1997; Keele et al. 2003). For example, despite concurrently performing a secondary task, participants could have developed different levels of awareness to the repeating sequence (which would be difficult to track by directly asking participants at the end of the task).

Is There a Common “Implicit Motor Learning” Component?

Studies of individual differences in motor control and learning have a long history. One prominent claim has been that differences are task specific, a hypothesis supported by studies using large test batteries (for example, Parker and Fleishman 1960) or studies of expertise (Bachman 1961; Chase and Simon 1973; Mann et al. 2007). An alternative perspective, advocated by Franklin Henry's “specificity hypothesis” (see Henry 1968), is that some component of individual differences arises from a set of core operations that are shared across tasks. Drawing on this idea, Keele and colleagues (Ivry and Keele 1989; Keele et al. 1985, 1987) provided evidence that individual differences in motor control might reflect variation in how consistent people are in controlling certain parameters of movement such as timing, force, or rate. For example, people who were consistent in timing repetitive movements also exhibited consistent timing when producing isometric force pulses or in judging the duration of events. These ideas, in combination with evidence from neuropsychological studies (for example, Ivry and Keele 1989), led to models in which different neural systems were associated with particular component operations.

Extending the logic of that line of work, we asked here if “implicit motor learning” might constitute a core component of skill acquisition (see Conway et al. 2010). To this end, we looked at between-task correlations. Given the reliability in the VMA and ASRT tasks, we combined the results from the two runs in making these comparisons. We also included the SRT task, although these data should be viewed cautiously given the lack of reliability in the measure of learning. The results revealed no correlation between the learning measures on the different tasks, arguing against the notion of a common implicit learning process shared across motor learning tasks, at least for visuomotor adaptation and sequence learning.

The lack of correlation might be surprising given that learning in both tasks has been associated with cerebellar function. Patients with cerebellar pathology, from either focal insult or degeneration, have pronounced impairments in learning when tested on sensorimotor adaptation (Donchin et al. 2012; Martin et al. 1996; Rabe et al. 2009; Schlerf et al. 2013; Shin and Ivry 2003; Smith and Shadmehr 2005; Taylor et al. 2010; Tseng et al. 2007; Werner et al. 2010) and sequence learning tasks (Gómez-Beldarrain et al. 1998; Molinari et al. 1997; Pascual-Leone et al. 1993; Shin and Ivry 2003; but see Spencer and Ivry 2009). Neuroimaging studies in humans (Bernard and Seidler 2013; Danckert et al. 2008; Della-Maggiore and McIntosh 2005) also point to an essential role for the cerebellum, in generating the error signals to guide learning (Diedrichsen et al. 2005; Schlerf et al. 2013) and/or in generating the predictions of expected sensory events (Ramnani et al. 2000). Given the implicit nature of these tasks and the association of the cerebellum with both sensorimotor adaptation and sequence learning, one might have expected to observe a correlation in learning between the learning tasks.

However, several explanations might account for why the measures of learning were not correlated. First, based on computational considerations, adaptation and sequence learning require very different learning mechanisms and operations. Adaptation is error driven, entailing the modification of an internal model based on the difference between predicted and observed sensory feedback (Taylor and Ivry 2012). Error-based learning is likely to contribute minimally to sequence learning; here, learning involves the formation of associations between successive stimulus-response pairs, supporting the establishment of predictions from one S-R element to the next. This process, at least when arising implicitly, might be more of a Hebbian-like process (Lu et al. 1998; Nixon and Passingham 2000; Spencer and Ivry 2009). As such, adaptation involves changes in terms of refining execution, whereas sequence learning is more about priming for action selection.

Second, the linkage of both tasks through their association with the cerebellum is, at best, superficial. The cerebellum is a large structure, and although it has been associated with both adaptation and sequence learning, one need not assume that these two task domains engage similar regions and/or cerebellar operations. Indeed, the evidence suggests that adaptation and sequence learning tasks may engage distinct cerebellar regions and cortico-cerebellar loops (Buckner et al. 2011; Kelly and Strick 2003; Krienen and Buckner 2009; Strick et al. 2009). Neuropsychological and neuroimaging evidence point to the involvement of motor regions of the cerebellum in adaptation tasks, including cerebellar regions with relatively clear somatotopy. These regions exhibit strong functional connectivity with motor cortex (Bernard and Seidler 2013; Burciu et al. 2014), as was found even during sensorimotor adaptation tasks (Burciu et al. 2014; Rabe et al. 2009). Sequence learning, on the other hand, has been linked with neocerebellar regions that are functionally connected with premotor and prefrontal cortex (Bernard and Seidler 2013; Nixon and Passingham 2000; Ramnani et al. 2000; Seidler et al. 2002; although it remains unclear whether this holds for both explicit and implicit conditions, see Hazeltine et al. 1997). Moreover, it remains unclear whether the cerebellar contribution to sequence learning is directly related to learning per se or is indirect, related to the formation and/or maintenance of the stimulus-response associations (Nixon and Passingham 2000; Spencer and Ivry 2009).

In future work it will be interesting to exploit individual differences in comparing cerebellar contributions to adaptation and sequence learning. For example, we might expect that functional connectivity between cerebellar regions and primary motor cortex will be predictive of learning rates in sensorimotor adaptation (Bernard et al. 2012; although see Rabe et al. 2009), whereas functional connectivity between cerebellar regions and premotor/prefrontal cortex will be predictive of sequence learning.

We recognize that our assays of learning for visuomotor adaptation and sequence learning involve very different measures (spatial accuracy vs. RT). There are cases in which performance measured in different units and on different scales do correlate (for example, mathematical skill, verbal fluency, and spatial visualization, among others, composing a construct of general intelligence, g) (Spearman 1904). Thus the use of different measures does not inherently impose a bias against observing a relationship between the two domains of implicit learning. Nonetheless, it would be interesting to compare tasks of implicit learning in which more similar measures were employed, for example, by using adaptation to a temporal delay.

Within-Task Behavioral Predictors of Implicit Learning

The preceding discussion indicates that there is little commonality between processes involved in implicit adaptation and implicit sequence learning. A different question concerns predictors of each of these forms of learning. To address this question, we focused on baseline measures of performance, using data obtained prior to the onset of the perturbation in the VMA task or during the early stages of the sequence tasks when there was little evidence of learning. We looked at two features of baseline performance: speed and variability.

As a measure of performance speed, we used MT in the VMA task and RT in the sequence-learning task, the temporal measures that were emphasized in the instructions used for each task. There was no relationship between MT and the rate of adaptation. In contrast, RT was correlated with sequence learning. However, the direction of the correlation was in opposite directions for the two sequence learning tasks: For SRT, the correlation was negative, with faster responders exhibiting the largest degree of learning; for ASRT, the correlation was positive, with the slower responders exhibiting the largest degree of learning.

The ASRT task is consistent with other work showing that the benefits of associative retrieval processes become higher as RT increases (Chenery et al. 1994). A similar idea could account for the positive correlation between RT and learning in the ASRT task. However, this hypothesis would also predict a similar pattern in the SRT task, whereas here the correlation was reversed. It might be that the reversal is related to the concern discussed above, namely that some participants may have developed a degree of awareness in the SRT task. Awareness would not only lead to the largest cost on the Random blocks (high magnitude of learning) but should also lead to fast RTs (namely, expecting and even predicating the next stimulus-response pair). We recognize that our interpretations of these RT relationships are speculative and call for further study.

Next, we considered how performance variability was related to individual differences in learning. For variability, we used a measure of spatial variability for the VMA task, using the SD of the heading angle during the baseline block (no perturbation). For the sequence learning tasks, we used the SD of the RTs in the early blocks. Here we observed reliable correlations between measures of variability and learning on both the VMA and ASRT tasks. The rate of adaptation was negatively correlated with variability, such that faster learning was associated with more consistent reaches. In contrast, the magnitude of sequence learning was positively correlated with variability, such that the extent of learning was highest for participants who were most variable in RT. A similar pattern was also observed in the SRT task. We recognize that there are differences in our measures of variability for the two task domains; in particular, one is a spatial measure and the other a temporal measure. Nonetheless, we chose these variability measures since they are closest to the dependent variable related to learning on each task.

The negative relationship between variability and learning rate on the VMA task is consistent with models in which motor output or sensory noise modulates the weight given to an error signal (Baddeley et al. 2003; van Beers 2009; Burge et al. 2008; Körding and Wolpert 2004; Schlerf et al. 2013). In conditions of high noise, these models would predict that the motor system would reduce its learning rate because confidence (or certainty) in the sensory signal is low; the converse is true in conditions of low noise. We would expect this relationship to be especially pronounced in the present study given our use of a small perturbation, one in which learning was entirely implicit. Indeed, the size of the perturbation change from trial to trial never exceeded 2°, falling within 1 SD of the expected distribution of end points for reaches in the absence of any perturbation.

An error-based account does not seem appropriate when considering sequence learning, because the fundamental learning mechanism here entails an associative process, one that learns to predict successive elements in a chain of events. As such, the absence of a negative correlation between our performance measure of variability, the SD of RT, and sequence learning is not surprising. However, the reversal to a positive correlation is intriguing. Wu and colleagues (Wu et al. 2014) observed a similar relationship, albeit in measures of spatial variability, in a task in which participants had to learn a complex trajectory or force field. They hypothesized that higher variability enabled increased exploration of the workspace and thus allowed participants to discover the appropriate solution. An extension of the exploration idea to account for the positive correlation in the sequence learning tasks in the present study is not straightforward: It is not obvious how higher temporal variability promotes, or reflects, exploration. Perhaps temporal variability is indicative of a variable retrieval process and this variability helps with the formation of sequential associations. Related to this idea, temporal variability was correlated with mean RT in the ASRT task (even after normalizing the temporal variability by mean RT) and, as described above, longer (and more variable RTs) might have allowed greater spreading activation from one element to the next. Our sequence learning data suggest that motor variability should not be considered merely the inevitable consequence of signal-dependent neural noise in the motor system that ought to be overcome but can instead be viewed as a key ingredient of learning, centrally driven and actively regulated, that the motor system leverages during learning.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grants NS-092079 and NS-074917 to R. B. Ivry and NS-084948 to J. A. Taylor.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

A.S.-I. and M.R. performed experiments; A.S.-I. and M.R. analyzed data; A.S.-I., M.R., J.A.T., and R.B.I. interpreted results of experiments; A.S.-I. prepared figures; A.S.-I. drafted manuscript; A.S.-I., J.A.T., and R.B.I. edited and revised manuscript; A.S.-I., M.R., J.A.T., and R.B.I. approved final version of manuscript.