Hybrid positron emission tomography segmentation of heterogeneous lung tumors using 3D Slicer: improved GrowCut algorithm with threshold initialization

Abstract.

This paper presents an improved GrowCut (IGC), a positron emission tomography-based segmentation algorithm, and tests its clinical applicability. Contrary to the traditional method that requires the user to provide the initial seeds, the IGC algorithm starts with a threshold-based estimate of the tumor and a three-dimensional morphologically grown shell around the tumor as the foreground and background seeds, respectively. The repeatability of IGC from the same observer at multiple time points was compared with the traditional GrowCut algorithm. The algorithm was tested in 11 nonsmall cell lung cancer lesions and validated against the clinician-defined manual contour and compared against the clinically used 25% of the maximum standardized uptake value [SUV-(max)], 40% ${\mathrm{SUV}}_{\max }$, and adaptive threshold methods. The time to edit IGC-defined functional volume to arrive at the gross tumor volume (GTV) was compared with that of manual contouring. The repeatability of the IGC algorithm was very high compared with the traditional GrowCut ($p=0.003$) and demonstrated higher agreement with the manual contour with respect to threshold-based methods. Compared with manual contouring, editing the IGC achieved the GTV in significantly less time ($p=0.11$). The IGC algorithm offers a highly repeatable functional volume and serves as an effective initial guess that can well minimize the time spent on labor-intensive manual contouring.

1. Introduction

In recent years, ¹⁸fluoro-deoxyglucose (${}^{18}\mathrm{F}$-FDG) positron emission tomography (PET) has emerged as an essential imaging modality in staging, tumor volume delineation, prognosis assessment, and evaluation of treatment response of nonsmall cell lung cancer (NSCLC). The superior sensitivity and specificity of ${}^{18}\mathrm{F}$-FDG PET particularly help to differentiate atelectasis in lungs and identify the presence of malignant lymph nodes, which are often difficult to visualize with computed tomography (CT). Consequently, the amount of normal tissue included in the target volume decreases and geometric mass is reduced.¹ However, uncertainty in target definition still contributes to the majority of the errors in radiation oncology. The inclusion of biological imaging may have the highest impact in the reduction of interobserver variability in target definitions.² Since the early 2000s, there has been a surge of PET-based automatic and semiautomatic contouring methods that have been proposed to help delineate the metabolic tumor activity. The methods range from simple to complex methods.^1,3,4 The segmentation methods include but are not limited to constant and adaptive threshold methods,^5–9 region growing methods,^10–12 gradient-based methods,^13–15 fuzzy models,^16–18 and Gaussian mixture modeling.^10,19 All these methods offer different compromises in terms of versatility and performance and compare well against manual segmentations by clinicians or the pathological measurements with varying rates of success.³ Yet there is not enough consensus among the clinical community on algorithms that work well to be incorporated into commercially available imaging software and treatment planning systems.^3,4 Most of these state-of-the-art algorithms are proprietary and are currently unavailable for clinical use. There is a lack of adequate documentation for these methods and they often do not have user/developer support, which makes it difficult to replicate the results in a similar clinical setting. Other limitations include the methods being optimized for specific scanner properties, the results of which are often difficult to reproduce.²⁰ The segmentation task is further complicated when tumors display cellular heterogeneity.

In this study, we have tried to delineate heterogeneous lung tumors using the GrowCut algorithm made available in the freely accessible 3D Slicer software. However, the algorithm is dependent on the accuracy of user-defined initial labels. To overcome this limitation, we provide a threshold-based initial estimate of the tumor and a three-dimensional (3-D) background shell as the initial seeds. The objective of this study was to improve the existing GrowCut algorithm. We tested the repeatability of the improved GrowCut (IGC) algorithm from the same observer at multiple time points in comparison with the 3D Slicer GrowCut algorithm. We postulate that the IGC algorithm would be able to provide reliable functional NSCLC tumor volumes compared with the clinically used threshold-based methods. The algorithm was tested in 11 NSCLC heterogeneous lesions and validated against the clinician-defined manual contour and compared against the 25% of maximum standardized uptake value [SUV-(max)], 40% ${\mathrm{SUV}}_{\max }$, and adaptive threshold methods. We also tested whether the proposed IGC method could offer itself as an effective initial guess for the gross disease segmentation as an alternative to the manual segmentation currently employed to delineate the NSCLC. The time taken for manual gross tumor volume (GTV) contouring versus the time to edit the IGC contours was assessed as a measure of efficiency in this approach.

2. Materials and Methods

2.1. Data

The patients retrospectively included for this study were treated for advanced NSCLC and had PET/CT scans taken between July and December 2014. The patients were instructed to fast 10 to 14 h before the FDG injection was administered, after which the patients were encouraged to rest (no music, reading, or talking) in a cool (23°C to 24°C), dimly lit room. The total injected activity of FDG was expressed in MBq. The injected activity was $5\mathrm{MBq}/\mathrm{kg}$ of FDG for all patients and was dependent on the weight of the patient and limited at 370 MBq with the average adult dose range between 7 and 8 mCi. Free-breathing PET and CT images were acquired at 60 (50 to 70) min. The scans were done at the Christian Medical College, Vellore, India. The Institutional Review Board and the ethical committee of the hospital approved this study.

The data included 11 primary tumors of 9 patients (5 men and 4 women). The patient demographics are shown in Table 1. The PET/CT scans were performed on a Biograph 6 TruePoint HD (Siemens Medical Solutions Inc., Knoxville, Tennessee) PET scanner. The CT images were first acquired at 124 mAs, 130 kVp, and 400 mm field-of-view (FOV). The CT images were reconstructed with a transaxial plane resolution of $0.78\mathrm{mm}\times 0.78\mathrm{mm}$ and slice thickness of 2 mm per slice; the image size was $512\times 512\text{pixels}$. The PET images were acquired with a 700-mm FOV and reconstructed using attenuation weighted ordered subset expectation maximization reconstruction (3 iterations, 21 subsets, and 4-mm FWHM Gaussian filter). During the reconstruction, corrections for point spread function (TrueX), attenuation, and scatter were performed. The sinogram data were decay, dead time, and random corrected. The CT images were used for the attenuation correction. The resultant PET image size was $168\times 168\text{pixels}$ and the in-plane resolution is $4.07\mathrm{mm}\times 4.07\mathrm{mm}$. The slice thickness in seven patients was 2 mm and in two patients it was 2.1 mm.

Table 1.

Summary of patient demographics included in this study.

Patient no.	Sex	Age (years)	Activity (MBq)	Histology	Stage	Location	Time postinjection (min)
1	M	50	312.1	Moderately differentiated squamous cell carcinoma	T4N3	Right middle and lower lobe	60
2*	M	30	234.8	Poorly differentiated nonsmall cell carcinoma not otherwise specified	T3N2	Left upper lobe	60
3	F	34	315.9	Myoepithelial neoplasm with invasive carcinoma of squamous differentiation	T4N0	Trachea and mediastinum and bilateral main bronchus	70
5	F	61	267.4	Nonsmall cell adenocarcinoma	T2N2	Left upper lobe	55
6	F	62	261.2	Mucin secreting adenocarcinoma	T3N2	Right lower lobe	55
7	M	45	281.8	Adenocarcinoma	T4N2	Right lower lobe	60
8	M	65	268.2	Moderately differentiated squamous cell carcinoma	T4N2	Right upper lobe	70
9**	M	61	270.0	Moderately differentiated squamous cell carcinoma	T3N3	Right upper lobe	65

Note: Patients 2* and 9** had two lesions and three lesions, respectively, with high PET uptake.

The treating clinician manually segmented the gross disease once for each patient based on combined CT and PET information. The display protocol with a fixed window/level setting for the CT scan (lung window) and upper window set to ${\mathrm{SUV}}_{\max }$ in the lesion of interest, with the lower window set at 0 for PET images for delineation. Delineations were performed on the Eclipse™ treatment planning system (Varian Medical Systems Inc.). The clinician-defined volumes were used as the reference volume and henceforth are referred to as MANUAL contours.

2.2. GrowCut Algorithm

The GrowCut algorithm developed by Vezhnevets and Konouchine²¹ follows an iterative labeling procedure, where the user-defined “seed” pixels try to occupy the neighbors. The automaton defines a set of local transition rules, which determines the value of each cell given the value of the cells in its neighborhood. The commonly described neighborhood definitions are the 4-connected Von Neumann or the 8-connected Moore neighborhoods.

The GrowCut algorithm uses the image features to drive the transition function. The current state of each cell is given by the triplet $(l_p,{\theta }_p,I_p)$, where $l_p$ is the class label of the cell, ${\theta }_p$ is the strength of the cell, and $I_p$ is the cell feature vector, defined in our case as the pixel intensity. Assume there are two competing cells, one an attacker cell and the other the defender cell, each having strengths ${\theta }_p$ and ${\theta }_q$ and pixel intensities $I_p$ and $I_q$, respectively. The attack force is defined as the strength of the attacker ${\theta }_p$ and the distance between the pixel intensities for the attacker and defender cells. The local transition function between the cells is defined by the monotonically decreasing function $g$, bounded to [0,1] and given by the following equation:

$$g(x)=1-\left[\frac{x}{(\max {\Vert \stackrel{\rightharpoonup }{I}\Vert }_2)}\right].$$ (1)

Therefore, if the strength of the attacker is greater than that of the defender cell, the attacker overtakes the defender, leading to a change in its label and strength which are replaced by the function $g\Vert \overrightarrow{I_p}-\overrightarrow{I_q}\Vert {\theta }_q^t$. The algorithm is iterated till the automaton converges to a stable configuration and there are no more local label updates. The algorithm always converges since the cell strength is increasing and bound.

The iteration steps can be described in Algorithm 1.

Algorithm 1.

Pseudocode for GrowCut algorithm.

//for every cell p

for all p in the image

//copy the previous state

label_new = label;

strength_new = strength;

// all neighbors q of p attack

for all q neighbors

if [attack_force*strength (q)>strength_new (p)]

label_new (p) = label (q)

strength_new (p) = strength_new (q)

end if

end for

end for

To initiate the segmentation, the user has to specify the seeds corresponding to “foreground” and “background” using different colored brush strokes, which set the initial labels and strengths of seed pixels. The strength of the seed pixels is set to one and the neighboring pixel strength to zero. The seed pixels grow over the image until some contact is made with the edges of two different labels. From that point forward, the pixels try to occupy their neighbors following the transition rule.

The algorithm is simple to implement and allows the user to interactively guide the segmentation while the algorithm is still iterating. However, experiments have shown that the method is very sensitive to small changes in the user-defined seeds and often required many user seeds distributed over the entire image for an adequate segmentation.^22,23

2.3. Preprocessing of PET Images

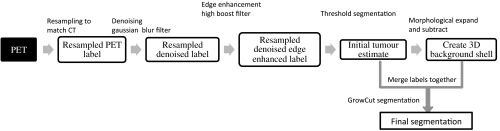
In the clinical setting, a trial-and-error method of initialization adds to the existing variability in target delineation. Hence, improvements were made to the initialization of the GrowCut algorithm in addition to some image preprocessing. The schematic diagram of the workflow is shown in Fig. 1 and the following sections describe the steps in detail. Although initially the workflow may seem complex, the steps can be easily learned.

Fig. 1.

Schematic workflow of the IGC algorithm implemented with 3D Slicer.

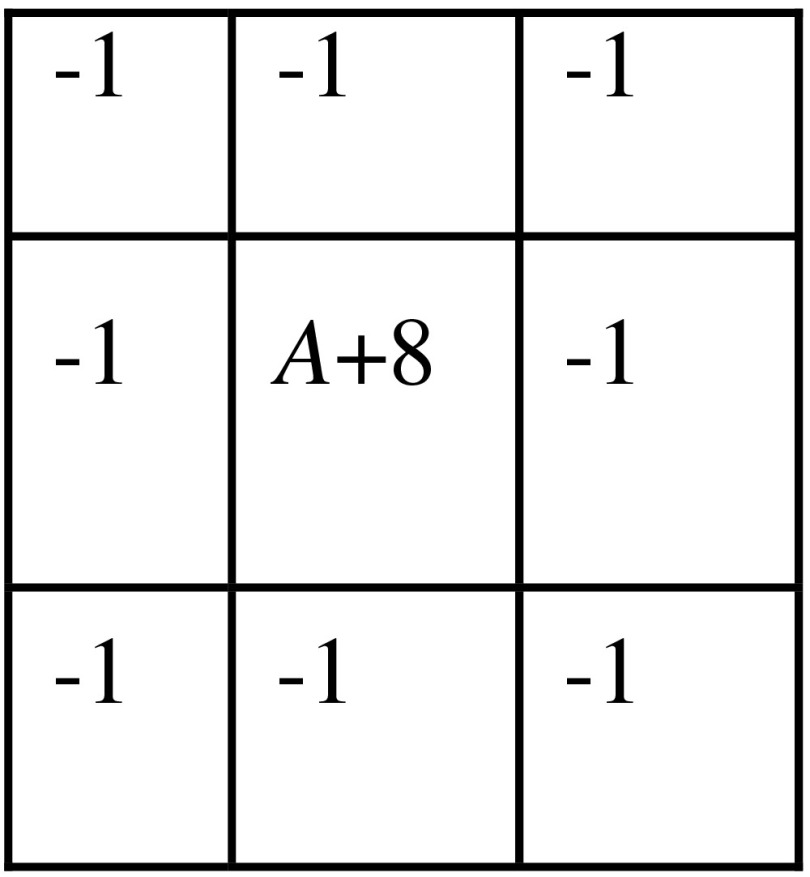
First, to improve the visual representation of the contours in the dataset, the PET images were upsampled to the finer CT image to match its transaxial dimensions using nearest-neighbor interpolation. The resampled PET images were convolved with a Gaussian blur filter ($\sigma =1.0$) to attenuate the sharp edges and noise. The denoised images were edge enhanced using a high boost filter with the convolution kernel given in Fig. 2.

Fig. 2.

High boost filter kernel. The amplification factor $A=2$.

If $A=1$, the kernel would basically represent a high-pass filter. For $A>1$, the darkening effect of the high-pass filter is nullified and the image appears more like an edge-enhanced original image. Therefore, the addition of the weighted version of the original image back to the high-pass filter ensured that the high frequencies were emphasized while retaining almost all the low-frequency components of the image. All the image preprocessing was done in the spatial image domain and was implemented in MATLAB R2012b (Mathworks Inc., USA). The MATLAB bridge module was used to integrate it in the 3D Slicer.

2.4. Improved GrowCut Segmentation Algorithm

As mentioned in Sec. 2.2, the GrowCut algorithm is dependent on the accuracy of user-marked input labels.^22,23 To overcome this limitation, the initialization has been automated in the IGC algorithm and the process is described in detail below. An initial estimate of the tumor is obtained by setting a threshold in the Segment Editor module of the 3D Slicer. The threshold effect uses vtkImageThreshold, which is a simple fixed threshold value of 25% of ${\mathrm{SUV}}_{\max }$. Next, a concentric 3-D shell background was defined around the initial tumor contour beginning at a distance of twice the FWHM of the PET Scanner and extending up to four times the FWHM. The FWHM for the PET scanner with TrueX reconstruction was 2 mm.²⁴ The contour was grown outward using a dilation morphological operator. The contour could be grown only in multiples of the voxel dimensions of the slices. The first dilation was made for 4 mm. Since the image size was $0.78\mathrm{mm}\times 0.78\mathrm{mm}$, the second dilation extent should ideally be 5.13 times (i.e., $4\mathrm{mm}/0.78\mathrm{mm}$) the first dilation. However, since the dilation is not performed in fractions, the actual extent of the dilated contour is either five or six times, which is 4.68 or 3.9 mm, respectively. Morphological subtraction was performed between the first and second dilations to produce a 3-D shell of 2-mm thickness in the $z$ plane and 0.78-mm thickness in the $x-y$ plane. The minimum space between the 3-D shell and the initial tumor estimate contour was 4 mm along the $z$ plane and 3.9 mm along the $x-y$ plane. A similar methodology for shell background has been discussed by Hofheinz et al.⁷ The space between the initial tumor contour and the inner edge of the shell warranted that the background voxels did not include the spill over voxels. The 3-D background shell was achieved using the morphology operators in SlicerRT module in the 3D Slicer.²⁵ The initial labels helped to provide enough information about the different pixel intensities that make up the tumor and the surrounding background, which aided the algorithm in the presence of heterogeneity. The tumor segmentation was performed using the GrowCut algorithm with preinitialization in the 3D Slicer software platform. The segmentation was executed on Apple MacBook Pro (2012) Intel Core i7 2.6 GHz PC with 16 GB RAM.

2.5. Repeatability of Improved GrowCut and 3D Slicer GrowCut Segmentation Methods

The repeatability of the IGC algorithm from the same observer at multiple time points was compared with the GrowCut algorithm made available in the 3D Slicer. The user provided the initial seeds for the 3D Slicer GrowCut algorithm as random brush strokes in two different colors. For the IGC method, the preinitialized initial tumor estimate and the 3-D background shell were provided as the initial seeds. The segmentations with both the methods were performed thrice with an average interval of 3 days between each run. An uncertainty region, as described in Ref. 26, was calculated as the difference between the union and intersection volumes of the three runs (represented as A, B, and C) for the GrowCut and IGC segmentation methods:

$$\text{Uncertainty region}=A\cup B\cup C-A\cap B\cap C.$$ (2)

If the contours had perfect agreement, the union and intersection volumes would be equal and there would be no regions of uncertainty. Lower uncertainty region volume meant there was less variability in defining the contours. The Wilcoxon signed rank test was used to compare the uncertainty differences between the 3D Slicer GrowCut and the proposed IGC segmentation method.

2.6. Validation of Improved GrowCut Segmentation Method and Comparison with Threshold-Based Segmentation Methods

To assess the merit of the proposed IGC method, the contours were compared with MANUAL contours using the following metrics: Dice similarity coefficient (DSC), the relative volume error (RVE), and the 95% Hausdorff distance.

DSC measures the spatial overlap of the pixels in the segmented contours ($S$) with the pixels in the MANUAL contour ($T$). A perfect agreement between contours results in value 1:

$$\mathrm{DSC}=2\times \frac{|S\cap T|}{|S|+|T|}.$$ (3)

The volume of the MANUAL contours is referred to as the true volume ($V_T$). The RVE is calculated as the fraction of difference between the segmented volume ($V_S$) and the true volume ($V_T$), as shown in the following equation:

$$\mathrm{RVE}=\frac{|V_S-V_T|}{V_T}.$$ (4)

The 95% Hausdorff distance measures the maximum distance between the reference points in the manual contour with the corresponding point in the automatically segmented contour, while excluding the longest 5% of distances.²⁷

The IGC segmentation method was also compared with threshold methods routinely reported for clinical use. For all the 11 lesions, 25% ${\mathrm{SUV}}_{\max }$ threshold ($T_{25}$), adaptive threshold ($T_{\text{Adaptive}}$), and 40% ${\mathrm{SUV}}_{\max }$ threshold ($T_{40}$) methods-based contours were generated. The adaptive threshold method used was of the form:

$$T=a\times \frac{1}{v}+b\times \frac{B}{T}+c,$$ (5)

where $a$ and $b$ are the correlation coefficients and $c$ is the constant, obtained from calibrated threshold-volume curves at a varying target-to-background ($S/B$) ratio acquired by phantom measurements optimized for the PET scanner used in this study. A detailed description of similar phantom measurements has been described in our earlier work.²⁸ The initial estimate volume for the adaptive threshold was obtained from $T_{25}$ threshold. The tracer uptake ratio in the source and background was obtained from the $T_{25}$ defined contour and the 3-D shell background, respectively.

The threshold-segmented contours were also compared against the MANUAL contours. The evaluation metrics for the IGC and threshold-based methods were compared using the Kruskal–Wallis test with the significance set at $p<0.05$.

2.7. Contour Edits for Gross Tumor Definition

The IGC contours were provided as a starting contour that could be edited by the clinician for defining the final GTV, which included composite information from CT and PET. The time taken for MANUAL GTV contouring versus the time to edit the IGC contours to create the GTV was assessed as a measure of clinical efficiency in this approach. The difference in contouring time and edit time was compared using Wilcoxon test and was considered significantly different when the $p$-value was lower than 0.05.

3. Results

3.1. Comparison of Improved GrowCut with 3D Slicer GrowCut Segmentation Method

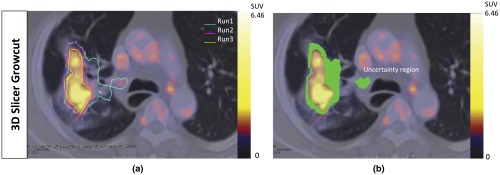
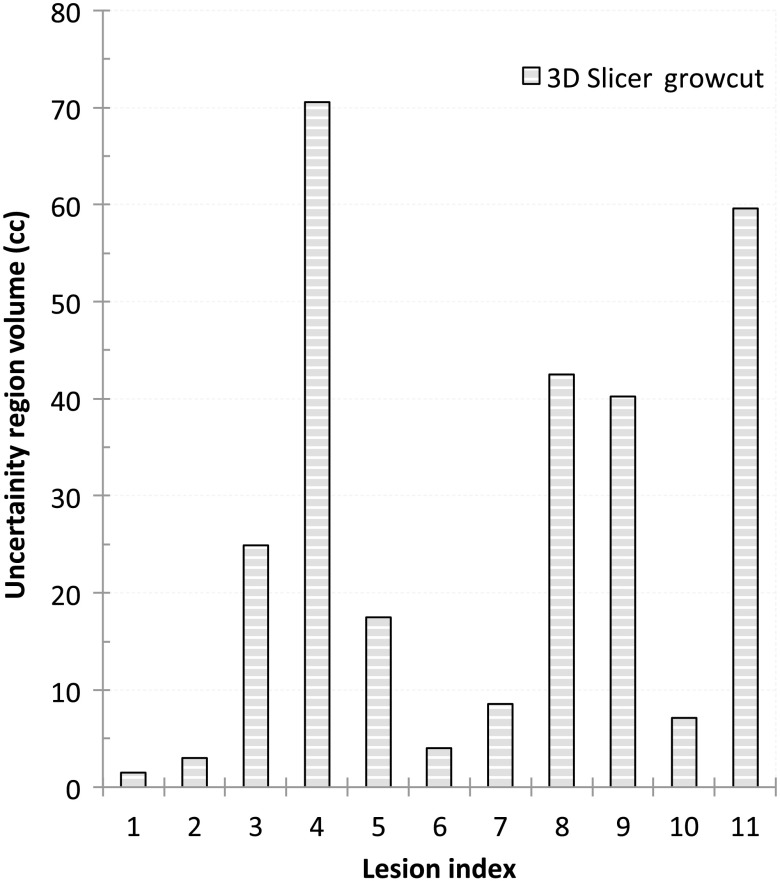
There were no observed variations between the contours generated with the IGC with multiple runs. Hence, there was no uncertainty volume for the IGC method. Large volume variations (median 17.34 cc, range 0 to 31.84 cc) were seen in the contours produced by the 3D Slicer GrowCut algorithm. There was a significant difference between the 3D Slicer GrowCut and IGC produced contours ($p=0.003$). Figure 3 shows the uncertainty volume with the 3D Slicer GrowCut method. Figure 4 shows the large volume uncertainty in contours when the lesions were separately delineated three times using the 3D Slicer GrowCut method.

Fig. 3.

A representative example of the uncertainty volume observed with the 3D Slicer GrowCut method. (a) The lesion was delineated in three separate runs. There was variability with each run and the composite error in the variability calculated as the uncertainty volume is highlighted in green in (b).

Fig. 4.

The uncertainty volumes as recorded when lesions were delineated using 3D Slicer GrowCut.

3.2. Comparison of Improved GrowCut with Threshold-Based Segmentation Methods

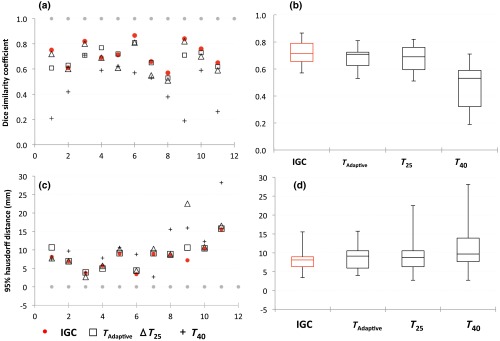
Figures 5(a) and 5(b) show the representative examples of differences in the IGC, $T_{\text{Adaptive}}$, $T_{25}$, and $T_{40}$ contours in comparison with the MANUAL contours. The median and interquartile range for the DSC and Hausdorff distances are reported in Table 2. The DSC values were found to be similar for IGC (0.71) and $T_{\text{Adaptive}}$ (0.71) suggesting a good overlap with the MANUAL contour. There was variability in the DSC values for $T_{25}$ (0.61) and $T_{40}$ (0.53) suggesting lower spatial overlap with the MANUAL contour. The IGC contours had the least 95% Hausdorff distances (8.1 mm) compared with the other threshold methods suggesting a better spatial overlap with the MANUAL contour. The median and interquartile range for the DSC and Hausdorff distances are reported in Table 2.

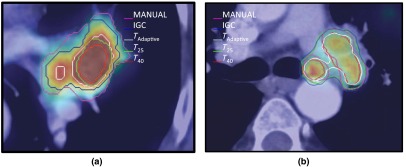
Fig. 5.

Representative examples showing differences in the IGC, $T_{\text{Adaptive}}$, $T_{25}$, and $T_{40}$ contours in comparison with the MANUAL contours. (a) Lesion (#10) where the MANUAL contour results in larger volumes than the automatic methods. (b) Lesion (#9) where the automatic methods result in larger volume compared with the MANUAL contour.

Table 2.

Descriptive statistics for evaluation metric.

Metric		IGC	$T_{\text{Adaptive}}$	$T_{25}$	$T_{40}$
DSC	Median	0.71	0.71	0.69	0.53
	Interquartile range (IQR)	0.7 to 0.8	0.62 to 0.73	0.6 to 0.8	0.3 to 0.6
95% Hausdorff distance (mm)	Median	8.1	9.1	8.8	9.7
	IQR	6.3 to 8.9	5.9 to 10.5	6.3 to 10.5	7.6 to 13.9

The evaluation metrics DSCs and Hausdorff distances measuring the spatial overlap of the automated contours with the manual contours were plotted for each lesion and are shown in the scatter plots in Figs. 6(a) and 6(c). The overall variability in the evaluation metrics for the cohort of lesions is represented in the box whisker plots in Figs. 6(b) and 6(d).

Fig. 6.

Evaluation metrics comparing automated segmentation contours (IGC, $T_{\text{Adaptive}}$ $T_{25}$, and $T_{40}$) with MANUAL contour. The scatter (a, c) and box whisker (b, d) plots showing the variability in the DSCs and Hausdorff distances for IGC, $T_{\text{Adaptive}}$, $T_{25}$, and $T_{40}$ segmentations against MANUAL defined contours. In (a) and (c), the gray dots indicate the ideal values at $\mathrm{DSC}=1.0\mathrm{mm}$ and $\text{Hausdorff distance}=0.0\mathrm{mm}$, respectively.

In Fig. 6, the scatter represents the variation for each lesion for the different autosegmentation methods considered. The box represents the range between the lower 25% quartile and the upper 75% quartile with the median represented by the line across the box. The most extreme values in the data within 1.5 times the interquartile range correspond to the whiskers extending from each end of the boxes. The filled gray dots in the scatter plots represent the ideal value for each metric.

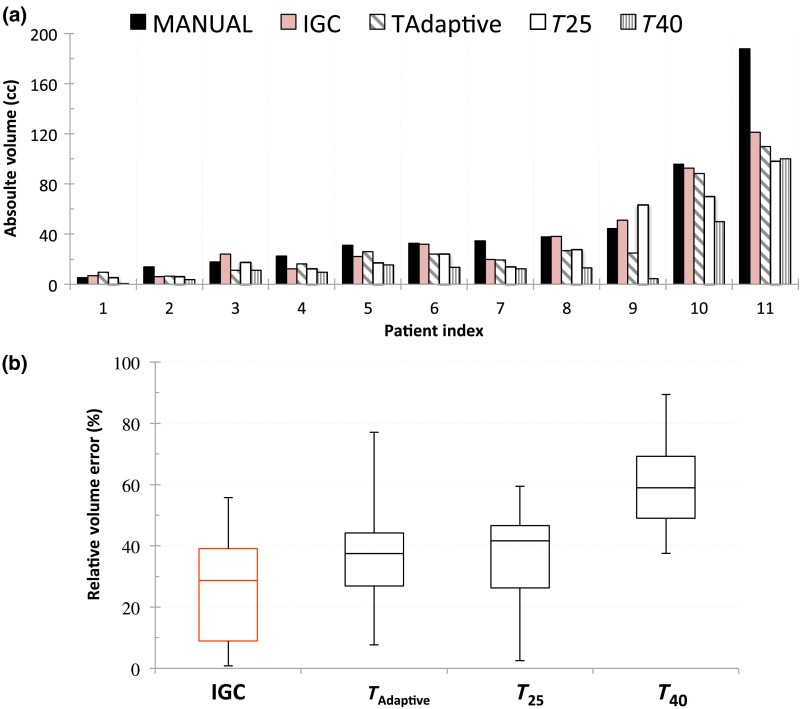
In Fig. 7(a), the absolute volumes of the autosegmented contours were compared with the clinician-defined manual contour volumes. Except for lesion 11, all the other volumes correlated well. The relative error in the tumor volumes for IGC, $T_{\text{Adaptive}}$, $T_{25}$, and $T_{40}$ segmentations against manual-defined contours is shown in the box whisker plots in Fig. 7(b).

Fig. 7.

Comparison of (a) absolute volume variability and (b) RVE for the IGC, $T_{\text{Adaptive}}$, $T_{25}$, and $T_{40}$ segmentations against MANUAL defined volume.

3.3. Contour Edits for Gross Tumor Definition

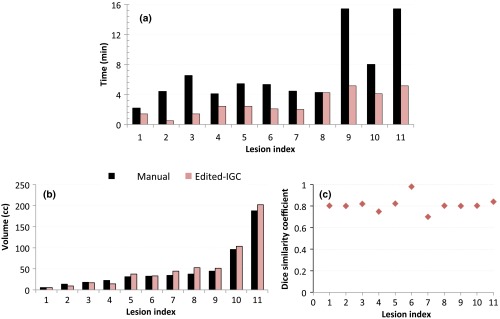
The manual contouring time and time taken to edit the IGC contour are represented in Fig. 8(a). There was significant reduction in the contouring time ($p=0.01$); the IGC method reduced the median manual contouring time from 4.46 to 2.45 min (45%). The volume of each lesion with the manual and the edited IGC contours was plotted in Fig. 8(b) and was not significantly different ($p=0.110$). The Dice similarity between the manual and the edited IGC contours was plotted in Fig. 8(c). The median DSC was 0.8 (range 0.7 to 0.98) suggesting that the shape of the contours was satisfactorily maintained.

Fig. 8.

Comparison of MANUAL contour and edited IGC contour: (a) time taken to edit given the IGC contour as the starting point for delineation; (b) volume of the contours; and (c) DSC.

4. Discussion

PET has been increasingly used as an adjuvant imaging modality with anatomical imaging for tumor delineation to provide complementary information. The limiting factor often is the difficulty associated with reliable PET segmentation methods. Although many automated methods have been proposed, manual delineation is still the clinical norm because it is quite simple to use and most vendors provide the required tools to export PET tumor contours as RT structures to the treatment planning system.⁴ Hybrid imaging of PET/CT with standardized protocols has helped to reduce the observer variability for NSCLC tumor segmentation,⁶ but the process of manual contouring itself poses a large source of variation. On the other hand, the clinical standard manual contouring done slice-by-slice is both labor intensive and time consuming,²⁹ an average of 4.46 min per lesion in this study.

In this study, we present a segmentation framework to delineate NSCLC tumors having heterogeneous FDG uptake. It was developed as a combination algorithm that integrates the benefits of threshold and automatic region growing segmentation methods, while mitigating their respective weaknesses. Intuitively, since FDG PET images show substantial contrast in glucose utilization between normal tissue and neoplastic tissue, threshold-based segmentation is one of the easier methods to adopt and implement.^{20,28,30–32} However, most threshold methods ($T_{25}$ and $T_{40}$) fail to identify a single threshold that includes the entire tumor in the presence of pronounced heterogeneities.⁷ To overcome this methodological shortcoming, we used the interactive GrowCut algorithm implemented in the 3D Slicer. Velazquez et al.²⁶ have shown some robust results for CT-based segmentation of NSCLC and we tried to extend it to segment the functional volume from FDG PET images. However, the algorithm is dependent on the correctness of user-marked labels.^22,23 To address this limitation, we provide a threshold-based initial estimate of the tumor and a 3-D background shell as the initial seeds. This automation has helped to reduce the intraobserver variability caused by the choice of initial seeds provided by the user. Some preprocessing steps like resampling, denoising, and edge enhancement have been included prior to the segmentation to help the GrowCut algorithm perform well. The intraobserver repeatability tests of the proposed IGC compared with the 3D Slicer GrowCut produced no regions of uncertainty on different trials. The IGC algorithm does not require any manual intervention except to select the segmented lesions or any prior optimization experiments to be implemented in the clinic. The IGC outperformed the threshold methods that are currently in clinically use and produced comparable tumor volumes that were more congruent with reference physician-defined contour.

The manual editing of the IGC contour was suggested since the proposed method only addresses the metabolic tumor volume as seen on the PET. However, the clinician would need to include the anatomical extent of the tumor for the gross disease, too. The performance statistics suggest that with minimal editing of the IGC contour, the clinician was able to arrive at statistically comparable ($p=0.11$) contours ($\mathrm{DSC}=0.81$) to the MANUAL contour in less time ($\text{mean time}=2.5\min$). From the clinician’s perspective, starting from an automated PET-based contour reduced the time spent in contouring the lesion in PET/CT compared with contouring without this initial guess to arrive at a similar GTV.

In comparison with the work on PET segmentation of heterogeneous tumor described earlier by various groups,^12,16,33 the present work does not describe elaborate mathematical models. Instead, this work was aimed at being simple and clinically implementable using widely used 3D Slicer software.^25,34 A detailed investigation of ways to improve the definition of the background, which was the limiting factor in our previous work,²⁸ led to the idea of the automated background. From our extended use of the method, we found that the background shell all around the tumor provided ample information about the tissue surrounding the tumor instead of random spheres to estimate the representative uptake values in the background. The space between the initial tumor contour and the inner edge of the shell ensured that the background voxel does not include the tumor voxels that may lie within the spill-out region due to partial volume effects. The background voxels were considered to extend beyond twice the FWHM based on the available resolution of the PET imaging system. The definition also allowed the contour to increase in volume using the GrowCut method from the initial tumor estimation to the actual extent of the tumor. Hofheinz et al.⁷ described a similar method of describing the radius of the background shell such that the reference voxel being determined is not localized at the boundary of the lesion.

Even though manual contour in PET has its limitations of inter- and intraobserver variability owing to various window level settings used by different operators, the clinician-defined tumor volume takes into account all contextual information about the tumor from multiple imaging modalities and pathological findings. It has been argued that the clinicians usually outperform computer algorithms in the high-level task of tumor recognition.³⁵ This was our motivation to use manual segmentation as the gold standard to validate computerized image segmentation techniques in the absence of the surgical specimen of the tumor that serves as the gold standard.³⁶ Due to practical difficulties in finding more experienced clinicians in contouring lung lesions based on PET imaging, we had to use a single clinician-defined volume for validation. Comparison against multiple clinician-defined tumor volumes may be part of our future studies.

Presently, the segmentation pipeline is not fully automated, which makes the whole process seem too long. The total computational time for the preprocessing and segmentation recorded is less than 10 s. The majority of the time is spent in loading the images and choosing the appropriate parameters involved in the workflow. This limitation would be addressed when we automate the steps into a click and use module in the near future.

Another limitation of this study is that the IGC algorithm fails to perform well in lesions surrounded by high-metabolic uptake regions, e.g., brain lesions. Predominantly, this is due to the limitation of the fixed threshold of 25% to provide the initial estimate. This may be addressed by attempting a different initialization approach in future studies. Since this method is currently validated only in lung cancer patients, further testing is required if it is intended for other anatomical tumor sites.

The impact of the PET-based segmentation method to delineate treatment volumes for the purpose of PET-guided radiation therapy treatment planning on patient management and clinical outcome is still not clear. It may be answered only with further clinical trials involving a larger sample of patients. Nevertheless, in comparison with the threshold segmentations that are in current clinical use and with no additional requirements of phantom experiments for implementation, the IGC algorithm could be used as a reliable starting point to delineate GTVs, which helps to reduce the inter- and intraobserver variability. When the IGC contour was provided, the clinician often only needed to incorporate the anatomical regions from the CT that are not part of the metabolic volume which resulted in less contouring time. It also helped in identifying regions that are often difficult to gauge on CT alone (atelectasis).

5. Conclusion

The proposed segmentation method improves the interactive semiautomatic GrowCut algorithm using a threshold-based initialization. This removes any variability in the contours due to the user inputs. This study demonstrates that the IGC segmentation algorithm could be easily implementable in the freely available 3D Slicer platform to achieve reliable and highly repeatable functional volumes with no user inputs required for the initialization of the GrowCut algorithm. The IGC algorithm also shows promise to serve as an effective initial guess that can well minimize the time spent on labor-intensive manual GTV delineation.

Biographies

Hannah Mary T. Thomas received her PhD from VIT University, Vellore, India, in 2016. She is currently a senior research fellow in the Department of Developmental Paediatrics at Christian Medical College Vellore. Her research interests include incorporating multimodality imaging with an aim to improve radiotherapy treatment planning.

Devadhas Devakumar received his PhD from MGR Medical University, Chennai, India. He is an associate professor in medical physics in the Department of Nuclear medicine at Christian Medical College, Vellore. His current interests include preprocessing and segmentation of PET, MRI, SPECT, and CT for radiotherapy treatment planning and surgical planning, preoperative risk evaluation, and epileptic focus localization using EEG source imaging and fMRI.

Balukrishna Sasidharan received his master’s degree in radiation oncology from MGR Medical University, Chennai, India. He is an associate professor of radiation oncology at the Christian Medical College, Vellore. He is a clinician and researcher with interests in treating and caring for patients with solid malignancies, particularly in head and neck, esophagus and lung. His research interests include design and conduct of clinical trials and improvising treatment planning and related tools.

Stephen R. Bowen received his PhD in medical physics from the University of Wisconsin in 2011. He is an assistant professor in the Departments of Radiation Oncology and Radiology at the University of Washington and is certified by the American Board of Radiology in therapeutic medical physics. His current research interests include quantitative molecular imaging of cancer and normal tissue for precision oncology strategies, including outcome prediction and biologically adaptive therapy.

Danie Kingslin Heck is a senior technologist in the Department of Nuclear Medicine at the Christian Medical College, Vellore. His research interests are in optimization of PET scanners, networking, and clinical data management.

E. James Jebaseelan Samuel received his PhD from Manonmaniam Sundaranar University, Tirunelveli, India. He is a senior professor of physics at the VIT University. His current research interests include medical gel dosimetry and radiotherapy treatment planning.

Disclosures

Authors have no relevant financial interests in the manuscript and no other potential conflicts of interest to disclose.