Rational Design of a Low-Cost, High-Performance Metal–Organic Framework for Hydrogen Storage and Carbon Capture

Abstract

We present the in silico design of a MOF-74 analogue, hereon known as M₂(DHFUMA) [M = Mg, Fe, Co, Ni, Zn], with enhanced small-molecule adsorption properties over the original M₂(DOBDC) series. Constructed from 2,3-dihydroxyfumarate (DHFUMA), an aliphatic ligand which is smaller than the aromatic 2,5-dioxidobenzene-1,4-dicarboxylate (DOBDC), the M₂(DHFUMA) framework has a reduced channel diameter, resulting in higher volumetric density of open metal sites and significantly improved volumetric hydrogen (H₂) storage potential. Furthermore, the reduced distance between two adjacent open metal sites in the pore channel leads to a CO₂ binding mode of one molecule per two adjacent metals with markedly stronger binding energetics. Through dispersion-corrected density functional theory (DFT) calculations of guest–framework interactions and classical simulation of the adsorption behavior of binary CO₂:H₂O mixtures, we theoretically predict the M₂(DHFUMA) series as an improved alternative for carbon capture over the M₂(DOBDC) series when adsorbing from wet flue gas streams. The improved CO₂ uptake and humidity tolerance in our simulations is tunable based upon metal selection and adsorption temperature which, combined with the significantly reduced ligand expense, elevates this material’s potential for CO₂ capture and H₂ storage. The dynamical and elastic stabilities of Mg₂(DHFUMA) were verified by hybrid DFT calculations, demonstrating its significant potential for experimental synthesis.

Introduction

Porous materials have been extensively studied as potential adsorbents in energy and environmental applications including hydrogen storage and carbon capture.¹⁻⁷ Among the various porous solids, metal–organic frameworks (MOFs), which are typically constructed from building blocks including inorganic metal (oxide) secondary building units (SBUs) and organic ligands, have attracted significant interest since their composition (i.e., chemical functionality) and structure (e.g., pore topology and sizes and internal surface areas) are highly tunable.⁸ Hence their performance for a given application can be systematically improved by rational materials design.⁹⁻¹⁴ With respect to hydrogen storage and carbon capture (e.g., from flue gas) applications, one of the most important factors which dictates the amount of H₂ and CO₂ that can be adsorbed in a MOF material is the adsorbate–adsorbent interactions, with MOF-74 being considered as one of the best performing MOFs because of the presence of a high density of open metal sites that interact strongly with H₂ and CO₂ molecules.¹⁵⁻¹⁷

Despite the many advantages of MOFs that result from high tunability of chemistry and structure, the cost of MOF production is still a major factor that impedes their large-scale industrial applications. Apart from the capital investment in infrastructures, the cost of MOF production consists largely of raw materials (including metal salts and organic ligands) and processing, which include but are not limited to nonreusable organic solvents and cost associated with activation. For MOF-74 with a molecular formula M₂(DOBDC) (M = Mg, Zn, Fe, etc. and DOBDC = 2,5-dioxido-1,4-benzenedicarboxylate), the major cost of raw materials comes from the organic ligand (i.e., DOBDC). Taking Mg-MOF-74 as an example, the cost of metal salts, usually MgCl₂, can almost be neglected; i.e., it accounts for only a small percentage of the expense of organic ligands. Indeed, MOFs built from much cheaper organic ligands will need to be developed before they can be widely used in industry in large quantities. Generally speaking, larger and longer aromatic organic ligands are more expensive than smaller and shorter aliphatic ligands. However, the majority of the MOFs synthesized so far features aromatic organic ligands because the coordination-driven self-assembly of building blocks to produce porous crystalline MOFs requires the molecular precursor to be rigid and possess proper directionality.¹⁸ Such properties are more likely to appear in conjugated organic ligands, e.g., DOBDC and BDC (BDC = 1,4-benzenedicarboxylate), both of which are frequently used in the synthesis of MOFs. On the other hand, most of the aliphatic ligands are flexible and do not have sites to form directional metal–ligand bonds, and they are less likely to form porous and crystalline solids with metal centers. Therefore, aliphatic ligands are rarely employed in MOF synthesis. Nevertheless, there are still several MOFs based on aliphatic ligands,¹⁹⁻²¹ including the commercially available aluminum fumarate (Basolite A520).²² However, there are no open metal sites in these MOFs, thereby limiting their CO₂ and H₂ storage potential at low and ambient pressures. It would be extremely useful to develop a MOF-74 analogue featuring both open metal sites, which lead to enhanced adsorbate–adsorbent interactions and higher gas uptake at ambient pressure, and cheap aliphatic linkers, which lower the overall raw materials cost. To the best of our knowledge, all the MOF-74 analogues which have been experimentally synthesized so far were constructed from longer, aromatic organic linkers and are therefore likely to be more expensive with limited improvement on gas adsorption capacity in low to ambient pressure regimes.

Another popular approach to increase the gas adsorption capacity of MOFs is to synthesize MOFs with expanded pores and larger internal surface areas, e.g., by replacing the DOBDC linker in MOF-74 with longer linkers.²³ We investigated the effectiveness of pore expansion in MOF-74 analogues in one of our recent high-throughput screening studies,²⁴ whereby we developed a novel in silico crystal assembly algorithm that differed from previous approaches²⁵⁻²⁹ to create a library of MOF-74 analogues which exhibit 1-D metal-oxide rod building units.³⁰ We found that the gravimetric uptake of CO₂ dropped significantly in MOF-74 analogues with higher pore volumes due to the spatial and gravimetric dilution of the open metal sites which serve as the strong adsorption sites for CO₂ molecules. Thus, the increased pore volume in these analogues (which results from construction with extended ligands) sacrifices gravimetric uptake and further complicates synthesis by introducing more complex organic molecule building units and by potentially reducing mechanical stability. Therefore, larger pore sizes are not always desirable. While many efforts have been made to tune and improve upon the exceptional small molecule adsorption properties of the original MOF-74 framework,³¹⁻³⁵ we undertake a rational design approach to further improve the gas adsorption capabilities in MOF-74 analogues by increasing the density of open metal sites, e.g., by replacing the DOBDC linker with a smaller molecule. While DOBDC represents the smallest aromatic molecule that satisfies the topological requirement of MOF-74, an even smaller molecule can be identified from the thousands of aliphatic molecules which are smaller in size than DOBDC.

In this work, we rationally design in silico a MOF-74 analogue based on a cheaper and commercially available aliphatic ligand, i.e., DHFUMA (DHFUMA = 2,3-dihydroxyfumarate), and simulate its H₂, CO₂, and H₂O adsorption properties, based on extensive previous work dedicated to describing the energetic interactions of small molecules in the MOF-74 framework.³⁶⁻⁴⁰ Namely, we predict significantly improved H₂ volumetric storage capacity, increased low-pressure CO₂ adsorption, and higher CO₂:H₂O selectivity in the M₂(DHFUMA) series than the M₂(DOBDC) series. The cost (per mol) of DHFUMA is lower than that of DOBDC by more than 80% from the commercial vendor Sigma-Aldrich, and the volumetric density of open metal sites in M₂(DHFUMA) is twice of that of M₂(DOBDC). Typical protocols used to synthesize M₂(DOBDC) have been tested and shown to result in a crystalline material that is not the desired M₂(DHFUMA) product (see Supporting Information); however, calculation of the elastic constants and vibrational frequencies demonstrates the dynamical and mechanical stability of M₂(DHFUMA) and provides justification that the material can be synthesized. M₂(DHFUMA), if it can be synthesized in large quantities, has the potential to be a better candidate than M₂(DOBDC) for industrial applications including hydrogen storage and carbon capture.

Methods

In Silico Crystal Design

Part of our recent work has focused on the in silico crystal design of 1-D rod MOFs.²⁴ The building blocks of these MOFs are embedded in three-dimensional space by an optimization routine that is constrained by geometric rules that must hold for a 1-D rod MOF. Utilizing this method allows for facile substitution of DOBDC for DHFUMA into the MOF-74 framework and quickly creates an accurate starting crystal structure for DFT optimization. Figure 1 demonstrates the analogous connectivity groups in DHFUMA and DOBDC. We believe this to be the smallest possible ligand with which a MOF-74 analogue can be constructed. Dispersion-corrected DFT optimization was performed to relax the M₂(DOBDC) and M₂(DHFUMA) frameworks and obtain partial atomic charges for each unique atom type in the framework.

Figure 1.

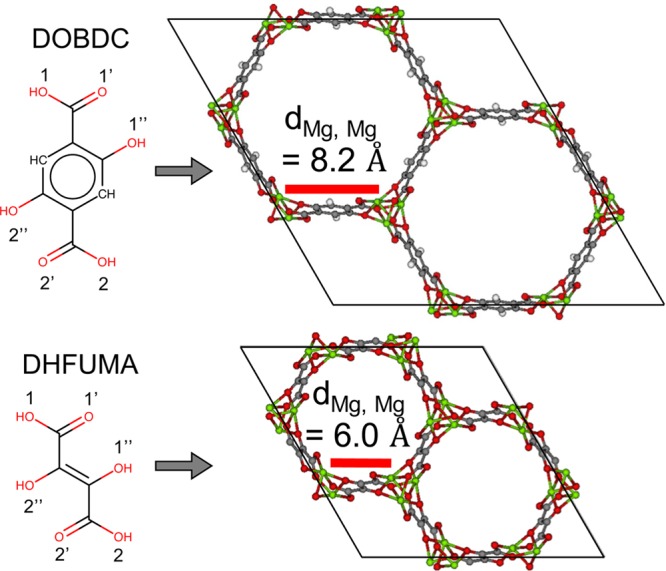
DOBDC ligand and framework is visually compared to the DHFUMA ligand and framework. (1, 1′, 1″) oxygens connect to one metal rod in the MOF-74-type framework, and (2, 2′, 2″) connect to an adjacent metal rod. The distance between adjacent open metal sites is shown to be 2 Å shorter in the Mg₂(DHFUMA) framework.

DFT Calculations

A majority of the periodic density functional theory calculations, including geometry and cell optimizations, have been performed using the CP2K code which uses a mixed Gaussian/plane-wave basis set.^41,42 We have used both gradient-corrected (i.e., PBE⁴³) and hybrid density functional (i.e., PBE0^44,45 with 25% Hartree–Fock exchange) methods. It is known that a correct description of the dispersion interactions is important to predict the MOF structures and host–guest interactions in MOFs.^46,47 In this work, we have used one of the most popular pairwise additive descriptions of the dispersion interactions as developed by Grimme et al., i.e., the D3 method⁴⁸ with the Axilrod–Teller–Muto three-body terms, in combination with the conventional PBE and PBE0 functionals. The same method was used in our previous work on MIL-53,^49,50 UiO-66,⁵¹ and MOF-74²⁴ types of MOFs, and we achieved very good agreement between theory and experimental results on structures and calorimetric measurements. We note that a hybrid functional is necessary here to provide a correct description of the electronic structures and host–guest interactions of MOF-74 materials featuring M²⁺ cations with unpaired electrons, including Mn²⁺, Fe²⁺, Co²⁺, Ni²⁺, and Cu²⁺. The Hartree–Fock exchange calculations, which are part of the hybrid DFT functional PBE0, were performed and significantly accelerated using the auxiliary density matrix method (ADMM),⁵² which enables us to consider relatively large systems (with the largest system containing 489 atoms) at the hybrid DFT level. The partial atomic charge analysis was performed using the REPEAT method proposed by Campana et al.,⁵³ which was recently implemented into the CP2K code based on a restrained electrostatic potential framework.⁵⁴ The REPEAT method calculates partial atomic charges from electrostatic potentials determined from DFT calculations, and only the grid points outside the van der Waals radii of each atom were included in the fitting. We have used partial atomic charges determined using the REPEAT scheme in our recent work on MOF-74, in which very good agreement was obtained between theory and experiment on the adsorption isotherms of CO₂ molecules.²⁴ The vibrational frequency and elastic constant calculations were performed using the CRYSTAL code^55,56 with the B3LYP hybrid functional.⁵⁷ More details of the calculations are included in the Supporting Information.

Classical Simulations and Pore Characterization

A critical component in the classical molecular simulation of nanoporous materials is the parametrization of classical potential energy functions (or force fields) that can accurately describe the energetics of host−guest systems. Many times off-the-shelf force fields such as UFF⁵⁸ or Dreiding⁵⁹ are used in lieu of a more accurate alternative, but this approach breaks down with MOFs that contain complex electronic structure features such as open metal sites.³⁷ Several different approaches have been used specifically to generate force fields which successfully describe gas interactions in MOF-74 type frameworks which contain these open metal sites.^37,60,61 Pham et al. used a many-body polarization approach to classically capture the complex H₂–open metal site interactions in the Mg₂(DOBDC) framework and later extended their force field development to the entire metal series.^40,62 In this work, the model of Pham was used to model H₂ adsorption in Mg₂(DOBDC) and Mg₂(DHFUMA), and we refer the reader to these publications for further details. The grand canonical Monte Carlo (GCMC) simulations of H₂ with many-body polarization were calculated with the RASPA2 software package.⁶³

Mercado et al. used a recently developed approach to parametrize the potential energy surface for the isoreticular series M₂(DOBDC) [M = Mg, Mn, Fe, Co, Ni, Zn] such that classical molecular simulation of CO₂ and H₂O could be performed for the entire metal series for the first time.³⁹ The parametrization was peformed by calculating DFT single-point energies along the path of minimum repulsion between unique guest–host pairwise types to accurately capture the repulsive behavior between the guest and the excess electon density at the open metal sites. We adopt this force field parametrization for studying the adsorption properties of CO₂ and H₂O in DHFUMA and refer the reader to this publication for specific details and the parameters themselves. The unique types assigned to each atom in the DHFUMA crystal structure and their correspondence to the atom types of Mercado’s force field are shown in the Supporting Information, in addition to a justification for the transferability of the force field. GCMC simulations were executed to calculate adsorption isotherms and isosteric heats of adsorption of the frameworks under consideration. An annealing minimization scheme was used to determine the classical binding energy of adsorbates in all analogues. In this scheme, an NVT ensemble Monte Carlo simulation consisting of one asorbate molecule is successively quenched from T = 298 K to T = 1 K. The potential energy of the final configuration in the T = 1 K simulation then corresponds to the classical binding energy. The porosity characterization of all frameworks was performed with the Zeo++ application using the high accuracy settings.^64,65

Results

Porosity Characterization

The channel geometry of the Mg analogues of the DHFUMA and DOBDC series were analyzed by Zeo++ to demonstrate the differences in porosity which are later shown to have a significant impact on the adsorption properties of the two frameworks. A probe radius of 1.65 Å was used which corresponds to the kinetic diamter of CO₂. Table 1 summarizes these important geometric quantities. We note that the distance between the centers of two metal rods opposite each other in a single hexagon of DHFUMA, i.e., the approximate diameter of a single channel, is equal to 12.6 Å. When accounting for the Van der Waal’s radii of the framework atoms in DHFUMA, the largest free and included spheres are close to half of this diameter as shown in Table 1. Interestingly, the typical diameter of single-wall carbon nanotubes (SWNTs), depending on the chirality indices, can range from 6.2 (n + m = 8) to 12.2 (n + m = 18) for the lowest energy tube for each combination of chirality indices.⁶⁶ We have therefore designed a MOF with a channel geometry that is essentially comparable to a SWNT but with a significantly higher degree of chemical diversity due to the presence of oxygens and open metal sites decorating the inside of the channel. The proximity and increased volumetric density of open metal sites in the DHFUMA structure compared to the DOBDC structure will later be shown to result in a new CO₂ binding configuration. The volumetric densities of open metal sites in Mg₂(DHFUMA) and Mg₂(DOBDC) are 0.0084 Mg/ų and 0.0044 Mg/ų, respectively. One in every six atoms in DHFUMA is an open metal site, whereas one in every nine atoms in DOBDC is an open metal site. With nearly two times the volumetric metal site density and one and a half times the molar metal site density of DOBDC (in addition to the reduced interatomic distance between adjacent Mg atoms in each channel), DHFUMA contains a spatial configuration of open metal sites that is more favorable for hydorgen storage and CO₂ capture. Additional pertinent crystallographic data for Mg₂(DOBDC) and Mg₂(DHFUMA) are included in the Supporting Information.

Table 1. Accessible Surface Area (ASA), Accessible Volume (AV), Largest Included Sphere (D_I), Largest Free Sphere (D_F), Open Metal Site Volumetric Density (ρ_Mg), and Open Metal Site Weight Percent of Two Frameworks: Mg₂(DHFUMA) vs Mg₂(DOBDC).

	ASA	AV	DI	DF	ρMg	wt % Mg
ligand	[m2/g]	[cm3/g]	[Å]	[Å]	[Mg/Å3]	[%]
DOBDC	1782	0.350	11.8	11.1	0.0044	20.0
DHFUMA	1043	0.095	7.6	6.3	0.0084	25.2

Predictions on Material Stability

To verify whether M₂(DHFUMA) is stable and therefore has the potential to be synthesized experimentally, we calculated the vibrational frequencies and elastic constants. Our calculated vibrational frequencies and the full elastic matrix of Mg₂(DHFUMA) are shown in the Supporting Information. We find all the vibrational modes of Mg₂(DHFUMA) have positive frequencies, demonstrating its dynamical stability. We further verify the elastic stability of Mg₂(DHFUMA) against the Born stability criteria,⁶⁷ and we find the calculated elastic constants of Mg₂(DHFUMA) satisfy all the necessary and sufficient stability conditions (see the Supporting Information),⁶⁸ demonstrating Mg₂(DHFUMA) to be mechanically stable. We expect M₂(DHFUMA) based on other metals to have the same behavior and suggest these materials have the potential to be synthesized in future experiments. The results of the mechanical and dynamical stability calculations are not surprising, especially since the metal oxide rod M–O coordination environment is identical to M₂(DOBDC) and since DHFUMA is an experimentally validated ligand with a fully conjugated backbone exhibiting a planar geometry between the two connection groups (see Figure 1). The synthetic difficulties arise in finding the necessary reaction conditions to yield the correct crystalline M₂(DHFUMA) product, the details of which are elaborated in the Supporting Information.

Enhanced H₂ Storage Potential

The doubling of the volumetric density of open metal sites results in a factor of 2 increase in the simulated volumetric H₂ storage capacity of Mg₂(DHFUMA) over Mg₂(DOBDC) at cryogenic temperatures. Utilizing the many-body polarization scheme implemented in the RASPA2 package and the polarizable model of Pham et al.⁴⁰ to compute H₂ potential energy interactions in Mg₂(DOBDC), we simulate the adsorption isotherms of both Mg₂(DOBDC) and Mg₂(DHFUMA) at 77 K. We assumed that the force field is transferable and adopt all model parameters of Pham with the exception of the frameworks’ partial atomic charges for which we use the values derived from our REPEAT analysis which are summarized in the Supporting Information. Figure 2(a) demonstrates a good agreement of our isotherm with the theoretical isotherm of Pham et al. and the experimental isotherm of Dietzel et al. (data extracted from ref (40) and ref (69), respectively) for Mg₂(DOBDC) at 77 K. Our simulated isotherm as generated by RASPA2 slightly overpredicts the gravimetric uptake (by ∼20% at 1 bar) shown by the experimental results and simulated by Pham et al. which we further discuss in the Supporting Information.

Figure 2.

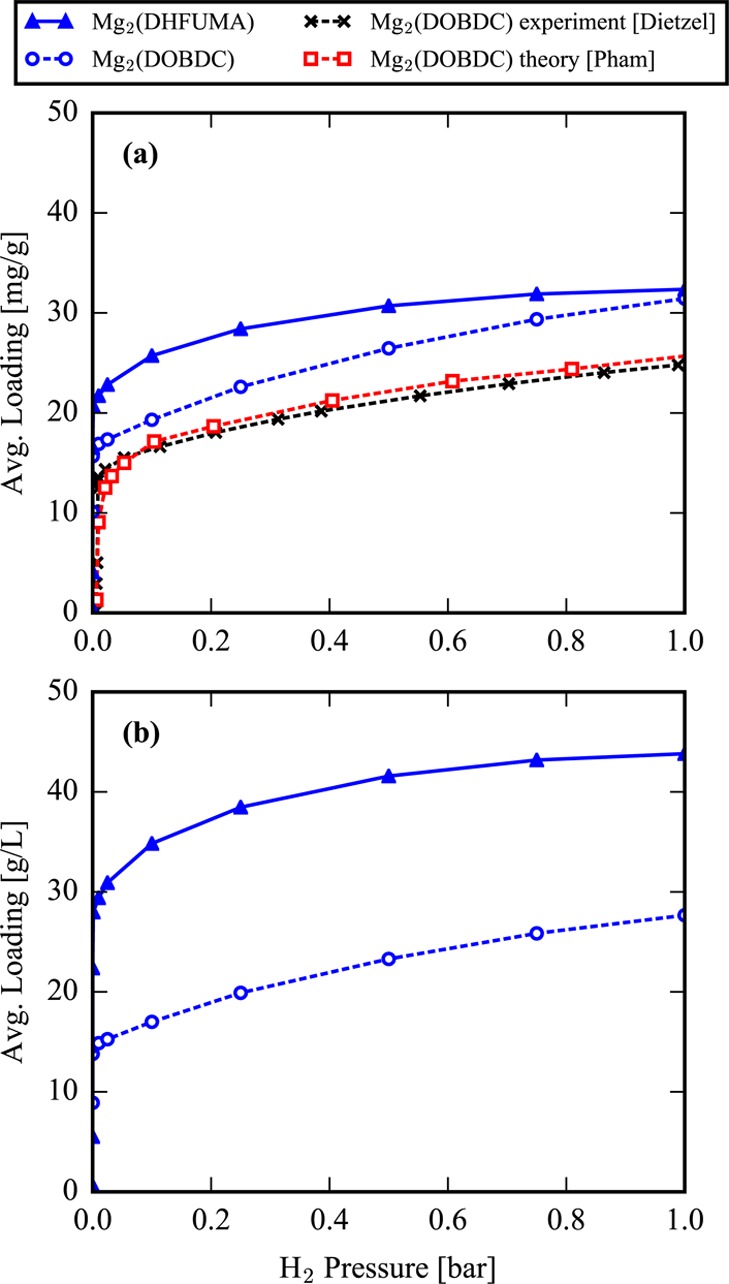
H₂ isotherms computed at T = 77 K. (a) Mg₂(DOBDC) isotherms computed in this work, by Pham et al. (extracted from ref (40)), and measured by Dietzel et al. (extracted from ref (69)) and the predicted Mg₂(DHFUMA) assuming a transferable force field. Isotherms are in units of amount adsorbed per framework mass. (b) Mg₂(DHFUMA) and Mg₂(DOBDC) simulated isotherms from this work in units of amount adsorbed per framework volume.

Since the weight compositions of Mg in DHFUMA (25.2 wt %) and DOBDC (20.0 wt %) differ slightly, the amount of H₂ loaded per framework weight in DHFUMA is marginally better than DOBDC at low pressure but does not represent a remarkable improvement as shown in Figure 2(a). The strong H₂–open metal site interactions dominate the adsorption at low temperatures and pressures, and weak H₂–H₂ interactions are not sufficient to provide the strong cooperative binding effects observed with CO₂ which are later discussed in the section on enhanced CO₂ heat of adsorption. In other words, H₂ gravimetric adsorption is not significantly improved in DHFUMA at low pressures, and the framework displays H₂ saturation behavior at significantly lower pressures than in DOBDC as one would expect from the reduced channel volume. Nevertheless, the advantage of Mg₂(DHFUMA) for H₂ storage lies exactly in this reduced channel volume and the doubling of volumetric open metal site density. As can be seen from Figure 2(b), the H₂ storage capacity on a volumetric basis (in which the amount loaded is expressed per total volume of adsorbent) is approximately twice that of Mg₂(DOBDC). Not only would a Mg₂(DHFUMA)-based storage device require half the volume to achieve approximately the same H₂ storage by weight percent but also the ligand is drastically cheaper. At the cryogenic temperature of 77 K and extremeley low pressure of 0.5 bar, Mg₂(DHFUMA) is predicted to achieve a volumetric uptake of 41.5 g H₂/L which is sufficient to surpass the DOE’s 2020 H₂ volumetric storage target of 40 g H₂/L. We note that Mn-BTT (BTT^3– = 1,3,5-benzenetristetrazolate), one of the best performing MOFs for volumetric hydrogen uptake, has been reported to achieve uptake of 43 g H₂/L but at the higher pressure of 1.2 bar.⁴

DFT Predicted Binding Geometries and Energies

We list our calculated lattice parameters of the all the MOFs considered in this work in Table 2, and we compare the data on M₂(DOBDC) with available experimental results (taken from ref (36); see references therein) from which we find that the errors of our theoretically predicted lattice parameters of M₂(DOBDC) are within ∼1%. We also find that for the same metal the a lattice parameter of M₂(DHFUMA) is proportionally smaller than that of M₂(DOBDC) by 27–29%, and the c lattice parameter of M₂(DHFUMA) is almost the same as that of M₂(DOBDC), with the biggest difference to be only 0.16 Å (Cu and Zn). Indeed, the decreased unit cell volume of M₂(DHFUMA), i.e., by ∼50% in comparison with M₂(DOBDC), is mainly due to the shortening of the lattice parameter along the a and b axes, and a direct result of that is the doubling of the density of open metal sites. We will see that the shortening of the a lattice parameter and the doubling of the density of open metal sites in M₂(DHFUMA) have a significant effect on the optimal binding configuration of CO₂ in M₂(DHFUMA).

Table 2. Lattice Parameters (in Å) of M₂(DOBDC) and M₂(DHFUMA) from Theory and Experiment.

	DHFUMA (theory)		DOBDC (theory)		DOBDC (expt)		a/a′
metal	a	c	a′	c′	a′	c′	(theory)
Mg	18.86	6.88	26.17	6.95	25.89	6.87	72%
Mn	18.70	7.14	26.22	7.01	26.23	7.04	71%
Fe	18.93	6.75	26.11	6.85	26.10	6.85	73%
Co	18.67	6.77	25.91	6.82	25.89	6.81	72%
Ni	18.59	6.65	25.73	6.75	25.72	6.74	72%
Cu	18.85	6.13	25.84	6.29	26.00	6.26	73%
Zn	19.01	6.72	26.18	6.88	25.93	6.84	73%

Taking Mg as an example, we show our theoretical optimized binding configuration of CO₂ in Mg₂(DOBDC) and Mg₂(DHFUMA) in Figures 3a and 3b, respectively. From Figure 3, we can find that a single CO₂ molecule has very different binding modes in Mg₂(DOBDC) and Mg₂(DHFUMA). In Mg₂(DOBDC), one terminal oxygen of CO₂ binds to Mg of Mg₂(DOBDC) with a short binding distance of 2.33 Å, while the other terminal oxygen of CO₂ is aligned with the DOBDC linker and points toward the open pore space of Mg₂(DOBDC). However, in Mg₂(DHFUMA), because of the much shorter interchain Mg···Mg distance (i.e., 6.03 Å in comparison with 8.26 Å in Mg₂(DOBDC)), both terminal oxygens of CO₂ are able to bind to two neighboring Mg²⁺ cations simultaneously, with similar binding distances (i.e., 2.59–2.60 Å). Such a unique binding mode results in a much enhanced binding energy of CO₂ in Mg₂(DHFUMA), i.e., 50.1 kJ/mol, which is 20% (8.8 kJ/mol) stronger than that in Mg₂(DOBDC). We show a detailed comparison of the binding energies and relevant O···M binding distances of CO₂ in M₂(DOBDC) and M₂(DHFUMA) with different metals in Table 3, in which we also list available experimental data on CO₂ adsorption in M₂(DOBDC).⁷⁰ We further looked at the adsorption of a single H₂O molecule in both M₂(DOBDC) and M₂(DHFUMA) with different metals, and we show a detailed comparison of the binding energies and relevant O···M binding distances in Table 4. Interestingly, the binding energies of a single H₂O molecule in M₂(DOBDC) and M₂(DHFUMA) with the same metal are almost identical. Taking Mg as an example, the binding energies of H₂O are 88.6 and 87.4 kJ/mol in Mg₂(DOBDC) and Mg₂(DHFUMA), respectively. This is because H₂O has only one central oxygen, and it interacts with both Mg₂(DOBDC) and Mg₂(DHFUMA) through a single-contact O···Mg interaction. Comparing the whole series of CO₂ and H₂O adsorption in M₂(DOBDC) and M₂(DHFUMA) with different metals, we can find that the trend is the same; CO₂ tends to have much stronger binding in M₂(DHFUMA) than that in M₂(DOBDC) with the same metal, while H₂O tends to have almost the same binding strength in M₂(DHFUMA) and M₂(DOBDC) with the same metal. This would lead to improved selectivity of CO₂ in a CO₂:H₂O mixture in M₂(DHFUMA) than that in M₂(DOBDC).

Figure 3.

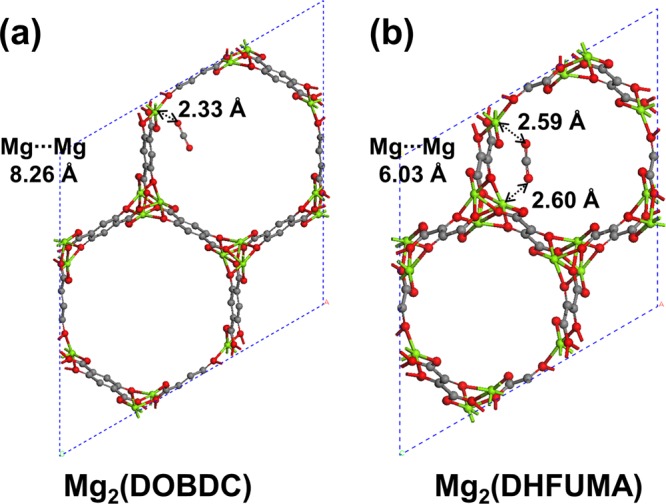
DFT optimized binding configurations of CO₂ in (a) Mg₂(DOBDC) and (b) Mg₂(DHFUMA).

Table 3. Binding Energies (in kJ/mol) and Relevant O···M Binding Distances (in Å) of CO₂ in M₂(DOBDC) and M₂(DHFUMA) from Theory and Experiment.

	DHFUMA (theory)		DOBDC (theory)		DOBDC (expt)		Eb – Eb′
metal	Eb	dO···M	Eb′	dO···M′	Eb′	dO···M′	(theory)
Mg	50.1	2.59/2.60	41.3	2.33	43.5	2.27	8.8
Mn	40.5	2.64/2.75	29.2	2.57	31.7	2.51	11.3
Fe	40.9	2.56/2.76	30.0	2.43	33.2	2.29	10.9
Co	41.1	2.49/2.79	29.3	2.43	33.6	2.23	11.8
Ni	46.1	2.46/2.69	34.8	2.32	38.6	2.29	11.3
Cu	32.0	2.69/2.80	19.9	2.74	22.1	2.86	12.1
Zn	37.6	2.76/2.83	31.3	2.66	26.8	2.43	6.3

Table 4. Binding Energies (in kJ/mol) and Relevant O···M Binding Distances (in Å) of H₂O in M₂(DOBDC) and M₂(DHFUMA) from Theory.

	DHFUMA (theory)		DOBDC (theory)
metal	Eb	dO ··M	Eb′	dO···M′
Mg	87.4	2.19	88.6	2.16
Mn	73.5	2.26	73.3	2.29
Fe	77.5	2.20	77.1	2.21
Co	79.4	2.17	78.9	2.17
Ni	89.2	2.12	89.4	2.11
Cu	68.1	2.22	62.5	2.24
Zn	74.9	2.22	68.4	2.23

Enhanced CO₂ Adsorption

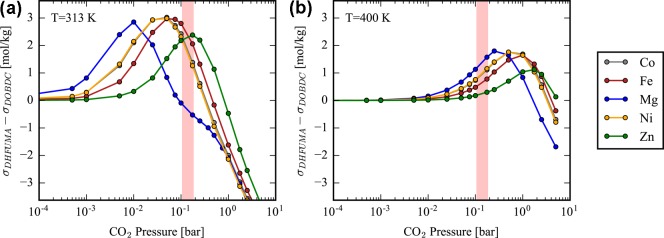
We demonstrate in the Supporting Information that the force field of Mercado can reproduce the ab initio potential energy landscape of CO₂ in our set of analogues as shown by the agreement of both binding energies and binding geometries. With confirmation of the force field’s tranferability, Henry coefficients of the M₂(DOBDC) and M₂(DHFUMA) structures were computed at temperatures of 313.0 and 400.0 K, shown in Table 5. An order of magnitude increase is observed in DHFUMA structures over DOBDC structures for a given metal substitution. It is also worthwhile to note that, for a given metal substitution, the M₂(DHFUMA) structure achieves the same order of magnitude (and only slightly lower) Henry coefficient at 400 K as its DOBDC counterpart at 313 K in all frameworks except for the Mg analogues. This large decrease in the free energy of a single adsorbed CO₂ molecule in DHFUMA is a direct result of the decreased potential energy of the one molecule per two open metal sites binding mode, which has been demonstrated in our DFT optimization and GCMC simulations. GCMC simulations were utilized to simulate the CO₂ uptake in M₂(DOBDC) and M₂(DHFUMA) structures and calculate isotherms for each material. The higher density of open metal sites and enhanced binding energy results in larger uptake at low pressures; however, the reduced channel volume results in quicker saturation of the DHFUMA adsorbent. The CO₂ isotherms in Mg₂(DOBDC) and Mg₂(DHFUMA) in Figure 4 visualize this trend. Thus, at low pressures DHFUMA performs significantly better in total CO₂ uptake but performs worse in total uptake at higher pressures. A detailed view of all CO₂ isotherms is provided in the Supporting Information. Due to the favorable enhancement of the binding energy, DHFUMA analogues are able to capture significantly more CO₂ in any pressure range relevant to industrial CO₂ capture from flue gas where P_CO2 = 0.15 bar. Figure 5 demonstrates the excess amount of CO₂ captured by each metal analogue of DHFUMA in comparison to its DOBDC analogues across a pressure range applicable to flue gas conditions. The excess value peaks at low pressures and then quickly drops to large negative values after the DHFUMA framework saturates with CO₂. It is also significant that DHFUMA analogues continue to load approximately 2 mol/kg more CO₂ at an elevated temperature of 400 K since high-temperature adsorption can be used to mitigate competitive water adsorption, as will be seen in later discussion.

Table 5. Henry Coefficients (K_H) × 10^–3 [mol/kg/Pa] of CO₂ in the M₂(DHFUMA) vs M₂(DOBDC) Series at 313 and 400 K.

	DHFUMA		DOBDC
metal	313 K	400 K	313 K	400 K
Mg	10.7	0.22	1.56	0.064
Fe	1.8	0.07	0.20	0.017
Co	3.2	0.11	0.26	0.021
Ni	3.0	0.12	0.27	0.021
Zn	0.39	0.028	0.076	0.009

Figure 4.

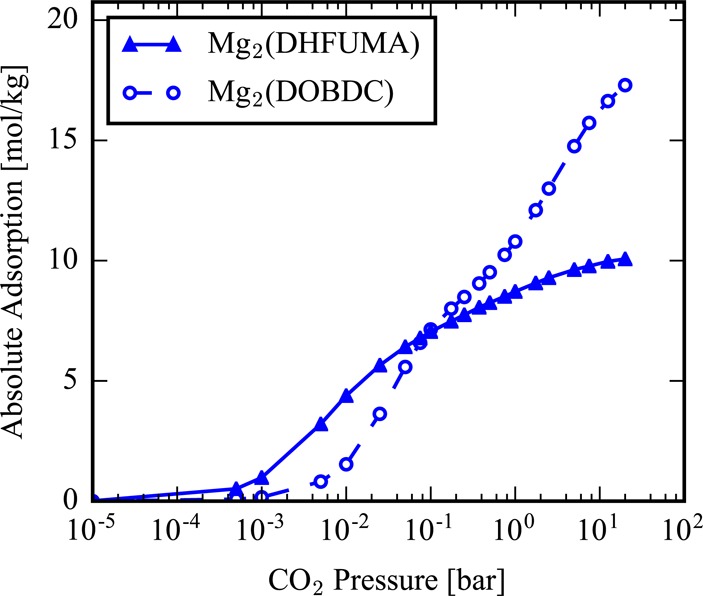
Absolute CO₂ adsorption in Mg₂(DHFUMA) vs the absolute CO₂ adsorption in Mg₂(DOBDC) at 313 K. The DHFUMA structure significantly outperforms the DOBDC structure in CO₂ uptake at low pressures but has far lower capacity of CO₂ in the limit of saturation.

Figure 5.

Absolute CO₂ adsorption in DHFUMA minus the absolute CO₂ adsorption in DOBDC (a) at 313 K and (b) at 400 K. The pressure region in pink corresponds to the typical partial pressure of CO₂ (P = 0.15 bar) in the exhaust from a coal-fired power plant. For each metal a temperature exists betweeen 313 and 400 K which maximizes the excess CO₂ uptake in the DHFUMA structure.

Enhanced CO₂ Heat of Adsorption

The isosteric heat of adsorption, ΔH_Ads, as a function of loading is a measure of the enthalpy gained on average by adsorbing one additional molecule in the adsorbent system at a specified loading. Conversely, the isosteric heat of desorption, ΔH_Des, as a function of loading is the amount of enthalpy required to desorb one additional molecule at a specified loading. In Figure 6 we observe an interesting feature of CO₂ adsorption in the DHFUMA structure that shows a monotonic increase in the heat of desorption as a function of loading from zero to saturation loading. A molecule that adsorbs when the framework is close to saturation (0.8–0.9 molec/M²⁺) releases nearly 10 kJ/mol more enthalpy than the first molecule to adsorb. In other words, the cooperative binding of CO₂ is very strong (due to the proximity of the primary binding sites) and increases in strength monotonically with loading. This leads to the nonintuitive property that the enthalpy penalty to desorb CO₂always decreases as the loading decreases from saturation to empty framework. Notably, Mg₂(DHFUMA) does not exhibit this trend because the binding energy of one CO₂ molecule is so strong that cooperative adsorption is only favorable enough to maintain a constant ΔH_Des as a function of loading. The same phenomenon does not exist with the DOBDC series. Only a 1–2 kJ/mol increase in ΔH_Des is observed in all DOBDC analogues between the limit of 0 loading and the inflection point at 1 molecule per open metal site. Thus, cooperative adsorption at loadings below 1 molecule per open metal site is negligible in the DOBDC frameworks when compared to the DHFUMA frameworks.

Figure 6.

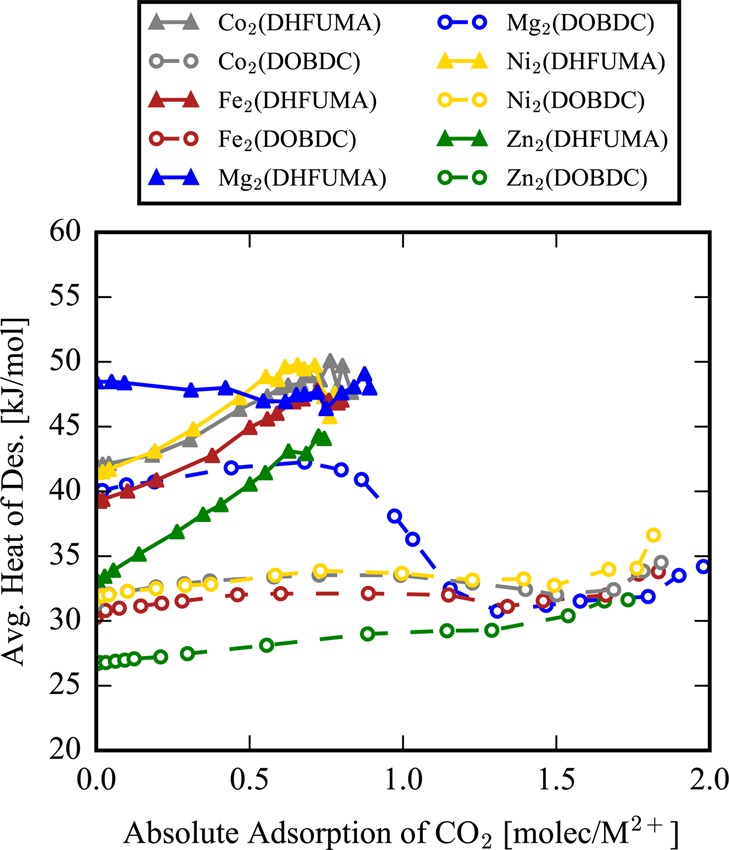
Heat of desorption as a function of loading for the M₂(DOBDC) and M₂(DHFUMA) analogues. The DHFUMA structures, with the exception of the Mg analogue, exhibit a 7–10 kJ/mol increase in the ΔH_Des between the limit of zero loading and saturation.

Optimizing CO₂ Capture in Binary CO₂:H₂O Mixtures

Enhanced CO₂ uptake in the range of partial pressures relevant to adsorption from a coal-fired flue stream does not necessarily indicate an improved potential for industrial-scale CO₂ capture.⁷¹ A multitude of other factors must be considered such as CO₂:H₂O selectivity, compression work of the CO₂-enriched waste stream, and the energy required for adsorbent regeneration, and these attributes can be quantified through a metric known as the parasitic energy.⁷² However, the deleterious effects of water on CO₂ uptake are often overlooked when evaluating materials for CO₂ capture potential via the parasitic energy.⁷³ For this reason we investigated water adsorption in the DHFUMA and DOBDC series as well since creative strategies such as high-temperature adsorption and low-temperature desorption (HALD⁷⁴) have been proposed to mitigate the parasitic energy when adsorbing CO₂ from humid flue gas streams. Pure component water isotherms and binding geometries are shown in the Supporting Information.

More relevant to carbon capture, we performed a CO₂:H₂O binary mixture analysis to investigate each structure’s potential performance for carbon capture in the presence of water. GCMC simulations were performed at a fixed reservoir pressure of 0.15 bar, and the molar composition of CO₂:H₂O of the reservoir was varied at different temperatures. Note that N₂ was not simulated in the mixture as its uptake in the MOF-74 framework series has been shown to be negligible in comparison to the uptake of CO₂ and H₂O at flue gas adsorption conditions.^38,39 The same stepped feature of water adsorption occurs in this binary analysis as in the pure component H₂O isotherms, and at a certain critical pressure, water condenses within the pore. In the case of this binary mixture analysis, the condensation of H₂O is sufficient to entirely remove any adsorbed CO₂ at equilibrium. Figure 7 demonstrates the loss in CO₂ uptake capacity that occurs after the molar composition of water (at fixed total pressure) in the reservoir becomes too high.

Figure 7.

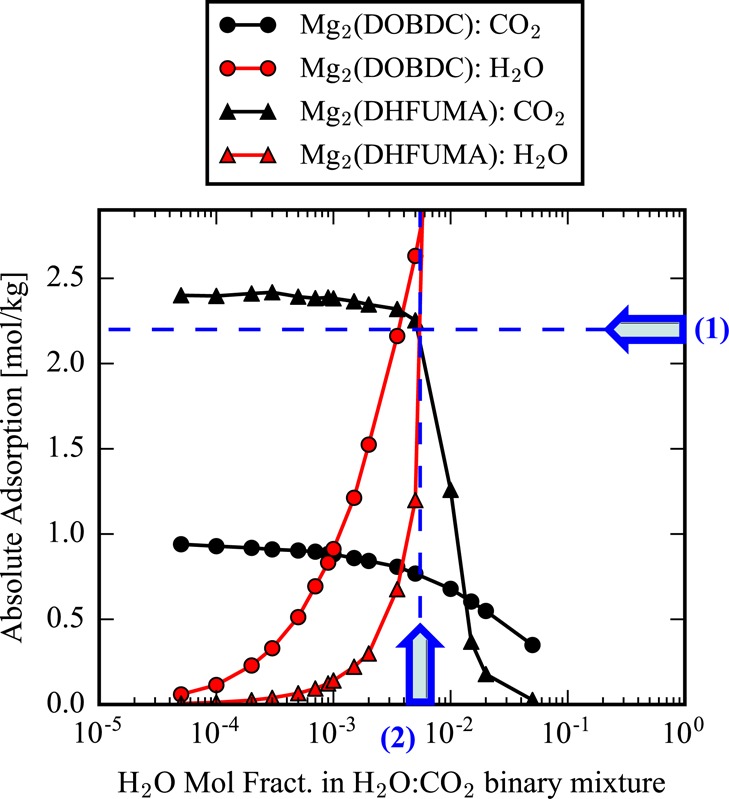
Mixture analysis of CO₂ and H₂O adsorption in the Mg analogues of DHFUMA and DOBDC. Each data point represents an equilibrated absolute adsorption loading from a GCMC simulation at 400 K and fixed total pressure of 0.15 bar, while the molar composition of H₂O to CO₂ is varied between simulations. For each analogue, two values are extracted, and (1) and (2) demonstrate the values extracted for Mg₂(DHFUMA). (1) Corresponds to the CO₂ uptake that is equal to 90% of the uptake in the limit of 0 mole fraction of H₂O. (2) Corresponds to the H₂O mole fraction at which the total CO₂ uptake has decreased by 10%.

Yet at higher temeprature, the onset of the water step is shifted to a significantly higher mole fraction. A reduction in CO₂ uptake capacity follows from this temperature increase, yet this uptake loss is mitigated in the DHFUMA structure due to the enhanced CO₂ affinity. An entire summary of the mixture anlaysis for each structure at various temperatures is presented in the Supporting Information. From one mixture analysis at a specified temperature, we can extract two values of importance which are visualized in Figure 7: the water mole fraction just before water condensation occurs and the amount of CO₂ loaded at that specific water mole fraction. These represent competing process design variables. To increase the water mole fraction at which condensation occurs, we must raise the temperature, which consequently reduces the amount of CO₂ loaded. These two quantities are plotted for each analogue structure across a range of adsorption temperatures (313–400 K for M = [Co, Fe, Ni, Zn] and 400–473 K for M = [Mg]) in Figure 8. From a carbon capture process design perspective, the ideal material would be located in the top right corner of Figure 8 where the material loads large amounts of CO₂ in the presence of extremely high water mole fractions. Since the x and y quantities of Figure 8 represent competing variables (but we desire to maximize both of them), we can interpret this summary as a problem of Pareto optimality, and a Pareto frontier can be observed for Co₂(DHFUMA). This means that regardless of the adsorption temperature chosen for our capture process there is no material that can simultaneously achieve a higher water tolerance and CO₂ uptake capacity at thermodynamic equilibrium than Co₂(DHFUMA). Therefore, regardless of the selected operating temperature, Co₂(DHFUMA) will have the best uptake and water tolerance as is easily visualized in Figure 8. In more physical terms, a Pareto optimal material in this context of CO₂ capture in the presence of humidity will be the material which delicately balances two factors. First, CO₂ uptake must remain the highest with increasing temperature, which fundamentally arises from the highest CO₂ Henry coefficient, which in turn arises from the strength of CO₂ interactions at the open metal site(s). Second, H₂O condensation must occur at the highest water mole fraction, which arises from a combination of the weakest possible H₂O interactions with the open metal site and the largest pore size. Hence we can see the competing nature of these two factors since the strengths of CO₂ binding and H₂O binding at the open metal site are highly correlated, and the advantage of DHFUMA becomes immediately clear since we selectively strengthen the binding energetics of CO₂ across all metals due to the one molecule per two open metal site binding mode. Thus, we also notably observe that each M₂(DHFUMA) represents a Pareto frontier over its DOBDC counterpart. For example, Ni₂(DOBDC) cannot maximize either water tolerance or CO₂ uptake above Ni₂(DHFUMA) regardless of our specification of the adsorption temperature.

Figure 8.

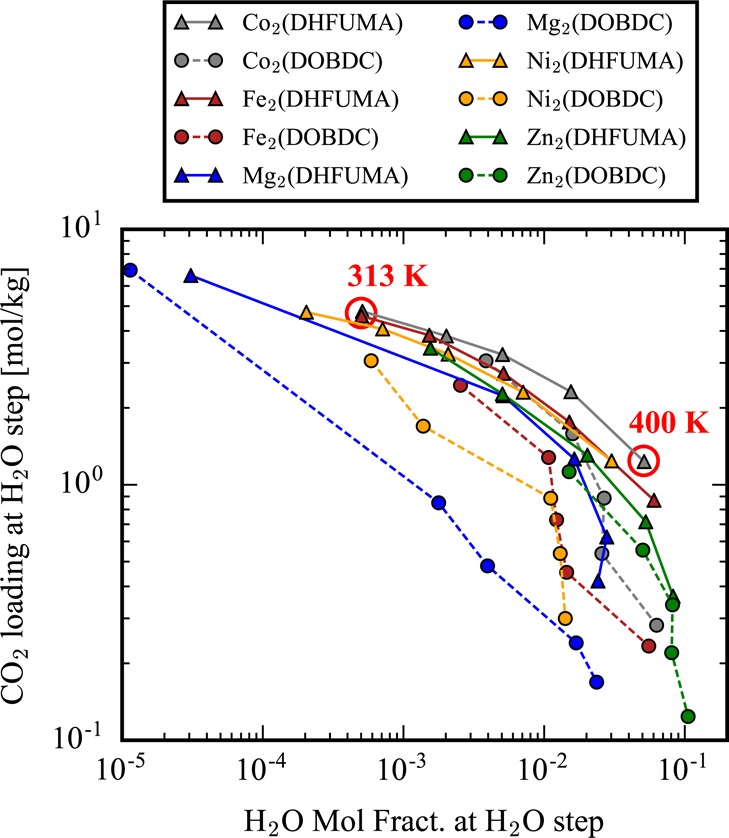
Mixture analysis of all analogues demonstrating the competing nature of CO₂ uptake and water tolerance. The y-axis corresponds to value (1) extracted from Figure 7, and the x-axis corresponds to value (2). The ideal material for CO₂ capture would have a data point corresponding to 313 K at the top right corner of the plot.

Conclusions

We have demonstrated the in silico design of a new MOF-74 analogue based on the aliphatic DHFUMA ligand. We predict exceptional small-molecule adsorption properties via a combination of ab initio electronic structure calculations and classical molecular simulation techniques in conjunction with the extensive previous research efforts to create simulation methods that accurately predict guest molecule behavior in MOF-74-type frameworks. Namely we have predicted (1) a doubling of the volumetric storage capacity of H₂ in Mg₂(DHFUMA) over Mg₂(DOBDC) at the cryogenic temperature of 77 K and pressures below 1 bar (and can meet the 2020 DOE target of 40 g/L at ∼0.5 bar); (2) a marked enhancement of CO₂ uptake in low-pressure regimes over the DOBDC analogue series; and (3) a selective increase of CO₂ binding energy (i.e., stronger CO₂ binding with no change in H₂O binding energy), the basis for which we propose an industrial-scale CO₂ capture process inspired by the HALD scheme (see the Supporting Information). These enhancements are a direct result of the open metal site properties of the M₂(DHFUMA) frameworks.

This material contains double the volumetric density of open metal sites over DOBDC analogues, leading to a remarkable simulated volumetric H₂ storage capacity. Additionally, the distance between two adjacent open metal sites in each channel is reduced from 8.3 Å in DOBDC to 6.0 Å in DHFUMA. CO₂ binds to two open metal sites in the M₂(DHFUMA) framework, resulting in a significantly stronger binding energy than in M₂(DOBDC). The confined pore channel results in significant cooperative adsorption of CO₂, with an isosteric heat of adsorption that is ∼15 kJ/mol stronger at saturation than in the limit of zero loading. Furthermore, since H₂O still can only bind to one open metal site in M₂(DHFUMA), the ab initio calculated quantity of ΔE_bind,H2O – ΔE_bind,CO2 in the DHFUMA series is typically ∼10 kJ/mol higher than in the DOBDC series, indicating that the DHFUMA series has more selective CO₂ binding energetics relative to H₂O. This enhanced selectivity for CO₂ is exploited in our classical GCMC simulations, and adsorption at high temperatures is proposed, allowing for a theoretical process by which CO₂ can be captured in appreciable amounts (∼1–2 mol/kg) in the presence of nontrace amounts of water (∼0.1–1 mol %). The water tolerance and amount of CO₂ captured is dependent on metal choice and adsorption temperature. Finally, an 80% decrease in ligand expense (per mol) suggests that an M₂(DHFUMA) analogue may in the future represent an economically improved path forward for large scale H₂ storage or CO₂ capture from flue gas.

The theoretical work in this paper should motivate efforts to experimentally synthesize M₂(DHFUMA) analogues and confirm our simulated volumetric H₂ storage capacity and adsorption behavior of CO₂:H₂O mixtures. We note the synthesis of M₂(DOBDC) is usually very challenging.³¹ Thus far, our efforts to synthesize M₂(DHFUMA) are unsuccessful. However, we do not see any obvious reason why M₂(DHFUMA) cannot be synthesized experimentally, considering the dynamical and mechanical stabilities of these materials as well as the availabilities and chemical stabilities of the metal and organic precursors. We also believe this framework could be useful for a variety of other separations or storage applications relevant to clean energy. In the future we plan to investigate a range of topics such as selective adsorption of components from light olefin mixtures which are small enough to fit into the DHFUMA channel network if the material can be synthesized.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.6b10363.

• Crystallographic data for Mg₂(DOBDC) and Mg₂(DHFUMA) (ZIP)

• Additional computational details; calculated vibrational frequencies and elastic constants of Mg₂(DHFUMA); structure files and charges; additional crystallographic data; force field parametrization details; CO₂ force field transferability; CO₂ isotherms; H₂O isotherms; H₂O:CO₂ mixture analysis; attempted synthetic procedures (PDF)

Author Contributions

^# M.W. and S.L. contributed equally to this work

The authors declare no competing financial interest.