Abstract
In a randomized clinical trial (RCT), it is often of interest not only to estimate the effect of various treatments on the outcome, but also to determine whether any patient characteristic has a different relationship with the outcome, depending on treatment. In regression models for the outcome, if there is a non-zero interaction between treatment and a predictor, that predictor is called an “effect modifier”. Identification of such effect modifiers is crucial as we move towards precision medicine, that is, optimizing individual treatment assignment based on patient measurements assessed when presenting for treatment. In most settings, there will be several baseline predictor variables that could potentially modify the treatment effects. This article proposes optimal methods of constructing a composite variable (defined as a linear combination of pre-treatment patient characteristics) in order to generate an effect modifier in an RCT setting. Several criteria are considered for generating effect modifiers and their performance is studied via simulations. An example from a RCT is provided for illustration.
Keywords: Biosignature, Moderator, Precision medicine, Treatment decision, Value
1. Introduction
Precision medicine focuses on making treatment decisions for an individual patient based on the patient’s measures (e.g., clinical and biological features). The idea underlies a long history of attempts to identify characteristics that exhibit interaction with treatment assignment in a regression model for the outcome of interest. Such baseline characteristics, called “treatment effect modifiers”, indicate that the outcome under one treatment compared to another treatment depends on these characteristics. Measures with such interactions can aid decisions about which treatment to prescribe (Gail and Simon, 1985; Wellek, 1997; Song and Pepe, 2004; Wang and Ware, 2013).
Interest in precision medicine is growing rapidly, both in clinical research and in statistical methodology. An important component of precision medicine is the notion of an “optimal treatment regime”, first formalized by Murphy (2003) and Robins (2004). Given a vector 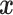 of baseline covariates, a treatment decision can be based a decision function
of baseline covariates, a treatment decision can be based a decision function 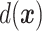 that maps
that maps 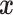 to a treatment indicator, say
to a treatment indicator, say 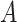 . Treatment decisions can be compared using the “value” of a decision
. Treatment decisions can be compared using the “value” of a decision  , denoted
, denoted 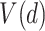 . The value of a decision is the expected value of an outcome variable
. The value of a decision is the expected value of an outcome variable 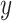 (with respect to the joint distribution of
(with respect to the joint distribution of 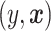 ) when all patients are treated according to a decision function
) when all patients are treated according to a decision function 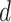 and Qian and Murphy (2011) show that the value can be expressed as
and Qian and Murphy (2011) show that the value can be expressed as
| (1.1) |
where 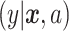 is the outcome of a patient given treatment
is the outcome of a patient given treatment 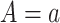 with covariates
with covariates 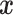 . Here we consider outcome variables
. Here we consider outcome variables 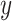 that are continuous, where higher values of
that are continuous, where higher values of 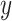 are preferred, as per convention. Determining optimal individual treatment decisions using data from RCTs is a topic that is the subject of active research (see Robins and others, 2008; Zhao and others, 2012; Zhang and others, 2012b; Kang and others, 2014; Zhao and others, 2015, among others). The “optimal treatment decision” is the one that, when applied to the target population, has the largest value.
are preferred, as per convention. Determining optimal individual treatment decisions using data from RCTs is a topic that is the subject of active research (see Robins and others, 2008; Zhao and others, 2012; Zhang and others, 2012b; Kang and others, 2014; Zhao and others, 2015, among others). The “optimal treatment decision” is the one that, when applied to the target population, has the largest value.
It has long been recognized that features that are important for predicting outcome might not be necessarily be useful for making treatment decisions (e.g., Wellek, 1997; Song and Pepe, 2004). Much recent research has focused on identification of individual baseline covariates related to the treatment effect (i.e., variables that exhibit interactions with the treatment indicator in predicting treatment outcome) in contrast to being important in the baseline model. A major challenge in precision medicine is that most baseline measures typically have small moderating effects and individually contribute little to informed treatment decisions. Unconstrained regression models with 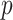 predictors (plus treatment and predictor- by-treatment interactions) become unwieldy, unstable and difficult to interpret when
predictors (plus treatment and predictor- by-treatment interactions) become unwieldy, unstable and difficult to interpret when 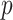 is moderate to large. Various strategies have been proposed to deal with the problem (see Qian and Murphy, 2011; Gunter and others, 2011; Lu and others, 2011, among others). Extensions of the methodology that allow functional data objects to be incorporated as baseline features have also been developed (e.g., McKeague and Qian, 2014; Ciarleglio and others, 2015).
is moderate to large. Various strategies have been proposed to deal with the problem (see Qian and Murphy, 2011; Gunter and others, 2011; Lu and others, 2011, among others). Extensions of the methodology that allow functional data objects to be incorporated as baseline features have also been developed (e.g., McKeague and Qian, 2014; Ciarleglio and others, 2015).
A parsimonious alternative to these previous methods that has received little attention is to use a simple model with only a single “composite” predictor. Herein, a methodology is developed for combining several baseline predictors into a single treatment effect modifier in the context of the classic linear model, which we call a generated effect modifier (GEM). Given a vector of 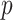 predictors
predictors 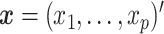 , we consider linear combinations of the predictors
, we consider linear combinations of the predictors 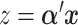 for
for 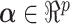 as potential GEMs. The idea of combining covariates was proposed by Tukey (1991, 1993) for balancing and increasing the precision of the estimates of treatment effect in RCTs. A closely related approach was proposed by Tian and Tibshirani (2011) who developed a method of constructing binary “markers” from continuous variables (via cut-off values) and forming an index to detect treatment–marker interactions. Emura and others (2012) introduced a compound covariate approach for predicting survival time in the case when there are too many covariates, for example, gene expression data. In contrast to this work, we propose to combine covariates with the goal of obtaining a single moderating variable, a GEM, that would aid in deciding which treatment is appropriate for any particular patient. Although the GEM model is more restrictive than an unconstrained model, it provides a parsimonious single index approach for making individualized treatment decisions.
as potential GEMs. The idea of combining covariates was proposed by Tukey (1991, 1993) for balancing and increasing the precision of the estimates of treatment effect in RCTs. A closely related approach was proposed by Tian and Tibshirani (2011) who developed a method of constructing binary “markers” from continuous variables (via cut-off values) and forming an index to detect treatment–marker interactions. Emura and others (2012) introduced a compound covariate approach for predicting survival time in the case when there are too many covariates, for example, gene expression data. In contrast to this work, we propose to combine covariates with the goal of obtaining a single moderating variable, a GEM, that would aid in deciding which treatment is appropriate for any particular patient. Although the GEM model is more restrictive than an unconstrained model, it provides a parsimonious single index approach for making individualized treatment decisions.
Alternative approaches to optimal treatment decision estimation have been proposed that fall in the realm of machine learning and can often be framed in the context of classification problems (Zhang and others, 2012a). Examples are the outcome weighted learning (OWL) (e.g., Zhao and others, 2015; Song and others, 2015) based on support vector machines, tree-based classification (e.g. Laber and Zhao, 2015), and the Kang and others (2014) method based on adaptive boosting. Although these approaches can be appealing options in many settings, we base our general approach on the linear model as it is most frequently utilized in practice and lends itself very well to interpretability. This paper fulfills the practical need of providing a simple treatment effect modifier methodology in the classic linear model setting for making precision medicine decisions. Also, the GEM approach provides the benefit of a visual presentation that is familiar to clinicians.
In efficacy studies, after the primary analysis of treatment efficacy has been performed, the usual practice is to seek individual effect modifiers (single patient baseline characteristics) with the ultimate goal of informing treatment decisions. When no single variable has a strong modifying effect, the GEM is an appealing and novel approach for secondary exploratory analysis to find a strong treatment effect modifier. The GEM can be particularly useful for analysis of studies designed to discover biosignatures for treatment response.
2. Criteria for choosing a GEM
Here we introduce several optimality criteria for defining a GEM 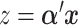 . For notational simplicity, we present the model in terms of the centered (at zero within treatment group) outcomes
. For notational simplicity, we present the model in terms of the centered (at zero within treatment group) outcomes 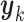 and predictors matrix
and predictors matrix 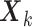 . The unrestricted linear model for the
. The unrestricted linear model for the 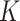 treatment groups is
treatment groups is
| (2.2) |
while the GEM model under consideration can be parameterized as
| (2.3) |
where 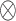 denotes the Kronecker product. The vector
denotes the Kronecker product. The vector 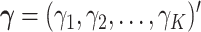 is the vector of the scaling coefficients for the GEM model (2.3). Because the predictors might be measured on different scales, a natural constraint that ensures identifiability is that the GEM
is the vector of the scaling coefficients for the GEM model (2.3). Because the predictors might be measured on different scales, a natural constraint that ensures identifiability is that the GEM 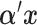 has a unit variance constraint
has a unit variance constraint
| (2.4) |
where 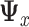 denotes the predictor covariance matrix (assumed equal across treatment groups as in a RCT). An unrestricted multiple regression model for
denotes the predictor covariance matrix (assumed equal across treatment groups as in a RCT). An unrestricted multiple regression model for 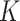 treatment groups (e.g. model (2.2)) with
treatment groups (e.g. model (2.2)) with 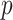 predictors and all interactions between treatment indicators and predictors, has
predictors and all interactions between treatment indicators and predictors, has 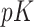 regression coefficients (not counting intercepts), whereas the restricted GEM model (2.3) is more parsimonious with only
regression coefficients (not counting intercepts), whereas the restricted GEM model (2.3) is more parsimonious with only 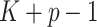 parameters (constraint (2.4) reduces the number of free parameters in
parameters (constraint (2.4) reduces the number of free parameters in 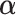 by one). Model (2.3) was considered by Follmann and Proschan (1999), but from a different perspective, where the vectors of regression coefficients
by one). Model (2.3) was considered by Follmann and Proschan (1999), but from a different perspective, where the vectors of regression coefficients 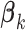 from (2.2) are all equal under the null hypothesis and (2.3) is the alternative hypothesis model. In addition to being more parsimonious and providing an intuitive interpretation with easy visualization, GEMs can also be used for making straightforward treatment decisions. When
from (2.2) are all equal under the null hypothesis and (2.3) is the alternative hypothesis model. In addition to being more parsimonious and providing an intuitive interpretation with easy visualization, GEMs can also be used for making straightforward treatment decisions. When 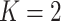 , for a new subject with covariates
, for a new subject with covariates 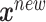 , the estimated treatment decision based on an unrestricted regression model is
, the estimated treatment decision based on an unrestricted regression model is 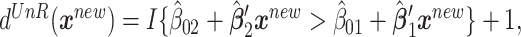 where
where 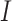 is an indicator function and
is an indicator function and 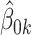 and
and 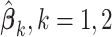 are the least squares (LS) estimates of the regression coefficients of model (2.2) written for the uncentered outcomes and predictors. Under a GEM model, the treatment decision is
are the least squares (LS) estimates of the regression coefficients of model (2.2) written for the uncentered outcomes and predictors. Under a GEM model, the treatment decision is 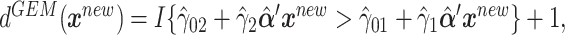 where
where 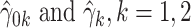 are the LS estimates of the scaling coefficients in model (2.3) for non-centered outcomes and predictors.
are the LS estimates of the scaling coefficients in model (2.3) for non-centered outcomes and predictors.
Since the GEM is defined as a linear combination of predictors, the GEM model lends itself most naturally to continuous predictors. In the results that follow, there is nothing that precludes the use of discrete predictors; only care must be taken in how discrete predictors are coded and how the corresponding GEM is to be interpreted. It is very common in clinical practice that categorical variables are actually discretized versions of continuous variables. If this is the case, we recommend that the original variable is used in the GEM instead of its discretized version.
There are several principled criteria one can use for choosing 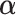 for optimizing the GEM. A natural choice obviously, in terms of moderator analysis, is to maximize the magnitude of interaction in the GEM model. Alternatively,
for optimizing the GEM. A natural choice obviously, in terms of moderator analysis, is to maximize the magnitude of interaction in the GEM model. Alternatively, 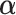 can be choosen to provide the best fit to the data using a GEM model which is consistent with the classic goal in linear models of minimizing the error sum of squares. A third approach, also consistent with the linear model framework, is to determine
can be choosen to provide the best fit to the data using a GEM model which is consistent with the classic goal in linear models of minimizing the error sum of squares. A third approach, also consistent with the linear model framework, is to determine 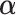 that maximizes the statistical significance of the interaction effects via an
that maximizes the statistical significance of the interaction effects via an 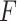 -test. Summarizing, we consider the following three criteria, which we refer to as the “numerator” (N), “denominator” (D) and “
-test. Summarizing, we consider the following three criteria, which we refer to as the “numerator” (N), “denominator” (D) and “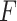 -ratio” (F) criteria, respectively:
-ratio” (F) criteria, respectively:
(N)Maximizing the interaction effect: Maximize the variability in the GEM scaling coefficients
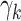 ’s in (2.3), corresponding to maximizing the Numerator of an
’s in (2.3), corresponding to maximizing the Numerator of an 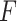 -test for significance of interaction effects. When there are
-test for significance of interaction effects. When there are 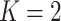 treatment groups, this is the same as maximizing the squared difference between the scaling coefficients
treatment groups, this is the same as maximizing the squared difference between the scaling coefficients 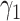 and
and 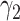 in the GEM model.
in the GEM model.(D)Fidelity to the data: Minimize the sum of squared residuals in the GEM model (2.3). This corresponds to the Denominator of an
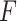 -test for significance of interaction effects.
-test for significance of interaction effects.(
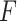 )
)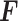 -ratio: Combine the first two criteria and maximize the ratio of the variability of the GEM scaling coefficients relative to the sum of squared residuals for the GEM model. This criterion corresponds to choosing
-ratio: Combine the first two criteria and maximize the ratio of the variability of the GEM scaling coefficients relative to the sum of squared residuals for the GEM model. This criterion corresponds to choosing 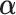 to maximize the
to maximize the 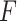 -test statistic when testing significance of interactions in the GEM model.
-test statistic when testing significance of interactions in the GEM model.
The method of LS is used to estimate the parameters of models (2.2) and (2.3). The common covariance matrix 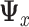 can be estimated by the pooled estimate of the predictor covariance matrix:
can be estimated by the pooled estimate of the predictor covariance matrix:
| (2.5) |
where 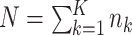 , where
, where 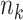 is the sample size in group
is the sample size in group 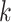 . The following notation will be used: let
. The following notation will be used: let 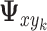 denote the vector of covariances between
denote the vector of covariances between 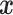 and the
and the 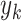 and
and 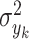 denote the variance of
denote the variance of 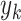 in the
in the 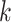 th group. Then the usual unconstrained vector of slope coefficients in the
th group. Then the usual unconstrained vector of slope coefficients in the 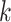 th treatment group in terms of population parameters and the weighted average coefficient vector are respectively
th treatment group in terms of population parameters and the weighted average coefficient vector are respectively
| (2.6) |
With a randomized experiment, equal weights (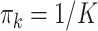 ) are used for
) are used for 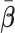 and that is the convention used in this article (although more flexible choices for weights are also possible). The GEM scaling coefficients
and that is the convention used in this article (although more flexible choices for weights are also possible). The GEM scaling coefficients 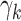 in (2.3) can be expressed equivalently, using (2.4), as
in (2.3) can be expressed equivalently, using (2.4), as
2.1. The “numerator” criterion: maximizing the interaction effect
This section derives the expression for 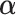 in the GEM model that maximizes the variance of a discrete random variable taking values
in the GEM model that maximizes the variance of a discrete random variable taking values 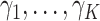 with respective probabilities
with respective probabilities 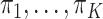 (i.e., the variance of the GEM slopes) which is given by
(i.e., the variance of the GEM slopes) which is given by
| (2.7) |
Denote the “between” group covariance matrix for the unconstrained slope coefficients as
| (2.8) |
Using (2.4), we seek 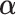 that maximizes
that maximizes 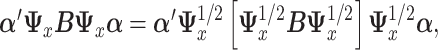 where
where 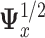 is the symmetric square-root of
is the symmetric square-root of 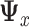 . The solution is
. The solution is 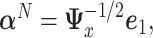 where
where 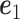 is the eigenvector of
is the eigenvector of 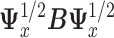 that is associated with the largest eigenvalue. To obtain an estimator
that is associated with the largest eigenvalue. To obtain an estimator 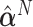 , we can apply the plug-in principal, use the pooled estimator
, we can apply the plug-in principal, use the pooled estimator 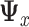 from (2.5) and the usual unrestricted LS estimators
from (2.5) and the usual unrestricted LS estimators 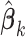 in place of the
in place of the 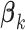 ’s. The GEM
’s. The GEM 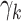 ’s and intercepts can be estimated via LS.
’s and intercepts can be estimated via LS.
In the case of 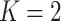 groups,
groups, 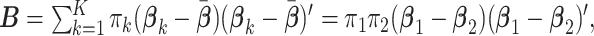 is a rank one matrix with eigenvector proportional to
is a rank one matrix with eigenvector proportional to 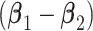 , in which case
, in which case
| (2.9) |
Section 1.1 of the supplementary material shows that for 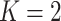 , in terms of population parameters, the treatment decision based on the unrestricted regression is equivalent to the treatment decision based on the numerator GEM model. Minor differences in the empirical decision rules from these two methods are due to differences in the LS estimates using the GEM predictor versus using the original predictors in the unrestricted model.
, in terms of population parameters, the treatment decision based on the unrestricted regression is equivalent to the treatment decision based on the numerator GEM model. Minor differences in the empirical decision rules from these two methods are due to differences in the LS estimates using the GEM predictor versus using the original predictors in the unrestricted model.
2.2. The “denominator” criterion: minimizing the residual error
This subsection gives the LS expression for 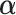 that minimizes the sum of squared residuals in a GEM model, that is, that provides the best fitting GEM model. Under the assumption of normality, the LS estimator coincides with the maximum likelihood estimator in the GEM linear model.
that minimizes the sum of squared residuals in a GEM model, that is, that provides the best fitting GEM model. Under the assumption of normality, the LS estimator coincides with the maximum likelihood estimator in the GEM linear model.
The sum of squared residuals from a standard linear model using LS can be written as 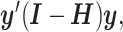 where
where 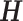 is the hat matrix and
is the hat matrix and 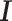 is an identity matrix. This sum of squared residuals (when divided by its associated degrees of freedom) is an estimate of the quantity
is an identity matrix. This sum of squared residuals (when divided by its associated degrees of freedom) is an estimate of the quantity 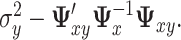 In the GEM model (2.3) with
In the GEM model (2.3) with 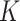 treatment arms, the hat matrix in the
treatment arms, the hat matrix in the 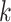 th group is
th group is 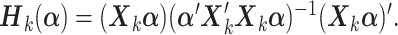 Letting
Letting 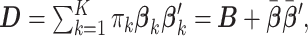 Section 1.2 of the supplementary material available at Biostatistics online shows that the
Section 1.2 of the supplementary material available at Biostatistics online shows that the 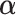 minimizing the “denominator” criterion is given by
minimizing the “denominator” criterion is given by 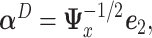 where
where 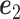 is the leading eigenvector of
is the leading eigenvector of 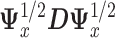 . As before,
. As before, 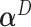 can be estimated by plugging in the LS estimators for
can be estimated by plugging in the LS estimators for 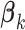 in the expression for
in the expression for 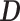 and using the sample covariance matrix of the pooled predictors (2.5) to estimate
and using the sample covariance matrix of the pooled predictors (2.5) to estimate 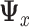 .
.
2.3. The “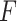 -criterion”: maximizing the
-criterion”: maximizing the 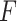 -statistic
-statistic
This section determines 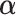 that maximizes the strength of the statistical evidence for the interaction effect in the GEM model (2.3) via an
that maximizes the strength of the statistical evidence for the interaction effect in the GEM model (2.3) via an 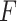 -test. With
-test. With 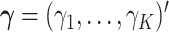 , we can consider the general linear hypothesis of
, we can consider the general linear hypothesis of 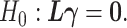 If
If 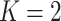 and
and 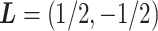 , the null hypothesis above states that the two groups have the same coefficients with respect to the GEM
, the null hypothesis above states that the two groups have the same coefficients with respect to the GEM 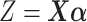 (i.e., no interaction). Thus, the goal is to determine
(i.e., no interaction). Thus, the goal is to determine 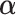 that maximizes the
that maximizes the 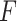 -ratio for testing
-ratio for testing 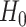 . From the two previous subsections, the
. From the two previous subsections, the 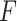 -ratio is proportional to the ratio with (2.7) in the numerator and a denominator corresponding to the residual sum-of-squares. The value of
-ratio is proportional to the ratio with (2.7) in the numerator and a denominator corresponding to the residual sum-of-squares. The value of 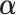 satisfying the “
satisfying the “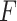 -ratio” criterion is
-ratio” criterion is 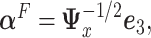 where
where 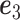 is the leading eigenvector of
is the leading eigenvector of
| (2.10) |
The derivation is in Section 1.3 of the supplementary material. Once again, 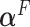 can be estimated by plugging parameter estimates into (2.10) and extracting the leading eigenvector.
can be estimated by plugging parameter estimates into (2.10) and extracting the leading eigenvector.
3. Fitting a GEM when the GEM model is misspecified
The GEM model allows us to combine several predictors into a single linear combination that has good treatment effect moderator properties. Generally, we do not expect the GEM model to be the true data generating model and (based on the above expressions), the “true” 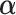 for the three criteria would differ. Consider two cases with
for the three criteria would differ. Consider two cases with 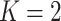 groups and
groups and 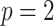 predictors
predictors 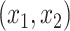 from a Gaussian distribution with means
from a Gaussian distribution with means 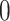 , variances 1 and 2, respectively, and a covariance 0.2:
, variances 1 and 2, respectively, and a covariance 0.2:
The deviation from a GEM model is measured by the angle 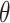 between the coefficient vectors
between the coefficient vectors 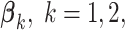 :
: 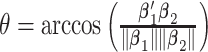 . In Case 1,
. In Case 1, 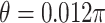 , and in Case 2,
, and in Case 2, 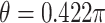 , so Case 1 is very “close” to a GEM model (
, so Case 1 is very “close” to a GEM model (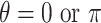 ), while Case 2 is almost as far away from GEM as possible (
), while Case 2 is almost as far away from GEM as possible (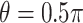 ). The “true”
). The “true” 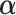 ’s are:
’s are:
From (2.10),  depends on the error variance; the results above are for a coefficient of determination
depends on the error variance; the results above are for a coefficient of determination 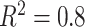 . As expected, the
. As expected, the 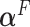 is closer to
is closer to 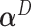 when the data is from a GEM model since the GEM regression fits the data well in this case, while when the model is far from a GEM model,
when the data is from a GEM model since the GEM regression fits the data well in this case, while when the model is far from a GEM model, 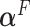 is closer to
is closer to 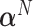 . This observation together with results from simulations suggest the use of the
. This observation together with results from simulations suggest the use of the 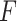 -criterion in practice.
-criterion in practice.
4. Permutation testing for the interaction in a GEM model
The GEM model estimation seeks to determine a linear combination of predictors that maximizes the evidence of an interaction effect using one of the three criteria described above. If there are no interaction effects between predictors and treatment indicators, then the GEM procedure would tend to generate anti-conservative 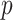 -values. A straightforward remedy to this problem is to fit the GEM model on many data sets with permuted treatment labels. A permutation
-values. A straightforward remedy to this problem is to fit the GEM model on many data sets with permuted treatment labels. A permutation 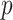 -value for testing an interaction effect can then be calculated as
-value for testing an interaction effect can then be calculated as
Theoretical details for using permutation tests for interaction effects in the presence of possible main effects have been investigated previously in the literature (e.g., Wang and others, 2015, p. 2046).
5. Simulation studies
An appealing feature of the GEM model is its utility for making individual treatment decisions, especially when 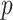 is large. In this subsection we investigate the value (1.1) of treatment decisions based on the three GEM criteria for both GEM and non-GEM generating models. Data sets were simulated under a variety of parameter settings. We varied the coefficient of determination
is large. In this subsection we investigate the value (1.1) of treatment decisions based on the three GEM criteria for both GEM and non-GEM generating models. Data sets were simulated under a variety of parameter settings. We varied the coefficient of determination 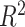 to be small (0.2), medium (0.5), and large (0.8). Another useful measure in the “effect size” (ES) of a moderator. For a regression model
to be small (0.2), medium (0.5), and large (0.8). Another useful measure in the “effect size” (ES) of a moderator. For a regression model 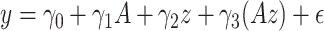 , with
, with 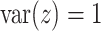 and a treatment indicator
and a treatment indicator 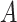 (
(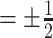 ), the ES (Kraemer, 2013) of
), the ES (Kraemer, 2013) of 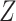 as an effect modifier is the proportion of the outcome variance (after removing the variance due to treatment) that is explained by the different relationships between
as an effect modifier is the proportion of the outcome variance (after removing the variance due to treatment) that is explained by the different relationships between 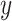 and
and 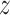 in the two treatment groups, that is,
in the two treatment groups, that is,
| (5.11) |
where 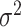 is the error variance (assuming equal error variances for all values of
is the error variance (assuming equal error variances for all values of  ). The simulations are similar for the GEM and non-GEM settings, except that the GEM models are characterized with respect to the effect size of
). The simulations are similar for the GEM and non-GEM settings, except that the GEM models are characterized with respect to the effect size of 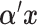 (using ES = 0.1 and 0.3), while the non-GEM cases are characterized with respect to the angle between the vectors of regression coefficients as described in Section 3; we use a small (
(using ES = 0.1 and 0.3), while the non-GEM cases are characterized with respect to the angle between the vectors of regression coefficients as described in Section 3; we use a small (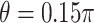 ) and a large (
) and a large (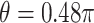 ) deviation from GEM.
) deviation from GEM.
The sample sizes per treatment group considered are 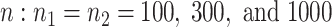 , mimicking typical situations in medical research. For each sample size, the number of predictors used were
, mimicking typical situations in medical research. For each sample size, the number of predictors used were 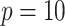 and
and 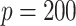 (except when
(except when 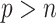 , namely
, namely 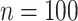 and
and 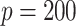 ). The predictors are generated from
). The predictors are generated from 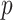 -variate normal distributions with mean zero and variances equal to 1, and small pairwise correlations (from
-variate normal distributions with mean zero and variances equal to 1, and small pairwise correlations (from  0.2 to 0.2) randomly selected, while ensuring a positive definite correlation matrix. For each
0.2 to 0.2) randomly selected, while ensuring a positive definite correlation matrix. For each 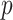 ,
, 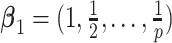 . Under GEM,
. Under GEM, 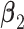 is computed to satisfy the respective
is computed to satisfy the respective 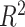 and
and 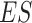 . Under non-GEM,
. Under non-GEM, 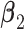 is obtained by adding random noise to the
is obtained by adding random noise to the 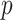 coefficients in
coefficients in 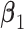 and computing the angle
and computing the angle 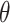 between
between 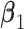 and
and 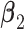 . More details about the values of
. More details about the values of 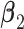 are given in Section 3.2 of the supplementary material. For each combination of
are given in Section 3.2 of the supplementary material. For each combination of 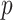 and the
and the 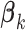 ’s (
’s (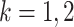 ), a large sample (
), a large sample ( ) is generated with known outcome values under both treatments and it is used to evaluate the “true” optimal population average outcome
) is generated with known outcome values under both treatments and it is used to evaluate the “true” optimal population average outcome 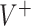 , which is the highest achievable value of any decision.
, which is the highest achievable value of any decision.
For each simulation configuration (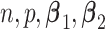 ,
, 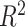 and ES),
and ES), 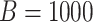 data sets are generated and estimates of
data sets are generated and estimates of 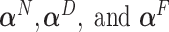 are computed, as well as
are computed, as well as  and
and 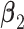 coefficients of the unrestricted regression model (2.2). These estimates are used to define treatment decisions as described in Section 2. These decisions are applied to the
coefficients of the unrestricted regression model (2.2). These estimates are used to define treatment decisions as described in Section 2. These decisions are applied to the 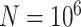 cases in the large data set to obtain the estimated values
cases in the large data set to obtain the estimated values 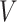 of the respective decisions
of the respective decisions 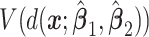 ,
, 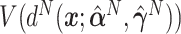 ,
, 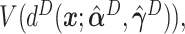 and
and 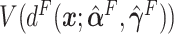 . For the sake of comparison, these values are expressed as a proportion of the “true” optimal average outcome
. For the sake of comparison, these values are expressed as a proportion of the “true” optimal average outcome 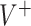 , and also taking into account the the worst average outcome
, and also taking into account the the worst average outcome 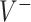 , which is obtained by choosing the worst (lower) outcome for each subject in the large data set. For example, the values of the treatment decision based on the “numerator” GEM approach are reported as
, which is obtained by choosing the worst (lower) outcome for each subject in the large data set. For example, the values of the treatment decision based on the “numerator” GEM approach are reported as 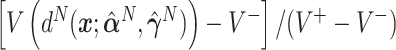 .
.
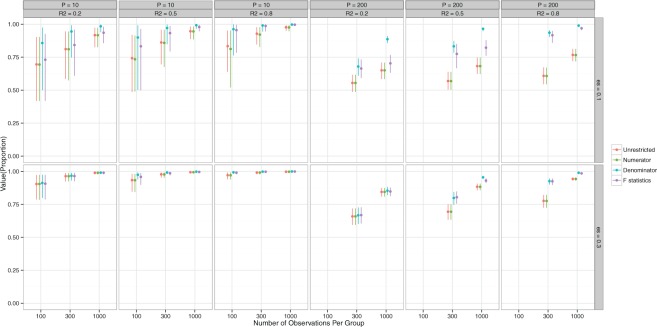
Figure 1 shows the means and the 95% Monte Carlo (MC) confidence intervals for the value of the decisions in the case of data generation from GEM models. A general observation is that for small ES of the GEM, the estimated decisions produce values that are about 10-20% lower than the “true” optimal value 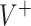 for
for 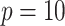 and still lower for
and still lower for 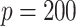 . How much worse the estimated decisions are compared with the “true” optimal average population outcome depends on the sample size and
. How much worse the estimated decisions are compared with the “true” optimal average population outcome depends on the sample size and 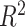 (performance improves with increasing sample size and
(performance improves with increasing sample size and 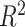 ). The “denominator” method is superior to the other two approaches, especially for larger
). The “denominator” method is superior to the other two approaches, especially for larger 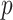 ’s and smaller ES’s, which is not be surprising since the denominator criterion is equivalent to the MLE objective when the error is normal and the true model is a GEM, as is the case here.
’s and smaller ES’s, which is not be surprising since the denominator criterion is equivalent to the MLE objective when the error is normal and the true model is a GEM, as is the case here.
Figure 1.
GEM data generation model. Mean and 95% Monte Carlo (MC) confidence intervals (based on the 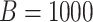 MC runs) of the values
MC runs) of the values 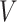 of the decisions, as a proportion
of the decisions, as a proportion 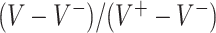 , for
, for 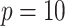 (left half of panels) and 200 (right half of panels), and for ES = 0.1 (top half of panels) and ES=0.3 (bottom half of panels). The three panels per (
(left half of panels) and 200 (right half of panels), and for ES = 0.1 (top half of panels) and ES=0.3 (bottom half of panels). The three panels per (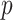 , ES) combination correspond to
, ES) combination correspond to 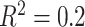 on the left,
on the left, 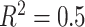 in the middle and
in the middle and 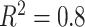 on the right. The method based on the unrestricted regression and the three GEM approaches are denoted as: (i) unrestricted—red color, most left; (ii) numerator criteria—green, second from left; (iii) denominator criterion—blue, third from left; (iv)
on the right. The method based on the unrestricted regression and the three GEM approaches are denoted as: (i) unrestricted—red color, most left; (ii) numerator criteria—green, second from left; (iii) denominator criterion—blue, third from left; (iv) 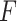 criterion—purple, most right. The “Number of observations” on the bottom horizontal axis is the sample size per group.
criterion—purple, most right. The “Number of observations” on the bottom horizontal axis is the sample size per group.
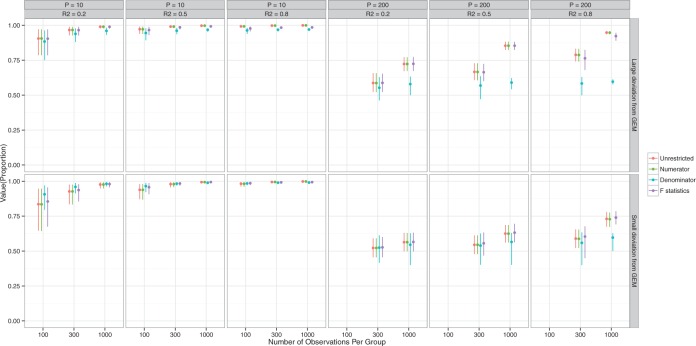
Figure 2 presents information similar to that on Figure 1, but here the data are generated under a general linear non-GEM model (2.2). It shows that even when the data is not generated from a GEM model, the criteria perform quite well for relatively small number of covariates 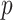 . For larger
. For larger 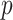 , larger sample sizes and larger
, larger sample sizes and larger 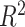 are needed to achieve good performance. The values of the decisions based on the denominator criterion are meaningfully inferior to the values of the decisions from the other methods as the deviation from GEM becomes large. The denominator’s inferiority becomes more pronounced as
are needed to achieve good performance. The values of the decisions based on the denominator criterion are meaningfully inferior to the values of the decisions from the other methods as the deviation from GEM becomes large. The denominator’s inferiority becomes more pronounced as 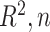 , and
, and 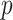 increase. Regardless of the data generating model, the values produced by the
increase. Regardless of the data generating model, the values produced by the 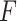 method are either the best or very close to the best values produced by either of the other methods compared here. Additionally, simulations were run using the non-GEM generating model except that a subset of predictors were discretized to be binary (5 out of 10 for
method are either the best or very close to the best values produced by either of the other methods compared here. Additionally, simulations were run using the non-GEM generating model except that a subset of predictors were discretized to be binary (5 out of 10 for 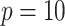 and 20 out of 200 when
and 20 out of 200 when 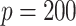 ); the results are very similar to those when all predictors are continuous—details are provided in the supplementary material.
); the results are very similar to those when all predictors are continuous—details are provided in the supplementary material.
Figure 2.
Non-GEM data generation model. Mean and 95% Monte Carlo (MC) confidence intervals (based on the 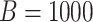 MC runs) of the values
MC runs) of the values 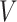 of the decisions, as a proportion
of the decisions, as a proportion 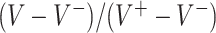 , for
, for 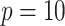 (left half of panels) and 200 (right half of panels), and for small deviation from GEM (top half of panels) and large deviation from GEM (bottom half of panels). The three panels per (
(left half of panels) and 200 (right half of panels), and for small deviation from GEM (top half of panels) and large deviation from GEM (bottom half of panels). The three panels per (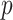 , deviation from GEM) combination correspond to
, deviation from GEM) combination correspond to 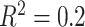 on the left,
on the left, 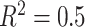 in the middle and
in the middle and 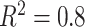 on the right. The method based on the unrestricted regression and the three GEM approaches are denoted as: (i) unrestricted—red color, most left; (ii) numerator criteria—green, second from left; (iii) denominator criterion—blue, third from left; (iv)
on the right. The method based on the unrestricted regression and the three GEM approaches are denoted as: (i) unrestricted—red color, most left; (ii) numerator criteria—green, second from left; (iii) denominator criterion—blue, third from left; (iv) 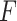 criterion—purple, most right. The “Number of observations” on the bottom horizontal axis is the sample size per group.
criterion—purple, most right. The “Number of observations” on the bottom horizontal axis is the sample size per group.
Section 4 of the supplementary material available at Biostatistics online presents results on the performance of the GEM methods in the case when the data generation is not from the linear model (2.2). There we show simulation results based on a doubly-robust estimation procedure using an augmented inverse probability weighted estimator (AIPWE) of the value 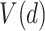 (Robins and others, 1994; Zhang and others, 2012b). Although the GEM approach based on the AIPWE does marginally worse than the unrestricted approach described in Zhang and others (2012b) using an example with
(Robins and others, 1994; Zhang and others, 2012b). Although the GEM approach based on the AIPWE does marginally worse than the unrestricted approach described in Zhang and others (2012b) using an example with 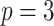 predictors, their approach becomes computationally infeasible for larger values of
predictors, their approach becomes computationally infeasible for larger values of 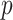 . In cases with large
. In cases with large 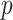 , the GEM reduces the dimensionality of the predictor space to
, the GEM reduces the dimensionality of the predictor space to 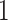 making the AIPWE approach fast and feasible.
making the AIPWE approach fast and feasible.
6. Application to data from a RCT
We illustrate the three GEM procedures using data from a RCT for the treatment of depression comparing antidepressants of the class of selective serotonin reuptake inhibitors (SSRI) against placebo. In addition to establishing the overall efficacy of the SSRI, the investigators were interested in finding biosignatures for SSRI treatment response. The investigators defined “biosignature” as a baseline patient characteristic or a combination of such characteristics, that constitutes a moderator of the treatment effect of SSRI vs. placebo.
Data from 76 and 72 subjects randomized to placebo and SSRI, respectively, were available. The outcome was the change from baseline (week 0) to 8 week of treatment on the Hamilton Rating Scale for Depression (HRSD). High values of HRSD indicate higher depression severity and thus positive change (week 0–week 8) indicate reduction of depression. The following baseline clinical measures were proposed as potential moderators: (i) level of anxiety (ii) severity of anger attack; (iii) suicidal risk; (iv) medical comorbidity score; and (v) experience of pleasure score.
Outcome was modeled as a linear function of a baseline measure, treatment indicator (SSRI 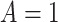 vs. placebo
vs. placebo 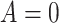 ) and the interaction between them for each measure individually. None of the interaction terms were statistically significant, see Table 1. A comparison of a full unrestricted model with all five predictors and their interactions with treatment against a reduced model without the interactions, yielded a non-significant
) and the interaction between them for each measure individually. None of the interaction terms were statistically significant, see Table 1. A comparison of a full unrestricted model with all five predictors and their interactions with treatment against a reduced model without the interactions, yielded a non-significant 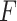 -test for the interactions (
-test for the interactions (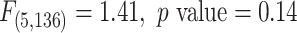 ). Thus, the usual approaches of treating each predictor separately or a full unrestricted model for all predictors fail to find evidence for heterogeneous effect of SSRI and consequently fails to identify patients who stand to benefit from or be harmed by it.
). Thus, the usual approaches of treating each predictor separately or a full unrestricted model for all predictors fail to find evidence for heterogeneous effect of SSRI and consequently fails to identify patients who stand to benefit from or be harmed by it.
Table 1.
SSRI Clinical biosignature: potential moderators of the efficacy of treatment with SSRI vs. placebo with respect to change in HRSD from baseline to week 8. The 3rd column gives the 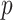 -values for the interaction predictor-by-treatment term and the 4th column gives the effect size of the predictor as a moderator of treatment effect from a regression model with only that variable as a predictor in addition to treatment. The last two columns give the regression coefficients from models with all five baseline measures as predictors for treatment
-values for the interaction predictor-by-treatment term and the 4th column gives the effect size of the predictor as a moderator of treatment effect from a regression model with only that variable as a predictor in addition to treatment. The last two columns give the regression coefficients from models with all five baseline measures as predictors for treatment 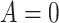 (placebo) and
(placebo) and 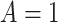 (SSRI) respectively
(SSRI) respectively
| Mean | St. dev. | Interaction | Effect | Reg. coefs | ||
|---|---|---|---|---|---|---|
| p value | size | 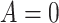 |
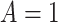 |
|||
| Anxiety | 5.36 | 1.80 | 0.797 | 0.020 | 1.06 | 1.44 |
| Anger attack | 3.05 | 2.12 | 0.671 | 0.034 |
 0.59 0.59 |
 0.09 0.09 |
| Suicide risk | 5.42 | 2.37 | 0.155 | 0.113 | 1.00 |
 0.38 0.38 |
| Medical comorbidity score | 2.01 | 2.78 | 0.092 | 0.140 | 0.11 |
 0.58 0.58 |
| Life pleasure score | 33.17 | 5.51 | 0.065 | 0.148 |
 0.20 0.20 |
0.04 |
Next, the linear combinations 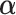 for the 3 GEM criteria were estimated, see Table 2. The numerator and
for the 3 GEM criteria were estimated, see Table 2. The numerator and 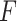 -criteria give similar results, but only the
-criteria give similar results, but only the 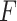 -criterion has a statistically significant permutation
-criterion has a statistically significant permutation 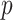 value (
value (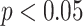 ). Note, that the effect sizes for the GEMs based on the numerator and the
). Note, that the effect sizes for the GEMs based on the numerator and the 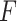 -criterion (which are very similar, both
-criterion (which are very similar, both 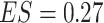 ), are double that of any individual predictor. The denominator GEM, on the other hand, does not produce a significant interaction
), are double that of any individual predictor. The denominator GEM, on the other hand, does not produce a significant interaction 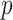 value (and also has a very small estimated ES), which is consistent with the observation that, since the angle between the unrestricted regression coefficient vectors is relatively large (
value (and also has a very small estimated ES), which is consistent with the observation that, since the angle between the unrestricted regression coefficient vectors is relatively large (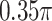 ), the model deviates quite a bit from a true GEM model.
), the model deviates quite a bit from a true GEM model.
Table 2.
GEM Model for SSRI clinical biosignature. The estimated GEMs of the SSRI treatment effect on change in HRSD. The bottom rows give the GEM effect sizes (row 6), permutation-adjusted 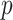 -values (row 7); the estimated value (1.1) of the decision based on GEM criteria along with a 95% cross-validated bootstrap confidence interval (CI) (row 8); the difference in value and 95% cross-validated bootstrap CI for the difference between the decision based on the respective GEM and the decision (i) give everyone placebo (row 9), (ii) give everyone SSRI (row 10), and (iii) give everyone SSRI or placebo at random (row 11).
-values (row 7); the estimated value (1.1) of the decision based on GEM criteria along with a 95% cross-validated bootstrap confidence interval (CI) (row 8); the difference in value and 95% cross-validated bootstrap CI for the difference between the decision based on the respective GEM and the decision (i) give everyone placebo (row 9), (ii) give everyone SSRI (row 10), and (iii) give everyone SSRI or placebo at random (row 11).
Estimated 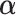
|
|||
|---|---|---|---|
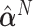 |
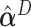 |
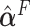 |
|
| Anxiety | 0.12 | 0.55 | 0.12 |
| Anger attack | 0.15 |
 0.15 0.15 |
0.15 |
| Suicide risk |
 0.42 0.42 |
0.14 |
 0.42 0.42 |
| Medical comorbidity score |
 0.21 0.21 |
 0.10 0.10 |
 0.21 0.21 |
| Life pleasure score | 0.07 | -0.04 | 0.07 |
| Effect size | 0.27 | 0.01 | 0.27 |
Permutation 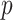 -value -value |
0.061 | 0.895 | 0.048 |
| Value of GEM | 8.03 | 7.60 | 8.03 |
| (95% CI) | (6.28, 9.78) | (5.62, 9.43) | (6.21, 9.68) |
Value of GEM  Value of placebo Value of placebo |
2.02 | 1.57 | 2.00 |
| (95% CI) | (1.97, 2.06) | (1.52, 1.62) | (1.96, 2.05) |
Value of GEM  Value of SSRI Value of SSRI |
0.52 | 0.07 | 0.50 |
| (95% CI) | (0.48, 0.55) | (0.04, 0.10) | (0.46, 0.54) |
Value of GEM  Value of random Value of random |
1.29 | 0.84 | 1.27 |
| (95% CI) | (1.25, 1.32) | (0.80, 0.87) | (1.24, 1.31) |
For the sake of comparison, estimates of the value for the three GEM criteria were obtained using an Inverse Probability Weighted Estimator (IPWE) 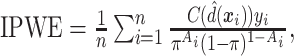 where
where 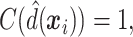 if the treatment assignment
if the treatment assignment 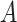 and treatment decision
and treatment decision 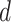 coincide for subject
coincide for subject 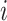 with covariates
with covariates 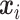 . Here,
. Here, 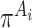 is the probability of treatment assignment, which will be a constant for a RCT and is 0.5 in this example. Row 8 of Table 2 gives a 95% cross-validation bootstrap confidence interval (using 1000 bootstrap samples) for the value of each GEM criterion. The CIs were computed using a 10-fold cross-validation on each bootstrap sample, where treatment decisions were estimated by applying the respective GEM approach to 9 of 10 non-overlapping subsamples of equal size, and then applied to the remaining 10th subsample to obtain an estimate of the value of the treatment decision and finally averaging those estimates across the 10 folds of the cross-validation. As Table 2 shows, the
is the probability of treatment assignment, which will be a constant for a RCT and is 0.5 in this example. Row 8 of Table 2 gives a 95% cross-validation bootstrap confidence interval (using 1000 bootstrap samples) for the value of each GEM criterion. The CIs were computed using a 10-fold cross-validation on each bootstrap sample, where treatment decisions were estimated by applying the respective GEM approach to 9 of 10 non-overlapping subsamples of equal size, and then applied to the remaining 10th subsample to obtain an estimate of the value of the treatment decision and finally averaging those estimates across the 10 folds of the cross-validation. As Table 2 shows, the 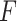 and numerator approaches produce very similar bootstrap confidence intervals for the value of the decision, while the denominator criterion results in a lower decision value that has a wider 95% CI. The last three rows of Table 2 show the differences between the values of the treatment decisions derived from each the three GEM approaches and the value of three commonly used comparison decisions (i) give everyone placebo; (ii) give everyone SSRI; and (iii) give placebo and SSRI at random estimated by the same cross-validation approach based on 1000 bootstrap samples.
and numerator approaches produce very similar bootstrap confidence intervals for the value of the decision, while the denominator criterion results in a lower decision value that has a wider 95% CI. The last three rows of Table 2 show the differences between the values of the treatment decisions derived from each the three GEM approaches and the value of three commonly used comparison decisions (i) give everyone placebo; (ii) give everyone SSRI; and (iii) give placebo and SSRI at random estimated by the same cross-validation approach based on 1000 bootstrap samples.
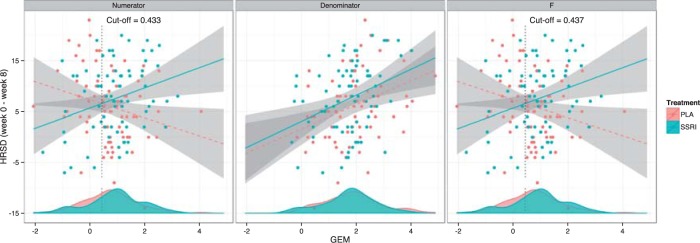
The results from the GEM approaches are visually presented in Figure 3. The GEM analysis using the 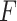 -ratio criterion (similar to the numerator criterion) results in the conclusion that 30.4% of the target population (to the left of the vertical lines at GEM
-ratio criterion (similar to the numerator criterion) results in the conclusion that 30.4% of the target population (to the left of the vertical lines at GEM 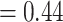 ) does not benefit from SSRI treatment. The decision based on the
) does not benefit from SSRI treatment. The decision based on the 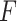 GEM could be not to prescribe SSRI to those subjects with
GEM could be not to prescribe SSRI to those subjects with 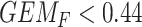 ; alternatively, one might choose to give SSRI only to patients with a
; alternatively, one might choose to give SSRI only to patients with a 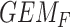 scores in the range where the 95% CIs for placebo and SSRI GEM regressions do not overlap, that, GEM
scores in the range where the 95% CIs for placebo and SSRI GEM regressions do not overlap, that, GEM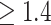 . These results are consistent with the fact that many antidepressant trials fail to show efficacy, or show only small benefits, for example, about 25–30% difference in response rates of the antidepressants vs. placebo (60–65% vs. 30–35% respectively).
. These results are consistent with the fact that many antidepressant trials fail to show efficacy, or show only small benefits, for example, about 25–30% difference in response rates of the antidepressants vs. placebo (60–65% vs. 30–35% respectively).
Figure 3.
The relationship between the GEMs obtained from the three criteria and the change in depression (HRSD) from baseline to week 8 for the SSRI (blue) and placebo (red) interventions. The GEMs corresponding to each of the criteria are plotted on the horizontal axis. The lines are the LS lines and the shaded areas indicate the 95% pointwise CIs. The densities of the respective GEMs for the two treatment groups are indicted at the lower part of each panel. The vertical lines indicate the cut-off point on the linear combinations of predictors above which a depressed patient would benefit from treatment with SSRI.
7. Discussion
This article has shown how to combine several baseline characteristics into a single generated effect moderator in the context of the classic linear model. Closed-form expressions have been derived for these GEMs that do not require complex iterative computations. The GEM offers a straightforward approach to determine beneficial treatments for patients. From this perspective, GEMs can be viewed as indices for treatment decisions. Of the three criteria, we generally recommend the 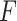 -criterion, because it simultaneously maximizes the interaction effect (the numerator) and also minimizes the prediction error (denominator) in the class of GEM models. Additionally, from our results, the
-criterion, because it simultaneously maximizes the interaction effect (the numerator) and also minimizes the prediction error (denominator) in the class of GEM models. Additionally, from our results, the 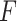 -criterion’s performance is either optimal or very close to optimal with respect to making rules for treatment decisions with highest values.
-criterion’s performance is either optimal or very close to optimal with respect to making rules for treatment decisions with highest values.
In practice, after conducting the main hypotheses testing in efficacy studies, investigators attempt to discover baseline patient features that moderate the effect of treatment. Given that (if present) variables with large moderating effects of treatments for most illnesses have already been discovered, it is not surprising that researchers regularly fail to discover other moderators in studies where the primary goal is to establish efficacy. The proposed methods show that combining patient characteristics with little to no moderating effects of a treatment can result in a strong treatment effect modifier that can help with making treatment decisions. Of course, any treatment decision has to be validated in properly designed studies; for example, a 3-arm RCT where the experimental treatment, the control treatment and treatment according to the investigated treatment decision are compared. The proposed methodology is expected to be of particular utility in studies specifically designed to discover biosignatures for response to treatment, as discussed in the Introduction.
Several generalizations of the GEM procedure are currently under development, such as extending the GEM to generalized linear models and longitudinal outcomes. Work is also underway to allow the outcome to depend on nonparametric functions of GEMs, similar to generalized additive models. It will be useful to compare the linear GEM model developed here and a more flexible nonparametric GEM model to other methods for precision medicine for providing guidance in making treatment decisions.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org
Acknowledgements
The authors are thankful to the editors and three reviewers whose feedback has greatly improved this article. Conflict of interest: None declared.
Funding
National Institutes of Health grant R01 MH099003.
References
- Ciarleglio A., Petkova E., Tarpey T. and Ogden R. T. (2015). Treatment decisions based on scalar and functional baseline covariates. Biometrics 71, 884–894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emura T., Chen, Y.-H. and Chen, H.-Y. (2012). Survival prediction based on compound covariate under cox proportional hazards models. PLoS One 7, 247627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Follmann D. A. and Proschan M. A. (1999). A multivariate test of interaction for use in clinical trials. Biometrics 55, 1151–1155. [DOI] [PubMed] [Google Scholar]
- Gail M. and Simon R. (1985). Testing for qualitative interactions between treatment effects and patient subsets. Biometrics 41, 361–372. [PubMed] [Google Scholar]
- Gunter L., Zhu J. and Murphy S. A. (2011). Variable selection for qualitative interactions in presonalized medicine while controlling the family-wise error rate. Journal of Biopharmaceutical Statistics 21, 1063–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang C., Janes H. and Huang Y. (2014). Combining biomarkers to optimize patient treatment recommendations. Biometrics 70, 695–707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraemer H. C. (2013). Discovering, comparing, and combining moderators of treatment on outcome after randomized clinical trials: a parametric approach. Statistics in Medicine 32, 1964–1973. [DOI] [PubMed] [Google Scholar]
- Laber E. B. and Zhao Y.-Q. (2015). Tree-based methods for individualized treatment regimes. Biometrika 102, 501–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu W., Zhang H. H. and Zeng D. (2011). Variable selection for optimal treatment decision. Statistical Methods in Medical Research 22, 493–504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKeague I. W. and Qian M. (2014). Estimation of treatment policies based on functional predictors. Statistica Sinica 24, 1461–1485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy S. A. (2003). Optimal dynamic treatment regimes (with discussion). Journal of the Royal Statistical Society, Series B 58, 331–366. [Google Scholar]
- Qian M. and Murphy S. (2011). Performance guarantees for individualized treatment rules. Annals of Statistics 39, 1180–1210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robins J. M. (2004). Optimal structured nested models for optimal sequential decisions. In: Heagerty P. J. and Lina D. Y.. (editors) Proceedings of the Second Seattle Symposium on Biostatistics. New York: Springer, pp. 189–326. [Google Scholar]
- Robins J., Orellana L. and Rotnizky A. (2008). Estimation and extrapolation of optimal treatment and testing strategies. Statistics in Medicine 27, 4678–4721. [DOI] [PubMed] [Google Scholar]
- Robins J. M., Rotnitzky A. and Zhao L. P. (1994). Estimation of regression coefficients when some regressors are not always observed. Journal of the American Statistical Association 89, 846–866. [Google Scholar]
- Song R., Kosorok M., Zeng D., Zhao Y., Laber E. B. and Yuan M. (2015). On sparse representation for optimal individualized treatment selection with penalized outcome weighted learning. Stat 4, 59–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song X. and Pepe M. S. (2004). Evaluating markers for selecting a patient’s treatment. Biometrics 60, 874–883. [DOI] [PubMed] [Google Scholar]
- Tian L. and Tibshirani R. J. (2011). Adaptive index models for market-based risk stratification. Biostatistics 12, 68–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tukey J. W. (1991). Use of many covariates in clinical trials. International Statistical Review 59, 123–137. [Google Scholar]
- Tukey J. W. (1993). Tightening the clinical trial. Controlled Clinical Trials 14, 266–285. [DOI] [PubMed] [Google Scholar]
- Wang R., Schoenfeld D. A., Hoeppner B. and Evins A. E. (2015). Detecting treatment-covariate interactions using permutation methods. Statistics in Medicine 34, 2035–2047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang R. and Ware J. H. (2013). Detecting moderator effects using subgroup analyses. Prevention Science 14, 111–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wellek S. (1997). Testing for absence of qualitative interactions between risk factors and treatment effect. Biometrical Journal 39, 809–821. [Google Scholar]
- Zhang B., Tsiatis A. A., Davidian M., Zhang M. and Laber E. (2012a). Estimating optimal treatment regimes from classification perspective. Stat 1, 103–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B., Tsiatis A. A., Laber E. B. and Davidian M. (2012b). A robust method for estimating optimal treatment regimes. Biometrics 68, 1010–1018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y., Zeng D., Rush A. J. and Kosorok M. P. (2012). Estimating individualized treatment rules using outcome weighted learning. Journal of the American Statistical Association 107, 1106–1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y., Zheng D., Laber E. B. and Kosorrok M. R. (2015). New statistical learning methods for estimating optimal dynamic treatment regimes. Journal of the American Statistical Association 110, 583–598. [DOI] [PMC free article] [PubMed] [Google Scholar]