Abstract
Marginal structural models (MSMs) are a general class of causal models for specifying the average effect of treatment on an outcome. These models can accommodate discrete or continuous treatments, as well as treatment effect heterogeneity (causal effect modification). The literature on estimation of MSM parameters has been dominated by semiparametric estimation methods, such as inverse probability of treatment weighted (IPTW). Likelihood-based methods have received little development, probably in part due to the need to integrate out confounders from the likelihood and due to reluctance to make parametric modeling assumptions. In this article we develop a fully Bayesian MSM for continuous and survival outcomes. In particular, we take a Bayesian nonparametric (BNP) approach, using a combination of a dependent Dirichlet process and Gaussian process to model the observed data. The BNP approach, like semiparametric methods such as IPTW, does not require specifying a parametric outcome distribution. Moreover, by using a likelihood-based method, there are potential gains in efficiency over semiparametric methods. An additional advantage of taking a fully Bayesian approach is the ability to account for uncertainty in our (uncheckable) identifying assumption. To this end, we propose informative prior distributions that can be used to capture uncertainty about the identifying “no unmeasured confounders” assumption. Thus, posterior inference about the causal effect parameters can reflect the degree of uncertainty about this assumption. The performance of the methodology is evaluated in several simulation studies. The results show substantial efficiency gains over semiparametric methods, and very little efficiency loss over correctly specified maximum likelihood estimates. The method is also applied to data from a study on neurocognitive performance in HIV-infected women and a study of the comparative effectiveness of antihypertensive drug classes.
Keywords: Causal inference, Dirichlet process, Gaussian process, g-Formula, Observational studies, Sensitivity analysis
1. Introduction
Marginal structural models (MSMs; Robins, 2000) are a class of marginal (not conditional on confounders) causal models. The causal effect parameters represent contrasts between population average causal outcomes. The models are flexible enough to allow discrete or continuous treatments and interactions with baseline covariates. A variety of semiparametric estimation methods have been developed for these models. The most widely used method involves inverse probability of treatment weighted (IPTW; Robins, Hernán, and Brumback, 2000) estimation or augmented IPTW estimation (Scharfstein and others, 1999; van der Laan and Robins, 2003). The latter has the advantage of having the double robustness property—only one of the outcome model or propensity score model needs to be correctly specified in order for the causal effect estimator to be consistent. Other semiparametric methods include those based on empirical likelihood (Tan, 2010) and targeted maximum likelihood (TMLE; Rosenblum and van der Laan, 2010).
Likedhood-based approaches to estimation of MSM parameters can potentially result in efficiency gains over semiparametric approaches. Among likelihood-based approaches, Bayesian methods have some additional appealing features, including obtaining full posterior distributions rather than simply point estimates and standard errors and the ability to capture uncertainty in assumptions via prior distributions; the final point is particularly important since all causal inference approaches require the analyst to make data-uncheckable assumptions. Despite these potential advantages, few maximum likelihood or Bayesian approaches have been developed for MSMs. A general framework for estimating causal effects using likelihood-based methods is the g-formula (Robins, 1986). Several recent papers have demonstrated the g-formula approach, though using fully parametric models in the different context of estimation of causal effects of dynamic treatment regimes. (Young and others, 2011; Wahed and Thall, 2013). Saarela and others (2015) recently proposed a Bayesian-like approach for MSM estimation. Their method differs from ours in that they take a Bayesian approach for IPTW, but do not specify a fully Bayesian MSM in general. As pointed out by Robins, Hernán, and Wasserman (2015), a fully Bayesian approach cannot be a function of the propensity score. Karabatsos Walker (2012) and Hoshino (2013) developed Bayesian nonparametric (BNP) models for the narrower problem of estimating an average causal effect between two treatment groups with no effect modification. Hill (2011) proposed the use of Bayesian adaptive regression trees (BART) for estimating causal effects in the point treatment setting. BART allows flexible modeling of the mean function (function of treatment and confounders). However, that work differed from ours in that it focused primarily on conditional, rather than marginal effects, and required a normal distribution assumption for the outcome. Our work is most similar to Xu and others (2015) in terms of the BNP approach, but their method was developed for a different problem (dynamic treatment regimes).
There are several challenges with specifying a fully Bayesian MSM. One is that we would like to minimize parametric assumptions about the distribution of the outcome given treatment and confounders. Another is that the potential outcomes are assumed to be exchangeable given all confounders, but the causal model is specified marginally (not conditional on confounders). Thus, the confounders have to be integrated out from the likelihood in a way that preserves the assumed causal structure. We deal with these challenges as follows. We specify a dependent Dirichlet process (DDP) for the outcome given confounders (MacEachern, 1999). This DDP is set up in such a way to ensure compatibility between the conditional distribution and assumed MSM and to facilitate “simple” computations. For the mean model, we use a Gaussian process (GP; Neal, 1998). The GP model allows for nonparametric estimation of the mean function of confounders.
We apply the methods to data from two studies—one with continuous outcomes and one with a survival outcome. The first example is a study of neurocognitive performance of human immunodeficiency (HIV)-sero positive women after being treated with either a highly active antiretroviral therapy (HAART) drug regimen or a non-HAART drug regimen (Cohen and others, 2001). The participants of this study were a subset of the prospective HIV Epidemiology Research (HER) Study (Smith and others, 1997) who had severely impaired immune function and who had at least two neurocognitive exams in 1993–1999. The outcome was the change in score on various neurocognitive tasks over time. Previous analyses of the data relied on parametric assumptions about the mean function of covariates (Roy and others, 2003) or the outcome distribution (Cohen and others, 2001). However, there is no prior reason to believe that the outcome distribution will be normal. In addition, there are several important confounding variables, including age, depression score, and intravenous drug use, and it is not apparent what kind of relationships with the outcome are reasonable to assume. Our BNP model allows for flexible modeling of these distributions and estimation of effect modification by recent alcohol use.
In the second example, we analyzed data from a study of the comparative effectiveness of angiotensin-converting enzyme inhibitors (ACEI) versus angiotensin II receptor blockers (ARBs) for treatment of hypertension (Roy and others, 2012). The data are from Geisinger Clinic electronic health records of an incident cohort of patients who were prescribed either an (ACEI) or ARB between 2001 and 2008. The outcome is all cause mortality, modeled as a (possibly censored) survival time.
In Section 2 we review MSMs for the point treatments setting. The BNP method is developed in Section 3, including Gibbs sampling steps and sensitivity analysis. Section 4 presents several simulation studies that are used to evaluate the BNP approach and compare its performance with other approaches. The methods are applied to the two studies in Section 5. Finally, there is a discussion in Section 6.
2. MSMs for Point Treatments
We consider the situation where there is treatment 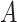 , confounders
, confounders 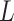 , and an outcome
, and an outcome 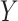 . Treatment is measured at one time and could be continuous or discrete. Treatment assignment might have depended on baseline, pretreatment, variables
. Treatment is measured at one time and could be continuous or discrete. Treatment assignment might have depended on baseline, pretreatment, variables 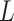 . The outcome
. The outcome 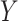 is measured sometime after baseline, and for this article we restrict it to continuous or survival cases.
is measured sometime after baseline, and for this article we restrict it to continuous or survival cases.
Denote by 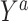 the potential outcome if the subject had been assigned to treatment level
the potential outcome if the subject had been assigned to treatment level 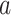 . For example, in the binary treatment case each subject would have two potential outcomes
. For example, in the binary treatment case each subject would have two potential outcomes 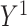 if they receive treatment and
if they receive treatment and 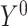 if they do not.
if they do not.
MSMs are a popular class of causal models (Robins, 2000; Robins, Hernán, and Brumback, 2000). They are models for the marginal mean of potential outcomes (or for the mean given a subset of covariates). Let 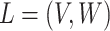 so that
so that 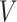 and
and 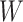 are subsets of the covariates
are subsets of the covariates 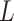 . The covariates
. The covariates 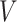 are covariates that we want to condition on as part of the causal model, possibily from the perspective of effect modification. Covariates
are covariates that we want to condition on as part of the causal model, possibily from the perspective of effect modification. Covariates 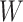 are simply other covariates that we need to control for. The full set of covariates
are simply other covariates that we need to control for. The full set of covariates 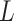 are necessary to control for confounding, and can be selected using standard methodology (Sauer and others, 2013). We consider MSMs of the form
are necessary to control for confounding, and can be selected using standard methodology (Sauer and others, 2013). We consider MSMs of the form
| (2.1) |
for all 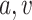 , where
, where 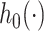 and
and 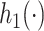 are known functions and
are known functions and 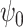 and
and  are unknown parameters. The
are unknown parameters. The 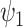 parameters represent causal treatment effects and are of primary interest.
parameters represent causal treatment effects and are of primary interest.
For example, consider the special case of a linear model with binary treatment and no covariates 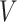 that we wish to condition on. We could write model 2.1 as
that we wish to condition on. We could write model 2.1 as 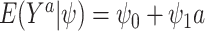 , for
, for 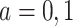 . Thus, the average causal effect (ACE) is
. Thus, the average causal effect (ACE) is 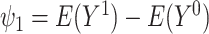 .
.
As an alternative example, consider a continuous treatment (e.g., dose of a drug) and a single binary effect modifier 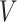 . Here we might assume
. Here we might assume 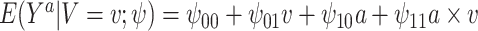 . Thus, among subjects with
. Thus, among subjects with  , each unit increase in
, each unit increase in 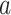 would increase the mean of the potential outcome by
would increase the mean of the potential outcome by 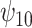 . This causal slope would differ between subjects with
. This causal slope would differ between subjects with 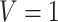 and
and  by
by 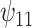 .
.
To identify the causal parameters, we make three standard causal assumptions. The first is consistency, which is that 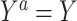 among subjects with
among subjects with 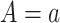 , for all
, for all 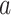 . This assumption implies that
. This assumption implies that 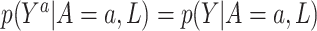 . The next assumption is positivity
. The next assumption is positivity 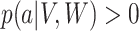 , which states that each treatment level has nonzero probability for every confounder level. The final assumption is ignorability:
, which states that each treatment level has nonzero probability for every confounder level. The final assumption is ignorability: 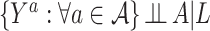 . This assumption implies that
. This assumption implies that 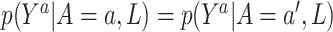 . In other words, given confounders
. In other words, given confounders 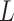 , treatment can be thought of as randomly assigned. This is also known as the “no unmeasured confounders” assumption. Because this assumption is not checkable and might be violated in practice, it is important to carry out a sensitivity analysis. We develop a sensitivity analysis method in Section 3.3 and demonstrate its application in Section 5.1.2.
, treatment can be thought of as randomly assigned. This is also known as the “no unmeasured confounders” assumption. Because this assumption is not checkable and might be violated in practice, it is important to carry out a sensitivity analysis. We develop a sensitivity analysis method in Section 3.3 and demonstrate its application in Section 5.1.2.
3. The Model and Inference
Our goal is to develop a flexible model for 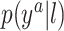 that enforces the MSM structure. The model we propose has flexibility both in terms of the mean function and the residual distribution.
that enforces the MSM structure. The model we propose has flexibility both in terms of the mean function and the residual distribution.
We model the conditional distribution 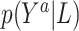 and constrain it to ensure that the MSM in (2.1) holds. We consider a dependent DP (DDP; (DDP; MacEachern, 1999; Gelfand and others, 2005; Xu and others, 2015) that accommodates the MSM constraint. Specifically, we assume
and constrain it to ensure that the MSM in (2.1) holds. We consider a dependent DP (DDP; (DDP; MacEachern, 1999; Gelfand and others, 2005; Xu and others, 2015) that accommodates the MSM constraint. Specifically, we assume
| (3.1) |
where 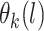 (a function of covariates) and
(a function of covariates) and 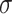 are the mean and standard deviation of the
are the mean and standard deviation of the 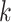 th component of the mixture model. We will derive
th component of the mixture model. We will derive 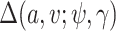 below, but for now we can think of it as a function of
below, but for now we can think of it as a function of 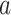 and
and 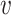 , but not
, but not 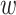 . Notice that this is an infinite mixture of normals, with weight
. Notice that this is an infinite mixture of normals, with weight 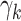 corresponding to the
corresponding to the 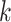 th mixture component,
th mixture component, 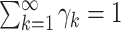 . The prior distribution for the weights,
. The prior distribution for the weights, 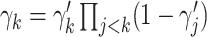 , is specified as
, is specified as 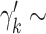 Beta
Beta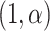 . Given a correctly specified mean function,
. Given a correctly specified mean function, 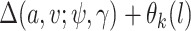 , we have an ordinary DP mixture for the outcome
, we have an ordinary DP mixture for the outcome 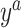 . This specification should be flexible enough to handle multiple modes, skewness, etc.
. This specification should be flexible enough to handle multiple modes, skewness, etc.
We next specify a flexible model for the mean function 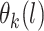 . We assume the following GP prior for
. We assume the following GP prior for 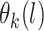 ,
, 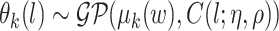 (Neal, 1998; Xu and others, 2015). A GP is a distribution over a function, here
(Neal, 1998; Xu and others, 2015). A GP is a distribution over a function, here 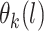 . For any set of points
. For any set of points 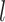 , the joint distribution
, the joint distribution 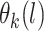 is multivariate normal. We specify the prior mean function as a linear regression
is multivariate normal. We specify the prior mean function as a linear regression 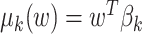 where the
where the 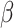 ’s are unknown regression coefficients, but more complex forms of this prior mean are also possible. Next, we define the covariance function as follows. The
’s are unknown regression coefficients, but more complex forms of this prior mean are also possible. Next, we define the covariance function as follows. The 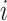 th row and
th row and 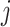 th column of
th column of 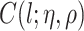 is
is 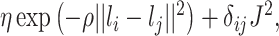 where
where 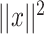 is the squared Euclidean distance of
is the squared Euclidean distance of 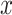 ,
, 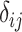 , Kronecker’s delta, takes a value of 1 if and only if
, Kronecker’s delta, takes a value of 1 if and only if 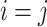 ,
, 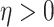 and
and 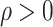 are unknown parameters, and
are unknown parameters, and 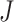 is set to a small value (we use 0.1). To help understand the model, imagine that the
is set to a small value (we use 0.1). To help understand the model, imagine that the 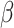 ’s have a prior mean of 0 with variance
’s have a prior mean of 0 with variance 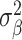 and that the
and that the 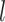 ’s have mean 0. Then, the prior covariance between the mean function at
’s have mean 0. Then, the prior covariance between the mean function at 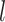 and
and 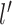 is
is
where 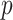 is the number of covariates in
is the number of covariates in 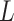 . The first term allows for nonstationarity. The second term is a function of the squared distance between
. The first term allows for nonstationarity. The second term is a function of the squared distance between 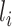 and
and 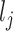 , leading to a larger covariance for smaller distances. The size of
, leading to a larger covariance for smaller distances. The size of 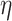 determines how much the mean function varies from linearity. Finally, the last term is necessary simply to ensure a positive definite matrix (variance larger than the covariance between two subjects who have same
determines how much the mean function varies from linearity. Finally, the last term is necessary simply to ensure a positive definite matrix (variance larger than the covariance between two subjects who have same 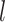 ’s). We will assume informative prior distributions for
’s). We will assume informative prior distributions for 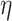 and
and 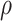 . Because inversion of
. Because inversion of 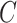 will be necessary, it will be important for
will be necessary, it will be important for 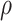 to not be too small (small values of
to not be too small (small values of 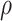 lead to higher correlations between
lead to higher correlations between 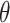 ’s). In general, larger values of
’s). In general, larger values of 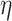 lead to more variation of the mean away from the linearity assumption. Essentially, large values of
lead to more variation of the mean away from the linearity assumption. Essentially, large values of 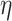 will lead to better a fit, but the log
will lead to better a fit, but the log that is part of the likelihood will act as a penalty term (preventing overfitting). The
that is part of the likelihood will act as a penalty term (preventing overfitting). The 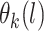 for the data is an
for the data is an 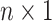 vector
vector 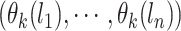 , where
, where 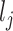 is the
is the 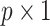 vector. Note that more complicated forms of
vector. Note that more complicated forms of 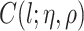 could be specified, providing added flexibility. Some of these forms are described in Neal (1998). However, having additional parameters in the covariance function can greatly increase computing time.
could be specified, providing added flexibility. Some of these forms are described in Neal (1998). However, having additional parameters in the covariance function can greatly increase computing time.
We next derive the form of 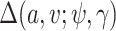 . Note that
. Note that 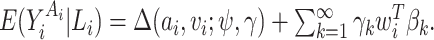 This implies that
This implies that
where 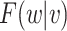 is the conditional distribution of
is the conditional distribution of 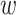 given
given 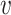 . This equation along with (2.1) imply
. This equation along with (2.1) imply
| (3.2) |
For solving the integral in 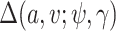 , we use the empirical distribution of
, we use the empirical distribution of 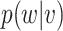 . This should work well if, as is usually the case,
. This should work well if, as is usually the case, 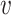 is discrete and of low dimension. Specifically, we can write
is discrete and of low dimension. Specifically, we can write
| (3.3) |
and then approximate the integral
for all 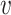 , where
, where 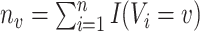 . Finally, denote by
. Finally, denote by 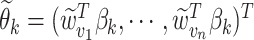 the corresponding
the corresponding 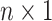 vector. The form of (3.3) greatly simplifies posterior computations (details in Section 1 of the supplementary materials).
vector. The form of (3.3) greatly simplifies posterior computations (details in Section 1 of the supplementary materials).
Prior distributions. For the coefficients of 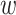 in the GP model,
in the GP model, 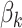 , we assume normal priors
, we assume normal priors 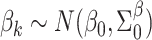 , where
, where 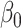 and
and 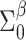 are known. These can be chosen following recommendations by Taddy (2008). We assume diffuse normal priors for the MSM parameters
are known. These can be chosen following recommendations by Taddy (2008). We assume diffuse normal priors for the MSM parameters 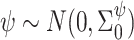 , where
, where 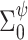 is a diagonal matrix with large values on the diagonal. For the DP precision parameter
is a diagonal matrix with large values on the diagonal. For the DP precision parameter 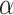 , we assume
, we assume 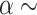 inv-Gam
inv-Gam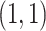 . This prior is centered at a relatively low value, but has a longer tail than a Gam
. This prior is centered at a relatively low value, but has a longer tail than a Gam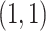 distribution. For the prior correlation-like parameter in the GP
distribution. For the prior correlation-like parameter in the GP 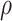 , we assume
, we assume 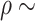 Gam
Gam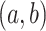 . The values we choose here depend on the application, but in some cases it is computationally beneficial to have less prior weight near 0 (as
. The values we choose here depend on the application, but in some cases it is computationally beneficial to have less prior weight near 0 (as 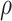 very close to 0 leads to a near singular covariance matrix). For the variance parameters, we assume the following:
very close to 0 leads to a near singular covariance matrix). For the variance parameters, we assume the following: 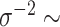 Gam
Gam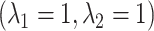 and
and 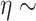 Gam
Gam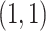 .
.
Posterior computations. We develop a Gibbs sampler for obtaining draws from the marginal posterior distribution of the parameters. Let 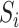 denote a multinomial latent variable that can take values
denote a multinomial latent variable that can take values 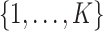 with probability
with probability 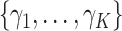 . This variable represents allocation of the cluster of the mixture model (i.e., if
. This variable represents allocation of the cluster of the mixture model (i.e., if 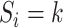 then subject
then subject 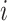 is in cluster
is in cluster 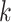 ). The Gibbs sampling algorithm alternates between drawing a cluster value
). The Gibbs sampling algorithm alternates between drawing a cluster value 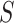 for each subject and updating the parameters, given
for each subject and updating the parameters, given 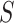 . In practice we will approximate the infinite sum in (3.1) with a finite sum up to
. In practice we will approximate the infinite sum in (3.1) with a finite sum up to 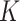 ,
, 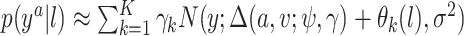 , where
, where 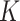 is chosen using the method of Ishwaran and James (2001), and
is chosen using the method of Ishwaran and James (2001), and 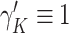 . Full details of the Gibbs sampler steps are given in Section 1 of the supplementary materials.
. Full details of the Gibbs sampler steps are given in Section 1 of the supplementary materials.
Sensitivity analysis. Here we develop a sensitivity analysis for departures from the ignorability assumption. Starting with the observed data likelihood and applying the consistency and ignrrability assumptions, we have 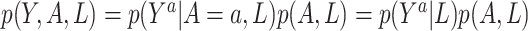 . Thus, to assess sensitivity to the ignorability assumption, we can modify model (3.1) to condition on
. Thus, to assess sensitivity to the ignorability assumption, we can modify model (3.1) to condition on  :
: 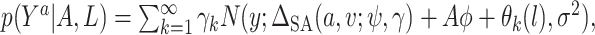 where
where 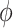 is a sensitivity parameter and the “SA” in
is a sensitivity parameter and the “SA” in 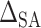 is meant to distinguish the
is meant to distinguish the 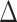 function in the sensitivity analysis from the one previously defined. We now need to integrate over both
function in the sensitivity analysis from the one previously defined. We now need to integrate over both 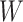 and
and 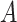 to derive
to derive 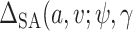 ),
),
which implies
We can estimate the above integrals using the empirical distribution:
In the Gibbs sampler, we can use 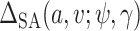 rather than
rather than 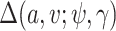 and otherwise proceed with the algorithm in Section 1 of the supplementary materials inserting the term,
and otherwise proceed with the algorithm in Section 1 of the supplementary materials inserting the term, 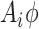 , where necessary. If
, where necessary. If 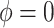 , then the ignorability assumption holds.
, then the ignorability assumption holds.
For binary 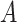 ,
, 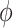 can be thought of as the average difference in
can be thought of as the average difference in 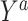 (for
(for 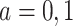 ) among subjects assigned
) among subjects assigned 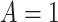 compared with subjects assigned
compared with subjects assigned 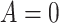 , who have the same covariates
, who have the same covariates 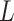 . We can assign an informative prior distribution for
. We can assign an informative prior distribution for 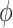 (representing our expectation about unmeasured confounding, as well as our uncertainty about it) and assess how that impacts inference about
(representing our expectation about unmeasured confounding, as well as our uncertainty about it) and assess how that impacts inference about 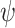 . This is an important advantage of the Bayesian approach.
. This is an important advantage of the Bayesian approach.
To calibrate 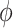 , we first calculate the total variance in
, we first calculate the total variance in 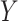 explained by
explained by 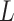 (but not
(but not 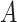 ). Denote this by
). Denote this by 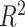 . We then assume that
. We then assume that 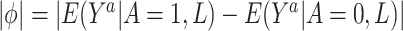 is less than
is less than 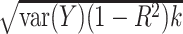 (i.e., unmeasured confounding would account for less than k% of the remaining variance). We can then specify a prior distribution for
(i.e., unmeasured confounding would account for less than k% of the remaining variance). We can then specify a prior distribution for 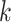 .
.
4. Simulation Studies
We conducted simulation studies to examine the performance of the proposed BNP approach described in Section 3 under three scenarios: (1) an outcome simulated from a normal distribution with a complicated mean function of confounders; (2) an outcome simulated from a bimodal distribution with a simplified mean function of confounders; and (3) a model with many confounders and a complicated relationship with the outcome. In each scenario, the simulated data consisted of a binary treatment, 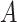 , a binary effect modifier
, a binary effect modifier 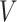 , other confounders
, other confounders 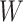 or
or 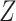 , and a continuous outcome
, and a continuous outcome 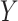 . The true causal model was
. The true causal model was 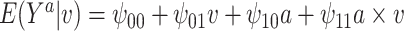 . Our primary interest was in the estimation of
. Our primary interest was in the estimation of 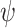 , and in particular,
, and in particular, 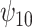 and
and 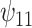 .
.
In each simulation scenario we compared the BNP approach to several other methods. The general methods we compared were IPTW estimator with stabilized weights; IPTW with stabilized weights truncated at 2nd and 98th percentiles (IPTWtr); augmented IPTW (IPTWaug); TMLE that used Super Learner (van der Laan and others, 2007) in the outcome model. Super Learner is an ensemble machine learning method that uses cross-validation to weigh different prediction algorithms. We used four algorithms (glm, step, gam, randomforest) and implemented TMLE using the R package tmle (Gruber and van der Laan, 2012). To compare the efficiency of the methods, we also fit a regression model relating the outcome to the confounders (REG). For augmented IPTW, we used the estimation method specified (van der Laan and Robins, 2003, p. 328).
For each scenario, we generated 1000 datasets. For the first 2 scenarios we used a small sample size of 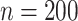 . For scenario 3 we tested a larger sample size of
. For scenario 3 we tested a larger sample size of 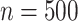 . For the BNP approach, we estimated the posterior distributions using the Gibbs sampling steps described in Section 1 of the supplementary materials and determined that 1000 draws was a sufficient burn-in period and 14000 additional draws yielded sufficiently small Monte Carlo (MC) error for all three scenarios. Furthermore, under each scenario, we first simulated a small number of datasets to determine a value for
. For the BNP approach, we estimated the posterior distributions using the Gibbs sampling steps described in Section 1 of the supplementary materials and determined that 1000 draws was a sufficient burn-in period and 14000 additional draws yielded sufficiently small Monte Carlo (MC) error for all three scenarios. Furthermore, under each scenario, we first simulated a small number of datasets to determine a value for 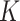 and then used that value of
and then used that value of 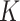 for all simulated datasets in that scenario.
for all simulated datasets in that scenario.
We compared the BNP approach with the existing methods in terms of bias, coverage probability and empirical standard deviation (ESD). For the BNP approach, we calculated the bias as the difference between the true value and the median of the posterior distribution, the ESD as the standard deviation of the posterior medians, and the coverage probability as the percentage of equal tail 95% credible intervals that contain the true values.
Simulation 1: normal outcome, complex mean function. In scenario 1, we simulated data under somewhat simple conditions, that is a normally distributed outcome with a complicated but linear relation between the outcome and confounders. We generated data as follows:
where 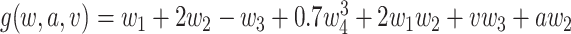 and
and 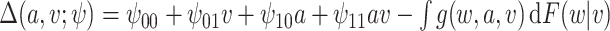 [note that here the integral is 0]. We set
[note that here the integral is 0]. We set 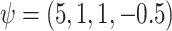 .
.
In the BNP approach, the number of clusters, 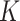 , was set to 10 as the number of uniquely observed values of
, was set to 10 as the number of uniquely observed values of 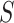 was 2 or 3 for the majority of draws. The correctly specified regression model (REG) was a regression of
was 2 or 3 for the majority of draws. The correctly specified regression model (REG) was a regression of 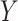 on
on 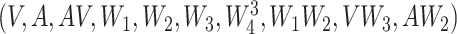 . While, in practice, it is unlikely that anyone would have correctly specified this model, it is used to compare the other approaches with this best performing model. The propensity score was correctly specified for IPTW, IPTWtr, IPTWaug, and TMLE.
. While, in practice, it is unlikely that anyone would have correctly specified this model, it is used to compare the other approaches with this best performing model. The propensity score was correctly specified for IPTW, IPTWtr, IPTWaug, and TMLE.
The bias, coverage probability, and ESD for the estimators of 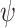 comparing the existing estimators with the BNP approach in scenario 1 are summarized in Table 1. For the causal parameter,
comparing the existing estimators with the BNP approach in scenario 1 are summarized in Table 1. For the causal parameter, 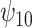 , which describes the average effect of treatment when
, which describes the average effect of treatment when  , the BNP approach performs well relative to the other causal methods with relatively low bias, coverage at approximately the nominal 95% level, and very small ESD (second only to that of the correctly specified regression model). The ESDs from the BNP model are in between those from the correctly specified regression model (which is the best one could achieve, as it is obtained by maximizing the true likelihood) and IPTWtr, which was the best performing of the semiparametric methods (much closer to the most efficient estimator). Of the existing methods, IPTWtr exhibited the largest bias for
, the BNP approach performs well relative to the other causal methods with relatively low bias, coverage at approximately the nominal 95% level, and very small ESD (second only to that of the correctly specified regression model). The ESDs from the BNP model are in between those from the correctly specified regression model (which is the best one could achieve, as it is obtained by maximizing the true likelihood) and IPTWtr, which was the best performing of the semiparametric methods (much closer to the most efficient estimator). Of the existing methods, IPTWtr exhibited the largest bias for 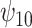 , although this was a trade-off for the smaller ESD. The coverage of the TMLE estimators was much lower. Because of this result, we decided to also report coverage based on bootstrapping the TMLE estimators (TMLEboot). This fixed the undercoverage problem. For the causal effect modification parameter
, although this was a trade-off for the smaller ESD. The coverage of the TMLE estimators was much lower. Because of this result, we decided to also report coverage based on bootstrapping the TMLE estimators (TMLEboot). This fixed the undercoverage problem. For the causal effect modification parameter 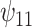 , the results were similar, except the IPTW methods had smaller bias than TMLE and BNP. Again, the ESD from the BNP approach was only slightly larger than from REG.
, the results were similar, except the IPTW methods had smaller bias than TMLE and BNP. Again, the ESD from the BNP approach was only slightly larger than from REG.
Table 1.
Results from simulation scenario 1 (1000 data sets, n = 200)
| Parameter | Method | Bias | Coverage | ESD |
|---|---|---|---|---|
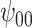 : Intercept : Intercept |
REG | 0.01 | 0.93 | 0.72 |
| IPTW | - 0.05 | 0.93 | 1.31 | |
| IPTWtr | - 0.14 | 0.93 | 1.06 | |
| IPTWaug | 0.02 | 0.95 | 1.05 | |
| TMLE | - 0.05 | 0.90 | 1.08 | |
| TMLEboot | - 0.05 | 0.94 | 1.08 | |
| BNP | - 0.07 | 0.97 | 1.00 | |
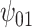 : V : V
|
REG | - 0.03 | 0.94 | 1.05 |
| IPTW | - 0.07 | 0.92 | 2.25 | |
| IPTWtr | - 0.13 | 0.93 | 1.67 | |
| IPTWaug | - 0.01 | 0.96 | 1.75 | |
| TMLE | 0.14 | 0.86 | 1.93 | |
| TMLEboot | 0.14 | 0.94 | 1.93 | |
| BNP | 0.13 | 0.96 | 1.27 | |
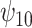 : A : A
|
REG | - 0.04 | 0.95 | 1.16 |
| IPTW | 0.34 | 0.91 | 2.05 | |
| IPTWtr | 0.74 | 0.91 | 1.52 | |
| IPTWaug | - 0.05 | 0.95 | 1.86 | |
| TMLE | 0.42 | 0.70 | 2.22 | |
| TMLEboot | 0.42 | 0.93 | 2.22 | |
| BNP | 0.16 | 0.96 | 1.24 | |
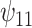 : A × V : A × V
|
REG | 0.04 | 0.95 | 1.53 |
| IPTW | - 0.06 | 0.91 | 3.11 | |
| IPTWtr | - 0.17 | 0.94 | 2.31 | |
| IPTWaug | 0.03 | 0.95 | 2.58 | |
| TMLE | - 0.39 | 0.71 | 3.28 | |
| TMLEboot | - 0.39 | 0.94 | 3.28 | |
| BNP | - 0.37 | 0.96 | 1.60 |
The true values were: 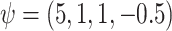 . REG is the correctly specified regression model. IPTW and IPTWtr use a correctly specified propensity score. IPTWaug uses a correctly specified outcome and propensity score model. TMLE uses a correctly specified propensity score and Super Learner for the outcome model. TMLEboot uses bootstrap confidence intervals, rather than asymptotic intervals. BNP is the proposed method. Bias is the absolute bias and ESD is the empirical standard deviation.
. REG is the correctly specified regression model. IPTW and IPTWtr use a correctly specified propensity score. IPTWaug uses a correctly specified outcome and propensity score model. TMLE uses a correctly specified propensity score and Super Learner for the outcome model. TMLEboot uses bootstrap confidence intervals, rather than asymptotic intervals. BNP is the proposed method. Bias is the absolute bias and ESD is the empirical standard deviation.
Simulation 2: bimodal outcome. In this scenario, we simulated a bimodal outcome distribution by generating data such that the error terms are from a mixture distribution consisting of two normal distributions with different means. We first generated A, V, and 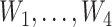 in the same way as in scenario 1. Then the outcome was generated from
in the same way as in scenario 1. Then the outcome was generated from 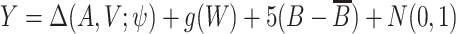 , where
, where 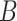 is Bernoulli(0.5),
is Bernoulli(0.5), 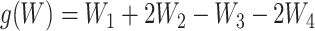 ,
, 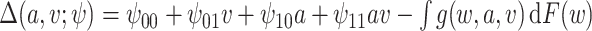 . Note that this is a simplified mean function compared with scenario 1. For example, there is no squared or cubic term for
. Note that this is a simplified mean function compared with scenario 1. For example, there is no squared or cubic term for 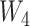 . The reason for this is we wanted to focus on the error distribution, rather than the mean function. We set
. The reason for this is we wanted to focus on the error distribution, rather than the mean function. We set 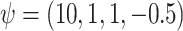 . For all of the analyses,
. For all of the analyses, 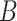 is treated as unobserved. For the BNP approach,
is treated as unobserved. For the BNP approach, 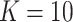 was sufficient as the majority of the observations fell into two clusters. We compared the same estimators as in scenario 1.
was sufficient as the majority of the observations fell into two clusters. We compared the same estimators as in scenario 1.
The performance of the BNP approach and the existing methods is summarized in Table 2. Of note is the very small ESD of the BNP approach compared with the existing methods, especially for the causal parameters. Note that in this scenario, for the REG method, the error distribution was assumed to be normal. In addition, while all of the methods had very low bias, the BNP approach has the smallest bias for three of four parameters. The coverage was approximately the nominal 95% for all of the causal inference methods, but was too large for REG.
Table 2.
Results from simulation scenario 2: outcome simulated from a bimodal distribution with simplified mean function of confounders.
| Parameter | Method | Bias | Coverage | ESD |
|---|---|---|---|---|
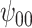 : Intercept : Intercept |
REG |
 0.02 0.02 |
1.00 | 0.38 |
| IPTW |
 0.01 0.01 |
0.97 | 0.51 | |
| IPTWtr | 0.00 | 0.97 | 0.50 | |
| IPTWaug |
 0.02 0.02 |
0.97 | 0.45 | |
| TMLE |
 0.02 0.02 |
1.00 | 0.45 | |
| BNP |
 0.01 0.01 |
0.99 | 0.44 | |
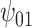 : : 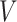
|
REG | 0.04 | 1.00 | 0.61 |
| IPTW | 0.05 | 0.94 | 0.99 | |
| IPTWtr | 0.10 | 0.94 | 0.95 | |
| IPTWaug | 0.03 | 0.95 | 0.81 | |
| TMLE | 0.05 | 1.00 | 0.80 | |
| BNP | 0.02 | 0.96 | 0.60 | |
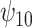 : : 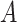
|
REG | 0.02 | 1.00 | 0.55 |
| IPTW | 0.01 | 0.98 | 0.81 | |
| IPTWtr | 0.04 | 0.98 | 0.75 | |
| IPTWaug | 0.01 | 0.95 | 0.60 | |
| TMLE | 0.01 | 0.93 | 0.58 | |
| BNP | 0.00 | 0.97 | 0.38 | |
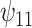 : : 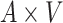
|
REG |
 0.04 0.04 |
1.00 | 0.79 |
| IPTW |
 0.05 0.05 |
0.95 | 1.37 | |
| IPTWtr |
 0.07 0.07 |
0.95 | 1.29 | |
| IPTWaug |
 0.02 0.02 |
0.96 | 0.88 | |
| TMLE |
 0.04 0.04 |
0.93 | 0.87 | |
| BNP | 0.00 | 0.96 | 0.53 |
The true values were 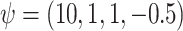 . Results are from 1000 simulated datasets of size
. Results are from 1000 simulated datasets of size 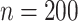 .
.
Simulation 3: many covariates and complex outcome For this scenario, we simulated data for 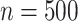 subjects with 10 binary and 10 continuous covariates. The outcome is a complex mixture, with some nonlinear components and interactions. Details of the data generation steps are given in Section 2 of the supplementary materials. The true value of
subjects with 10 binary and 10 continuous covariates. The outcome is a complex mixture, with some nonlinear components and interactions. Details of the data generation steps are given in Section 2 of the supplementary materials. The true value of 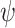 was
was 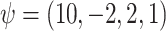 .
.
For the semiparametric methods, a correctly specified propensity score was used. For the regression method, the mean was specified as an additive linear function of the 20 covariates 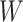 , along with
, along with 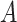 ,
, 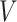 , and
, and 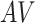 . For the BNP approach,
. For the BNP approach, 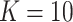 was found to be sufficiently large.
was found to be sufficiently large.
The results are given in Table 3. For the causal main effect 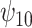 , BNP had the smallest bias. Coverage for all of the methods were a little low (about 0.90 for all except TMLE, which was 0.79). The ESD was smallest for REG (0.43) and IPTWaug (0.44) and largest for IPTW (0.75). For the causal interaction
, BNP had the smallest bias. Coverage for all of the methods were a little low (about 0.90 for all except TMLE, which was 0.79). The ESD was smallest for REG (0.43) and IPTWaug (0.44) and largest for IPTW (0.75). For the causal interaction 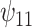 , IPTW had the smallest bias. The absolute bias for REG, TMLE, and BNP were similar (0.23, 0.33, and 0.27, respectively). Coverage for REG, IPTWaug, and BNP were close to the nominal level. The ESD was smallest for REG and BNP (1.39) and largest for TMLE (2.59).
, IPTW had the smallest bias. The absolute bias for REG, TMLE, and BNP were similar (0.23, 0.33, and 0.27, respectively). Coverage for REG, IPTWaug, and BNP were close to the nominal level. The ESD was smallest for REG and BNP (1.39) and largest for TMLE (2.59).
Table 3.
Results from simulation scenario 3: many confounders and complex outcome.
| Parameter | Method | Bias | Coverage | ESD |
|---|---|---|---|---|
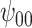 : Intercept : Intercept |
REG |
 0.04 0.04 |
0.89 | 0.34 |
| IPTW |
 0.02 0.02 |
0.94 | 0.62 | |
| IPTWtr |
 0.10 0.10 |
0.94 | 0.43 | |
| IPTWaug |
 0.18 0.18 |
0.92 | 0.34 | |
| TMLE | 0.22 | 0.84 | 0.49 | |
| BNP |
 0.08 0.08 |
0.92 | 0.34 | |
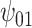 : : 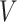
|
REG |
 0.29 0.29 |
0.90 | 1.29 |
| IPTW | 0.01 | 0.81 | 2.13 | |
| IPTWtr | 0.08 | 0.86 | 1.69 | |
| IPTWaug | 0.17 | 0.94 | 1.38 | |
| TMLE |
 0.33 0.33 |
0.73 | 2.47 | |
| BNP | 0.25 | 0.89 | 1.25 | |
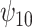 : : 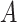
|
REG | 0.24 | 0.90 | 0.43 |
| IPTW | 0.31 | 0.91 | 0.75 | |
| IPTWtr | 0.36 | 0.89 | 0.52 | |
| IPTWaug | 0.27 | 0.91 | 0.44 | |
| TMLE |
 0.20 0.20 |
0.79 | 0.62 | |
| BNP | 0.12 | 0.90 | 0.51 | |
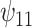 : : 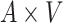
|
REG |
 0.23 0.23 |
0.94 | 1.39 |
| IPTW |
 0.09 0.09 |
0.84 | 2.24 | |
| IPTWtr |
 0.14 0.14 |
0.89 | 1.79 | |
| IPTWaug |
 0.19 0.19 |
0.95 | 1.49 | |
| TMLE | 0.33 | 0.61 | 2.59 | |
| BNP |
 0.27 0.27 |
0.92 | 1.39 |
The true values were 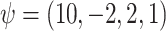 . Results are from 1000 simulated datasets of size
. Results are from 1000 simulated datasets of size 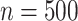 .
.
Conclusions. Across the three scenarios, BNP had consistently good performance. It had the best performance in scenario 2, where the outcome was bimodal. In the other scenarios, it was competitive with the other causal methods in terms of bias and coverage. BNP had consistently smaller ESD than the semiparametric methods, and not much larger than the ESD from correctly specified regression models. It is important to emphasize that for both IPTW and TMLE, correctly specified propensity score models were used, whereas for BNP we did not use knowledge about how the data were generated.
In Section 3 of the supplementary materials, we present one additional simulation study. Data were generated following a model proposed by Kang and Schafer (2007). In that scenario, some treatments have extremely high or extremely low probability for some subjects (i.e., near violation of the positivity assumption—an assumption that is typically necessary for models that involve inverse probability of treatment weighting). The BNP model had good coverage and was more efficient than IPTW and TMLE.
5. Data Analyses
We applied the methods to two datasets. We present here the analysis of data from a study of the neurocognitive effects of HAART. In the supplementary materials (Section 5), we present results from a study of the comparative effectiveness of ACEIs and ARBs.
We apply the BNP approach to estimate the average causal effect of a HAART drug regimen versus a non-HAART regimen on neurocognitive outcomes in HIV-seropositive women with severely impaired immune function (as measured by low CD4 cell count). In addition, we are interested in differences in effect between women with a recent history of alcohol use and those without as Durvasula and others (2006) have shown that recent heavy alcohol use is associated with decreased neurocognitive function in HIV-seropositive African American US men.
The participants are a subset from the HER Study (Smith and others, 1997), a multisite study of the natural history of HIV in US women. For women with CD4 cell count 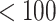 cells/
cells/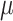 L, neurocognitive exams were administered every 6 months beginning with a baseline exam at 3 months after this threshold was reached (Cohen and others, 2001). Potential a priori confounders collected at enrolment are age (continuous), intravenous drug use in the past six months (yes/no), any previous use of opiates, cocaine, amphetamines, barbiturates, and/or hallucinogens (yes/no), depression severity measured using The Center for Epidemiology Scale of Depression (continuous), and CD4 cell count (continuous). A potential effect modifier of interest is alcohol use in the past 6 months (yes/no).
L, neurocognitive exams were administered every 6 months beginning with a baseline exam at 3 months after this threshold was reached (Cohen and others, 2001). Potential a priori confounders collected at enrolment are age (continuous), intravenous drug use in the past six months (yes/no), any previous use of opiates, cocaine, amphetamines, barbiturates, and/or hallucinogens (yes/no), depression severity measured using The Center for Epidemiology Scale of Depression (continuous), and CD4 cell count (continuous). A potential effect modifier of interest is alcohol use in the past 6 months (yes/no).
Treatment is the first initiation of a HAART drug regimen defined using the guidelines of the US Public Health Service (Smith and others, 1997; Centers for Disease Control, 1999) as a combination of either protease inhibitor plus two nucleoside analog reverse transcriptase inhibitors or a protease inhibitor plus a nucleoside analog reverse transcriptase inhibitor plus a nonnucleoside reverse transcriptase inhibitor. Non-HAART consisted of monotherapy or dual nucleoside therapy without the above combinations.
During the semiannual neurocognitive exam, multiple tasks were given including the Grooved Pegboard total time (GPB), Color Trail Making 1 total time (CTM), and Controlled Oral Word Generation Test total words (COWAT). The outcomes we consider are the changes in the scores (continuous) over time. We define the observed outcomes: 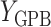 = GPB(last exam) – GPB(baseline exam),
= GPB(last exam) – GPB(baseline exam), 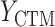 = CTM(last exam) – CTM(baseline exam), and
= CTM(last exam) – CTM(baseline exam), and 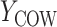 = COWAT(last exam) – COWAT(baseline exam). The potential outcomes if a woman is put on a HAART drug regimen (a=1) are
= COWAT(last exam) – COWAT(baseline exam). The potential outcomes if a woman is put on a HAART drug regimen (a=1) are 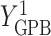 ,
, 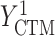 , and
, and 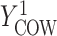 , and
, and 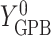 ,
, 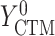 , and
, and 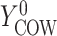 if put on a non-HAART drug regimen (
if put on a non-HAART drug regimen (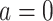 ). Improvement is indicated by a negative change in time to complete the task for GPB and CTM, but a positive change in total words for COWAT which measures verbal fluency.
). Improvement is indicated by a negative change in time to complete the task for GPB and CTM, but a positive change in total words for COWAT which measures verbal fluency.
We consider the 126 women with CD4 cell count 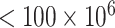 cells/L who completed at least two neurological exams in 1993–1996. We further excluded one woman with unknown treatment, four women with unknown CD4 cell count, and one woman with a CTM change in time more than 21 standard deviations from the median, for a final sample size of 120.
cells/L who completed at least two neurological exams in 1993–1996. We further excluded one woman with unknown treatment, four women with unknown CD4 cell count, and one woman with a CTM change in time more than 21 standard deviations from the median, for a final sample size of 120.
In this analysis, we model each of the potential outcomes separately. For each, our MSM consists of main effects for recent alcohol use and a HAART drug regimen and an interaction term (e.g., 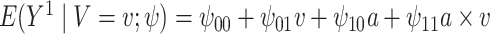 ). The interpretation of
). The interpretation of 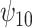 is the difference in mean of the potential outcome comparing HAART versus non-HAART among women with no recent alcohol use (
is the difference in mean of the potential outcome comparing HAART versus non-HAART among women with no recent alcohol use (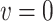 ). Furthermore,
). Furthermore, 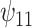 indicates modification of this difference by recent alcohol use.
indicates modification of this difference by recent alcohol use.
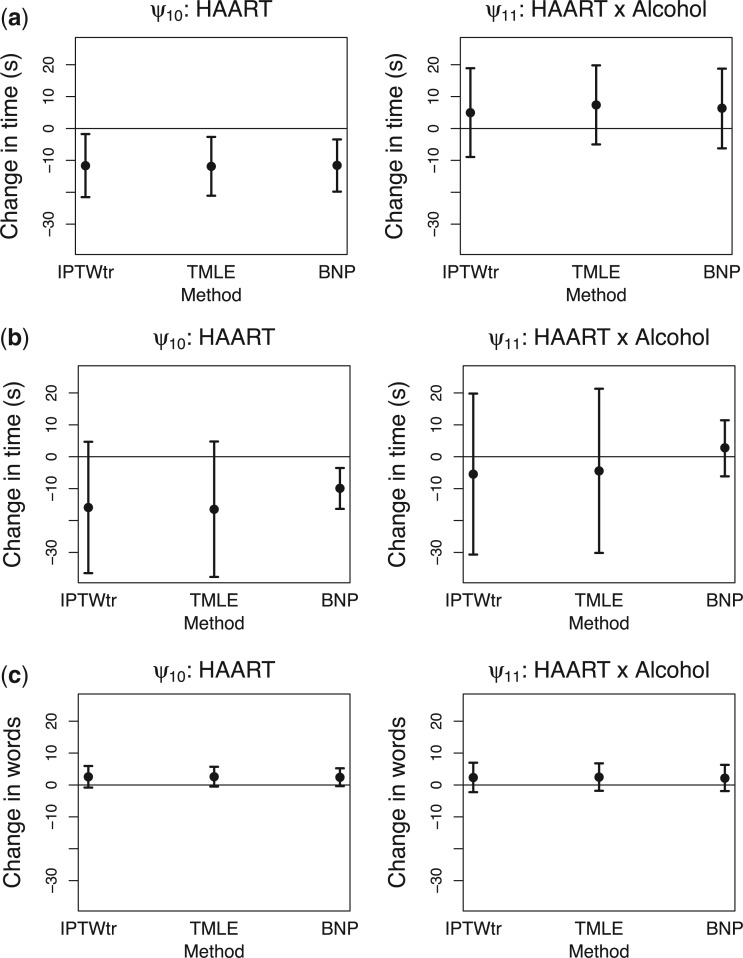
Results. In Figure 1, we compare the posterior medians and 95% equal tail credible intervals of the causal parameters fit using the BNP approach with the point estimates and 95% confidence intervals fit using IPTW with stabilized weights truncated at 2nd and 98th percentiles (IPTWtr) and TMLE. The estimates from the BNP approach are also given in Table 4 in the row labeled 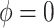 . For the CTM task (Figure 1(a)), the estimates of
. For the CTM task (Figure 1(a)), the estimates of 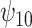 from all three approaches are similar and indicate that treatment with a HAART drug regimen was significantly associated with faster times in women without recent alcohol use. The estimates of
from all three approaches are similar and indicate that treatment with a HAART drug regimen was significantly associated with faster times in women without recent alcohol use. The estimates of 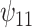 indicate that recent alcohol use counteracted this improvement though not significantly. Similar results were found for
indicate that recent alcohol use counteracted this improvement though not significantly. Similar results were found for 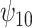 and
and 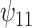 using the BNP approach for the GPB task (Figure 1(b)). For the GPB task, the distribution was not Gaussian and the payoff of using the BNP approach, even for small datasets, can be seen in the smaller credible intervals which do not include the null for
using the BNP approach for the GPB task (Figure 1(b)). For the GPB task, the distribution was not Gaussian and the payoff of using the BNP approach, even for small datasets, can be seen in the smaller credible intervals which do not include the null for 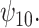 For the COWAT task (Figure 1(c)), the results from all three approaches show an association between treatment with a HAART drug regimen and increase in number of words in women without recent alcohol, although all of the intervals included the null.
For the COWAT task (Figure 1(c)), the results from all three approaches show an association between treatment with a HAART drug regimen and increase in number of words in women without recent alcohol, although all of the intervals included the null.
Fig 1.
Results for example on neurocognitive effects of a HAART versus non-HAART drug regimen. Comparison of point estimates and 95% confidence intervals of causal parameters (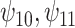 ) from IPTW with stabilized weights truncated at 2nd and 98th percentiles (IPTWtr) and TMLE, compared with posterior median and 95% credible intervals from the proposed BNP approach. Models were fit separately for three outcomes: change in score on (a) Color Trail Making 1 total time (CTM), (b) Grooved Pegboard total time (GPB), and (c) Controlled Word Association Test total words (COWAT) tasks. For CTM and GPB tasks, a negative change in time (s) indicates improvement while for the COWAT task, a positive change (words) indicates improvement. Restricted to 120 HIV seropostive women with CD4 cell count
) from IPTW with stabilized weights truncated at 2nd and 98th percentiles (IPTWtr) and TMLE, compared with posterior median and 95% credible intervals from the proposed BNP approach. Models were fit separately for three outcomes: change in score on (a) Color Trail Making 1 total time (CTM), (b) Grooved Pegboard total time (GPB), and (c) Controlled Word Association Test total words (COWAT) tasks. For CTM and GPB tasks, a negative change in time (s) indicates improvement while for the COWAT task, a positive change (words) indicates improvement. Restricted to 120 HIV seropostive women with CD4 cell count 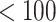 cells/
cells/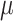 L,
L, 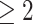 neurocognitive exams, known drug regimen, known baseline CD4 cell count, and nonoutlying CTM change.
neurocognitive exams, known drug regimen, known baseline CD4 cell count, and nonoutlying CTM change.
Table 4.
Sensitivity analysis for example on neurocognitive effects of a HAART versus non-HAART drug regimen.
| Change in CTM total time | |||||||||||||
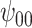 : Intercept : Intercept |
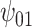 : Alcohol : Alcohol |
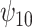 : HAART : HAART |
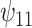 : HAART : HAART 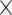 Alcohol Alcohol |
||||||||||
| Sensitivity parameters | Median | 95% CI | Median | 95% CI | Median | 95% CI | Median | 95% CI | |||||
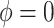 |
5.10 | (- 1.21, | 11.30) | - 0.03 | (- 9.71, | 9.99) | - 12.01 | (- 21.30, | - 3.15) | 6.51 | (- 7.25, | 21.67) | |
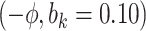 |
3.32 | (- 2.70, | 9.37) | - 1.37 | (- 11.12, | 8.00) | - 7.72 | (- 16.32, | 0.91) | 7.14 | (- 6.04, | 21.25) | |
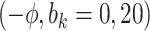 |
2.75 | (- 3.28, | 8.97) | - 3.52 | (- 13.05, | 6.88) | - 6.17 | (- 15.42, | 2.55) | 9.95 | (- 4.11, | 23.11) | |
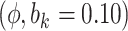 |
7.40 | (0.67, | 13.89) | - 2.96 | (- 12.48, | 6.62) | - 16.22 | (- 25.88, | - 6.47) | 9.44 | (- 4.54, | 23.86) | |
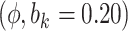 |
8.20 | (1.06, | 15.41) | - 1.80 | (- 11.98, | 8.63) | - 18.45 | (- 29.16, | - 7.58) | 8.37 | (- 6.36, | 23.66) | |
| Change in CTM total time | |||||||||||||
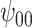 : Intercept : Intercept |
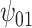 : Alcohol : Alcohol |
 : HAART : HAART |
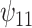 : HAART : HAART 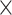 Alcohol Alcohol |
||||||||||
| Sensitivity parameters | Median | 95% CI | Median | 95% CI | Median | 95% CI | Median | 95% CI | |||||
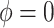 |
7.35 | (3.29, | 11.28) | - 6.37 | (- 12.08, | - 0.27) | - 9.88 | (- 16.35, | - 3.53) | 2.83 | (- 6.15, | 11.44) | |
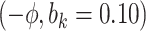 |
2.42 | (- 3.85, | 8.36) | - 5.27 | (- 13.41, | 3.65) | - 3.87 | (- 12.81, | 5.25) | 4.56 | (- 8.71, | 16.34) | |
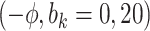 |
5.26 | (- 2.45, | 12.64) | - 6.57 | (- 16.82, | 5.00) | - 5.46 | (- 17.10, | 5.92) | - 0.99 | (- 17.49, | 14.59) | |
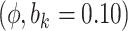 |
9.89 | (3.44, | 15.87) | - 4.10 | (- 13.19, | 5.21) | - 15.80 | (- 24.98, | - 5.38) | - 0.89 | (- 15.37, | 11.43) | |
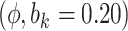 |
11.55 | (2.34, | 17.54) | - 4.75 | (- 13.67, | 7.58) | - 21.10 | (- 30.30, | - 9.77) | 3.13 | (- 11.58, | 15.20) | |
| Change in CTM total time | |||||||||||||
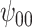 : Intercept : Intercept |
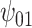 : Alcohol : Alcohol |
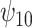 : HAART : HAART |
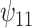 : HAART : HAART 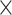 Alcohol Alcohol |
||||||||||
| Sensitivity parameters | Median | 95% CI | Median | 95% CI | Median | 95% CI | Median | 95% CI | |||||
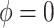 |
- 1.37 | (- 3.43, | 0.66) | - 0.98 | (- 3.83, | 1.81) | 2.43 | (- 0.30, | 5.15) | 2.08 | (- 2.00, | 6.13) | |
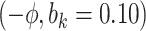 |
- 1.96 | (- 4.06, | 0.10) | - 0.98 | (- 3.95, | 1.86) | 3.71 | (0.87, | 6.63) | 2.06 | (- 2.03, | 6.20) | |
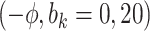 |
- 2.45 | (- 4.51, | - 0.33) | - 0.64 | (- 3.52, | 2.14) | 4.26 | (1.30, | 7.09) | 1.91 | (- 1.99, | 5.92) | |
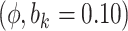 |
- 0.95 | (- 3.01, | 1.11) | - 0.96 | (- 3.78, | 1.86) | 1.25 | (- 1.66, | 4.16) | 2.14 | (- 1.93, | 6.19) | |
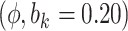 |
- 0.62 | (- 2.67, | 1.42) | - 1.09 | (- 3.88, | 1.72) | 0.79 | (- 2.18, | 3.71) | 2.07 | (- 1.97, | 6.23) | |
Posterior median and 95% credible intervals of 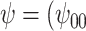 ,
,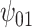 ,
,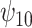 ,
,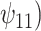 were estimated using the proposed BNP approach applied separately for different combinations of sensitivity parameters and for each outcome. The row,
were estimated using the proposed BNP approach applied separately for different combinations of sensitivity parameters and for each outcome. The row, 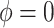 , corresponds to the results under the ignorability assumption. Outcome was change in score from baseline exam to last exam. For Color Trail Making 1 (CTM) and Grooved Pegboard (GPB) tasks, a negative change in time (s) indicates improvement, while for Controlled Word Association Test (COWAT) a positive change (words) indicates improvement. Alcohol (binary) represented use in the past 6 months. Restricted to 120 HIV seropostive women with CD4 cell count
, corresponds to the results under the ignorability assumption. Outcome was change in score from baseline exam to last exam. For Color Trail Making 1 (CTM) and Grooved Pegboard (GPB) tasks, a negative change in time (s) indicates improvement, while for Controlled Word Association Test (COWAT) a positive change (words) indicates improvement. Alcohol (binary) represented use in the past 6 months. Restricted to 120 HIV seropostive women with CD4 cell count 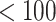 cells/
cells/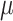 L,
L, 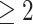 neurocognitive exams, known drug regimen, known baseline CD4 cell count, and nonoutlying CTM change.
neurocognitive exams, known drug regimen, known baseline CD4 cell count, and nonoutlying CTM change.
Sensitivity Analysis. For sensitivity to the ignorability assumption, we use the method described in Section 3.3. We consider two uniform priors for 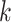 :
: 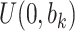 , with
, with 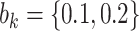 , which represent our prior belief that up to 10 or 20%, respectively, of the remaining unexplained variance is explained by unmeasured confounding, and that any value between 0% and the upper bound,
, which represent our prior belief that up to 10 or 20%, respectively, of the remaining unexplained variance is explained by unmeasured confounding, and that any value between 0% and the upper bound,  , are equally likely. In addition, because we require that
, are equally likely. In addition, because we require that 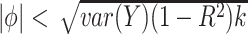 , we consider both positive and negative values of
, we consider both positive and negative values of 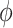 . A negative value, for example, would indicate that subjects in the HAART group had a lower value of each potential outcome than did subjects in the non-HAART group.
. A negative value, for example, would indicate that subjects in the HAART group had a lower value of each potential outcome than did subjects in the non-HAART group.
The estimates of 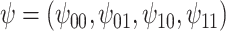 for four combinations of the sensitivity parameters are shown in Table 4 along with the estimates fit under the ignorability assumption (
for four combinations of the sensitivity parameters are shown in Table 4 along with the estimates fit under the ignorability assumption (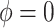 ). For both the CTM and GPB tasks, under the ignorability assumption, the estimate of
). For both the CTM and GPB tasks, under the ignorability assumption, the estimate of 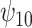 was negative and the credible interval did not include 0. If we relax this assumption and assume
was negative and the credible interval did not include 0. If we relax this assumption and assume 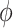 is positive, the posterior distribution of
is positive, the posterior distribution of 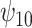 is more negative, indicating treatment with HAART is associated with a stronger improvement in women without alcohol use; however, if we assume
is more negative, indicating treatment with HAART is associated with a stronger improvement in women without alcohol use; however, if we assume 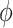 is negative, the posterior median is still negative but the 95% credible interval for
is negative, the posterior median is still negative but the 95% credible interval for 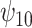 includes zero for both values of
includes zero for both values of 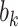 . For the COWAT task, under ignorability, the estimate of
. For the COWAT task, under ignorability, the estimate of 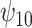 was positive but the credible interval included 0. If we assume
was positive but the credible interval included 0. If we assume 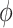 is positive, the estimate of
is positive, the estimate of 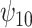 decreases, although the posterior median is still positive; while, if we assume
decreases, although the posterior median is still positive; while, if we assume 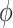 is negative, the posterior distribution of
is negative, the posterior distribution of 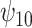 increases farther away from 0, resulting in credible intervals that no longer include 0. Overall this agrees with the results of the other tasks, since positive values of change in words on the COWAT task indicate improvement. Focusing on the GPB outcome, the credible intervals for all of the parameters were wider in each of the sensitivity analyses. For
increases farther away from 0, resulting in credible intervals that no longer include 0. Overall this agrees with the results of the other tasks, since positive values of change in words on the COWAT task indicate improvement. Focusing on the GPB outcome, the credible intervals for all of the parameters were wider in each of the sensitivity analyses. For 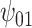 in particular, under the ignorability assumption, the 95% credible interval was entirely below 0; however, in each of the sensitivity analyses, the interval widened to include 0.
in particular, under the ignorability assumption, the 95% credible interval was entirely below 0; however, in each of the sensitivity analyses, the interval widened to include 0.
6. Discussion
In this article we proposed a BNP approach to MSM inference in the point treatment setting. Advantages of the approach include efficiency gains due to using a likelihood-based approach, the ability to incorporate prior information into the model, and obtaining full posterior distributions for the causal parameters of interest. Simulation studies showed good performance of our approach under a variety of scenarios. We also developed and demonstrated a sensitivity analysis approach, that allows for uncertainty in the ignorability assumption to be accounted for via informative prior distributions.
While the proposed BNP approach requires more computation resources, there are several ways that this can be improved. One option is to assume a limited, discrete space for the parameters 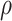 and
and 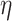 , invert
, invert 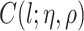 for each unique
for each unique 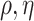 , store those inverted matrices and recall them as needed. Another option is to use an alternative to the GP model, such as treed GP models (Gramacy and Lee, 2008).
, store those inverted matrices and recall them as needed. Another option is to use an alternative to the GP model, such as treed GP models (Gramacy and Lee, 2008).
In this article we focused on the common situation of continuous outcomes (including censored survival) and point treatments. An appealing aspect of semiparametric methods, such as IPTW and TMLE, is estimation of MSM parameters in longitudinal and discrete outcome situations is realtively straightforward (with the cost of having to correctly specify a propensity score model or an outcome model). BNP extensions to these settings need to be developed. In the common situation where the treatment variable is categorical, a BNP approach could be used to model the joint distirbution of observed data, with the g-formula used to obtain posterior distributions for the causal effect parameters. This is an area of ongoing research.
The BNP approach developed here does not require explicit specification of interactions between the confounders in the outcome model (this is handled via the Gaussian process). However, as pointed out by a referee, the model implicitly assumes no interactions between treatment (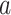 ) and confounders (
) and confounders (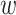 ). This is in contrast to IPTW, where any interactions between treatment and confounders are automatically averaged over. If treatment is categorical (not continuous), then the BNP approach proposed here can be refined to eliminate the assumption of no interactions between
). This is in contrast to IPTW, where any interactions between treatment and confounders are automatically averaged over. If treatment is categorical (not continuous), then the BNP approach proposed here can be refined to eliminate the assumption of no interactions between 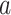 and
and 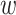 . We describe this approach in Section 4 of the supplementary material.
. We describe this approach in Section 4 of the supplementary material.
Acknowledgements
The authors thank members of the Penn Causal Inference Reasearch Group for helpful comments. Conflict of Interest: None declared.
Supplementary Material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
The research was funded by NIH grants R01GM112327 and R01CA183854.
References
- CENTERS FOR DISEASE CONTROL. (1999). HIV-AIDS surveillance report. Morbidity and Mortality Weekly Report 11, 1–44. [Google Scholar]
- Cohen, R.A., Boland, R., Paul, R., Tashima, K.T., Schoenbaum, E.E., Celentano, D.D., Schuman, P, Smith, D. K. AND Carpenter, C. C.. (2001). Neurocognitive performance enhanced by highly active antiretroviral therapy in HIV-infected women. AIDS 16 , 341–345. [DOI] [PubMed] [Google Scholar]
- Durvasula, R.S., Myers, H. F, Mason, K. AND Hinkin, C.. (2006). Relationship between alcohol use/abuse, HIV infection and neuropsychological performance in African American men. Journal of Clinical and Experimental Neuropsychology 28, 383–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelfand, A.E., Kottas, A. AND Maceachern, S. N.. (2005). Bayesian nonparametric spatial modeling with dirichlet process mixing. Journal of the American Statistical Association 100, 1021–1035. [Google Scholar]
- Gramacy, R. B AND Lee, H. K. H.. (2008). Bayesian treed gaussian process models with an application to computer modeling. Journal of the American Statistical Association 103, 1119–1130. [Google Scholar]
- Gruber, S. AND Van Der Laan, M. J.. (2012). tmle: an R package for targeted maximum likelihood estimation. [Google Scholar]
- Hill, J. L. (2011). Bayesian nonparametric modeling for causal inference. Journal of Computational and Graphical Statistics 20 (1), 217–240. [Google Scholar]
- Hoshino, T. (2013). Semiparametric Bayesian estimation for marginal parametric potential outcome modeling: application to causal inference. Journal of the American Statistical Association 108, 1189–1204. [Google Scholar]
- Ishwaran, H. AND James, L. F.. (2001). Gibbs sampling methods for stick-breaking priors. Journal of the American Statistical Association 96, 161–173. [Google Scholar]
- Kang, J.D.Y. AND Schafer, J. L.. (2007). Demystifying double robustness: a comparison of alternative strategies for estimating a population mean from incomplete data. Statistical Science 22, 523–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karabatsos, G. AND Walker, S. G.. (2012). A Bayessian nonparametric causal model. Journal of Statistical Planning and Inference 142, 925–934. [Google Scholar]
- Maceachern, S. N. (1999). Dependent nonparametric processes. ASA Proceedings of the Section on Bayesian Statistical Science, Alexandria, VA: American Statistical Association, pp. 50–55. [Google Scholar]
- Neal, R. M. (1998). Regression and classification using gaussian process priors. Bernardo, J. and others (editors), Bayesian Statistics 6. Oxford, UK: Oxford University Press. [Google Scholar]
- Robins, J. M. (1986). A new approach to causal inference in mortality studies with sustained exposure periods— applications to control of the healthy worker survivor effect. Mathematical Modeling 7, 1393–1512. [Google Scholar]
- Robins, J. M. (2000). Marginal structural models versus structural nested models as tools for causal inference. Halloran, M. E. AND Berry, D. (editors), Statistical Models in Epidemiology, the Environment, and Clinical Trials, Vol. 116, The IMA Volumes in Mathematics and its Applications. New York: Springer, pp. 95–133. [Google Scholar]
- Robins, J.M., HernáN, M. A. AND Brumback, B.. (2000). Marginal structural models and causal inference in epidemiology. Epidemiology 11, 550–560. [DOI] [PubMed] [Google Scholar]
- Robins, J.M., HernáN, M. A. AND Wasserman, L.. (2015). Discussion of “On Bayesian estimation of marginal structural models”. Biometrics 71, 296–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenblum, M. AND Van Der Laan, M. J.. (2010). Targeted maximum likelihood estimation of the parameter of a marginal structural model. International Journal of Biostatistics 6, Article 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy, J., Lin, X. AND Ryan, L. M.. (2003). Scaled marginal models for multiple continuous outcomes. Biostatistics 4, 371–383. [DOI] [PubMed] [Google Scholar]
- Roy, J., Shah, N.R., Wood, G.C., Townsend, R. AND Hennessy, S.. (2012). Comparative effectiveness of angiotensin-converting enzyme inhibitors and angiotensin receptor blockers for hypertension on clinical end points: a cohort study. The Journal of Clinical Hypertension 14, 407–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saarela, O., Stephens, D. A, Moodie, E. Eand Klein, M. B.. (2015). On Bayesian estimation of marginal structural models. Biometrics 71, 279–288. [DOI] [PubMed] [Google Scholar]
- Sauer, B.C., Brookhart, M.A., Roy, J. AND Vander Weele, T.. (2013). A review of covariate selection for non-experimental comparative effectiveness research. Pharmacoepidemiology & Drug Safety 22, 1139–1145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scharfstein, D.O., Rotnitzky, A. and Robins, J. M.. (1999). Rejoinder to adjusting for nonignorable drop-out using semiparametric nonresponse models. Journal of the American Statistical Association 94, 1135–1146. [Google Scholar]
- Smith, D.K., Warren, D.L., Vlahov, D., Schuman, P., Stein, M.D., Greenberg, B. L. AND Holmberg, S. D.. (1997). Design and baseline participant characteristics of the human immunodeficiency virus epidemiology research (HER) study: a prospective cohort study of human immunodeficiency virus infection in us women. American Journal of Epidemiology 146, 459–469. [DOI] [PubMed] [Google Scholar]
- Taddy, M. A. (2008). Bayesian nonparametric analysis of conditional distributions and inference for Poisson point processes [Ph.D. Thesis]. Santa Cruz, CA: University of California. [Google Scholar]
- Tan, Z. (2010). Nonparametric likelihood and doubly robust estimating equations for marginal and nested structural models. Canadian Journal of Statistics 38, 609–632. [Google Scholar]
- Van Der Laan, M.J., Polley, E. C AND Hubbard, A. E.. (2007). Super learner. Statistical Applications in Genetics and Molecular Biology 6, 25. [DOI] [PubMed] [Google Scholar]
- Van Der Laan, M. J. AND Robins, J. M.. (2003). Unified Methods for Censored Longitudinal Data and Causality, Springer Series in Statistics. Springer. [Google Scholar]
- Wahed, A. S. AND Thall, P. F.. (2013). Evaluating joint effects of induction–salvage treatment regimes on overall survival in acute leukaemia. Journal of the Royal Statistical Society: Series C 62, 67–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, Y., MüLler, P., Wahed, A. AND Thall, P.. (2015). Bayesian nonparametric estimation for dynamic treatment regimes with sequential transition times. Journal of the American Statistical Association, doi: 10.1080/01621459.2015.1086353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young, J.G., Cain, L.E., Robins, J.M., O’Reilly, E. J. and Hernán. M. A.,. (2011). Comparative effectiveness of dynamic treatment regimes: an application of the parametric g-formula. Statistics in Biosciences 3, 119–143. [DOI] [PMC free article] [PubMed] [Google Scholar]