Summary
The development of next-generation sequencing technologies has allowed researchers to study comprehensively the contribution of genetic variation particularly rare variants to complex diseases. To date many sequencing analyses of rare variants have focused on marginal genetic effects and have not explored the potential role environmental factors play in modifying genetic risk. Analysis of gene–environment interaction (GxE) for rare variants poses considerable challenges because of variant rarity and paucity of subjects who carry the variants while being exposed. To tackle this challenge, we propose a hierarchical model to jointly assess the GxE effects of a set of rare variants for example, in a gene or regulatory region, leveraging the information across the variants. Under this model, GxE is modeled by two components. The first component incorporates variant functional information as weights to calculate the weighted burden of variant alleles across variants, and then assess their GxE interaction with the environmental factor. Since this information is a priori known, this component is fixed effects in the model. The second component involves residual GxE effects that have not been accounted for by the fixed effects. In this component, the residual GxE effects are postulated to follow an unspecified distribution with mean 0 and variance 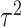 . We develop a novel testing procedure by deriving two independent score statistics for the fixed effects and the variance component separately. We propose two data-adaptive combination approaches for combining these two score statistics and establish the asymptotic distributions. An extensive simulation study shows that the proposed approaches maintain the correct type I error and the power is comparable to or better than existing methods under a wide range of scenarios. Finally we illustrate the proposed methods by a exome-wide GxE analysis with NSAIDs use in colorectal cancer.
. We develop a novel testing procedure by deriving two independent score statistics for the fixed effects and the variance component separately. We propose two data-adaptive combination approaches for combining these two score statistics and establish the asymptotic distributions. An extensive simulation study shows that the proposed approaches maintain the correct type I error and the power is comparable to or better than existing methods under a wide range of scenarios. Finally we illustrate the proposed methods by a exome-wide GxE analysis with NSAIDs use in colorectal cancer.
Keywords: Burden and variance component tests, Colorectal cancer, Kernel machine, Rare genetic variants, Score test
1. Introduction
Both genetic and environmental factors contribute to the development of complex diseases. Understanding the interplay between genes and environment is of great interest in genetic epidemiology, as it may help researchers elucidate the underlying biology and devise effective clinical prevention and intervention strategies. Many methods have been proposed to enhance power for detecting genome-wide gene-environment interaction (GxE) effects for individual common variants (Thomas, 2010; Hsu and others, 2012 and references therein). However, these methods do not provide adequate power for GxE testing on rare variants. In some instances, because few individuals carry variant alleles and have environmental exposure, the asymptotic-based inference becomes unreliable. To improve both type I error and power, variants are aggregated by a priori defined sets (e.g., genes and functional classes). Instead of testing GxE variant-by-variant, the GxE testing will be performed set-by-set. The idea is then to combine several signals in the set that would otherwise be difficult to detect individually.
Limited work has been done on testing for the interaction between a set of rare genetic variants and an environmental factor. A natural approach is to test for the overall association of the set with the outcome by standard 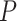 -degrees of freedom likelihood ratio or score tests. However, when the genetic variants are rare, such tests may not keep the correct type I error and the power is also limited. To improve type I error and power, Lin and others (2013) used the kernel machine regression framework by imposing the GxE effects to follow an arbitrary distribution with mean 0 and variance
-degrees of freedom likelihood ratio or score tests. However, when the genetic variants are rare, such tests may not keep the correct type I error and the power is also limited. To improve type I error and power, Lin and others (2013) used the kernel machine regression framework by imposing the GxE effects to follow an arbitrary distribution with mean 0 and variance 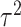 and test
and test 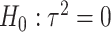 for heterogeneity of GxE effects with an extension that allows for correlated GxE effects (Lin and others, 2016). Tzeng and others (2011) developed a set-based GxE test for continuous traits based on similarity matrices, similar to the variance component test as in Lin and others (2013). We also proposed a set-based GxE test where the variant alleles are summed over the set of genetic variants with weight informed by the screening statistics (burden) (Jiao and others, 2013), and recently extended it to allow for heterogeneous GxE effects (Jiao and others, 2015). However, our works treated genetic main effects as fixed, and the type I error may be inflated when the variants are rare. Generally speaking, the variance component-based test is powerful when both positive and negative directions of GxE effects exist, whereas the burden test is powerful when the variants in the set have the same direction of GxE. Since the pattern of the GxE effects for a set of variants is typically complex and unknown, it is important to devise a unified approach that combines test statistics that capture a particular feature of GxE effects, where a feature can be a priori defined variant functions or some generic distributional assumption of GxE effects. By this the combined test statistic may be powerful under a wide range of scenarios for GxE.
for heterogeneity of GxE effects with an extension that allows for correlated GxE effects (Lin and others, 2016). Tzeng and others (2011) developed a set-based GxE test for continuous traits based on similarity matrices, similar to the variance component test as in Lin and others (2013). We also proposed a set-based GxE test where the variant alleles are summed over the set of genetic variants with weight informed by the screening statistics (burden) (Jiao and others, 2013), and recently extended it to allow for heterogeneous GxE effects (Jiao and others, 2015). However, our works treated genetic main effects as fixed, and the type I error may be inflated when the variants are rare. Generally speaking, the variance component-based test is powerful when both positive and negative directions of GxE effects exist, whereas the burden test is powerful when the variants in the set have the same direction of GxE. Since the pattern of the GxE effects for a set of variants is typically complex and unknown, it is important to devise a unified approach that combines test statistics that capture a particular feature of GxE effects, where a feature can be a priori defined variant functions or some generic distributional assumption of GxE effects. By this the combined test statistic may be powerful under a wide range of scenarios for GxE.
In this article we introduce a unified hierarchical regression framework for modeling GxE effects that account for a priori information about variant characteristics such as functional features and data-driven screening statistics as fixed effects, and heterogeneous GxE effects as random effects. We show that all previously proposed tests can be derived under this framework by constraining certain parameters to 0. Under this regression framework we develop a novel and rigorous approach to deriving independent score statistics for fixed effects and the variance component. The approach is broadly applicable to any mixed effects model where the hypothesis of interest is to test both the fixed and random effects equal to 0. Our proposed score statistics have two advantages: (1) both score statistics have trackable asymptotic distributions, and (2) the score statistics corresponding to the fixed effects and the random effects are asymptotically independent. The independence of score statistics is very desirable, because it not only allows study of the properties of various combinations of independent statistics with trackable asymptotic distributions but also facilitates the search of optimum within a particular class of combinations of the two score statistics. Towards this end we proposed two data-adaptive approaches to optimally combine two independent score statistics. Our framework and tests provide, nearly uniformly, more powerful approaches to identifying GxE of rare variants.
The rest of the article is organized as follows. In Section 2 we describe the hierarchical model for GxE interaction effects, derive the independent score statistics for fixed and random effects, respectively. The two data-driven combination approaches for combining the score statistics are also presented. The results from an extensive simulation study are presented in Section 3. The proposed methods are applied to a large exome-wide study of GxE analysis with NSAIDs use in colorectal cancer (CRC) in Section 4, and finally, the article is concluded with some remarks.
2. Methods
2.1. Notation and model
Consider an outcome 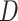 , which can be binary or continuous. Let
, which can be binary or continuous. Let 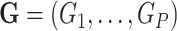 be a set of variants where
be a set of variants where 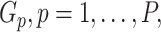 is a function of the
is a function of the 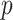 th variant genotype (e.g., the number of copies of the variant allele), and
th variant genotype (e.g., the number of copies of the variant allele), and 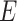 an environmental factor. The model for GxE is
an environmental factor. The model for GxE is
| (2.1) |
where 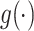 is a link function, which depends on the type of outcome. For binary outcome, a commonly used link function is logit. For continuous outcome, linear or log transformation may be used. In this model,
is a link function, which depends on the type of outcome. For binary outcome, a commonly used link function is logit. For continuous outcome, linear or log transformation may be used. In this model, 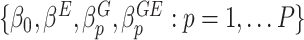 are the intercept, the main effects of E and G, and the interaction effects, respectively. The main parameters of interest in this article are the interaction effects between the
are the intercept, the main effects of E and G, and the interaction effects, respectively. The main parameters of interest in this article are the interaction effects between the 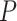 genetic variants and
genetic variants and 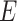 ,
, 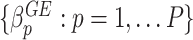 .
.
A direct approach for drawing statistical inference on 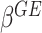 ’s is based on the likelihood ratio test treating
’s is based on the likelihood ratio test treating  ’s as fixed effects. However, this approach may yield an inflated type I error and lose power when the variants are rare and the number of the variants
’s as fixed effects. However, this approach may yield an inflated type I error and lose power when the variants are rare and the number of the variants 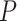 is large. To overcome these issues, we propose a hierarchical model to reduce the dimension of parameters while leveraging information across
is large. To overcome these issues, we propose a hierarchical model to reduce the dimension of parameters while leveraging information across 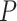 variants. Specifically, let
variants. Specifically, let 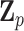 denote
denote 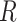 known attributes associated with the
known attributes associated with the  th variant. These attributes can be functional annotations such as whether a variant is missense, nonsense, or other characteristics. It can be data-driven weights such as those based on minor allele frequency or screening statistics of marginal association of
th variant. These attributes can be functional annotations such as whether a variant is missense, nonsense, or other characteristics. It can be data-driven weights such as those based on minor allele frequency or screening statistics of marginal association of 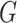 with disease risk and correlation between
with disease risk and correlation between 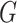 and
and 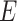 that were shown to be informative for GxE yet independent of GxE interaction tests (Hsu and others, 2012). Under the hierarchical modeling, we model the genetic main and interaction effects as a function of these variant attributes as following
that were shown to be informative for GxE yet independent of GxE interaction tests (Hsu and others, 2012). Under the hierarchical modeling, we model the genetic main and interaction effects as a function of these variant attributes as following
| (2.2) |
where 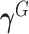 and
and 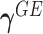 are
are 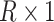 row vectors of regression coefficients associated with the R attributes for the main and interaction effects, respectively, and
row vectors of regression coefficients associated with the R attributes for the main and interaction effects, respectively, and 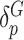 and
and 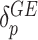 are the respective variant-specific main and interaction effects that cannot be explained by
are the respective variant-specific main and interaction effects that cannot be explained by 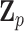 . To further leverage the information across variants allowing for robust statistical inference for rare variants and improving power, we assume these residual variant-specific effects,
. To further leverage the information across variants allowing for robust statistical inference for rare variants and improving power, we assume these residual variant-specific effects,  and
and 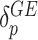 , follow arbitrary distributions with mean 0 and variance
, follow arbitrary distributions with mean 0 and variance 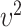 and
and 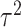 , respectively. Plugging model (2.2) into model (2.1), we obtain
, respectively. Plugging model (2.2) into model (2.1), we obtain
| (2.3) |
It becomes clear that 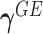 characterizes the interaction effects of
characterizes the interaction effects of 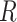 genetic risk (or burden) scores weighted by one of the variant attributes, whereas
genetic risk (or burden) scores weighted by one of the variant attributes, whereas  is the variance of the residual GxE effects. For example, suppose
is the variance of the residual GxE effects. For example, suppose 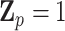 , a scalar, for all variants, then
, a scalar, for all variants, then 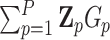 is the number of variant alleles that a subject carries. For another example, let
is the number of variant alleles that a subject carries. For another example, let  if the
if the 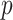 th variant is missense and 0 otherwise, for
th variant is missense and 0 otherwise, for 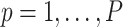 . Then
. Then 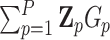 is the total number of missense variant alleles that a subject carries, and
is the total number of missense variant alleles that a subject carries, and 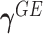 characterizes the “dosage” interaction effect of (missense) variant alleles with
characterizes the “dosage” interaction effect of (missense) variant alleles with 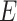 . To guard against the possibility that such “dosage” interaction effect may not fully account for the interaction effect, the remaining variant-specific interaction effects are captured by
. To guard against the possibility that such “dosage” interaction effect may not fully account for the interaction effect, the remaining variant-specific interaction effects are captured by 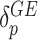 , which are assumed to follow an arbitrary distribution with mean 0 and variance
, which are assumed to follow an arbitrary distribution with mean 0 and variance 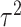 . Testing the interaction effect between
. Testing the interaction effect between 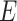 and a set of variants
and a set of variants 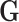 therefore amounts to test
therefore amounts to test 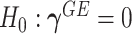 and
and 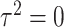 , and the number of tested parameters is
, and the number of tested parameters is 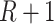 , which is typically smaller than if we were to test
, which is typically smaller than if we were to test  variant GxE.
variant GxE.
Model (2.3) encompasses scenarios that give rise to previously proposed tests. If we set 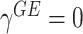 , testing GxE is to test
, testing GxE is to test 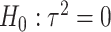 , which is the variance component test proposed by Lin and others (2013). If
, which is the variance component test proposed by Lin and others (2013). If 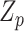 is a screening statistics-based weight with
is a screening statistics-based weight with 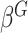 as fixed effects, the score statistic for GxE derived under this model is same as our early works on screening informed GxE tests assuming
as fixed effects, the score statistic for GxE derived under this model is same as our early works on screening informed GxE tests assuming 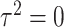 (Jiao and others, 2013) and
(Jiao and others, 2013) and 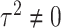 (Jiao and others, 2015). Further if
(Jiao and others, 2015). Further if 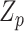 is 1 for all variants, then our model is same as the random effects model in Lin and others (2016), where the interaction effects have an exchangeable correlation.
is 1 for all variants, then our model is same as the random effects model in Lin and others (2016), where the interaction effects have an exchangeable correlation.
Model (2.3) provides a basis for a general framework for modeling the interaction effect of 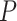 variants with
variants with 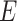 . It can straightforwardly include adjustment of other covariates, for example, principal components to account for population substructure. It can be further generalized to allow for non-linear genetic effects by replacing
. It can straightforwardly include adjustment of other covariates, for example, principal components to account for population substructure. It can be further generalized to allow for non-linear genetic effects by replacing  and
and 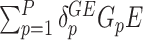 by
by 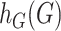 and
and 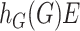 , respectively, where
, respectively, where 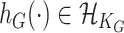 is an unknown function belonging to the functional space
is an unknown function belonging to the functional space 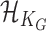 implicitly specified by some positive definite kernel function
implicitly specified by some positive definite kernel function 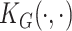 (Cristianini and Shawe-Taylor, 2000). Common examples of kernel functions include the polynomial kernel, identity-by-state, and the Gaussian Kernel (Schaid, 2010). Without loss of generality, we focus on the generalized linear regression model (2.3) for the development of proposed GxE test statistics.
(Cristianini and Shawe-Taylor, 2000). Common examples of kernel functions include the polynomial kernel, identity-by-state, and the Gaussian Kernel (Schaid, 2010). Without loss of generality, we focus on the generalized linear regression model (2.3) for the development of proposed GxE test statistics.
2.2. Proposed score statistics
Computation remains one of the foremost considerations in large-scale genome-wide discovery because of the large sample size and the large number of variants being tested. It is important that test statistics are quick to compute, and their p values can be obtained based on asymptotic distributions. Maximum likelihood or Bayesian approaches based on the mixed effects model (2.2) involve 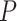 -dimensional integration, for which the required computation can be intensive for genome-wide discovery. We therefore propose to use score statistics to test GxE interaction effects because they only depend on the null and are easy to compute with trackable asymptotic distributions.
-dimensional integration, for which the required computation can be intensive for genome-wide discovery. We therefore propose to use score statistics to test GxE interaction effects because they only depend on the null and are easy to compute with trackable asymptotic distributions.
Consider the data consist of 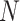 subjects such that
subjects such that 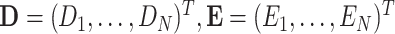 , and
, and 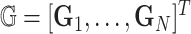 . These subjects can be sampled randomly from the population or under a retrospective sampling scheme such that cases (diseased) and controls (non-diseased) are randomly selected from their respective subpopulations. We establish the asymptotic distributions under both scenarios and the proof are provided in Section A in the supplementary material available at Biostatistics online. We denote
. These subjects can be sampled randomly from the population or under a retrospective sampling scheme such that cases (diseased) and controls (non-diseased) are randomly selected from their respective subpopulations. We establish the asymptotic distributions under both scenarios and the proof are provided in Section A in the supplementary material available at Biostatistics online. We denote 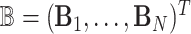 to be the (weighted) burden scores, where
to be the (weighted) burden scores, where 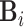 is a
is a 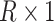 vector of
vector of 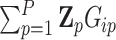 , for
, for 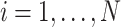 . Further, we denote the score statistics for
. Further, we denote the score statistics for 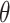 by
by 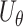 .
.
The usual approach for deriving score statistics is to take the partial derivatives of the log-likelihood function with respect to the parameters of interest under the null hypothesis. Here, we propose a novel modification to the derivation of score statistics. Specifically, we derive the score statistic 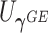 for
for 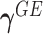 corresponding to the burden scores under
corresponding to the burden scores under 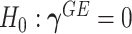 and
and 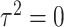 as usual. However, for the score statistic
as usual. However, for the score statistic 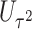 , we propose to derive it under
, we propose to derive it under  without constraining
without constraining 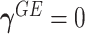 , instead of
, instead of 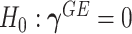 and
and 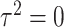 . This seemingly simple modification to
. This seemingly simple modification to 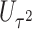 has an important property: the resulting score
has an important property: the resulting score 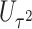 is independent of
is independent of 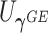 asymptotically. In fact, it is asymptotically orthogonal to the projection of the score statistics
asymptotically. In fact, it is asymptotically orthogonal to the projection of the score statistics 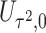 for
for  onto the space of
onto the space of  under
under 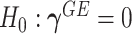 and
and 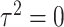 .
.
To explicitly express the two score statistics, additional notation is introduced as follows. Define 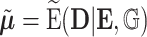 to be the fitted value of
to be the fitted value of 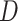 under
under 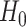 , and
, and 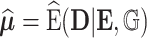 to be the fitted value of
to be the fitted value of 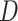 under
under 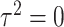 without constraining
without constraining  . Then the score statistics for
. Then the score statistics for 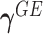 and
and 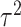 can be written as
can be written as
| (2.4) |
| (2.5) |
where 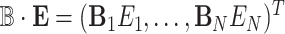 ,
, 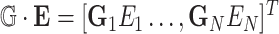 , and
, and  is a covariance matrix of
is a covariance matrix of 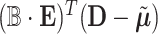 and is equal to
and is equal to 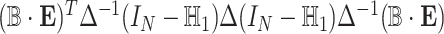 , where
, where 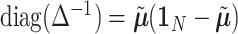 with
with 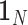 is a
is a 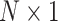 vector of 1,
vector of 1, 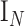 is an
is an 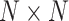 identity matrix, and
identity matrix, and 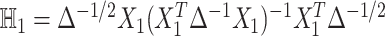 with
with 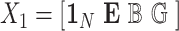 . We term the score statistics for testing both the fixed and random interaction effects as Mixed effects Score Tests for interaction (MiSTi).
. We term the score statistics for testing both the fixed and random interaction effects as Mixed effects Score Tests for interaction (MiSTi).
As the fitted value 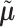 and
and 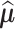 involve the random main effects for the variants, maximum posterior estimate (MPE) (also known as best linear unbiased prediction, BLUP, in the context of linear mixed effects model) can be used; however, it requires calculation of the posterior distribution of the random effects given observed data and estimation of variance
involve the random main effects for the variants, maximum posterior estimate (MPE) (also known as best linear unbiased prediction, BLUP, in the context of linear mixed effects model) can be used; however, it requires calculation of the posterior distribution of the random effects given observed data and estimation of variance 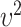 , for which the computation can be intensive especially under the generalized linear model because
, for which the computation can be intensive especially under the generalized linear model because 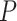 -dimensional integration is required and there is no closed form for the integration. Instead, we propose to use ridge regression estimators (Hastie and others, 2005) for estimating the random effects. Note that for linear models, the ridge regression estimator is equivalent to the BLUP for a given penalty (de Vlaming and Groenen, 2015). Furthermore, the ridge regression estimator is
-dimensional integration is required and there is no closed form for the integration. Instead, we propose to use ridge regression estimators (Hastie and others, 2005) for estimating the random effects. Note that for linear models, the ridge regression estimator is equivalent to the BLUP for a given penalty (de Vlaming and Groenen, 2015). Furthermore, the ridge regression estimator is 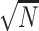 -consistent if the penalty grows at the rate of
-consistent if the penalty grows at the rate of 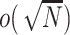 (Knight and Fu, 2000). Following these results, it is easy to show that as
(Knight and Fu, 2000). Following these results, it is easy to show that as 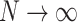 ,
, 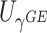 follows a
follows a 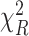 distribution with
distribution with 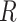 degrees of freedom and
degrees of freedom and 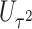 follows a weighted sum of
follows a weighted sum of 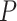 i.i.d.
i.i.d. 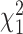 distributions with weights being eigen-values of
distributions with weights being eigen-values of 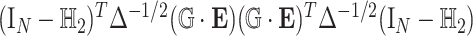 , where
, where 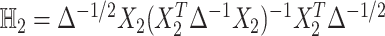 with
with 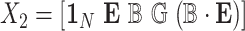 , the design matrix of proposed logistic model (2.3) under
, the design matrix of proposed logistic model (2.3) under 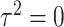 .
.
2.3. Combinations of score statistics
The asymptotic independence of 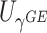 and
and 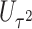 offers many possibilities for combining these two statistics. For example, since each score statistic has an asymptotic distribution, we can obtain the p value based on each score statistic and combine these p values using for example, the commonly used Fisher’s or Tippett’s combinations. However, unlike in the conventional meta-analysis where the combined components are from different studies but test the same parameter,
offers many possibilities for combining these two statistics. For example, since each score statistic has an asymptotic distribution, we can obtain the p value based on each score statistic and combine these p values using for example, the commonly used Fisher’s or Tippett’s combinations. However, unlike in the conventional meta-analysis where the combined components are from different studies but test the same parameter,  and
and 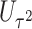 do not test the same parameters. The score statistic
do not test the same parameters. The score statistic 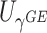 tests the association of weighted burden scores when
tests the association of weighted burden scores when 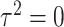 , whereas the score statistic
, whereas the score statistic 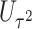 tests
tests 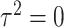 . Hence, a usual weighting for combining test statistics in the meta-analysis, which often involves sample sizes of individual studies, does not apply here. In the following we propose two data-driven combination approaches: grid-search optimal linear combination and adaptive weighted linear combination.
. Hence, a usual weighting for combining test statistics in the meta-analysis, which often involves sample sizes of individual studies, does not apply here. In the following we propose two data-driven combination approaches: grid-search optimal linear combination and adaptive weighted linear combination.
2.3.1. Gird-search-based optimal linear combination
The perhaps most straightforward approach for combining the two score statistics is to take the weighted sum of 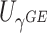 and
and 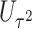 as
as  , where
, where 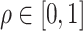 controls the relative contribution of the burden score versus the variance components. A natural approach to choosing the optimal value of
controls the relative contribution of the burden score versus the variance components. A natural approach to choosing the optimal value of 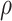 is by minimizing the p values as
is by minimizing the p values as 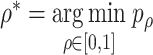 , where
, where 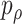 is the p value based on
is the p value based on 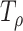 for a given
for a given 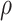 . We call the corresponding test statistic,
. We call the corresponding test statistic, 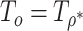 , oMiSTi with “o” referring to optimal. Now let
, oMiSTi with “o” referring to optimal. Now let 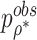 be the observed minimal p value obtained from data we can show that under the null
be the observed minimal p value obtained from data we can show that under the null
| (2.6) |
where 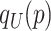 stands for the 100
stands for the 100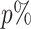 -th quantile of the random variable
-th quantile of the random variable 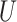 , and the expectation is with respect to
, and the expectation is with respect to 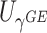 . We refer to Section B in the supplemental material available at Biostatistics online for a detailed derivation of (2.6). It is clear that the independence between
. We refer to Section B in the supplemental material available at Biostatistics online for a detailed derivation of (2.6). It is clear that the independence between 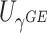 and
and 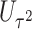 facilitates an easy evaluation of the above conditional probability of
facilitates an easy evaluation of the above conditional probability of 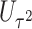 given
given 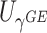 . We employ a numerical method proposed by Liu and others (2009) to approximate the distribution of
. We employ a numerical method proposed by Liu and others (2009) to approximate the distribution of 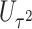 that is a weighted sum of i.i.d.
that is a weighted sum of i.i.d. 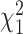 random variables by a skewed
random variables by a skewed 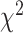 distribution with skewness and degrees of freedom obtained by matching the fourth moment while minimizing the third moment between the two distributions. This numerical method has been applied in SKAT-related methods and shown to perform well in the rare variants association analysis with finite sample sizes Lee and others, 2012. The expectation can be obtained by numerical integration on
distribution with skewness and degrees of freedom obtained by matching the fourth moment while minimizing the third moment between the two distributions. This numerical method has been applied in SKAT-related methods and shown to perform well in the rare variants association analysis with finite sample sizes Lee and others, 2012. The expectation can be obtained by numerical integration on 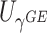 , which is very fast for univariate integrals.
, which is very fast for univariate integrals.
In practice, evaluating the conditional probability in (2.6) for all 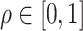 can be computationally intensive. To ease this, we consider a grid-search method to evaluate the conditional probability on a set of pre-specified grid points
can be computationally intensive. To ease this, we consider a grid-search method to evaluate the conditional probability on a set of pre-specified grid points 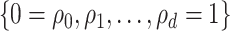 , and the search of optimal
, and the search of optimal 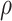 is restricted on this given set of grid points. Based on our numerical experiences, a set of 20 grid points usually achieves good performance at a reasonable computational cost.
is restricted on this given set of grid points. Based on our numerical experiences, a set of 20 grid points usually achieves good performance at a reasonable computational cost.
2.3.2. Adaptive weighted linear combination
Since each of the score statistics 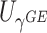 and
and  has an asymptotic distribution, it is natural to first calculate the p value based on each score statistic and then combine the two independent p values. Fisher’s combination (Fisher and others, 1970) is a very popular approach for combining independent p values. This can be represented by
has an asymptotic distribution, it is natural to first calculate the p value based on each score statistic and then combine the two independent p values. Fisher’s combination (Fisher and others, 1970) is a very popular approach for combining independent p values. This can be represented by 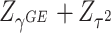 , where
, where 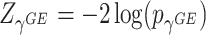 and
and 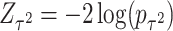 . It is expected that Fisher’s combination is very powerful when both the burden and variance components are non-null, but could potentially lose power when only one is non-null. To allow for flexibility of the combined test to accommodate the evidence of association mainly from either the burden or variance component, we propose an adaptive weighted linear combination with weights determined by
. It is expected that Fisher’s combination is very powerful when both the burden and variance components are non-null, but could potentially lose power when only one is non-null. To allow for flexibility of the combined test to accommodate the evidence of association mainly from either the burden or variance component, we propose an adaptive weighted linear combination with weights determined by 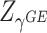 and
and 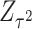 , respectively. Specifically, the adaptive weighted linear combination can be represented as
, respectively. Specifically, the adaptive weighted linear combination can be represented as
| (2.7) |
where the subscript 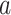 refers to “adaptive”. We term this combination as aMiSTi. Note that
refers to “adaptive”. We term this combination as aMiSTi. Note that 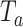 is equivalent to the square of
is equivalent to the square of 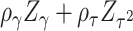 , where
, where 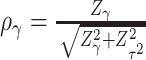 and
and 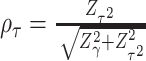 . Interestingly, the weights
. Interestingly, the weights 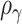 and
and 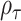 are equivalent to the sine and cosine functions of the angle between the direction of the observed 2D test statistics
are equivalent to the sine and cosine functions of the angle between the direction of the observed 2D test statistics 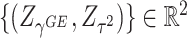 and the x-axis. We note that a similar idea of adaptive weighting has been proposed in set-based association testing for main effects (see e.g., Cai and others, 2012). Compared to the grid-search weighted combination, the adaptive weighting has the advantage that it does not require a prior decision on the number and placement of grid points. The nice property of
and the x-axis. We note that a similar idea of adaptive weighting has been proposed in set-based association testing for main effects (see e.g., Cai and others, 2012). Compared to the grid-search weighted combination, the adaptive weighting has the advantage that it does not require a prior decision on the number and placement of grid points. The nice property of 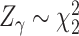 and
and 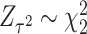 , and the independence between the two components facilitate an easy way to calculate the p value for
, and the independence between the two components facilitate an easy way to calculate the p value for 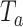 through numerical integration at low computational cost.
through numerical integration at low computational cost.
3. Simulation
We conducted an extensive simulation study to evaluate the performance of our proposed combinations 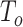 (oMiSTi) and
(oMiSTi) and 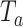 (aMiSTi), Fisher’s combination
(aMiSTi), Fisher’s combination 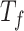 (fMiSTi) and an existing approach, iSKAT (Lin and others, 2016). To help understand the performance of various combination methods, we also included tests based on the burden component only (
(fMiSTi) and an existing approach, iSKAT (Lin and others, 2016). To help understand the performance of various combination methods, we also included tests based on the burden component only (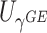 ) and the variance component only (
) and the variance component only (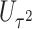 ). We evaluated the performance of all tests for both continuous and binary outcomes. Here we are focused on results for binary outcome because in our real data application the phenotype is binary and it is also generally more challenging than continuous outcome. The results for continuous outcome are provided in Section D, supplementary materials available at Biostatistics online. Briefly, all tests maintain correct type I error and MiSTi’s are generally more powerful than or as powerful as iSKAT. When the signals mainly come from either the burden or the variance component, oMiSTi and aMiSTi are slightly more powerful than fMiSTi. On the other hand, when the signals come from both components, fMiSTi is slightly more powerful, probably due to the cost of estimating the weight from the data for oMiSTi and aMiSTi.
). We evaluated the performance of all tests for both continuous and binary outcomes. Here we are focused on results for binary outcome because in our real data application the phenotype is binary and it is also generally more challenging than continuous outcome. The results for continuous outcome are provided in Section D, supplementary materials available at Biostatistics online. Briefly, all tests maintain correct type I error and MiSTi’s are generally more powerful than or as powerful as iSKAT. When the signals mainly come from either the burden or the variance component, oMiSTi and aMiSTi are slightly more powerful than fMiSTi. On the other hand, when the signals come from both components, fMiSTi is slightly more powerful, probably due to the cost of estimating the weight from the data for oMiSTi and aMiSTi.
Specifically, we generated the binary outcome according to logistic regression model
| (3.1) |
We generated 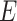 from
from 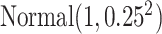 independently from
independently from 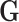 . We generated
. We generated 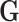 under two different scenarios. The first scenario was to generate
under two different scenarios. The first scenario was to generate 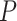 =
= 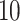 or
or 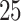 independent SNPs with minor allele frequencies (MAF) equally spaced from
independent SNPs with minor allele frequencies (MAF) equally spaced from 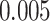 to
to 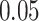 . The purpose of this simulation was to study how all methods perform under various alternatives without being confounded by complicated genetic structures. To save space, the results are presented in Section D.3, supplementary material available at Biostatistics online. Here we only provide a brief summary. All tests maintain correct type I error across all settings considered under this scenario. The various combinations of MiSTi’s have comparable power, and they all have greater power than iSKAT. The pattern and strength of the genetic main effects do not affect the general pattern of the powers across all methods.
. The purpose of this simulation was to study how all methods perform under various alternatives without being confounded by complicated genetic structures. To save space, the results are presented in Section D.3, supplementary material available at Biostatistics online. Here we only provide a brief summary. All tests maintain correct type I error across all settings considered under this scenario. The various combinations of MiSTi’s have comparable power, and they all have greater power than iSKAT. The pattern and strength of the genetic main effects do not affect the general pattern of the powers across all methods.
The second scenario is to mimic a more realistic genetic structure by generating 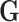 based sequencing data from the Dallas Heart Study (DHS, DHS, Victor and others, 2004). Specifically, haplotypes were inferred based on the sequencing data on a candidate gene ANGPTL5 for 3409 subjects and randomly paired to achieve a desirable sample size. There are a total
based sequencing data from the Dallas Heart Study (DHS, DHS, Victor and others, 2004). Specifically, haplotypes were inferred based on the sequencing data on a candidate gene ANGPTL5 for 3409 subjects and randomly paired to achieve a desirable sample size. There are a total 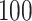 genetic variants in ANGPTL5. Of these,
genetic variants in ANGPTL5. Of these, 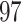 variants have MAF
variants have MAF
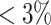 , and
, and 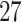 are functional variants. Unless otherwise stated, a total of 10 000 simulated data sets were generated each with 5000 cases and 5000 controls to mimic our real data example. The type I error and power were evaluated at three significance levels
are functional variants. Unless otherwise stated, a total of 10 000 simulated data sets were generated each with 5000 cases and 5000 controls to mimic our real data example. The type I error and power were evaluated at three significance levels 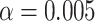 ,
, 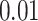 , and
, and 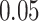 .
.
Type I error We considered two settings for the genetic main effects: (1) Null, 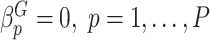 , (2) Sparse, 20% of
, (2) Sparse, 20% of 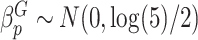 and 0 otherwise. The set of variants is defined in two different ways:
and 0 otherwise. The set of variants is defined in two different ways: 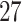 functional variants only and all
functional variants only and all 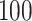 variants in the gene. When all
variants in the gene. When all 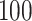 variants are tested for GxE, we also assessed the type I error with and without including a function indicator, which is 1 if the variant is functional and 0 otherwise. Ridge regression was used in fitting the null models and the penalty was selected by generalized cross validation following the suggestion in Lin and others (2013). Overall, the type I error of all MiSTi combinations are well within the 95% confidence intervals of the true type I error (Table 1). iSKAT also has correct type I error; however, the type I error is somewhat inflated when
variants are tested for GxE, we also assessed the type I error with and without including a function indicator, which is 1 if the variant is functional and 0 otherwise. Ridge regression was used in fitting the null models and the penalty was selected by generalized cross validation following the suggestion in Lin and others (2013). Overall, the type I error of all MiSTi combinations are well within the 95% confidence intervals of the true type I error (Table 1). iSKAT also has correct type I error; however, the type I error is somewhat inflated when 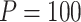 . We also examined the type I error of the proposed methods at the exome-wide significance level. A large scale simulation with 1 000 000 datasets was conducted. Figure 1 shows the estimated type I error of MiSTi’s at various significance levels ranging from
. We also examined the type I error of the proposed methods at the exome-wide significance level. A large scale simulation with 1 000 000 datasets was conducted. Figure 1 shows the estimated type I error of MiSTi’s at various significance levels ranging from 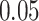 to the exome-wide significance level
to the exome-wide significance level 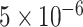 . All MiSTi’s appear to keep a correct type I error all the way to the exome-wide significance level.
. All MiSTi’s appear to keep a correct type I error all the way to the exome-wide significance level.
Fig. 1.
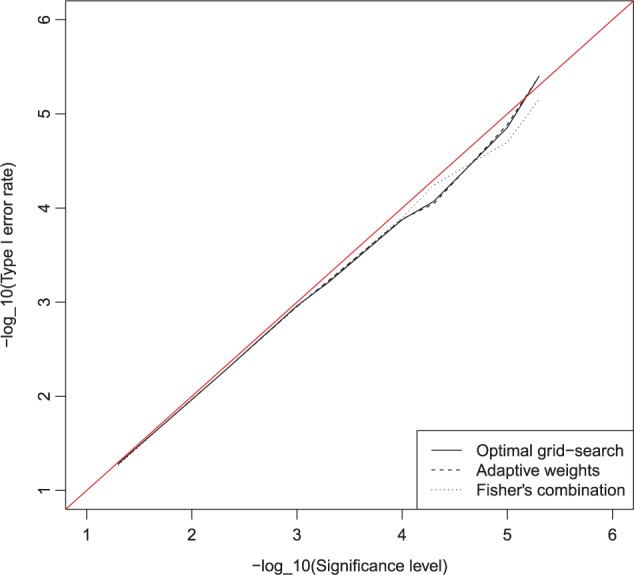
Type I error rate of three different combination approaches for DHS genetic structure on the 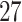 functional variants under genetic main effects as setting 2n. Sample size is 10 000 and the number of simulation runs is 10 00 000.
functional variants under genetic main effects as setting 2n. Sample size is 10 000 and the number of simulation runs is 10 00 000.
Table 1.
Type I error of four combinations oMiSTi, aMiSTi, fMiSTi, and iSKAT as well as tests for burden (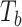 ) and variance component (
) and variance component (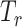 ) at significance level
) at significance level 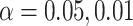 , and
, and 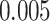 for binary outcome. A total of
for binary outcome. A total of 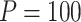 variants are in the gene-set, and
variants are in the gene-set, and 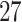 are functional. For
are functional. For 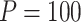 , the type I error for MiSTi’s with and without incorporating the functional indicator, denoted by FA and No FA, respectively, are also shown.
, the type I error for MiSTi’s with and without incorporating the functional indicator, denoted by FA and No FA, respectively, are also shown.
| Null genetic main effects | Sparse genetic main effects | ||||||
|---|---|---|---|---|---|---|---|
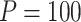 |
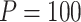 |
||||||
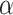 |
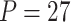 |
No FA | FA | 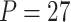 |
No FA | FA | |
| 0.05 | |||||||
| oMiSTi | 0.0519 | 0.0519 | 0.0499 | 0.0515 | 0.0483 | 0.0484 | |
| aMiSTi | 0.0522 | 0.0516 | 0.0487 | 0.0512 | 0.0490 | 0.0476 | |
| fMiSTi | 0.0554 | 0.0529 | 0.0505 | 0.0517 | 0.0512 | 0.0498 | |
| iSKAT | 0.0568 | 0.0555 | — | 0.0548 | 0.0589 | — | |
 |
0.0496 | 0.0519 | 0.0498 | 0.0518 | 0.0521 | 0.0510 | |
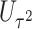 |
0.0546 | 0.0519 | 0.0480 | 0.0530 | 0.0469 | 0.0467 | |
| 0.01 | |||||||
| oMiSTi | 0.0107 | 0.0120 | 0.0121 | 0.0107 | 0.0110 | 0.0108 | |
| aMiSTi | 0.0107 | 0.0116 | 0.0118 | 0.0105 | 0.0109 | 0.0104 | |
| fMiSTi | 0.0116 | 0.0116 | 0.0115 | 0.0104 | 0.0107 | 0.0093 | |
| iSKAT | 0.0125 | 0.0134 | — | 0.0118 | 0.0143 | — | |
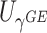 |
0.0093 | 0.0121 | 0.0117 | 0.0091 | 0.0111 | 0.0104 | |
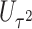 |
0.0121 | 0.0107 | 0.0103 | 0.0113 | 0.0100 | 0.0095 | |
| 0.005 | |||||||
| oMiSTi | 0.0051 | 0.0060 | 0.0065 | 0.0060 | 0.0053 | 0.005 | |
| aMiSTi | 0.0053 | 0.0057 | 0.0066 | 0.0062 | 0.0052 | 0.0048 | |
| fMiSTi | 0.0054 | 0.0059 | 0.0062 | 0.0055 | 0.0054 | 0.0045 | |
| iSKAT | 0.0065 | 0.0079 | — | 0.0070 | 0.0084 | — | |
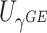 |
0.0046 | 0.0066 | 0.0064 | 0.0044 | 0.0056 | 0.0055 | |
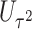 |
0.0060 | 0.0060 | 0.0058 | 0.0063 | 0.0054 | 0.0051 | |
Power To compare power among different tests, we randomly selected two functional variants to have GxE. We considered two scenarios, the GxE effects of the two variants are in same direction (GxE same direction) and opposite direction (GxE opposite direction). The results of power comparison are shown in Table 2. All MiSTi tests are much more powerful than iSKAT with MiSTis having comparable power with each other, and oMiSTi and aMiSTi being more powerful than fMiSTi when the signal is from only the variance component as in the GxE opposite direction model. When all 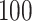 variants are included in the set, all tests lose power; however, iSKAT still has lower power than MiSTi tests in most of the cases. Furthermore, incorporating an indicator for whether or not a variant is functional can improve power for MiSTi tests considerably when the functional indicator is informative, as in the case of the GxE same direction model. Importantly, we note that the power of the burden component is much greater after incorporating the functional indicator, suggesting that the interaction signals are mainly from the functional variants. This demonstrates that using the mixed effects model leveraging functional annotation, if known and informative, cannot only improve power for detecting the overall association, but also help identify sources of the signals that may inform the follow-up studies.
variants are included in the set, all tests lose power; however, iSKAT still has lower power than MiSTi tests in most of the cases. Furthermore, incorporating an indicator for whether or not a variant is functional can improve power for MiSTi tests considerably when the functional indicator is informative, as in the case of the GxE same direction model. Importantly, we note that the power of the burden component is much greater after incorporating the functional indicator, suggesting that the interaction signals are mainly from the functional variants. This demonstrates that using the mixed effects model leveraging functional annotation, if known and informative, cannot only improve power for detecting the overall association, but also help identify sources of the signals that may inform the follow-up studies.
Table 2.
Power of various methods without and with functional annotations: 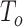 ,
, 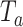 ,
, 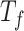 ,
, 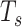 ,
,  , and
, and 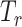 for dichotomous outcomes for 27 functional variants (FV Only) and 100 variants (All) from the DHS without or with functional annotations (No FA and FA, respectively) under scenarios with no main effects and two settings of interaction effects on two variants with same and opposite directions respectively (GxE Same Direction and GxE Opposite Direction). The significance levels
for dichotomous outcomes for 27 functional variants (FV Only) and 100 variants (All) from the DHS without or with functional annotations (No FA and FA, respectively) under scenarios with no main effects and two settings of interaction effects on two variants with same and opposite directions respectively (GxE Same Direction and GxE Opposite Direction). The significance levels 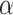 are 0.05, 0.01, and 0.005, respectively
are 0.05, 0.01, and 0.005, respectively
| GxE same direction | GxE opposite direction | ||||||
|---|---|---|---|---|---|---|---|
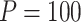 |
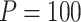 |
||||||
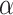 |
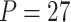 |
No FA | FA | 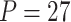 |
No FA | FA | |
| 0.05 | |||||||
| oMiSTi | 0.798 | 0.151 | 0.370 | 0.726 | 0.063 | 0.077 | |
| aMiSTi | 0.813 | 0.159 | 0.365 | 0.727 | 0.069 | 0.072 | |
| fMiSTi | 0.842 | 0.160 | 0.396 | 0.703 | 0.079 | 0.078 | |
| iSKAT | 0.554 | 0.086 | — | 0.633 | 0.064 | — | |
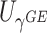 |
0.439 | 0.066 | 0.373 | 0.062 | 0.053 | 0.056 | |
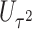 |
0.745 | 0.193 | 0.133 | 0.810 | 0.083 | 0.093 | |
| 0.01 | |||||||
| oMiSTi | 0.576 | 0.054 | 0.181 | 0.480 | 0.010 | 0.016 | |
| aMiSTi | 0.590 | 0.053 | 0.172 | 0.484 | 0.011 | 0.017 | |
| fMiSTi | 0.647 | 0.056 | 0.186 | 0.454 | 0.013 | 0.017 | |
| iSKAT | 0.241 | 0.022 | — | 0.316 | 0.014 | — | |
 |
0.230 | 0.015 | 0.201 | 0.013 | 0.013 | 0.011 | |
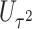 |
0.498 | 0.068 | 0.024 | 0.581 | 0.013 | 0.016 | |
| 0.005 | |||||||
| oMiSTi | 0.486 | 0.031 | 0.124 | 0.394 | 0.007 | 0.009 | |
| aMiSTi | 0.490 | 0.032 | 0.122 | 0.397 | 0.007 | 0.009 | |
| fMiSTi | 0.542 | 0.031 | 0.131 | 0.354 | 0.006 | 0.009 | |
| iSKAT | 0.166 | 0.011 | — | 0.222 | 0.007 | — | |
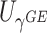 |
0.164 | 0.007 | 0.146 | 0.006 | 0.005 | 0.006 | |
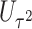 |
0.408 | 0.042 | 0.013 | 0.480 | 0.006 | 0.010 | |
4. Application to genome-wide exome chip GxE analysis
CRC is a commonly diagnosed cancer, and has a sizable genetic component and well-established environmental risk factors. Identifying GxE is key to understand the interplay between genes and environment and their role in the development of CRC. We applied our proposed MiSTi’s and iSKAT to the case–control data from the Genetics and Epidemiology of Colorectal Cancer Consortium (GECCO) (Peters and others, 2013). In particular, this data set includes exome-wide genotyping on 17 864 white study participants (9135 CRC cases and 8729 controls) from 11 studies. The description of these studies is provided in supplementary Table S6 available at Biostatistics online. To illustrate, we assessed association of exome-wide interaction with nonsteroidal anti-inflammatory drugs (NSAIDs) use (nonuser, regular user) with CRC risk. A logistic regression model was used, adjusting for study, age, sex, and three major principal components to account for population substructure. NSAIDS use is associated with decreased risk of CRC with odds ratio (OR) 0.71 (95% confidence interval: 0.66–0.76).
We aggregated rare variants (MAF
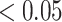 ) by gene and assessed the interaction effect of each gene with NSAIDs use on CRC risk. Genes with two or fewer rare variants were excluded, resulting a total of 7600 genes. The number of variants ranges from 3 to 357, with an average of 4.8. Since the colorectal tissue specific functional annotation database is still under development in GECCO, detailed annotation is not yet available for analysis. To illustrate, we simply set
) by gene and assessed the interaction effect of each gene with NSAIDs use on CRC risk. Genes with two or fewer rare variants were excluded, resulting a total of 7600 genes. The number of variants ranges from 3 to 357, with an average of 4.8. Since the colorectal tissue specific functional annotation database is still under development in GECCO, detailed annotation is not yet available for analysis. To illustrate, we simply set 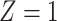 for all variants, creating a burden score (B) that is the sum of variant alleles in a gene. The MiSTi’s test both the BxE and the variance component for GxE equal to 0.
for all variants, creating a burden score (B) that is the sum of variant alleles in a gene. The MiSTi’s test both the BxE and the variance component for GxE equal to 0.
Two genes are identified at the exome-wide significance level 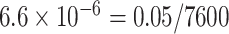 : PTCHD3 at 10p12.1 and TELO2 at 16p13.3 (Table 3). The interaction of PTCHD3xNSAIDs is only detected by fMiSTi, and the pvalues of oMiSTi and aMiSTi are close to the threshold (
: PTCHD3 at 10p12.1 and TELO2 at 16p13.3 (Table 3). The interaction of PTCHD3xNSAIDs is only detected by fMiSTi, and the pvalues of oMiSTi and aMiSTi are close to the threshold (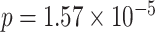 and
and 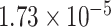 , respectively). However, the p value for iSKAT is 0.0189, which is highly non-significant. Gene TELO2 is identified by both fMiSTi and iSKAT at the exome-wide significance level, though the p values of oMiSTi and aMiSTi are close to the threshold. No other genes have reached exome-wide significance by any test.
, respectively). However, the p value for iSKAT is 0.0189, which is highly non-significant. Gene TELO2 is identified by both fMiSTi and iSKAT at the exome-wide significance level, though the p values of oMiSTi and aMiSTi are close to the threshold. No other genes have reached exome-wide significance by any test.
Table 3.
P-values of MiSTi’s, iSKAT, burden 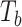 and variance component
and variance component 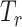 for the interaction of PTCHD3 and TELO2 with NSAIDs use from the analysis of GECCO exome chip data
for the interaction of PTCHD3 and TELO2 with NSAIDs use from the analysis of GECCO exome chip data
| Gene | oMiSTi | aMiSTi | fMiSTi | iSKAT | 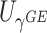 |
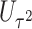 |
| PTCHD3 | 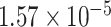 |
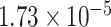 |
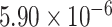 |
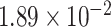 |
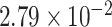 |
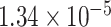 |
| TELO2 | 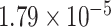 |
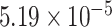 |
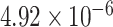 |
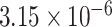 |
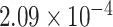 |
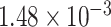 |
Gene PTCHD3 has been previously reported by Jiao and others (2013). There are eight rare variants in PTCHD3 with MAF ranging from 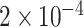 to
to 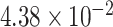 (see supplementary Table S7 available at Biostatistics online). A ridge regression model on the eight variants in PTCHD3 and MSAIDs with interactions shows that the NSAIDs use has no protective effect if a subject carries any minor allele in PTCHD3 (see supplementary Table S8 available at Biostatistics online). For TELO2, there are seven rare variants with MAF ranging from
(see supplementary Table S7 available at Biostatistics online). A ridge regression model on the eight variants in PTCHD3 and MSAIDs with interactions shows that the NSAIDs use has no protective effect if a subject carries any minor allele in PTCHD3 (see supplementary Table S8 available at Biostatistics online). For TELO2, there are seven rare variants with MAF ranging from 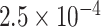 to
to 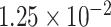 . A ridge regression with GxE shows that NSAIDs use has a stronger protective effect if the subject does not carry any minor allele in any of the seven variants (OR = 0.69 =
. A ridge regression with GxE shows that NSAIDs use has a stronger protective effect if the subject does not carry any minor allele in any of the seven variants (OR = 0.69 = 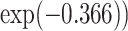 than subjects who carry at least one minor allele (
than subjects who carry at least one minor allele (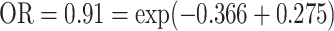 ). For both genes, the interaction appears to be driven by a few variants as shown in single variant GxE test, and there is substantial variability on the individual variant GxE effects, where both positive and negative effects exist. The variance component test would be more powerful than the burden test under this scenario. However, our approach suggests that despite highly heterogeneous GxE effects, there appears to be a concerted GxE as shown in the burden GxE. A search of literature suggests that TELO2 encodes a protein that is a regulator of the DNA damage response and associated with telomere maintenance (Takai and others, 2007), which could potentially be modified by NSAIDs use. Though these findings are very preliminary and need to be replicated in an independent data set, it is clear that our proposed tests are able to detect as many, if not more, genes than the existing test.
). For both genes, the interaction appears to be driven by a few variants as shown in single variant GxE test, and there is substantial variability on the individual variant GxE effects, where both positive and negative effects exist. The variance component test would be more powerful than the burden test under this scenario. However, our approach suggests that despite highly heterogeneous GxE effects, there appears to be a concerted GxE as shown in the burden GxE. A search of literature suggests that TELO2 encodes a protein that is a regulator of the DNA damage response and associated with telomere maintenance (Takai and others, 2007), which could potentially be modified by NSAIDs use. Though these findings are very preliminary and need to be replicated in an independent data set, it is clear that our proposed tests are able to detect as many, if not more, genes than the existing test.
5. Discussion
In this article, we proposed a mixed effects model for assessing the association of GxE for a set of genetic variants and a novel approach for constructing score test statistics for testing both the fixed effect and the variance component equal to 0. Our novel construction ensures that the score statistics corresponding to fixed and random effects are asymptotically independent, which enables one to combine these two score statistics efficiently with p values that can be easily computed. We also proposed two data-adaptive combinations: linear combinations based on grid-search and adaptive weighted. Extensive simulation shows that these two and Fisher’s combination all have comparable power and they are more powerful than existing tests under a wide range of scenarios. This is particularly appealing for genome-wide search of GxE, as all possible interaction models could exist.
Model (2.2) has fixed and random effects for both the main genetic effects and GxE. As the focus here is on testing GxE, there is no need to model the main effects of 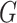 as in (2.2). Instead we can directly estimate
as in (2.2). Instead we can directly estimate 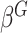 by ridge regression. This is because tests for GxE are valid, as long as the main effects of
by ridge regression. This is because tests for GxE are valid, as long as the main effects of 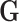 and
and 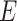 are adequately modeled. In fact, we show that the fitted values from the two ridge regression modeling on the genetic main effects are asymptotically equivalent if the penalty term is
are adequately modeled. In fact, we show that the fitted values from the two ridge regression modeling on the genetic main effects are asymptotically equivalent if the penalty term is 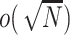 (see Section C supplementary material available at Biostatistics online). However, if the interest is in GxE effects, it is important that the main effects and GxE have the same models to ensure the hierarchical structure and interpretable estimates.
(see Section C supplementary material available at Biostatistics online). However, if the interest is in GxE effects, it is important that the main effects and GxE have the same models to ensure the hierarchical structure and interpretable estimates.
Sample size determination for set-based GxE is important in the study design phase. The power of a set-based GxE test depends on the size of the set and the number of causal variants with GxE in the set, as well as the effect sizes and MAFs of the causal variants, and the underlying linkage disequilibrium structure among the variants. One needs to balance out between not missing causal variants that would require a larger set and not including too many neutral variants that would require a smaller set. We note that when a set includes many neutral variants, if the functional annotation is somewhat informative, our proposed mixed effects score tests can improve power significantly. A closed form of power calculation would be desirable for determining the sample size required for particular scenarios; however, it is difficult to derive such a formula because the power depends on many factors. It would be more realistic to calculate power based on simulations for any particular scenarios that investigators deem to be reasonable. As our score statistics have asymptotic distributions, it is computationally feasible to conduct such a simulation-based study to assess the power with given sample size. As a back-of-the-envelope calculation, we may calculate power by a “composite” single variant GxE, where the MAF of the composite variant is the sum of the MAFs of rare variants in the set and the effect size 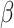 for the composite variant would be such that the explained variation, that is,
for the composite variant would be such that the explained variation, that is, 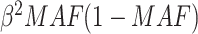 is equivalent to the total sum of variation explained by the hypothesized causal variants. By doing this transformation, we can then easily calculate the power for single variant GxE using the popular power calculator Quanto (http://biostats.usc.edu/Quanto.html). For example, under the first scenario in Table 2, the back-of-the-envelop power calculations give the power estimates 0.863, 0.689, and 0.603, respectively, when
is equivalent to the total sum of variation explained by the hypothesized causal variants. By doing this transformation, we can then easily calculate the power for single variant GxE using the popular power calculator Quanto (http://biostats.usc.edu/Quanto.html). For example, under the first scenario in Table 2, the back-of-the-envelop power calculations give the power estimates 0.863, 0.689, and 0.603, respectively, when 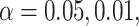 and
and 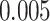 , which are largely consistent with the power as shown for MiSTi’s.
, which are largely consistent with the power as shown for MiSTi’s.
Acknowledgments
authors would like to thank the GECCO Coordinating Center for their generosity of providing the data for illustrating the methods. The detailed funding and acknowledgement for studies that contribute to GECCO are provided in the Supplementary Materials (Section F). Conflict of Interest: None declared.
Supplementary material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
The work is supported by the grants from the National Institute of Health (R01 CA189532, R01 CA195789, R21 ES022332, P01 CA53996, R21 CA195789). The GECCO Coordinating Center is funded by the grants from the National Institute of Health (R01 CA189532, R21 ES022332, P01 CA53996, U01 CA137088, R01 CA59045, U01 CA164930).
References
- Cai, T., Lin, X. and Carroll, R. J. (2012). Identifying genetic marker sets associated with phenotypes via an efficient adaptive score test. Biostatistics 13, 776–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cristianini, N. and Shawe-Taylor, J. (2000). An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge, U.K.: Cambridge University Press; ISBN 0-521-78019-5. [Google Scholar]
- de Vlaming, R. and Groenen, P. J. F. (2015). The current and future use of ridge regression for prediction in quantitative genetics. BioMed Research International 2015, 143712 doi:10.1155/2015/143712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher, S. R. A., Genetiker, S., Fisher, R. A., Genetician, S., Britain, G., Fisher, R. A. and Généticien, S. (1970). Statistical Methods for Research Workers, Volume 14. Edinburgh: Oliver and Boyd. [Google Scholar]
- Hastie, T., Tibshirani, R., Friedman, J. and Franklin, J. (2005). The elements of statistical learning: data mining, inference and prediction. The Mathematical Intelligencer 27, 83–85. [Google Scholar]
- Hsu, L., Jiao, S., Dai, J. Y., Hutter, C., Peters, U. and Kooperberg, C. (2012). Powerful cocktail methods for detecting genome-wide gene-environment interaction. Genetic Epidemiology 36, 183–194. PMCID: PMC3654520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiao, S., Hsu, L., Bézieau, S., Brenner, H., Chan, A. T., Chang-Claude, J., Le Marchand, L., Lemire, M., Newcomb, P. A., Slattery, M. L.. and others (2013). Siberia: set based gene environment interaction test for rare and common variants in complex diseases. Genetic Epidemiology. PMCID: PMC3713231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiao, S., Peters, U., Berndt, S., Bézieau, S., Brenner, H., Campbell, P. T., Chan, A. T., Chang-Claude, J., Lemire, M., Newcomb, P. A., Potter, J. D., Slattery, M. L.. and others (2015). Powerful set-based gene-environment interaction testing framework for complex diseases. Genetic Epidemiology 39 (8), 609–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight, K. and Fu, W. (2000). Asymptotics for lasso-type estimators. The Annals of Statistics 28, 1356–1378. [Google Scholar]
- Lee, S., Wu, M. C. and Lin, X. (2012). Optimal tests for rare variant effects in sequencing association studies. Biostatistics 13, 762–775. PMCID: PMC3440237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin, X., Lee, S., Christiani, D. C. and Lin, X. (2013). Test for interactions between a genetic marker set & environment in generalized linear models. Biostatistics 14 (4), 667–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin, X., Lee, S., Wu, M. C., Wang, C., Chen, H., Li, Z. and Lin, X. (2016). Test for rare variants by environment interactions in sequencing association studies. Biometrics 72 (1), 156–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, H., Tang, Y. and Zhang, H. H. (2009). A new chi-square approximation to the distribution of non-negative definite quadratic forms in non-central normal variables. Computational Statistics and Data Analysis 53, 853–856. [Google Scholar]
- Peters, U., Jiao, S., Schumacher, F. R., Hutter, C. M., Aragaki, A. K., Baron, J. A., Berndt, S. I., Bézieau, S., Brenner, H., Butterbach, K.. and others (2013). Identification of genetic susceptibility loci for colorectal tumors in a genome-wide meta-analysis. Gastroenterology 144 (4), 799–807.e24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaid, D. J. (2010). Genomic similarity and kernel methods ii: methods for genomic information. Human Heredity 70, 132–140. PMCID: N/A (no NIH grant funding cited). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takai, H., Wang, R. C., Takai, K. K., Yang, H. and De Lange, T. (2007). Tel2 regulates the stability of pi3k-related protein kinases. Cell 131, 1248–1259. [DOI] [PubMed] [Google Scholar]
- Thomas, D. (2010). Gene–environment-wide association studies: emerging approaches. Nature Reviews Genetics 11, 259–272. PMCID: PMC2891422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzeng, J.-Y., Zhang, D., Pongpanich, M., Smith, C., McCarthy, M. I., Sale, M. M., Worrall, B. B., Hsu, F.-C., Thomas, D. C. and Sullivan, P. F. (2011). Studying gene and gene-environment effects of uncommon and common variants on continuous traits: a marker-set approach using gene-trait similarity regression. The American Journal of Human Genetics 89, 277–288. PMCID: PMC3155192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Victor, R. G., Haley, R. W., Willett, D. W. L., Peshock, R. M., Vaeth, P. C., Leonard, D., Basit, M., Cooper, R. S., Iannacchione, V. G., Visscher, W. A.. and others (2004). The Dallas Heart Study: a population-based probability sample for the multidisciplinary study of ethnic differences in cardiovascular health. The American Journal of Cardiology 93, 1473–1480. [DOI] [PubMed] [Google Scholar]


