Ancient human disturbances may be skewing our understanding of Amazonian forests

Significance

The Amazon harbors thousands of species and plays a vital role in the Earth’s climate and carbon cycles. Much of what we know about the Amazon is based on censuses of only a small number of forest inventory plots, an even smaller number of which are censused repeatedly and used to study forest dynamics and carbon fluxes. The effects of ancient human impacts have never been properly assessed or accounted for in studies of Amazonian plots. New spatial analyses show that plots significantly oversample areas with high abundances of archaeological evidence of past human activities. This suggests that our interpretations of the Amazon’s structure, composition, and function are based disproportionately on forests still reflecting the legacies of past human disturbances.

Abstract

Although the Amazon rainforest houses much of Earth’s biodiversity and plays a major role in the global carbon budget, estimates of tree biodiversity originate from fewer than 1,000 forest inventory plots, and estimates of carbon dynamics are derived from fewer than 200 recensus plots. It is well documented that the pre-European inhabitants of Amazonia actively transformed and modified the forest in many regions before their population collapse around 1491 AD; however, the impacts of these ancient disturbances remain entirely unaccounted for in the many highly influential studies using Amazonian forest plots. Here we examine whether Amazonian forest inventory plot locations are spatially biased toward areas with high probability of ancient human impacts. Our analyses reveal that forest inventory plots, and especially forest recensus plots, in all regions of Amazonia are located disproportionately near archaeological evidence and in areas likely to have ancient human impacts. Furthermore, regions of the Amazon that are relatively oversampled with inventory plots also contain the highest values of predicted ancient human impacts. Given the long lifespan of Amazonian trees, many forest inventory and recensus sites may still be recovering from past disturbances, potentially skewing our interpretations of forest dynamics and our understanding of how these forests are responding to global change. Empirical data on the human history of forest inventory sites are crucial for determining how past disturbances affect modern patterns of forest composition and carbon flux in Amazonian forests.

Amazonian rainforests encompass an area of >5 million km², harbor much of Earth’s biodiversity, and directly or indirectly support global society through vital ecosystems services, such as water cycling and carbon sequestration (1–4). Several decades of inventorying and monitoring of forest plots have provided invaluable information concerning, for example, the total number of trees (5), species diversity (6–8), and estimates of carbon stocks and dynamics (1, 4, 9) in the Amazon. That said, many important questions remain concerning the drivers of forest dynamics and functioning, and how the Amazon may be responding to global changes, such as increasing atmospheric concentrations of CO₂, rising temperatures, and changes in precipitation patterns (10–14). Notably, recensuses of hundreds of forest plots have revealed increases in their aboveground biomass, suggesting that the Amazon forest is acting as a large carbon sink (15, 16); however, both the generality of biomass increases and the underlying cause(s) remain matters of active debate, owing to such factors as sparse data and environmental heterogeneity (17–20).

One of the primary sources of uncertainty in estimating forest dynamics and function is the fact that forest plots directly sample only a very small fraction (<0.0005%) of the total area of Amazonia (21), and thus there is a strong potential for biases toward certain conditions or types of forests (15, 22, 23). Another source of uncertainty is the use of short-term monitoring to track changes in forest dynamics that can be influenced by processes occurring over much longer time scales. Amazonian tree lifespans often exceed 400 y (24), with some trees living more than 1,400 y (25); as such, disturbances that occurred in past centuries or millennia may still be affecting the patterns and processes observed in modern ecological surveys (26).

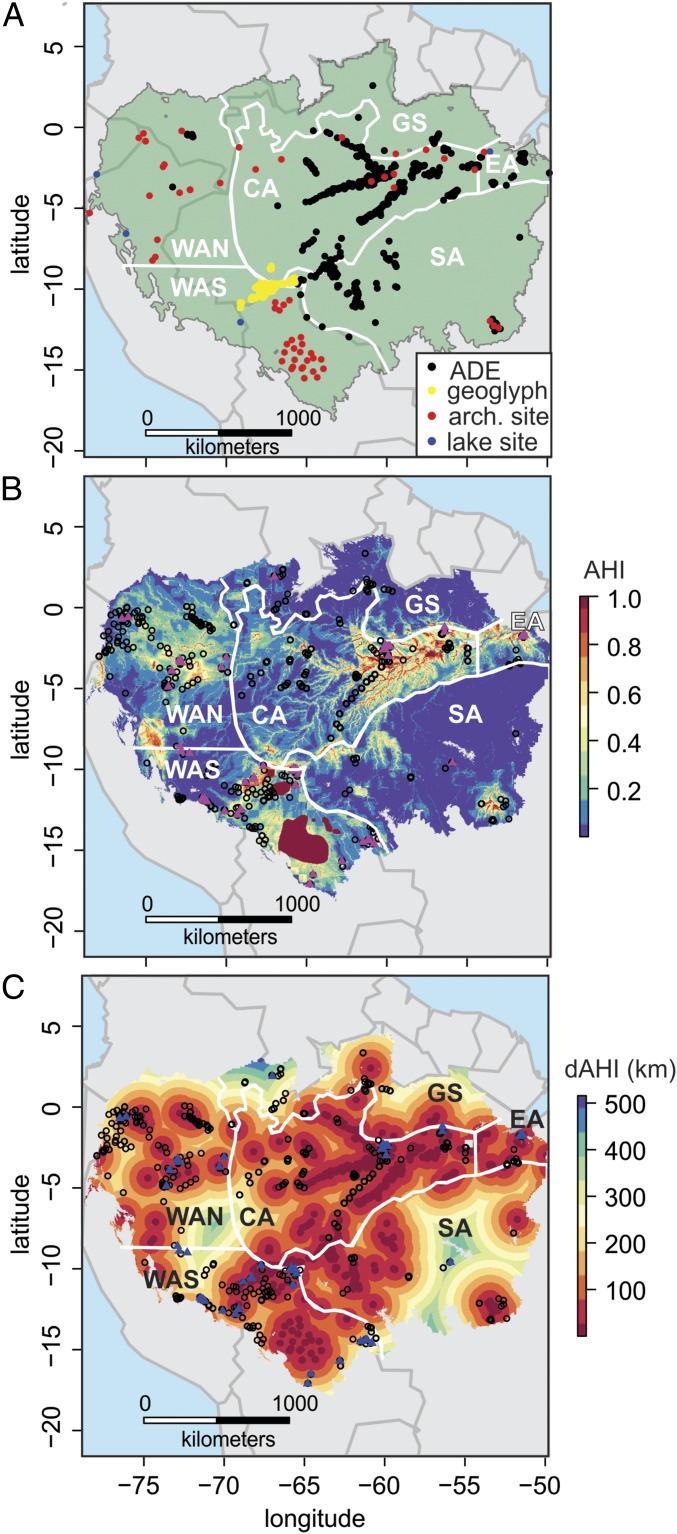
A likely source of past large-scale disturbances on these time scales is ancient people, who actively modified landscapes (27–29) and have been cultivating crops in some regions of the Amazon since at least 6,000 y ago (30, 31). The Llanos de Moxos region in Bolivia contains abundant evidence of ancient people in the form of fish weirs, berms, and raised canals (28). The most common legacy of ancient peoples on these landscapes, however, is Amazonian Dark Earths (ADEs; also referred to as “terras pretas”), which contain elevated nutrient levels, pottery sherds, and abundant charcoal (32–34) (Fig. 1A). ADEs have been associated with altered abundances of several species of Amazonian trees, particularly palms (35–37). Ancient people also constructed geoglyphs, geometric earthworks sometimes several hundred meters in diameter that often occur in clusters in regions of southwestern Amazonia (27, 38). Other archaeological sites have also been compiled and mapped (39, 40) (Fig. 1A), and approximately one half of all lake sediment records analyzed for pollen in Amazonia contained evidence of ancient human activity (41).

Fig. 1.

Amazonia sensu stricto and regional divisions (sensu 5) shown with locations containing AHIs used to create the AHI models and dAHI raster (A), modern forest inventory and recensus plot locations overlain on AHI model output (B), and modern forest inventory and recensus plot locations overlain on the dAHI raster (C). Black circles in B and C represent single-census plot locations. Pink triangles in B and dark-blue triangles in C represent recensus plot locations from Johnson et al. (53). Regional divisions of Amazonia are shown with white lines and are labeled with white text (CA, central; EA, eastern; GS, Guiana Shield; SA, southern; WAN, northwestern; WAS, southwestern) (5). In B, the large dark-red polygon in WAS represents the Llanos de Moxos in Bolivia, which has extensive ancient earthworks and landscape transformations (28, 68).

Before European colonization in the 1500s, an estimated 8–20 million people inhabited Amazonia (42–44). These ancient people and their impacts on the forest were not homogenously distributed, however, and people were associated with specific forest types, abiotic conditions, or access to transportation and other resources (45–47). Given that both ancient and modern humans tend to focus activities around areas close to waterways and other means of access, there exists the strong possibility that forest inventory plots have been established disproportionately in areas with high likelihoods of ancient human impact (AHI). If this hypothesis is correct, and forest inventories are indeed oversampling forests that are only one to two tree generations into succession, then our understanding of forest processes and dynamics may be highly skewed.

In this study, we assessed the degree to which forest plot networks in Amazonia sensu stricto (hereinafter Amazonia) potentially reflect legacies of human-modified landscapes by comparing the locations of forest inventory plots with probability models of AHI. Given the heterogeneity of both abiotic conditions and the distribution of known AHI across Amazonia, we conducted our analyses at both basin-wide and regional scales. We also analyzed the potential for AHI in a smaller subset of plots that have been recensused multiple times and are used to study forest dynamics and carbon fluxes.

Results

By combining the published locations of 882 Amazonian forest plots (hereinafter inventory plots) and a subset of 115 plots that have been recensused multiple times (hereinafter recensused plots) with probability models of predicted AHI (i.e., pre-Columbian) and locations of known ancient human activity (Fig. 1 B and C), we determine the degree to which plots are situated along gradients of ancient disturbance across the basin (Methods and SI Methods). The forest inventory plots are located in forests with AHI values ranging from 0.0008 (low probability of AHI) to 1 (high probability of AHI), with a median value of 0.23 and median absolute deviation of ±0.23. The plots ranged from 0 to 379 km away from the nearest-known evidence of ancient human activity (dAHI), with a median distance of 55 km and a median absolute deviation of ±65 km.

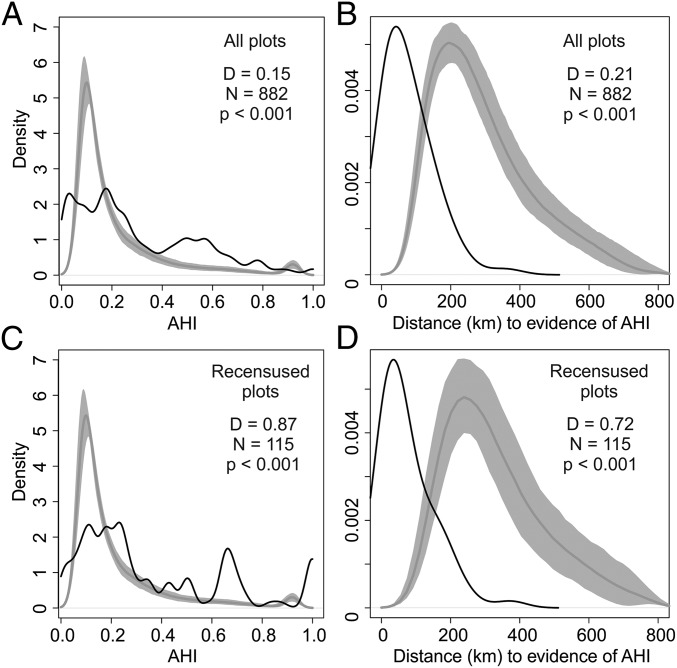
The density distributions of AHI values and dAHI values differed significantly from null expectations based on the density distributions generated in the 500 simulations of random sampling points (Fig. 2 A and B). The probability densities of AHI values were lower than the simulated densities of random points when AHI values were <0.2, but exceeded the density values of random points when AHI values were >0.2 (Fig. 2A). In other words, forest inventory plots tend to undersample forests with low probability of AHI, but to oversample forests with intermediate to high probability of AHI [but also to undersample areas in the Bolivian Beni with extremely high (e.g., AHI = 1.0) probability of AHI]. Probability densities of dAHI values from the forest inventory plots exceeded the expected density of random points at distances <100 km, and were significantly lower than the expected densities at distances between 100 and 800 km (Fig. 2B). Thus, the plots oversample forests close to sites known to have supported ancient humans and undersample forests at intermediate to high distances from sites with known disturbances.

Fig. 2.

Density of AHI probabilities for the 882 forest inventory plots (A and B) and a subset of 115 recensused plots (C and D), in Amazonia (black line) compared with density values generated from 500 simulations of random points across Amazonia (gray line and shading). The dark-gray line represents the median of the simulated densities, and the light-gray shading represents the upper and lower 95% confidence intervals. Bandwidths for density functions were 0.025 for AHI densities (A and C), and 45 for dAHI densities (B and D).

The subset of recensused plots is located in forests with AHI values ranging from 0.01 to 1, with a median AHI of 0.24 and median absolute deviation of ±0.23. The probability densities of AHI values from recensused plots tended to be lower than random at AHI values <0.2, and significantly exceeded null expectations at most AHI values >0.2 (Fig. 2C). Thus, the recensused plots markedly oversampled areas that likely contained ancient human activity. The dAHI values for the recensused plots ranged from 1 to 377 km, with a median distance of 39.5 km and a median absolute deviation of ±49 km. The densities of dAHI values also exceeded random expectation at distances <125 km, similar to the full set of inventory plots (Fig. 2 B and D). Collectively, these results reinforce the idea that plot locations, particularly those that are surveyed repeatedly, tend to be closer to areas of the Amazon that contain higher levels of ancient human disturbance than would be expected by chance (Fig. 2 C and D).

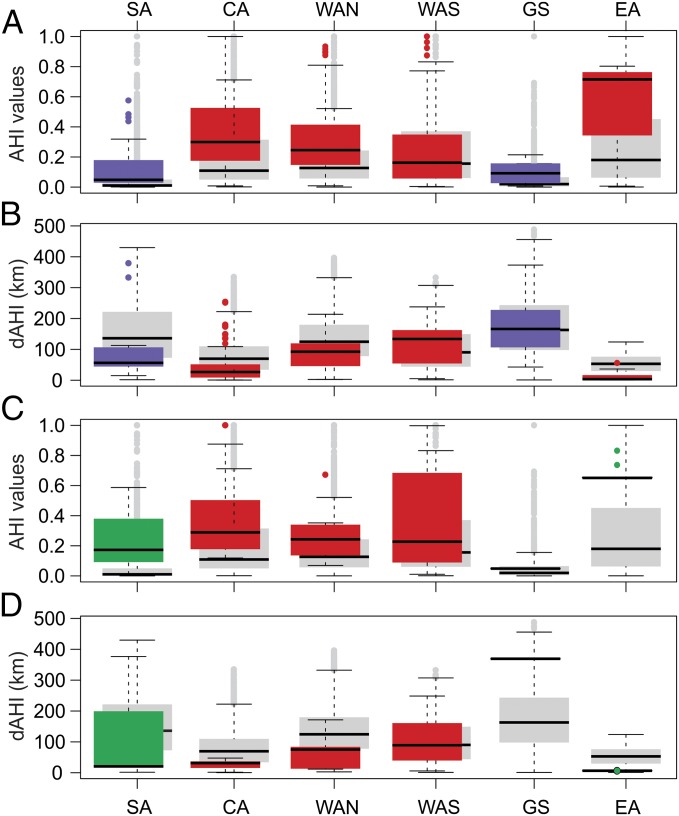
The central, western, and eastern regions of Amazonia (sensu 5) were oversampled with inventory plots compared with null expectations (i.e., these regions contained significantly more plots than would occur if plots were distributed randomly across the basin), whereas southern Amazonia and the Guiana Shield were undersampled (Fig. 3 A and B and Table S1). Inventory plots had significantly higher AHI values and significantly lower dAHI values in eastern and central Amazonia (both oversampled) compared with plots in the western, and southern Amazonia and Guiana Shield regions (AHI: χ² = 143, df = 5, P < 0.001; dAHI: χ² = 343, df = 5, P < 0.001) (Fig. 3 A and B; a full set of Nemenyi post hoc test results is presented in Table S2). Inventory plots also had significantly different distributions of AHI values compared with random points in all regions (Fig. 3A and Table S2). dAHI values were lower than random expectation for inventory plots in all regions except the Guiana Shield and southwestern Amazonia (Fig. 3B and Table S2).

Fig. 3.

Regional distribution of AHI values and dAHI values for forest inventory sites, recensused inventory sites, and random points. Regional divisions are as shown in Fig. 1, and boxplots include medians with 0.75 quantile ranges. Regions are ordered by their relative proportion of the total area of Amazonia, from largest to smallest (Table S1). Plots are color-coded by sampling effort relative to total area: red, oversampled; green, adequately sampled; purple, undersampled (Table S1). (A and B) AHI values (A) and dAHI values (B) for the 882 forest inventory sites compared with random point distributions (gray boxplots). (C and D) AHI values (C) and dAHI values (D) for 115 recensus plots compared with random point distributions. Numbers of sites and random points included in forest and recensused regional analyses are listed in Table S1.

Table S1.

Forest inventory and recensus plot characteristics in different Amazonian regions

Characteristic	SA	CA	WAN	WAS	GS	EA
Proportion of total area	0.256	0.247	0.195	0.147	0.13	0.025
Observed inventory plots	47	366	216	166	60	27
Simulated inventory plots, 0.25 quantile	218	209	164	123	108	19
Simulated inventory plots, median	226	218	171	130	115	22
Simulated inventory plots, 0.75 quantile	234	227	178	137	122	25
Observed recensus plots	4	26	24	50	1	10
Simulated recensus plots, 0.25 quantile	3	3	3	3	3	4
Simulated recensus plots, median	12	5	12	5	5	6
Simulated recensus plots, 0.75 quantile	23	21	23	17	22	18

The proportion of total area of Amazonia sensu stricto, the observed number of inventory and recensus plots, and the quantile ranges of 500 simulated distributions of plot locations are provided for each region. CA, central; EA, eastern; GS, Guiana Shield; SA, southern; WAN, northwestern; WAS, southwestern.

Table S2.

Interregional comparisons of AHI and dAHI values from forest inventory plots (n = 882)

Region	No. of plots	SA	CA	WAN	WAS	GS	EA	Random	No. of random points
Inventory plots: interregional comparison of AHI values
SA	47	NA	< 0.001	< 0.001	0.012	0.982	< 0.001	< 0.001	2,434
CA	366	< 0.001	NA	0.300	< 0.001	< 0.001	0.134	< 0.001	2,385
WAN	216	< 0.001	0.300	NA	0.005	< 0.001	0.013	< 0.001	1,870
WAS	166	0.012	< 0.001	0.005	NA	< 0.001	< 0.001	< 0.001	1,395
GS	60	0.982	< 0.001	< 0.001	< 0.001	NA	< 0.001	< 0.001	1,229
EA	27	< 0.001	0.134	0.013	< 0.001	< 0.001	NA	< 0.001	246
Inventory plots: Interregional comparison of dAHI values
SA	47	NA	< 0.001	0.885	0.020	< 0.001	< 0.001	< 0.001	2,435
CA	366	< 0.001	NA	< 0.001	< 0.001	< 0.001	0.007	< 0.001	2,385
WAN	216	0.885	< 0.001	NA	0.010	< 0.001	< 0.001	< 0.001	1,870
WAS	166	0.020	< 0.001	0.010	NA	0.252	< 0.001	0.07	1,395
GS	60	< 0.001	< 0.001	< 0.001	0.252	NA	< 0.001	0.27	1,229
EA	27	< 0.001	0.007	< 0.001	< 0.001	< 0.001	NA	< 0.001	246

Comparisons are P values from Nemenyi post hoc tests. Kruskal–Wallis tests indicated significant regional differences in both AHI values (χ² = 143, df = 5, P < 0.001) and dAHI values (χ² = 343, df = 5, P < 0.001). CA, central; EA, eastern; GS, Guiana Shield; NA, not applicable; SA, southern; WAN, northwestern; WAS, southwestern. “Random” is the P value from the Kolmogorov–Smirnov test that compared the number of plots in each region with the distribution of random points.

The recensused plots were oversampled in the central and western Amazonia regions and undersampled in the Guiana Shield region, compared with random expectation (Fig. 3 C and D). Sample numbers in the southern Amazonia and the Guiana Shield regions were too low to enable statistical comparisons, and thus were excluded from the regional comparisons of recensused plots. AHI values in recensused plots differed significantly across some regions (χ² = 13, df = 3, P = 0.004; a full set of Nemenyi post hoc test results is presented in Table S3), and were highest in eastern and central Amazonia (Fig. 3C). The distributions of AHI values also were significantly higher than random in all regions (Fig. 3C and Table S3). The dAHI values from the recensused plots were significantly lower in eastern and central Amazonia compared with other regions (χ² = 45, df = 3, P < 0.001) (Fig. 3D; a full set of post hoc results is presented in Table S3), and were also lower than would be expected by chance in all regions except southwestern Amazonia (Fig. 3D and Table S3).

Table S3.

Interregional comparisons of AHI and dAHI values from recensused forest plots (n = 115)

Region	No. of plots	SA		CA	WAN	WAS	GS	EA	Random	No. of random points
Recensus plots: Interregional comparison of AHI values
SA	47	NA		NA	NA	NA	NA	NA	NA	2,434
CA	366	NA		NA	0.695	0.627	NA	0.071	< 0.001	2,385
WAN	216	NA		0.695	NA	0.999	NA	0.007	< 0.001	1,870
WAS	166	NA		0.627	0.999	NA	NA	0.003	< 0.001	1,395
GS	60	NA		NA	NA	NA	NA	NA	NA	1,229
EA	27	NA		0.071	0.007	0.003	NA	NA	< 0.001	246
Recensus plots: Interregional comparison of dAHI values
SA	47	NA		NA	NA	NA	NA	NA	NA	2,435
CA	366	NA		NA	0.073	< 0.001	NA	0.097	< 0.001	2,385
WAN	216	NA		0.073	NA	0.264	NA	< 0.001	< 0.001	1,870
WAS	166	NA		< 0.001	0.264	NA	NA	< 0.001	0.02	1,395
GS	60	NA		NA	NA	NA	NA	NA	NA	1,229
EA	27	NA		0.097	< 0.001	< 0.001	NA	NA	< 0.001	246

Comparisons are P values from Nemenyi post hoc tests. Kruskal–Wallis tests indicated significant regional differences in both AHI values (χ² = 13, df = 3, P = 0.004) and dAHI values (χ² = 45, df = 3, P = < 0.001). CA, central; EA, eastern; GS, Guiana Shield; NA, not applicable; SA, southern; WAN, northwestern; WAS, southwestern. “Random” is the P value from the Kolmogorov–Smirnov test that compared the number of plots in each region with the distribution of random points.

SI Methods

Overview of the AHI Model.

The AHI model is the summed probability of (i) a previously published Maxent model that predicts ADEs (45), (ii) a previously published Maxent model that predicts geoglyphs (earthworks constructed by ancient people in Amazonia) (46), (iii) a newly generated Maxent model of smaller archaeological sites and the locations of lake sediment records containing ancient maize agriculture (30, 31, 39, 40, 60), and (iv) the location of the Llanos de Moxos archaeological region in Bolivia. Each Maxent model is based on occurrence points and a set of predictor variables, described below and in Table S4. Each Maxent model output is on a logistic scale (from 0 to 1) and represents the likelihood that a specific location contained the modeled archaeological feature. The polygon of the Llanos de Moxos in Bolivia (dark-red area in Fig. 1B), a well-studied archaeological region (28, 66–68), is assigned a value of 1 within its boundaries and 0 outside of its boundaries. The likelihood values for each of the three Maxent models are summed and added to the Llanos de Moxos values to create the AHI values, which are then rescaled to 1 (Fig. 1B). AHI is calculated on a 1-km² spatial grid across the 5,799,721 km² of Amazonia sensu stricto (59).

Table S4.

Characteristics of outputs and predictor variables for Maxent models of ADEs (ADE model), geoglyphs (G model), and archaeological-paleoecological sites (A-P model)

Maxent model feature	ADE model	G model	A-P model
Occurrence points	917	255	63
Training AUC	0.96	0.99	0.95
Testing AUC	0.96	0.98	0.86
Predictor variables, permutation importance, %
BIO3 = isothermality (BIO2/BIO7) (* 100)	1.2	0.5	0
BIO4 = temperature seasonality (SD *100)	0.4	2.8	9
BIO6 = minimum temperature of coldest month	2.7	0	0.2
BIO9 = mean temperature of driest quarter	2.4	2.4	0.5
BIO13 = precipitation of wettest month	0.6	0.1	0
BIO14 = precipitation of driest month	2.7	0.2	7
BIO15 = precipitation seasonality (coefficient of variation)	3.4	0.2	0.9
BIO16 = precipitation of wettest quarter	0.6	0.1	0.1
BIO17 = precipitation of driest quarter	0.1	8.3	4.2
Elevation	61.5	0.2	2.5
Roughness	0.7	0.3	0
Distance to roughness >25 m	4.8	2.6	2.7
Distance to roughness >50 m	0.8	0.5	16.8
Geological province (polygon)	5.6	0.1	25
Distance to river	4.6	NA	6.2
Size of nearest river	0.8	NA	2.6
Distance to bamboo forest	NA	79.7	6
Subsoil cation exchange content	0.1	0.7	13.8
Subsoil gravel	1.9	0.1	0.5
Subsoil organic carbon	2.6	0	0
Subsoil pH	0.5	0	0
Subsoil reference bulk density	1	0	0.1
Topsoil organic carbon	0.2	0.4	2

AUC scores represent model performance, and the permutation importance of each variable from the Maxent model output is reported. Further details and references for each predictor variable are provided in SI Methods.

Occurrence Points for the Maxent Models.

Occurrence locations for the ADE Maxent model were retrieved from the publicly available WinklerPrins and Aldrich ADE database (33) and a set of ADE sites surveyed by Neves (45) (n = 917). Locations for the geoglyph Maxent model were obtained from McMichael et al. (46) and references therein (n = 255). Archaeological site locations were obtained from previously and newly synthesized archaeological datasets (39, 40) (n = 59), and locations of ancient maize agriculture were compiled from previously published paleoecological datasets (n = 4; n = 63) (30, 31, 60). Because Maxent models link environmental characteristics with occurrence locations they require a degree of geographical certainty, but have been shown to perform well with occurrence locations with spatial uncertainty on spatial scales of ∼5 km² (69). Thus, studies in which the geographic coordinates of the site locations were not given within a certainty of at least 5 km² were excluded from our analysis. The exclusion of sites from the analysis is not problematic; Maxent has been shown to be quite robust in dealing with sample sizes <25 (70), and has outperformed other species distribution models when dealing with even smaller sample sizes (71, 72). Our smallest sample size was 63, and thus sample numbers should not influence model outputs.

Predictor Variables for the Maxent Models.

Twenty-two predictor variables were used in the Maxent models of ADEs, geoglyphs, and archaeological/paleoecological sites (Table S4). These variables included nine bioclimatic predictors, seven geographical predictors, and six soil characteristic predictors. To account for autocorrelation between bioclimatic variables across the Amazonian landscape, we narrowed the original set of 19 variables (73) down to a subset of nine using cross-correlation matrices (45, 74). The six soil parameters used were selected from the 16 available parameters (75) based on a similar cross-correlation analysis, and because subsoil and topsoil characteristics were highly correlated, we chose primarily the subsoil characteristics for inclusion in the model (45).

Because the Maxent models were aimed at predicting distributions of ancient humans across the Amazonian landscape, we also included additional geographic predictor variables that are known to influence the spatial patterning of ancient human activity. We included “distance to river” and “size of nearest river” because the locations of pre-Columbian settlement sites have been suggested to be associated with the main Amazonian river courses, particularly on the bluffs overlooking those rivers (76, 77). The HydroSHEDS dataset (www.hydrosheds.org) was used to obtain global hydrological data. Rivers were defined as water courses having “upcell” values, an attribute of the HydroSHEDS dataset that represents the flow accumulation for a defined location along the water course, of greater than 25,000 (45). We chose this threshold value to define rivers because it corresponds with permanently navigable rivers in Amazonia (i.e., waterways that do not dry up seasonally). The size of nearest river predictor variable was also calculated based on the upcell value for each location along each river (45). “Roughness,” the average difference in the elevation of a given pixel with all of its neighboring pixels (78), was calculated and used as a predictor variable representing high ground above the floodplain (e.g., river bluffs). The distance to roughness >25 m and distance to roughness >50 m metrics were calculated to use as predictor variables that identify areas close to larger and smaller changes in topography that may be preferable as high-ground areas (45).

Although Amazonia lacks large changes in elevation, we also used elevation as a predictor variable to indicate a potential preference of sites on higher ground, including on the flank of the Andes up to a maximum of 500 m above sea level. Elevation data were obtained from the Shuttle Radar Topography Mission (SRTM), available from the US Geological Survey (eros.usgs.gov), and all roughness metrics were also calculated from the SRTM data. Geological province (the underlying parental material of the soils), which indicates the amount of soil weathering, was also used as a predictor variable (US Geological Survey; https://webgis.wr.usgs.gov/globalgis/datasets.htm). Distance to bamboo forest was used as a predictor variable in the geoglyph Maxent model and contributed the most information (79.7% of the permutation importance) to the overall predicted distribution of geoglyphs (46). This predictor was also used in the newly generated Maxent model for archaeological/paleoecological sites, but its contribution to the model was relatively small (e.g., 6% permutation importance) (Table S4).

This array of predictor variables was chosen to provide intermediate model complexity, and to not be overly simplistic or overly complex to the degree at which the number of predictor variables approached the number of occurrence points (79).

Setup of the Maxent and AHI Models.

All Maxent models were run using MaxEnt version 3.3.3 (61) or the R dismo package (73) with default settings. Input parameters were the occurrence point locations and predictor variables described above. The full number of occurrence points was not used in Maxent models, because the model removes duplicate occurrences falling within a 1-km² pixel (our defined spatial resolution) to prevent overfitting. Model outputs included a logistic prediction across the sampling area of the likelihood of occurrence of the modeled archaeological feature, which is derived from maximum entropy algorithms (61, 63, 80). Model assessments were based on the AUC values (a commonly used method of assessing distribution models) of the testing and training datasets, with 60% of the occurrence locations used to train the model and the remaining 40% used to test the model (63, 80). Further information about the responses of each archaeological feature to specific predictor variables is provided in the original literature on the ADE and geoglyph models (45, 46) and in Table S4. The ADE Maxent model was also tested against a subset of independent ADE and ADE-free locations (n = 2,879) (45, 81), and it performed with 89% accuracy (45), highlighting the model’s robustness to capture the distribution of archaeological features in Amazonian ecosystems.

We established our Maxent prediction of likelihood at a 1-km² spatial grid to account for some of the uncertainty associated with archaeological site locations in the newly generated Maxent model (39, 40), as well as some of the uncertainty associated with the ADE sites (33). Thus, the original models of ADE and geoglyphs were resampled to a 1-km² spatial resolution from their original 90-m² resolution as described previously (45, 46). The probabilistic (logistic) outputs of the ADE, geoglyph, and archaeological/paleoecological datasets at the 1-km² spatial resolution were then summed across Amazonia, and combined with presence-absence (binary 1-0) raster of the location of the Llanos de Moxos region in Bolivia (Fig. 1A) to create the spatial prediction of AHI (Fig. 1B).

Generating the dAHI Raster.

We also generated a raster of dAHI, based on the geographic distance of each 1-km² grid cell across Amazonia to all known locations of ADEs, geoglyphs, archeological sites, and paleoecological archives of ancient maize cultivation. The dAHI raster was generated from pure geographical distance, and did not account for environmental changes over geographic distance. The dAHI raster did not exclude occurrence locations found within 1 km² of each other, and thus had a greater number of overall occurrence points compared with the AHI model. For the dAHI raster, we used 1,359 ADE sites (33, 45), 255 geoglyph sites (27, 46), 59 archaeological sites (39, 40), and 4 paleoecological sites (30, 31, 60) (n = 1,677). Both the AHI and dAHI rasters were used to compare with forest inventory and recensus plot locations to assess the likelihood of AHI in ecologically surveyed areas.

Discussion

In Amazonia sensu stricto, fewer than 1,000 forest inventory plots, typically 1 ha or smaller in size, represent ∼5 million km² of hyperdiverse tropical rainforests (Fig. 1 B and C). Although the networks of forest plots extend across the entire basin, our analysis suggests that these plots are spatially biased toward areas that are more likely to have been impacted by ancient human activity (Figs. 2 and 3 and Tables S2 and S3). Given that human activities, even from hundreds of years ago, can have marked legacies on forest composition, structure, and dynamics (42, 48), these biases may have profound implications for our interpretation of ecological processes and dynamics in the Amazon.

The tendencies of inventory and recensus plots to be located in areas with higher likelihoods of AHI is especially prevalent in central and eastern Amazonia (Fig. 3 and Tables S2 and S3), where ADEs are the most frequent legacy of ancient peoples (Fig. 1). Of the 882 inventory plots, 134 (15%) are located within 10 km of a known ADE site, as are 13 of the 115 recensus sites (11%). The formation of ADEs required amendments of soil charcoal, which was accomplished by burning forests near settlement sites (32). Fire transforms Amazonian systems because most species are not evolutionarily adapted to handle it (49), and repeated burning at a site can induce up to a 90% turnover of tree species (50).

The AHI models were constructed based on empirical archaeological and paleoecological data, including evidence of human activity for the last 10,000 y, although site frequency was highest primarily from 2000–500 y ago (30, 31, 39, 45, 46) (Fig. 1 B and C and Methods). Modern peoples show similar spatial patterns of occupation across the Amazon as ancient peoples (47), and it is likely that early European settlers, including those who entered during the Amazonian rubber boom (1850–1920 A.D.), also disproportionately affected forests in areas with higher AHI values (Fig. 1B). Thus, a large proportion of the forest inventory and recensus plots actually may be in recovery from even more recent anthropogenic disturbances.

It is critical that the possible influences of AHI be accounted for in both conservation-based and ecological studies of the Amazon. For example, plot inventory data indicate that some tree species are much more common than others, and that a small suite of just 227 species, termed “hyperdominants,” collectively account for one half of all individual trees in the Amazon (5, 51). Many of these hyperdominant species are positively associated with human activities, providing food or other resources, and their growth or reproduction can be actively encouraged. Given that the existing forest plots are oversampling areas of the Amazon most likely influenced by human activities, it is possible that the calculated abundances of these human-preferred species is inflated over and above what would be calculated based on unbiased sampling of forests across the full gradient of human disturbance.

Amazonian rainforests play an important role in Earth’s carbon budget (e.g., accounting for ∼14% of the total carbon fixation in the global biosphere; ref. 52), and are widely believed to act as a large carbon sink, helping to offset emissions. However, field-based estimates of ecological change and carbon flux in Amazonia are derived from a network of fewer than 200 total recensused inventory plots (4, 16, 53–55). Our results suggest that these recensused plots may be even more spatially biased toward areas with likely AHI than the full network of forest inventory plots (Figs. 2 and 3). This exaggerated bias toward areas with high AHI is likely due to the fact that recensused plots need to be maintained and monitored over time, thereby making ease of access even more important than in nonpermanent plots.

The extreme bias of the recensused plots toward areas with high probability of AHI is especially worrisome given that tropical forests can take decades to centuries, if not longer, to reach equilibrium (26, 56, 57). Indeed, some 100-y-old secondary forests still show patterns of increasing biomass accumulation and recovery (58). In other words, the actual strength of the tropical carbon sink may be significantly less than currently estimated if plots that were disturbed by ancient (and perhaps more recent) human impacts are still in postdisturbance recovery and accumulating biomass at a faster rate than less-disturbed forests. More generally, if the observed dynamics of forest census plots do not accurately represent basin-wide patterns, then estimates of the Amazon’s role in the global carbon budget will need to be reevaluated (26).

We stress that our results do not suggest that all forest plot locations have experienced large-scale past disturbances, or that all of the results based on inventory or recensused plots are invalidated. What our results do show is that these forest plot locations are more likely than randomly located sites to have been disturbed over the last centuries to millennia. Indeed, as more archaeological sites in Amazonia are unveiled, it is possible that the spatial bias of inventory and recensused sites toward forests in postdisturbance recovery will be revealed to be even stronger than that estimated here. Paired archaeological, paleoecological, and forest surveys on local and regional scales would further our understanding of long-term disturbance dynamics in Amazonia by increasing the detectability of the more nuanced AHI; empirically assessing how the spatial extensiveness, intensity, and duration of past disturbances affect modern forest composition and dynamics; and providing an avenue for incorporating the human legacy on ecosystems into ecological and conservation-based modeling. As researchers continue to expand forest plot networks throughout the Amazon and other tropical forests, care should be taken to situate plots to better capture the full variation in past and present anthropogenic disturbances so that we can refine our overall understanding of the interplay of human history and forest dynamics and functioning on longer timescales.

Methods

The locations of published forest inventory plots, in which measurements of tree size and identity are used to assess characteristics of forest structure and composition, were collated from the Amazonian Forest Inventory Network (www.rainfor.org), the Amazon Tree Diversity Network (atdn.myspecies.info/), Forestplots.net (https://www.forestplots.net/), the Tropical Ecology Assessment and Monitoring Network (www.teamnetwork.org/about-team/), and the Smithsonian Institute’s Center for Tropical Forest Science (www.forestgeo.si.edu/). Census plots duplicated in multiple repositories were removed, and only forest inventory plot locations from within Amazonia sensu stricto (59), which includes lowland tropical forests below 500 m above sea level and within the drainage of the Amazon River, were included in the analyses. This resulted in a total of 882 Amazonian forest plots. Of these plots, 115 have been recensused multiple times and are used in studies of forest and carbon dynamics (53) (Fig. 1 B and C).

We compared the locations of the inventory and recensused plots with a predictive model of pre-Columbian human impacts in Amazonia (37). The prediction of AHI (hereinafter the AHI model) is the summed probability of (i) a probabilistic model of ADEs (45), (ii) a probabilistic model of geoglyphs (earthworks constructed by ancient people in Amazonia) (46), (iii) a probabilistic model of smaller archaeological sites and locations of lake sediment records containing ancient maize agriculture (30, 31, 39, 40, 60), and (iv) the known locations of major archaeological sites (37) (Fig. 1A and SI Methods). The components of the AHI model were constructed separately because they overlap temporally (primarily 2,000–500 y ago) (27, 34), although not spatially (37), and appear culturally different.

Maximum entropy models (hereinafter Maxent models) (61), which require presence-only data, are commonly used in ecological and macroecological research to predict species distributions across landscapes (62, 63). Maxent models have been used to model archaeological features in other geographic regions of the world (64, 65), and were used to create each probabilistic component of the summed probability AHI model. Each model used the georeferenced occurrence points of the archaeological feature (e.g., geoglyphs, ADEs) (Fig. 1A) and a set of predictor variables that represent environmental and climatic conditions at 1-km² spatial resolution across Amazonia (Table S4) (45, 46). Further details on the construction of the probabilistic models and the summed probability AHI model are provided in SI Methods.

We also constructed a raster of dAHI based on the compilation of known locations of ADEs, geoglyphs, archaeological sites, and lake sediment records containing evidence of ancient maize cultivation (n = 1,677) to compare with forest inventory and recensus locations. Details on the occurrence locations and their references are provided in SI Methods.

We extracted the AHI and dAHI values for each of the forest inventory and recensused plots (Fig. 1 B and C), then compared the density distributions of the extracted AHI and dAHI values for the inventory and recensus sites with null expectations by creating 500 simulated distributions based on the random placement of 882 and 115 plots, respectively. Observed versus random distributions were compared using a Kolmogorov–Smirnov test.

Because the floristic patterns of hyperdominance were shown to vary on regional scales, we divided Amazonia into northwestern, southwestern, central, eastern, southern, and Guiana Shield regions (sensu 5) (Fig. 1), and compared intraregional and interregional AHI and dAHI values. We used the Kruskal–Wallis test with Nemenyi post hoc test to determine whether the AHI or dAHI differed significantly between regions, and the Kolmogorov–Smirnov test to determine whether the distribution of AHI or dAHI values in forest inventory plots and recensus plots differed from a distribution of random points within each region. Finally, we classified the regions as “undersampled,” “oversampled,” or “adequately sampled” by calculating whether the number of inventory and recensus plots in each region was lower than the 0.25 quantile, higher than the 0.75 quantile, or ranged between the 0.25 and 0.75 quantiles, respectively, of 500 simulated distributions.