Thermodynamics of Hydrophobic Amino Acids in Solution: A Combined Experimental–Computational Study

Abstract

We present a joint experimental–computational study to quantitatively describe the thermodynamics of hydrophobic leucine amino acids in aqueous solution. X-ray scattering data were acquired at a series of solute and salt concentrations to effectively measure interleucine interactions, indicating that a major scattering peak is observed consistently at q = 0.83 Å^–1. Atomistic molecular dynamics simulations were then performed and compared with the scattering data, achieving high consistency at both small and wider scattering angles (q = 0–1.5 Å^–1). This experimental–computational consistence enables a first glimpse of the leucine–leucine interacting landscape, where two leucine molecules are aligned mostly in a parallel fashion, as opposed to antiparallel, but also allows us to derive effective leucine–leucine interactions in solution. Collectively, this combined approach of employing experimental scattering and molecular simulation enables quantitative characterization of effective intermolecular interactions of hydrophobic amino acids, critical for protein function and dynamics such as protein folding.

The interaction between hydrophobic amino acids is a key driving force in protein folding, for example, by forming a hydrophobic core of several amino acids during the initial collapse of a protein peptide chain.¹⁻⁵ Our knowledge regarding these hydrophobic amino acids has been centered around the long-existing Miyazawa–Jernigan energetics that was statistically derived from a database of protein structures.⁶⁻⁹ An accurate, experimental data-based description of how they interact, for example, during a folding process, however, is still lacking. Achieving this quantification of amino acid interactions remains of fundamental importance in studying protein dynamics.

Efforts toward characterizing effective interactions between amino acids have been advancing on two fronts. One is a top-down approach where microscopic parameters are derived from protein structure databases or empirical thermodynamic data. Examples include the aforementioned Miyazawa–Jernigan statistical potentials^{6−8,10−17} and, more recently, an alternative Martini force field optimized in part to be consistent with macroscopic thermodynamic measurements.¹⁸⁻²¹ In these efforts, the accuracy of the parameters is limited by the presumption that the knowledge derived from protein crystal structures would apply to unfolded protein chains. The other is an alternative bottom-up approach where physical properties are optimized on the basis of highly detailed atomistic knowledge. For example, the force matching and Boltzmann inversion methods use atom-level simulation trajectories to derive residue-level energetic parameters;²²⁻²⁸ the UNRES force field is a set of simulation- and physics-based, residue-level potentials.²⁹ The accuracy of this approach is similarly limited by the fidelity of atomistic simulations used in the derivation.

In this Letter, we describe a joint experimental–computational study to investigate the thermodynamics of hydrophobic leucine in an aqueous solution. Specifically, we use experimental X-ray scattering data to guide the optimization of atomistic molecular dynamics (MD) simulation and subsequently construct an effective residue-level leucine–leucine interaction. It should be noted that two main aspects of this current work are not completely new. For instance, X-ray scattering has been used previously to measure the leucine pair-distance distribution,³⁰ although little attempt was made to derive leucine–leucine energetics from that data. This use of experimental X-ray scattering data provides an alternative approach for testing amino acid interactions in aqueous solution that has mostly relied on osmotic pressure measurements in the past.³¹⁻³⁴ There has also been a systematic study by Elcock and colleagues to derive effective potentials from atomistic MD simulations.³⁵ Inspired by these previous works, we now take advantage of experimental X-ray scattering data that guide the optimization of parameters used in atomic-level simulations to derive effective amino acid interactions.

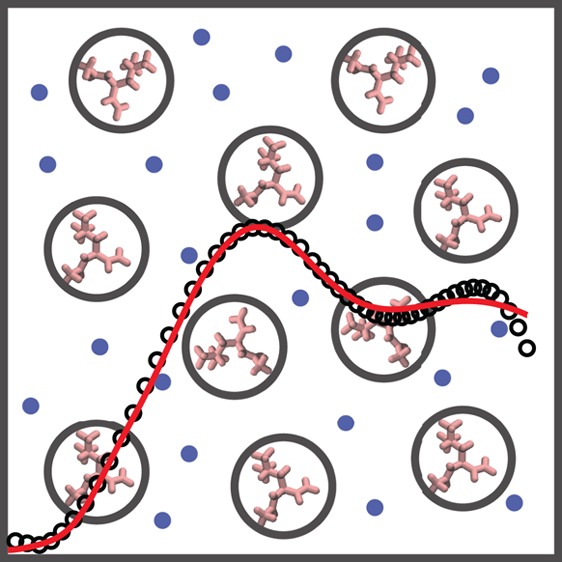
The total X-ray scattering intensity of leucine amino acids in solution (illustrated in Figure 1) is given by

1

where I₁(q) is the contribution from intermolecular scattering between leucine and water and I₂(q) is from leucine amino acids themselves, intramolecularly and intermolecularly. They are given as follows

2a

2b

where ρ_a is the number density of amino acids and q is the magnitude of X-ray momentum transfer during the scattering (see more details in the Supporting Information). The form factors F(q) ≡ ∑_i f_i(q) exp(iq · r_i) effectively describe internal structures of each molecule (amino acid or water), where f_i(q) is the form factor for each atom within its corresponding residue group and an excluded-volume correction is applied to F_a(q).³⁶ The orientational average of the intramolecular scattering is given by the Debye Formula, 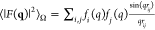(more details about deriving I(q) can be found in the Supporting Information).

Figure 1.

Schematic representation of leucine amino acids in solution showing that the total scattering intensity I(q) (left) consists of intermolecular (middle) and intramolecular (right) contributions.

A key component of I(q) is the structure factor S(q) originating from intermolecular correlations (S_aa(q) for leucine–leucine and S_aw(q) for leucine–water, respectively), which is related to a radial distance distribution function g(r) via a Fourier transform

3a

3b

Here, ρ_w is the number density of water, and g_aa(r) and g_aw(r) are the leucine–leucine and leucine–water pairwise distance distribution functions, respectively. The structure factor S_aa(q) shows characteristic behavior of an ideal gas at a high-q limit (where S_aa(q) → 1 and there is a peak at around q = 1.1 Å^–1, corresponding to a favorable intermolecular distance of r = 6.5 Å in g_aa(r)), while S_aw(q) shows a minor bump in its medium-q region (Figures S1 and S2). As discussed later, a weighting factor w was used to describe the excess electron density of solvent in such a crowded environment compared to a regular bulk solvent, as we demonstrated previously,^36,37 and a shape factor β(q) ≡ 1 + c(|⟨F_a(q)⟩_Ω|²/⟨|F_a(q)|²⟩_Ω – 1) was used to account for the nonspherical nature of leucine molecular shapes.

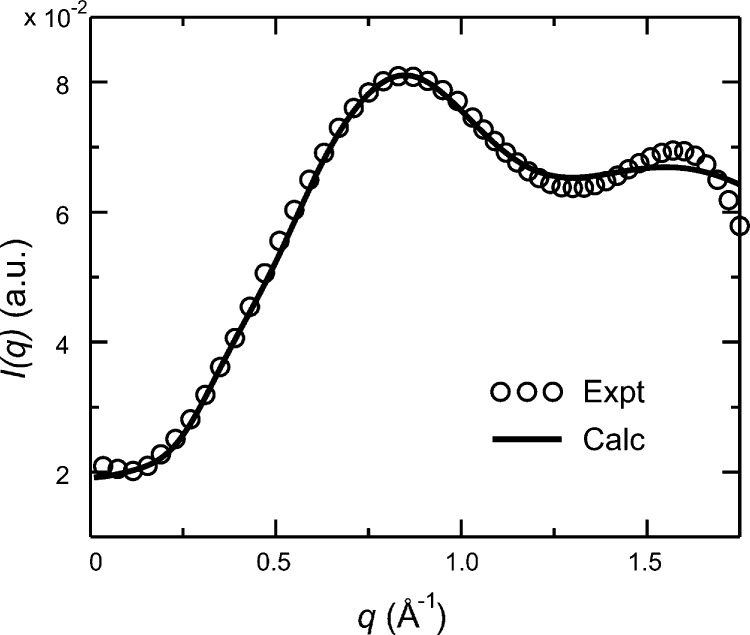
Experimental X-ray scattering measurements were performed to measure the pair distance distributions between the leucine amino acids in solution (see details in the Supporting Information). Figure 2a shows the scattering data acquired for a series of three leucine concentrations, represented by leucine-to-water ratios of 1:35, 1:50, and 1:75, respectively. Consistently, there is a major scattering peak at q = 0.83 Å^–1, which originates from the solute–solute structure, as we shall see. Note that all I_expt(q) measurements reported here were after buffer subtraction. The fact that this peak remains invariant among the scattering data of different leucine concentrations indicates that a stable and ordered solute–solute distribution is reached under such a wide range of concentrations. It should be mentioned that the positioning of this peak is also consistent with a similar observation by Head-Gordon and colleagues, where a scattering peak was reported at q = 0.8 Å^–1.³⁰ Note that the scattering data shown in Figure 2a were obtained in the absence of salt. To examine the effect of different salt concentrations, scattering data were collected for a leucine-to-water solution of 1:35, under three NaCl concentrations of 50, 150, and 500 mM. Figure 2b shows the scattering data of these leucine–salt solutions. Clearly, while there is some minor difference below q < 0.4 Å^–1, little deviation is observed in general, especially at higher scattering regions, indicating that the salt concentration has a negligible effect on the overall scattering intensity I(q). For this reason, the scattering data of the 1:35 leucine in the presence of 150 mM NaCl, shown in Figure 2b, will be used for the rest of this Letter.

Figure 2.

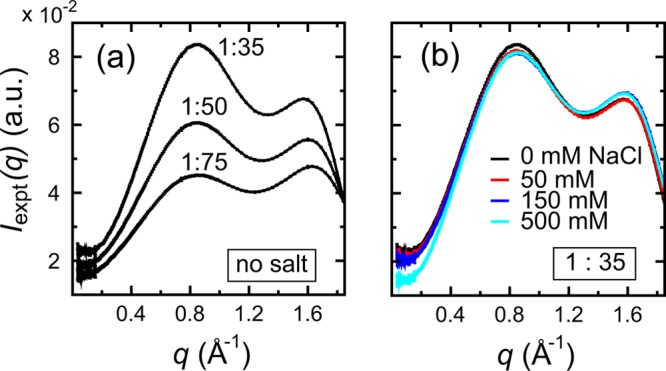
Scattering intensity I_expt(q) of leucine amino acids at a series of leucine-to-water ratios, 1:35, 1:50, and 1:75, in the absence of salt (a), and at a series of NaCl concentrations, 0, 50, 150, and 500 mM, for the 1:35 leucine solution (b). Note that all scattering profiles were reported after buffer subtraction.

To make an effective comparison with experimental data, two sets of MD simulations were carried out for such concentrated leucine solutions. One was based on a standard simulation protocol, where the Amber ff99SB force field³⁸ and the TIP3P water model³⁹ were used. Figure S1 shows the resulting g_aa(r) for pairwise leucine molecules (as marked by a dashed line), where a strong intermolecular correlation observed at large distance separations indicates a signature of molecular aggregation, as reported previously by Head-Gordon and colleagues,³⁰ although no sign of aggregation was shown based on our experimental scattering measurements.

The other simulation set is adopted to address this nonrealistic aggregation issue by adjusting the strength of solute–solvent interactions. In fact, this aggregation issue, presumably due to inaccurate solvation energetics,⁴⁰⁻⁴² has been alleviated by modifying a single parameter of solute–solvent interactions in the force field, as recently proposed by Best and colleagues.⁴¹ This is achieved by increasing a well-depth of its attractive interaction potentials by⁴¹

4

where ε_o and ε_i are the Lennard-Jones well depths for water’s oxygen and any leucine atom i, respectively, as used in the Amber force field with a standard Lorentz–Berthelot rule.³⁸ The value of λ = 1.1 was used in this modified simulation protocol,⁴¹ as opposed to λ = 1.0 used in the first control simulation set. More recently, the use of this parameter λ = 1.1 has been shown toward a more accurate description of disordered proteins,⁴² presumably due to well-controlled balancing between protein–protein and protein–water interactions. In that sense, this concept is in accord with the efforts by Elcock and colleagues on reducing the attraction between amino acids for better agreement in the case of their villin headpiece simulations.³⁵ When applied for the leucine simulations, this improved procedure (eq 4) appears to overcome the aggregation symptom and improve the leucine–leucine correlation g_aa(r) considerably (Figure S1).

The improvement in the modified simulation allows us to examine the extent to which simulation results are consistent with experimental scattering data. To that end, theoretical scattering intensity I(q) was calculated from simulation trajectories. Specifically, radial distribution functions of leucine–leucine (g_aa) and leucine–water (g_aw) were computed from simulation snapshots to evaluate the aforementioned structure factors (Figure S2) and finally the scattering intensity (eqs 1–3).

Figure 3 shows the final scattering intensity I_calc(q) calculated from S_aa(q) and S_aw(q) and its comparison with experimental intensity I_expt(q). Notably, some discrepancy was found in the region of q > 1.2 Å^–1, although it is rather clear that the calculated I_calc(q) is in good agreement with experimental data I_expt(q). This is demonstrated by reasonable agreement near the major scattering peak at around q = 0.83 Å^–1, which is well reproduced by the MD simulations that properly capture the key feature of leucine–leucine distance distributions contributing to experimental scattering. Note that there is a minor peak in the experimental curve at q = 1.6 Å^–1. The amplitude and positioning of this peak are not faithfully reproduced by our scattering calculations, presumably due to the atomic-level details neglected in deriving the form factor of leucine amino acid. It is worth pointing out that the simulations were performed at 300 K and the experimental setup was cooled at 283 K, although it is unlikely that this temperature difference contributes to the discrepancy in scattering. Also, it should be noted that a weighting factor of w = 8% was used to account for the excess solvent density surrounding the solute (eq 3b). On the basis of our previous comparison with various experimental data, the value of w = 8% was found to best reproduce experimental scattering data.^36,37,43 In addition, a shape factor of β(q) = 1 + c[β_a(q) – 1] was included to consider the proper shape of leucine molecules, where c is a shape-related parameter between 0 and 1. When c = 0, no shape effect is considered; when c = 1, a perfect globular shape is assumed for each atom within the leucine amino acid, which is likely to misrepresent the realistic shape of the molecule. While it is nontrivial to estimate the c value for leucine, a value of c = 0.25 was used to reasonably represent its shape contribution to the total scattering (Figure S3). Overall, the improved atomistic simulations, highly consistent with experimental scattering measurements, are capable of providing reliable information on the thermodynamic feature of hydrophobic leucine amino acids in solution.

Figure 3.

Theoretical scattering intensity I_calc(q) and experimental intensity I_expt(q) of leucine amino acids in solution. Note that I_calc(q) was rescaled by a multiplying constant to match I_expt(q) at the peak position of q = 0.83 Å^–1.

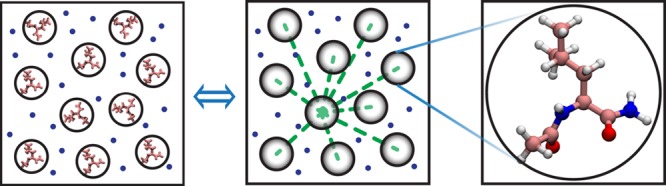
This agreement not only provides validation of the modified atomistic simulation but more importantly allows us to derive effective interleucine interactions. Here, we adopted a similar procedure of coarse-graining used by Elcock and colleagues applied to massive simulation trajectories.³⁵ This was achieved via the so-called iterative Boltzmann inversion,²⁵ where the g(r) values of coarse-grained particles are repeatedly optimized against their atomistic counterparts. Specifically, the entire leucine system used in MD simulations is structurally simplified into two major groups/beads for each leucine residue: one bead for its backbone (denoted by BB) and the other for its side chain (SC). Note that the acetyl (ACE) and amide (NH2) capping groups are also coarse-grained into a single bead, each at the center-of-mass of their corresponding groups of atoms (Figure S4), respectively, and all explicit water molecules are averaged out. The resulting effective potentials between these leucine beads reach convergence after 150 iterations of Monte Carlo sampling implemented in the MagiC program,²⁵ essentially based on the convergence of the g(r) of coarse-grained beads. During this procedure, the effective potential between a pair of coarse-grained leucine beads is updated repeatedly by U⁽ⁱ⁺¹⁾(r) = U⁽ⁱ⁾(r) + k_BT ln[g⁽ⁱ⁾(r)/g(r)], where U⁽ⁱ⁾ and g⁽ⁱ⁾(r) are the potential and distribution function at the iteration step i.

The coarse-graining results are quite informative. Figure 4a shows the converged g(r) distributions for nonbonded BB–BB, SC–SC, and BB–SC beads (solid lines) and their corresponding g(r) distributions from atomic simulation trajectories (open circles), respectively. The fact that these g(r) distributions reach convergence indicates that this form of coarse-graining is able to provide structural properties with regards to their thermodynamic energetics. Figure 4b shows the resulting effective potentials U(r) for BB–BB, SC–SC, and BB–SC interactions of nonbonded leucine, respectively. Apparently, U_SC–SC(r) has the deepest well depth of 0.75 kcal/mol located at r = 5.4 Å. Also note that there is an energetic bump of 0.16 kcal/mol at r = 7.3 Å, which presumably corresponds to the desolvation barrier that has been extensively studied in protein folding.^44,45 On the other hand, U_BB–BB(r) displays a less favorable short-range attraction, having a well depth of −0.44 kcal/mol at r = 4.7 Å, but agrees well with the interaction between the BB of valine amino acids shown by Elcock and colleagues,³⁵ despite a minor difference in the well depth itself. For U_BB–SC(r), it has a similar but slightly shallower potential well compared to U_BB–BB(r) (Figure 4b). While the dominating U_SC–SC(r) has a slightly weaker attraction, compared to the corresponding Lennard-Jones potential with a well depth of −1.25 kcal/mol at r = 7.75 Å,⁹ which was optimized on the basis of the Miyazawa–Jernigan statistical potentials,⁶⁻⁸ the collective sum of all three potentials seems to be comparable. In addition, a simpler one-bead model of coarse-graining has resulted in a well depth of 0.5 kcal/mol at r = 5.4 Å (Figures S4 and S5). The fact that a single-bead representation is able to retain the overall feature of U_SC–SC(r) suggests that such a single-bead model captures the essential energetics between a pair of amino acids, at least for leucine, although a more detailed BB–SC two-bead representation can be useful to yield knowledge regarding their relative orientation.

Figure 4.

(a) Converged radial distance distributions g(r) for BB–BB, SC–SC, and BB–SC nonbonded interactions. The g(r) distributions from coarse-grained and atomistic trajectories are represented by solid lines and open circles, respectively. (b) Resulting effective potentials U(r) for nonbonded interactions of BB–BB, SC–SC, and BB–SC leucine beads, where r is the distance between a pair of beads, each positioned at the center-of-mass of its corresponding atomic groups.

As a byproduct, the experimentally consistent simulation data further allow us to examine the energy landscape for a pair of interacting leucine amino acids. Figure 5a shows the two-dimensional contour plot of a center-of-mass distance R_com between two leucine amino acids and its corresponding angle θ (in cosine) between the orientations of SCs (each defined by a vector pointing from the center-of-mass of the BB to the center-of-mass of the SC). For each pair of leucine residues, the effective potentials (including U_BB–BB(r), U_BB–SC(r), and U_SC–SC(r) shown in Figure 4) were used to evaluate the total nonbonded interacting energy. It is clear that three energy minima are located at R_com = 4.9, 6.8, and 8.5 Å, respectively, and each has its preferred orientational angle. For example, at R_com = 4.9 Å, the pair has a tendency to be aligned at cos(θ) ≈ 1, while the other two (at R_com = 6.8 and 8.5 Å) energetically prefer perpendicular or antialigned orientations. Figure 5b shows the contour plot of R_com and a center-of-mass distance R_SC–SC between their SCs to further illustrate their relative orientation. Note that the configurations at the three energy minima in Figure 5a have a similar value of R_SC–SC = 5.5 Å.

Figure 5.

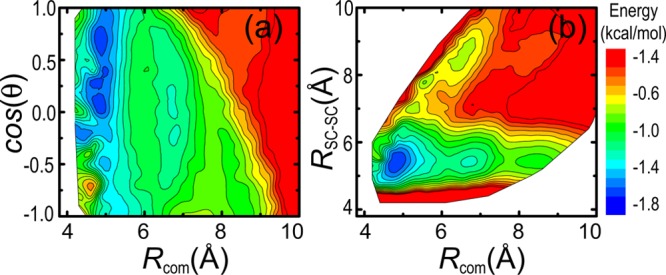
Two-dimensional energy landscape of two interacting leucine amino acids as a function of the center-of-mass distance R_com and their relative angle θ (a) and of R_com and a SC–SC distance R_SC–SC (b). The color bar represents the lowest interacting energy that each configuration can have at its corresponding location.

By using a joint experimental–computational study, we have been able to determine the thermodynamics of hydrophobic leucine amino acids in solution. Specifically, the fact that X-ray scattering experiments and atomistic MD simulations reach a quite reasonable consistence provides the opportunity to derive effective interactions of hydrophobic leucine amino acids in solution. By coarse-graining the simulation data via a bottom-up iterative Boltzmann inversion, we are now able to derive the effective leucine–leucine interactions for an accurate understanding of this critically important system concerning the fundamental hydrophobic interaction of amino acids. From a broad perspective, this combined approach of optimizing simulations against experimental scattering is set to be straightforwardly generalized to other important amino acid interactions, which could have a profound implication on the MD of protein folding and disorder where long-range hydrophobic interaction matters.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.6b02673.

• Details of X-ray scattering experiments, atomistic molecular dynamics simulations, derivation of I(q), and coarse-graining via a two-bead and single-bead model (PDF)

The authors declare no competing financial interest.