Abstract
The physiologically based pharmacokinetic (PBPK) model for liver transporter substrates has been established previously and used for predicting drug–drug interactions (DDI) and for clinical practice guidance. So far, nearly all the published PBPK models for liver transporter substrates have one or more hepatic clearance processes (i.e., active uptake, passive diffusion, metabolism, and biliary excretion) estimated by fitting observed systemic data. The estimated hepatic clearance processes are then used to predict liver concentrations and DDI involving either systemic or liver concentration. However, the accuracy and precision of such predictions are unclear. In this study, we try to address this question by using the PBPK model to generate simulated compounds for which we know both systemic and liver profiles. We then developed an approach to assess the accuracy and precision of predicted liver concentration. With hepatic clearance processes estimated using plasma data, model predictions of liver are typically accurate (i.e., true value is bounded by predicted maximum and minimum); however, only for a few compounds are predictions also precise. The results of the current study indicate that extra attention is required when using the current PBPK approach to predict liver concentration and DDI for transporter substrates dependent upon liver concentrations.
Electronic supplementary material
The online version of this article (doi:10.1208/s12248-016-9895-0) contains supplementary material, which is available to authorized users.
KEY WORDS: identifiability analysis, liver transporter, physiologically based pharmacokinetic (PBPK) model
INTRODUCTION
Modeling and simulation of tissue pharmacokinetics for new chemical entities are key tasks to support rational drug design, candidate selection, and risk assessment in preclinical animal studies and clinical studies. Traditionally, assuming that the unbound drug concentration in a non-clearance tissue is equivalent to the unbound systemic plasma concentration, several empirical or mechanistic approaches based on static or dynamic models have been applied in simulating tissue pharmacokinetics (1). However, such an assumption is not valid for the compounds with liver transporter-mediated disposition. This is particularly problematic in modern drug discovery where medicinal chemistry efforts to reduce CYP-mediated clearance or to design compounds specifically targeting liver tissue have led to an increased prevalence of transporter-mediated clearance. In an attempt to address this challenge, physiologically based pharmacokinetic (PBPK) models for liver transporter substrates have been developed for preclinical animals and human (2,3). Generally, these models have similar model structures, where drug distribution in non-liver tissues are perfusion limited, whereas distribution in liver is permeability limited achieved by using liver blood and liver tissue compartments incorporating active transport, passive diffusion, metabolism, and biliary excretion.
Most PBPK models for liver transporter substrates require in vivo hepatic clearance processes or empirical in vitro–in vivo extrapolation (IVIVE) scaling factors estimated from systemic plasma concentration profiles of a single (4) or multiple compounds (5). The subsequent simulations for pharmacokinetics, pharmacodynamics and drug–drug interactions (DDI) within liver are made based on the estimated hepatic clearance processes (2). Hence, it is very important to know if the model can reasonably simulate the liver pharmacokinetics, when the model is only trained with observed plasma pharmacokinetics. However, due to the challenge in acquiring data in tissues, particularly in human tissues, the answer to this question is largely unknown.
In an attempt to answer this question, we first validated the robustness of the current PBPK model structure using published rat liver and plasma data of 12 structurally diverse compounds. The rat pharmacokinetic data are chosen to validate the model because liver concentrations for most compounds are only available in rat. The structural identifiability of the model is analyzed. A case example is then given to demonstrate how the PBPK model trained only by systemic plasma data may confound simulated drug concentration in the liver tissue and DDI. Finally, multiple “pseudo” compounds with “known” systemic and liver profiles are generated with this model structure under different scenarios. The hepatic clearance processes are estimated using only systemic profiles and then used to predict liver profiles. The predicted liver distribution is compared with the known values.
METHODS
The Structural Model
The structure of the PBPK model (6) and the values for physiological parameters for rat (7) have been described before. To enable modeling enterohepatic recirculation for compounds with biliary excretion, the bile flow rate for a 250 g rat is fixed at 22.5 mL/day (8). The liver is modeled with five sequential pairs of sub-compartments for liver blood and tissue that mimic the acinar structure and approximate the partial differential equation dispersion model (3). The liver blood volume includes reported liver plasma and blood cell volumes, while the tissue volume includes reported liver cellular, interstitial, and endosomal volumes (7). The compound distribution into non-liver tissues is assumed to be driven by passive processes and predicted using an in silico approach (9,10).
The values and references for pKa, logD 7.4, fraction unbound in the plasma (f u,p) and blood-to-plasma ratio (R BP) of the 12 real compounds are given in the supplemental materials, Table S1. The fraction unbound in the liver tissue (f u,t) is calculated using Lukacova approach published in (11). Compound transport between the liver blood and tissue compartments is mediated by both unbound active uptake (CL act) and unbound passive diffusion clearance (CL pass). The compound in the liver tissue compartments is eliminated through unbound metabolism (CL met) or unbound biliary clearance (CL bile). To simplify the problem, all processes are assumed to be linear. To validate the model structure is robust enough to describe both liver and systemic concentration, the hepatic clearance processes are estimated by simultaneously fitting both observed liver and systemic concentration-time profiles, with a numerical global optimizer as described before (6). The drug concentration-time profiles in both liver and systemic plasma are then simulated and plotted as overlays on the observations digitized from publications and scaled to dosing 1 mg/kg body weight (the sources of pharmacokinetic data are given in Table S1).
The Structural Identifiability Analysis
To test if quantification of three hepatic processes is possible from a given set of ideal noise-free systemic data, we performed a structural identifiability analysis, using DAISY (12). Because of the high algebraic computational cost, in this analysis, we reduced the full model to a simplified model that still contains the essence of the problem. Briefly, all tissues except for liver, gut, and spleen are merged into a single tissue compartment. The gut and spleen are merged into the new gut compartment. The venous and arterial blood compartments are merged into the new blood compartment. The liver is modeled as either one or two pairs of sub-compartments for liver blood and tissue. For this analysis, the observation (output in DAISY) is only available in the blood compartment. Details about the reduced model and DAISY input file are given in the supplemental material.
A Case Study
Systemic plasma concentration time course (i.e., 10, 20, 30, 40, and 50 min, and 1, 2, 3, 4, 6, 9, and 12 h) data are generated using the current PBPK model with hepatic CL act, CL pass, and CL met values of 10, 0.10, and 0.46 L/h, respectively. pKa, logD 7.4, f u,p, R BP, and f u,t are fixed at 4.5 (acidic), 1, 0.01, 0.7, and 0.0925. Hepatic CL act, CL pass, and CL met are then reestimated based on the generated systemic data. Two sets of fitted clearance values that can reasonably describe the systemic data (sum of squared error in log space less than 0.13) are picked to simulate liver pharmacokinetics and DDI. Biliary excretion is fixed at zero here and below unless otherwise indicated. Active basolateral efflux is fixed at zero for all modeling in this study.
Generating More Pseudo Compounds
Systemic plasma data for pseudo compounds are generated using the following approach. The hepatic clearance processes (i.e., CL act, CL pass, and CL met) are predefined with K possible values uniformly distributed in a bounded log-transformed space (e.g., 10−3, 10−1.5, 100, 101.5, and 103 L/h for which K is 5). Hence, in total, there are K 3 permutation sets of hepatic clearance processes, which are considered as “true” values, and assigned to K 3 pseudo compounds. For all compounds, pKa, logD 7.4, f u,p, R BP, and f u,t are fixed at 4.5 (acidic), 1, 0.01, 0.7, and 0.0925, respectively, while biliary and renal clearances are assumed to be zero. The systemic plasma concentrations after intravenous bolus dosing (1 mg per 1 kg body weight) are generated for each compound at 10, 20, 30, 40, and 50 min, and 1, 2, 3, 4, 6, 9, and 12 h using the PBPK model, unless otherwise indicated. With certain values of hepatic clearance processes, the simulated concentration at later time points may exceed the error tolerance of the differential equation solver, leading to numerical errors; any pseudo compound with such a value is dropped from the analysis. Prediction intervals for the drug concentrations in the systemic plasma are generated using Eqs. 1 and 2.
| 1 |
| 2 |
Y is the natural log-transformed systemic plasma concentration at the specified time point. SD and SD i are population and individual standard deviations of Y. The standard deviations digitized from individual reports are usually given at normal scale. As such, SD i at natural log scale is approximated by using reported coefficients of variation. SD is approximated as the pooled variance given in Eq. 2, where n i is the number of replicates for a reported concentration and N is the sum of n i. In each individual study, along the time course profile, several different SD i values may be reported, but we assume that they are all associated with the same n i value. The SD estimated from observations is 0.297.
Reestimating Hepatic Clearance Processes of Pseudo Compounds
CL act, CL pass, and CL met for each compound are reestimated from its plasma concentration-time profile, using the following approach developed based on a previous report (13). Values for CL act, CL pass, and CL met are randomly generated from a uniform distribution at log10 scale bounded by their true values divided by 103 or multiplied by 103. The systemic plasma concentration-time profiles are simulated using randomly generated hepatic clearance processes values. The sets of random values will be accepted only if they can lead to plasma concentrations within the predefined prediction intervals described above. The random value generation will stop when 100 sets of random values are accepted. However, if the computation time has been 1 h but there are less than 100 sets accepted, and all the accepted values so far are within the interval bounded by the true values divided by 102 and multiplied by 102, then the boundaries of uniform distribution for random value generation will shrink to the true values divided by 102 and multiplied by 102. Similarly, if the number of accepted sets are still less than 100 at computation time of 2 h, and all the accepted values are within the interval bounded by the true values divided by 10 and multiplied by 10, then the boundaries of uniform distribution for random value generation will further shrink to the true values divided by 10 and multiplied by 10. The random values will be generated in this final interval until 100 accepted values are identified. The protocol described here is also presented in the flow chart (Supplemental Material Fig. S1).
Calculate Pseudo Steady-State Unbound Liver Tissue to Systemic Plasma Partition Coefficient (Kpuu)
To simplify the comparison between true and predicted liver profiles, liver Kp uu (the ratio between free liver and free systemic plasma concentrations after a single intravenous bolus dosing), rather than a liver concentration-time course, is simulated after constant intravenous infusion for 1000 h. Because the systemic concentration is bounded by predefined intervals, changes in Kp uu values largely reflect changes in liver concentrations. The true Kp uu is generated with true hepatic clearance processes, while 100 predicted Kp uu values are generated from the accepted random hepatic clearance processes. If the true value is bounded by the maximum and minimum predicted Kp uu values, the predicted values are considered to be accurate. If the ratio between maximum and minimum predicted Kp uu values is less than 10, the predicted values are considered to be precise. Accurate and precise estimates of hepatic clearance processes are defined in the same way.
Modeling with Human Parameters
Analyses are performed using human physiological parameter values (6). For modeling rosuvastatin in humans, enterohepatic recirculation is included in the model as described before (6), but with a slightly different empirical absorption model (Eq. 3 to 6) to better describe data after intravenous and oral dosing.
| 3 |
| 4 |
| 5 |
| 6 |
F absorption,1 is the fraction of absorbed drug going to compartment 1, k a,1 and k a,2 are absorption rates, and F a is the total fractional absorption. These parameters are estimated simultaneously with three hepatic clearance processes by fitting systemic data. F g is the fraction that escapes from metabolism or efflux in the GI tract and assumed to be 1. C bile, C a, and C gut are the concentrations in the bile, arterial blood, and gut compartment. Q bile is the liver bile flow, V gut is the volume of gut, Q gut is the blood flow, and Kp gut is the tissue to plasma partition coefficient. Values of these parameters are given in the previous publication (6). The mean plasma concentration is simulated using best fitted hepatic clearance processes and absorption values mentioned above. With Eqs. 1 and 2, the prediction interval of plasma concentration is constructed using mean simulated concentration and an observed average coefficient of variation of 0.333 (14). The renal clearance is fixed at the observed value (14). Values of CL act, CL pass, and CL bile are randomly generated within the predefined intervals with width of 106 centered at the best fitted values, while k a,1 and k a,2 are randomly generated within the intervals with width of 102 centered at the best fitted values, and F absorption,1 and F a are bounded by 0.01 and 1.
Results
The Model Structure and the Structural Identifiability Analysis
When the model is properly parameterized, the simulations can reasonably reproduce the observed drug concentration-time profiles in both systemic plasma and liver tissue (Fig. 1). As such, the model structure is considered to be robust enough for the purpose of generating systemic and liver pharmacokinetic data for the pseudo compounds with known parameter values. Using DAISY, the model with two pairs of liver sub-compartments is determined to be structurally globally identifiable (DAISY result file is given in the supplementary material). The model with one pair of liver sub-compartments is also structurally globally identifiable (data not shown).
Fig. 1.
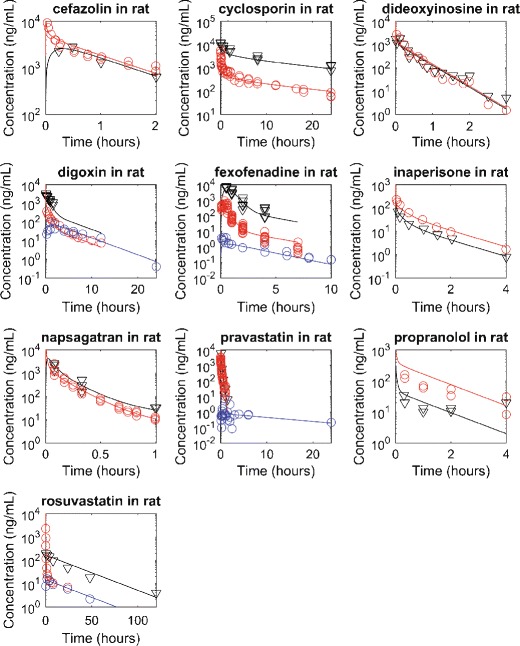
Observed and simulated rat systemic and liver concentration-time profiles. Red, blue, and black represent systemic concentration after intravenous dosing, systemic concentration after oral dosing, and liver concentration, respectively. The markers and lines represent observations and simulations. The dosing amounts have been scaled to 1 mg/kg, assuming linear clearances
A Case Example Where the PBPK Model Trained by Systemic Plasma Data May Have Large Uncertainty in Simulating Liver Concentration and DDI
In this example, two sets of different values of hepatic clearance processes (i.e., CL act, CL pass, and CL met are 10.7, 0.103, and 0.411 L/h for set 1, and 7.69, 0.100, and 55.3 L/h for set 2, respectively), combined with the same values for all other model parameters, can equally well describe systemic plasma time course data generated with the parameters noted in the methods (Fig. 2). On the other hand, these different values of hepatic clearance processes lead to substantially different concentrations in liver tissue with set 1 accumulating more free compound in the liver compared to plasma and set 2 producing free liver concentrations lower than free plasma. As such, for pharmacodynamic response and DDI (when the compound is perpetrator) in the liver, the two sets of values are likely to result in different predictions, depending on the IC50 values. For DDI in the liver where the compound is the victim, it is not straightforward to see if the two sets of values will lead to different systemic profiles. We perform simple simulations assuming that an inhibitor can lead to a 90% inhibition of hepatic metabolic clearance constantly over the time. In these simulations, with the same inhibitory effect, the two sets of hepatic clearance processes values result in different systemic profiles, as well as different liver profiles (Fig. 2). Although the inhibitor changes liver profiles of both Set 1 and 2, it only changes systemic profiles of Set 1. The systemic profile of Set 2 is not significantly affected by the inhibitor.
Fig. 2.
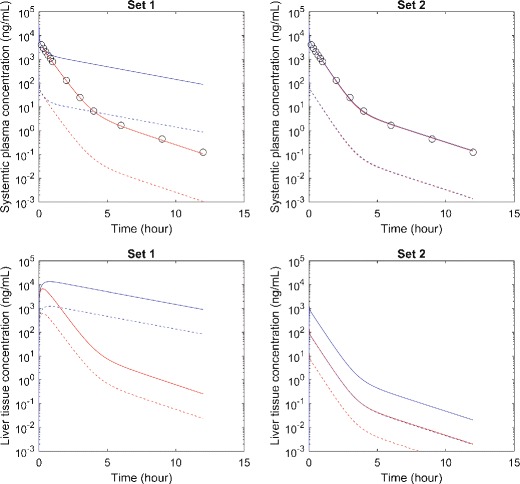
Two simulated compounds result in similar plasma concentrations with different liver concentrations that also are differentially altered by metabolic inhibition. Circles represent synthesized data. Red solid and dashed lines represent simulated total and free concentrations without metabolic inhibitor. Blue solid and dashed lines represent predicted total and free concentrations with metabolic inhibitor, assuming that constant inhibitory effect leads to hepatic clearance reduced to 10% of the control values
Estimating Hepatic Clearance Processes and Predicting Kpuu from Generated Plasma Data
The predefined hepatic clearance processes include 10 possible values: 10−3, 10−2.33, 10−1.67, 10−1, 10−0.33, 100.33, 101, 101.67, 102.33, and 103 L/h, leading to in total 1000 permutation sets of hepatic clearance processes (i.e., 1000 synthetic compounds), within which 190 compounds are dropped due to numerical error. Among the 810 surviving compounds, 12.7, 11.6, 12.7, and 4.4% have precise predictions on Kp uu, CL act, CL pass, and CL met, respectively. All estimates of hepatic clearance processes and Kp uu predictions are accurate but may not be precise. That is to say, the true values of hepatic clearance processes or Kp uu are always bounded by the maximum and minimum of the estimated values; however, the ratio between estimated maximum and minimum may be greater than our criterion (i.e., 10). As such, in the text below, when the word “precise” is used, it means precise and accurate.
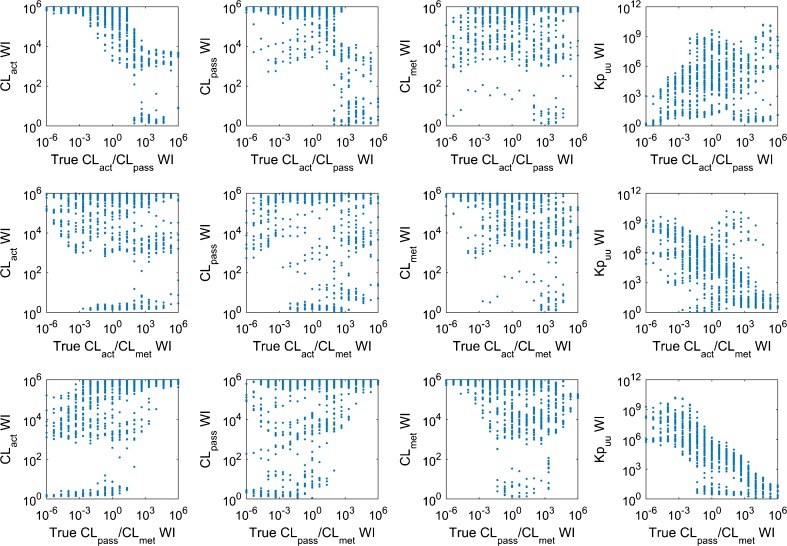
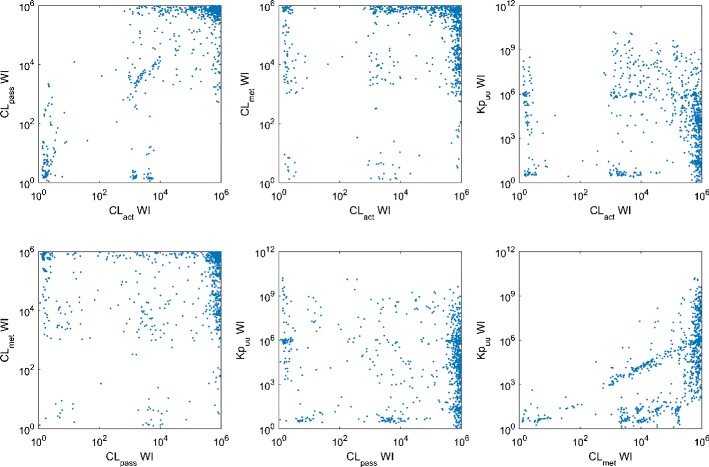
Precise estimates of CL met are very likely to result in the precise prediction of Kp uu (Fig. 3), although to have a precise prediction of Kp uu, it is not necessary to have precise estimate of any hepatic clearance process. Hence, precise estimates of CL met may be used as an indicator for precise prediction of Kp uu. No other obvious relation is identified among the precision of estimated values for Kp uu, CL act, CL pass, and CL met. The relations between ratios of the true values of the hepatic clearance processes and the precision of estimated hepatic clearance processes and Kp uu are also analyzed (Fig. 4). We find that compounds with large values of CL pass/CL met are more likely to have precise estimate of Kp uu. There is no obvious correlation between the true value of hepatic clearance processes and the intervals of their estimates, although it seems that compounds with higher Kp uu are slightly more likely to have precise prediction of Kp uu (Fig. 5). Considering that the current PBPK model is more likely to be applied to a compound with significant asymmetric liver distribution, we reanalyze 164 compounds with Kp uu greater than 10, where the percentage of compounds with precise Kp uu, CL act, CL pass, and CL met increased to 43.9, 31.1, 25.0, and 18.3%.
Fig. 3.
Scatter plots showing the relations among the widths of intervals (WI) of estimated values of CL act, CL pass, CL met, and Kp uu
Fig. 4.
Scatter plots showing the relations between ratios of hepatic clearances and widths of prediction intervals (WI)
Fig. 5.
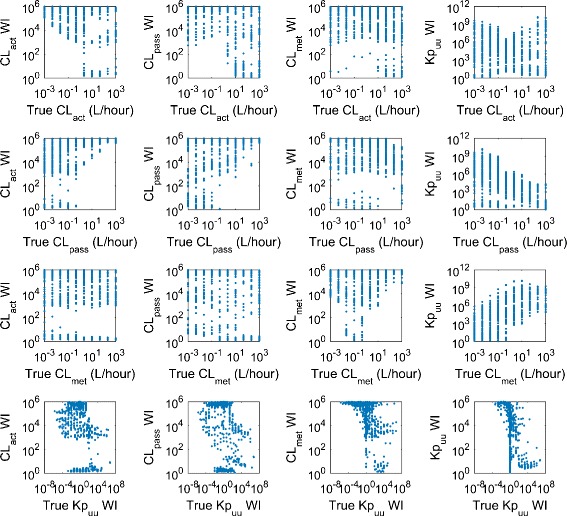
Scatter plots showing the relations between true values of hepatic clearances and Kp uu, and widths of prediction intervals (WI)
To make the hepatic clearance processes of pseudo compounds more comparable to the real compounds (Table S1), during compound generation, the possible values for clearances are narrowed to 10−1, 10−0.67, 10−0.33, 100, 100.33, 100.67, 101, 101.33, 101.67, and 102 L/h for CL act and CL pass, and 10−2, 10−1.67, 10−1.33, 10−1, 10−0.67, 10−0.33, 100, 100.33, 100.67, and 101 L/h for CL met. However, this does not increase the percentage of compounds with precisely estimated hepatic clearance processes or Kp uu (data not shown).
All the results with 1000 permutation sets are very similar to results with 125 permutation sets derived from a sparser grid over the same parameter range (the predefined hepatic clearance processes include five possible values: 10−3, 10−1.5, 100, 101.5, and 103 L/h); hence, in the analyses below, we only use 125 pseudo compounds to decrease computation time.
Predicting Kpuu with One Hepatic Clearance Process Fixed at True Value
The result that compounds with precise estimates of CL met are more likely to have precise prediction of Kp uu leads to a question: Can Kp uu be more precisely predicted, when CL met is fixed at its true value? We perform the analysis with only CL act and CL pass estimated by fitting systemic data, and predict Kp uu. In this scenario, the number of compounds with precise prediction of Kp uu is greatly increased to 63 (i.e., 64.3% of 98 survived compounds). However, there are still 35 compounds that do not have precise estimates of Kp uu, among which the ratio between estimated maximal and minimal CL act is always greater than 103, as is the ratio between maximal and minimal CL pass.
We also fix CL act or CL pass at its true value, estimate the other two hepatic clearance processes, and predict Kp uu by fitting systemic data. The number of compounds that have precise predictions of Kp uu is only 16 (16.3% of 98 survival compounds) when CL act is fixed and 27 (27.5% of 98 survival compounds) when CL pass is fixed. If CL met can be estimated precisely, the predicted Kp uu is more likely to be precise.
It is worth noting that if one hepatic clearance process is fixed at a wrong value, then the estimates of the other two hepatic clearance processes and predictions of Kp uu may be precise but may not be accurate. As an example, we fix CL met at values three times greater than the true values, while CL act and CL pass are estimated and Kp uu is predicted. There are four compounds (4.1% of 98 survival compounds) for which no CL act and CL pass values can be identified to reasonably describe systemic pharmacokinetic data (i.e., no randomly generated CL act and CL pass values are accepted according to the criteria described above). Among compounds for which there are CL act and CL pass values that can reasonably describe systemic data, 8 compounds (8.2% of 98 survival compounds) have true CL act values outside estimated CL act intervals, 11 compounds (11.2% of 98 survival compounds) have true CL pass values outside estimated intervals, and 41 compounds (41.8% of 98 survival compounds) have true Kp uu values outside predicted intervals.
Predicting Kpuu Using Systemic Data Generated with Different pKa and Lipophilicity Values
We performed similar analysis with different pKa and lipophilicity (e.g., pKa of 9 (basic) and logD 7.4 of 2 versus 4.5 (acidic) and 1 in the current analysis), which govern the distribution into tissues except for liver, but the results are similar (data not shown).
Predicting Kpuu with Decreased SD of Systemic Data
We decreased SD of systemic data to some unrealistically low values (i.e., 30 and 10% of original value). As such, the intervals of systemic concentrations constructed as the acceptance criterion are narrower than before. With smaller SD and narrower intervals, more pseudo compounds can have precisely estimated clearances and precisely predicted Kp uu, but the majority of the compounds still do not (Table I). It indicates that for some compounds, the unidentifiability of their clearances or Kp uu is more, if not entirely, due to the shape of concentration-time course, rather than the variability existing in data.
Table I.
The Number of Sets of Clearances Leading to Precise Estimates of Kp uu and Clearances, with Different SD of Generated Systemic Data
| SD of systemic data | |||
|---|---|---|---|
| 0.297 (determined from observations) | 0.0891 (30% of 0.297) | 0.0297 (10% of 0.297) | |
| Sets without producing numerical error | 98 | 98 | 98 |
| Sets with precise estimate of CL act | 13 | 19 | 31 |
| Sets with precise estimate of CL pass | 16 | 20 | 39 |
| Sets with precise estimate of CL met | 4 | 7 | 12 |
| Sets with precise prediction of Kp uu | 12 | 27 | 40 |
Human Implications
Assuming that the same model structure can also simultaneously describe the human systemic and liver pharmacokinetics, similar analyses are performed after changing physiological parameter values to values for human (6), with 10 predefined values for CL act, CL pass, and CL met (i.e., 10−1, 10−0.33, 100.33, 101, 101.67, 102.33, 103, 103.67, 104.33, and 105 L/h), leading to 925 compounds that do not have numerical error. Among these compounds, 6.59, 7.78, 7.03, and 0.865% have precise predictions on Kp uu, CL act, CL pass, and CL met, respectively. Results of other analyses are similar to the analyses performed with rat physiological values (data not shown).
We further analyzed uncertainty in estimating human hepatic CL act, CL pass, and CL bile and predicting liver tissue concentration based on human systemic pharmacokinetic data of rosuvastatin, a compound that is heavily used to test PBPK models for transporter substrates. Values of CL act, CL pass, CL bile, and parameters for enterohepatic recirculation (Table II) are initially estimated by numerically fitting systemic pharmacokinetic data (Fig. S2) (6). We collect one thousand sets of parameter values (with maximum and minimum given in Table II) which can generate systemic concentration-time profiles within the prediction intervals. These values are then used to predict liver concentrations (Fig. 6) and calculate Kp uu (Table II).
Table II.
Best Fitted, Minimal, and Maximal Values of Parameters in the Human PBPK Model for Rosuvastatin and Resulting Kp uu Values
| Parameter | Best fitted value | Minimum | Maximum |
|---|---|---|---|
| CL act (L/h) | 2266 | 137 | 3260000 |
| CL pass (L/h) | 6.63 | 0.0552 | 6420 |
| CL bile (L/h) | 2.51 | 0.518 | 46.3 |
| F a | 0.380 | 0.0989 | 0.835 |
| k a,1 (h−1) | 0.0147 | 0.00147 | 0.143 |
| k a,2 (h−1) | 0.509 | 0.0510 | 4.53 |
| F abosprition,1 | 0.382 | 0.0671 | 0.969 |
| Kp uu | 454 | 4.36 | 2662 |
Fig. 6.
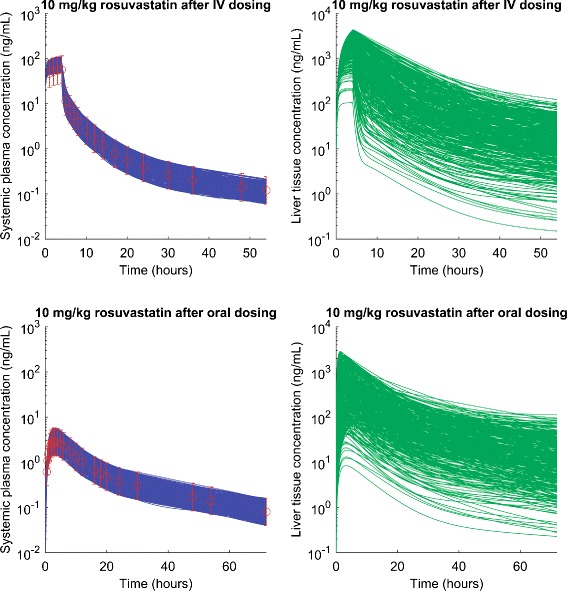
Simulated human plasma and predicted liver concentration-time profiles for rosuvastatin. Circles represent the simulated mean systemic plasma concentration using best fitted parameter values given in Table II. Error bar represents the prediction intervals using observed average standard deviation. Green solid lines represent 1000 predicted liver concentration-time profiles, using parameter values with which model can generate systemic concentration-time profiles (blue solid lines) within the prediction intervals
Discussion
When a PBPK model is only trained with systemic plasma data but is used to simulate liver profiles, a key question we need to address is how much confidence we have in the prediction. In this study, we try to address the question by generating pseudo compounds for which we know both systemic and liver profiles. We then developed an approach to assess the accuracy and precision of predicted liver concentration. We find that in all scenarios, after training with plasma data, model predictions of liver are always accurate (i.e., true value is bounded by predicted maximum and minimum); however, only for a few compounds are predictions also precise. Although this study does not cover the entire space of hepatic clearance processes, and the real compounds may not be uniformly distributed in the space we defined, the results here still indicate that, one should not assume that the hepatic clearance processes or liver concentration can always be precisely estimated using a PBPK model calibrated using exclusively plasma data. Uncertainty in estimating hepatic clearance and liver concentration will be carried into DDI prediction in the liver, as shown in the case example. These results generated with the rat PBPK model are well preserved in a human model.
Recently, PBPK models have been widely used by the pharmaceutical industry and regulatory agencies for human DDI assessments for substrates of liver transporters, with hepatic clearance processes estimated by fitting systemic data. This may lead to biased conclusions about DDI or misleading guidance for clinical practice when both transporters and metabolic enzymes are acting on liver concentrations. Predicted DDI dependent upon plasma concentrations, such as hepatic uptake transporter inhibition for compounds whose clearance is mainly driven by hepatic active uptake, should be minimally affected, as well as very permeable compounds for which free liver concentration is about the same as free plasma concentration.
It is worth noting that here, to simplify the problem, we fixed parameters except for hepatic clearance processes at the “true” values, such that the analysis results are not confounded by the values of these parameters. In analyzing real-world compounds, if some of these parameters are fixed at “wrong” values, the Kp uu prediction may be precise but may not be accurate. However, under such a scenario, it may not be possible to estimate Kp uu or free tissue concentration with any other approach either (including the direct measurement of drug concentration in the tissue, such as a positron emission tomography study or terminal study). In the analysis, it is interesting to see that a precise prediction of Kp uu is possible, even if all three hepatic clearance processes cannot be precisely estimated. The following equation may help understand this phenomenon. To simplify the problem, assuming the impact of hepatic blood flow, f u,p, and R BP on Kp uu is minimal, Kp uu can be approximated using Eq. 7 (4).
| 7 |
Hence, Kp uu can be uniquely determined, as far as the ratio between CL act + CL pass and CL pass + CL met is uniquely defined by systemic data, even if every single parameter in the equation is not uniquely identifiable.
In the analyses, the compounds with precise estimate of CL met are more likely to have precise estimates of Kp uu; however, when fixing CL met at true values, there are still about 40% compounds that do not have precise prediction of Kp uu. It may be because the CL met exerts its influence on systemic concentration through changes it makes on liver concentration. As such, if CL met is influential on the systemic data, then it must also be influential on the liver concentration, making a precise estimate of CL met a sufficient condition for precise estimates of Kp uu. On the other hand, if CL met is influential on the liver concentration, it may not be influential on the systemic data (e.g., active uptake limited plasma clearance). In such a case, neither CL met nor Kp uu can be confidently estimated. In addition, there are cases where CL met is not influential enough on the liver concentration; as such, even if CL met is fixed at true value, Kp uu cannot be precisely predicted, or even if CL met is not precisely estimated, Kp uu can still be precisely predicted. If CL act and/or CL pass is also influential on liver concentrations, then precise Kp uu prediction also requires precise CL act and/or CL pass estimates. However, because these two clearances have direct impact on systemic concentration, even if precise estimates of them are achieved, it does not guarantee that Kp uu can be precisely predicted.
Nevertheless, when fitting systemic data of individual compounds, the chance to have a precise Kp uu prediction will be greatly increased with precise CL met prediction as shown in results. This may be achieved by using the product of in vitro metabolic clearance, physiological scaling factor, and empirical scaling factor. The empirical scaling factor, which captures all differences between in vitro and in vivo that are not described by physiological scaling factor, hence, is an important parameter. The challenge is that these scaling factors are not always readily determined to be assured of good estimates. An attempt to address this challenge has been published previously (5). In addition to CL met, the in vitro assays may also provide information about permeability and transporter activity. For compounds showing high permeability and not being transporter substrates in the assays, the permeability limited liver model with three free parameters (CL act, CL pass, and CL met) can be reduced to a perfusion-limited well-stirred liver model with only one free parameter (CL met). In such cases, at steady state, the free liver concentration can be approximated as the same as the observed free plasma concentration for compounds with low extraction. In the current analysis, we assume a linear model to simplify the problem. For compounds with saturable transport or metabolism processes, a similar but compound-specific analysis with additional parameters can be performed.
In this study, the PBPK model with permeability-limited liver compartment is determined to be structurally globally identifiable (i.e., quantification of parameters is possible from a set of ideal noise-free data (15)). Even if the models are structurally identifiable, they may not be numerically identifiable, potentially because the data are not ideal. The current study focuses more on the numerical identifiability, which addresses the question of whether practical quantification of parameters is possible when the data are real with noise (15). The results that the parameter estimation and liver concentration prediction are precise for only certain pseudo compounds, and with smaller SD and narrower intervals, more pseudo compounds can have precisely estimated clearances and precisely predicted Kp uu, are consistent with the conclusion that the model is structurally identifiable but may not be numerically identifiable for some data.
Conclusion
In this study, we generated systemic and liver concentration profiles for pseudo compounds with predefined values of hepatic clearance processes and a PBPK model structure validated by rat systemic and liver data. Then, the hepatic clearance processes are reestimated by fitting systemic data and used to predict liver concentrations. The accuracy and precision of estimated hepatic clearances and predicted liver concentration are analyzed. With hepatic clearance processes estimated using plasma data, model predictions of liver are always accurate but less likely to be precise. The results of the current study indicate that extra attention is required when using the current PBPK approach for transporter substrates to predict liver concentrations and DDI dependent upon those liver concentrations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
(DOCX 267 kb)
Acknowledgments
The authors greatly appreciate the sincere help on structural identifiability analysis from Dr. Nicolette Meshkat at Santa Clara University and Dr. Joe DiStefano III at University of California, Los Angeles.
References
- 1.Peters SA. Physiologically based pharmacokinetic (PBPK) modeling and simulations : principles, methods, and applications in the pharmaceutical industry. Hoboken: Wiley; 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rose RH, Neuhoff S, Abduljalil K, Chetty M, Rostami-Hodjegan A, Jamei M. Application of a physiologically based pharmacokinetic model to predict OATP1B1-related variability in pharmacodynamics of rosuvastatin. CPT Pharmacometrics Syst Pharmacol. 2014;3 doi: 10.1038/psp.2014.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Watanabe T, Kusuhara H, Maeda K, Shitara Y, Sugiyama Y. Physiologically based pharmacokinetic modeling to predict transporter-mediated clearance and distribution of pravastatin in humans. J Pharmacol Exp Ther. 2009;328(2):652–62. doi: 10.1124/jpet.108.146647. [DOI] [PubMed] [Google Scholar]
- 4.Li R, Barton HA, Varma MV. Prediction of pharmacokinetics and drug-drug interactions when hepatic transporters are involved. Clin Pharmacokinet. 2014;53(8):659–78. doi: 10.1007/s40262-014-0156-z. [DOI] [PubMed] [Google Scholar]
- 5.Li R, Barton HA, Yates PD, Ghosh A, Wolford AC, Riccardi KA, et al. A “middle-out” approach to human pharmacokinetic predictions for OATP substrates using physiologically-based pharmacokinetic modeling. J Pharmacokinet Pharmacodyn. 2014;41(3):197–209. doi: 10.1007/s10928-014-9357-1. [DOI] [PubMed] [Google Scholar]
- 6.Li R, Barton HA, Maurer TS. Toward prospective prediction of pharmacokinetics in OATP1B1 genetic variant populations. CPT Pharmacometrics Syst Pharmacol. 2014;3 doi: 10.1038/psp.2014.50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shah DK, Betts AM. Towards a platform PBPK model to characterize the plasma and tissue disposition of monoclonal antibodies in preclinical species and human. J Pharmacokinet Pharmacodyn. 2012;39(1):67–86. doi: 10.1007/s10928-011-9232-2. [DOI] [PubMed] [Google Scholar]
- 8.Davies B, Morris T. Physiological parameters in laboratory animals and humans. Pharm Res. 1993;10(7):1093–5. doi: 10.1023/A:1018943613122. [DOI] [PubMed] [Google Scholar]
- 9.Rodgers T, Leahy D, Rowland M. Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate-to-strong bases. J Pharm Sci. 2005;94(6):1259–76. doi: 10.1002/jps.20322. [DOI] [PubMed] [Google Scholar]
- 10.Rodgers T, Rowland M. Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci. 2006;95(6):1238–57. doi: 10.1002/jps.20502. [DOI] [PubMed] [Google Scholar]
- 11.Poirier A, Funk C, Scherrmann JM, Lave T. Mechanistic modeling of hepatic transport from cells to whole body: application to napsagatran and fexofenadine. Mol Pharm. 2009;6(6):1716–33. doi: 10.1021/mp8002495. [DOI] [PubMed] [Google Scholar]
- 12.Bellu G, Saccomani MP, Audoly S, D’Angio L. DAISY: a new software tool to test global identifiability of biological and physiological systems. Comput Methods Prog Biomed. 2007;88(1):52–61. doi: 10.1016/j.cmpb.2007.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Spear RC, Bois FY. Parameter variability and the interpretation of physiologically based pharmacokinetic modeling results. Environ Health Perspect. 1994;102(Suppl 11):61–6. doi: 10.1289/ehp.94102s1161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Martin PD, Warwick MJ, Dane AL, Brindley C, Short T. Absolute oral bioavailability of rosuvastatin in healthy white adult male volunteers. Clin Ther. 2003;25(10):2553–63. doi: 10.1016/S0149-2918(03)80316-8. [DOI] [PubMed] [Google Scholar]
- 15.DiStefano JJ. Dynamic systems biology modeling and simulation. First edition. ed. Amsterdam: Elsevier, Academic Press; 2013. xxii, 859 pages p.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX 267 kb)