Whole-genome analysis of Alu repeat elements reveals complex evolutionary history

Abstract

Alu repeats are the most abundant family of repeats in the human genome, with over 1 million copies comprising 10% of the genome. They have been implicated in human genetic disease and in the enrichment of gene-rich segmental duplications in the human genome, and they form a rich fossil record of primate and human history. Alu repeat elements are believed to have arisen from the replication of a small number of source elements, whose evolution over time gives rise to the 31 Alu subfamilies currently reported in Repbase Update. We apply a novel method to identify and statistically validate 213 Alu subfamilies. We build an evolutionary tree of these subfamilies and conclude that the history of Alu evolution is more complex than previous studies had indicated.

Alu repeats are a family of short interspersed elements (SINEs) that replicate via LINE-mediated reverse transcription of an RNA polymerase III transcript (Rogers 1983; Mathias et al. 1991; Dewannieux et al. 2003). Each Alu element is roughly 280 bp long, followed by a poly-A tail of variable length. Thus, the more than 1 million Alu elements comprise roughly 10% of the human genome (International Human Genome Consortium 2001). Although Alu repeats have no known biological function (Schmid 2003), the study of the Alu repeat family has many ramifications. Alu insertions and Alu-mediated unequal recombination contribute to a significant proportion of human genetic disease (Deininger and Batzer 1999). Alu-mediated unequal recombination is believed to be responsible for the enrichment of gene-rich segmental duplications in humans versus other sequenced organisms (Bailey et al. 2003). Alu repeats have been used to study the history of substitution patterns in the human genome (Arndt et al. 2003), and polymorphic Alu insertions have been used as markers to determine genetic distances between human sub-populations (Watkins et al. 2003). Recently, a phylogenetic analysis of Alu elements belonging to the Alu Ye5 subfamily has provided the strongest evidence yet that the chimp is humans' closest living relative (Salem et al. 2003). Virtually all areas of Alu research rely on the classification of Alu subfamilies, and this paper provides strong evidence that the existing classification is incomplete.

Early analyses, prior to the assembly of the human genome, identified a small number of Alu subfamilies, each characterized by a few diagnostic positions in its consensus sequence (Willard et al. 1987; Britten et al. 1988; Deininger and Slagel 1988; Jurka and Smith 1988; Quentin 1988; Matera et al. 1990a; Batzer and Deininger 1991; Jurka and Milosavljevic 1991). These analyses led to the conjecture that all Alu repeat elements have arisen from the replication of either “a single master gene” (Shen et al. 1991), or “an extremely small group of master genes” (Deininger et al. 1992). The conjecture of a single master gene was shown to be incorrect (Matera et al. 1990b; Jurka and Milosavljevic 1991; Leeflang et al. 1992), but it remains widely believed that “only a few human Alu elements... seem to be retrotransposition competent” (Batzer and Deininger 2002). In this paper, we will refer to Alu elements that have (or previously had) the ability to replicate as source elements (Matera et al. 1990b); we note that many different definitions of the terms “source gene” and “master gene” have been used previously (Matera et al. 1990b; Shen et al. 1991; Deininger et al. 1992; Deininger and Batzer 1995). As a source element evolves over time, it may produce a lineage of more than one subfamily (Leeflang et al. 1993). The Repbase Update database (Jurka 1998, 2000) keeps a record of known Alu subfamilies, each defined by a consensus sequence. New Alu sub-families have been added to the database as recently as 2002, and there are 31 Alu subfamilies currently reported in the database. 2

With the sequence of the human genome now assembled (International Human Genome Consortium 2001), Alu repeats can be analyzed on a genome-wide scale. In our genome-wide analysis, we have identified and statistically validated 213 Alu subfamilies, each defined by a consensus sequence. Our novel method recursively splits subfamilies whose members fail a statistical uniformity test. After identifying Alu subfamilies, we built an evolutionary tree of these subfamilies. Our evolutionary tree describes the path of evolution from AluJ subfamilies to AluS subfamilies, and from AluS subfamilies to AluY subfamilies, at a much finer granularity than previous analyses. Our evolutionary tree also contains a large number of completely new branches. We conclude that the history of Alu evolution is more complex than previous studies had indicated.

The existing set of repeat subfamily identification algorithms is quite limited. Recent algorithms such as RepeatMasker (A.F.A. Smit and P. Green, http://repeatmasker.org), REPuter (Kurtz et al. 2000), RepeatFinder (Volfovsky et al. 2001), RECON (Bao and Eddy 2002), and RepeatGluer (Pevzner et al. 2004) are successful at finding individual repeat elements or identifying repeat families, but they do not address the problem of identifying very similar subfamilies of a repeat family. The only previous algorithm for identifying repeat subfamilies that we are aware of is the MASC algorithm (Milosavljevic et al. 1989; Jurka and Milosavljevic 1991), which was applied to a limited Alu data set to identify 6 Alu subfamilies. In this application to repeat subfamily identification, the MASC algorithm recursively splits subfamilies into two clusters that maximize a likelihood function and is similar to hierarchical application of the k-means clustering algorithm (Lloyd 1982). We recognize the pioneering contribution of the MASC algorithm to repeat subfamily identification; however, we believe that k-means clustering is not well suited to solving this problem. Indeed, our own efforts to analyze Alu repeats on a genome-wide scale using hierarchical k-means yielded inconsistent results, for reasons we will explain below.

New ideas

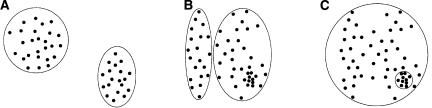
A natural approach to repeat subfamily identification is to define a cluster of repeat elements by its profile of nucleotide frequencies at each position, and search for a fixed number of clusters maximizing the likelihood of generating the data from these clusters. This approach is similar to the popular k-means clustering algorithm (Lloyd 1982). k-means clustering is good at identifying disjoint clusters of similar size (Fig. 1A); however, it has known limitations (Bishop 1996). In particular, it is not good at identifying small subfamilies nested inside large subfamilies, a typical scenario in our application to Alu repeat subfamilies, because it prefers to split off a larger cluster (Fig. 1B). We would like to be able to identify such nested subfamilies (Fig. 1C).

Figure 1.

Applicability of k-means clustering to different kinds of clustering problems. Disjoint clusters of similar size are easily identified (A). Small subfamilies nested inside large subfamilies, a typical scenario in Alu repeat subfamilies, are not easily identified, because there is a tendency to split off a larger cluster (B) instead of identifying the nested subfamily (C).

We illustrate with an example using real data. Suppose we analyze the set of all Alu repeat elements, looking only at the five nucleotide positions with diagnostic mutations in the Ya5 subfamily. The nucleotide frequency profile of all Alus at these 5 positions is listed in Table 1A; this profile has consensus values T,C,G,C,G, which are the consensus values of nearly every Alu subfamily at these positions. Applying k-means clustering 3 with k = 2, we split the data into two clusters. The frequency profiles for these two clusters are listed in Table 1B; the two clusters are defined by whether the second nucleotide is an A or C (cluster 1), or a G or T (cluster 2). The frequency profiles at the remaining nucleotide positions, however, are similar for these two clusters. Thus, the second cluster may be explained by random mutation of the second nucleotide to a G or T, and no new subfamily has been found.

Table 1.

Finding the Ya5 subfamily in the set of all Alu elements

(A) All Alus: nucleotide frequencies
	1	2	3	4	5
A	0.01	0.02	0.06	0.03	0.31
C	0.02	0.87	0.01	0.63	0.02
G	0.00	0.02	0.91	0.03	0.64
T	0.96	0.08	0.01	0.31	0.02

(B) k-means clustering
	Cluster 1 (90% of Alus)
	1	2	3	4	5
A	0.01	0.03	0.06	0.03	0.31
C	0.02	0.97	0.01	0.63	0.03
G	0.00	0.00	0.91	0.03	0.64
T	0.96	0.00	0.01	0.31	0.02

	Cluster 2 (10% of Alus)
	1	2	3	4	5
A	0.01	0.00	0.07	0.03	0.34
C	0.02	0.00	0.01	0.64	0.02
G	0.00	0.22	0.91	0.03	0.63
T	0.98	0.78	0.02	0.31	0.02

(C) All Alus: binucleotide frequencies relative to expected
	1,2	1,3	1,4	1,5	2,3	2,4	2,5	3,4	3,5	4,5
A,A	1	1	1	1	5	1	1	1	1	1
A,C	1	1	1	1	1	1	12	1	5	1
A,G	1	1	1	1	1	1	1	1	1	1
A,T	1	1	1	1	1	2	1	1	1	1
C,A	12	5	1	1	1	1	1	1	1	1
C,C	1	1	1	11	1	1	1	1	1	1
C,G	1	1	1	1	1	1	1	1	1	1
C,T	1	1	2	1	1	1	1	1	1	1
G,A	1	1	1	2	2	1	1	1	1	1
G,C	1	1	1	1	1	1	1	1	1	1
G,G	1	1	1	1	1	1	1	1	1	1
G,T	1	1	1	1	1	1	1	1	1	1
T,A	1	1	1	1	1	1	1	1	1	1
T,C	1	1	1	1	1	1	1	1	1	2
T,G	1	1	1	1	1	1	1	1	1	1
T,T	1	1	1	1	1	1	1	1	1	1

(D) Our algorithm
	Cluster 1 (99.3% of Alus)
	1	2	3	4	5
A	0.01	0.02	0.06	0.03	0.32
C	0.02	0.88	0.01	0.64	0.02
G	0.00	0.02	0.92	0.03	0.64
T	0.97	0.08	0.01	0.30	0.02

	Cluster 2 (0.7% of Alus)
	1	2	3	4	5
A	0.01	0.98	0.95	0.00	0.02
C	0.95	0.01	0.00	0.06	0.91
G	0.00	0.01	0.05	0.00	0.07
T	0.05	0.00	0.00	0.93	0.00

For simplicity, we considered only the 5 Alu positions with diagnostic mutations in the Ya5 subfamily (positions 91, 98, 146, 175, and 238, assuming that positions of the AluSx consensus sequence are labeled from 1 to 282). In each table, entries corresponding to the Ya5 consensus are underlined. In (A), entries corresponding to the Alu consensus are indicated in boldface type. In (B) and (D), entries corresponding to the consensus of each respective cluster are indicated in bolface type. (A) The nucleotide frequency profile of all Alus. (B) Frequency profiles for the 2 clusters returned by k-means clustering with k = 2, which does not find the Ya5 subfamily. (C) Ratio of actual versus expected biprofile frequencies at each pair of positions, rounded to the nearest integer. (D) Frequency profiles for the 2 clusters found by our algorithm, which finds the Ya5 subfamily.

Because k-means clustering does not succeed, finding the Alu Ya5 subfamily requires a different approach. One possibility is to look for a frequent nucleotide value different from the consensus and assign Alu elements with that value to a new cluster. The highest frequencies for non-consensus nucleotide values are 0.31 for T at position 4 and 0.31 for A at position 5; however, these are readily explained by frequent mutation of CpG dinucleotides. If we exclude frequent CpG mutations, the highest frequency for a non-consensus nucleotide value is 0.08 for T at position 2. As we have already seen from the results of the k-means clustering in Table 1B, however, Alu elements with a T at position 2 are no different from usual at the remaining nucleotide positions. Thus, the frequency of 0.08 for T at position 2 may be explained by random mutation, and no new subfamily has been found. Indeed, rates of random mutation vary widely for different Alu positions. Without a priori knowledge of random mutation rates at each Alu position, there is no reason to believe a frequent nonconsensus nucleotide value is different from random and indicative of a new subfamily. We conclude that the frequency profile in Table 1A contains no clues for the existence of the Ya5 subfamily.

We propose instead to look for overrepresented pairs of nonconsensus nucleotide values, at distinct positions, by computing biprofiles (Keich and Pevzner 2002), that is, frequencies of pairs of nucleotide values. Upon doing this, we observe that Alu elements have both a C at position 1 and an A at position 2 with frequency 0.0068. This is extremely surprising. In fact, this is 12 times as many instances as we would expect based on the individual frequencies of C at position 1 and A at position 2 (0.024 · 0.023 = 0.00055), under the null hypothesis that the positions are independent. In Table 1C, we list all such ratios of actual versus expected biprofile frequencies. The peaks in the table are nearly in 1:1 correspondence with the entries corresponding to the Ya5 subfamily, and immediately point to the Ya5 consensus values C,A,A,T,C. In particular, the peak with value 12 for a C at position 1 and an A at position 2 has a P value of less than 1e^-2000 under the null hypothesis, according to our statistical test. We split the set of Alu elements accordingly, eventually obtaining the two clusters whose frequency profiles are listed in Table 1D. The second cluster is precisely the Ya5 subfamily.

Identifying new subfamilies by searching for overrepresented pairs (or, more generally, triples or even n-tuples) of nonconsensus nucleotide values has numerous advantages: We can identify nested subfamilies without a priori knowledge of underlying mutation rates, validate their existence with a high level of statistical confidence, and assign individual Alu elements to these subfamilies accurately and unambiguously. This approach, however, cannot identify subfamilies that differ at only a single diagnostic position. Thus, after using overrepresented pairs of nonconsensus nucleotide values to build a scaffold of the space of Alu subfamilies, we use this scaffold to calibrate Alu mutation rates at each position and identify additional Alu subfamilies by looking for overrepresented individual mutations within each subfamily of the scaffold.

Results

We generate a multiple alignment of roughly 480,000 full-length Alu elements (see Methods). Starting with a single subfamily containing all of these Alu elements, we recursively split subfamilies whose members fail a statistical uniformity test. We first split subfamilies containing overrepresented pairs of nonconsensus nucleotide values to build a scaffold of the space of Alu subfamilies, performing an additional validation step to verify that the union of two or more subfamilies fails the uniformity test, using a P-value threshold of 0.001 (see Methods). The resulting scaffold contains 60 Alu subfamilies. We then use the resulting calibration of Alu mutation rates at each position to split subfamilies containing overrepresented individual mutations, again using a P-value threshold of 0.001 (see Methods). This procedure identifies 153 additional subfamilies. Thus, we identify a total of 213 Alu subfamilies. The size of each subfamily ranges from roughly 50 to 60,000 Alu elements, with most subfamilies containing at least a few hundred elements. P-values for each subfamily range from below 1e^-6000 to near our P-value threshold of 0.001, with most subfamilies having a P-value below 1e^-40.

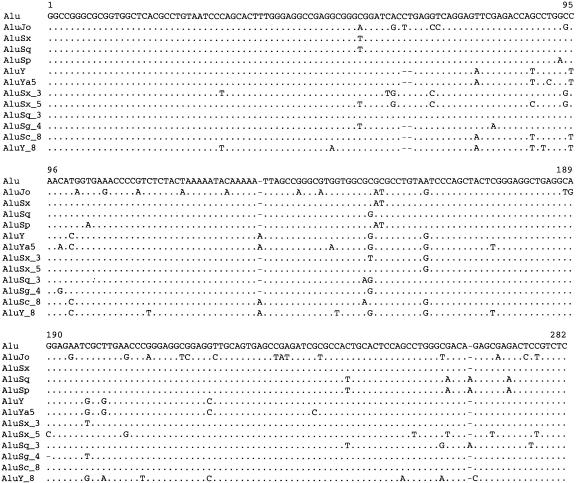
We have chosen a sample of 12 Alu subfamilies identified by our algorithm to describe here, including six subfamilies that are currently reported in Repbase Update (Jurka 1998; Jurka 2000) and six novel subfamilies from our scaffold of 60 Alu subfamilies. We list the aligned consensus sequences of these 12 subfamilies in Figure 2, and their sizes and P-values in Table 2. Consensus sequences for all 213 subfamilies identified by our algorithm are listed elsewhere (see online Supplemental materials).

Figure 2.

Aligned consensus sequences of selected subfamilies. (Top) The consensus sequence of the entire Alu family, with positions labeled from 1 to 282. (Middle) The consensus sequences of six Alu subfamilies we identified that are currently reported in Repbase Update: AluJo, AluSx, AluSq, AluSp, AluY, and AluYa5; the few discrepancies between our consensus sequences and the consensus sequences reported in Repbase Update occur mostly at CpG dinucleotide positions, which are ill-determined because of frequent mutation. (Bottom) The consensus sequences of six Alu subfamilies we identified that are not currently reported in Repbase Update: AluSx_3, AluSx_5, AluSq_3, AluSg_4, AluSc_8, and AluY_8.

Table 2.

Sizes and P-values of selected subfamilies

Subfamily	Size	P-value
AluJo	7,266	8e-1841
AluSx	39,724	6e-4770
AluSq	4,035	2e-62
AluSp	28,063	7e-4520
AluY	27,023	2e-6924
AluYa5	3,257	4e-2813
AluSx_3	3,292	8e-1841
AluSx_5	401	3e-150
AluSq_3	1,956	2e-779
AluSg_4	1,904	1e-679
AluSc_8	9,588	1e-5959
AluY_8	107	1e-48

We list the size and P-value for each of the 12 subfamilies whose aligned consensus sequences are listed in Figure 2. Some Repbase Update subfamilies, particularly the AluSq subfamily, contain fewer elements in our allocation of Alu elements to subfamilies than in the allocation of Alu elements to Repbase Update subfamilies only, because many elements have been reallocated to neighboring subfamilies not in Repbase Update.

We build an evolutionary tree of Alu subfamilies that describes the history of Alu evolution. In contrast to the typical scenario in phylogenetic tree reconstruction in which the input data contains only external nodes of the tree, our Alu subfamilies may be either internal or external nodes of the evolutionary tree; this is because Alu repeat elements in the genome give us a fossil record of Alu subfamilies from the past as well as the present. Thus, traditional methods for phylogenetic tree reconstruction are not applicable here. We instead define the evolutionary tree of Alu subfamilies to be their Minimum Spanning Tree (Kruskal 1956) (see Methods). The resulting evolutionary tree of the 31 subfamilies currently reported in Repbase Update is displayed in Figure 3, and the evolutionary tree of the 213 subfamilies we have identified is displayed in Figure 4.

Figure 3.

Evolutionary tree of the 31 subfamilies currently reported in Repbase Update. (Large nodes) Subfamilies with more than 10,000 elements; (medium nodes) 1000 to 10,000 elements; (small nodes) less than 1000 elements. Each of the 6 Repbase Update subfamilies listed in Figure 2 is labeled. The AluJ, AluS, and AluY classes of subfamilies are contained in boxes.

Figure 4.

Evolutionary tree of the 213 subfamilies we identified. (Large nodes) Subfamilies with more than 10,000 elements; (medium nodes) 1000 to 10,000 elements; (small nodes) less than 1000 elements. Subfamilies listed in Repbase Update are colored blue, and the 6 novel subfamilies listed in Figure 2 are colored red. Each of the subfamilies listed in Figure 2 is labeled. A rendition of this tree with every node labeled is available in the Supplementary materials online. The AluJ, AluS, and AluY classes of subfamilies are contained in boxes; not all subfamilies fit into one of these classes. A timeline roughly depicting the average divergence of each subfamily from its consensus sequence and the approximate age obtained by applying a constant scaling factor of 4 million years per 1% divergence from consensus sequence are included at right.

As an Alu source element evolves over time, it may produce a lineage of more than one Alu subfamily (thus the number of Alu subfamilies may exceed the number of Alu source elements) but these subfamilies must correspond to a single path in the Alu evolutionary tree. Thus, by counting the number of leaves in the tree, we obtain a lower bound on the number of source elements. Our evolutionary tree of 213 subfamilies implies that there are at least 143 Alu source elements. In contrast, the evolutionary tree of the 31 subfamilies currently reported in Repbase Update implies the existence of only 14 Alu source elements.

Discussion

We have identified a total of 213 Alu subfamilies. Our evolutionary tree of these subfamilies describes the path of evolution from AluJ subfamilies to AluS subfamilies, and from AluS subfamilies to AluY subfamilies, at a much finer granularity than previous analyses. For example, the path of evolution from AluJ subfamilies to AluS subfamilies includes the novel AluSx_3 subfamily,4 and the path of evolution from AluS subfamilies to AluY subfamilies includes the novel AluSc_8 subfamily. Our evolutionary tree also contains a large number of completely new branches, revealing a complex evolutionary history. The abundance of previously undiscovered subfamilies in the earlier phases of Alu evolution is particularly striking; because their elements have mutated significantly from the consensus sequence, most of these subfamilies can only be detected by a rigorous whole-genome analysis. Looking in detail at the remaining novel subfamilies listed in Figure 2, the novel AluSx_5 subfamily, a descendant of the AluSx_3 subfamily, can be viewed as a cousin of the AluSx subfamily; the novel AluSq_3 and AluSg_4 subfamilies are moderately large and quite different from their ancestors (AluSq and AluSg) in Repbase Update; and the novel AluY_8 subfamily is very different from its ancestor (AluY) in Repbase Update.

Our results are partially, but not entirely, consistent with existing theories of Alu evolution. Our lower bound of 143 Alu source elements is much larger than previous studies had indicated; we further speculate that there are many Alu subfamilies that we have not identified, either because they are not statistically discernible or because of limitations in our algorithm. We conjecture that there may be thousands of Alu subfamilies, and thousands of Alu source elements. Previous studies had suggested a mostly linear Alu evolution pattern in which most parallel subfamily formations involve very low copy number or short-lived subfamilies (Deininger and Batzer 1995); Figure 4 does contain many short, low-copy-number branches but also contains many major branches that have propagated a large number of Alu copies. Our results are consistent with a model in which a large number of Alu copies are themselves source elements, replicating at widely varying rates; however, these hundreds (or perhaps thousands) of Alu source elements represent a tiny fraction of the more than 1 million Alu elements. It remains clear that the majority of Alu elements are not retrotransposition competent; a common explanation for this is that appropriate upstream sequence is required for efficient Alu transcription (Ullu and Weiner 1985). The abundance of short branches in the Alu evolutionary tree suggests that many source elements are retrotransposition competent for only a short time, perhaps because mutations to the CpG dinucleotides of an Alu source element, or to its poly-A tail, may eliminate their retrotransposition capability (Batzer and Deininger 2002).

Our algorithm has several known limitations. For technical reasons, we exclude insertion/deletion mutations, frequent CpG mutations, and mutations to nucleotide values already present in other subfamilies as a means of identifying new subfamilies (see Methods), making subfamilies characterized by these mutations difficult to identify. In addition, the partition of the set of Alu elements into statistically distinguishable subfamilies need not be unique, and there may exist subfamilies whose elements are distributed across more than one member of our partition, making them difficult to identify. There is no immediate fix to these limitations in our algorithm; they are important directions of our ongoing research. Because of these limitations, our algorithm identifies only 19 of the 31 subfamilies currently reported in Repbase Update. Combining the 213 Alu subfamilies identified by our algorithm with the 12 Alu subfamilies in Repbase Update not identified by our algorithm (which each belong to minor branches of the AluY subfamily), there are a total of 225 previously and presently identified Alu subfamilies. A complete list of these subfamilies is given in the Supplemental materials.

An improved characterization of Alu subfamilies and their evolutionary history will benefit numerous applications, such as analysis of segmental duplications induced by Alu recombination (Bailey et al. 2003), and phylogenetic inference using Alus. Recently, a phylogenetic analysis of Alu elements in the Ye5 subfamily has provided the strongest evidence yet that the chimp is humans' closest living relative (Salem et al. 2003). We hope that the novel Alu subfamilies we have identified may lead to phylogenetic inferences involving other primate species. Furthermore, our methods can be used to identify subfamilies of other repeat families in non-primate species, an open problem. SINE elements have already been used to make phylogenetic deductions about cetartiodactyls (Nikaido et al. 1999) and cichlid fish (Takahashi et al. 2001), and an improved characterization of repeat subfamilies may aid such efforts in the future.

Methods

We generated a data set of Alu elements via a BLAST search (Tatusova and Madden 1999) of Build 34 of the human genome (International Human Genome Consortium 2001) against the AluSx consensus sequence reported in Repbase Update (Jurka 1998, 2000); equivalently, this data set can be generated using RepeatMasker (A.F.A. Smit and P. Green, http://repeatmasker.org). We multiply aligned the Alu elements in our data set by tabulating the nucleotide value of each Alu element at each position of the AluSx consensus sequence, with insertions recorded separately. Because our method assumes that the nucleotide value of each Alu element at each position is known, we excluded Alu elements whose alignment to AluSx is missing more than 5 bases at the beginning or end. After imposing this restriction, there were roughly 480,000 full-length Alu elements in our data set.

We split subfamilies containing overrepresented pairs of non-consensus nucleotide values as follows. Let μ₁ and μ₂ be two mutations from the consensus sequence. Let N be the number of repeat elements in the subfamily, N_i be the number of repeat elements with mutation i (for i = 1,2), and N₁₂ be the number of repeat elements with both mutations. If the two mutations are unlinked, we expect

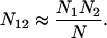If

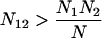then the ratio of the actual versus expected frequency of both mutations, which equals

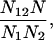quantifies the extent of the linkage (as in Table 1C). We computed a P-value for the linkage using a nonparametric P-value computation, which makes no assumptions about the underlying probability distributions: the probability of at least N₁₂ repeat elements with both mutations occurring by chance is

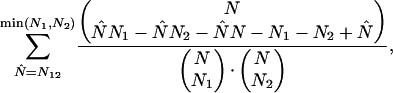where the denominator represents the total number of ways to allocate the two mutations to the sequences, and the multinomial coefficient in the numerator represents the number of allocations with exactly N̂ sequences containing both mutations. The above expression, which we denote ξ_μ1,μ2, is a P-value for the observed linkage of μ₁ and μ₂ under the null hypothesis of uniformity. Thus, ξ = min_μ1,μ2ξ_μ1,μ2 gives an overall P-value for the uniformity of the subfamily. If ξ is below a threshold, which we set at 0.001, the subfamily fails the uniformity test and we split it accordingly. We ensure that the assignment of all Alu repeat elements to one of the resulting subfamilies is consistent, that is, that the consensus sequence defining each subfamily matches the consensus sequence of its members: At each step of the algorithm, we iteratively reassign all Alu repeat elements to subfamilies and recompute the consensus of each subfamily, until this process converges.

To insure the validity of our P-value computation, we addressed several important details. First, for a given subfamily, we computed ξ_μ1,μ2 for many different pairs of mutations (μ₁,μ₂). To compensate for the possibility of obtaining a low value of ξ_μ1,μ2 by chance, we applied a Bonferroni correction, multiplying each ξ_μ1,μ2 by the number of pairs (μ₁,μ₂) tested. To verify that this Bonferroni correction was sufficient, we simulated a uniform data set from the probability profile of all Alu repeat elements and observed that P-values computed from this data set were all greater than 1, after the Bonferroni correction. Second, in our application to Alu repeat subfamilies, a single source element might produce copies over a long span of time, thus producing older copies with many mutations from the consensus and newer copies with fewer mutations from the consensus. This would bias any two mutations μ₁ and μ₂ into being linked, because Alu copies with mutation μ₁ would be likely to be older and thus have mutation μ₂ also. Routine calculations showed that this effect could bias the number of repeat elements with both μ₁ and μ₂ upwards by a factor of up to 4/3. We modified the computation of ξ_μ1,μ2 to account for this bias. Third, because insertion/deletion mutations violate our assumption that distinct positions mutate independently and cause further technical problems, we excluded the case of two indel mutations in our P-value computation and imposed a minimum distance of 10 nucleotides between any two mutations μ₁ and μ₂. Fourth, the Alu consensus sequence contains many CpG dinucleotides, which are highly prone to methylation and subsequent mutation to TpG or CpA (Labuda and Striker 1989). These mutations violate our independence assumption and complicate the computation of the correct consensus sequence (e.g., a dinucleotide with frequent occurrences of both TpG and CpA has correct consensus CpG, but its consensus computed under the independence assumption may equal TpG or CpA). Thus, we excluded CpG → TpG and CpG → CpA mutations and the reverse of these mutations in our P-value computation. Fifth, we excluded mutations to nucleotide values already present in other subfamilies; this very conservative restriction is necessary to avoid falsely assigning mosaic Alu elements formed by Alu–Alu recombination to separate subfamilies. Sixth, we excluded pairs of mutations (μ₁,μ₂) for which the number N₁₂ of repeat elements is <50, thus imposing a minimum subfamily size of 50; this insures that a small number of copies of a repeat element formed by segmental duplication will not be assigned to a separate subfamily.

After we finished splitting all subfamilies containing over-represented pairs of nonconsensus nucleotide values, we verified that the union of two or more subfamilies fails the uniformity test, otherwise we merged subfamilies accordingly. Because it is not computationally feasible to perform a separate check for every possible union of two or more subfamilies, we checked only the unions formed when building the Minimum Spanning Tree (see below). We defined the P-value for each subfamily in the resulting scaffold as the P-value obtained by testing the uniformity of the union of that subfamily with its parent in the Minimum Spanning Tree.

After building a scaffold of Alu subfamilies, we calibrated Alu mutation rates at each position from a given consensus value to every other value by averaging over the elements of all subfamilies in the scaffold that have that consensus value; the mutation rates were computed relative to the overall divergence of a sub-family from its consensus sequence, which serves as our proxy for its age. This calibration allowed us to split subfamilies containing overrepresented individual mutations. We computed P-values using a simple binomial test, and split each subfamily containing an overrepresented individual mutation with a P-value below 0.001, assigning this P-value to the newly created subfamily. As before, we applied an appropriate Bonferroni correction, excluded insertion/deletion and frequent CpG mutations, and imposed a minimum subfamily size of 50. We excluded mutations to nucleotide values already present in other subfamilies, unless the nucleotide value was present in an adjacent subfamily of the Minimum Spanning Tree of Alu subfamilies (see below), in which case splitting with respect to that mutation would simply add an intermediary subfamily.

Because traditional methods for phylogenetic tree reconstruction are not applicable here, we defined the evolutionary tree of Alu subfamilies to be their Minimum Spanning Tree, that is, the tree with Alu subfamilies as nodes that minimizes the sum of edge distances. We built the Minimum Spanning Tree of Alu subfamilies using Kruskal's algorithm (Kruskal 1956), iteratively connecting the two closest subfamilies in different connected components of the tree. We defined the distance between two subfamilies to be the Hamming distance between their consensus sequences, ignoring CpG → TpG and CpG → CpA mutations, with a higher penalty for insertions and deletions. We rooted the tree by selecting the oldest subfamily, that is, the subfamily with highest average divergence from its consensus sequence, as the root.