Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2004 Nov;14(11):2336–2346. doi: 10.1101/gr.2657504

A novel method for multiple alignment of sequences with repeated and shuffled elements

Benjamin Raphael 1,1, Degui Zhi 1, Haixu Tang 1, Pavel Pevzner 1
PMCID: PMC525693  PMID: 15520295

Abstract

We describe ABA (A-Bruijn alignment), a new method for multiple alignment of biological sequences. The major difference between ABA and existing multiple alignment methods is that ABA represents an alignment as a directed graph, possibly containing cycles. This representation provides more flexibility than does a traditional alignment matrix or the recently introduced partial order alignment (POA) graph by allowing a larger class of evolutionary relationships between the aligned sequences. Our graph representation is particularly well-suited to the alignment of protein sequences with shuffled and/or repeated domain structure, and allows one to construct multiple alignments of proteins containing (1) domains that are not present in all proteins, (2) domains that are present in different orders in different proteins, and (3) domains that are present in multiple copies in some proteins. In addition, ABA is useful in the alignment of genomic sequences that contain duplications and inversions. We provide several examples illustrating the applications of ABA.

Multiple sequence alignment (MSA) is arguably among the most studied (Sankoff 1975; Waterman et al. 1976; Feng and Doolittle 1987; Higgins and Sharp 1988; Lipman et al. 1989; Schuler et al. 1991; Vingron and Argos 1991; Kececioglu 1993; Thompson et al. 1994; Morgenstern et al. 1996; Pei et al. 2003; Schwartz et al. 2003a; Darling et al. 2004) and difficult (Wang and Jiang 1994) problems in computational biology. An optimal MSA of t sequences, each of length n, can be computed in Θ((2n)t) time by dynamic programming (Sankoff 1975; Waterman et al. 1976). However, such an approach is not practical for more than a few sequences. Consequently, a large body of research exists for the design of efficient heuristics for MSA; see Notredame (2002) for a recent review. Currently, popular programs include CLUSTALW (Thompson et al. 1994), T-COFFEE (Notredame et al. 2000), DIALIGN (Morgenstern et al. 1998), MultiPiPMaker(Schwartz et al. 2003a), and MACAW (Schuler et al. 1991). However, these programs (and the majority of alignment algorithms) consider the sequences to be aligned as having resulted from an evolutionary process that includes only point mutations and (small) insertions/deletions. Accordingly, an MSA of t sequences is often represented in row–column format: The sequences are listed in t rows with “space characters” (dashes) inserted in positions of indels, and columns indicating aligned positions.

This representation of the alignment as a linear sequence of alignment columns implicitly assumes that all regions of all sequences are similar over their entire length. However, for many biological sequences this assumption does not hold. For example, multidomain protein families evolve not only through mutation of individual amino acids but also through operations such as domain duplications and domain recombinations (Doolittle 1995). Experienced users of multiple alignment programs often manually clip their sequences into similar blocks and compute a global alignment of each block (Eddy 1998). In a sense, this manual procedure attempts to overcome the limitations of the alignment program by trimming the sequences to the parts that are related by point mutations and small indels. A more attractive alternative is to change the alignment program to include a larger set of operations that more accurately reflect the changes that occur in biological sequences.

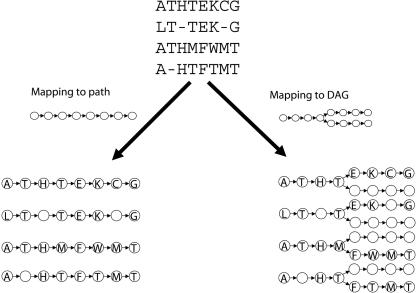
Recently, in a pioneering paper, Lee et al. (2002) asked the question “Should MSAs be linear?” In answer to this question, they proposed partial order alignment (POA), an algorithm that replaces the row–column representation of a multiple alignment by a directed acyclic graph (DAG). Figure 1 illustrates the intuition behind the POA approach. An alignment is a mapping from a set of sequences to a graph. In row–column alignment, the graph is always a single directed path, whereas the POA approach expands the allowable graph structures to include DAGs. The POA approach opens a new perspective on the multiple alignment problem by removing the rigid structure of the linear row–column representation that has been the basis for multiple alignment research over the three decades. POA permits domain recombinations, making it a useful tool for the alignment of multidomain proteins and ESTs.

Figure 1.

Figure 1.

Open in a new tab

An alignment is a mapping from a set of input sequences to a directed graph. Positions that map to the same vertex are aligned. Standard MSA programs map each sequence to a single path. Each vertex on the path contains either a letter or a gap character from each sequence. POA maps each sequence to a DAG. The structure of the DAG permits alignments where a subset of the sequences is aligned at a position.

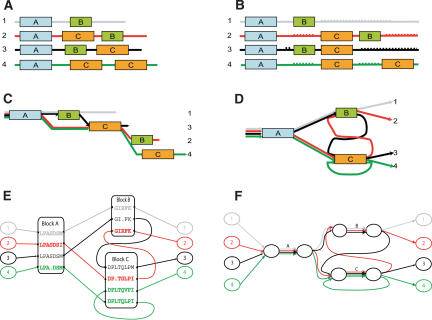
However, even the DAG representation used in POA is not flexible enough to capture the full complexity of the similarities between biological sequences. For example, related protein sequences frequently share common domains, but the order of the domains may be different in different proteins (shuffled domains), or a single domain may be repeated in a single protein (repeated domains). To represent shuffled or repeated domains, the alignment representation must permit directed cycles (Fig. 2). Hence, neither the row–column representation nor the DAG representation provides an accurate representation of shuffled or repeated domains. We take the approach of Lee et al. (2002) a step further and ask “Should multiple alignments be represented by acyclic graphs?” In the case of proteins with repeated or shuffled domains, the answer is no.

Figure 2.

Figure 2.

Open in a new tab

(A) Four “protein” sequences containing three “domains” (A, B, and C; shown as boxes) and unique regions (shown as lines). (B) A row–column multiple alignment introduces gaps (dotted lines) to align domains A and C but cannot represent the alignment of all three domains. (C) The POA graph improves the alignment in B by reducing the number of gaps but does not align all copies of the domains. (D) A representation of the domain structure as a graph with cycles. (E) We obtain a representation of the multiple alignment of the four sequences by “gluing” together similar regions in the sequences. However, the sequences do not align over their entire length, and the shuffled domains create cycles in the resulting graph. (F) A simplified representation of the ABA graph shows the domains as edges of high multiplicity, and the unaligned regions as edges of multiplicity one.

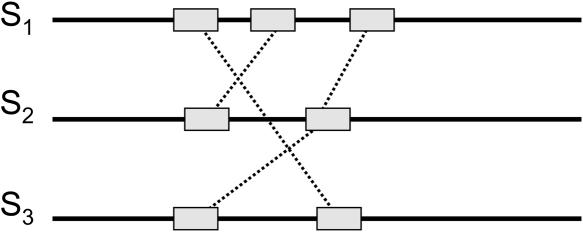
We emphasize that the real multiple alignment problem is more difficult that the schematic representation in Figure 2. For example, when aligning multidomain protein sequences, the delineation of the sequences into domains is not known in advance and needs to be derived from raw protein sequences. Neuwald et al. (1997) recognized this problem and developed a program that can automatically identify local blocks of significant multiple alignment. However, their program restricts the blocks to be in the same order and converges onto a single strongest domain. Different domains may have different lengths in different proteins, and pairwise alignments between them are often inconsistent. Resolving these inconsistencies is a major challenge in multiple alignment. In proteins with preserved domain order, local similarities should not “cross” (Fig. 3). However, alignments of proteins with shuffled domains often contain many such crossing similarities. Because a row–column or POA does not permit crossing similarities, in building such an alignment one must decide which of the crossing similarities to represent in the alignment. Once we allow cycles in our alignment representation, crossing local similarities are permissible, and distinguishing the crossing similarities that indicate domains from “spurious” similarities becomes much more difficult. Therefore, the problem of dealing with crossing local similarities calls for development of a new MSA approach that adequately reflects the varieties of domain architectures in different proteins.

Figure 3.

Figure 3.

Open in a new tab

With a row–column or partial order representation, any local similarities that “cross” are inconsistent. In our representation, these local similarities are permissible and lead to cycles in the alignment.

In this article, we describe a new representation for a multiple alignment as a weighted directed graph (possibly containing cycles) called the A-Bruijn graph. The A-Bruijn graph was recently introduced and applied to fragment assembly and de novo repeat identification (Pevzner et al. 2004). Our work is the first application of the A-Bruijn graph to MSA. The A-Bruijn graph is an extension of the classical de Bruijn graph that has been successfully applied to many bioinformatics problems (Pevzner 1989; Pevzner et al. 2001; Heber et al. 2002; Pe'er et al. 2002; Shamir and Tsur 2002; Böcker 2003; Li and Waterman 2003). Zhang and Waterman (2003) pioneered the use of the de Bruijn graph approach for global multiple alignment of DNA sequences. However, the question of how to generalize their approach for highly diverged DNA or protein sequences remained open. In this article, we show how the notion of A-Bruijn graph addresses this problem. We describe A-Bruijn Aligner (ABA), a program to produce an alignment representation from the A-Bruijn graph. We apply ABA to multidomain protein sequences and genomic sequences with repeated and shuffled elements. The alignment representation produced by ABA is similar to the threaded blocksets recently introduced by Blanchette et al. (2004) to represent the complex multiple alignments of large genomic sequences. We demonstrate that ABA provides a solution to the open problem posed by Blanchette et al. (2004) of how to automatically generate threaded blocksets. The ABA software is available at http://nbcr.sdsc.edu/euler/.

Results

The MSA problem involves two tasks: finding a graph that represents the domain structure and finding a mapping of each sequence to this graph. Our approach constructs this graph based on a predetermined set of local similarities (e.g., pairwise alignments) between the input sequences. Intuitively, the A-Bruijn graph is obtained for a collection of pairwise alignments by “gluing” the aligned positions.

Although Figure 2F is illustrative of the alignment representation that we wish to obtain, it is not immediately clear how to obtain such a representation. The major challenge is the determination of the regions of similarity that should be “glued together” in the graph to represent the protein domains (boxes in Fig. 2). One cannot use a stringent criterion for similarity, such as exact 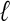Inline graphic-tuple matches, because relatively few, if any, exact matches are present in distantly related sequences. Therefore, the traditional de Bruijn graph approach that is based on perfect 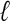Inline graphic-tuple matches does not work for this application. With a less stringent criteria (e.g., local alignments), local similarities will frequently be inconsistent, and one must decide which local similarities to respect in the multiple alignment, a nontrivial task. Morgenstern et al. (1996) give a mathematical condition for the consistency of a set of local similarities among sequences. A number of heuristics have been proposed for selecting sets of consistent local similarities and building alignments from these sets (Vingron and Argos 1991; Sammeth et al. 2003). The problem is compounded by our desire to permit directed cycles that result from crossing alignments that indicate domain structures. In the ABA approach, we distinguish crossing alignments from local inconsistencies by using graph heuristics that remove the short cycles resulting from local inconsistencies, whereas retaining longer cycles that result from multidomain organization.

The A-Bruijn and ABA graphs

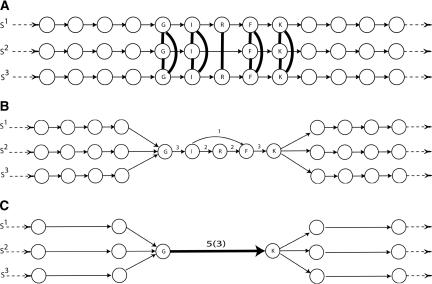
ABA represents an alignment of t sequences, S1, S2,..., St, as a directed graph (possibly containing cycles) with t source and t sink vertices. Each sequence Si corresponds to a directed path in the graph from the ith source to the ith sink. Aligned regions from different sequences or repeated regions in a single sequence correspond to high multiplicity edges in the ABA graph. This latter feature—aligning regions in the same sequence—is not found in existing approaches to multiple alignment and is similar to the use of the A-Bruijn graph in repeat analysis (Pevzner et al. 2004). Thus, our representation reveals repeated and shuffled regions in the input sequences, features that are not apparent in a row–column or POA. The input to ABA is a set of t sequences and their pairwise alignments. We first construct the A-Bruijn graph of the alignments by “gluing” together the aligned positions in the sequences S1, S2,..., St in the following way. We model each sequence S = s1... sn as directed path on n vertices. Each pairwise local alignment between sequence Si and Sj can be viewed as a set of instructions for gluing together the paths corresponding to Si and Sj: glue together every pair of matched positions in the alignment (Fig. 4A). Application of this gluing process to all pairwise alignments between the input sequences results in a rather complex A-Bruijn graph, often containing many short cycles that result from “weak” and inconsistent alignments (Fig. 4B).

Figure 4.

Figure 4.

Open in a new tab

(A) Three linear paths represent three sequences: S1, S2, and S3. Vertices represent positions in each sequence and are labeled by the amino acid at that position. Vertices corresponding to aligned positions in the set of pairwise alignments are joined by dark edges. These edges give a set of “gluing” instructions, and we obtain the A-Bruijn graph by collapsing each set of glued vertices into a single vertex. (B) The resulting A-Bruijn graph contains a short (undirected) cycle on vertices I, R, and F. Edge labels indicate the multiplicity of the edge. (C) We remove short cycles and collapse each simple chain into a single edge, obtaining a simplified A-Bruijn graph. Each multiple edge has a label of the form l(m), where l is the length of the sequences represented by that edge and m is the multiplicity of the edge.

These short cycles occlude the recognition of domains in protein alignments or conserved segments in genomic alignments. Thus, we want to “clean” the A-Bruijn graph by removing these short cycles while retaining the large cycles that indicate multidomain organization. To accomplish this task, we simplify the A-Bruijn graph by solving the maximum subgraph with large girth (MSLG) problem as described in Pevzner et al. (2004). An optimal solution to the MSLG problem gives a maximum weight subgraph that does not contain any cycles of length less than a fixed parameter, the girth. After removing short cycles, we collapse each simple chain in the graph into a single edge, and record the number of vertices on the simple chain as the length of the edge (Fig. 4C).

Case study: Proteins with SH2, SH3, and Pkinase domains

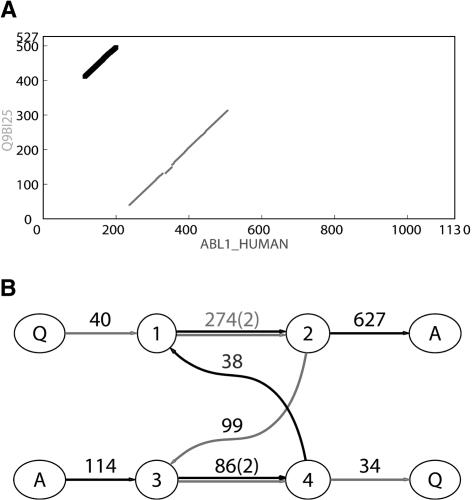
The ABA graph can represent alignments of proteins with shuffled domains. As an illustration, we first examine the pairwise alignment of two proteins: SHK1 protein in Dictyostelium (SWISS-PROT ID no. Q9BI25) and the ABL1 protein in human (SWISS-PROT ID no. ABL1_HUMAN). Both proteins function as kinases in signal transduction pathways and contain a protein kinase domain and SH2 domain, but in different order (Fig. 5A).

Figure 5.

Figure 5.

Open in a new tab

(A) Dot matrix representation of similarities between Q9BI25 and ABL1_HUMAN protein sequences as revealed by BLAST (Altschul et al. 1997). The two diagonals of length 274 and 86 represent two domains: Pkinase (gray) and SH2 (black). (B) The corresponding ABA graph. Each multiple edge has a label of the form l(m), where l is the length of the sequences represented by that edge, and m is the multiplicity of the edge. Each single edge is labeled simply as l (length) for brevity. Source/sink vertices are labeled A and Q for protein sequences ABL1 HUMAN and Q9BI25, respectively. Other vertices are numbered. The gray path through the graph corresponds to Q9BI25 and the black path through the graph corresponds to ABL1 HUMAN. The Pkinase domain corresponds to the edge (1 → 2) of length 274, and the SH2 domain corresponds the edge (3 → 4) of length 86.

The ABA graph reveals the shared domains as edges of multiplicity two (Fig. 5B). Furthermore, the ABA graph reflects the shuffled domain structure as a cycle consisting of two edges of multiplicity two—corresponding to the shared domains— and two edges of multiplicity one—corresponding to the unique interdomain regions in each sequence. This cyclic structure cannot be represented as a row–column alignment or as a POA graph.

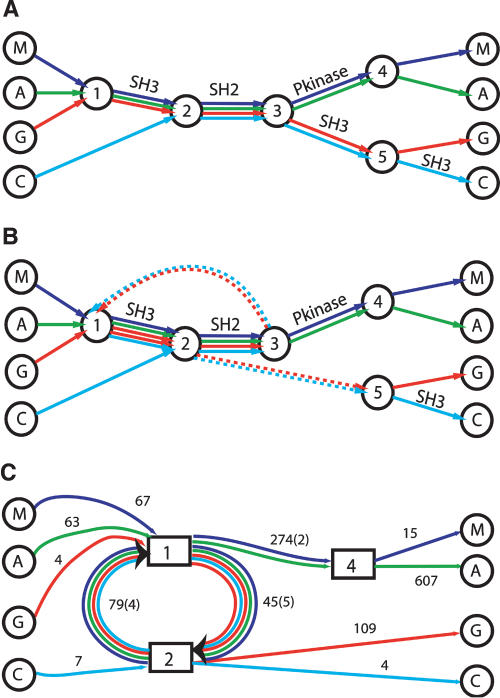
As a second example, we present an alignment of four human proteins: MATK, ABL1, GRB2, and CRKL. Lee et al. (2002) use this example to illustrate the ability of the POA graph to reveal domain structures and to demonstrate the advantage of the partial order representation over a row–column representation. In their representation (Fig. 6A), the alignment of the SH2 domains present in all four sequences is shown as an edge in the center of the graph. However, POA does not align the five SH3 domains present in these sequences. In fact, the acyclic property of the POA graph prohibits an alignment with the five SH3 domains aligned and the four SH2 domains aligned. The alignment of the four SH2 domains by POA forces the five SH3 domains into two alignments: one preceding the aligned SH2 domains, and one succeeding the aligned SH2 domains. This rigidity is not present in the ABA graph (Fig. 6B,C). The SH3 domains on both sides of the SH2 domains align in a single unit. As a result, the edges corresponding to the SH2 domain and SH3 domain form a cycle in the ABA graph.

Figure 6.

Figure 6.

Open in a new tab

Comparison of POA and ABA representations of the domain structure of four human SH2 domain containing proteins: MATK (M), ABL1 (A), GRB2 (G), and CRKL (C). (A) A simplified representation of the POA graph, as obtained in Lee et al. (2002). Each input sequence forms a path through the graph. Edges with a high multiplicity are labeled with protein domains. (B) A simplified representation of the ABA graph. Dotted edges have length zero and connect nodes that are glued together in the ABA graph. (C) The ABA graph with collapsed multiple edges. Boxed vertices represent small subgraphs that have been contracted (cf. Methods). In this graph, high multiplicity edges correspond to protein domains SH2, SH3, and Pkinase domains with estimated lengths of 79, 45, and 274 nucleotides, respectively.

To obtain the ABA graph, we identify pairwise local alignments between the four protein sequences by using the BLAST program with BLOSUM80 matrix. Hits with minimal length of 40 and at least 40% conserved (as defined by BLAST) are input to the ABA algorithm. The resulting ABA graph (Fig. 6C) clearly shows the domain structures as edges with high multiplicity. In the ABA graph, the edge (2 → 1) of multiplicity four corresponds to the SH2 domain shared by all four sequences. The edge (1 → 2) of multiplicity five corresponds to the five SH3 domains in four sequences. Notably, the two SH3 domains in GRB2 are glued together on this edge. As a result, the path through the graph corresponding to the GRB2 sequence contains a cycle signifying duplication of the SH3 domain. Also note that there is a second SH3 domain at the C-terminal end of CRKL that is not glued by ABA to the other SH3 domains. The reason for the isolation of this SH3 domain is that it is sufficiently diverged from the other SH3 domains so that there are no significant pairwise local alignments (satisfying our criteria above) between this SH3 domain and the other sequences detected by BLAST.

Case study: Proteins with GAF, Response_reg, GGDEF, and EAL domains

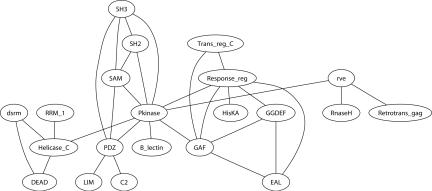
Because ABA has the ability to align proteins with shuffled domains, we wanted to explore the prevalence of domain shuffling in proteins from SWISS-PROT (Boeckmann et al. 2003), based on the SwissPfam domains annotation (Bateman et al. 2004). The domain shuffling network (Fig. 7) summarizes our findings. Vertices in the domain shuffling network are Pfam domains, and a pair of vertices are joined by an edge if they appear in different orders in some proteins in the SWISS-PROT database; that is, they are shuffled. The domain shuffling graph is similar to the domain network (Wuchty 2001) or the domain graph (Ye and Godzik 2004), in which domains (vertices) are linked if they appear in the same protein. Clearly, the domain shuffling network is a subgraph of the domain graph.

Figure 7.

Figure 7.

Open in a new tab

The largest connected component of the Domain Shuffling Network of Pfam domains. Only long, conserved, and common domains are shown. Pfam domains that appear in different orders in proteins from SWISS-PROT are connected by an edge. We omit loops in the network that indicate repeated domains.

To construct the domain shuffling network, we select a subset of Pfam domains (7316 domains, as at February 2004) according to the following criteria: (1) is >50 amino acids (aa); (2) is > 21% conserved; and (3) contained in at least 500 proteins. A total of 119 domains satisfy these criteria, and 47 of these appear in different orders in the Pfam annotation of some SWISS-PROT proteins. There are a total of 56 edges representing shuffles between these 47 domains. The network has 10 connected components. The largest connected component of the domain shuffling network (Fig. 7) prominently displays the protein kinase domain (Pkinase) as the highest degree vertex. This reflects the fact that domain shuffling is a common feature in the kinase family. However, the domain shuffling network reveals that shuffling of domains is not restricted to kinases. We now describe an example of domain shuffling and duplication outside the protein kinase family.

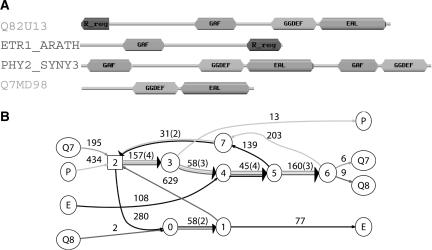
We analyzed the four proteins Q82U13, ETR1_ARATH, PHY2_SYNY3, and Q7MD98 from SWISS-PROT, each containing some but not all of the Pfam domains GAF, Response_reg, GGDEF and EAL (Fig. 8). The BLAST program with the BLOSUM80 matrix gives eight significant pairwise local alignments between these sequences that satisfy the constraints that alignment length is >40 aa and is >40% conserved. We inputed these alignments into the ABA program, and obtained the graph shown in Figure 8.

Figure 8.

Figure 8.

Open in a new tab

Four proteins with shuffled domains and their ABA graph. (A) The domain structures are derived from the SwissPfam database (Bateman et al. 2004). We show only well-annotated PfamA domains. Domains that appear in only one of the four sequences are not shown. (B) Cycles in the ABA graph reveal the extensive domain shuffling in these sequences.

Edges of high multiplicity (or a chain of high multiplicity edges) in the ABA graph corresponds to domains shared by the sequences. Table 1 shows four edges (chain of edges), each representing a significant local multiple alignment. We emphasize that the correspondence between these edges and known protein domains is approximate, because the edges result directly from significant alignments from BLAST. We can extract the subsequences corresponding to high multiplicity edges, and refine the multiple alignment using an existing tool like CLUSTALW. We remark that ABA eliminates a time-consuming, manual clipping procedure.

Table 1.

Four high multiplicity edges in the ABA graph

Domain occurrenceb
No. Edge Length Conservationa Domain(s) Q7 P E Q8
1 2 → 3 → 4 → 5 → 6 420 53% GGDEF-EAL 1 1 1
2 0 → 1 58 51% Response_reg 1 1
3 7 → 2 49c 60% GAF 1 1
4 2 → 3 157 43% GGDEF 2
Open in a new tab
a

Average pairwise percent of conserved amino acids

b

Number of occurrences of domain or domain combinations in the proteins

c

The alignment corresponding to this domain extends into block 2 in the graph (data not shown), and thus the alignment is longer than the length of the edge 7 → 2 in Figure 8B

Domain shuffling creates directed cycles in the ABA graph. In this example there are two domain shuffles: Response_reg versus GAF, and EAL versus GAF/GGDEF represented by two directed cycles (2 → 0 → 1 → 2 and 2 → 3 → 4 → 5 → 7 → 2) in Figure 8. The different domain orders in individual sequences are reflected by the different paths traversing the ABA graph that visit edges in different orders.

When we align these four sequences by using POA (Lee et al. 2002), we observe that the DAG representation used by POA cannot adequately represent the shuffled domain structure (Supplemental Fig. S1a,b). Among the four significant local alignments listed in Table 1, POA correctly identifies the first one: an alignment between the GGDEF-EAL domains in the three sequences. However, depending on the order that the sequences were input into the iterative alignment procedure, POA detects either alignment 2 or 3 in Table 1, but not both. Alignment 4 (self-alignment) is always missing. We emphasize that the ABA graph (Supplemental Fig. S1c), in contrast to the POA graph, is independent of the order in which the sequences are considered.

Case study: Proteins with condensation, AMP-binding, and PP-binding domains

We use ABA to align 16 protein sequences from SWISS-PROT containing the condensation domain. Supplemental Table S1 gives the SWISS-PROT ID for each of the 16 proteins. The condensation domain is 249 aa long and is found in multidomain enzymes that synthesize peptide antibiotics. Many of these proteins also contain an AMP-binding domain, a 330-aa-long domain that covalently binds AMP to their substrates in an ATP-dependent manner, and a PP-binding domain, a short domain (65 aa) that serves as a “swinging arm” for the attachment of activated fatty acid and amino-acid groups.

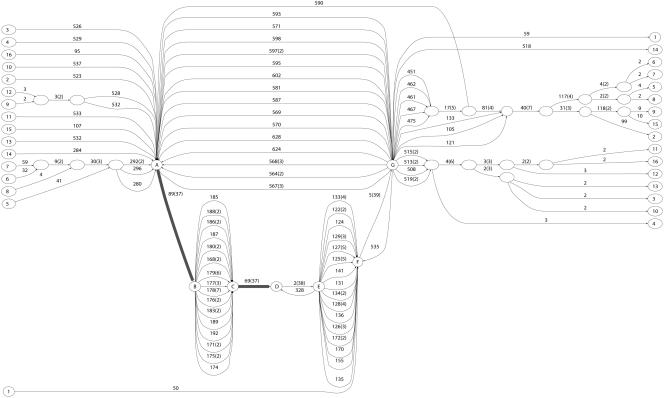
We obtain the ABA graph shown in Figure 9 by using the same BLAST parameters as the previous case studies. Most of the long edges in the graph correspond to the long domains: condensation and AMP-binding. These domains are typically not well conserved over their full length, and ABA reveals the well conserved parts as high multiplicity edges (e.g., A → B and C → D) and splits the less conserved parts into multiple edges, for example, B → C, E → F, and G → A.

Figure 9.

Figure 9.

Open in a new tab

ABA graph of 16 proteins, each containing a condensation domain. Edges A → B and C → D (highlighted) indicate well-conserved parts of the AMP-binding domain. A long directed cycle (A → B → C → D → E → F → G → A) indicates repetition of these well-conserved sequences.

Genomic sequences

ABA is also applicable to the alignment of genomic sequences, and the ABA graph directly reveals duplications and inversions that are often found in alignments of long mammalian genomic sequences. The input to ABA is a set of t DNA sequences (with the t reverse complements) and the pairwise local alignments between the 2t sequences. The resulting ABA graph is a collection of 2t paths—corresponding to the t input sequences and their t reverse complements—that are glued together according to the local alignments. A duplication in a single sequence corresponds to a directed cycle in the path corresponding to this sequence, whereas an inversion corresponds to a gluing of the direct strand of one sequence to the reverse strand of another sequence.

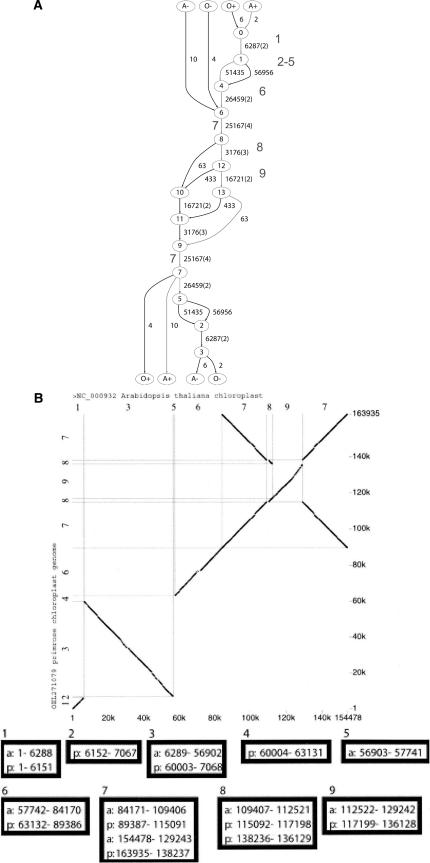
We apply ABA to a pair of plant chloroplast genomes, Arabidopsis thaliana and Oenothera elata, and produce the graph in Figure 10A. We compare our results to the alignment obtained by the Threaded Blockset Aligner (TBA) of Blanchette et al. (2004) (Fig. 10B). TBA represents a multiple alignment as a set of alignment blocks (a blockset) that is ordered according to one of the input sequences; namely, one “threads” one of the input sequences through the set of blocks. Blocksets in TBA are analogous to long edges in the ABA graph. We observe a striking correspondence between long edges in the ABA graph of the chloroplast genomes (Fig. 10A) and the blocks obtained by Blanchette et al. (2004) (Fig. 10B). A single block (block 3) is missing from the ABA graph, which probably could be rescued by a more sensitive parameter setting when computing the pairwise BLASTZ alignments that are input to ABA. Thus, in this example ABA automatically generates threaded blocks as long edges of high multiplicity in the ABA graph.

Figure 10.

Figure 10.

Open in a new tab

Alignment of genomes of chloroplasts Arabidopsis thaliana and Oenothera elata. (A) ABA graph. We use BLASTZ (Schwartz et al. 2003b) with parameter “B = 1C = 2” to generate pairwise local alignments. Gray path corresponds to the direct strand of Arabidopsis DNA. The number in bold font close to an edge corresponds to the block number in B, the blockset of Blanchette et al. (2004) (Reproduced from Figure 2A in Blanchette et al. [2004]). (B, top) A dot plot of the Arabidopsis genome (horizontal axis) and Oenothera genome (vertical axis). (middle, bottom) Nine “alignment blocks”; each block contains sequence segments labeled by the genome of origin (a) = Arabidopsis, (p) = Oenothera and the coordinates of the segment in the genome.

We note that the current implementation of TBA produces a limited type of threaded blockset, namely, TBA “does not accommodate inversions2 and duplications, and it is restricted to finding matches that occur in the same order and orientation in the given sequences”. ABA has no such restrictions. Indeed, in the ABA graph of the chloroplast genomes, block 7 appears twice along the path corresponding to the Arabidopsis genome, once in the direct strand and once in the reverse strand. (TBA now can handle reverse-strand matches and inversions [W. Miller, pers. comm.]).

To further our comparison of the blocks extracted from the long edges of the ABA graph with the blocks produced by TBA, we examined the human, mouse, and rat sequences from the NISC target region T1. The complete set of sequences from 12 species was first analyzed in Thomas et al. (2003). The ABA graph (Supplemental Fig. S3) contains 13536 edges (for both strands of the three genomic sequences), whereas TBA generates 4445 blocks. When projected on the direct strand of human genome, the ABA graph (Supplemental Fig. S2) has 3726 multiple edges (i.e., edges of multiplicity larger than one) and TBA has 1624 multiple blocks (i.e., blocks containing more than one sequence). We display the ABA and TBA blocks in the UCSC genome browser (Kent et al. 2002) as custom tracks (http://www.cse.ucsd.edu/groups/bioinformatics/browser-tba-aba-human.bed) for a visual comparison. A region surrounding the CAV2 gene along human genome is shown in Figure 11.

Figure 11.

Figure 11.

Open in a new tab

Comparison of blocks produced by TBA and ABA. A region on human genome surrounding the CAV2 gene is displayed on the “zoo genome” (NISC target region T1) of the UCSC genome browser (Kent et al. 2002). We use BLASTZ with parameters “B = 1 C = 2” to include reverse strand matches. Blocks of multiplicity greater than one are shown with shades of gray indicating the multiplicity of the blocks. Most of the blocks have multiplicity of three, corresponding to three-way alignments. Darker gray blocks indicate higher multiplicity and include duplications and inversions (matches on the reverse strands).

ABA and TBA use different algorithmic approaches to blockset generation (discussed below), yet most of the blocks produced by TBA and ABA have significant overlaps. However, we observe three differences. First, ABA generates blocks of multiplicity higher than three (dark gray blocks in Fig. 11), demonstrating the ability of ABA to handle duplications and inversions. Second, TBA detects a few blocks that are missed by ABA: These blocks represent short three-way alignments. ABA misses these short alignments because it uses only pairwise alignments, whereas TBA implements a progressive multiple alignment engine (MULTIZ). Third, ABA generally produces longer blocks (or concatenations of blocks).

The above results demonstrate that (1) ABA is able to automatically generate threaded blocksets for genomic sequence alignment, and (2) ABA handles duplications and matches of sequences that are in different orders in different genomes. A more detailed comparison of the two approaches and the possibility of synergistic combinations of both approaches are important questions for future study.

Discussion

The important feature of ABA is the ability to produce multiple alignments of sequences that include shuffled and repeated regions, a feature lacking in other alignment methods. We now compare ABA with other approaches to MSA, and describe further applications and extensions of ABA.

Alignment representation

ABA represents a multiple alignment as a directed graph, possibly containing cycles. This is in contrast to most existing alignment programs that use a linear row–column representation. Recently, Lee et al. (2002) introduced POA that uses a variation of network alignment (first presented in Sankoff and Kruskal [1983] and analyzed in Myers [1996]) to align a sequence to a DAG representation of an alignment. The method is order dependent, as each sequence is aligned to the graph in turn. In a later article, Grasso and Lee (2004) generalized the method to include alignment of two partial order graphs and thus implement a progressive alignment. However, their partial order graph is not able to represent shuffled or repeated domains.

Lee et al. (2002) commented that their partial order representation “expresses a more complex set of relationships than can easily be discovered by phylogenetic tree”, and accordingly introduced a new edit operator: domain recombination. In a similar fashion, ABA implements two other operations: domain rearrangement (change in order of two domains in a single sequence) and domain duplication (repetition of a domain in a single sequence). Both domain rearrangement and domain duplication are common in protein sequences. Domain rearrangement is similar to “string edit distance with moves” (Cormode et al. 2000) or block edit distance (Ergün et al. 2003) studied in string matching. However, to our knowledge, ABA is the first multiple alignment program that implements the domain rearrangement operation.

Zhang and Waterman (2003) were the first to propose a multiple alignment method based on the de Bruijn graph approach for DNA sequences. Following the Eulerian method for fragment assembly in DNA sequencing (Idury and Waterman 1995; Pevzner et al. 2001), their EulerAlign algorithm starts with the de Bruijn graph of k-mers contained in the set of sequences to be aligned. Their algorithm transforms the de Bruijn graph into a DAG and then aligns all sequences to a consensus represented by a high weight path through the DAG. Thus, their method aligns all sequences to a single consensus and removes all cycles present in the de Bruijn graph.

The Zhang and Waterman (2003) algorithm presents a powerful new technique for alignment of similar DNA sequences that eliminates the time-consuming task of performing pairwise alignments. Thus, their method is suitable for aligning a large number of DNA sequences. However, the question of how to generalize their method to align highly diverged DNA sequences (e.g., DNA sequences that are <70% to 80% similar) remains open. Furthermore, although the similarity between DNA sequences can often be captured by shared k-mers, protein sequences typically share very few k-mers and the similarity between protein sequences often requires nontrivial scoring matrices. Furthermore, shared k-mers are very sensitive to indels. Our A-Bruijn graph approach bypasses these limitations by abandoning the k-mer analysis.

Very recently, Blanchette et al. (2004) introduced the TBA for multiple alignment of megabase-sized regions of genomic sequences. The development of TBA and ABA share a common philosophy: overcoming the limitations of the row–column representation of a multiple alignment. The blocksets used by TBA are analogous to the high multiplicity edges in the ABA graph, and the threading procedure in TBA to create “ref-blocksets” is analogous to following the path in the ABA graph from source i to sink i. However, the current implementation of TBA—similar to POA—handles only alignments of blocks that occur in the same order and orientation in the sequences. They leave open the problem of “automatically, accurately, and reliably” identifying blocksets in genomic sequences that resulted from inversions, duplications, and other complex rearrangements. We demonstrate that ABA solves this problem for protein and genomic sequences, and it is possible to use ABA to automatically generate blocksets for TBA.

The algorithmic approach of TBA is very different from ABA. TBA progressively aligns input sequences along a phylogenetic tree from leaves to the root. The blocks in the blockset at a parent node result from intersections or exclusive-ORs of the blocks at its children. The blocks are only split into smaller blocks during the progressive steps of TBA. There is no mechanism to merge blocks—TBA follows the maxim “Once a block boundary, always a block boundary.” In contrast, ABA permits the merging and simplification of very small blocks.

Every blockset represented by TBA is a somewhat simplified linear view of a multiple alignment. In reality, some alignments within a blockset may extend over several blocks, whereas other alignments may be significantly shorter. In a sense, the individual blocks in a blockset have the same limitations as the row–column alignment, in comparison to a DAG alignment that was discussed in the introduction. ABA has a more flexible approach to defining the block boundaries that are expressed as “tangles” in the ABA graph.

Applications and extensions

ABA integrates well with existing multiple alignment tools and can serve as a preprocessor for these multiple alignment programs. For example, given a set of sequences with complex domain structure, we can first run ABA to uncover this structure and then apply an existing multiple alignment program such as CLUSTALW to refine the alignments given by high multiplicity edges in the ABA graph. In this scenario, ABA automates the time-consuming clipping of sequences frequently recommended for multiple alignment tools and performs this clipping in a rigorous way.

The ability of the ABA graph to succinctly represent proteins with shuffled and repeated domains makes it useful for de novo domain finding and studies of domain structure. Galperin and Koonin (1998) highlighted how the multidomain organization of proteins can trigger mistakes in functional annotation, and thus ABA graphs may be useful in this context. Because some protein domains cannot be determined solely from pairwise similarity, alternative similarity measures will be necessary for these applications. ABA can use different measures of similarity in the construction of the A-Bruijn graph. In this article, we focus on similarities given by pairwise sequence alignments, but we can also use k-way similarities, or similarity measures given by profiles (e.g., PSI-BLAST), structural comparisons, Hidden Markov Models, etc. In particular, we can use reverse position–specific BLAST (rpsBLAST) with profiles found in domain libraries such as the Conserved Domain Database (Marchler-Bauer et al. 2003). Use of rpsBLAST will reveal alignments corresponding to known domains. Other high multiplicity edges in the ABA graph might suggest novel domains.

Further refinements in the ABA algorithm will be required to extend its application. One possible improvement to ABA is the implementation of an iterative refinement procedure: After we construct the initial ABA graph using pairwise similarities, we identify the important edges and refine the alignment at each important edge using more accurate alignment procedures. Finally, we rethread individual sequences through the important edges; if the topology of the graph changes, the procedure is repeated.

Methods

We describe the construction of the A-Bruijn and ABA graphs that we use to represent a multiple alignment. Our presentation follows that in Pevzner et al. (2004). Let S1, ..., St denote the sequences to be aligned. The goal is to obtain a directed multigraph with multiple edges corresponding to the aligned regions in the sequences. We begin with a similarity matrix (dot matrix) that describes a set of similarities between the sequences S1, ...,St. For simplicity, we assume that we use pairwise similarities, but our model is more general and may include any l-way similarity with l ≤ t.

Let 𝒜 denote the set of significant pairwise local alignments between the sequences. For convenience, we concatenate S1,..., St into a single sequence S = s1s2... sN of total length N. We represent these alignments 𝒜 in a similarity matrix A. We set entry aij of A equal to one if positions si and sj are aligned in at least one alignment in 𝒜; otherwise we set aij equal to zero. We think of the similarity matrix A as the adjacency matrix (incidence matrix) of a graph, called the A-graph. The vertices of the A-graph are the positions s1, s2,..., sN of S, and (si,sj) is an edge if and only if aij = 1.

The main obstacle to combining these local similarities into an alignment is finding consistent sets of similarities. We now form a multigraph G = (V,E) with vertices that are the connected components of the A-graph. Accordingly, let V denote the connected components of the A graph, and for si in S, let vi denote the connected component containing si. The set E of edges of G are (vi → vi + 1) for i = 1,..., |S| – 1 provided si and si + 1 belong to a single sequence Sk; that is, we do not have edges that cross the sequence boundaries in the concatenate S. The resulting graph G is a directed multigraph, containing at most t sources and t sinks.3 The directed path in the graph from source i to sink i correspond to the sequence Si for 1 ≤ i ≤ t.2

In the case of inconsistent and “weak” alignments the resulting A-Bruijn graph is often very complex and contains many short cycles. We distinguish directed short cycles, whirls, and undirected cycles, bulges. Whirls result from inconsistencies in pairwise alignments. Often these inconsistencies can be removed by moving gaps or removing matches in the alignment. Bulges result from gaps in pairwise alignments. Bulges and whirls can form complex structures of overlapping bulges/whirls, complicating their removal. We solve the MSLG problem, using the method described in Pevzner et al. (2004), to remove bulges and whirls from the graph, setting the parameter girth equal to 50.

After removing bulges and whirls, the resulting graph may still contain many short edges, due to ambiguities at the ends of aligned regions. These edges add unnecessary complexity to the A-Bruijn graph. To reveal aligned regions, we are interested in important edges: edges of high multiplicity and edges with length greater than some threshold. Therefore, we apply a two-step rethreading procedure: (1) remove the unimportant edges, and (2) thread each sequence Si through the remaining important edges.

Finally, for visual display purposes, we apply a short edge removal heuristic that simply collapses any connected component of short edges in the graph into a single super-vertex, represented by boxes in the figures. We use the Graphviz package (Gansner and North 1999) to draw the resulting ABA graph. As an illustration, the construction of the ABA graph in Figure 8 is shown in Supplemental Figure S4.

For short sequences (e.g., protein sequences) the running time of ABA is negligible compared to the time taken in computing all local pairwise alignments that form the input to ABA. For longer sequences (e.g., megabase-sized genomic sequence), the major constraint is memory. The human–mouse–rat sequences considered above required 2 h of processing time and three gigabytes of memory on an Alpha ES40 workstation. Improvements in memory usage will be necessary for scaling ABA to larger genomic regions. We are currently implementing a version of ABA with reduced memory requirements.

Acknowledgments

We are greatly indebted to Nick Grishin, Eugene Koonin, Webb Miller, and Yuri Wolf for critical readings of the manuscript. We also thank Neil Jones and Michele Day for helpful discussions. This work is supported by NHGRI grant 1 R01 HG02366. B.R. is supported by a fellowship from the Alfred P. Sloan Foundation.

Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.2657504.

Footnotes

[Supplemental material is available online at www.genome.org.]

2

To avoid the situation when two sources or two sinks are glued into a single vertex (i.e., when the ends of two different sequences are aligned in one alignment in 𝒜), we add virtual vertices at the ends of a sequence with zero length edges.

References

  1. Altschul, S.F., Madden, T.L., Schaffer, A.A., Zhang, J., Zhang, Z., Miller, W., and Lipman, D.J. 1997. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 25: 3389-3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bateman, A., Coin, L., Durbin, R., Finn, R.D., Hollich, V., Griffiths-Jones, S., Khanna, A., Marshall, M., Moxon, S., Sonnhammer, E.L., et al. 2004. The Pfam protein families database. Nucleic Acids Res. 32: D138-D141. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Blanchette, M., Kent, J.W., Riemer, C., Elnitski, L., Smit, A.F., Roskin, K.M., Baertsch, R., Rosenbloom, K., Clawson, H., Green, E.D., et al. 2004. Aligning multiple genomic sequences with the threaded blockset aligner. Genome Res. 14: 708-715. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Böcker, S. 2003. Sequencing from compomers: Using mass spectrometry for DNA de-novo sequencing of 200+ nt. In: Third workshop on algorithms in bioinformatics, Vol. 2812 of Lecture Notes in Computer Science, pp. 476-497. Springer, New York.
  5. Boeckmann, B., Bairoch, A., Apweiler, R., Blatter, M., Estreicher, A., Gasteiger, E., Martin, M., Michoud, K., O'Donovan, C., Phan, I., et al. 2003. The SWISS-PROT protein knowledgebase and its supplement TrEMBL in 2003. Nucleic Acids. Res. 31: 365-370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cormode, G., Paterson, M., Sahinalp, S., and Vishkin, U. 2000. Communication complexity of document exchange. In: Proceedings of the 11th annual ACM-SIAM symposium on discrete algorithms, pp. 197-206. Society for Industrial and Applied Mathematics, Philadelphia.
  7. Darling, A.C., Mau, B., Blattner, F.R., and Perna, N.T. 2004. Mauve: Multiple alignment of conserved genomic sequence with rearrangements. Genome Res. 14: 1394-1403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Doolittle, R.F. 1995. The multiplicity of domains in proteins. Annu. Rev. Biochem. 64: 287-314. [DOI] [PubMed] [Google Scholar]
  9. Eddy, S.R. 1998. Multiple-alignment and sequence searches. Trends Guide to Bioinformatics, pp. 15-18. Elsevier Science, Amsterdam.
  10. Ergün, F., Muthukrishnan, S., and Sahinalp, S.C. 2003. Comparing sequences with segment rearrangements. FST TCS 2003: Foundations of software technology and theoretical computer science, Vol. 2914 of Lecture Notes in Computer Science, pp. 183-194. Springer, New York.
  11. Feng, D.F. and Doolittle, R.F. 1987. Progressive sequence alignment as a prerequisite to correct phylogenetic trees. J. Mol. Evol. 25: 351-360. [DOI] [PubMed] [Google Scholar]
  12. Galperin, M.Y. and Koonin, E.V. 1998. Sources of systematic error in functional annotation of genomes: Domain rearrangement, non-orthologous gene displacement and operon disruption. In Silico Biol. 1: 55-67. [PubMed] [Google Scholar]
  13. Gansner, E.R. and North, S.C. 1999. An open graph visualization system and its applications to software engineering. Software-Practice and Experience. http://www.research.att.com/sw/tools/graphviz/.
  14. Grasso, C. and Lee, C. 2004. Combining partial order alignment and progressive multiple sequence alignment increases alignment speed and scalability to very large alignment problems. Bioinformatics 20: 1546-1556. [DOI] [PubMed] [Google Scholar]
  15. Heber, S., Alekseyev, M., Sze, S.H., Tang, H., and Pevzner, P.A. 2002. Splicing graphs and EST assembly problem. Bioinformatics 18(Suppl 1): S181-S188. [DOI] [PubMed] [Google Scholar]
  16. Higgins, D.G. and Sharp, P.M. 1988. CLUSTAL: A package for performing multiple sequence alignment on a microcomputer. Gene 73: 237-244. [DOI] [PubMed] [Google Scholar]
  17. Idury, R.M. and Waterman, M.S. 1995. A new algorithm for DNA sequence assembly. J. Comput. Biol. 2: 291-306. [DOI] [PubMed] [Google Scholar]
  18. Kececioglu, J. 1993. The maximum weight trace problem in multiple sequence alignment. Combinatorial pattern matching (Padova, 1993), Vol. 684 of Lecture Notes in Computer Science, pp. 106-119. Springer, New York.
  19. Kent, J., Sugnet, C., Furey, T., Roskin, K., Pringle, T., Zahler, A.M., and Haussler, D. 2002. The Human Genome Browser at UCSC. Genome Res. 12: 996-1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lee, C., Grasso, C., and Sharlow, M.F. 2002. Multiple sequence alignment using partial order graphs. Bioinformatics 18: 452-464. [DOI] [PubMed] [Google Scholar]
  21. Li, X. and Waterman, M.S. 2003. Estimating the repeat structure and length of DNA sequences using 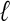Inline graphic-tuples. Genome Res. 13: 1916-1922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lipman, D.J., Altschul, S.F., and Kececioglu, J.D. 1989. A tool for multiple sequence alignment. Proc. Natl. Acad. Sci. 86: 4412-4415. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Marchler-Bauer, A., Anderson, J.B., DeWeese-Scott, C., Fedorova, N.D., Geer, L.Y., He, S., Hurwitz, D.I., Jackson, J.D., Jacobs, A.R., Lanczycki, C.J., et al. 2003. CDD: A curated Entrez database of conserved domain alignments. Nucleic Acids Res. 31: 383-387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Morgenstern, B., Dress, A., and Werner, T. 1996. Multiple DNA and protein sequence alignment based on segment-to-segment comparison. Proc. Natl. Acad. Sci. 93: 12098-12103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Morgenstern, B., Frech, K., Dress, A., and Werner, T. 1998. DIALIGN: Finding local similarities by multiple sequence alignment. Bioinformatics 14: 290-294. [DOI] [PubMed] [Google Scholar]
  26. Myers, E.W. 1996. Approximate matching of network expressions with spacers. J. Comput. Biol. 3: 33-51. [DOI] [PubMed] [Google Scholar]
  27. Neuwald, A.F., Liu, J.S., Lipman, D.J., and Lawrence, C.E. 1997. Extracting protein alignment models from the sequence database. Nucl. Acids Res. 25: 1665-1677. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Notredame, C. 2002. Recent progress in multiple sequence alignment: A survey. Pharmacogenomics 3: 131-144. [DOI] [PubMed] [Google Scholar]
  29. Notredame, C., Higgins, D.G., and Heringa, J. 2000. T-Coffee: A novel method for fast and accurate multiple sequence alignment. J. Mol. Biol. 302: 205-217. [DOI] [PubMed] [Google Scholar]
  30. Pe'er, I., Arbili, N., and Shamir, R. 2002. A computational method for resequencing long DNA targets by universal oligonucleotide arrays. Proc. Natl. Acad. Sci. 99: 15492-15496. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Pei, J., Sadreyev, R., and Grishin, N. 2003. PCMA: Fast and accurate multiple sequence alignment based on profile consistency. Bioinformatics 19: 427-428. [DOI] [PubMed] [Google Scholar]
  32. Pevzner, P.A. 1989. 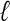Inline graphic-tuple DNA sequencing: Computer analysis. J. Biomol. Struct. Dyn. 7: 63-73. [DOI] [PubMed] [Google Scholar]
  33. Pevzner, P.A., Tang, H., and Waterman, M.S. 2001. An Eulerian path approach to DNA fragment assembly. Proc. Natl. Acad. Sci. 98: 9748-9753. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Pevzner, P.A., Tang, H., and Tesler, G. 2004. De novo repeat classification and fragment assembly. In: Proceedings of the fifth ACM conference on computational molecular biology (RECOMB), pp. 213-222. ACM Press, New York.
  35. Sammeth, M., Morgenstern, B., and Stoye, J. 2003. Divide-and-conquer multiple alignment with segment-based constraints. Bioinformatics 19(Suppl 2): II189-II195. [DOI] [PubMed] [Google Scholar]
  36. Sankoff, D. 1975. Minimal mutation trees of sequences. SIAM J. Appl. Math. 28: 35-42. [Google Scholar]
  37. Sankoff, D. and Kruskal, J.B., eds. 1983. Time warps, string edits, and macromolecules: The theory and practice of sequence comparison. Addison-Wesley, Boston.
  38. Schuler, G., Altschul, S., and Lipman, D. 1991. A workbench for multiple alignment construction and analysis. Proteins 9: 180-190. [DOI] [PubMed] [Google Scholar]
  39. Schwartz, S., Elnitski, L., Li, M., Weirauch, M., Riemer, C., Smit, A., Green, E.D., Hardison, R.C., and Miller, W. 2003a. MultiPipMaker and supporting tools: Alignments and analysis of multiple genomic DNA sequences. Nucleic Acids Res. 31: 3518-3524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Schwartz, S., Kent, W.J., Smit, A., Zhang, Z., Baertsch, R., Hardison, R.C., Haussler, D., and Miller, W. 2003b. Human–mouse alignments with BLASTZ. Genome Res. 13: 103-107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Shamir, R. and Tsur, D. 2002. Large scale sequencing by hybridization. J. Comput. Biol. 9: 413-428. [DOI] [PubMed] [Google Scholar]
  42. Thomas, J.W., Touchman, J.W., Blakesley, R.W., Bouffard, G.G., Beckstrom-Sternberg, S.M., Margulies, E.H., Blanchette, M., Siepel, A.C., Thomas, P.J., McDowell, J.C., et al. 2003. Comparative analyses of multi-species sequences from targeted genomic regions. Nature 424: 788-793. [DOI] [PubMed] [Google Scholar]
  43. Thompson, J.D., Higgins, D.G., and Gibson, T.J. 1994. CLUSTAL W: Improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 22: 4673-4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Vingron, M. and Argos, P. 1991. Motif recognition and alignment for many sequences by comparison of dot-matrices. J. Mol. Biol. 218: 33-43. [DOI] [PubMed] [Google Scholar]
  45. Wang, L. and Jiang, T. 1994. On the complexity of multiple sequence alignment. J. Comput. Biol. 1: 337-348. [DOI] [PubMed] [Google Scholar]
  46. Waterman, M.S., Smith, T.F., and Beyer, W.A. 1976. Some biological sequence metrics. Adv. Math. 20: 367-387. [Google Scholar]
  47. Wuchty, S. 2001. Scale-free behavior in protein domain networks. Mol. Biol. Evol. 18: 1694-1702. [DOI] [PubMed] [Google Scholar]
  48. Ye, Y. and Godzik, A. 2004. Comparative analysis of protein domain organization. Genome Res. 14: 343-353. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Zhang, Y. and Waterman, M.S. 2003. An Eulerian path approach to global multiple alignment for DNA sequences. J. Comput. Biol. 10: 803-819. [DOI] [PubMed] [Google Scholar]

WEB SITE REFERENCES

  1. http://nbcr.sdsc.edu/euler/; EULER Project Homepage.
  2. http://www.cse.ucsd.edu/groups/bioinformatics/browser-tba-aba-human.bed; ABA and TBA blocks for human–mouse–rat sequences.

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES