Arterial input functions in dynamic contrast-enhanced magnetic resonance imaging: which model performs best when assessing breast cancer response?

Abstract

Objective:

To evaluate the performance of six models of population arterial input function (AIF) in the setting of primary breast cancer and neoadjuvant chemotherapy (NAC). The ability to fit patient dynamic contrast-enhanced MRI (DCE-MRI) data, provide physiological plausible data and detect pathological response was assessed.

Methods:

Quantitative DCE-MRI parameters were calculated for 27 patients at baseline and after 2 cycles of NAC for 6 AIFs. Pathological complete response detection was compared with change in these parameters from a reproduction cohort of 12 patients using the Bland–Altman approach and receiver-operating characteristic analysis.

Results:

There were fewer fit failures pre-NAC for all models, with the modified Fritz-Hansen having the fewest pre-NAC (3.6%) and post-NAC (18.8%), contrasting with the femoral artery AIF (19.4% and 43.3%, respectively). Median transfer constant values were greatest for the Weinmann function and also showed greatest reductions with treatment (−68%). Reproducibility (r) was the lowest for the Weinmann function (r = −49.7%), with other AIFs ranging from r = −27.8 to −39.2%.

Conclusion:

Using the best performing AIF is essential to maximize the utility of quantitative DCE-MRI parameters in predicting response to NAC treatment. Applying our criteria, the modified Fritz-Hansen and cosine bolus approximated Parker AIF models performed best. The Fritz-Hansen and biexponential approximated Parker AIFs performed less well, and the Weinmann and femoral artery AIFs are not recommended.

Advances in knowledge:

We demonstrate that using the most appropriate AIF can aid successful prediction of response to NAC in breast cancer.

INTRODUCTION

Neoadjuvant chemotherapy (NAC) for locally advanced breast cancer has a long-established role in the reduction of primary tumour size, facilitating conservative surgery and the treatment of micrometastatic disease. Clinical studies using dynamic contrast-enhanced MRI (DCE-MRI) have established that changes in kinetic parameters after 1–2 cycles of NAC can predict for clinical and pathological response¹ as well as disease-free and overall survival.² Quantitative kinetic parameters, and in particular changes in forward transfer constant (K^trans), provide the majority of the evidence for clinical utility in the setting of NAC for breast cancer.³

To calculate quantitative DCE-MRI kinetic parameters, the concentration of the contrast medium in the vasculature supplying the tumour, known as the arterial input function (AIF), needs to be defined.⁴ There are a number of methods available to define the AIF. Direct arterial sampling can be performed, but this is impractical and highly invasive. A second option is to measure the AIF for individual patients, often with a degree of automation, using MRI, as described by Parker et al.⁴ This is non-invasive but is time-consuming, is restricted to major vessels such as the aorta (which may be some distance from the tumour such as in breast cancer), can still have quantification errors and requires extra doses of the contrast agent. Another method uses normal reference tissue sampling (e.g. muscle) and knowledge of leakage space to infer the AIF (Kovar method⁵). The most commonly used and convenient method is to use assumed or population-based AIFs. These mathematical models allow readily available solutions to the definition of AIFs to be applied to kinetic modelling. Since the latter is not based on the individual patient in question, it introduces a systematic error to kinetic parameter outputs.

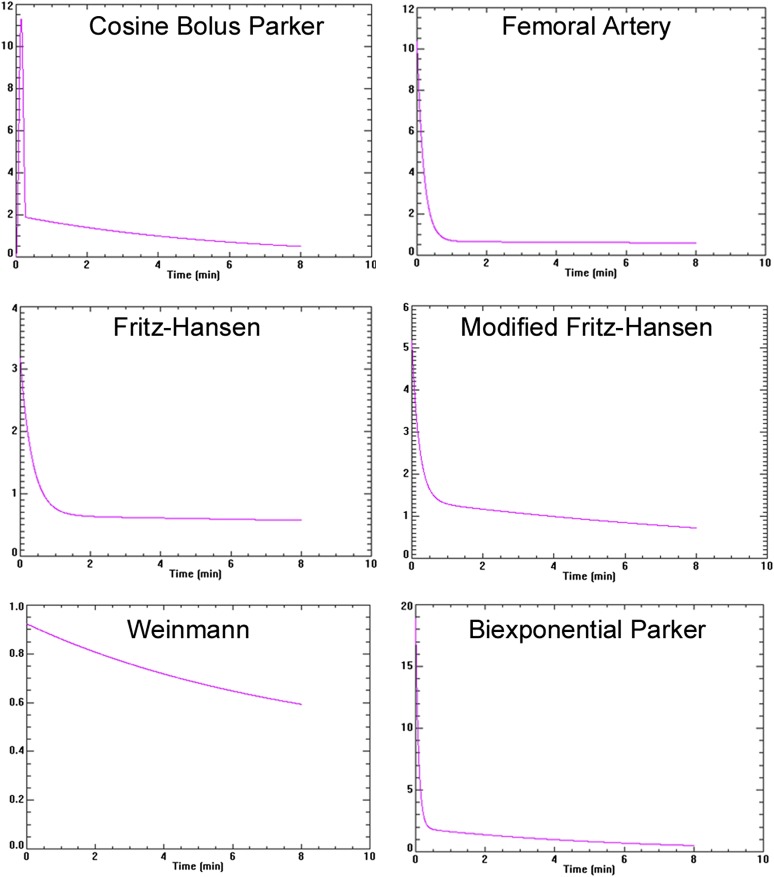
Assumed AIFs take different mathematical forms that account for the changes in plasma concentration over time. There are a number of assumed AIFs in current use. These include the data reported by Fritz-Hansen,⁶ a combination of the data of Weinmann and Fritz-Hansen known as the modified Fritz-Hansen,⁷ the biexponential approximated form of Parker⁴ (“biexponential Parker”), femoral artery,⁸ the mathematical equivalent AIF to the Parker (“Cosine Bolus Parker”)⁹ and the now rarely used Weinmann function¹⁰ (Figure 1). Using differing AIFs will have effects on the DCE-MRI modelling process and the outputs generated. The description of the assumed or measured AIF in terms of the peak arterial concentration and subsequent decay rate combined with model components has profound effects on the numeric value (and biologic meaning) of the derived DCE-MRI kinetic parameters, including the K^trans. Thus, for a given DCE-MRI experiment, the use of an AIF with lower initial concentration and decay such as the Weinmann AIF used in the classic Tofts model yields higher K^trans values (implying increased contributions from perfusion). For the same DCE-MRI data, employing a higher initial AIF concentration and faster decay AIF (Parker) leads to lower K^trans values. Given these complex interactions, it is therefore important to fix the kinetic model and vary only the AIF model to assess effects on the modelling pipeline and the extracted kinetic parameters. This should be performed using DCE-MRI data sets that are representative of real-world tumour data with intrinsic heterogeneity before and after therapy, to see the effects of varying the AIF on a defined model's test performance.

Figure 1.

Curve shape for each arterial input function (AIF): the y-axis is plasma gadolinium concentration. The maximum concentration is different between each AIF (the differing scales can be noted) with a similar minimum concentration. The rates of decay are also different, in particular with the Weinmann AIF.

However, there are little data comparing the performance of different assumed AIFs in terms of their ability to produce physiological meaningful results, for model fitting to patient data and for their ability to yield meaningful results in terms of clinical outcome performance. We therefore investigated, in patients with primary breast cancer receiving NAC, how well the differing assumed AIFs allowed patient DCE-MRI data to be fitted by the Tofts kinetic model,¹¹ provided physiologically plausible data and assessed the ability to detect pathological outcomes.

METHODS AND MATERIALS

Study design

Institutional ethics committee approval was given, and informed consent was obtained from all participants. Patients with histologically proved locally advanced non-metastatic breast cancer were recruited consecutively to undergo dynamic MRI before and after two cycles of NAC between August 2002 and September 2008 as part of two sequential prospective studies. All patients received docetaxel-based chemotherapy (100 mg m⁻² every 21 days) for either three cycles followed by anthracycline chemotherapy with i.v. 5-fluorouracil (600 mg m⁻²), epirubicin (60 mg m⁻²) and cyclophosphamide (600 mg m⁻²) or adriamycin (60 mg m⁻²) and cyclophosphamide (600 mg m⁻²) three times weekly for three cycles, or a total of four cycles of docetaxel alone. These regimens were the standard of care at that time in our institution. Patients were excluded if they were pregnant or if they had any contraindications to MRI. At completion of NAC, patients subsequently received further treatment with surgery (wide local excision or mastectomy with axillary nodal clearance), post-operative external beam radiation therapy to the breast or chest wall, endocrine therapy if the tumour had positive hormone receptor status and adjuvant trastuzumab if the tumour had positive HER2 status, as was the standard of care at the time.

In addition, 12 patients (from both this cohort of patients and a previous cohort¹²) had a second MRI scan performed within 1 week of the baseline study, and prior to any systemic therapy, to produce a reproducibility cohort group.

MRI data acquisition and analysis

Our MRI protocol is as follows: MRI was performed with a 1.5-T scanner (Symphony; Siemens Healthcare, Erlangen, Germany) using a dedicated bilateral breast coil. Initial morphologic T₁ and T₂ weighted images were obtained followed by proton density-weighted gradient-recalled echo images (350-/4.7-ms repetition time/echo time, 6° flip angle and 8-mm-thick sections) for three tumour sections. 40 sets of dynamic T₁ weighted images were then acquired every 12 s for a total imaging time of 8 min. The sequence was based on two-dimensional fast low-angle shot imaging (11/4.7 ms, 35° flip angle and 256 × 256 pixel matrix). Gadopentetate dimeglumine (Magnevist; Bayer-Schering, Newbury, UK) was injected intravenously at a dose of 0.1 mmol kg⁻¹ body weight at 4 ml s⁻¹ using a power injector during the fifth acquisition time point followed by 20-ml flush of normal saline. The proton density and T₁ weighted dynamic series of images were acquired to calculate tissue T₁ and contrast agent concentration.¹³ Images were analyzed using the specialist DCE-MRI software MR Imaging Workbench v. 4.3 (Institute of Cancer Research, London, UK)¹⁴ with whole tumour regions of interest drawn on T₁ weighted subtraction images by one observer (ARP), an oncology-trained radiologist with a special interest in breast cancer MRI and over 20 years' experience, on pre-/post-treatment scans. Data from all slices were analyzed on a voxel-by-voxel basis.

Quantitative DCE-MRI analysis was performed using pharmacokinetic modelling according to the Tofts¹¹ model. Biexponential approximations to the following input AIFs were used: Fritz-Hansen,⁶ modified Fritz-Hansen,⁷ Weinmann,¹⁰ Parker,⁴ femoral artery⁸ and a computationally efficient raised cosine model AIF approximating Parker⁹ (Figure 1), in order to calculate the following quantitative kinetic parameters: K^trans (measured in min⁻¹), the volume of extracellular extravascular space per unit volume of tissue (v_e), or the leakage space, in % and rate constant (k_ep) (measured in min⁻¹). Changes (in %) in median parameter values of all fitting voxels containing tumour were calculated after two cycles of NAC for each tumour.

Fit failures

The MR Imaging Workbench software uses a non-linear least-squares Levenberg–Marquardt algorithm to fit the data and perform internal consistency checks to filter out parameter values which are not physiologically reasonable.¹⁴ We defined non-enhancing (NE) fails as fit fails which are likely to arise from tissue physiology such as fibrotic tissue, necrosis etc. and all other fail reasons as computational fit fails, i.e. voxels which do not fit the model or produce non-physiological values; for example, v_e >90% and K^trans >5 min⁻¹. All non-failing model fits provide fitting residuals.

Statistical analysis

Pathological complete response (pCR) rates and pathological response rates after NAC were measured according to the well-established histological criteria of residual tumour at the end of NAC.¹⁵

The Bland–Altman¹⁶ approach was used to calculate the measurement error of K^trans for the reproducibility cohort using all six AIFs. Statistics were generated as per Galbraith et al¹⁷ including the mean K^trans, the repeatability coefficient (r), r as a percentage of the mean where any differences below this value would occur in fewer than 5% of observations and therefore be statistically significant and the within-patient coefficient of variation (wCV). This methodology has been used previously to assess the reproducibility of AIFs.^18,19 The number of pathological complete responders and non-responders correctly assessed using r (as a % of the mean) were calculated and receiver-operating characteristic curves were used to assess the relative test performance.

Statistical significance was set at a two-tailed p-value of <0.05. All statistical analyses were performed using SPSS statistical software v. 21.0 (IBM Corp., New York, NY; formerly SPSS Inc., Chicago, IL), and additional figures were produced with StatsDirect software (StatsDirect Ltd, Sale, UK).

RESULTS

Patient characteristics and response to neoadjuvant chemotherapy

27 patients were included in this study, and the patient and disease characteristics are shown in Table 1. The median age at diagnosis was 44 years (range, 22–62 years) and the median tumour size was 55 mm (range, 25–100 mm). Most females were pre-menopausal (70%), with most exhibiting tumours of the invasive ductal subtype (78%).

Table 1.

Baseline patient demographics and tumour characteristics

Characteristic		Number of patients (n = 27) (%)
Age at diagnosis (years)	<50	19 (70)
	≥50	8 (30)
Menopausal status	Pre-menopausal	19 (70)
	Post-menopausal	6 (22)
	Perimenopausal	1 (4)
	Unevaluable	1 (4)
Histological characteristic	Invasive ductal carcinoma	21 (78)
	Invasive lobular carcinoma	4 (15)
	Other or not otherwise specified	2 (7)
Grade	I	2 (7)
	II	13 (48)
	III	11 (41)
	Unknown or unevaluable	1 (4)
Clinical tumour stage	T2	13 (48)
	T3	11 (41)
	T4	3 (11)
Clinical nodal stage	Positive	15 (56)
	Negative	12 (44)
Oestrogen receptor status	Positive	15 (56)
	Negative	12 (44)
Progesterone receptor status	Positive	12 (44)
	Negative	13 (48)
	Unknown or unevaluable	2 (8)
Human epidermal growth factor receptor 2 (HER2) status	Positive	6 (22)
	Negative	20 (74)
	Unknown or unevaluable	1 (4)

All patients received docetaxel-based chemotherapy for either 3–4 cycles followed by anthracycline chemotherapy with i.v. 5-fluorouracil, epirubicin and cyclophosphamide (n = 13) or adriamycin and cyclophosphamide three times weekly for three to four cycles (n = 6) or a total of four cycles of docetaxel alone (n = 8).

13 patients underwent breast-conserving surgery and 14 patients underwent a total mastectomy. Overall, 22 (81%) of the 27 patients showed a pathological response and were classified as pathological responders. 8 (30%) of the 27 patients achieved a complete pathological response to chemotherapy. 14 (52%) out of the 27 patients had a pathological partial response to chemotherapy. 5 (19%) of the 27 patients did not show any pathological response to chemotherapy and were labelled pathological non-responders.

Model fitting

Voxels which failed to fit the model were counted and calculated as a percentage for each AIF, for both pre-NAC and after two cycles of NAC (Table 2, Figure 2). All models had fewer fit failures pre-chemotherapy than after two cycles of NAC with the femoral artery AIF having a pre-chemotherapy fit failure rate of 19.4% and a post-chemotherapy fit failure rate of 43.3%, contrasting with the modified Fritz-Hansen values of 3.6% and 18.8%, respectively. When looking at the cause of fit fails (Table 2, Figure 2), all models except the modified Fritz-Hansen had a greater number of fit fails owing to computation failure rather than NE pre-NAC, although in absolute terms, the number of NE fit fails for this AIF was still very low. Post-NAC, the patterns of fit fails was more heterogeneous with only one AIF (femoral artery) having a much greater number of computation fit fails, two AIFs having roughly similar numbers of NE and computation fit fails (Fritz-Hansen and cosine bolus) and others having a greater number of NE failures.

Table 2.

Average fitting failure % for each arterial input function (AIF)

AIF	Pre-NAC		Post-two cycles of NAC
	Fit fails (% of total voxels)	Fails attributable to computational failure to fit (% of total voxels)	Fit fails (% of total voxels)	Fails attributable to computational failure to fit (% of total voxels)
Weinmann	8.1	6.3	18	3.3
Biexponential Parker	5.8	3.6	25.7	10.9
Modified Fritz-Hansen	3.6	1.3	18.8	3.6
Fritz-Hansen	12.2	10	26.7	12.3
Femoral artery	19.4	17.3	43.3	30.8
Cosine bolus Parker	9.4	6.6	29.5	15.6

NAC, neoadjuvant chemotherapy.

Figure 2.

The average fit failure for each arterial input function as a %. Non-enhancing (NE) fails are fit fails which are likely to arise from tissue physiology such as fibrotic tissue, necrosis etc. All other fail reasons are computational fit fails. NAC, neoadjuvant chemotherapy.

Kinetic parameter values

Median K^trans, v_e and k_ep values for each patient pre- and post-two cycles of NAC for all six AIFs are displayed as box plots in Figure 3 and are shown for K^trans in Table 3. For both K^trans and k_ep, the greatest spread is seen in the Weinmann AIF, whereas for v_e, the spread is similar between all of the variables. The largest absolute values of K^trans were for the Weinmann AIF, which also showed the largest percentage reduction after two cycles of NAC at −68% (Table 3). The other AIFs show a broadly similar range of K^trans reductions (−42.6 to −51.5%).

Figure 3.

Box plots of transfer constant, leakage space and rate constant pre- and post-two cycles of neoadjuvant chemotherapy.

Table 3.

Transfer constant (K^trans) values for each arterial input function (AIF) at baseline and after two cycles of neoadjuvant chemotherapy (mean of patient median K^trans)

AIF	Ktrans baseline mean	Ktrans post-chemotherapy mean	Change in Ktrans mean (%)
Weinmann	1.068	0.342	0.725 (−68)
Biexponential Parker	0.13	0.07	0.06 (−46.2)
Modified Fritz-Hansen	0.241	0.117	0.124 (−51.5)
Fritz-Hansen	0.333	0.175	0.157 (−47.4)
Femoral artery	0.170	0.095	0.075 (−44.1)
Cosine bolus Parker	0.115	0.066	0.048 (−42.6)

Reproducibility and response assessments

Data from the 12 patients in the reproducibility cohort are displayed in Table 4. The wCV, repeatability coefficient (r) and r as % of the mean (r%) showed that K^trans reproducibility was worst for the Weinmann AIF (r = −49.7%), with the rest falling into the range of −27.8% (cosine bolus Parker) to −39.2% (modified Fritz-Hansen). These pharmacokinetic reproducibility data allow meaningful changes to be defined and are in keeping with previously published data.^18,19

Table 4.

Reproducibility statistics of transfer constant (K^trans) data for each arterial input function (AIF) (n = 12) used to detect individual patient responses and receiver-operating characteristic (ROC) analysis

AIF	wCV (%)	r	r% used to assess response	Pathological complete response correctly predicteda	Non-responders correctly predicteda	Sensitivity (%)	Specificity (%)	Area under ROC curve
Weinmann	28.1	0.69	−49.7	6/8	7/19	75	37	0.70
Biexponential Parker	11.9	0.04	−33	7/8	8/19	87.5	42	0.73
Modified Fritz-Hansen	14.2	0.09	−39.2	7/8	9/19	87.5	47	0.74
Fritz-Hansen	15.9	0.41	−33.6	7/8	9/19	87.5	47	0.73
Femoral artery	18.3	0.47	−37.3	6/8	8/19	75	42	0.69
Cosine bolus Parker	12.5	0.33	−27.8	7/8	8/19	87.5	42	0.72

r, reproducibility statistic; wCV, within-patient coefficient of variation.

^aprediction based on median K^trans changes in relation to reproducibility values.

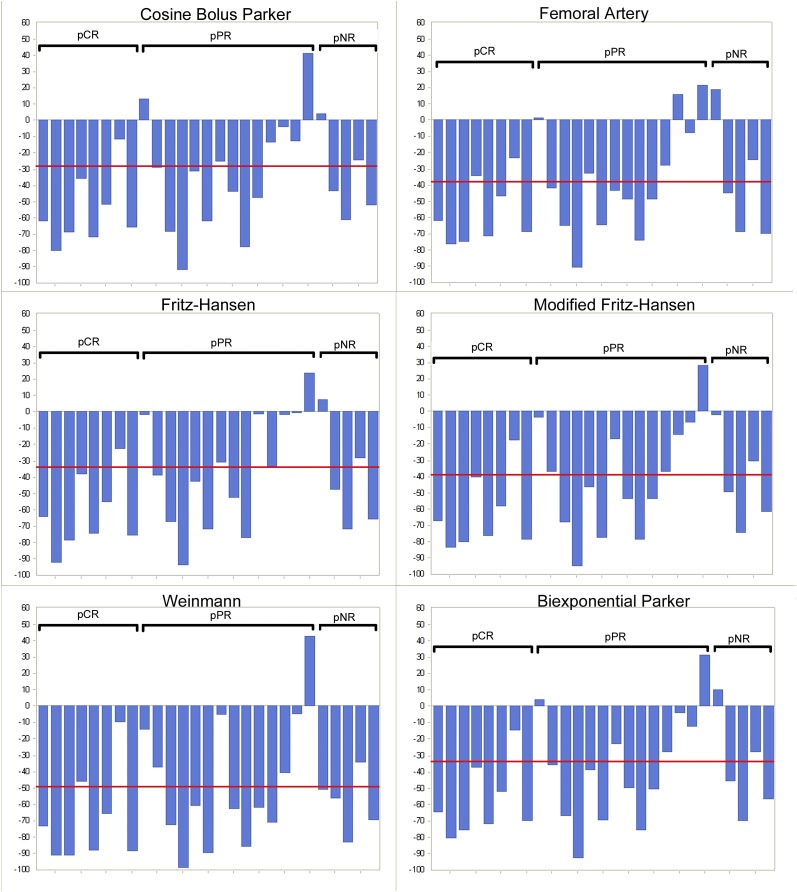
Using the reproducibility data (r%) to apply significance to changes in K^trans, their ability to detect pCR (n = 8) and non-complete response (n = 19) was calculated (Table 4). Using the Fritz-Hansen and modified Fritz-Hansen AIFs, K^trans was able to detect 7/8 pCRs and 9/19 non-responders, giving a sensitivity of 87.5% and a specificity of 47%. Individual patient percentage changes in K^trans for each AIF are shown in Figure 4 alongside the r% cut-off line. Test performance was broadly similar for all AIFs (Table 4), with the modified Fritz-Hansen model performing best.

Figure 4.

Histogram showing change in the transfer constant by arterial input function (AIF) for each patient before and after neoadjuvant chemotherapy. Patients are grouped into those with pathological complete response (pCR), those with pathological partial response (pPR) and those with pathological non-response (pNR): repeatability r (as a % of the mean) lines are displayed for each AIF (from the reproducibility cohort shown in Table 4).

DISCUSSION

Our study has addressed the question of which is the best performing modelled/population AIF from six found in the literature. We used three criteria: (1) the ability of the AIF to minimize the number of computational fit fails, (2) the ability of the AIF to produce physiologically valid parameters and (3) detection of pathological response (a predictor for disease-free and overall survival²⁰), to NAC chemotherapy in a well-defined population of advanced breast cancer.

Regarding fit fails, the modified Fritz-Hansen AIF performed best pre-chemotherapy, and the Weinmann performed best post-chemotherapy. The worst performing AIF was the femoral artery with a fit failure rate of 19.4% pre-chemotherapy and 43.3% after two cycles of NAC. Overall, the best performing AIF was the modified Fritz-Hansen with a fit failure rate of 3.6% pre-NAC and 18.8% post-two cycles of NAC.

NE fit failures can be ascribed to voxels containing de novo fibrosis, cysts, necrosis etc. Post-chemotherapy NE fit fails may be due to therapy-induced fibrosis and/or necrosis. NE fit failures at a particular time point has to be the same, so the only thing that varies is the model used to assess it and any treatment-related effects.

Our data show that the patterns of fit failure differ between AIF models and are also affected by NAC (Figure 2). The Weinmann AIF had a high proportion of fit fails owing to computational failure pre-NAC, but the vast majority post-NAC were NE failures. Both the biexponential Parker model and the cosine bolus AIF had a similar pattern with over half the pre-NAC failures being due to computational fit fail, but more NE fails post-NAC. The modified Fritz-Hansen, which had a low number of fit failures overall, mainly had NE failures both pre- and post-NAC, the only AIF to exhibit this pattern. Using the Fritz-Hansen and femoral artery AIFs, we observed the majority of fit fails pre-NAC were due to computational failure, but post-NAC, about half of the Fritz-Hansen failures were due to computation fails compared with two-thirds of the femoral artery failures.

The intention of the modelled AIFs is to allow the production of physiologically valid data. There are limited data correlating DCE-MRI parameters with tissue studies using accepted correlates of perfusion including quantitative autoradiography.²¹ One study used [¹⁴C]aminoisobutyric acid to validate K^trans,²² and another study used similar methods to measure v_e.²³ Another study has correlated the intracellular and extracellular space parameters on MR spectroscopy with classical radiolabelling methods (³H₂O and [¹⁴C]insulin),²⁴ suggesting that MR findings have physiological validity. The range of our v_e data of the cosine bolus, biexponential Parker and modified Fritz-Hansen AIFs is mostly in keeping with the ranges of values produced from the data in the literature, suggesting that these have physiological plausibility. This shows that not all modelled AIFs are equally capable of yielding plausible values, with the choice of AIF being key to obtaining meaningful data.

The poor reproducibility and fitting capability of the Weinmann AIF confirms that it is the least physiologically realistic of the AIFs for locally advanced breast cancer. It is a simple biexponential that largely represents k_ep related to extracellular equilibrium and renal excretion over 8 min (Figure 1) and does not have the initial concentration which occurs during the first pass of bolus. Both the biexponential form of Parker (biexponential Parker) and the cosine form of Parker (cosine bolus Parker) have the best reproducibility values, suggesting that they are more reliable and robust. In addition, the cosine bolus Parker AIF more accurately reproduces the shape of an i.v. bolus of the contrast (Figure 1) and is considered to be the most physiologically realistic.

In terms of response assessment, the best performing AIF model is the modified Fritz-Hansen, originally derived from a combination of the data reported by Weinmann and Fritz-Hansen.⁷ However, three other AIFs performed almost equally well, biexponential Parker, cosine bolus Parker and Fritz-Hansen. The use of these models allowed the correct detection of seven out of eight patients who had a pCR to NAC, giving a sensitivity of 87.5%. The detection of non-complete responders was 8–9 out of 19, giving a specificity of 42–47%. The Weinmann and femoral artery AIFs performed poorly in detecting pathological response.

Even though the data from our study have suggested which are the best performing AIFs, we have not been able to show the robust predictive accuracy of any of the AIFs for use in routine clinical practice. In particular, they did not predict those who were non-complete responders, which are a useful group to establish in clinical practice. This does limit the potential clinical impact of the study, although using the best AIF would still be important for future research or clinical use.

Limitations

Although this study assesses the relative performance of various AIFs, some caution should be applied to the use of these results being extrapolated to prospectively acquired data. This is because the 27 patients were selected, on the basis of the use of the same chemotherapy agents, from a pool of 60 patients in 2 studies and were not consecutive patients. This retrospective cohort was chosen to test the relative performance of detected AIFs in predicting pathological response. However, it was not designed to assess the ability of DCE as an overall technique to assess pathological response, which has been explored by other studies.^1,2

As discussed previously, there are a number of methods to measure the AIF and this study addressed only the use of differing population AIFs. Although this is the most commonly used technique, there are others in use, and the comparison with these also needs to be made.

We have used median K^trans as a comparator, as it has been shown to have the best prognostic value of DCE parameters.² There are, however, other parameters which we did not evaluate including k_ep (rate constant) and IAUGC (initial area under the gadolinium concentration–time curve) whose test performance may be affected.

The numbers of patients in this study are limited, which might have a bearing on the ability to extrapolate our results. This also did not allow statistically appropriate comparisons to be made within our patient population such as assessments of the impact of differing immunophenotypes of the tumour. It is possible that the modelling for ductal carcinomas and lobular carcinomas are different. All patients had the same chemotherapy agent, which gives a more homogeneous cohort of patients, but this means that our data may not be able to be extrapolated to other regimens.

CONCLUSION

The use of the best performing AIF is essential in order to produce valid data for the interpretation of dynamic parameters in DCE-MRI. This applies to its use in assessing treatment response, as demonstrated in this study, and also in the imaging of de novo disease or Phase I studies where antiangiogenic or vascular targeting agents are being evaluated. In the absence of measured AIFs, we would recommend the use of either the modified Fritz-Hansen or cosine bolus Parker AIFs for imaging breast cancers, as they have a low overall percentage of fit fails, physiological plausibility and demonstrate robust predictive accuracy. The biexponential Parker and the Fritz-Hansen functions also perform reasonably well and their use would be acceptable. The femoral artery and Weinmann AIF models should be noted for their poor performance, particularly in their inability to detect response to treatment and the high percentage of fit failures. These AIFs were earlier versions of other AIFs, which represent incremental improvements on their predecessors. It is uncertain how much these recommendations could be extended to other tumour types and anatomical locations.