Abstract
Objective:
This article considered why the proton therapy (PT) relative biological effect (RBE) should be a variable rather than a constant.
Methods:
The reasons for a variable proton RBE are enumerated, with qualitative and quantitative arguments. The heterogeneous data sets collated by Paganetti et al (2002) and the more homogeneous data of Britten et al (2013) are further analyzed using linear regression fitting and RBE-inclusive adaptations of the linear–quadratic (LQ) radiation model.
Results:
The in vitro data show RBE increasing as dose per fraction is lowered. In the Paganetti et al (2002) data sets, the differences between observed and expected effects are smaller when the LQ model is used, but with such data heterogeneity, firm statistical conclusions cannot be obtained. The more homogeneous data set shows an unequivocal variation in RBE with dose per faction. The in vivo data are inappropriate for assessments of late normal tissue effects in radiotherapy. Also, if there is the same degree of uncertainty in an RBE of 1.1 or in an RBE of 2–3 for C ions, the fractional and biological effective doses can vary considerably and be greater in the proton case. So, errors in RBE assignment are important for protons, just as with C ions.
Conclusion:
Further experimental programmes are proposed, including late normal tissue end points. Better RBE allocations might further improve PT outcomes.
Advances in knowledge:
This study provides a rigorous critique of the 1.1 RBE used for protons, from theoretical and practical standpoints. Data analysis shows that the LQ model is more appropriate than simple linear regression. Comprehensive research programmes are suggested.
INTRODUCTION
Uniquely in external beam radiotherapy, the dose prescription process in proton therapy (PT) includes a radiobiological concept called the relative biological effect (RBE). The dose given to the patient is the intended photon-equivalent physical dose divided by the RBE; so, if RBE allocations to different tissues and tumours are incorrect, there will be an inevitable underdosage or overdosage in the tumour and/or in the normal tissues. The clinical significance of this will vary owing to a variety of reasons such as the physical dose and volume distributions, local anatomy, medical history and other factors that may change normal tissue tolerances or influence tumour control. The dose variations caused by an incorrect RBE assignment can not only exceed those in the International Commission on Radiation Units and Measurements (ICRU) prescription guidelines (of −5 to +7% of the prescribed dose), but also those allowed within the legal requirements for dose precision of around 2% in most countries.1,2 This is a sensitive issue in the clinic, since there are implications that inappropriate doses are given, although there can be no fault in law, since this is presently the international standard of practice.
The conventional use of a constant RBE of 1.1 in all tissues and tumours and at all levels of dose and linear energy transfer (LET), which has been endorsed by ICRU,2 has been questioned for some time, with recent calls for a reassessment of this policy.3–8 The decision to adopt this single value was made on the basis of some well-intended radiobiological experiments; it also followed previous decisions made in fast neutron therapy, principally in the UK, to use a single RBE value, despite extensive evidence that RBE varied with dose per fraction.9–11 When these decisions were taken, the treatment planning systems could not have accommodated a variable RBE easily, and the easier alternative option of reallocating tissue tolerances was also not adopted owing to the necessary complexity and lack of three-dimensional dose distributions.
This article considers the reasons why the RBE of protons, or indeed any higher LET radiation, must be a variable rather than a constant, by referring to basic radiobiological principles within the overall framework of the linear–quadratic (LQ) model. The most pertinent consideration is that the increased clustering of ionization events with increasing LET produces a higher proportion of unrepairable damage, which confers greater radiosensitivity and reduced fraction sensitivity than that with lower LET radiation. Another potentially misleading aspect is the definition of the boundary between “low” and “high” LET, which can be misleading in the case of protons where elevations in RBE can occur at what are deemed to be low LET values (from 1 to 10 keV μm−1).12,13 In the present article, high LET will refer to any LET which exceeds the control low LET value which should be in the 0.5–1.5 keV μm−1 range, since there is a steep increase in RBE beyond this value, and more so in the case of protons than other ions12,13 where the gradient of RBE with LET is less marked.
METHODS AND MATERIALS
The justification for a variable rather than constant proton RBE is considered from several standpoints in this article. These are:
standard radiobiological principles, beginning with the definition of RBE and how the ratio changes for different cell/tissue types
LQ model considerations
the multifactorial nature of RBE
the investigation of changes in biological effective dose (BED) per fraction for incremental errors in RBE close to one [protons in mid-spread-out Bragg peak (SOBP)] compared with those for much higher RBEs such as C ions
-
a critique of the proton experimental data used to justify the 1.1 RBE.
a further analysis of the data of Britten et al13 to find the relationship between RBE and dose per fraction at various depths in the beam. The published radiosensitivities of the control and test cells were used to provide the limit of RBE at high dose (RBEmax) and limit of RBE at low dose (RBEmin) values, which were then used in Equation (A7) of the Appendix A to provide the RBE plots.
A reanalysis of the data of Paganetti et al,14 since this data set was influential in determining the continuation of the 1.1 RBE during the past 15 years. Linear regression models (with standard error weighting where possible) have been used to provide a linear fit of the form RBE = m.dose + c, where m is slope and c is the intercept. Also, the LQ model in its BED form (Appendix A) was used to define isoeffective conditions for plots of RBE against dose per fraction, using least-squared non-linear fitting techniques on Mathematica software (Wolfram, Champaign, IL). Statistical comparisons were made using absolute residual values by comparing observed and expected data results and the summated χ2 statistic. The distribution-free Kolmogorov–Smirnov (K-S) test was used to provide probability estimates for goodness of fit, since the data form was unsuitable for a χ2 probability estimation or for any of the statistical tests that rely on a Gaussian distribution, although the χ2 statistic is given. The data sets were analyzed separately for (a) all data and (b) data where RBE exceeded one, which eliminates all experiments where low kiloelectron volt photon controls are used, since the latter may have a higher LET than the proton LET in the SOBP, thus causing an “inverted” RBE below one. Although this may introduce a bias, there is a good scientific a priori reason for not using such data; but the original data set is biased since these inappropriate experiments were included. This is because the control irradiation should preferentially be megavoltage photons or very well-filtered 250-keV X-rays as a poor second choice, otherwise RBE values less than one may be found. Data with equivocal or no standard error estimates were also excluded from the present analysis, unlike in Paganetti et al. Again, the Appendix A provides the relevant equations used for the LQ model fits to provide RBEmax and RBEmin for the data with RBE greater than unity.
RESULTS
The definition of RBE refers to its measurement as the low LET (reference) dose divided by the high LET dose,
when the same bioeffect is achieved by each quality of radiation (i.e. when both are isoeffective). The numerator dose is very dependent on repair proficiency, the denominator less so because of the greater proportion of unrepairable damage, depending on the particle and operative LET. To meet isoeffective conditions for a specified high LET denominator dose, the required low LET numerator dose per fraction will be much larger in the case of a more radioresistant cell/tissue (with high repair capacity) than in the case of a more radiosensitive cell/tissue system (with lower repair capacity). In this way, slower growing/more radioresistant systems (which have large fraction sensitivities associated with low α/β ratios, where α and β are the radiosensitivity coefficients in the linear quadratic model) will have the highest RBEs. Conversely, cells that are highly radiosensitive, with a high α/β ratio, will require a lower numerator dose and the high LET dose will not differ much, since the absence of repair proficiency will not matter so much where there is a higher proportion of unrepairable damage, resulting in a lower RBE which can approach unity in highly radiosensitive repair-deficient mutant cells. For example, the data of Weyrather et al15 show that the low LET radiosensitivity correlates inversely with RBE. The RBE ratio consequently depends mostly on the intrinsic radiosensitivity/repair proficiency of the cell/tissue type, being scaled mostly by the numerator dose. It follows that in the more radiosensitive/rapidly growing cells/tissues, or with reduced DNA repair capacity, the changes in RBE with dose per fraction will be small. Since repair capacities and radiosensitivities are determined by a large number of genes, it follows that RBE must be a variable. This is similar to population frequency distributions of height, body weight, blood pressure etc., where multifactorial influences inevitably contribute to variation.
Another reason is provided by the mathematical boundary conditions for RBE. These extreme RBE limits are defined by radiosensitivity ratios of the higher LET radiosensitivity state divided by the control LET radiosensitivity. This is represented by the separate non-linear increments in α and β which occur with increasing LET. Derivations are provided in the Appendix A. Fast neutron experiments are appropriate for the simulation of proton RBE in the Bragg peak region, since most of the ionization occurs due to the formation of recoil protons. Examples are provided in the fast neutron data16–18 and the proton data of Britten et al,13 where α increases with LET to a much greater extent than β. The maximum RBE is then given by αH/αL, found at very low doses, since the α radiosensitivity parameter dominates cell killing at low doses. The minimum RBE is given by √βH/√βL at very high doses, where the β component of cell kill dominates. For all doses between these limits, the RBE must be of a variable intermediate value, which depends on the dose itself (owing to the changing contribution of α and β to cell kill with dose). Also, since the intrinsic variability of the low LET α and β values, which increase non-linearly with LET, will further contribute to RBE variations.
RBE will depend on the following physical factors:
particle charge (z) and energy
depth/position within the patient
treatment volume (owing to the superimposition of low and high LET regions off and within Bragg peaks, respectively)
beam contamination with neutrons and γ radiation.
For all these reasons, it follows that RBE will be a continuous variable. There will be an infinite number of RBEs in any practical treatment plan, just as with dose, although for convenience, dose and RBEs can be binned into ranges.
It is commonly assumed that because the measured proton RBE in experiments is so close to unity, then further deviations are insignificant, especially if compared with ion beams having higher RBEs of around 3. This rationale is often used to support the use of a constant proton RBE on the grounds that small deviations either greater or less than 1.1 might not be significant in clinical practice, especially since the megavoltage photon control radiation by definition has an RBE of 1. This simplistic argument can be counteracted by considering the effect of a change in dose on the BED.19 It is shown (in Table 1) that the use of assumed deviations (x) of RBE from 1.1 gives similar and sometimes greater BED modification when compared with the same deviations in radiations associated with a higher RBE such as carbon ions. In other words, a 10% error in RBE will produce a broadly similar change in relative dose fluctuations for an RBE of 1.1 compared with a similar error around an RBE of 3. Further details of the BED calculation methods are given in the Appendix A. In the case of protons (with assumed RBEmax = 1.3, RBEmin = 1.02), the equivalent dose to 2 Gy is estimated to be 1.749 Gy, which yields a BED difference of only 0.037 Gy3 over 30 fractions when compared with the photon-equivalent BED, but a comparison of the 1.749-Gy dose per fraction with the dose (if given by the standard RBE 1.1) of 1.82-Gy fractions gives a BED difference of 5.44 Gy3. Similarly, for C ions (with assumed RBEmax = 4, RBEmin = 1.2), the equivalent dose to 2 Gy is estimated to be 0.76 Gy, which yields a BED difference of only 0.057 Gy3 over 30 fractions when compared with the photon-equivalent BED, but a comparison of the 0.76-Gy dose per fraction with the dose (using a standard RBE of 2.5) of 0.8-Gy fractions gives a BED difference of 5.26 Gy3.
Table 1.
Results for protons and C ions for variations in parameter x, the relative biological effect (RBE) uncertainty factor (for example, x = 1.2 indicates a 20% RBE increment, x = 1 indicates an RBE of 1 etc.), for intended 2-Gy-equivalent fractional doses
| x = 0.95 | x = 1.0 | x = 1.05 | x = 1.1 | x = 1.15 | x = 1.20 | x = 1.25 | |
|---|---|---|---|---|---|---|---|
|
Protons | |||||||
| dH (Gy) | 1.91 | 1.82 | 1.73 | 1.65 | 1.58 | 1.51 | 1.45 |
| % change (=dH/1.82×100) | (105.3) | (100) | (95.2) | (90.9) | (87.0) | (83.3) | (80) |
| ΔdH (Gy) (=dH −1.82) | 0.1 | 0 | −0.09 | −0.17 | −0.24 | −0.30 | −0.36 |
| BED Gy3 per fraction | 3.20 | 3.42 | 3.65 | 3.88 | 4.12 | 4.36 | 4.61 |
| % BED change (compared with x = 1) | 93.7 | 100 | 106.8 | 113.6 | 120.5 | 127.6 | 134.9 |
|
Carbon ions | |||||||
| dH (Gy) | 0.84 | 0.8 | 0.76 | 0.73 | 0.70 | 0.67 | 0.64 |
| % change (=dH/1.82 × 100) | (105.3) | (100) | (95.2) | (90.9) | (87.0) | (83.3) | (80) |
| ΔdH (Gy) (=dH −1.82) | 0.04 | 0 | −0.04 | −0.07 | −0.10 | −0.13 | −0.16 |
| BED Gy3 per fraction | 3.14 | 3.32 | 3.50 | 3.68 | 3.86 | 4.05 | 4.23 |
| % BED change (compared with x = 1) | 94.6 | 100 | 105.4 | 110.9 | 116.5 | 122.2 | 127.6 |
BED, biological effective dose.
dH is the dose of the particle radiation, which is 1.82 Gy (protons) and 0.8 Gy (C ions).
Δ is the physical change in the dose.
Gy3 is the BED units for the case of α/β=3Gy.
The experimental data sets are considered separately as follows:
Britten et al data set
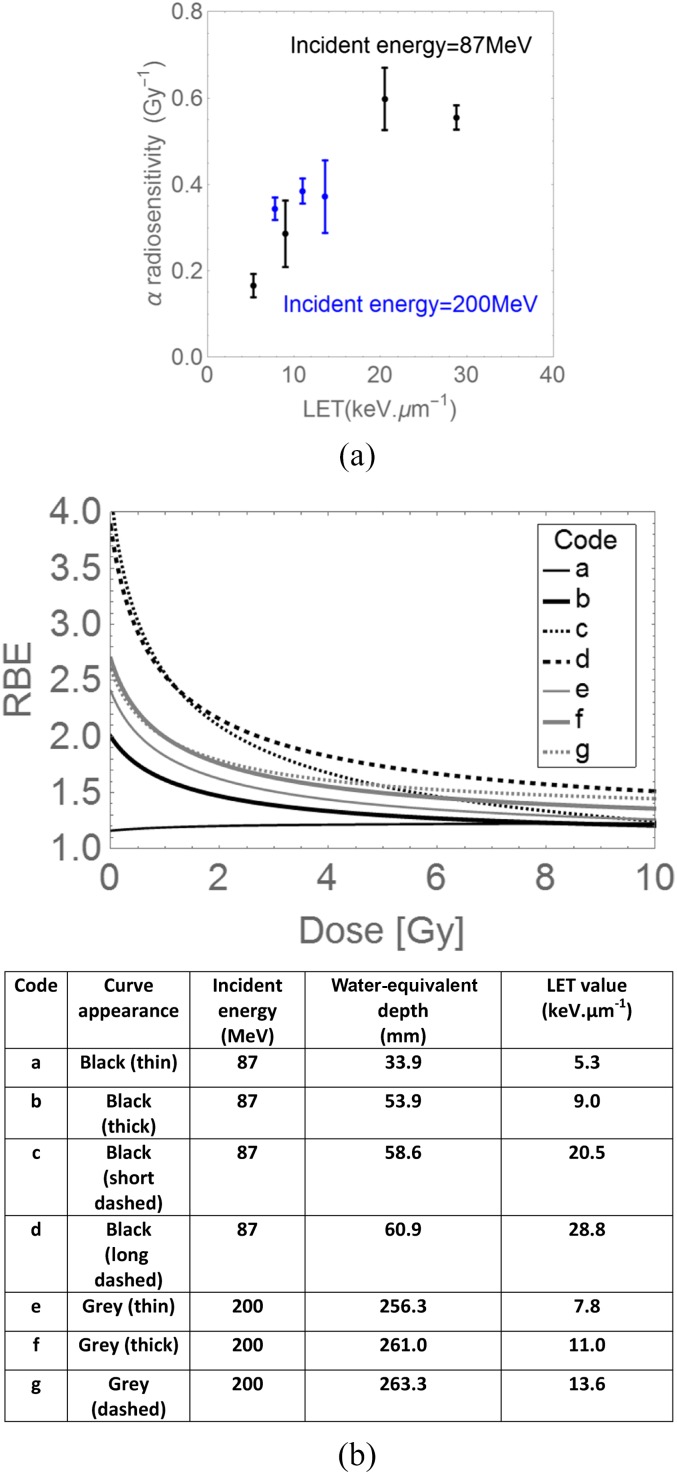
Most proton RBE experiments have measured RBE using single-fraction experiments conducted in the mid spread-out Bragg peak region of a single field. Higher LET and RBE values will inevitably occur towards the end of SOBP range.5,8,13 The detailed study of Britten et al,13 where experiments were performed at different depth/ranges and LET values. The reported changes in the α radiosensitivity parameter with LET in human Hep-2 cell line are shown in Figure 1a, where the values depend on the initial incident energy as well as LET (determined by energy and target depth). There are insufficient data points to determine the true position of the α radiosensitivity and LET turnover points, although this limited data set does suggest that the turnover point LET possibly depends on incident energy, but further experiments are necessary to confirm whether this is so. Also, the increase in α-radiosensitivity appears to be inversely related to the incident energy. Only the lower incident energy characteristics appear to be similar to the data of Belli et al,8,12 where turnover occurs at an LET value of around 30.5 keV μm−1. The RBE variation with depth and dose per fraction for each incident energy in this study is shown in Figure 1b. These curves show the large variation of RBE with dose per fraction and LET in different parts of a proton beam. The points shown in Figure 1b are the published RBE values for a surviving fraction of 0.1: these fit on each curve almost exactly, although the curves are not fitted by using these points, thus increasing the overall confidence in the LQ model with modification by RBEmax and RBEmin interpretation (as given in the Appendix A and in other publications).4,8,10,20 The K-S test statistic for goodness of fit approaches 1, the prediction accuracy being averaged at 0.998 ± 0.002.
Figure 1.
Further analysis of data of Britten et al13 for (a) α radiosensitivity in Hep-2 cells with changes in linear energy transfer (LET), for two different values of the initial incident energy. (b) Relative biological effect (RBE) plots with dose per fraction calculated using Equation (A7) in the Appendix A, constructed from the α and β radiosensitivities found at various positions in spread-out Bragg peaks and obtained using two different incident energies. The coded letters (a–g) refer respectively to different irradiation parameters given in the table.
The Paganetti et al data sets
Both in vitro and in vivo data sets show a modest increase in mean and median values of RBE, when RBE values below unity are excluded, as shown in Table 2. For this reason, the further analysis contains only the RBE results greater than unity and excludes experiments where the control radiation used relatively low kiloelectron volt photons in the photoelectric energy range. The in vitro data further analyzed contain 4 exclusions and the in vivo data contain 14 exclusions.
Table 2.
Comparisons of mean and median values of data characterized as relative biological effect (RBE) > 0 and RBE > 1
| In vitro RBE | Dose (Gy) | In vivo RBE | Dose (Gy) | |
|---|---|---|---|---|
|
Data RBE > 0 | ||||
| Mean (SD) | 1.21 (0.20) | 4.8 (2.69) | 1.08 (0.14) | 12.2 (9.02) |
| Median | 1.20 | 5.37 | 1.05 | 12.4 |
|
Data RBE > 1 | ||||
| Mean (SD) | 1.22 (0.18) | 5.0 (2.68) | 1.12 (0.07) | 8.7 (8.04) |
| Median | 1.23 | 5.6 | 1.12 | 10.07 |
SD, standard deviation.
In vitro assays
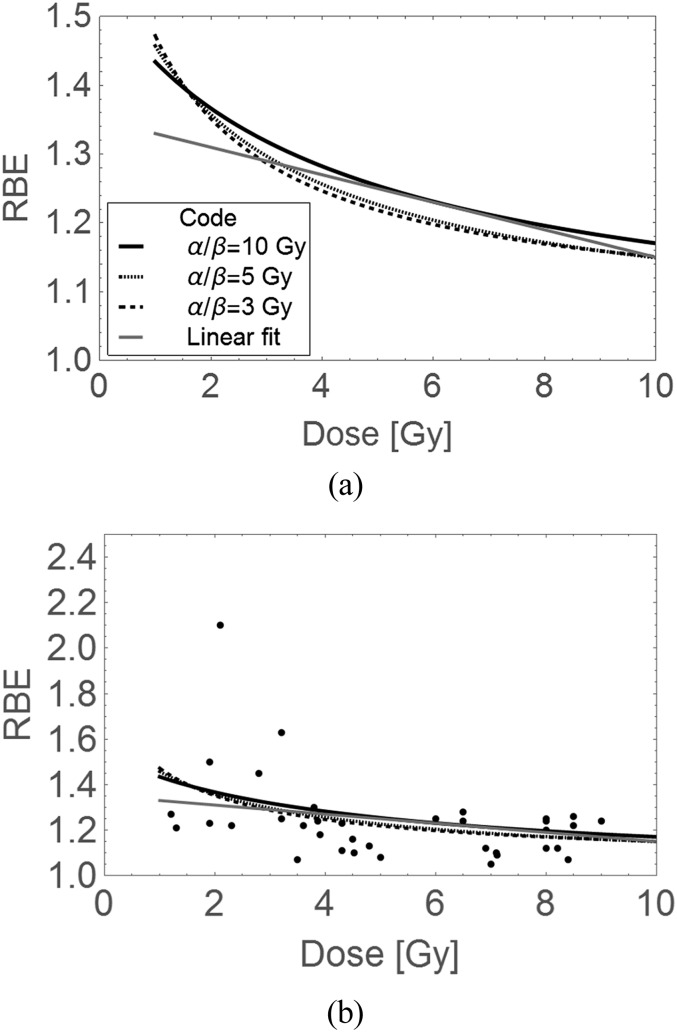
In the publication,14 there are considerable variations in proton RBE. Some data points at low dose per fraction exceed 1.1, with small error bars. However, a greater number of experiments were performed at high dose per fraction where lower RBEs predominate. These experiments can be criticized from the radiotherapy standpoint, since most of the cell lines tested are from the Chinese hamster ovary, with a lower chromosome numbers than in each human cell. In vitro cell growth conditions also favour proliferation, which confers increasing photon radiosensitivity, which will drive down RBE. The range of cells used is very limited and based on low-cost assays, rather than using a pool of human cell lines with a wide spectrum of cell kinetics and intrinsic radiosensitivities. Even so, the data does show an inverse relationship with dose, which may be fitted by simple linear or LQ model functions (Figure 2a,b).
Figure 2.
Displays of relative biological effect (RBE) and dose data from Paganetti et al,14 with modelled plots of dose per fraction and RBE plots using parameters obtained from the weighted least squares fitted 1.35 – 0.02d linear regression model (the straight line) and the linear–quadratic (LQ) model (for varying α/β ratios), which provides curves for in vitro data with RBEs > 1; (a) a magnified view of plotted models and (b) with superimposed data over a larger scale using the same codes. Owing to frequent overlapping, error bars are omitted in order to improve visual inspection, but can be seen in the original reference. The LQ RBE plots with dose per fraction are constructed using Equation (A7) in the Appendix A.
In vivo assays
In general, in vivo tissue assays can be divided into two types: acute and late tissue reactions. Each have different mechanisms. The acute reaction is due to cellular depopulation and acute inflammatory reactions in tissues. In contrast, the late reaction depends on chronic inflammatory processes, with late-developing vascular insufficiency along with the development of progressive fibrosis resulting in tissue dysfunction, and which typically occur at intervals of at least 6 months to many years after treatment.21,22 Late reactions are important since they determine the long-term quality of life in patients cured of cancer; they are highly fraction sensitive, with low radiosensitivity and α/β values, with a high repair capacity, so that RBE values are expected to be higher on the basis of the statements made above.
After exposures to fast neutrons (and so recoil protons), the late reactions showed by far the greatest changes in RBE with dose per fraction compared with very little change in RBE with dose per fraction in acute-reacting tissues with high α/β ratios.9–11,18 For convenience, the acute upper intestinal crypt assay became used for neutron beam intercomparisons as a beam quality assurance check in fast neutron and PT: it is the most rapid animal clonogenic tissue assay, with a high low LET α/β ratio of around 10 Gy.23 Later onset and more clinically relevant effects, such as narrowing of the bowel lumen (stricture), ulceration and perforation, with α/β of around 3 Gy, are not checked by this assay. It is the predominant assay used in the in vivo data of Paganetti et al14
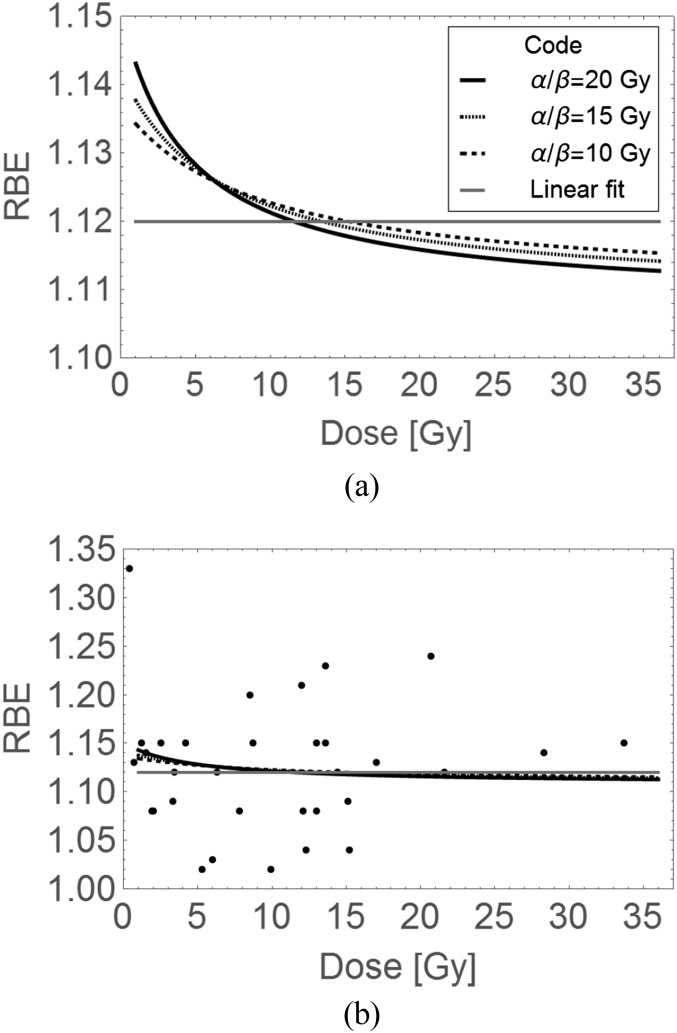
For the above reasons, this data set is unlikely to show significant changes in RBE with dose per fraction (Figure 3a,b). Some other tissues in the same data set did include later effects, such as the lens of the eye, which represents dose-related protein opacification and not a cellular clonogenic response associated with repair, and so is not a suitable assay to make any general conclusions. The few lung assays include early and later pneumonitis (but not the later development of lung fibrosis) and there are some delayed skin reactions (these show consequential late effects in animals and so, the overall RBE could reflect the severity of the acute reaction). These assays, when taken together, cannot adequately represent classical late tissue reactions in a variety of human tissues (e.g. kidney, heart, central nervous system and gut). Also, many of the experiments on these tissues were performed at between 9 and 12 Gy per fraction (because such large doses were in use for proton eye treatments). This is a dose range which should reveal low RBE values compared with those expected below 2.5 Gy per fraction. It is concluded that the most appropriate experiments for defining a range of clinically relevant RBEs remain to be performed for late-reacting normal tissues.
Figure 3.
Dose per fraction and relative biological effect (RBE) plots using parameters obtained from the linear fit of 1.12 + 0.d (shown as the straight line) and the linear–quadratic (LQ) model (for varying α/β ratios), which provides curves, for in vivo data with RBEs > 1: (a) a magnified view of plotted models and (b) with superimposed data over a larger scale using the same codes. Error bars are omitted in order to improve visual inspection, but can be seen in the original reference. The LQ RBE plots with dose per fraction are constructed using Equation (A7) in the Appendix A.
Both of the Paganetti14 data sets are summarized in Tables 2–4 and displayed with fitted lines and curves in Figures 2 and 3. Only RBE values above unity were included in the figures, since the data for all values of RBE showed larger residuals. For the in vitro data with RBE > 1, larger absolute residuals and ∑χ2 (sum of each Chi-squared statistic) values are found for the linear model when compared with the LQ model (at all assumed α/β values). For the in vivo data, for all RBEs, the absolute residual counts are marginally higher for the LQ model than for the simple linear fit, but the ∑χ2 values are slightly smaller for the LQ fits.
Table 4.
In vivo data analysis summary for relative biological effect (RBE) > 1
| RBEs > 1 | |
∑χ2 | Total residuals | K-S Test p-value | Adjusted R2 | ||
|---|---|---|---|---|---|---|---|
| Linear fit |
1.12–0.00d SEM = 0.02 |
0.13 | 1.59 | <0.001 | 0.997 | ||
| RBEmax (SEM) | RBEmin (SEM) | ||||||
| α/β = 15 | 1.14 (0.03) | 1.11 (0.03) | 0.12 | 1.60 | 0.02 | 0.996 | |
| α/β = 10 | 1.15 (0.03) | 1.11 (0.03) | 0.12 | 1.60 | 0.02 | 0.996 | |
| α/β = 7 | 1.16 (0.04) | 1.11 (0.02) | 0.12 | 1.60 | 0.02 | 0.996 | |
| α/β = 5 | 1.17 (0.04) | 1.11 (0.02) | 0.12 | 1.62 | 0.02 | 0.996 | |
| α/β = 3 | 1.20 (0.05) | 1.11 (0.02) | 0.18 | 1.97 | <0.001 | 0.996 | |
K-S, Kolmogorov–Smirnov; RBEmax, limit of RBE at high dose; RBEmin, limit of RBE at low dose; SEM, standard error of the mean.
Table 3.
In vitro data analysis summary for relative biological effect (RBE) > 1
| RBEs > 1 | |
∑χ2 | Total residuals | K-S test p-value | Adjusted R2 | |
|---|---|---|---|---|---|---|
| Linear fit |
1.35 – 0.02d SEM (0.05, 0.007) |
0.87 | 4.30 | 0.03 | 0.99 | |
| RBEmax (SEM) | RBEmin (SEM) | |||||
| α/β = 10 | 1.54 (0.11) | 1.00 (0.12) | 0.82 | 4.48 | 0.01 | 0.98 |
| α/β = 7 | 1.60 (0.13) | 1.00 (0.10) | 0.80 | 4.39 | 0.04 | 0.98 |
| α/β = 5 | 1.67 (0.16) | 1.03 (0.09) | 0.80 | 4.36 | 0.04 | 0.98 |
| α/β = 4 | 1.73 (0.18) | 1.04 (0.08) | 0.81 | 4.33 | 0.04 | 0.98 |
| α/β = 3 | 1.82 (0.22) | 1.06 (0.07) | 0.81 | 4.29 | 0.04 | 0.98 |
K-S, Kolmogorov–Smirnov; RBEmax, limit of RBE at high dose; RBEmin, limit of RBE at low dose; SEM, standard error of the mean.
It can be seen that there is greater variation in RBEmax for the in vitro data than for the in vivo data, presumably because of greater heterogeneity in the former.
However, all models provide a small K-S test p-value showing that the fit quality is not good and varies little with α/β ratio, presumably owing to data heterogeneity. The differences between each modelling variant are best shown in Figures 2b and 3b, where it can be seen that the LQ fits lead to the highest RBEs at low dose, even if these are minimized by data heterogeneity.
DISCUSSION
The existing data on proton RBEs refer to in vitro and acute reaction in vivo experiments, which are likely to underestimate the RBE in late-reacting tissues, especially at lower doses per fraction. It is the latter class of tissues that contribute to long-term quality of life after all forms of radiotherapy, and their tolerances must be respected in the prescription process. Paganetti et al14 indicate how difficult it would be to detect deviations in RBE from an assumed value of 1.1: this would be especially true in experimental or clinical series, where deviations in RBE may produce clinically important changes only in a small proportion of patients, depending on the degree of normal tissue sparing and the tumour dose achieved in each patient.24 For example, excess toxicity in the regions close to the planning target volume would be expected if the RBE error were to override the degree of normal tissue sparing obtained. It is difficult to assess the true clinical significance, but the unexpected outcome results might occur in 5–15% of all patients. Dasu and Toma-Dasu7 have performed interesting clinical simulations, with significant implications for patient safety. For tissues within the planning target volume, the RBE error may apply to all patients, but may not be clinically significant depending on the volume treated and the tissue functionality. For this to be detectable amid the large variation inherent in outcome studies, between 200 and 1000 patients might be required, even in the context of randomized studies.25 An alternative and complimentary better approach might be to study all unexpected outcomes on an international basis and compare observed vs expected results, with a detailed analysis of LET, dose distributions, medical histories etc., in order to identify which RBE uncertainties may be responsible. This is especially relevant to proton irradiations in the central nervous system, which has low α/β ratios of 2 Gy and where the RBE is predicted to be the highest.5,8,18,19
The analysis also shows that further in vitro and in vivo work may be helpful to define to what extent the RBE changes with dose per fraction in many different cell and tissue types. This can be ascertained from cell survival experiments which estimate α and β as accurately as possible, using large numbers of experiments to reduce the standard errors, in a wide panel of cells with different radiobiological characteristics. This would involve the same overall experimental plan as in Britten et al,13 but with greater numbers of LET variations in order to discern whether the LET–radiosensitivity turnover point position varies with incident energy, as there are suggestions in Figure 1a that this might be so. Such work would contribute to solving the remaining enigma about changes in RBE with depth in beams with different incident energies and with different scanning modes8,26,27. LET–RBE turnover points, where RBE is at a maximum, are important since these can be used as a reference to scale all other RBEs.8,20
Experimental programmes should aim to predict as accurately as possible the relationship between low LET radiosensitivities and those at higher LET, sufficient to supply RBEmax and RBEmin and define the relationship between dose per fraction and RBE with LET changes, as suggested elsewhere.8,20,26–28 In vivo studies must include true late-reacting tissue effects: this imposes a burden of responsibility on particle beam centres which also possess in vivo research facilities.
Where future RBE experiments are performed, it will be essential to pursue experiments across the same broad range of dose and LET for each cell/tissue type and to analyze them independently rather than perform a combined analysis of all systems. This principle can be seen in the work of Sørensen et al,29 where combined displays of data do not reveal what is most clearly shown for individual cell types and individual ions. Only then will the data provide useful parameters for each cell/tissue type, since the LET–RBE turnover points are unique for each ion species and the RBE magnitude is dependent on cell type.20 Care must therefore be taken in the analysis of data sets such as Friedrich et al,30 which consists of many different ionic beams, each with unique radiobiological properties. The data analysis presented in this article shows that analyzing heterogeneous systems will arguably provide results which do not reflect well what may be occurring in individual systems. When LQ fits are so similar in a heterogeneous population, it is inevitable that LQ-generated curves would show greater differences if derived from more individualized experiments.
The question must be asked as to why a constant RBE is adopted in the first place? The UK fast neutron authors9–11 adopted a constant “prescription” tumour RBE, which applied in all tissues and at all doses within the patient. This was because the neutron radiotherapy was planned using the coplanar “hand-planning” technique, where the depth dose distribution from each beam was manually added for each field and sometimes weighted to produce as uniform a tumour dose as possible. The RBE would have also required knowledge of what the photon dose would have been in the same tumour and normal tissue locations. Further corrections of the dose per fraction by inclusion of a variable rather than a fixed RBE would have been extremely difficult to implement, as well as time consuming. For PT, the same essential decision was also taken, influenced by in vivo data already presented, which apply to single-field mid-SOBPs, where LET is expected to be low.
There is now a greater appreciation that LET varies considerably in a complex treatment plan, for example, using multiple treatment field directions or with intensity-modulated pencil beams. It follows, from the RBE definitions and if a constant RBE is chosen, that PT will not completely achieve its intended promise. This can be assessed within the formal ICRU definitions of treatment volumes,2,8 with potential increases in effective dose in normal tissue volumes, as well as possibilities that radiosensitive tumours (with very low predicted RBE values <1.1) may be underdosed.8,31 In the absence of dose escalation, improved clinical outcomes will be achieved only if the tumour RBE exceeds that of the prescribed RBE, and also if the prescribed RBE is equal or less than the RBE assumed in each of the critical late-reacting normal tissues. These differences should also be contrasted with the potential advantages of proton therapy which in most instances include a substantial reduction in integral dose, which must influence low-dose vascular and carcinogenic late effects over a much wider volume of interest. To make improvements possible, it will be necessary to allocate individual RBEs to different tissues and for different tumour types, from the knowledge of the LET and dose per fraction they receive.
In comparison with the formal requirements for animal drug testing in the pharmaceutical industry, the past PT experiments would be considered inadequate in terms of the range of tissues tested and the end points used. This is not necessarily a critique of particle therapy, since this also applies to other newer techniques in radiotherapy which are not subjected to a battery of approved radiobiological pre-clinical experiments.
Inclusion of flexible relative biological effects in treatment plans
Nowadays, it would be possible to include a variable RBE within the treatment planning process, but this would require considerable changes within the software. An easier and short-term solution would be to use the existing inbuilt 1.1, but with a carefully considered reduction of the tolerance doses applied to critical late-reacting normal tissues. For very radiosensitive tumours such as many forms of children's cancer, it might be preferable either not to include any RBE correction or use a lesser correction of say 1.05 for the tumour itself. This is because the RBE may be significantly <1.1, which may result in underdosage, since the RBE is used to divide the photon-equivalent dose to provide the physical dose of protons used.8,30 But, care must be taken not to overdose important late-reacting normal tissues where a higher RBE should be applied. The eventual gold standard might be to use dose and LET maps to provide a more appropriately weighted dose, using agreed radiobiological input data. At the present time, greater resources are being devoted to clinical reporting and analysis of LET and RBE,32,33 although sharing of human data nationally or internationally may provide greater statistical power to detect subtle but important findings.
In the future, there may be further predictive assays which feed into RBE values beyond what is now possible by taking assumed α/β ratios (as used in standard clinical radiobiological modelling), or likely values of α and β, especially since gene expression patterns and DNA methylation are markedly different after PT in comparison with conventional therapy X-rays.6,34–37 Such changes, in response to more clustered DNA damage in Bragg peak regions, may influence cell killing and ultimately the RBE dose ratio. It is possible that indications for proton beam therapy in certain tumour types may alter on this basis. It is also intriguing that the oxygen enhancement ratio may also reduce in the Bragg peak regions to the same extent as fast neutrons, because the latter cause ionization mostly by means of recoil protons.
In summary, there is an urgent need for co-ordinated in vitro and in vivo experiments that concentrate on a realistic dose range of 1.5–6 Gy per fraction in clinically relevant tissues such as the spinal cord, lung, kidney and intestine for true late effects. Also, in vitro experiments must be used to test a wide range of human cancer cells in resting and growth conditions, to further investigate the relationship between LET, repair capacity, radiosensitivity and dose per fraction influences on RBE.
Acknowledgments
ACKNOWLEDGMENTS
I wish to thank all my past and present colleagues and coauthors who have stimulated my interest in this field of knowledge, a number too numerous to mention individually. I am indebted to the Award of Guest Professor at the European Centre for Nuclear Medicine (CERN), Geneva, 2015–2016.
APPENDIX A
Using suffixes L and H for low and a higher LET, respectively, isoeffective doses can be represented as:
| (A1) |
As dH approaches zero, β terms can be neglected; so, the RBE (the ratio dL/dH) becomes αH/αL, denoted as RBEmax.
If dL becomes large, α terms are neglected; so, the RBE approaches √βH/√βL, denoted as RBEmin.
It follows that at all intermediate doses, RBE will have a value between those of RBEmax and RBEmin.
For high LET biological effective dose (BED) estimations,10,11,19 the following equation is used:
| (A2) |
where k is the low LET α/β ratio and RBEmax and RBEmin are the limits of RBE at low and high dose, respectively. The low LET (control) radiation BED is given by
| (A3) |
For an isoeffect for each form of radiation, Equations (A5) and (A6) are combined, when n is the same for both treatments, as:
| (A4) |
For a dL value of 2 Gy, the solution for dH can then be found, using k = 3 Gy for most normal tissue late effects, RBEmax = 1.35 and 4, RBEmin = 1.02 and 1.2 for protons and carbon ions, respectively. Then, the RBE values at 2 Gy per fraction of the control radiation are 1.14 and 2.63 Gy, which provide 2-Gy-equivalent doses of 1.75 and 0.76 Gy for protons and carbon ions, respectively. These doses are used in the BED equations to estimate the changes due to RBE uncertainties, where we assume that x operates equally on both RBEmax and RBEmin, so that the high LET BED for each fraction is:
| (A5) |
The change in percentage BEDs are normalized to the values for 1.82 Gy protons and 0.8 Gy carbon ions, which are assumed to be isoeffective with 2-Gy fractions for megavoltage X-rays.
The difference in dose between the dose using the assumed single value of RBE and the dose when x is introduced is given as Δd in results.
To determine RBE from changes in radiosensitivity, it is convenient to use a BED isoeffective equation,
| (A6) |
where k is the low LET α/β ratio.
The solution for dL is obtained, and then divided by dH to provide the RBE as
| (A7) |
This last equation is used to fit the data sets of RBE plotted against dose per fraction, using the non-linear fitting programme in Mathematica.
REFERENCES
- 1.Dale RG, Jones B, Cárabe-Fernández A. Why more needs to be known about RBE effects in modern radiotherapy. Appl Radiat Isot 2009; 67: 387–92. doi: 10.1016/j.apradiso.2008.06.013 [DOI] [PubMed] [Google Scholar]
- 2.International Commission on Radiation Units and Measurements. Prescribing, recording, and reporting proton-beam therapy. (ICRU Report 78). Bethesda, USA: NIH; 2010. [Google Scholar]
- 3.Blomquist E, Russell KR, Stenerlöw B, Montelius A, Grusell E, Carlsson J. Relative biological effectiveness of intermediate energy protons. Comparisons with 60Co gamma-radiation using two cell lines. Radiother Oncol 1993; 28: 44–51. doi: 10.1016/0167-8140(93)90184-A [DOI] [PubMed] [Google Scholar]
- 4.Jones B, Dale RG. Estimation of optimum dose per fraction for high LET radiations: implications for proton radiotherapy, Int J Radiat Oncol Biol Phys 2000; 48: 1549–57. [DOI] [PubMed] [Google Scholar]
- 5.Paganetti H. Relative biological effectiveness (RBE) values for proton beam therapy. Variations as a function of biological endpoint, dose, and linear energy transfer. Phys Med Biol 2014; 59: R419–72. doi: 10.1088/0031-9155/59/22/R419 [DOI] [PubMed] [Google Scholar]
- 6.Tommasino F, Durante M. Proton radiobiology. Cancers (Basel) 2015; 7: 353–81. doi: 10.3390/cancers7010353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dasu A, Toma-Dasu I. Impact of variable RBE on proton therapy. Med Phys 2013; 40: 011705. doi: 10.1118/1.4769417 [DOI] [PubMed] [Google Scholar]
- 8.Jones B. Towards achieving the full clinical potential of proton therapy by inclusion of LET and RBE models. Cancers (Basel) 2015; 7: 460–80. doi: 10.3390/cancers7010460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hornsey S, Field SB. The RBE of cyclotron neutrons for effects on normal tissues. Eur J Cancer 1974; 10: 231–4. doi: 10.1016/0014-2964(74)90180-7 [DOI] [PubMed] [Google Scholar]
- 10.Carabe-Fernandez A, Dale RG, Jones B. The incorporation of the concept of minimum RBE (RBEmin) into the linear-quadratic model and the potential for improved radiobiological analysis of high-LET treatments. Int J Radiat Biol 2007; 83: 27–39. doi: 10.1080/09553000601087176 [DOI] [PubMed] [Google Scholar]
- 11.Carabe-Fernandez A, Dale RG, Hopewell JW, Jones B, Paganetti H. Fractionation effects in particle radiotherapy: implications for hypo-fractionation regimes. Phys Med Biol 2010; 55: 5685–700. doi: 10.1088/0031-9155/55/19/005 [DOI] [PubMed] [Google Scholar]
- 12.Belli M, Bettega D, Calzolari P, Cera F, Cherubini R, Dalla Vecchia M, et al. Inactivation of human normal and tumour cells irradiated with low energy protons. Int J Radiat Biol 2000; 76: 831–9. [DOI] [PubMed] [Google Scholar]
- 13.Britten RA, Nazaryan V, Davis LK, Klein SB, Nichiporov D, Mendonca MS, et al. Variations in the RBE for cell killing along the depth-dose profile of a modulated proton therapy beam. Radiat Res 2013; 179: 21–8. doi: 10.1667/RR2737.1 [DOI] [PubMed] [Google Scholar]
- 14.Paganetti H, Niemierko A, Ancukiewicz M, Gerweck LE, Goitein M, Loeffler JS, et al. Relative biological effectiveness (RBE) values for proton beam therapy. Int J Radiat Oncol Biol Phys 2002; 53: 407–21. doi: 10.1016/S0360-3016(02)02754-2 [DOI] [PubMed] [Google Scholar]
- 15.Weyrather WK, Ritter S, Scholz M, Kraft G. RBE for carbon track-segment irradiation in cell lines of differing repair capacity. Int J Radiat Biol 1999; 75: 1357–64. [DOI] [PubMed] [Google Scholar]
- 16.Warenius HM, Britten RA, Peacock JH. The relative cellular radiosensitivity of 30 human in vitro cell lines of different histological type to high LET 62.5 MeV (p-->Be+) fast neutrons and 4 MeV photons. Radiother Oncol 1994; 30: 83–9. doi: 10.1016/0167-8140(94)90013-2 [DOI] [PubMed] [Google Scholar]
- 17.Jones B. The apparent increase in the β-parameter of the linear quadratic model with increased linear energy transfer during particle irradiation. Br J Radiol 2010; 83: 433–6. doi: 10.1259/bjr/68792966 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jones B, Dale RG, Deehan C, Hopkins KI, Morgan DA. The role of biologically effective dose (BED) in clinical oncology. Clin Oncol (R Coll Radiol) 2001; 13: 71–81. [DOI] [PubMed] [Google Scholar]
- 19.Jones B, Underwood TSA, Carabe-Fernandez A, Timlin C, Dale RG. Further analysis of fast neutron relative biological effects and implications for charged particle therapy. Br J Radiol 2011; 84: S11–18. doi: 10.1259/bjr/67509851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jones B. A simpler energy transfer efficiency model to predict relative biological effect for protons and heavier ions. Front Oncol 2015; 5: 184.. Available from: http://journal.frontiersin.org/article/10.3389/fonc.2015.00184 + Corrigendum (in press). doi: 10.3389/fonc.2015.00184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Trott KR, Doerr W, Facoetti A, Hopewell J, Langendijk J, van Luijk P, et al. Biological mechanisms of normal tissue damage: importance for the design of NTCP models. Radiother Oncol 2012; 105: 79–85. doi: 10.1016/j.radonc.2012.05.008 [DOI] [PubMed] [Google Scholar]
- 22.Dörr W. Radiobiology of tissue reactions. Ann ICRP 2015; 44(Suppl. 1): 58–68. doi: 10.1177/0146645314560686 [DOI] [PubMed] [Google Scholar]
- 23.Gueulette J, Octave-Prignot M, De Costera BM, Wambersie A, Grégoire V. Intestinal crypt regeneration in mice: a biological system for quality assurance in non-conventional radiation therapy. Radiother Oncol 2004; 73(Suppl. 2): S148–54. [DOI] [PubMed] [Google Scholar]
- 24.Jones B, Underwood TS, Dale RG. The potential impact of relative biological effectiveness uncertainty on charged particle treatment prescriptions. Br J Radiol 2011; 84: S61–9. doi: 10.1259/bjr/36792876 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bentzen SM. Radiobiological considerations in the design of clinical trials. Radiother Oncol 1994; 32: 1–11. doi: 10.1016/0167-8140(94)90443-X [DOI] [PubMed] [Google Scholar]
- 26.Calugaru V, Nauraye C, Noël G, Giocanti N, Favaudon V, Mégnin-Chanet F. Radiobiological characterization of two therapeutic proton beams with different initial energy spectra used at the Institut Curie Proton Therapy Center in Orsay. Int J Radiat Oncol Biol Phys 2011; 81: 1136–43. doi: 10.1016/j.ijrobp.2010.09.003 [DOI] [PubMed] [Google Scholar]
- 27.Grassberger C, Trofimov A, Lomax A, Paganetti H. Variations in linear energy transfer within clinical proton therapy fields and the potential for biological treatment planning. Int J Radiat Oncol Biol Phys 2011; 80: 1559–66. doi: 10.1016/j.ijrobp.2010.10.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dosanjh M, Jones B, Myers S. A possible biomedical facility at the European Organization for Nuclear Research (CERN). Br J Radiol 2013; 86: 20120660. doi: 10.1259/bjr.20120660 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sørensen BS, Overgaard J, Bassler N. In vitro RBE-LET dependence for multiple particle types. Acta Oncol 2011; 50: 757–62. doi: 10.3109/0284186X.2011.582518 [DOI] [PubMed] [Google Scholar]
- 30.Friedrich T, Scholz U, Elsässer T, Durante M, Scholz M. Systematic analysis of RBE and related quantities using a database of cell survival experiments with ion beam irradiation. J Radiat Res 2013; 54: 494–514. doi: 10.1093/jrr/rrs114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jones B. Patterns of failure after proton therapy in medulloblastoma. Int J Radiat Oncol Biol Phys 2014; 90: 25–6. doi: 10.1016/j.ijrobp.2014.05.054 [DOI] [PubMed] [Google Scholar]
- 32.Giantsoudi D, Sethi RV, Yeap BY, Eaton BR, Ebb DH, Caruso PA, et al. Incidence of CNS injury for a cohort of 111 patients treated with proton therapy for medulloblastoma: LET and RBE associations for areas of injury. Int J Radiat Oncol Biol Phys 2016; 95: 287–96. doi: 10.1016/j.ijrobp.2015.09.015. [Epub ahead of print]. [DOI] [PubMed] [Google Scholar]
- 33.Yock TI, Yeap BY, Ebb DH, Weyman E, Eaton BR, Sherry NA, et al. Long term toxic effects of proton radiotherapy for paediatric medulloblastoma: a phase 2 single arm study. Lancet Oncol 2016; 17: 287–298. doi: http://dx.doi.org/org/10.1016/S1470-2045(15)00167-9 [DOI] [PubMed] [Google Scholar]
- 34.Chaudhary P, Marshall TI, Currell FJ, Kacperek A, Schettino G, Prise KM. Variations in the processing of DNA double-strand breaks along 60-MeV therapeutic proton beams. Int J Radiat Oncol Biol Phys 2016; 95: 86–94. doi: 10.1016/j.ijrobp.2015.07.2279. [Epub ahead of print]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chaudhary P, Marshall TI, Perozziello FM, Manti L, Currell FJ, Hanton F, et al. Relative biological effectiveness variation along monoenergetic and modulated Bragg peaks of a 62-MeV therapeutic proton beam: a preclinical assessment. Int J Radiat Oncol Biol Phys 2014; 90: 27–35. doi: 10.1016/j.ijrobp.2014.05.010 [DOI] [PubMed] [Google Scholar]
- 36.Girdhani S, Sachs R, Hlatky L. Biological effects of proton radiation: what we know and don't know. Radiat Res 2013; 179: 257–72. doi: 10.1667/RR2839.1 [DOI] [PubMed] [Google Scholar]
- 37.Girdhani S, Sachs R, Hlatky L. Biological effects of proton radiation: an update. Radiat Prot Dosimetry 2015; 166: 334–8. doi: 10.1093/rpd/ncv178 [DOI] [PubMed] [Google Scholar]