Motion-Robust Reconstruction based on Simultaneous Multi-Slice Registration for Diffusion-Weighted MRI of Moving Subjects

Abstract

Simultaneous multi-slice (SMS) echo-planar imaging has had a huge impact on the acceleration and routine use of diffusion-weighted MRI (DWI) in neuroimaging studies in particular the human connectome project; but also holds the potential to facilitate DWI of moving subjects, as proposed by the new technique developed in this paper. We present a novel registration-based motion tracking technique that takes advantage of the multi-plane coverage of the anatomy by simultaneously acquired slices to enable robust reconstruction of neural microstructure from SMS DWI of moving subjects. Our technique constitutes three main components: 1) motion tracking and estimation using SMS registration, 2) detection and rejection of intra-slice motion, and 3) robust reconstruction. Quantitative results from 14 volunteer subject experiments and the analysis of motion-corrupted SMS DWI of 6 children indicate robust reconstruction in the presence of continuous motion and the potential to extend the use of SMS DWI in very challenging populations.

1 Introduction

Diffusion-weighted magnetic resonance imaging (DWI) is the technique of choice for the analysis of neural microstructure and structural connectivity in the brain. While early works focused on a diffusion tensor imaging (DTI) model to describe major fiber bundles, models and techniques have evolved to characterize the complex underlying structure of the neural anatomy including crossing fibers and free water compartments [1, 2]. Fitting more complex models requires relatively dense q-space sampling which can be extremely time consuming. Acceleration through simultaneous multi-slice (SMS) acquisition with multiband excitation and controlled aliasing [3] has played a significant role in routine use of these techniques in large-scale projects such as the human connectome project [4].

Accelerations of a factor of two or more are achieved by SMS DWI, but these scans are still lengthy and generate loud noise and vibration that is not easily tolerated by non-cooperative patients, children, and newborns, who may move continuously during a DWI scan. Extensive research has been done on motion-robust sequences and motion correction methods in MRI [5], but the use of these methods is limited by the the type and amount of motion that can be corrected, and the challenges in implementation or setup. Motion correction in DWI is currently performed at the volume level either retrospectively using volume-to-volume registration [6] or prospectively using navigators [7]. These techniques are slow and do not perform well when motion is continuous and fast.

There has been some promising work on slice-level motion correction in DWI to deal with continuous motion [8–11]. While robust motion estimation is a challenge in these techniques, SMS DWI, which is being increasingly used, holds the potential to facilitate slice-level motion correction by the novel approach proposed in this paper. We achieve this by 1) integrating a model of motion with image registration that particularly takes advantage of rigidly-coupled simultaneously acquired multiple slices to strengthen slice-level motion tracking and estimation; 2) detecting and rejecting intra-slice motion; and 3) robust reconstruction of multi-compartment models from motion-corrected SMS DWI data. This work extends our earlier work on motion-robust DTI reconstruction [11].

2 Materials and Methods

An SMS DWI scan is performed by interleaved 2D echo-planar imaging with M_B multi-band excitations. Therefore, at the smallest time step, k-space data is acquired for M_B slices simultaneously from multiple receiver coils and is used to reconstruct slice images through unaliasing. Subject motion can occur between excitations (i.e. inter-slice motion) or within excitation-sampling (i.e. intra-slice motion). The latter results in signal loss or distortion in all M_B slices. Our approach constitutes tracking the dynamics of motion through slice-level image registration, and detecting and excluding slices corrupted by intra-slice motion.

2.1 Slice-Level Motion Tracking and Estimation

Slice-to-volume registration, used previously for inter-slice motion correction and image reconstruction, is often initialized by volume-to-volume registration. This is suboptimal and is not robust. In contrast, we introduce the notion of slice-level motion tracking, where image registration is used to capture the dynamics of motion. We formulate the problem as a dynamic state-space model estimation where slices, as observations, are used in image registration to estimate motion parameters considered to be the hidden states. We take advantage of slice timing profile and the 3D coverage of the anatomy provided by multiple slices acquired simultaneously in an SMS acquisition (see Fig. 1a).

Fig. 1.

(a) Three slices are acquired simultaneously by a 3-band SMS DWI: as compared to a single slice, these rigidly-coupled slices provide a multi-plane (3D) coverage of the anatomy, therefore they mitigate the ill-posed problem of slice-to-volume registration. (b) Pairs of arrows point at intra-slice motion artifacts seen in simultaneously acquired slices in a 2-band axial SMS DWI. Partial signal loss is observed in a corrupted axial slice on the right. (c) Outliers of the proposed mean and median metrics on a difference filtered image are used to detect intra-slice motion (x-axis is the slice number).

Assuming that one set of simultaneous slices y_k = {y₁, y₂, …, y_MB} are acquired at a time k, we show the relative position of the head at time k by the hidden states x_k, where x_k in this case is a vector of 6 rigid transformation parameters. Given a finite sequence of observations (slice acquisitions), our goal is to estimate the states x_k of motion dynamics governed by a stochastic equation:

$${\mathbf{x}}_k={\mathbf{x}}_{k-1}+{\omega }_{k-1},\hspace{1em}{\mathbf{y}}_k=\mathrm{H}({\mathbf{x}}_k)+{\nu }_k$$ (1)

where ω_k and ν_k are the process and measurement noise and represent uncertainty in the modeling of motion dynamics and measurements, respectively. H is a function that relates states x_k to the measurements y_k. In other words, H is a generative function for the slices y_k acquired at time k at head position x_k.

We aim to use Kalman filter for state estimation, so we separate the non-linear output model from the filtering process, rewrite it as z_k = x_k + ν_k, and integrate it with image registration that estimates z_k by matching the observations (as target) and the reference image (as source) transformed by p; i.e. ${\mathbf{z}}_k=\underset{\mathbf{P}}{\text{argmax}}\mathit{\text{Sim}}(\mathrm{H}(\mathbf{p}),{\mathbf{y}}_k)$, where Sim(․) is a similarity metric between the set of M_B slices (y_k) and the transformed source image. Simultaneous slices in y_k are in maximum distance to each other and provide 3D multi-plane coverage of the anatomy, thus enable 3D image-based navigation as opposed to a single slice that only provides a single-plane coverage. Image registration based on y_k is thus much more robust than slice-to-volume registration based on a single slice. The output of image registration is z_k, which is then used in state estimation.

For robust state estimation in the presence of nonlinearity and registration errors, we use an outlier-robust Kalman filter [12], which assumes a Gaussian distribution for the process noise, i.e. ω_k~𝒩(0, Q), but updates the measurement noise (ν_k~𝒩(0, S_k)) based on sequential observations by estimating its covariance S_k at time k. S_k is sampled from a Wishart distribution as ${\mathrm{S}}_k^{-1}$ ~ 𝒲 (R⁻¹/s, s), where Λ ≻ 0 is a precision matrix with s degrees of freedom. The prior mean of 𝒲 (Λ, s) is sΛ where s quantifies the concentration of the distribution around its mean [12]. Algorithm 1 shows the pseudo code of the entire process.

2.2 Intra-Slice Motion Detection and Rejection

Intra-slice motion at time k results in signal loss and distortion in all slices that are acquired at k. Fig. 1b shows an example. To detect it, we rely on the fact that SMS DWI slices are acquired in an interleaved manner and fast intra-slice motion occurs occasionally. As such, we use inter-slice intensity discontinuity [13] to detect motion-corrupted slices. In this approach, we compute an intensity difference image I_d by subtracting the image from a filtered version of it based on a morphological closing filter. We use robust statistics to detect intra-slice motion; i.e. a slice is considered to be affected by intra-slice motion if its median in I_d is greater than 0 or its mean is an outlier (Fig. 1c) [11]. When intra-slice motion is detected at time k, all M_B rejected.

Algorithm 1.

Pseudo-code of the slice-level motion estimation algorithm

Input: H, yk = {y1 y2, … yMB}, x̂k−1
Output: x̂k
1:	register source to simultaneous slices: ${\mathbf{z}}_k\leftarrow \underset{\mathbf{p}}{\text{max}}\mathit{\text{Sim }}(\mathrm{H}(\mathbf{p}),{\mathbf{y}}_k)$; p0 = x̂k−1
2:	predict states: ${\hat{\mathbf{x}}}_k^{-}\leftarrow {\hat{\mathbf{x}}}_{k-1},\hspace{1em}{\hat{\mathbf{x}}}_k\leftarrow {\hat{\mathbf{x}}}_k^{-};\hspace{1em}{\mathrm{P}}_k^{-}\leftarrow {\mathrm{P}}_{k-1}+\mathrm{Q},\hspace{1em}{\mathrm{P}}_k\leftarrow {\mathrm{P}}_k^{-}$
3:	repeat
4:	update noise: δ = zk − x̂k ; Λk = (sR + δδT + Pk)/(s + 1)
5:	update states: ${\mathrm{K}}_k={({\mathrm{P}}_k^{-}+{\Lambda }_k)}^{-1}{\mathrm{P}}_k^{-1};\hspace{1em}{\hat{\mathbf{x}}}_k={\hat{\mathbf{x}}}_k^{-}+{\mathrm{K}}_k^T({\mathbf{z}}_k-{\hat{\mathbf{x}}}_k^{-})$
6:	${\mathrm{P}}_k={\mathrm{K}}_k^T{\Lambda }_k{\mathrm{K}}_k+{(\mathrm{H}-{\mathrm{K}}_k)}^T{\mathrm{P}}_k^{-}(\mathrm{H}-{\mathrm{K}}_k)$
7:	until converged
8:	return x̂k

2.3 Model Reconstruction from Motion-Corrected Data

We aim to fit a model to motion-corrected DWI data from non-diffusion weighted scans S₀ and diffusion-weighted scans S_i (b_i ≠ 0) with gradients g_i and b values b_i. We formulated the problem based on a ball-and-stick model [1] (but a similar approach can be used for other multi-compartment models and DTI):

$$S_i=S_0\sum _{j=0}^N{f}_j{e}^{-b_i{g}_i^T{\mathbf{D}}_j{g}_i},$$ (2)

where D_js are 3 × 3 symmetric positive definite (SPD) matrices, and f_j ∈ [0,1] are sum-of-unity fractions of occupancy. This model assumes that all D_js have equal first eigenvalues (λ₁), a single ball compartment quantifies isotropic water fraction, and the stick compartments quantify fibers. The model has 3N + 1 degrees-of-freedom. To ensure estimation of SPD matrices we parameterized the tensors D_j in the log-domain by setting L = (log(D₁), …,log(D_N)).

To estimate model parameters, we used maximum a posteriori (MAP) estimation at the voxel level, i.e. $\{\hat{\mathbf{L}},\hat{\mathbf{f}}\}=\underset{\mathbf{L},\mathbf{f}}{\text{argmax}}p(\mathbf{L},\mathbf{f}|{\mathbf{S}}_{\mathbf{i}})$, where f = (f₁, … f_N) is the vector of the compartment fractions. The issue here is that due to motion and slice-level motion correction, voxels from S₀ and S_i slices are not spatially aligned and are scattered in 3D space; therefore, the q-space is differently sampled at every voxel. To handle this, we built a 3D high-resolution vector-class image in the space of S₀ (i.e. V₀) from motion-corrected DWI slices. Each voxel of this image (v ∈ V₀) is a variable-length vector (of length M_v) of a class that contains the intensity values (C_is), g_is corrected by the estimated rotation matrices (from estimated slice motion parameters), b_is, and finally the physical coordinates and direction, of all M_v DWI voxels mapped to the neighborhood (one-voxel radius) of v after motion correction. We assumed a uniform distribution for the a priori probability distribution functions and a zero-mean normal distribution with variance σ² around the unknown modeled signal S_i:

$$P(\mathbf{C}|\mathbf{L},\mathbf{f})=\prod _{v\in V_0}\frac{1}{\sigma \sqrt{2\pi }}\text{exp}(\frac{-{\sum }_{i=1}^{M_v}{\omega }_i{\Vert S_i(e^{{\mathbf{L}}_v},{\mathbf{f}}_v)-C_i\Vert }^2}{2{\sigma }^2})$$ (3)

The weights (w_i) are calculated by the distance between neighborhood voxels and the reference voxel by a Gaussian kernel that models the point-spread-function of the DWI slice acquisition. We used numerical optimization [14] and gradually increased the complexity of the model from a single stick to the ball-and-stick.

3 Experimental Results

For quantitative evaluation, first we performed 14 volunteer subject motion experiments with different amounts and types of head motion up to 30° rotation in 2 volunteers; we also acquired 3 motion-free DWI scans for each volunteer, which were used as gold standard (GS). Each DWI scan involved 6 b = 0 and 30 b ≠ 0 volumes, and a multi-band factor of 2, for which we fit a DTI model. We used normalized cross correlation similarity metric for slice-level motion estimation in both b = 0 and b ≠ 0 images, and mutual information to register the reconstructed S₀ and S_i images. The amount of motion was estimated for each experiment using $d=\sqrt{x^2+y^2+z^2+{(cr)}^2}$, where x, y and z are the translation parameters, c = 50 mm, and r is the Euler angle of the estimated motion, which is computed from 3 rotation angles based on Euler's rotation theorem.

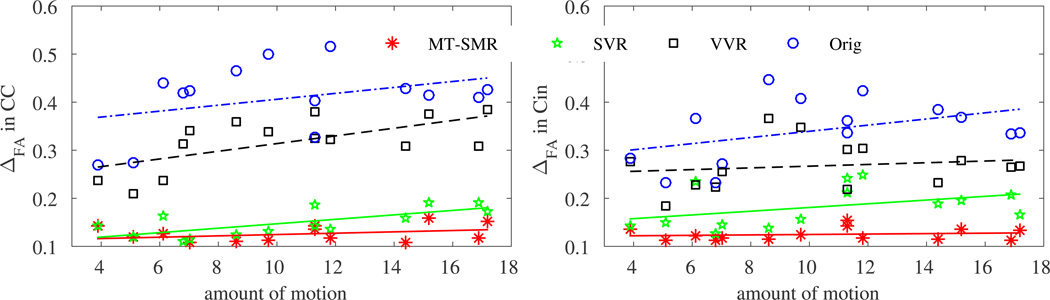
We compared the performance of our motion tracking based on simultaneous multi-slice registration (MT-SMR) to the original reconstruction without motion correction (Orig), reconstruction with volume-to-volume registration (VVR) [6], and slice-to-volume registration (SVR) initialized by VVR [8]. Fig. 2 shows sample DTI results: color-coded fractional anisotropy (FA) maps. We calculated the difference in FA values (Δ_FA), mean diffusivity (Δ_MD), and angular difference of first eigenvectors (Δ_Dir) between each method and the GS in four regions-of-interest (ROIs): corpus callosum (CC), cingulum (Cin), limbs of the internal capsule (LIC), and the lateral ventricles (Vent). The average results, given in Table 1, show consistently lower errors by MT-SMR compared to the other methods. We plotted Δ_FA in the CC and Cin ROIs vs. the estimated amount of motion in Fig. 3. While the errors were high in VVR, SVR, and Orig, MT-SMR generated lower errors in a robust manner regardless of the amount of motion.

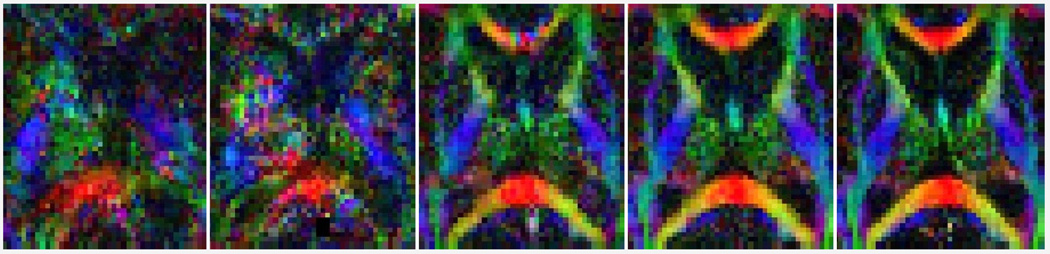
Fig. 2.

Axial (top) and sagittal (bottom) views of color FA in a volunteer. MT-SMR generated FA very similar to the GS (motion-free) and outperformed other methods.

Table 1.

The mean of Δ_FA, Δ_Dir and Δ_MD error metrics in corpus callosum (CC), cingulum (Cin), limbs of the internal capsule (LIC) and ventricles (Vent) regions. MT-SMR consistently generated the lowest errors in all regions (highlighted in bold).

	ΔFA				ΔDir				ΔMD(×103)
	Orig	VVR	SVR	SMR	Orig	VVR	SVR	SMR	Orig	VVR	SVR	SMR
CC	0.41	0.32	0.15	0.12	0.75	0.76	0.36	0.30	1.16	1.05	0.56	0.50
Cin	0.34	0.27	0.18	0.12	0.93	0.92	0.53	0.36	0.22	0.27	0.15	0.09
LIC	0.26	0.23	0.11	0.10	0.54	0.56	0.30	0.27	0.27	0.19	0.09	0.08
Vent	0.13	0.11	0.08	0.07	0.87	0.86	0.83	0.82	0.91	0.72	0.25	0.22

Fig. 3.

FA value differences (Δ_FA) between the gold-standard (GS) and each motion-correction method in the CC and Cin ROIs based on the amount of motion (mm). Regardless of the amount of motion, MT-SMR generated low errors in all experiments.

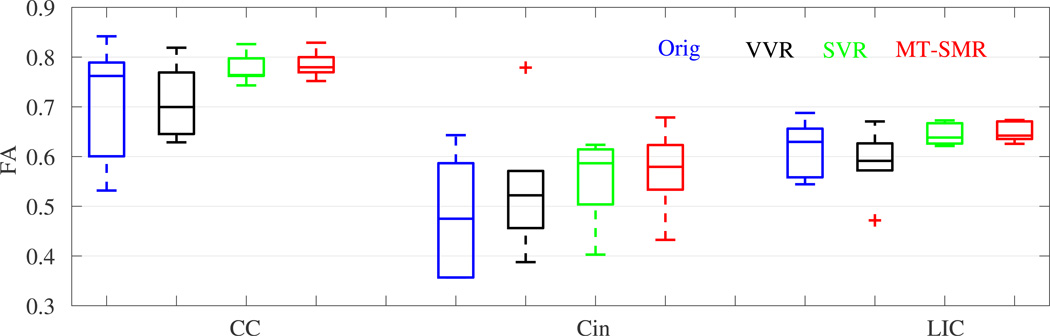
Next, we applied our method to multi b-value, 90-direction, motion-corrupted DWI scans of 6 children (between 3 and 14 years old), who significantly moved during DWI scans. We fit a single tensor model as well as a ball-and-stick model with N = 3. Based on a single tensor model, we calculated FA in the CC, Cin, and LIC ROIs. Motion blurs the images and reduces FA in these fiber-rich regions. On the other hand, if motion is corrected and FA is robustly reconstructed, we expect high FA in these regions. Fig. 4 shows boxplot analysis of the results, which indicates superior performance of MT-SMR compared to the other methods. Fig. 5 shows multiple fascicles and isotropic water fraction compartments detected by different methods from motion-corrupted DWI of a 5 year old child. The structure and direction of crossing fibers is correctly identified by MT-SMR.

Fig. 4.

Boxplot analysis of the FA of 4 methods in 3 ROIs (CC, Cin, LIC) using DWI of 6 children who moved during scans. The high FA values with low variance by MT-SMR in these fiber-rich ROIs indicate robust reconstruction in the presence of motion.

Fig. 5.

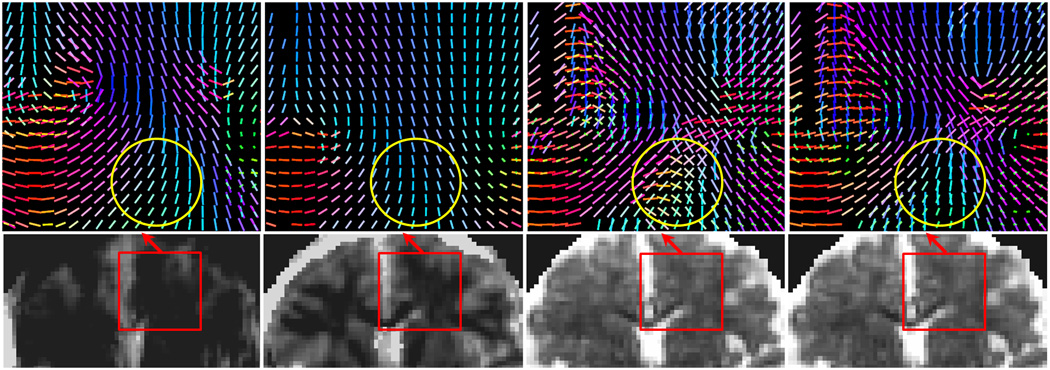
Top: multiple fascicles, and bottom: isotropic water fraction, detected by the ball-and-stick model by different methods. The results from MT-SMR (d) comply with our knowledge of the anatomy in this region where fascicles from CC, corticospinal tracts, and the superior longitudinal fasciculus cross. Orig and VVR generated blurred, inaccurate isotropic water fraction maps, and failed to find crossing fibers in many regions, and SVR (c) generated wrong angles in the ROI highlighted by circles.

4 Discussions and Conclusion

We developed a slice-level motion tracking and estimation technique that takes advantage of the 3D coverage of the anatomy at multiple image planes provided by simultaneously acquired slices in SMS DWI. We showed that this technique outperforms slice-to-volume registration as it performs 3D registration based on data from multiple planes rather than a single plane. This technique also outperforms the current routinely-used volume-to-volume registration techniques as it enables faster motion tracking which results in more efficient use of DWI data. In this work, we reported retrospective analysis of motion-corrupted data, but our motion tracking and estimation system is causal, therefore, with sufficient computation power it can be implemented and used in real-time for prospective motion tracking and correction. This technique can extend the use of SMS DWI to populations that move near continuously during lengthy DWI scans.