Intrinsic α helix propensities compact hydrodynamic radii in intrinsically disordered proteins

Abstract

Proteins that lack tertiary stability under normal conditions, known as intrinsically disordered, exhibit a wide range of biological activities. Molecular descriptions for the biology of intrinsically disordered proteins (IDPs) consequently rely on disordered structural models, which in turn require experiments that assess the origins to structural features observed. For example, while hydrodynamic size is mostly insensitive to sequence composition in chemically denatured proteins, IDPs show strong sequence-specific effects in the hydrodynamic radius (R_h) when measured under normal conditions. To investigate sequence-modulation of IDP R_h, disordered ensembles generated by a Hard Sphere Collision model modified with a structure-based parameterization of the solution energetics were used to parse the contributions of net charge, main chain dihedral angle bias, and excluded volume on hydrodynamic size. Ensembles for polypeptides 10 to 35 residues in length were then used to establish power-law scaling relationships for comparison to experimental R_h from 26 IDPs. Results showed the expected outcomes of increased hydrodynamic size from increases in excluded volume and net charge, and compaction from chain-solvent interactions. Chain bias representing intrinsic preferences for α helix and polyproline II (PP_II), however, modulated R_h with intricate dependence on the simulated propensities. PP_II propensities at levels expected in IDPs correlated with heightened R_h sensitivity to even weak α helix propensities, indicating bias for common (φ, ψ) are important determinants of hydrodynamic size. Moreover, data show that IDP R_h can be predicted from sequence with good accuracy from a small set of physicochemical properties, namely intrinsic conformational propensities and net charge.

INTRODUCTION

Structural characterizations of intrinsically disordered proteins (IDPs) provide key molecular details from which to understand the broad range of biological tasks that have been associated with this protein class.^1-4 Identified by a persistent lack of tertiary stability, intrinsic disorder is common in eukaryotic proteins and protein domains.¹ Functionally, IDPs have roles regulating gene expression,^5,6 cellular communication,^7-9 and subcellular spatial organization,^10-12 as well as mechanical duties like maintaining curvature in the cell bilayer.¹³ Molecular descriptions of IDP biology and its associated human disorders^6,9,14 thus depend on an accurate accounting of the features and properties of disordered protein structures.

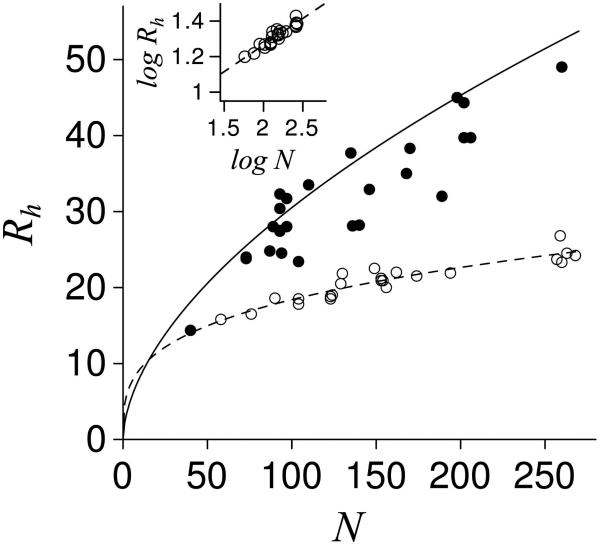
Hydrodynamic size, as represented by the radius of gyration, R_g, or the hydrodynamic radius, R_h, has been widely used for quantifying protein structures^15-17 and other polymers.^18-20 R_h measured under normal conditions and from published reports for IDPs^21-39 and folded proteins^16,40,41 are provided in Figure 1. When comparing sets of R_h (or R_g), logarithmic plots of R_h and N, the number of subunits in a polymer (e.g., the number of amino acids in a protein), are useful since the y-axis intercept and slope in the dataset trend provide a pre-factor (R_o) and exponent (v) for a power-law scaling relationship that can be used to numerically approximate R_h from N; R_h ~ R_o·N^v. More importantly, v, sometimes referred to as the Flory exponent, provides information on the nature of the molecular interactions governing the observed R_h.^42,43 For v less than 0.5, polymers are considered to be in ‘poor’ solvents where chain-chain intramolecular interactions dominate relative to chain-solvent intermolecular interactions. For example, a log-log plot of R_h and N for the folded proteins in Figure 1 (see inset) yields v = 0.3, indicating that the hydrodynamic dimensions of folded proteins are established mostly from intramolecular chain-chain contacts (e.g., hydrogen bonds, ionic pairs, packing interactions) that form owing to folding and the accompanying burial of atomic surfaces. If folded proteins are transferred to solutions with high concentrations of urea or guanidine hydrochloride, causing denaturation of native folds, v increases to ~ 0.6.^15,16 Polymers are considered to be in ‘good’ solvents where chain-solvent interactions dominate relative to chain-chain interactions when v is greater than 0.5.^42,43 The observed v for chemically-denatured proteins thus predicts well-solvated structures with few stable tertiary contacts and minimal burial of atomic surfaces.

Figure 1.

R_h trends with N in proteins. Solid and open circles are IDPs^21-39 and folded proteins,^16,40,41 respectively. The trend for folded proteins, R_h = 4.65·N^0.30, was determined from the inset plot and is shown by the dashed line. The trend for chemically denatured proteins, R_h = 2.21·N^0.57, from Wilkins¹⁶ is shown by the solid line. R_h is reported in Å. Inset: Plot of log R_h and log N for the folded proteins, which gave a linear slope and y-intercept of 0.298 (v ~ 0.30) and 0.667 (R_o = antilog (0.667) ~ 4.65), respectively.

When comparing R_h from IDPs under normal conditions to the expected hydrodynamic size of a protein in a poor solvent, given by the power-law scaling relationship for folded proteins (see Figure 1), it is not surprising that IDP R_h are noticeably larger relative to folded proteins of similar N. IDP structures are mostly lacking in stable, tertiary contacts^1-4 that are hallmarks of folded and globular proteins and, accordingly, should exhibit larger v and concomitant larger R_h. Likewise, since normal aqueous solutions are poor solvents for polypeptides relative to concentrated urea or guanidine hydrochloride solutions, as demonstrated with solubility studies^44-46 and fluorescence correlation spectroscopy experiments,⁴⁷ it may not be surprising that IDPs exhibit R_h that are usually, but not always, smaller than the trend for chemically-denatured proteins. From the reference of folded and chemically-denatured proteins, R_h that have been observed for IDPs are reasonable.

In contrast to chemically denatured proteins, which yield R_h and R_g that are mostly insensitive to details of amino acid sequence,^15,16 IDPs with similar N often show large differences in R_h. For example, R_h ranges from ~ 24-32 Å for IDPs with N ~ 90 in the dataset of Figure 1. The molecular origins for these differences in R_h could be owing to coulombic interactions between charged side chains, since the spacing⁴⁸ and sequential patterns⁴⁹ of charged groups in disordered structures are known to influence R_h. Biases in main chain dihedral angles, such as propensities for (φ, ψ) associated with type II polyproline helix (PP_II), are also thought to modulate R_h in disordered structures.^21,48 Overall, these data indicate that certain sequence details are capable of modulating the structural features of disordered proteins under normal conditions. Identifying the influential physical properties and determining their relative strengths (i.e., energetics) and additivities are thus prerequisites for a quantitative description of IDP structures.

Here, we investigate the effects of net charge, main chain dihedral angle bias, and excluded volume on the hydrodynamic dimensions of IDPs as reported by R_h. The term ‘excluded volume’ is used to represent the exclusion of chain conformations from steric restrictions associated with atomic volumes. Computer simulation of disordered structures using a Hard Sphere Collision (HSC) model developed by Richards⁵⁰ and modified to approximate chain-solvent interactions using the solvent accessible surface area (SASA) parameterization of Hilser and Freire⁵¹ provided a theoretical construct from which to parse and combine these structural effectors. Simulations were used to generated large conformational ensembles of disordered polypeptides ranging in size from 10 to 35 residues that were then used to establish power-law scaling relationships for comparison to the set of IDP R_h in Figure 1. Since prior experiments and calculations have shown that the hydrodynamic sizes of disordered ensembles are indeed sensitive to sequence details associated with net charge and intrinsic PP_II propensities,^{21,48,49,52-54} experimental R_h from IDPs with net charge and chain bias for PP_II that are statistically elevated relative to dataset norms were verified using dynamic light scattering (DLS) and analytical size exclusion chromatography (SEC) techniques. These verifications of experimental R_h were performed to control for data that could be strongly influential in our comparative study.

The results indicated that excluded volume effects owing to sequence differences were generally minor for establishing hydrodynamic size differences among IDPs. Net charge effects on R_h were mostly consistent across the IDP dataset, whereby increases in net charge correlated with increased R_h, showing agreement with previous reports.^52-54 The IDP with the highest net charge, prothymosin-α, however, trended separately from the other IDPs in the dataset when assessing apparent R_h sensitivity to net charge. An important structural parameter for establishing R_h in disordered ensembles seemed to be main chain dihedral angle bias. R_h sensitivity to chain bias for α helix was detected in both a sequence analysis of the IDP dataset and computer generated ensembles simulated with the HSC model. Of note, the effects on R_h from α helix propensities, which caused compaction, were stronger when combined with PP_II propensities. Overall, the results indicate a key role provided by intrinsic chain bias for determining the hydrodynamic size and show that, at least under normal conditions, IDP R_h can be described accurately from sequence-based estimates of intrinsic conformational propensities and net charge.

MATERIALS AND METHODS

Computer Generation of Disordered Structures

Conformers for polypeptide chains restricted to the 20 normal amino acids were generated by a random search of conformational space using the HSC model.^40,50 A detailed description of the computer algorithm is available elsewhere.⁵⁵ Briefly, this model uses van der Waals atomic radii^56,57 as the only scoring function to eliminate grossly improbable conformations. The procedure to generate a random conformer starts with a unit peptide and all other atoms for a chain are determined by the rotational matrix.⁵⁸ Backbone atoms are generated from the dihedral angles φ, ψ, and ω and the standard bond angles and bond lengths.⁵⁹ To sample conformational space efficiently, (φ, ψ) are restricted to the allowed Ramachandran regions.⁶⁰ For peptide bond dihedral angles (ω), non-PRO amino acids were given 100% trans form (180°) and PRO sampled the cis form (0°) at a rate of 10% if the preceding amino acid was non-PRO, and at a rate of 6% if the preceding amino acid was PRO.⁶¹ The dihedral angle ω was given a Gaussian fluctuation of ± 5° around the value of 180° or 0°. Of the two possible positions of the C_β atom, the one corresponding to L-amino acid residues was used throughout the studies. The positions of all other side chain atoms were determined from random sampling of rotamer libraries.⁶² To calculate state distributions typical of protein ensembles, a structure-based energy function parameterized to solvent-accessible surface areas was used to population-weight the generated structures.^63-71

Expression and purification of recombinant protein

Genes coding for Hdm2-ABD and prothymosin-α, each including an N-terminal histidine tag and thrombin cleavage site, were cloned into plasmid expression vectors by DNA 2.0 (Menlo Park, California). Hdm2-ABD and prothymosin-α were individually expressed, isolated from bacterial lysate, and affinity tag removed using the expression and purification protocols described elsewhere for recombinant human p53(1-93).⁷² The same expression and purification protocols were used for recombinant wild type human p53(1-93) and the PRO⁻ and ALA⁻PRO⁻ variants.²¹ Recombinant PGR was provided as a gift from Andrew Herr (Cincinnati Children’s Hospital, Cincinnati, Ohio, USA). R_h for each IDP was measured by techniques based on dynamic light scattering (DLS) and size exclusion chromatography (SEC), described below. SEC methods require a linear relationship between K_D (distribution coefficient) and R_h for the tested range, which was demonstrated using the folded proteins Staphylococcal nuclease, bovine erythrocyte carbonic anhydrase, chicken egg albumin, and horse heart myoglobin. Nuclease was expressed and isolated using the protocols described elsewhere.⁷³ Carbonic anhydrase, albumin, and myoglobin were purchased from Sigma-Aldrich (St. Louis, MO) and further processed by ion exchange chromatography and extensive dialysis to remove residual contaminants.

DLS measured R_h

Dynamic light scattering readings used noninvasive backscatter optics and were measured using a Zetasizer Nano ZS with Peltier temperature control from Malvern Instruments (Worcestershire, UK). All measurements were performed at 25 °C and used 1-cm path-length quartz cuvettes, as described elsewhere.^21,40 Samples contained 600 μL of ~ 0.5 mg/mL protein and were filtered immediately prior to use by 0.2-μm PVDF syringe-driven filters. R_h reported for each protein was the average of at least 5 measurements.

SEC measured R_h

Size exclusion chromatography (SEC) experiments used Sephadex G-75 (GE Healthcare, Piscataway, NJ) equilibrated in 10 mM sodium phosphate, 100 mM sodium chloride, pH 7, following previously described protocols.^21,40 Elution volumes (V_e) for each protein were determined from chromatograms measured using a Bio-Rad BioLogic LP System equipped with a UV absorbance monitor (Hercules, CA). Each sample was 100 µL and contained 0.5–1 mg/mL protein in 10 mM sodium phosphate, 100 mM sodium chloride, pH 7 with 3 mg/mL blue dextran and 0.3 mg/mL 2,4-dinitrophenyl-L-aspartate added as indicator dyes for determining the void (V_o) and total (V_t) column volumes, respectively. For PGR and prothymosin-α, which lack PHE residues and have low absorbance at 280 nm, 250 µL samples containing 3-4 mg/mL of protein were used. K_D for each protein was determined as K_D = (V_e - V_o)/(V_t - V_o). K_D reported for each protein was the average of at least 3 room-temperature (~ 22 °C) measurements.

RESULTS

Composition of experimental R_h dataset

The hydrodynamic dimensions of disordered proteins under normal conditions are known to depend on sequence, specifically proline⁵⁴ and alanine content,²¹ chain length,⁵⁴ chain bias for PP_II,⁴⁸ net charge,^52-54 and charge distributions where mixing of positive and negative charged residues show compaction relative to linear stretches of like charges.^48,49 IDPs in the experimental dataset, which numbered 26, were selected to provide sequence-based variations associated with these known modulators of R_h. N ranged from 40 to 260 and net charge from 1 to 43, where low net charge was from mixing positive and negative groups (e.g., SNAP25 and securin) or from relatively few charged residues (e.g., ShB-C). The dataset includes IDPs known to aggregate under certain conditions (e.g., CFTR-R⁷⁴ and α-synuclein⁷⁵) or form dimers (e.g., sml1³⁹), as well as IDPs that have high monomeric solubility (e.g., p53 TAD²² and prothymosin-α²⁴). Sequence content among dataset IDPs was generally diverse (see Fig. S1 in Supporting Information) with, for example, the fractional number of PRO residues (i.e., (# PRO residues)/N) ranging from 0 to 0.29, ALA from 0 to 0.24, SER from 0.02 to 0.20, and GLU from 0.03 to 0.31. The identity, sequence, and experimentally determined R_h for each IDP is provided in Table S1 of the Supporting Information. R_h measured for proteins containing histidine affinity tags were avoided since these affinity tags are known to compact R_h.⁵⁴ Folded proteins destabilized by mutation (e.g., CTL9-I98A⁷⁶) were not included to limit the investigation to IDP sequences.

As mentioned above, numerous studies have demonstrated that increases in net charge correlate with increases in R_h for IDPs.^52-54 For each IDP in Table S1, net charge was estimated from sequence as the absolute value in the number of GLU and ASP residues minus the number of LYS and ARG residues. This sequence-estimated net charge was normalized to IDP size,

$$\text{net}\text{charge}\text{density}=\text{net}\text{charge}∕N^{0.5},$$ (1)

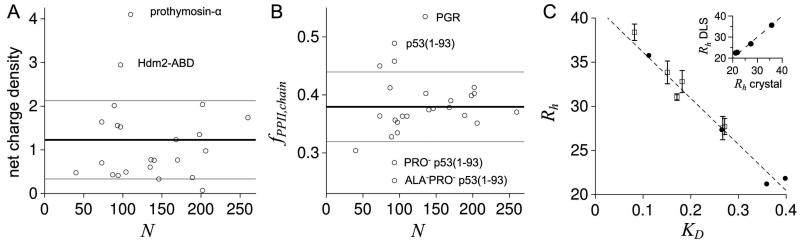
using N and the Flory exponent for IDPs⁵⁴ to calculate a net charge density. Figure 2A shows that net charge density calculated for 23 of 26 IDPs were within 1 standard deviation of the dataset average, 1.2 ± 0.9. Outlier IDPs are indicated in the figure and, of the 3, sequences from Hdm2-ABD and prothymosin-α gave net charge density values that were significantly above the dataset norm. Based on these data, charge effects on structure may be pronounced in Hdm2-ABD and prothymosin-α relative to the cumulative effects of charge on structure in the other dataset IDPs. Accordingly, experimental R_h from Hdm2-ABD and prothymosin-α may hold greater influence for assessing the effects on R_h owing to net charge. To verify R_h for these two IDPs, recombinant Hdm2-ABD and prothymosin-α were expressed, isolated from bacterial lysate, and R_h measured using DLS and SEC techniques. Results from these experiments are shown in Figure 2C and demonstrate that R_h for Hdm2-ABD and prothymosin-α were found to be 31.7 Å and 33.6 Å, respectively. Our measurements for prothymosin-α gave R_h that were practically identical to the literature reported value of 33.7 Å.²⁴ The literature reported value for Hdm2-ABD was 25.7 Å,⁷⁸ which was lower than our measurements. Changing solution conditions to match the prior report (10 mM sodium phosphate, 10 mM sodium chloride, pH 6) did not correct the discrepancy, yielding 34.2 Å for R_h for Hdm2-ABD when determined from SEC-measured K_D. We assume the increase in R_h for our second measurement was from decreased solution ionic strength, which could increase net electrostatic repulsion in Hdm2-ABD from its high net charge.

Figure 2.

A) Net charge density calculated from sequence for each dataset IDP. B) Chain-averaged PP_II propensity calculated from sequence for each dataset IDP using experimental propensities.⁷⁹ In A and B, bold lines are dataset averages, whereas grey lines are averages ± the standard deviation. C) R_h (in Å) and K_D for the IDPs identified in panels A and B and the folded proteins chicken egg albumin, bovine erythrocyte carbonic anhydrase, Staphylococcal nuclease, and horse heart myoglobin. Open squares are DLS-measured R_h, from largest to smallest, for the IDPs PGR (38.4 ± 0.9Å), prothymosin-α (33.8 ± 1.3Å), p53(1-93) (32.8 ± 1.2Å), Hdm2-ABD (31.0 ± 0.5Å), ALA⁻PRO⁻ p53(1-93) (27.7 ± 0.9Å), and PRO⁻ p53(1-93) (27.5 ± 1.3Å). Filled circles are R_h estimated as one-half the maximum C_α-C_α distance in the crystallographic structures of albumin,⁸¹ carbonic anhydrase,⁸² nuclease,⁸³ and myoglobin.⁸⁴ K_D is the distribution coefficient determined by SEC. Standard deviations from measuring K_D were < 0.007. The dashed line is a linear fit of R_h to K_D applied to the filled circles (folded proteins), which was used to estimate R_h from K_D for the IDPs. Table S1 lists the averages of the DLS-measured and K_D-estimated R_h for each of the 6 IDPs. Inset: Filled circles are R_h measured by DLS for the folded proteins compared to R_h estimated from crystal structures as one-half the maximum C_α-C_α distance, showing good agreement. DLS-measured R_h for each folded protein was: albumin (35.6 ± 0.5Å), carbonic anhydrase (26.8 ± 0.8Å), myoglobin (22.7 ± 0.8Å), and nuclease (22.4 ± 0.4Å).

IDP R_h have also been observed to trend with intrinsic propensities for PP_II helix.^21,48 To estimate chain bias for (φ, ψ) representative of PP_II structure for each dataset IDP, experimental propensities for the 20 common amino acids from Elam and colleagues⁷⁹ were used. Figure 2B shows the chain averaged propensity, f_PPII,chain, determined for each IDP sequence by summing the experimental propensities across a sequence and dividing by N. For the dataset, the average f_PPII,chain was 0.38 ± 0.06. The 135-residue intrinsically disordered Proline/Glycine-rich Region (PGR) of the cell surface protein Aap from Staphylococcus epidermidis⁸⁰ was included in the IDP dataset specifically because its sequence yields a value for f_PPII,chain that is much higher than average. Figure 2C shows that R_h measured for recombinant PGR using DLS and SEC methods gave an average of 37.7 Å. Other IDPs with calculated f_PPII,chain that were substantially outside the dataset norm were p53(1-93) and the PRO⁻ and ALA⁻PRO⁻ variants of p53(1-93). Since experimental R_h from these IDPs could hold greater influence for testing the effects on R_h owing to chain bias for PP_II, experimental R_h were verified using DLS and SEC. Results from these experiments are given in Figure 2C and demonstrate that R_h for wild type p53(1-93), PRO⁻ p53(1-93), and ALA⁻PRO⁻ p53(1-93) were 32.3 Å, 27.5 Å, and 27.4 Å, respectively, each of which were practically identical to the literature reported values.²¹

R_h calculated from simulated ensembles

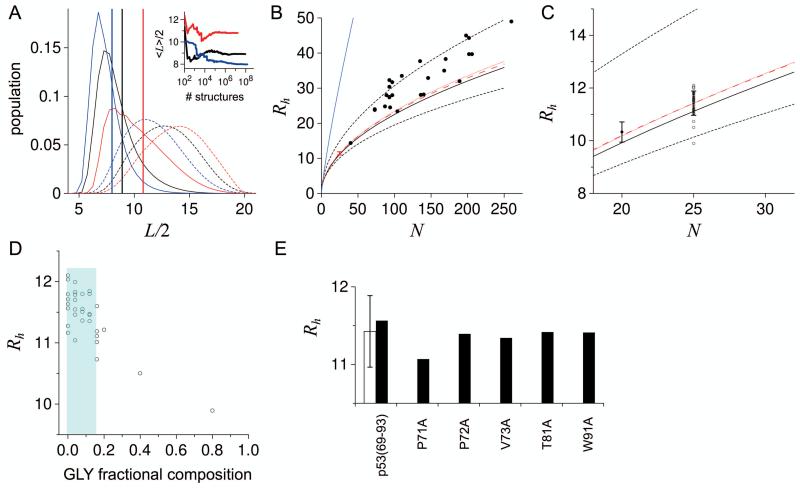
Conformers for polypeptide sequences were generated using the HSC model,^40,50 which builds structures from the standard bond angles and bond lengths,⁵⁹ a random sampling of backbone dihedral angles and side chain rotamer libraries,⁶² and discards those containing contact violations based on van der Waals atomic radii.^56,57 Each structure generated for a conformational ensemble is independent of previously generated structures. Figure 3A demonstrates typical HSC simulation output, using 15-residue poly-GLY, poly-ALA, and poly-PRO sequences as examples. Although any number of structural metrics could be presented, L/2 is used to represent an approximate R_h. L was calculated as the maximum C_α-C_α distance in a generated structure and <L> is the population-weighted average for an ensemble. The inset to Figure 2C shows that L/2 is a reasonable estimate for experimental R_h when the structure of a protein is known.

Figure 3.

R_h calculated from simulated conformational ensembles. A) L/2 distribution in ensembles of poly-GLY (blue), poly-ALA (black), and poly-PRO (red) with N = 15. Stippled curves were determined by giving each structure equal statistical weight; solid curves are probability-weighted distributions using equation 2. Vertical lines show <L>/2 calculated for each ensemble by equation 3. Inset: <L>/2 calculated for ensembles with increasingly larger numbers of simulated structures. B) Filled circles are experimental IDP R_h. Lower-stippled, solid, and upper-stippled black lines show the trend in R_h with N from ensembles simulated for poly-GLY, poly-ALA, and poly-PRO, respectively. Red dot with error bar at N = 25 is the average ± standard deviation in R_h calculated from ensembles simulated for IDP fragments. Red lines extrapolate the fragment average to larger N by using the poly-ALA scaling relationship (R_h = 2.16·N^0.509) with pre-factor or exponent modified for agreement with the fragment average at N = 25 (dashed line is R_o changed to 2.22 and v kept at 0.509; stippled line is R_o kept at 2.16 and v changed to 0.518). Blue line is the trend for poly-PRO when simulated with PP_II propensity of 0.95 at each residue position. C) Open circles show R_h from ensembles simulated for each 25-residue IDP fragment, with the average ± the standard deviation given by the error bar (11.4 ± 0.5 Å). R_h from ensembles simulated for IDP fragments with N = 20 give an average ± standard deviation of 10.3 ± 0.4 Å, shown by the filled circle with error bar. Lines match their panel B representations. D) Open circles are R_h from ensembles simulated for the 25-residue IDP fragments and the corresponding GLY compositions determined from sequence. Shading is the range in fractional GLY composition for the natural IDP sequences in the dataset. E) Open column with error bar is the average R_h (± standard deviation) from ensembles simulated for the 33 IDP fragments with N = 25. Black columns show R_h calculated from ensembles simulated for 6 different sequences based on the C-terminal 25-residue fragment from p53(1-93) wild type. Shown are p53(69-93) (left-most black column) and p53(69-93) with ALA point substitutions applied at the PRO-71, PRO-72, VAL-73, THR-81, and TRP-91 positions as labeled. R_h is in Å.

If the generated structures are given equal statistical weight, symmetric distributions are obtained for L/2 in ensemble populations. Relatively few conformers for an ensemble exhibit highly extended or highly compacted structures and most are structurally in-between these two extremes. To approximate the effects of chain-solvent interactions on an ensemble, a structure-based energy function that has been parameterized to SASA⁵¹ and tested extensively^63-71 was used to estimate the solution energetics of each generated conformer. This SASA-based energy function does not include terms accounting for the energetics of common intramolecular forces such as intra-chain hydrogen bonds and charge-charge interactions, which could be added separately.⁴⁸ The energy function calculates a Gibbs free energy for each structure (ΔG_i) and sets probabilities by the Boltzmann distribution,

$$P_i=K_i∕\Sigma K_i,$$ (2)

where P_i is the probability of structure i, K_i is the statistical weight from the relative Gibbs free energy (K_i = e^−ΔGi/RT, where R is the gas constant and T is absolute temperature), and the summation is over all structures in an ensemble. Ensemble populations for poly-GLY, poly-ALA, and poly-PRO favor compacted structures with application of the SASA-based energy function (see Fig. 3A), phenomenologically similar to the hydrophobic collapse expected of polypeptides in water.⁴⁷ Energy-weighted distributions tend to show a positive skew, with the population-weighted value,

$$<L>∕2=\Sigma (L_i\cdot P_i)∕2,$$ (3)

slightly higher than the distribution mode. To calculate R_h from a simulated ensemble for polypeptide sequences using this model, conformers were generated until <L> converged to a statistically stable value (Fig. 3A inset). <L> was considered stable if its value changed by less than 1% over a 10-fold increase in the number of conformers generated. For the computational results reported here, R_h was calculated from simulated ensembles as <L>/2 using equation 3.

Estimating excluded volume effects on R_h

Computer simulations using the HSC model to compute <L> were intractable for poly-ALA with N > 75,⁴⁰ and prohibit direct simulation of full sequences from each IDP in the dataset. Polypeptide sequences containing large, bulky side chains (e.g., PHE, TRP, PRO) also exhibit less efficient conformer sampling from generating steric conflicts at higher rates. To manage these computational limitations associated with polypeptide length, R_h (i.e., <L>/2) calculated from ensembles for short sequences were extrapolated to larger N. For example, simulation results for poly-ALA, poly-GLY, and poly-PRO are shown in Figure 3B and compared to IDP R_h from the experimental dataset. R_h for poly-GLY and poly-PRO were calculated from ensembles using N = 10, 15, 20, 25, and 35. Log-log plots of R_h and N were constructed to obtain the pre-factor (R_o) and exponent (v) for the poly-GLY and poly-PRO curves shown in the figure. For poly-ALA, the trend of R_h with N determined previously⁴⁰ was used.

Comparing R_h from simulated ensembles for poly-ALA, poly-PRO, and poly-GLY demonstrates the limits of sequence-based excluded volume effects on IDP R_h in this model. Removing a heavy atom (C_β) attached to the main chain at each residue position results in decreases in R_h at all N, as shown by poly-GLY relative to poly-ALA. In contrast, attaching an additional heavy atom (C_δ) directly to the main chain at each residue position increases R_h, as shown by poly-PRO relative to poly-ALA.

To estimate excluded volume effects on R_h owing to sequence differences among IDPs, 25-residue polypeptide fragments were selected from the IDP dataset using the following protocol. First, IDPs with the two highest and two lowest net charge density values (Fig. 2A) were selected. These were Hdm2-ABD, prothymosin-α, ShB-C, and securin. Next, IDPs with the two highest and two lowest f_PPII,chain values (Fig. 2B) were selected. These were PGR, p53(1-93), PRO⁻ p53(1-93), and ALA⁻PRO⁻ p53(1-93). Finally, the two IDPs with f_PPII,chain closest to the dataset average (Fos-AD and HIF1-α-530) and the two IDPs with net charge density closest to the dataset average (Fos-AD and tau-K45) were selected. The goal from the selection process was to obtain IDP sequences at the extremes and at the averages for physical properties known to modulate R_h. From each of these 11 different IDPs, 25 residue fragments from the N-terminus, C-terminus, and center of each sequence were extracted, producing 33 25-residue sequences that were simulated using the HSC model to compute R_h. A table is provided in Supporting Information listing the fragment sequences and R_h that were computed from simulation (Table S2). This table also provides net charge density and f_PPII,chain determined for each fragment for comparison to the parent sequences. Since the SASA-based energy function does not include terms for main chain dihedral angle bias or charge effects on structure, the variance in R_h for these fragments should provide a rough estimate of the extent of R_h differences among typical IDPs owing to sequence-based excluded volume effects on hydrodynamic size.

Figure 3C shows that R_h for the 25-residue fragments ranged from 12.1 Å to 9.9 Å in the simulations, and averaged 11.4 ± 0.5 Å. For comparison, R_h for poly-ALA and N = 25 should be ~ 11.1 Å, estimated from HSC simulations performed using identical methods.⁴⁰ R_h trended with GLY content (Fig. 3D) and fragments that reported the smallest and second smallest R_h had 80% and 40% GLY composition, respectively. Fragments producing the largest R_h in these simulations were those containing sequentially adjacent PRO residues and with higher compositions of branched (LEU, ILE, VAL) and aromatic (PHE, TRP, TYR) side chains (see Fig. S2). Each of the 4 fragments containing sequentially adjacent PRO residues were among the fragments with largest R_h, although no obvious correlation was observed when comparing R_h to fractional PRO composition (Fig. S2). Using the 25-residue fragment from the C-terminal end of p53(1-93) to showcase these effects, point substitution to ALA at PRO positions adjacent to and preceding another PRO residue generally produced larger reductions in R_h when compared to ALA substitutions at positions containing branched or aromatic residues (Fig. 3E). Also, no obvious correlation was observed when comparing R_h in these simulations to net charge or number of charged groups in a sequence (Fig. S2); a result that should be expected considering the energy function that was used. Overall, these data seemed to indicate that R_h generally follows the hydrodynamic dimensions of poly-ALA when only excluded volume effects on the chain are considered, with the exception of high fractional GLY composition (Fig. 3D) or the occurrence of sequentially adjacent PRO residues (Fig. S2). To demonstrate this, if the pre-factor (R_o) or exponent (v) for the poly-ALA scaling relationship is changed such that the poly-ALA curve agrees with the fragment average (11.4 Å) at N = 25, the red lines in Figures 3B and 3C are obtained (dashed line = pre-factor changed; stippled line = exponent changed). These results are consistent with reports that excluded volume effects on the structural dimensions of random polypeptide chains are sensitive mostly to the addition or subtraction of heavy atoms covalently attached to the main chain, i.e., PRO and GLY substitution effects.^85,86 Repeating these simulations for IDP fragments with N = 20 gave quantitatively similar results (Fig. 3C). It should be noted that there are only 14 instances of adjacent PRO residues out of 2958 total residue positions in the IDP dataset, when redundancy is removed owing to multiple variants of the N-terminal region of p53 and overlap in the Mlph(147-240) and Mlph(147-403) sequences. This indicates that adjacent PRO residues are not uncommon but also not over-represented among IDPs. Likewise, GLY content ranged from 0.01 (multiple IDPs) to 0.15 (PGR) in the natural IDP sequences of the dataset, with redundancy removed. For fractional GLY composition from 0 to 0.15, little to no correlation with R_h was apparent among the IDP fragments that were simulated (Fig. 3D).

Effects of main chain bias for PP_II on R_h

An issue with HSC-based simulations, as used above, is that energetic minima associated with main chain dihedral angles are not accounted for, though conformational bias for certain (φ, ψ) have been detected in experimental studies with disordered peptides^79,87-89 and surveys of protein structures.^86,90-92 To demonstrate this issue, the blue line in Figure 3B represents R_h for poly-PRO when the propensity for PP_II at each residue position was modeled as 95% in simulated ensembles.⁴⁰ Poly-PRO peptides are known to adopt PP_II under normal conditions.⁹³ Comparison of R_h for poly-PRO from PP_II-biased and non-biased ensembles shows that main chain dihedral angle preferences can affect R_h substantially in these simulations.

The effects of PP_II propensities on R_h calculated from HSC-simulated ensembles have been investigated systematically, whereby propensities for PP_II were modeled by applying a sampling bias to the main chain dihedral angles (φ, ψ).^40,48 For example, a 20% sampling bias for PP_II at residue position i was equivalent to 20% of (φ, ψ) at position i located in the region of (−75±10, 145±10) and 80% distributed randomly in the allowed Ramachandran areas outside of (−75±10, 145±10). Following the van der Waals check, the propensity, f_PPII,i, is calculated as the sum of the probabilities, given by equation 2, for structures with (φ, ψ) in the region (−75±10, 145±10) at position i. Since conformers containing contact violations are discarded and ensemble populations are weighted toward compacted structures (see Fig. 3A), f_PPII,i does not necessarily match the applied sampling bias.⁴⁰

For poly-ALA, R_h was observed in simulations to depend on the chain-averaged PP_II propensity by,

$$R_h=2.16\cdot N^{0.503-0.11\cdot \text{ln}(1-fPPII,chain)},$$ (4)

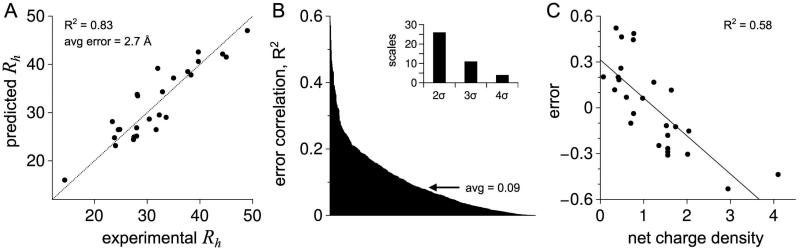
where R_h is in Å and f_PPII,chain is the sum of f_PPII,i over all residue positions and divided by N.⁴⁸ Accordingly, f_PPII,chain from a simulation is calculated in a manner analogous to its use in Figure 2B with intrinsic PP_II propensities applied to an IDP sequence. The structural relationship between R_h, N, and f_PPII,chain described by equation 4 was independent of position-specific patterns of PP_II bias and was capable of predicting IDP R_h with good agreement to the experimental value.⁴⁸ Figure 4A shows R_h predicted from sequence for each dataset IDP and compared to experimental R_h when using the intrinsic PP_II propensities of Elam and colleagues.⁷⁹ Good agreement (coefficient of determination, R² = 0.83) and a small average error (± 2.7 Å) were observed. It is important to recognize that equation 4 was derived solely from conformational ensembles simulated with the HSC model and the agreement between predicted and experimental R_h represents a key test.

Figure 4.

Predicting R_h from intrinsic PP_II propensities. A) Filled circles show R_h (in Å) predicted from sequence for each dataset IDP using equation 4. The stippled line is the identity line. B) Prediction error, normalized for IDP size using equation 5, was compared to 567 amino acid scales (544 from the Amino Acid Index database,⁹⁴ 20 representing fractional composition for the common amino acids, the net charge density, the net charge per residue, and κ). Scales from the Amino Acid Index database were summed by sequence and normalized to chain length. The correlation (R²) for each comparison is in rank order from left to right. Inset: Number of amino acids scales with R² greater than the average plus 2, 3, and 4 times the standard deviation (σ). C) Comparison of prediction error to net charge density for each dataset IDP. The line is the observed trend; error = −0.25·(net charge density) + 0.31.

The error in predicting R_h for IDPs by equation 4 has been compared to the net charge.⁴⁸ Since this error indeed correlated with net charge, as expected,^52-54 a simple search for other amino acid properties that could influence IDP R_h was conducted. To do this, the prediction error was normalized for IDP size by,

$$\text{error}=(\text{predicted}{R}_h-\text{experimental}{R}_h)∕N^{0.5}.$$ (5)

The error determined for each dataset IDP was then compared to 544 different amino acid scales available from the Amino Acid Index database.⁹⁴ To test for bias from sequence composition, the prediction error was also compared to the fractional composition of each amino acid type in each IDP. The fractional composition of each IDP sequence is provided in Figure S1, demonstrating substantial dataset variation. When comparing prediction error in the dataset to the various amino acid scales, the observed correlations were mostly weak (average R² = 0.09 ± 0.1; Figure 4B). A few exceptions, however, gave R² ≥ 0.5, but none exceeded the correlation observed for the net charge density (R² = 0.58).

Additional charge-based metrics commonly used to classify IDP sequences, net charge per residue and κ,⁴⁹ were also tested for correlation with the error. Since net charge per residue is determined from sequence almost identically to the net charge density, i.e., as the net charge divided by N rather than N^0.5, a similar error correlation was observed (R² = 0.57; Figure S3). For κ, which is a measure of the mixing of positive and negative charges in a sequence, correlation with the error was small and weaker than average (R² = 0.05; Figure S3). Generally, κ is used to compare sequences with similar charge composition.⁴⁹ κ ranges from 0 to 1, with values near 0 indicating that residues with opposite charge are well-mixed in a sequence. Values close to 1 are from sequences with segregated charge types, allowing for long-range attraction between oppositely charged regions of a disordered protein. The low correlation to the prediction error for κ here likely represents the diverse compositions and weak charge segregation among the IDP sequences in the dataset (dataset average = 0.211 ± 0.086 with minimum and maximum of 0.058 and 0.423, respectively). Values for net charge density, net charge per residue, and κ are provided in Table S3 for each IDP sequence.

Table I lists the ten highest ranking amino acid scales^95-101 in terms of R², each 3 standard deviations or more above the average. Net charge per residue was omitted from this list because of its high similarity to the net charge density. It is interesting to note that the list is dominated by physicochemical properties associated with charge (e.g., net charge density, ASP fractional composition, amino acid net charge) and main chain conformational bias (e.g., beta-structure-coil equilibrium, frequency as first residue in a turn, positional frequency in an α helix). Showing only slightly lower correlations were partial specific volume¹⁰² and apparent partial specific volume¹⁰³ with R² of 0.36 and 0.37, respectively. These results emphasize that while the HSC model seems to perform well for generating statistical ensembles of disordered polypeptide structures, the absence of specific terms in the energy function accounting for the effects of charge, non-ALA excluded volumes (i.e., when using poly-ALA derived relationships like equation 4), and preferences for certain main chain dihedral angles are serious limitations. Since the prediction error correlated best with the net charge density, the effects of net charge on IDP R_h were investigated in more detail. Contributions from other physicochemical properties to IDP R_h are also discussed below.

Table I.

Sequence properties and amino acid scales with best correlation (R²) to equation 4 error.

R 2	scale
0.58	net charge density
0.53	beta-structure-coil equilibrium95
0.50	ASP fractional composition
0.47	positional residue frequency at helix termini N' 96
0.46	helix initiator at position i-197
0.45	amino acid net charge98
0.44	frequency as 1st residue in turn99
0.43	amino acid isoelectric point100
0.43	positional residue frequency at helix termini N" 96
0.39	frequency in beta-bends101

Effects of net charge on R_h

The trend in the prediction error with net charge density was generally consistent across the IDP dataset (Fig. 4C). This could be considered surprising. While some studies have shown that IDP R_h are sensitive to net charge,^52-54 results from other studies indicate that describing charge effects on R_h via the net charge could prove inaccurate since changes in the spacing between⁴⁸ and the sequential patterns of charged groups⁴⁹ are capable of producing large changes in R_h in the absence of net charge changes.

To compare R_h sensitivity to net charge among the dataset IDPs, R_h predicted by equation 4 was corrected for apparent net charge effects using the observed linear error trend. From equations 1, 4, and 5, the trend-corrected R_h is,

$$R_h=2.16\cdot N^{0.503-0.11\cdot \text{ln}(1-fPPII,chain)}+0.25\cdot \text{Q}-0.31\cdot N^{0.5},$$ (6)

where 0.25 and 0.31 are from the slope and intercept, respectively, of the trend in Figure 4C, Q is the net charge from sequence (Table S1), and f_PPII,chain is the sequence sum, divided by N, of the experimental PP_II propensities⁷⁹ (Fig. 2B and Table S1). The goal is to identify charge patterns in the IDP dataset that influence R_h atypically by identifying IDPs that deviate from the dataset trend according to equation 6. Specifically, if R_h depends on the net charge strongly for an IDP, and if that dependence differs from the other dataset IDPs, removal of such an IDP from the training set should produce discernible changes in equation 6 that could be used to identify atypical structural behavior and/or sequence patterns.

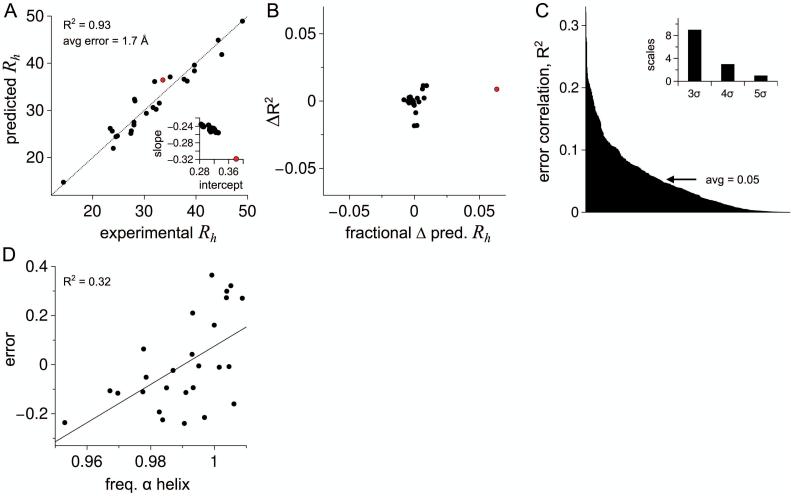
Figure 5A shows R_h predicted from sequence using equation 6 and compared to experimental R_h for each dataset IDP. Good agreement was observed, yielding an increased R² of 0.93 and a decreased average error of ± 1.7 Å, relative to the correlation and average error obtained when predicting R_h from sequence without the net charge correction (see Fig. 4A). Next, each IDP was removed from the dataset, individually, and R_h from sequence recalculated for the remaining IDPs. First, using equation 4 to regenerate the error trend with net charge density. The trend slope and trend intercept showed small variations with the removal of individual dataset IDPs (Fig. 5A inset), with the exception of removing prothymosin-α (highlighted red in Figs. 5A and B). As such, removing an IDP from the dataset produced commensurate changes in equation 6. R_h was then recalculated from sequence by equation 6, using new slope and intercept values, for the dataset IDPs. Figure 5B shows that the correlation between predicted and experimental R_h changed only slightly (± 0.02) when removing an individual IDP from the dataset, relative to the correlation obtained with the full dataset (R² = 0.93). R_h predicted by equation 6 also changed by 1% or less for most of the IDPs when one was removed from the training set and then equation 6, re-calculated, was applied to the missing IDP. Again, the exception was prothymosin-α that reported a 6.3% change. These results indicate that hydrodynamic size for IDPs can be well-estimated from sequence using equation 6, however, its use should be circumspect owing to apparent differences in R_h sensitivity to net charge among IDPs.

Figure 5.

Predicting R_h from intrinsic PP_II propensities and net charge. A) Filled circles show R_h (in Å) predicted from sequence for each dataset IDP using equation 6. The identity line is shown by the stippled line. Inset: slope and y-intercept for the linear trend in Fig. 4C when a singular IDP is removed from the training set. B) Each filled circle represents the removal of a singular IDP from the training set. The concomitant change in correlation for predicted and experimental R_h (ΔR²) is compared to the fractional change in predicted R_h for the removed IDP. C) Prediction error, normalized for IDP size by equation 5, was compared to 567 amino acid scales (same scales as Fig. 4B). The correlation (R²) for each comparison is in rank order from left to right. Inset: Number of amino acids scales with R² greater than the average plus 3, 4, and 5 times the standard deviation (σ). D) Comparison of prediction error to the best performing scale, normalized frequency of α helix in all α class,¹⁰⁴ showing the trend line.

The fractional composition of charged residues in prothymosin-α is very high (fractional composition = 0.57; from 53 GLU and ASP, 10 LYS and ARG, out of 110 total residues) when compared to the other dataset IDPs (average = 0.25 ± 0.05). Considering that net charge density is at the dataset maximum for prothymosin-α (Fig. 2A), it could be argued that charge effects on structure, in sum, should be pronounced in prothymosin-α more so than typical. Thus, it may be counter-intuitive to observe that the magnitude of the slope representing R_h sensitivity to Q increased by ~ 25% when prothymosin-α was removed from the training set (Fig. 5A inset). Specifically, these data indicate that the effects of net charge on R_h were weaker in prothymosin-α, on a per-charge basis, than for the other IDPs. Since prothymosin-α was a lone outlier in this analysis, additional tests are needed. If prothymosin-α is removed from the dataset and the entire resampling analysis repeated, removing a second IDP, no obvious outliers were detected (Fig. S4). At a minimum, these results argue that net charge is a poor metric from which to model charge effects on hydrodynamic size since Figure 5B predicts that some IDP structures respond differently than others to small changes in the net charge. Of note, prothymosin-α had the largest value for κ among the sequences in the IDP dataset (κ = 0.423). Larger κ values trend in molecular dynamics simulations with compacted disordered structures,⁴⁹ possibly providing an explanation for the somewhat reduced effect of net charge on R_h in prothymosin-α.

Effects of main chain bias for α helix on R_h

The HSC model has many limitations, as discussed above, and use of equation 6 for estimating IDP R_h will have errors from excluded volume and charge effects on structure, and possibly from position-specific perturbations to the intrinsic PP_II propensities from neighboring residues.⁸⁹ To test for additional error sources, R_h prediction error was again compared to 544 amino acid scales from the Amino Acid Index database,⁹⁴ the fractional composition of each amino acid type, net charge density, net charge per residue, and κ. Prediction errors from equation 6 were normalized for IDP size using equation 5 and the results are given in Figure 5C. Correlations of prediction error to amino acid properties were weak, with an average R² of 0.05 ± 0.05 and a maximum of 0.32. Amino acid properties that trend best with the prediction error were associated with α helix propensities, representing the 3 highest and 15 of the top 20 correlations (Table S4).^{96,99,101,104-115} Error correlation to net charge density, net charge per residue, and κ were 0, 0.0007, and 0.005, respectively.

The correlation of prediction error with α helix propensities could be another example of R_h sensitivity to intrinsic (φ, ψ) preferences, similar to the effects of intrinsic PP_II propensities on IDP R_h.^21,48 Figure 5D shows that increasing chain propensities for α helix seem to follow increasing prediction error, which was observed for each α helix propensity scale listed in Table S4 (Fig. S5). Inspection of equation 5 indicates that increasing prediction errors are associated with decreasing experimental R_h, providing a testable hypothesis. Specifically, these data predict R_h compaction with increasing α helix propensities.

To test this hypothesis, propensities for α helix were modeled using the same simulation strategy that was employed for PP_II propensities.^40,48 Briefly, a sampling bias was applied to main chain dihedral angles (φ, ψ) in simulations that computed R_h from HSC-generated ensembles of poly-ALA peptides. Surveys of α helix structures yield an average (φ, ψ) of (−64±7, −41±7).¹¹⁶ Accordingly, a sampling bias for α helix at residue position i, for example a 20% sampling bias, was equivalent to 20% of (φ, ψ) at position i located in the region of (−64±10, −41±10) and 80% distributed randomly in the allowed Ramachandran areas outside of (−64±10, −41±10). Following the van der Waals check, the α helix propensity, f_α,i, was calculated as the sum of the probabilities (equation 2) for structures with (φ, ψ) in the region (−64±10, −41±10) at position i. No provisions accounting for the favorable energetics of intra-chain hydrogen bonds were added to the energy function, though the authors recognize that intra-chain hydrogen bonds contribute to α helix structural stability.¹¹⁶

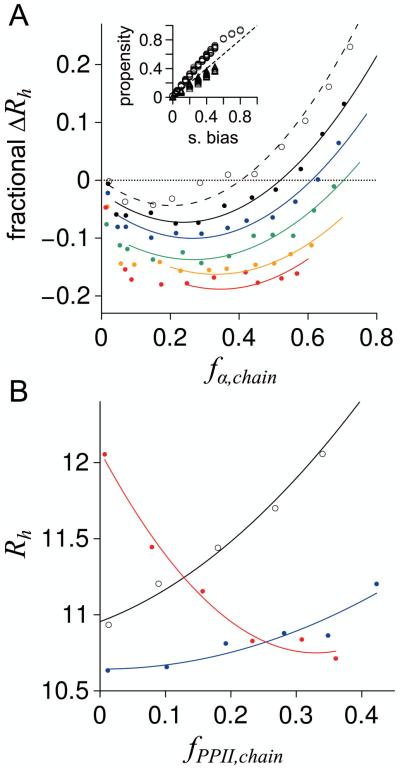
The effects of α helix propensities on R_h calculated from ensembles of poly-ALA peptides with N = 25 are shown in Figure 6. In these simulations, sampling biases were applied equally at each residue position, although the sampling bias for α helix did not necessarily match the applied sampling bias for PP_II in any particular ensemble. Of note, f_α,chain, calculated as the sum of f_α,i for each position i and divided by N, was generally greater than the applied sampling bias for α helix (Fig. 6A inset). In contrast, f_PPII,chain was smaller than the applied PP_II sampling bias, consistent with previous results.⁴⁰ For poly-ALA with no PP_II sampling bias, f_α,chain from 0.1 – 0.2 reduced R_h by ~ 5%, relative to R_h when no sampling preference for α helix was applied (Fig. 6A). For f_α,chain > 0.2, R_h gradually increased with increasing f_α,chain. When sampling biases for PP_II were applied, the percent reduction in R_h from α helix propensities generally increased with increasing PP_II bias.

Figure 6.

R_h for poly-ALA (N = 25) simulated with intrinsic propensities for α helix and PP_II. A) Open circles are ensembles with no applied sampling bias for PP_II. Filled circles are ensembles simulated with applied PP_II sampling biases of 0.10 (black), 0.20 (blue), 0.30 (green), 0.40 (orange), and 0.50 (red). Shown is the change in R_h relative to R_h expected from f_PPII,chain using equation 4. Curves in both panels (A and B) represent data fits to second order polynomials and have no physical meaning; they were provided to highlight trends. Inset: Chain propensities calculated for each ensemble, f_α,chain (circles) and f_PPII,chain (triangles), and compared to the applied sampling bias. The stippled line is the identity line. B) Open circles are ensembles with no applied sampling bias for α helix. Filled circles are ensembles simulated with applied α helix bias resulting in f_α,chain of ~ 0.05 – 0.07 (blue) and f_α,chain of ~ 0.50 – 0.60 (red).

Several observations from these simulations are noteworthy. First, R_h compaction was observed owing to α helix propensities, consistent with the motivating hypothesis from the observed dataset trend (Fig. 5D). Second, weak f_α,chain values produced substantial compaction in R_h. For ensembles with f_PPII,chain from 0.3 – 0.5, which should be expected for most IDPs (see Fig. 2B), chain averaged α helix propensities of just 0.05 – 0.1 resulted in 10 – 20% R_h compaction. This contrasts with simulation results for PP_II bias, whereby weak PP_II propensities (f_PPII,chain ≤ 0.1) produced relatively small changes in R_h.^40,48 Third, the effects of α helix propensities on R_h were modulated by PP_II propensities. And fourth, the reciprocal relationship was also observed where the effects of PP_II propensities on R_h were modulated by α helix propensities. Figure 6B shows that when no bias for α helix is applied to a poly-ALA chain, R_h increases with increasing chain propensity for PP_II. For f_α,chain of ~ 0.05 – 0.07, however, compaction occurs and increases in R_h from increasing PP_II propensities are reduced. When the chain bias for α helix was very high (f_α,chain ~ 0.50 – 0.60), the trend is reversed and increasing chain propensities for PP_II yield decreasing R_h. Considering that the trend among experimental R_h is for decreasing R_h with increasing α helix propensities (Fig. 5D) and increasing R_h with increasing PP_II propensities,²¹ these observations argue for intrinsic α helix propensities that are generally weak in IDPs, when averaged for a chain. In summary, these results predict that intrinsic bias to preferred (φ, ψ) regions in disordered polypeptides, even at levels below experimental^79,87-89,117 and computational^118,119 estimates for the common amino acids, are capable of establishing sequence-dependent variability in the structural dimensions of the disordered protein conformational ensemble and concomitant sequence-dependent effects on IDP R_h.

DISCUSSION

Identifying the molecular properties that regulate disordered protein structures, and to what extent, is critical for establishing molecular descriptions of IDP-mediated biology. Here, conformational ensembles of polypeptides were simulated using a model based on the HSC algorithm to assess the contributions of net charge, main chain dihedral angle bias, and excluded volume to the hydrodynamic dimensions of disordered structures. To test and evaluate simulation results, R_h calculated from simulated ensembles were compared to experimental R_h from 26 IDPs showing diverse sequence compositions, chain lengths, charge patterns, and net charge. There are benefits to using a HSC model for simulating disordered structures. First, it is reductionistic and thus useful for identifying salient phenomena by subtracting out uninteresting results. For example, the overall magnitude of R_h for a disordered ensemble may not be interesting, since its value is largely driven by excluded volume effects and chain-solvent interactions that are somewhat similar among different IDPs, at least in the simulated data (Fig. 3B). The deviations in experimental R_h from this random coil approximation accordingly could yield detail on the intra- and inter-molecular interactions that bias state distributions in the protein conformational ensemble. Second, proposed structural effectors, such as chain bias for (φ, ψ) representative of PP_II⁴⁰ and coulombic interactions between charged groups,⁴⁸ could be added to the model and the capabilities of these changes tested. The HSC model also has limitations. As used above, and in addition to the limitations already noted, it is not capable of establishing why there is a particular (φ, ψ) bias, or net charge effect on R_h, only that the comparative analysis indicates that these specific structural effectors are present in IDP systems.

The results of this study indicate that IDP R_h can be described from simple physicochemical properties associated with the polypeptide chain. The main structural determinants, other than N, seem to be excluded volume effects that can be reasonably approximated using poly-ALA (Fig. 3B), chain-solvent interactions that cause a general compaction in the hydrodynamic dimensions (Fig. 3A), charge effects that, when averaged across a dataset of IDP structures, cause a general expansion that trends with the net charge density (Fig. 4C), and bias in the main chain dihedral angles for common (φ, ψ) that have been associated with PP_II and α helix (Figs. 4A and 6). Most likely, this list of pertinent structural effectors is not complete and the identification of additional R_h sensitive properties awaits further study. For example, energetic preferences for (φ, ψ) in other areas of the allowed Ramachandran regions,^90-92 position-specific perturbations to the intrinsic conformational propensities from neighboring residues,⁸⁹ and a more accurate accounting of charge effects on structure than provided by the net charge density are probably needed and currently underestimated in the model (i.e., assumed to be negligible). In spite of the gross simplicity of this model, it is interesting to note that IDP R_h can be predicted accurately from sequence using just experimental PP_II propensities, an estimation of the protein net charge, and equation 6 (Fig. 5A).

The agreement between the observed IDP dataset trend, showing that experimental R_h generally compact with increasing chain propensities for α helix (Fig. 5D), with the effect on simulated R_h of a sampling bias to the canonical (φ, ψ) of α helix structures (Fig. 6A) offers compelling evidence for the hypothesis that main chain biases for common (φ, ψ) are key determinants for establishing hydrodynamic size in IDPs. Previously, it was shown that experimental PP_II propensities are capable of describing sequence-based differences in IDP R_h,^21,48 which was predicted from HSC simulations of disordered polypeptides.⁴⁰ Here, the simulated data predict that IDP R_h are modulated also by intrinsic α helix propensities. Weak α helix propensities (< 0.10) were capable of producing substantial compaction in the simulations, decreasing R_h by upwards of 20%, and the effects on R_h owing to α helix propensities were dependent on the chain propensity for PP_II. Likewise, PP_II effects on R_h were modulated by chain propensities for α helix. While experiments that directly test these predictions have yet to be provided, the results, overall, demonstrate how intrinsic structural propensities are capable of influencing the chain dimensions in disordered proteins.