The Lowdown on Linkage Disequilibrium

Flowering time varies among Arabidopsis accessions. Some of the genes that contribute to this polygenic trait have been localized using quantitative trait loci (QTL) mapping, eventually leading to the identification of genetic variants that contribute to observed differences in flowering time (El-Assal et al., 2001). Despite this and other similar successes with the positional cloning of QTL, the path from a mapped QTL to a gene underlying trait variation is fraught with obstacles. One obstacle is the lack of fixed genetic differences between parental lines used to create the mapping population. This “diversity hurdle” can be overcome by repeating QTL analyses in many mapping populations (or by mapping variance components in a number of families), but this approach is not feasible for most taxa and phenotypes. Linkage disequilibrium (LD) mapping steps into this void. Unlike traditional linkage mapping, which maps genes using gametic phase disequilibrium created in a single- or multiple-generation cross, LD mapping can rely on segregating variation in natural populations. As a result, LD mapping samples contain many more informative meioses (i.e., all those that have occurred in the history of the sample) than a traditional mapping population. Although not without its own problems (Lander and Schork, 1994), LD mapping holds great promise for fine-mapping genes and variants that contribute to a trait of interest, such as flowering time. Here, we briefly review LD (What is it? How is it measured? What biological and evolutionary factors shape its distribution?), summarize recent studies of LD in plant systems, and relate genomic patterns of LD to mapping genes that underlie variation in complex phenotypic traits.

MEASURING LD

LD is the nonindependence of alleles. Consider the two sets of single nucleotide polymorphisms (SNPs) in Figures 1A and 1B. Both data sets contain two SNP sites. In the first data set, the two sites are in complete LD because an A at the first SNP is associated with a G at the second SNP in all individuals examined. By contrast, the As and Gs are randomly associated in the second data set; in this data set, the sites are in linkage equilibrium.

Figure 1.

Two SNP Sites Typed from Eight Individuals.

Estimates of D, D′, and r² (see text) are provided for each data set.

(A) Complete LD between the two sites.

(B) Randomized data, implying recombination between sites.

(C) Unequal marginal frequencies between sites. Unequal frequencies do not imply that recombination has occurred; for example, the C may be a relatively new mutation that occurred on the T background. Because only three of four possible gametic types are found at the two sites, there is no need to invoke recombination to explain the pattern of variation.

(D) All four gametic types with the same marginal frequencies as in (C); the four gametic types imply recombination.

The metric D is a quantitative measure of allelic association. With respect to Figure 1,

D₁₂=p_1A2G−p_1Ap_2G

where D₁₂ is a measure of LD between sites 1 and 2, p_1A2G is the frequency of sequences that contain an A at site 1 and a G at site 2, p_1A is the marginal frequency of allele A at site 1, and p_2G is the marginal frequency of allele G at site 2. Using this formula, D = 0.5 − (0.5)(0.5) = 0.25 for the data in Figure 1A and D = 0.25 − (0.5)(0.5) = 0.00 for the data in Figure 1B. Note that the absolute value of D is symmetric, in that it does not matter which alleles are measured and associated. For example, one can measure the frequency of either A or T at site 1 to calculate D. Here, we demonstrate D on haplotypic data, but D also is estimated routinely from unphased diploid data.

D incorporates information about allelic association and allele frequencies. For example, imagine that only one of eight sequences in Figure 1A contained an A at site 1 and a G at site 2 (with the seven remaining sequences containing a T and a C). Although the two sites are still in complete disequilibrium, the change in frequency of the A and G alleles leads to D = 0.125 − (0.125)(0.125) = 0.109. Because of this frequency dependence, values of D are expected to vary widely over many pairs of SNPs, even when sites are in complete LD.

There are two ways to address the dependence of D on marginal allele frequencies. The first is to ignore low-frequency variants, which contribute inordinately to variation in D. Most empirical studies of LD ignore alleles with marginal frequencies of <5 or 10%. The second solution is to use measures of allelic association that are normalized, to some extent, with respect to allele frequencies. The most common normalized measure of D is Lewontin's D′ (Lewontin, 1964). D′ has the desirable property that its absolute value is equal to 1.0 if two SNPs are in complete LD or if there are only three gametic types in the sample (Figure 1). For this reason, D′ has intuitive appeal; with only three gametic types, one need not invoke recombination to explain patterns of variation (Figure 1). A drawback of D′ is that its sampling properties are poorly understood when |D′| < 1.0. A modern alternative to normalization, based on the likelihood of observed LD conditional on allele frequencies, is rapidly gaining acceptance (Hudson, 2001).

Another measure that deserves mention is r², which is equal to D² divided by the product of the allele frequencies at the two loci. Hill and Robertson (1968) deduced that

Er²=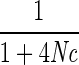

where c is the recombination rate in morgans between the two markers and N is the effective population size. This equation illustrates two important properties of LD. First, expected levels of LD are a function of recombination. This is easy to intuit: the more recombination between two sites, the more they are shuffled with respect to one another, decreasing LD. Second, LD is a function of N, emphasizing that LD is a property of populations. To arrive at this equation, Hill and Robertson assumed that the population was an “ideal” large, random-mating population without natural selection and mutation. When these assumptions are violated, the extent and pattern of LD may be affected (see below).

Given the empirical measurement of r², one can use the above equation to estimate 4Nc, a parameter that contains historical information about the population. It is important to note, however, that the relationship between r² and 4Nc has a large variance; for this reason, any single measure of LD between two SNPs does not allow accurate estimation of 4Nc. Because measures such as D and r² are pair-wise measures between two polymorphic sites, it also is difficult to obtain a summary statistic of LD across a region. Common approaches to summarize the distribution of LD in a genomic region are to plot r² (or an alternative LD measure) against physical distance (Figure 2) and to summarize pair-wise measures of LD in matrix form (Figure 2). These plots illustrate the rate at which LD decays with physical distance and often form the basis for comparison between studies. Newer methods estimate 4Nc for an entire region by integrating over the likely evolutionary histories of the sample (Fearnhead and Donnelly, 2001), but the methods can be computationally intractable with large data sets or high recombination rates. New methods also can obtain a composite measure of 4Nc for an entire region (Hudson, 2001); this approach has been extended to detect intervals with greater or fewer recombination events than predicted, given the interval size (http://genapps.uchicago.edu/axis/index.html).

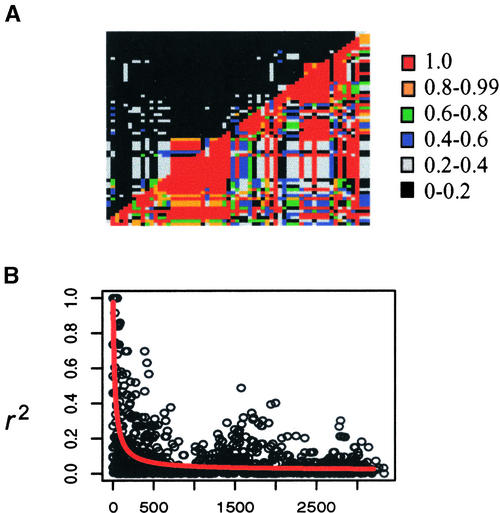
Figure 2.

Plots of LD across the Maize d3 Gene (Remington et al., 2001).

(A) Patterns of pair-wise LD between common polymorphisms with minor-allele frequencies of >0.05 in the d3 gene. LD estimates r² and D′ are plotted for each pair-wise comparison, with D′ below the diagonal and r² above it.

(B) A plot of r² versus distance (in bp) between pairs of sites. The line fitted to the data minimizes the sum of the squared differences between r² and its expected value, assuming recombination scales with physical distance.

EVOLUTIONARY FORCES THAT AFFECT LD

LD is affected by both biological factors, such as recombination, and historical factors that affect N. For example, population subdivision and blending (admixture) increase LD, but their effects depend on the number of populations, the rate of exchange between populations, and the recombination rate (Pritchard and Przeworski, 2001). Similarly, population bottlenecks and directional selection increase LD, but in the absence of other mitigating factors (such as population subdivision), their effect is short-lived (Przeworski, 2002; Wall et al., 2002).

Other factors that affect LD include selection, inbreeding, and fluxes in population size. Population bottlenecks increase LD, but in the absence of other mitigating factors (such as population subdivision), this effect should be short-lived (Wall et al., 2002). The same is true of directional selection; strong selection for a particular allele limits genetic diversity around a locus, resulting in a short-term increase in LD around the selected gene. With reasonable recombination rates, the duration of the increase in LD is short (i.e., on the order of <0.4N generations) (Przeworski, 2002).

The mating system also has a profound effect. Surprisingly, selfing species may have increased recombination rates per meiosis (Charlesworth and Charlesworth, 1979); for example, the recombination rate per base pair is estimated to be approximately twofold and sixfold higher in selfing Arabidopsis than in Drosophila and maize, respectively (L. Zhang and B.S. Gaut, unpublished data). However, selfing increases homozygosity, thereby limiting the number of double heterozygotes that can be shuffled by recombination. As a result, the effective rate of recombination is low in selfing species, genetic polymorphisms tend to remain correlated, and LD is expected to be maintained over long physical distances.

All of these factors affect the utility of LD for localizing QTL. Any evolutionary force that increases LD beyond that expected by chance in an ideal population will inflate the rate of false-positive associations.

LD IN TWO-MODEL PLANT SYSTEMS

To date, genetic diversity at the sequence level has been studied in only a handful of plant taxa, with maize and Arabidopsis the primary foci. These two species have different mating systems (outcrossing and selfing, respectively) and provide contrasting views of LD in plant genomes.

Maize

The first published LD study was based on survey of 21 loci on chromosome 1 (Tenaillon et al., 2001). Each locus was sampled in 25 individuals representing a “species-wide” sample of maize that included U.S. and exotic germplasm. Although the length of these genes was short (<1.5 kb), the rate of decay in LD was surprisingly rapid. On average, LD declined below nominal levels, which we arbitrarily define here as r² = 0.20, within 400 bp. By contrast, a subsample that included only U.S. inbred lines demonstrated a lower rate of decay over distance, reaching nominal LD levels in ∼1 kb. Higher LD in U.S. germplasm is consistent with the recent formation of these inbred lines and their relatively narrow genetic base.

A second study surveyed six genes of longer length (1.2 to 10 kb) in 102 inbred lines (Remington et al., 2001). These lines included tropical and semitropical lines and thus are more genetically diverse than samples of U.S. inbred lines alone but probably are less diverse than a species-wide sample. In this study, LD again declined rapidly; for five of six genes, LD was below the nominal level in 200 to 1500 bp. However, LD did not decay to nominal levels in ∼10 kb for one gene, shrunken1 (sh1). A subsequent study showed that sh1, an enzyme in the starch biosynthesis pathway, was under directional selection during either domestication or breeding (Whitt et al., 2002). Although LD decays rapidly in a gene after selection for a particular allele (Przeworski, 2002), the time scale of maize domestication (∼9000 years ago [Matsuoka et al., 2002]) may be such that an appreciable selective effect on LD remains. Another surprising aspect of this study was that a genome-wide sample of 47 simple sequence repeats demonstrated higher levels of LD than intergenic comparisons of SNPs. The reason for the apparent difference between SNPs and simple sequence repeats is unclear at present, but it may reflect differences in the type of historical information captured by markers with different mutation rates (Remington et al., 2001).

A more recent study examined LD in 18 genes based on a sample of 36 inbred lines, primarily from U.S. germplasm (Ching et al., 2002). Unlike previous studies, these data demonstrated an almost complete lack of LD decay over 500 bp. The lack of decline in LD probably reflects the narrow germplasm studied; levels of diversity in this sample were ∼50% of the levels in the species-wide sample. Another reason could be the genes chosen for analysis: as in sh1, recent artificial selection in these or tightly linked genes could increase LD. However, there was no strong evidence that any of the 18 genes had been subjected directly to recent selection. The overall result is that recombination in maize is sufficient to shuffle SNP polymorphisms on a very short physical scale, but this may not hold true in a sample of elite U.S. breeding germplasm.

Arabidopsis

LD extends over far greater distances in selfing Arabidopsis. In the region surrounding the flowering-time gene FRI, for example, LD declines to nominal levels only after ∼250 kb (Hagenblad and Nordborg, 2002). LD is even more pronounced in samples from local populations (Nordborg et al., 2002).

FRI may contribute to local adaptation and contain increased levels of LD as a result. Two recent studies suggest that this may be the case. The first is a study of diversity in the region surrounding the defense gene rps5 (Tian et al., 2002). For this region, LD breaks down in as little as 10 kb in a species-wide sample. Similarly, LD decays within 10 to 50 kb around the CLAVATA2 region (Shepard and Purugganan, 2003). However, these two regions, like FRI, also may be atypical; both regions appear to have been subjected to balancing selection, which retains distinct alleles within populations for long periods of time. When alleles are retained for substantially longer periods than expected for neutral genes, there is time to accumulate relatively high levels of diversity and ample opportunity for recombination among alleles.

Because FRI, rps5, and CLAVATA2 may be atypical, additional studies of the genomic patterns of Arabidopsis LD are merited. Nonetheless, one can draw two conclusions. The first is that LD in species-wide samples decays far more slowly over physical distance in this selfing species relative to outcrossing maize; this difference is consistent with the low effective recombination rate and the demographic consequences of selfing. The second is that selection on a particular gene, such as rps5, affects the distribution of genetic diversity in neighboring genes through genetic associations. The extent of these effects likely is stronger in selfing than in outcrossing taxa.

LD MAPPING

When LD declines rapidly with distance, LD mapping is potentially very precise. This idea has been best exploited in a series of studies that mapped the factors affecting the number of sensory hairs on the Drosophila thorax and abdomen (Lai et al., 1994; Long et al., 1998). In these studies, LD mapping localized causative variants to candidate genes that act in the development of the peripheral nervous system. Similar strategies can be applied to maize because the rapid decay of LD over physical distance in the species-wide maize samples suggests that most SNPs associated with phenotype will be located very near (within ∼1 kb) the causative genetic variant. By contrast, patterns of LD decay in Arabidopsis and in a narrow sample of maize U.S. germplasm suggest that LD mapping will be less precise (but perhaps no less helpful), likely narrowing causative variants to within an approximately 10- to 250-kb region. Quantifying levels and patterns of LD in germplasm of interest will facilitate the design of LD mapping studies.

The success of LD mapping depends on many additional factors, including the analytical methods used, the number of individuals examined, the recombination rate in target regions, and the proportion of phenotypic variance attributable to a causative polymorphism (Long and Langley, 1999). Population structure also is an important consideration; increased LD from population admixture can result in spurious associations between genotype and phenotype. Thus, it is important to correct for population structure in any association study (Pritchard et al., 2000), as exemplified in the landmark dwarf8 association study in maize (Thornsberry et al., 2001). However, the prospects for LD mapping are daunting, even with extensive knowledge of LD and population structure. When SNPs from hundreds or thousands of genes are tested for associations with characteristics of adaptive or agronomic importance, many false associations will be detected. Additional experiments will be required to replicate a positive association in an independent population and to functionally validate positive associations.

WHAT NEEDS TO BE DONE? FUTURE STUDIES OF LD

There is still much to learn about genomic patterns of LD. In maize, for example, there has been no study of the decay of LD over long (∼100-kb) distances. Such studies are important because recombination rates are not uniform across physical distances. Maize contains recombination hot spots within genes but recombinationally suppressed intergenic regions (Fu et al., 2002). Paradoxically, this pattern of recombination could result in the rapid breakdown of LD within genes but high residual levels of LD in intergenic regions, producing a punctuate pattern even more pronounced than that of the human major histocompatibility complex (Jeffreys et al., 2001). There also is relatively little knowledge of LD in plants on a chromosomal scale. LD should correlate with chromosome dynamics, such that low-recombination regions near centromeres contain relatively high levels of LD. Only one plant study has demonstrated this contrast explicitly, and there was no clear pattern between the levels of LD and physical estimates of recombination (Tenaillon et al., 2002). More studies are needed to generalize this result and to investigate the factors that influence LD. Finally, LD needs to be studied in more plant species, particularly economically important species such as rice, in which very little is known about SNP diversity. The success of LD mapping can be predicted in part by careful quantification of extant patterns of LD.