The Use of Entropy to Analyze Phyllotactic Mutants: A Theoretical Analysis

The mechanisms involved in phyllotactic regulation have been studied intensively from an experimental and theoretical point of view (Jean, 1994; Jean and Barabé, 1998; Reinhardt and Kuhlemeier, 2001; Reinhardt et al., 2003), so the discovery of genes that promote a change in phyllotactic patterns is certainly a breakthrough (Callos and Medford, 1994; Itoh et al., 2000; Reinhardt and Kuhlemeier, 2001). Phyllotactic systems are generally described using parameters such as divergence angle, plastochrone ratio, and number of sets of opposed visible spirals (parastichies). The main problem that emerges in the analysis of phyllotactic mutants is quantitatively describing altered degrees of order relative to the wild type. One possibility is to use a measure of order based on the principle of entropy, which is a mathematical function representing a measure of disorder in physical systems. A physical system evolving spontaneously toward equilibrium will correspond to an increase of its entropy. For example, a glass of water in which one introduces a drop of coloring fluid will spontaneously evolve toward a uniformly colored liquid.

Recently, Itoh et al. (2000) analyzed the pattern of leaf initiation in the shoot organization (sho) mutants in rice. Leaf primordia of sho mutants were initiated at nearly random positions on the shoot apex with a mean divergence angle of 110°. To quantify the degree of order of phyllotactic patterns appearing in these mutants they used the entropy of a partition, as defined in the context of information theory (Jean, 1979). To our knowledge, this represents the first time that this definition of entropy has been used to quantify the degree of order of a phyllotactic system and certainly constitutes an interesting avenue of research. However, there are limits in the degree to which entropy can characterize phyllotactic patterns, and it is problematic to use it to characterize the organization of the shoot apical meristem. More precisely, we use numerical simulations to demonstrate that the entropy of a partition cannot discriminate between an organized spiral system, for example with a divergence angle of 137.5°, and a random phyllotactic system. It is important to clarify that our theoretical analysis does not alter the biological conclusions reached by Itoh et al. (2000) or others studying mechanisms that underlie phyllotactic patterns. However, our theoretical simulations indicate that the entropy of a partition measure behaves in such a way (because of its mathematical definition) that it may not provide an adequate means to quantify alterations in phyllotactic patterns.

To measure the degree of organization of the stem apical meristem Itoh et al. (2000) used the following general formula of entropy:

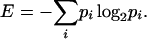The minus sign allows increasing positive values of E to be obtained.

In the entropy of a partition, the probability 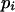is estimated by the frequency of the number of elements n_i placed in the sectori (n_i/n), where n represents the total number of elements. Then, in a centric representation, the apex being divided in h equal circular sectors (4 in Itoh et al., 2000), the value of the entropy is:

At equilibrium, the number of leaves appearing in each sector should theoretically be equal. Then n_i = n/h. Consequently, the formula of entropy becomes: The logarithm is in base 2 to agree with the information theory. This indicates that the value of the entropy increases when the number of the sectors increases. For example with 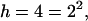the limit value of E is 2 (Table 1), and with , the limit value is 3 (Table 2).

Table 1.

Theoretical Value of E for Different Angles of Divergence in a Partition of Four Sectors

Divergence	n = 10	n = 20	n = 30	n = 50	n = 100	n = 200
60°	1.5710	1.5813	1.5850	1.5844	1.5848	1.5849
77.96°	1.971	1.9855	1.9968	1.9966	1.9988	1.9996
99.5°	1.971	1.9855	1.9968	1.9966	1.9994	1.9999
100°	1.9219	1.9589	1.9494	1.9709	1.9709	1.9739
120°	1.5710	1.5813	1.5850	1.5844	1.5848	1.5849
130°	1.9710	1.9855	1.9839	1.9896	1.9896	1.9912
137.51°	1.9219	1.9855	1.9968	1.9964	1.9988	1.9999
151.14°	1.9710	1.9589	1.9968	1.9988	1.9994	1.9999
180°	0	0	0	0	0	0
Random	1.9855	1.9037	1.9139	1.9787	1.9899	1.9904

h = 4; n, total number of leaves.

Table 2.

Theoretical Value of E for Different Angles of Divergence in a Partition of Eight Sectors

Divergence	n = 10	n = 20	n = 30	n = 50	n = 100	n = 200
60°	2.5219	2.5710	2.5850	2.5827	2.5844	2.5848
77.96°	2.9219	2.9332	2.9614	2.9918	2.9977	2.9985
99.5°	2.7219	2.9710	2.9899	2.9966	2.9976	2.9997
100°	2.7219	2.9464	2.9438	2.9661	2.9696	2.9738
120°	2.5219	2.5710	2.5850	2.5927	2.5844	2.5848
130°	2.7919	2.8710	2.9496	2.9828	2.9862	2.9902
137.51°	2.9219	2.9710	2.9899	2.9918	2.9988	2.9997
151.14°	2.7219	2.9710	2.9899	2.9966	2.9977	2.9994
180°	1	1	1	1	1	1
Random	2.4464	2.9710	2.8975	2.9535	2.9501	2.9701

h = 8; n, total number of leaves.

Let a theoretical phyllotactic system be divided in four sectors (Figure 1). Each sector is formed by two opposite angled sections of 45° each. The total entropy of the system (E) is the sum of the entropy (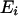) of each sector i dividing the circle in equal parts of:

For example, the sector 1 covers from the angle 337.5° to 22.5° and on the opposite side from the angle 157.5° to 202.5.5°. To calculate 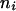we use an algorithm adding one unit (1 to n) to a sector i each time a new leaf is initiated in that sector at a given angle of divergence.

Figure 1.

Simulation of Different Phyllotactic Patterns.

The smallest values of E appear in whorled systems. For example, in alternate trimerous whorls (divergence of 60° between two whorls) and superposed trimerous whorls (divergence of 120° between elements of the same whorl) and E = 1. 58 for n = 30 (Table 1). In the case of a distichous systems (180°), E = 0. Note that in whorled systems the total number of leaves should theoretically be a multiple of the number of leaves in a whorl. For example, in a trimerous whorl the exact value of 1.58 is when n = 30. However, as n increases this constraint becomes insignificant. The entropy of whorled systems is always inferior to that of other types of systems. However, in all spiral systems (divergence angles of 77.96°, 95.5°,137.5°, and 151.14° in Tables 1 and 2) the entropy value rapidly reaches ∼1.9 with an increase in n. This limit value is already reached when n = 20. Therefore, there is a very small difference between the value of the entropy of a partition in spiral systems with respect to the angle of divergence and the number of primordia. It is interesting to see that the entropy of a random phyllotactic system (Figure 1) also quickly reaches this limit value of ∼1.9. The values of E random systems are generally inferior or equal to that of the spiral systems (Tables 1 and 2). Here, the entropy of a well organized system (spiral) is superior to that of a disorganized system (random). This indicates that the use of the entropy of a partition is problematical when it comes to determining the level of organization of a phyllotactic system when the number of leaves reaches the value of 20.

Therefore, except for whorled and distichous (wild-type) patterns, the entropy of a partition cannot give a precise representation of the degree of order in a phyllotactic system. This is not surprising considering that to characterize completely a phyllotactic system one needs to know at least two parameters among the four linked parameters used to define a phyllotactic system (Table 4.2 in Jean, 1994). In particular, the entropy of a partition does not take into account the number of opposed parastichies of the system (m, n). In regard to the problem of entropy, Jean (1994, 1998) developed a model based on a concept of hierarchy to represent the various spiral phyllotactic patterns (m, n), where (m, n) represent a visible parastichy pair. He used an entropy-like function E_b based on the set of hierarchies to calculate their energetic cost. The representation of the patterns (m, n) by hierarchies relates phyllotaxis to the general phenomenon of branching. In this model (Jean, 1994; Jean and Barabé, 2001), the entropy for each set of visible parastichies (m, n) is:

Parameter E_b represents the production cost of each type (m, n) of spiral pattern. The value of E_b increases as the number of parastichies increases, and there is no maximum value. However, this model is useless when the number of parastichies is not recognizable. It is impossible here to give a thorough presentation of this model; those readers who are interested are referred to Jean (1994, 1998, and 1999) and Jean and Barabé (2001) for its description and the predictions that can be made from it.

In conclusion, the entropy of a partition does not indicate the degree of order in the system with precision. For example, the value of E in a spiral phyllotactic pattern (n = 20) is not very different from that of a random system with the same number of leaves. With this formula, a spiral system will appear as disorganized even though it is a well-ordered pattern. Therefore, it is difficult to determine the degree of regularity of a system without the value of (m, n). Actually, in Jean's model it is not possible to determine the entropy of the phyllotactic system without knowing the number of opposed parastichies. To solve this problem, we are presently developing a probabilistic model that should quantify with precision the alteration degree of phyllotactic mutants. In this model, it will be possible to determine, within a confidence interval, to which phyllotactic system a given phyllotactic pattern belongs.