Contraction and stress-dependent growth shape the forebrain of the early chicken embryo

Abstract

During early vertebrate development, local constrictions, or sulci, form to divide the forebrain into the diencephalon, telencephalon, and optic vesicles. These partitions are maintained and exaggerated as the brain tube inflates, grows, and bends. Combining quantitative experiments on chick embryos with computational modeling, we investigated the biophysical mechanisms that drive these changes in brain shape. Chemical perturbations of contractility indicated that actomyosin contraction plays a major role in the creation of initial constrictions (Hamburger-Hamilton stages HH11–12), and fluorescent staining revealed that F-actin is circumferentially aligned at all constrictions. A finite element model based on these findings shows that the observed shape changes are consistent with circumferential contraction in these regions. To explain why sulci continue to deepen as the forebrain expands (HH12–20), we speculate that growth depends on wall stress. This idea was examined by including stress-dependent growth in a model with cerebrospinal fluid pressure and bending (cephalic flexure). The results given by the model agree with observed morphological changes that occur in the brain tube under normal and reduced eCSF pressure, quantitative measurements of relative sulcal depth versus time, and previously published patterns of cell proliferation. Taken together, our results support a biphasic mechanism for forebrain morphogenesis consisting of differential contractility (early) and stress-dependent growth (late).

1. Introduction

The embryonic brain emerges through a series of complex physical processes. Following neurulation, the anterior end of the neural tube expands to create the primitive brain, and circumferential constrictions, or sulci, divide the brain tube (BT) into three primary vesicles called the forebrain, midbrain, and hindbrain (Lowery and Sive, 2009). In the forebrain, additional constrictions form to separate the telencephalon, diencephalon, and the optic vesicles (Fig. 1). Meanwhile embryonic cerebrospinal fluid (eCSF) accumulates in the lumen, and the brain undergoes a period of rapid expansion and flexure. During these stages, insufficient growth of the forebrain can result in microcephaly (small brain) (Cox et al., 2006), and abnormal shaping has been linked to a range of neurodevelopmental disorders (Lowery and Sive, 2009).

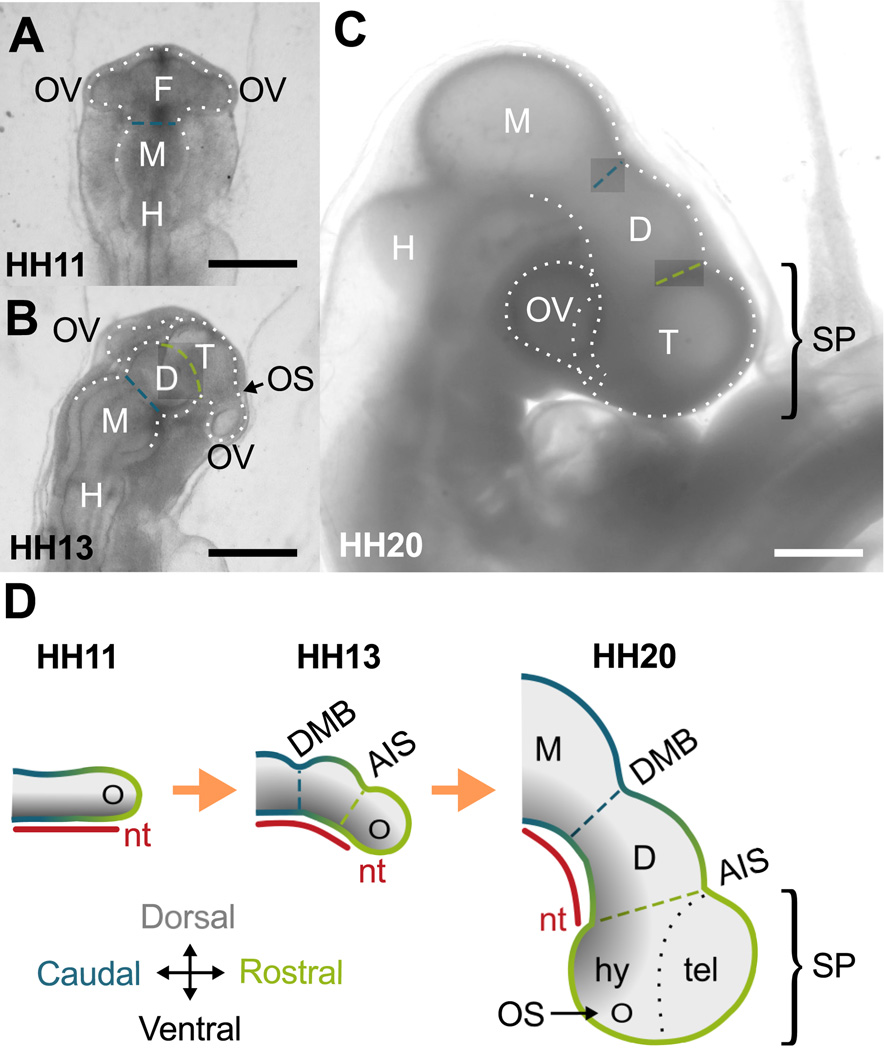
Figure 1.

Forebrain development in chick embryo. (A–C) Bright-field images of extracted embryos. (A) At HH11 (dorsal view), the brain tube (BT) is divided into three primary vesicles: forebrain (F), midbrain (M) and hindbrain (H). Optic vesicles (OVs) protrude bilaterally from the forebrain. (B) By HH13, the forebrain has further divided into diencephalon (D) and the telencephalon-hypothalamus complex (T). On each side the optic stalk (OS) has also constricted to separate OVs from T. (C) By HH20, a 90 degree rotation at the level of the spinal cord (not shown) results in a lateral instead of dorsal view of the BT. All sulci persist as the BT bends and expands. Scale bars: 500 µm. (D) Schematic of forebrain development (lateral view). The notochord (nt) and caudal-rostral axis (blue-to-green gradient) of the BT are relatively straight initially. As the BT grows, the notochord and BT bend ventrally, maintaining dorsal-ventral signaling (black-to-gray gradient) along the new curvature. Together the OVs, telencephalon (tel), and hypothalamus (hy) comprise the secondary prosencephalon (SP). DMB, diencephalon-midbrain boundary sulcus (blue dashed line); AIS, anterior intraencephalic sulcus (green dashed line).

This paper aims to explain secondary morphogenesis of the forebrain. On the dorsal side of the embryonic brain tube (Fig. 1A,B) the telencephalon and diencephalon are physically delineated by a constriction called the anterior intraencephalic sulcus, or AIS (Folgueira et al., 2012). On the ventral side, however, bending and bulging of the forebrain make subdivisions more difficult to interpret. As shown in Fig. 1C,D (right lateral view), the hypothalamus later appears as a ventral bulge in the curved forebrain. Optic vesicles also protrude from left and right sides of the forebrain to create the primitive eyes. Based on signaling patterns and fate-mapping, Puelles et al. (2012) propose that the telencephalon, hypothalamus, and optic vesicles all emerge from the rostral tip of the brain tube, a region named the secondary prosencephalon (SP). As shown in Fig. 1, the SP is morphologically distinct from the diencephalon and follows a dorsoventral pattern similar to the other brain vesicles.

The mechanisms responsible for secondary forebrain division remain poorly understood (Puelles et al., 2012). In the chick embryo, Filas et al. (2012) showed that actomyosin contraction likely creates the sulci between primary vesicles. A similar contractile mechanism is plausible within the forebrain, where actin is concentrated at the apical surface (Filas et al., 2012) and actin-binding proteins have been reported at sulci (Nicholson-Flynn et al., 1996). Yet evidence also suggests alternative or supplementary roles for pressure and growth (Gutzman and Sive, 2010; Lowery and Sive, 2009). Pressure from the eCSF inflates the brain tube viscoelastically and increases growth of the neuroepithelium (Alonso et al., 1998; Desmond and Jacobson, 1977; Desmond et al., 2014; Goodrum and Jacobson, 1981). Studies have also revealed increased proliferation in vesicles and dorsal regions of the normal embryonic chick brain (Layer and Sporns, 1987; Takamatsu and Fujita, 1987;Weikert et al., 1990).

This study focuses on the origin of the constrictions that separate the telencephalon-hypothalamus complex (T), diencephalon (D), and optic vesicles (OVs). Using the chick embryo as an experimental model, we determined the effects of actomyosin contraction and eCSF pressure on brain shape. Computational models incorporating experimentally measured F-actin alignment verify that a contractile mechanism is sufficient to initiate forebrain subdivision. However, our results suggest that an additional mechanism is needed to maintain and deepen sulci during subsequent brain inflation and bending (cephalic flexure). We propose that mechanical feedback, through the interaction of wall stress and growth, is instrumental in forebrain expansion and sulcal maintenance. To evaluate this hypothesis, we compare new experimental data with a model that includes contraction, eCSF pressure, bending, and stress-dependent growth. Our results highlight how the interplay of several common morphogenetic mechanisms can generate the complex structure of the early embryonic brain.

2. Materials and Methods

2.1. Embryo culture and perturbation

Fertilized white Leghorn chicken eggs were incubated at 37 ° C (90% humidity), and embryos were extracted using a filter paper carrier as described in Chapman et al. (2001). Embryos were staged according to the system of Hamburger and Hamilton (1951) (denoted HHxx) and cultured in Dulbecco’s Modified Eagle’s Medium (Sigma) with 10% chick serum (Sigma), 1% penicillin/streptomycin/neomycin (Invitrogen). During culture embryos were submerged under a thin layer of fluid and superfused with a mixture of 95% oxygen and 5% carbon dioxide (Voronov and Taber, 2002). All embryos were examined over the course of development under a Leica MZ8 microscope.

Altering actomyosin contractility

To alter contractility during initial forebrain subdivision, embryos were extracted at 40–42 h incubation (HH11) and cultured with blebbistatin (60 µM, Sigma) or calyculin A (30 nM, Sigma). Blebbistatin decreases contraction by inhibiting myosin II adenosine triphosphatase, while calyculin A enhances contraction by inhibiting myosin II phosphatase (Filas et al., 2012). As an alternate method of increasing contraction, several embryos were treated in media containing 5 mM adenosine triphosphate (ATP, Sigma) and 0.05% Triton-X 100 for 3 h. To rule out the effects of external forces, external mesenchyme and membranes were removed from several samples, which were then cultured for 6 h in control media or media containing calyculin A (30 nM). To observe effects at later stages, calyculin A was also added to culture medium of embryos after 50–60 h incubation (HH14–17) at concentrations of 30 nM or 100 nM.

Altering eCSF pressure

To relieve pressure during later stages of brain expansion, normal embryos (HH12) were intubated at the anterior neuropore with an open pulled glass micropipette (inner diameter = 40–60 µm) and cultured in media for 24 h (Desmond and Jacobson, 1977). Only embryos in which the tube remained intact and unblocked were used for subsequent analysis. In control embryos, pressure was similarly relieved at the equivalent end stage (HH17) using a glass capillary tube (inner diameter = 150 µm).

2.2. Morphological imaging and analysis

For quantitative analysis, optical coherence tomography (OCT) was used to record three-dimensional (3D) geometries in living embryos at multiple time points. With Fiji/ImageJ software, image stacks were oriented to yield cross sections along the axis of the BT (see Fig. S1 for details) (Schindelin et al., 2012). The perimeter δ of the lumen was traced and recorded for each cross section, and the average inner radius was computed as R = δ/2π. The average circumferential stretch ratio is given by λ_Θ = r/R, where R and r are the average radii in the initial and final configurations, respectively.

Relative constriction is defined as the ratio of vesicle radius to adjacent sulcus radius. Ratios are denoted by T/AIS (r_T/r_AIS), D/DMB (r_D/r_DMB), and M/DMB (r_M/r_DMB). According to this notation, a sulcus forms when the corresponding ratio is greater than unity, and the sulcus deepens as the ratio increases.

2.3. Actin imaging and analysis

To visualize F-actin on the apical surfaces, embryos were fixed with 3.7% formaldehyde, cut into dorsal and ventral halves, and stained with phalloidin (Filas et al., 2012). Three-dimensional images of the apical surface were recorded using a Zeiss LSM 710 confocal microscope with a 20× objective lens.

Fiji/ImageJ was used to divide image stacks into 50 µm by 50 µm squares, with the view angle reoriented manually to ensure images tangent to the apical surface. This method was designed to minimize tissue distortion associated with previous flat-mount techniques (Filas et al., 2012). For each square, the angular distribution of actin was calculated from its Fourier power spectrum using the directionality function in Fiji/ImageJ (Liu, 1991). The resulting histogram of actin directionality (N=90 bins spanning 0° to 180°) was converted into circumferential (0°) and longitudinal (90°) components, S_Θ and S_Z, respectively, as defined by the relations

$$S_{\mathrm{\Theta }}={\int }_0^{\pi }|\xi (\gamma )\text{ cos }\gamma |d\gamma \approx \sum _{n=1}^N|{\xi }_n\text{ cos }{\gamma }_n|$$

$$S_Z={\int }_0^{\pi }|\xi (\gamma )\text{ sin }\gamma |d\gamma \approx \sum _{n=1}^N|{\xi }_n\text{ sin }{\gamma }_n|.$$ (1)

Here γ is the fiber angle relative to the circumferential direction, and ξ is the angular distribution normalized to ${\int }_0^{\pi }\xi (\gamma )d\gamma ={\sum }_{n=1}^N{\xi }_n=1$ (Marquez, 2006). The total area fraction of actin was estimated by the number of bright pixels divided by total number of pixels in the image. Since actin generally outlines apical cell borders, cell density was also estimated as the number of cells in an image divided by the total image area.

2.4. Statistics

Statistical significance was evaluated between groups using SigmaPlot (Systat Software, San Jose, CA). Analysis of Variance (ANOVA) with post-hoc Tukey test was used to compare data between multiple groups. Student t-test was used to compare data between two groups where applicable. For all tests, P<0.05 was considered to be significant. All error bars denote standard deviation unless otherwise indicated.

2.5. Computational Modeling

Geometry and boundary conditions

To simulate forebrain morphogenesis, finite element models were created using ABAQUS Standard (v6.10, SIMULIA, Providence, RI). Initial three-dimensional geometries were based on dimensions from OCT images at HH11, before forebrain constriction.

We considered two idealized models for development from HH11 to HH12. The first model considers the main BT as a cylinder of length L = 0.5 mm, wall thickness h = 50 µm, and inner radius R = 0.1 mm, including a hemispherical cap for the forebrain but omitting optic vesicles (Fig. 4A, top). The second model considers only the SP (Fig. 4A, bottom), consisting of a middle spherical shell (telencephalon-hypothalamus complex) with inner radius R_T = 0.15 mm, optic vesicles with inner radius R_OV = 0.08 mm, wall thickness h = 50 µm, and total distance W = 0.6 mm between tips of the optic vesicles. In both models only the left half of the brain was simulated, using symmetry conditions at the cutting plane to reduce computation time. The open (midbrain) end of the BT model is constrained by roller boundary conditions, and the SP model assumes rostral-caudal symmetry. Walls are five elements thick and composed of C3D20R elements (20-node hexagonal elements with reduced integration). To capture full model behavior, 7115 elements are used in the BT model, and 3810 elements are used in the SP model.

A third, modified BT model was used to simulate morphogenesis beyond HH12 (omitting OVs), as the BT undergoes significant bending and growth. Flexure has been attributed in part to the notochord, which is a relatively stiff, rod-like structure attached along the ventral side of the BT (Fig. 1D) (Adams et al., 1990; Agero et al., 2010; Zhou et al., 2009). As the brain grows longer, the length of the notochord changes relatively little, which could cause the tube to bend (Fujita, 1986; Takamatsu and Fujita, 1987). Here the notochord is represented by a stiff, non-growing region on the ventral side of the BT with a shear modulus that decays from 100µ at the ventral midline to μ at its dorsal and lateral edges (Fig. 6A). This continuous representation, as opposed to a separate notochord, was implemented to minimize stress concentrations and improve convergence for models that include stress-dependent growth. Notably, bending requires a fully 3D analysis.

To simulate the one-cell-thick neuroepithelium, the walls of all models consist of an outer layer of passive, growing tissue and a relatively thin inner layer of contractile tissue (20% of the initial wall thickness) to represent the network of actomyosin fibers located at cell apices. In addition, a uniform pressure p = 30 Pa (Jelinek and Pexieder, 1968) is applied to the inner surface of each model. Pressure is ramped to its final value after contraction (HH12⁻ to HH12⁺), then held constant for all subsequent development up to HH20, in agreement with data of Desmond et al. (2005), who measured relative changes in eCSF pressure from HH12–26. For simplicity, stress-dependent growth is applied only after contraction and pressure have reached their final, maintained values (HH12⁺).

Kinematics

Contraction and growth were simulated in ABAQUS using a custom user subroutine based on the UMAT-generator of Young et al. (2010) for large deformations. Modifying the theory for volumetric growth (Rodriguez et al., 1994), we decompose the total deformation gradient tensor in the form

$$\mathbf{F}={\mathbf{F}}^{*}·\mathbf{C}·\mathbf{G},$$ (2)

where G, C, and F* are growth, contraction, and elastic deformation gradient tensors, respectively. With rigid-body rotation absorbed into F*, G = I corresponds to no net growth and C = I corresponds to passive tissue, where I is the identity tensor. Relative to the zero-stress configuration, the Lagrangian strain tensor is ${\mathbf{E}}^{*}=\frac{1}{2}({\mathbf{F}}^{*T}·{\mathbf{F}}^{*}-\mathbf{I})$.

Since the wall thickness of the early BT remains relatively unchanged throughout the stages considered here (Fig. S1D), we do not include contraction or growth in the radial (transverse normal) direction. We also assume that growth is transversely isotropic relative to the radial direction. For cylindrical geometry, these stipulations lead to the relations

$$\mathbf{C}={\mathbf{e}}_R{\mathbf{e}}_R+C_{\mathrm{\Theta }}{\mathbf{e}}_{\mathrm{\Theta }}{\mathbf{e}}_{\mathrm{\Theta }}+C_Z{\mathbf{e}}_Z{\mathbf{e}}_Z$$

$$\mathbf{G}={\mathbf{e}}_R{\mathbf{e}}_R+G{\mathbf{e}}_{\mathrm{\Theta }}{\mathbf{e}}_{\mathrm{\Theta }}+G{\mathbf{e}}_Z{\mathbf{e}}_Z.$$ (3)

Contraction is simulated by taking 0 < C_Θ < 1 and 0 < C_Z < 1 (C_Θ = C_Z = 1 for passive tissue), and G > 1 gives positive growth. For spherical and toroidal geometries, the Z direction is replaced by the more general meridional direction Φ.

Constitutive relations

In all models, the passive outer layer is taken as isotropic (Xu et al., 2010), while the contractile inner layer is represented by an active orthotropic material consisting of aligned fibers within an isotropic meshwork (cell membrane and disordered actomyosin fibers) (Murrell et al., 2015). To account for the relatively small volumes of water that enter or exit the tissue during deformation, both layers are assumed to be composed of nearly incompressible pseudoelastic materials (Xu et al., 2010).

The Cauchy stress tensor is given by (Taber and Perucchio, 2000)

$$\mathit{\sigma }=J^{*-1}{\mathbf{F}}^{*}·\mathbf{S}·{\mathbf{F}}^{{*}^T}$$ (4)

where Eq. (2) gives F* = F · G⁻¹ · C⁻¹, and

$$\mathbf{S}={\phi }_{\mathit{\text{iso}}}\frac{\partial W_{\mathit{\text{iso}}}}{\partial {\mathbf{E}}^{*}}+{\phi }_{\mathrm{\Theta }}\frac{\partial W_f}{\partial E_{\mathrm{\Theta }\mathrm{\Theta }}^{*}}{\mathbf{e}}_{\mathrm{\Theta }}{\mathbf{e}}_{\mathrm{\Theta }}+{\phi }_Z\frac{\partial W_f}{\partial E_{ZZ}^{*}}{\mathbf{e}}_Z{\mathbf{e}}_Z$$ (5)

is the second Piola-Kirchhoff stress tensor. Here, W_iso(E*) and $W_f(E_{\mathrm{\Theta }\mathrm{\Theta }}^{*},E_{ZZ}^{*})$ represent strain-energy density functions for isotropic constituents and aligned contractile fibers, respectively. In addition, J* = det F* is the elastic volume ratio, the e_i are unit base vectors in the initial configuration, and T denotes the transpose. The φ_k are volume fractions that satisfy the condition

$${\phi }_{\mathit{\text{iso}}}+{\phi }_{\mathrm{\Theta }}+{\phi }_Z=1.$$ (6)

In the passive outer layer, C = I, φ_iso = 1, and φ_Θ = φ_Z = 0.

For these early stages in the chick embryo, neuroepithelial tissue is relatively linear and can be treated as a modified neo-Hookean material (Xu et al., 2010). Here, we take

$$W_{\mathit{\text{iso}}}=\frac{\mu }{2}(\overline{I_1^{*}}-3)+\kappa [\frac{1}{2}(J^{*2}-1)-\text{ln }{J}^{*}]$$

$$W_f=\frac{1}{2}({\mu }_{\mathrm{\Theta }}{E}_{\mathrm{\Theta }\mathrm{\Theta }}^{*2}+{\mu }_Z{E}_{ZZ}^{*2}),$$ (7)

where $\overline{I_1^{*}}=J^{*-2/3}\text{ tr}(\mathbf{I}+2{\mathbf{E}}^{*})$ is the first strain invariant; μ, μ_Θ, and μ_Z are shear moduli; and κ is the bulk modulus. Using the measurements of Xu et al. (2010) for the embryonic chick brain (HH11–13), we set μ = 200 Pa and κ = 100μ for both layers. Values for the other moduli and volume fractions are discussed below.

Contraction parameters

To estimate the values of C_Θ and C_Z (or C_Φ), we modified the method of Filas et al. (2012), who modeled morphogenesis of the midbrain and hindbrain vesicles. Accordingly, contractile strength C is characterized by the relative change in apical surface area of the cells as given by

$$C=C_{\mathrm{\Theta }}{C}_Z=C_{\mathrm{\Theta }}{C}_{\mathrm{\Phi }}.$$ (8)

As C decreases from unity, strength of contraction increases. For normal development, we let C = 0.5 at peak contraction, consistent with measurements of Nakajima and Tanoue (2010) for mammalian epithelial cells. To check for consistency, model results were compared to the experimentally measured stretch ratio λ_Θ in the diencephalon. To calibrate contraction for the hypercontracted brain, C was decreased until λ_Θ reached the average value measured for embryos cultured in 30 nM calyculin A, corresponding to C = 0.3 for our case. In other systems undergoing apical constriction, such as during Drosophila gastrulation and avian lung budding, the relative change in area has been reported as low as 0.25 (Kim et al., 2013; Martin et al., 2009). We assume uniform C throughout the inner layer of our models, where colocalization of F-actin and phosphorylated myosin light chain (pMLC) has been reported previously (Filas et al., 2012).

Filas et al. (2012) assumed that contractile anisotropy is related to changes in cell shape. Here, however, we estimate anisotropy from our actin alignment data through the relations

$$C_{\mathrm{\Theta }}=\frac{S_Z}{S_{\mathrm{\Theta }}}\sqrt{C},\hspace{1em}{C}_Z=\frac{S_{\mathrm{\Theta }}}{S_Z}\sqrt{C},$$ (9)

which satisfy Eq. (8). As defined by Eqs. (1), S_Θ and S_Z represent the net fiber components oriented in the circumferential and longitudinal directions, respectively. According to these relationships, greater circumferential fiber content (increased S_Θ) corresponds to increased circumferential contractility (decreased C_Θ), and vice versa. This relationship is consistent with published findings that contractile force increases with fiber alignment in vascular smooth muscle cells and cardiomyocytes (Alford et al., 2011; Feinberg et al., 2012).

Actomyosin fibers also stiffen as they contract, due in part to the addition of myosin crosslinks (Salbreux et al., 2012; Stricker et al., 2010). To include this effect we assume that the fiber shear modulus increases with contraction (decreased C_Θ,C_Z) through the relations

$${\mu }_{\mathrm{\Theta }}=\mu C_{\mathrm{\Theta }}^{-\alpha },\hspace{1em}{\mu }_Z=\mu C_Z^{-\alpha }$$ (10)

where α > 0. Here we consider α = 4. For control embryos this relationship gives μ_Θ = μ_Z ≈ 4μ in isotropic regions but μ_Θ ≈ 13μ and μ_Z ≈ 1.2μ in aligned regions (for S_Θ/S_Z ≈ 1.3). For hypercontracted brains these relations yield μ_Θ = μ_Z ≈ 11μ in isotropic regions. Such increases are consistent with previously reported stiffening of the BT under contraction (Filas et al., 2011), as well as direct measurement of actin fiber stiffening in living endothelial cells (Lu et al., 2008). All values fall within the range of previously reported actin-fiber stiffness data (Salbreux et al., 2012; Stricker et al., 2010).

Since S_Θ and S_Z also represent fractional sums of all fiber components oriented in the Θ and Z directions, we use these quantities to estimate volume fractions in the relatively thin contractile layer. Actin image analysis indicates that fibers comprise about 50% of the apical surface area. To satisfy Eq. (6), we take φ_iso = 0.5 and

$${\phi }_{\mathrm{\Theta }}=\frac{0.5S_{\mathrm{\Theta }}}{S_{\mathrm{\Theta }}+S_Z},\hspace{1em}{\phi }_Z=\frac{0.5S_Z}{S_{\mathrm{\Theta }}+S_Z}.$$ (11)

Growth law

In the BT model for HH12–20, growth is included in the outer, passive layer through a rate equation of the form

$$Ġ=(g_0+g_{\sigma }\overline{\sigma })G$$ (12)

where g₀ ≥ 0 is the baseline growth rate and g_σ ≥ 0 is a coefficient for stress-dependent growth (Taber, 2009). In this equation, the nondimensionalized average stress is defined as

$$\overline{\sigma }=\frac{1}{2\mu }({\sigma }_{\mathrm{\Theta }\mathrm{\Theta }}+{\sigma }_{ZZ}).$$ (13)

Here we assume stress-dependent growth is triggered by tension only (g_σ = 0 for $\overline{\sigma }$ ≤ 0). As described in the Results section, values of the growth parameters were determined by fitting model results to experimental measurements of embryos cultured under control and zero-pressure conditions.

3. Results

Stage-dependent results are based on the system of Hamburger and Hamilton (1951), who divided the 21-day incubation period of the chick embryo into 46 stages based on morphological characteristics. Stage is a nonlinear function of time that depends on environmental and other factors. Thus, developmental stage in the following models is related to average midbrain radius (r_M) measured in chick embryos.

3.1. Contraction is necessary for AIS and OS formation

In the early chick embryo, the apical (inner) surface of the BT is lined with actin and myosin, which have been implicated in shaping the primary vesicles (Filas et al., 2012). To determine whether actomyosin contraction also partitions the forebrain (AIS and OS formation), embryos were cultured from HH11 to HH12 in control media (n=9), blebbistatin to reduce contractility (n=15), or calyculin A to increase contractility (n=12) (Fig. 2A–C). Morphological changes were measured from OCT cross sections (Fig. 2A’–C’, A”–C”). To rule out the influences of external factors, additional experiments were also conducted as outlined in Supplementary Data (Fig. S2). These include exposure to ATP (n=5), culture of isolated brain tubes in control media (n=3) or calyculin A (n=5), reduced eCSF pressure during boundary formation (n=3), and staining for cell death (n=21).

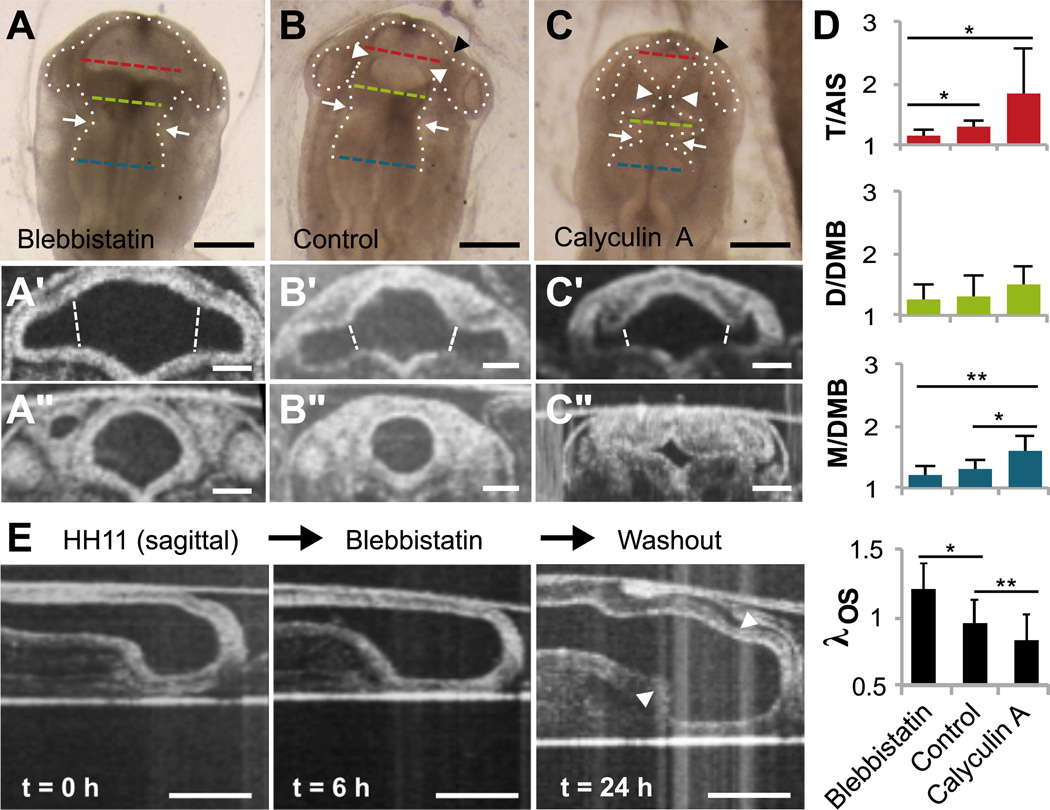
Figure 2.

Effects of actomyosin contraction on early forebrain morphogenesis (HH11–12). Stage HH11 embryos were cultured 6 h in media containing blebbistatin or calyculin A to inhibit or enhance contractility, respectively (control n=9, blebbistatin n=15, calyculin A n=12). (A–C) Bright-field images reveal altered BT morphology under each condition (dorsal view). White arrowheads indicate AIS, black arrowheads indicate the optic stalk (OS), and white arrows highlight previously formed DMB. Dashed lines indicate locations used to compute average radii for T (red), D (green) and M (blue). Scale bars: 200 µm. (A’–C’) Representative OCT cross sections of SP for each case. Dashed white lines indicate locations used to compute average radii for the OS, and the average radius of T was calculated considering lumen area between the optic stalks. Scale bars: 100 µm. (A”–C”) Representative AIS cross sections for each case. Scale bars: 100µm. (D) Relative constrictions based on average radii at locations indicated in (A–C), as well as relative OS stretch ratio λ_OS based on locations indicated in (A’–C’). *P<0.05, **P<0.001 (E) Representative sagittal cross sections before and after 6 h in blebbistatin, followed by washout (n=6). White arrowheads indicate AIS. Scale bars: 200 µm.

Exposure to blebbistatin significantly reduced relative AIS constriction (T/AIS) (P=0.001, Fig. 2D), which resumed after subsequent washout (n=6, Fig. 2E). Blebbistatin had relatively little effect on the DMB, which formed prior to HH11, suggesting that constriction may be at least partially irreversible (Filas et al., 2012). Due to the complex shape of the optic vesicle (see Fig. 1C), OS constriction could not be measured relative to the primitive eye. However, comparison of circumferential stretch, λ_OS, revealed that the optic stalk expanded when cultured in blebbistatin (Fig. 2A’–B’).

Exposure to calyculin A increased relative constriction of the DMB (M/DMB, P<0.001) and AIS (T/AIS, P=0.058) and caused significant shrinkage of the OS (λ_OS, P<0.001). The effect of calyculin A on T/AIS showed largest variability, with the AIS sometimes appearing similar to controls and other times almost entirely closing off the boundary. Because even embryos of the same stage show slight differences, we speculate that the embryos most affected by calyculin A were at an optimal point in development to allow hypercontraction. “Hinge-points” were also observed at the dorsal, ventral, and lateral corners of the AIS in hypercontracted embryos (Fig. 2C”), similar to those described in other regions by Filas et al. (2011). For simplicity our measures reflect only the change in total boundary circumference.

Embryos cultured with ATP showed hyperconstriction that was qualitatively similar to those cultured in calyculin A (Fig. S2A). Isolated BTs constricted slightly more than those of intact embryos in control media (Fig. S2B), but isolated BTs constricted drastically in calyculin A (Fig. S2C). Constrictions were observed even for embryos in which the neural tube failed to close, ruling out a need for eCSF pressure in sulcus initiation (Fig. S2D). Furthermore, no cell death was observed during early or late sulcus formation (Fig. S2E). These results suggest that the observed changes in morphology are likely caused by altered contractility within the neuroepithelium; external forces are not necessary for initial forebrain subdivision.

3.2. Actin is circumferentially aligned at forebrain constrictions

The importance of myosin II in forebrain subdivision motivated a closer look at its structural counterpart, F-actin. Staining for F-actin at the time of AIS formation (HH12, n=15) revealed localization at the apical surface throughout the forebrain (Fig. 3A–C). This appears similar to the midbrain and hindbrain, where colocalized F-actin and phosphorylated myosin light chain (pMLC) were found along the apical surface (Filas et al., 2012). Confocal imaging of the apical surface (Fig. 3A’–C’) revealed distinct patterns of actin alignment and three statistically significant groups (ANOVA P<0.001, n=5–6 per group). Actin fibers were circumferentially oriented (S_Θ/S_Z > 1) in circumferentially constricted regions (DMB and AIS), longitudinally oriented (S_Θ/S_Z < 1) on the dorsal side of the OS, and isotropically oriented (S_Θ/S_Z ≈ 1) elsewhere (D, T, and ventral OS). With the exception of the OS, no significant differences were observed between dorsal, ventral, and lateral sides of the BT. These patterns are summarized in Fig. 3E, and detailed distributions are shown in Fig. 4C.

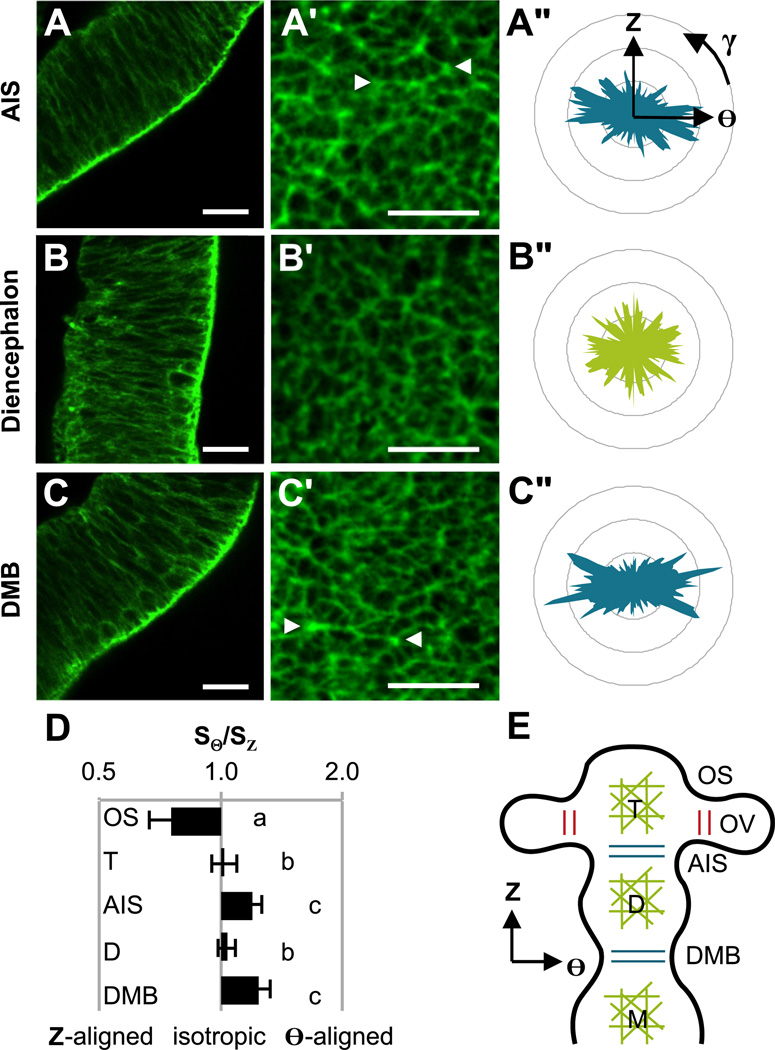
Figure 3.

Actin patterns in HH12 brain tube. (A–C) Phalloidin staining revealed F-actin concentrated along the entire apical surface of the forebrain vesicles and sulci. Representative images are shown for the wall of the AIS, D, and DMB, respectively. (A’–C’) The inner, apical surface of the forebrain was recorded and divided into 50 µm × 50 µm squares for analysis. Representative squares are shown for the AIS, D, and DMB, respectively. Arrowheads indicate actin cables that span multiple cells. (A”–C”) Histograms of fiber orientation for squares in (A’–C’). (D) Each histogram was decomposed into circumferential and longitudinal components, S_Θ and S_Z, relative to the BT. Fiber orientation, defined by S_Θ/S_Z, is compared across major regions (log scale). S_Θ/S_Z = 1 indicates isotropic fiber organization, S_Θ/S_Z > 1 indicates circumferentially aligned fibers, and S_Θ/S_Z < 1 indicates longitudinally aligned fibers. One-way ANOVA (P<0.001) with post-hoc Tukey test revealed three statistically different groups denoted by a, b and c (n≥5 per region, P<0.05). (E) Schematic summarizing observed fiber orientations. Isotropic fiber organization for the midbrain (M) has been previously described (Filas et al., 2012). Scale bars: 20 µm.

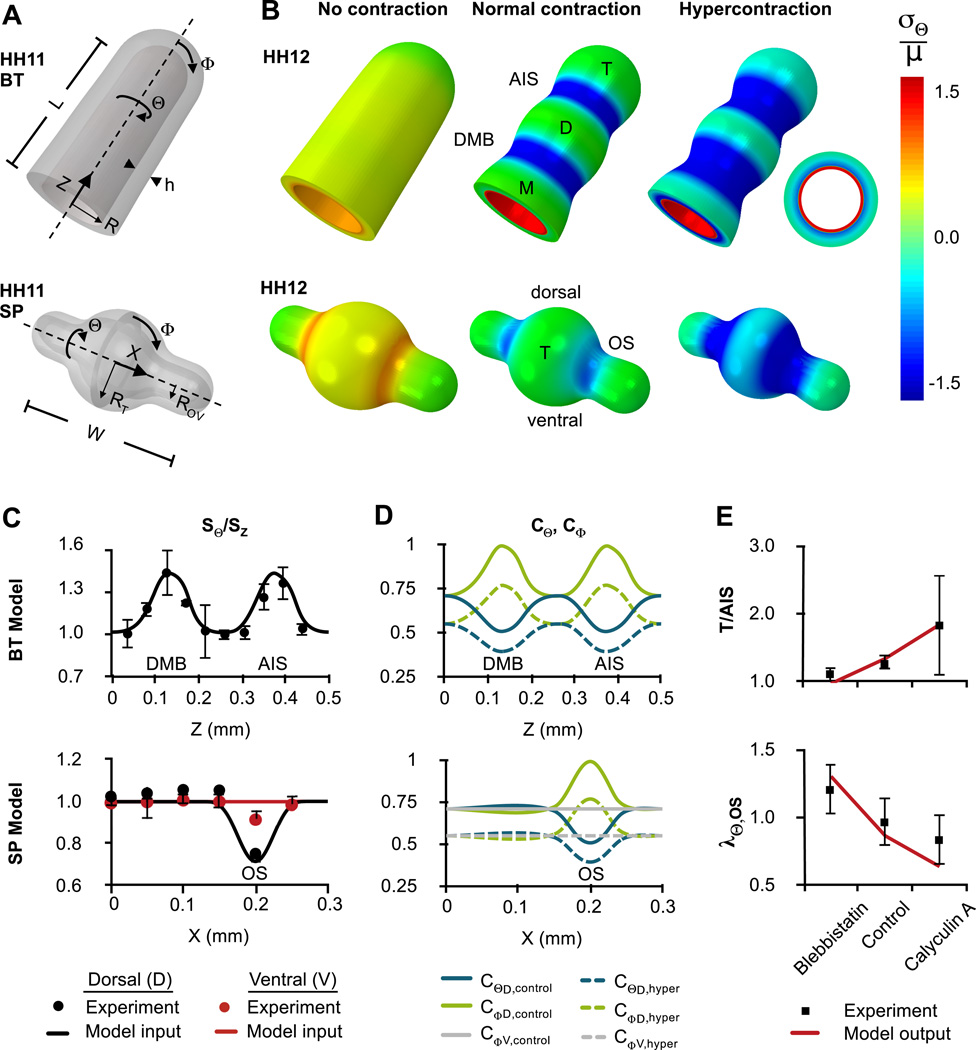
Figure 4.

Finite element models of initial forebrain subdivision (HH11–12). (A) Initial geometries approximate HH11 BT (omitting OVs, top) and SP (bottom). A thin contractile layer covers the inner surface (red in B, right) (B) Deformed geometry with normalized circumferential stress distributions for the cases of no contraction (blebbistatin), normal contraction (control), and hypercontraction (calyculin A). Representative cross section is shown at right. (C) Experimental actin alignment patterns were used as model input. Top: Patterns along the Z-axis of the BT indicate circumferential alignment at DMB (Z ≈ 0.13 mm) and AIS (Z ≈ 0.37 mm). Experimental data are shown for the dorsal midline, but no significant differences were observed between dorsal and ventral sides. Bottom: Patterns along the X-axis of the SP indicate circumferential alignment at dorsal but not ventral OS (X ≈ 0.2 mm). Bars represent standard error of the mean. (D) Resulting circumferential (C_Θ) and longitudinal (C_Φ) contraction tensor components plotted along the Z and X-axes for normal (C = 0.5) and hypercontracted (C = 0.3) cases. (E) Relative AIS depth (T/AIS) and OS stretch (λ_Θ,OS) plotted for model and experimentally measured values.

Since the OS is essentially a small cylinder protruding perpendicularly from the BT, the longitudinal direction relative to the BT is circumferential relative to the OS. As such, actin fibers are consistently oriented in the direction of maximum curvature at all constrictions. With this interpretation, the estimated alignment in the local circumferential direction is similar for the DMB, AIS and OS (Fig. 3D). As in Filas et al. (2012), actin is circumferentially aligned at persistent brain constrictions (MHB, DMB, AIS, OS), while it is relatively isotropic in brain vesicles (H, M, D, T).

3.3. Contraction initiates forebrain segmentation

To examine whether measured actin patterns could produce observed morphology, we simulated contraction in finite element models for the HH11–12 BT (without OVs) and SP (including OVs). Initial model geometries are based on OCT measurements (Fig. 4A, see Table S1 for parameter values). Material properties, eCSF pressure p, and contractile strength C were taken from published data (Jelinek and Pexieder, 1968; Nakajima and Tanoue, 2010; Xu et al., 2010), and directional contractilities were calculated from actin orientation using Eq. (9) (Fig. 4C,D). The resulting model contained only one free parameter, α, which determines how fiber shear modulus varies with C (see Eq. (10), calibration in Fig. S3). Since the size of the BT changes relatively little from HH11–12, growth was neglected during this step.

For α = 4, our BT model produced a shape resembling morphology of the HH12 BT (compare Fig. 4B to Fig. 2A–C). Relative constriction of the AIS agrees well with quantitative measurements under reduced, normal, and enhanced contraction (Fig. 4E, top). Using the same contraction parameters, the SP model gives similarly accurate results for OS constriction (Fig. 4E, bottom).

At these stages, wall stress is determined by a combination of lumen pressure, which produces tension, and apical contraction, which produces tension in the inner, contractile layer and compression in the outer, passive layer. Under normal contraction, the passive layer experiences circumferential compression at the sulci but minimal wall stress in the vesicles (Fig. 4B). As contraction increases, compression of the passive layer increases. Note that, while both model geometries are initially axisymmetric, differences between ventral and dorsal actin orientation at the OS produce slight asymmetry in final shape and stresses of the SP. (As shown in Fig. 1C, the OVs becomes quite asymmetric at later stages of SP development.)

For a pressurized tube, compliance generally increases with the ratio of radius to wall thickness. This ratio is relatively small at HH12; eCSF pressure causes elastic deformation of only ${\lambda }_{\mathrm{\Theta }}^{*}=1.1\pm 0.1$ in control embryos (vesicle radii measured from OCT before and after deflation, n=7). In embryos exposed to blebbistatin, however, the walls of the BT and SP are abnormally compliant. Similarly, in BT and SP models with no contraction, the active layer fails to stiffen and we see overexpansion. Our SP model reveals that the OS is particularly susceptible to overexpansion (Fig. 4B), consistent with experimental observations (Fig. 2A’).

3.4. Lumen pressure drives forebrain expansion via inflation and growth

The BT undergoes significant expansion in subsequent stages of normal development, with vesicle radii more than doubling from HH12–17. To separate the relative contributions of eCSF pressure and growth, we measured lumen radii across the BT for three cases: (1) embryos cultured from HH12 to HH17 with no pressure (n=6 intubated; Fig. 5B–C); (2) embryos cultured from HH12 to HH17 with normal pressure (n=8 control; Fig. 5E); and (3) control embryos immediately after deflation at HH17 (n=8; Fig. 5D). The relationships between each case are depicted schematically in Fig. 5A.

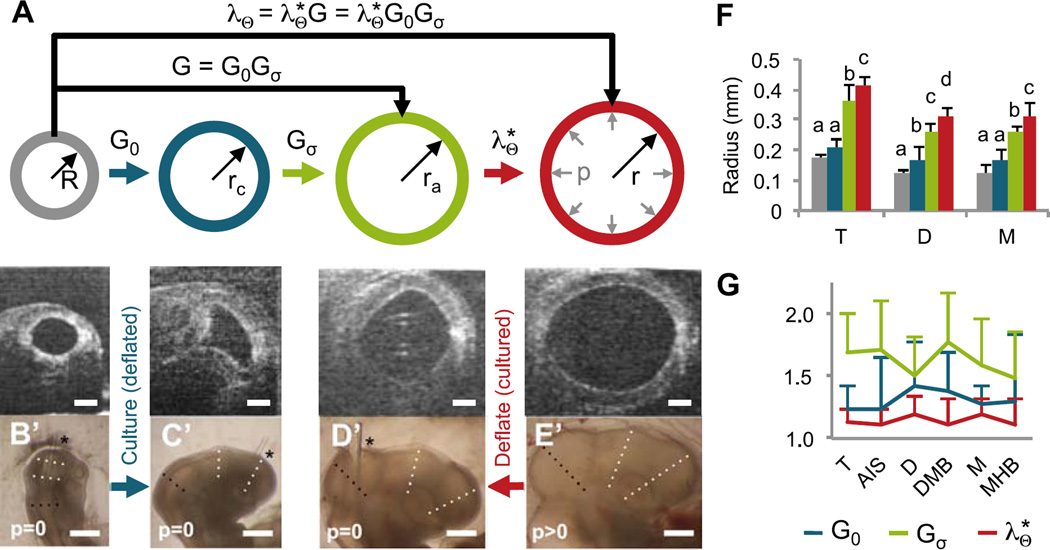
Figure 5.

Effects of eCSF pressure on forebrain development (HH12–17). (A) Schematic depicting analysis of growth and elastic deformation. Radius for each cross section was determined from images of brains shown below each section. These radii were used to compute baseline growth (G₀ = r_c/R), pressure-dependent growth (G_σ = r_a/r_c), and elastic stretch ratio $({\lambda }_{\mathrm{\Theta }}^{*}=r/r_a)$. (B–C) To determine baseline growth, embryos were intubated at HH12 (B) and cultured to HH17 (C, n=6). (D–E) To determine elastic stretch due to pressure, HH17 control embryos were imaged immediately before (E) and after intubation (D, n=8). Representative OCT cross sections shown for midbrain are shown (B’–E’). Bright field images (lateral view) for sections shown in B–E. Dotted lines indicate locations used to compute average radii for M (black), D and T (white); asterisks indicate location of tube insertion. (F) Measured radii for each case, where colors of each bar correspond to radii shown in (A). For each vesicle, one-way ANOVA (P<0.001) with post-hoc Tukey test revealed 3–4 statistically different groups denoted by a, b, c and d (P<0.05). (G) Estimated contributions of baseline growth G₀, stress-dependent growth G_σ, and elastic stretch $({\lambda }_{\mathrm{\Theta }}^{*})$ to total expansion from HH12 to HH17. No statistically significant differences were detected between regions. Scale bars: 0.1 mm for (B–E) and 0.5 mm for (B’–E’).

As shown in Fig. 5F, vesicle radii increased slightly during culture of intubated BTs, indicating low baseline growth in the absence of pressure (P=0.25, 0.02, and 0.13 for M, D, and T). However, these radii were significantly less than equivalent controls, indicating additional growth driven by eCSF pressure (P<0.001 for all vesicles).

Circumferential stretch and growth ratios were estimated from these radius measurements. As illustrated in Fig. 5A, we assume that the total stretch ratio λ_Θ = r/R can be decomposed into the following components: baseline growth G₀ = r_c/R for p = 0; pressure- or stress-dependent growth G_σ = r_a/r_c for p > 0; and elastic deformation ${\lambda }_{\mathrm{\Theta }}^{*}=r/r_a$ due to pressure. These quantities are related by ${\lambda }_{\mathrm{\Theta }}=G{\lambda }_{\mathrm{\Theta }}^{*}$, where the total growth is G = G₀G_σ. As shown in Fig. 5G, elastic inflation $({\lambda }_{\mathrm{\Theta }}^{*}\approx 1.1)$ contributed considerably less than total growth (G ≈ 2.1) to BT expansion. Pressure-dependent growth (G_σ ≈ 1.6) contributed considerably more to the total growth than baseline growth (G₀ ≈ 1.3), suggesting that pressure-dependent growth accounts for most brain expansion during stages HH12–17.

3.5. Stress-dependent growth can generate realistic brain tube morphology at later stages

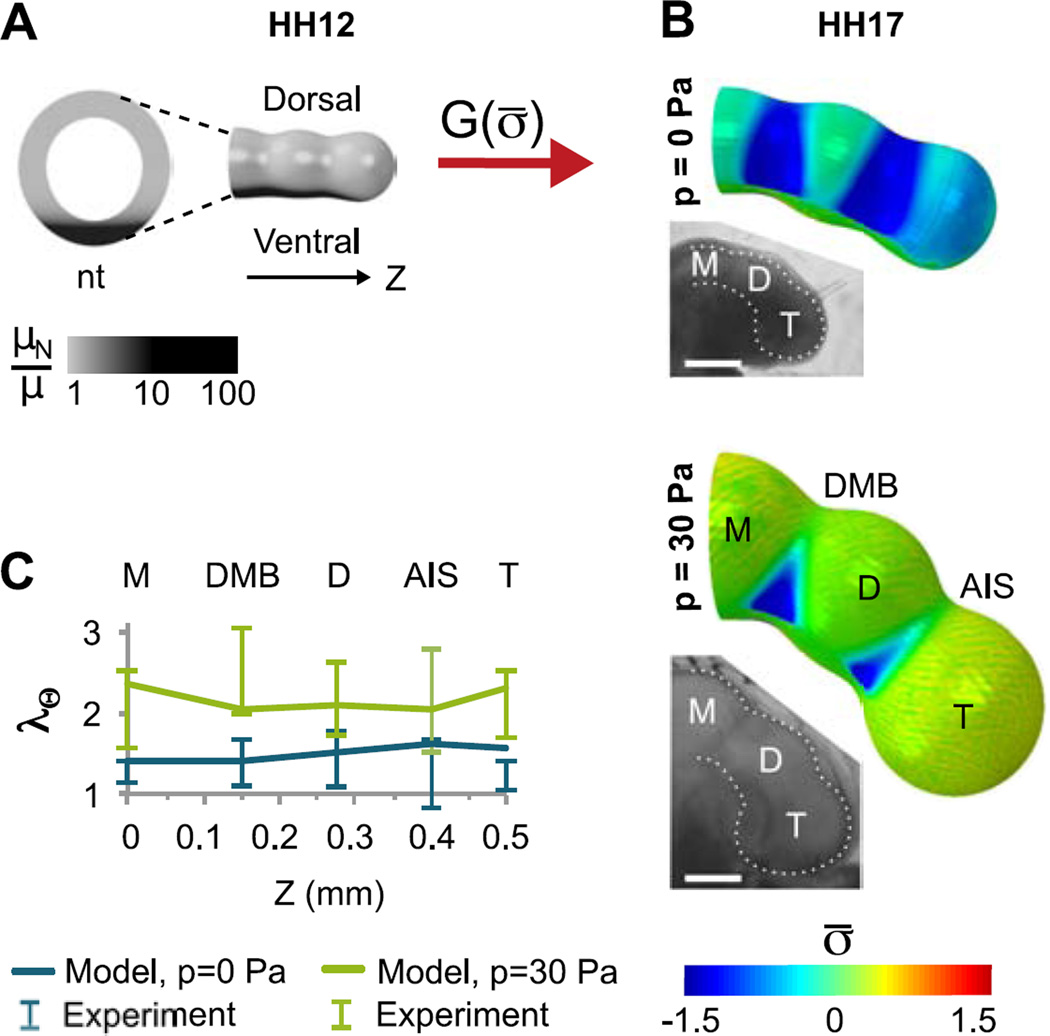
To determine whether the observed effects can be explained by mechanical feedback, we extended the BT model for HH12–20 to include stress-dependent growth, as well as a stiff notochord to account for bending (Fig. 6A). Intubated and control conditions were simulated by running the model with p = 0 Pa and p = 30 Pa, respectively.

Figure 6.

Finite element model of brain tube morphogenesis including flexure and stress-dependent growth (HH12–17). (A) Model geometry at HH12. A relatively stiff notochord (nt, modulus μ_N ≥ 10µ) is added to the model shown in Fig. 4A. The BT subsequently undergoes stress-dependent growth, but the notochord (black) does not grow or contract. (B) As the BT grows, both structures bend ventrally. For p=0, the passive outer layer remains compressed (σ̅ < 0) due to contraction of the actin layer, resulting in negligible stress-dependent growth throughout the brain. When pressure is included (p = 30 Pa), tension induces stress-dependent growth, particularly in the vesicles. Colors represent normalized average tangential stress (σ̅). Insets: Bright field images of intubated and control HH17 embryos shown for comparison (scale bar = 0.5 mm). (C) Model and experimentally measured circumferential stretch ratio (λ_Θ) in five regions of intubated (p = 0) and control (p = 30 Pa) BTs cultured from HH12 to HH17. As discussed in the text, these data were used to determine the growth-rate coefficients g₀ and g_σ, respectively.

The growth parameters in Eq. (12) were determined by approximately matching model predictions to the data in Fig. 5. To produce the growth ratio observed under intubated conditions (G₀), the baseline growth rate was calculated as g₀ = 0.02 hr⁻¹. To produce growth and inflation observed under normal conditions (λ_Θ), the stress-dependent rate constant was g_σ = 5g₀ (Fig. 6B–C). With these values, circumferential deformations in our model fall within experimentally measured ranges, except for a slight overestimation for the intubated telencephalon.

For both zero and normal eCSF pressure, the calibrated model yields morphology similar to experimental observations, including realistic differences in flexure (Fig. 6B). From OCT measurements of control embryos, we found that the dorsal length of the BT (measured from M to T) was approximately 1.8 times the ventral length at HH17 (n=8), slightly more than the value given by our model (≈ 1.5). As notochord stiffness is increased in our model, this flexure increases but model convergence suffers (Fig. S3). In the absence of pressure, our model predicts a decrease in bending (13%) comparable to that observed in intubated embryos (16%, n=6).

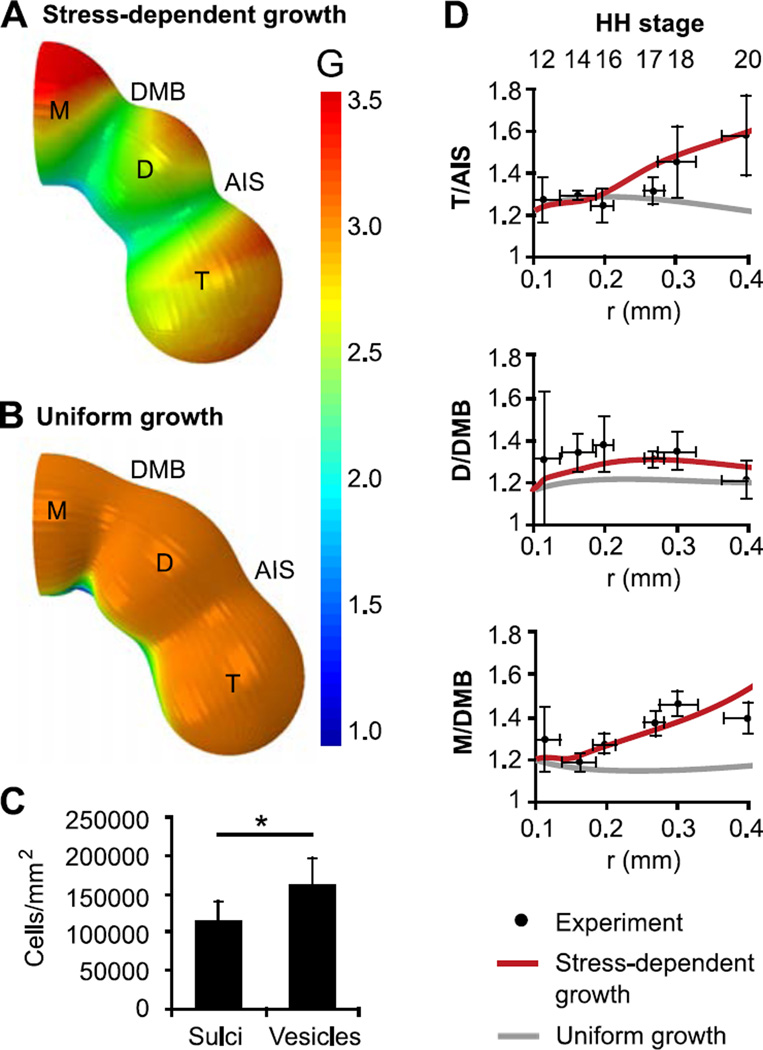
Since wall stresses in a pressurized vessel increase with radius, circumferential and longitudinal stresses increase as the BT grows. Wall stress is also higher in the vesicles than in the sulci, and cephalic flexure adds tension on the dorsal side of the BT while subtracting tension on the ventral side (Fig. 6B). Patterns of growth follow these stress distributions, leading to more growth and greater vesicle bulging on the dorsal side (Fig. 7A), in agreement with previous measurements of proliferation in chick embryos (Gutzman and Sive, 2010; Layer and Sporns, 1987; Takamatsu and Fujita, 1987; Weikert et al., 1990). Confocal imaging of late-stage embryos (HH17–18) also revealed increased cell density in dorsal vesicles (n=14) compared to sulci (n=10, P=0.02) (Fig. 7C), consistent with increased proliferation.

Figure 7.

Comparison of stress-dependent and uniform growth models. (A) Growth pattern from stress-dependent growth model at HH20 (g_σ > 0) (B) Growth pattern from uniform growth model at HH20 (g_σ = 0, g₀ chosen so midbrain radius is same as in (A)). (C) Based on F-actin staining (HH17–18), apical cell density was significantly higher in vesicles compared to sulci. (D) Relative constrictions, plotted as functions of midbrain radius with corresponding stages shown. Stress-dependent growth (red) predicts experimentally observed increases in relative constriction, or sulcal depth. Conversely, sulcal depths change relatively little for uniform growth (gray).

In our model, an important consequence of differential growth is that the AIS and DMB become more defined after HH16, similar to experimental measurements. Prior to this time, wall stress remains low as a result of initial contraction, and stress-dependent growth is inhibited. After HH16, pressure-induced tension starts to dominate and vesicle growth accelerates. This growth increases the ratios T/AIS and M/DMB, but D/DMB remains relatively constant (Fig. 7D). In our model, the closely spaced DMB and AIS constrain diencephalon expansion, keeping tension low and inhibiting growth.

For comparison we also ran our model without stress-dependent growth (g_σ = 0) and increased the baseline growth rate (g₀ = 0.03 hr⁻¹). In contrast to the deepening sulci produced by stress-dependent growth, relative sulcal depth remains low in the uniform growth model, contrary to our data (Fig. 7B,D). These results suggest that stress-dependent growth contributes to both size and shape of the early embryonic brain.

4. Discussion

Much is now known concerning the biophysical mechanisms that create the neural tube (Brodland and Clausi, 1995; Colas and Schoenwolf, 2001; Davidson and Keller, 1999) and those that drive cortical folding (Richman et al., 1975; Tallinen et al., 2016). However, processes that shape the brain between these two phases of neural development have received relatively little attention. The present study focuses on development of the early embryonic forebrain, finding that: (1) differential patterns of actomyosin contraction initiate constrictions between the telencephalon-hypothalamus complex, diencephalon, and optic vesicles (HH11–12); (2) stress-dependent growth can maintain and deepen sulci during subsequent expansion and flexure of the BT (HH12–20); and (3) regionally constrained growth likely produces cephalic flexure and contributes to dorsoventral growth patterns (HH12–20).

4.1. Organized actomyosin as initiator of brain constrictions

This study extends an earlier investigation of boundary formation, which found that differential contraction of apical actomyosin creates the constriction dividing the midbrain and hindbrain of the chick embryo (Filas et al., 2012). Results here suggest that similar patterns initiate segmentation of the forebrain. Together these studies support the notion that regional circumferential contraction forms sulci in the early BT, with the exception of the transient rhombomere boundaries of the hindbrain that have relatively smaller radii and may require a different contractile mechanism (Filas et al., 2012).

Our findings are backed by three main pieces of evidence. First, chemical perturbations that inhibit myosin-II activity (blebbistatin) prevent the formation of constrictions, whereas exposure to chemicals that enhance contractility (calyculin A, ATP) lead to deeper constrictions (Fig. 2). Second, apical actin exhibits predominately circumferential alignment in constricted regions, consistent with circumferential contraction, and relatively isotropic orientation elsewhere (Fig. 3). Third, computational models based on realistic parameters agree with quantitative measurements of both normal and hypercontracted BTs (Fig. 4).

Our results for F-actin orientation are similar to previous observations in the MHB (Filas et al., 2012), where both F-actin and cell shape were circumferentially oriented. Strikingly, all regions of aligned actin (MHB, DMB, AIS, OS) match regions of high molecular weight tropomyosin expression reported in the embryonic rat (Nicholson-Flynn et al., 1996). Tropomyosin stabilizes actin to form long, straight filaments (Gunning et al., 2005) similar to the long, circumferential filaments we observed at forebrain constrictions (Fig. 3A’, C’). Reports also suggest that binding of tropomyosin can increase actin bundle stiffness (Fujime and Ishiwata, 1971). This behavior is captured by Eqs. (9) and (10) in our models. In cultured epithelial cells, actin fibers have been shown to align in the direction of maximum curvature (Svitkina et al., 1995; Yevick et al., 2015), suggesting that circumferential alignment may occur naturally in situations where long, stable filaments of actin are allowed to form.

As shown in Fig. 4, circumferential contraction effectively minimizes circumferential tension in the BT and SP. Indeed, similar contractile mechanisms have been observed in embryonic wound healing (Bement et al., 1993) and gut morphogenesis (Burgess, 1982). In the zebrafish, Gutzman et al. (2008) found that basal constriction helps to form the MHB. However, important morphological differences between zebrafish and chick (or mammal) suggest that mechanisms may be species dependent (Filas et al., 2012).

4.2. Stress-dependent growth as a mechanism of vesicle maintenance during brain expansion

In cultured embryos, forebrain sulci continue to deepen after HH12 as the BT expands (Fig. 1B,C). This behavior contradicts our computational model with prescribed uniform growth, in which lumen pressure causes the DMB and AIS to become more shallow as the brain grows (Fig. 7B). The result may seem counterintuitive, since Laplace’s law predicts greater circumferential expansion in regions of larger radius, i.e., in the vesicles between constrictions. On the other hand, Laplace’s law also predicts longitudinal tension for a capped vessel such as the BT. This force tends to unbend the sulcal folds and dominate the relatively small difference in circumferential stretch. Cephalic flexure of the BT only exacerbates this behavior, further increasing longitudinal tension on the dorsal side of the brain tube.

One potential mechanism to counteract unfolding would be to increase contraction in sulci. However, our experiments do not support this possibility since exposure to calyculin A had no noticeable effect beyond stage HH14 (n=6 at 30 nM, n=5 at 100 nM; Fig. S2). We also note that uniform growth is not consistent with previously documented proliferation patterns (Gutzman and Sive, 2010; Layer and Sporns, 1987; Takamatsu and Fujita, 1987; Weikert et al., 1990), and predefined growth (uniform or patterned) does not predict documented increases in cell proliferation due to pressure (Desmond and Jacobson, 1977; Desmond et al., 2014, 2005).

Accordingly, we speculate that mechanical feedback, in the form of stress-dependent growth, is required to deepen sulci as the BT expands during HH12–20 and beyond. Elevated tension in vesicles relative to sulci (due to initial contraction, see Fig. 4B) would induce relatively higher growth rates in vesicles, deepening the sulci. As vesicles expand, increased wall stress (via Laplace’s law) would further accelerate their growth, causing sulci to deepen further. This idea is supported by multiple studies showing growth of the BT depends on eCSF pressure: Eliminating lumen pressure via intubation slows growth considerably (Desmond and Jacobson, 1977) (Fig. 5), and abnormally high pressure increases proliferation (Alonso et al., 1998; Desmond et al., 2014). Cell proliferation has been shown to increase with the degree of mechanical tension in tissues such as blood vessels and epithelia (Lehoux et al., 2005; Wyatt et al., 2015).

With a growth rate that depends linearly on average in-plane stress (Eq. (12)), our model yields morphology similar to that of experimental BTs for both p = 0 Pa and p = 30 Pa (Fig. 6B). In contrast to the uniform growth model, our stress-dependent growth model predicts temporal increases in relative AIS and DMB depth that are in remarkable agreement with experimental measurements for control embryos during stages HH12–20 (Fig. 7D). This model predicts differential growth patterns consistent with observations in both chick and zebrafish, which found higher proliferation in vesicles than sulci (Gutzman and Sive, 2010; Layer and Sporns, 1987; Weikert et al., 1990) and reduced proliferation in the ventral neuroepithelium during stages of flexure (Layer and Sporns, 1987; Takamatsu and Fujita, 1987).

At the molecular level, mechanical feedback may be regulated by focal adhesion kinases (FAKs), which act as mechanotransducers in vascular and epithelial systems (Chaturvedi et al., 2007; Lehoux et al., 2005). In Xenopus, Hens and DeSimone (1995) found FAK transcripts localized in the forebrain, midbrain, hindbrain, and optic vesicle. In the chick embryo, Desmond et al. (2014) showed that FAK and cell proliferation were upregulated and activated by eCSF pressure. The stress and growth patterns predicted by our model are consistent with these data (Figs. 6B and 7A).

4.3. Mechanical constraint by the notochord predicts bending and realistic growth patterns

For decades, researchers have speculated that differential growth drives flexure of the BT (Goodrum and Jacobson, 1981). Others have suggested that an external structure on the ventral side of the BT, e.g., the notochord or foregut, may constrain longitudinal growth and cause the tube to bend (Pikalow et al., 1994; Takamatsu and Fujita, 1987). None, however, have offered conclusive physical evidence for their theories.

Our model for stages HH12–20 includes a relatively stiff, non-growing notochord along the ventral side of the BT extending from midbrain to the telencephalon-hypothalamus complex (Fig. 6A). With a stiffness in the range of published data (Adams et al., 1990; Zhou et al., 2009), this structure provides sufficient constraint to force realistic bending of the BT as it grows (Fig. 6B). Since growth depends on stress, bending is slightly reduced in our model without lumen pressure (Fig. 6), similar to experimental observations. The notochord also springs apart when cut experimentally, indicating that it is under tension as predicted by our model (Fig. S4). In this model, stress and growth near the notochord decrease due to bending, which could explain previous reports of decreased proliferation on the ventral side of the BT (Layer and Sporns, 1987; Takamatsu and Fujita, 1987).

4.4. Limitations

While our stress-dependent growth model yields realistic trends, we cannot rule out other forms for the growth law (12). For example, we assume that growth is triggered by tension but reduced to baseline levels under compression. The first part of this assumption is supported by studies showing that proliferation in the BT increases with eCSF pressure (Alonso et al., 1998; Desmond and Jacobson, 1977; Desmond et al., 2014; Goodrum and Jacobson, 1981). We did not observe any indications of cell death (G < 1) in compressed regions (Fig. S2), but it is possible that cells in compression could proliferate at a further reduced rate. Future studies are warranted to address this issue. It is also plausible that growth depends on a different mechanical quantity, such as strain or strain rate (Cowin, 1996).

For simplicity, our model assumes that growth is transversely isotropic (isotropic tangent to the surface) and depends on the average in-plane stress. Future studies could determine whether differences exist in the circumferential and longitudinal directions, similar to previous studies of proliferation in epithelial tissue (Kim et al., 2013; Wyatt et al., 2015). Our model also assumes no changes in wall thickness due to growth or contraction. For growth, this choice is supported by minimal change in tissue thickness over time (Fig. S1D). For contraction, this implies no change in actin layer thickness as fibers are pulled toward and between each other, such that fluid which once occupied space between fibers is pushed out of the actin layer and into the cell body. While a multiscale model would ultimately be necessary to describe the interactions of actin, myosin, and fluid in the cell, here we have proposed a continuum approximation to describe critical aspects of the system.

Finally, our model does not consider additional subdivisions of the diencephalon and secondary prosencephalon that begin to emerge during the final stages of our analysis (HH18–20), and our model is limited to the physical mechanisms responsible for morphogenesis. While countless reports have revealed regionalizing effects of molecular signals such as Sonic hedgehog (SHH) and fibroblast growth factors (FGF8) (Puelles et al., 2012), their influences are outside the scope of the present study. Future work may consider how such signals apply to these or subsequent subdivisions.

4.5. A mechanistic model informs accurate patterning of the forebrain

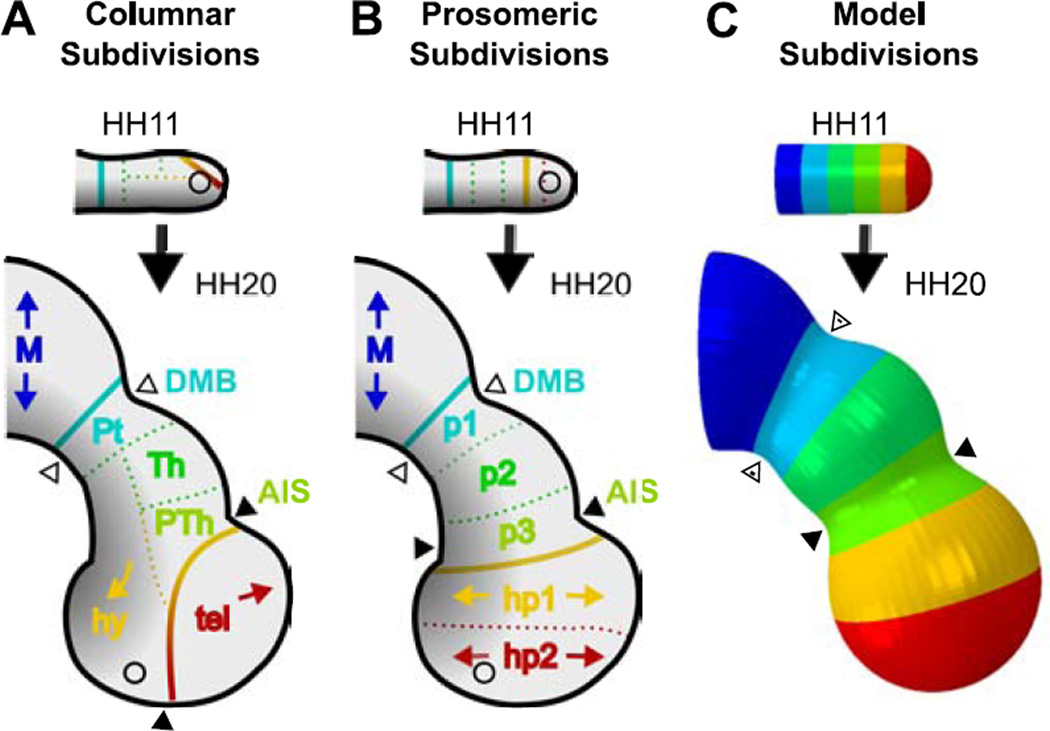
Historically, researchers have described the forebrain using columnar subdivisons first proposed by Herrick (1910) (Fig. 8A), which attributed the hypothalamus and optic vesicles to the diencephalon region. However, recent advances in fate-mapping have modified our understanding of brain organization (Folgueira et al., 2012; Puelles and Rubenstein, 2015), leading Puelles et al. (2012) to propose updated functional prosomeric subdivisions in the forebrain (or prosencephalon), as shown in Fig. 8B (Puelles et al., 2012; Puelles and Rubenstein, 2015). Comparing our model to the prosomeric subdivisions, regional morphogenesis emerges naturally from stress-dependent growth and bending (Fig. 8C), with prosomeres (p1–3, hp1–2) corresponding neatly to equally spaced regions in the HH11 BT.

Figure 8.

Forebrain regionalization in terms of columnar, prosomeric, and mechanistic subdivisions. (A–B) Proposed functional regions drawn onto forebrain tracings at HH11 and HH20. Black-to-gray gradient represents approximate ventral-to-dorsal signaling (Puelles et al., 2012), regions are denoted by color. Solid lines denote proposed functional boundaries between the diencephalon (middle) and adjacent vesicles, while dotted lines separate regions within each vesicle. Historically accepted columnar subdivisions are shown in (A) (Herrick, 1910), and prosomeric subdivisions (based on signaling patterns and fate mapping) are shown in (B) (Puelles and Rubenstein, 2015). Arrowheads represent expected bounds of physical sulci (black = AIS, white = DMB) for each. (C) Finite element model based on physical observations. Colors represent equally-spaced sections along the rostral-caudal axis at HH11. In this mechanistic model, physical sulci form in regions of circumferentially aligned actin, matching prosomeric regions p1 and p3. Bending of the BT and bulging of the hypothalamus result from constrained growth (constrained by the notochord). Vesicle inflation results from eCSF pressure and stress-dependent growth. M=midbrain, p1=Pt=pretectum, tel=telencephalon, hy=hypothalamus, Th=thalamus, PTh=prethalamus, hy=hypothalamus, p1–p3=diencephalon (prosomeric), hp1–hp2=secondary prosencephalon (SP, prosmeric). Circles represent location of optic stalk.

While discrepancies between anatomical subdivisions may seem trivial, they can become critical when attempting to understand physical morphogenesis. For example, if we assume all brain vesicles are roughly partitioned by a contractile ring, the outdated columnar subdivisions would lead us to expect circumferentially aligned actin between the telencephalon and hypothalamus. Alternatively, researchers might conclude that complicated, region-specific mechanisms are necessary to obtain the secondary forebrain shape (Goodrum and Jacobson, 1981). Instead, our analysis finds actin is circumferentially aligned along prosomere p3 to form the AIS, consistent with alignment along p1 to form the DMB. By considering the updated definitions of secondary prosencephalon, diencephalon, and their subdivisions (Puelles et al., 2012), we obtain a physical understanding of development that complements functional anatomic regions.

In this study, we have proposed a mechanistic model for early forebrain morphogenesis that is consistent with both structural and functional partitioning. In conjunction with experiments, our model provides new insight into how complex morphology can arise from simple mechanisms.

The following abbreviations are used throughout this paper

BT

brain tube

T

telencephalon-hypothalamus complex

D

diencephalon

M

midbrain (mesencephalon)

H

hindbrain (rhombencephalon)

SP

secondary prosencephalon

OS

optic stalk

AIS

anterior intraencephalic sulcus

DMB

sulcus at the diencephalon-midbrain boundary

MHB

sulcus at the midbrain-hindbrain boundary

HH

Hamburger Hamilton stage.