Automated detection of coarctation of aorta in neonates from two-dimensional echocardiograms

Abstract.

Coarctation of aorta (CoA) is a critical congenital heart defect (CCHD) that requires accurate and immediate diagnosis and treatment. Current newborn screening methods to detect CoA lack both in sensitivity and specificity, and when suspected in a newborn, it must be confirmed using specialized imaging and expert diagnosis, both of which are usually unavailable at tertiary birthing centers. We explore the feasibility of applying machine learning methods to reliably determine the presence of this difficult-to-diagnose cardiac abnormality from ultrasound image data. We propose a framework that uses deep learning-based machine learning methods for fully automated detection of CoA from two-dimensional ultrasound clinical data acquired in the parasternal long axis view, the apical four chamber view, and the suprasternal notch view. On a validation set consisting of 26 CoA and 64 normal patients our algorithm achieved a total error rate of 12.9% (11.5% false-negative error and 13.6% false-positive error) when combining decisions of classifiers over three standard echocardiographic view planes. This compares favorably with published results that combine clinical assessments with pulse oximetry to detect CoA (71% sensitivity).

1. Introduction

Critical congenital heart defects (CCHD) collectively refer to a group of life threatening heart defects that are present from birth. These require accurate and immediate diagnosis and are typically followed by catheter-based intervention or heart surgery.¹ The reported prevalence of CCHDs at birth ranges from 6 to 13 per 10,000 live births^2–6 and delayed diagnosis may result in poorer preoperative condition of the child, worse cardiopulmonary, and neurological outcomes after treatment⁷ increased mortality rates and increased healthcare costs.⁸ Recent mandate by the US Department of Health and Human Services prescribes newborn screening protocol to be observed in every delivery rooms setting within 24 h of birth. Screening for congenital heart diseases is usually based on history, physical examination, chest radiography or ultrasound imaging, and hyperoxia test.⁹ The last of these is performed using pulse oximetry and is recommended by the American Heart Association for screening of seven listed CCHD’s.^10,11 Unfortunately, these techniques have important limitations in their sensitivity to pick up many key defects especially when the delivery is conducted at tertiary/nonexpert birthing centers.^12,13

Among various imaging modalities, ultrasound is ubiquitously employed during the pre and postnatal stages of childbirth at various healthcare centers due to its portability, relative ease of use, and more importantly, due to safety considerations as it does not use ionizing radiation. Additionally, ultrasound provides several modes, such as brightness mode (B-mode), motion mode (M-mode), Doppler mode, and the color mode for imaging the heart. This makes two-dimensional (2-D) echocardiography the dominant imaging modality for assessing cardiac structure and function in both infant and adult populations.^14,15

The application of machine learning methods to medical imaging is a richly studied and rapidly growing field of research and development activities, and numerous semi- and fully automated methods, algorithms, and applications have been developed for various aspects of 2-D and three-dimensional (3-D) medical image processing. These include image segmentation, registration, fusion, guided therapy, and computer-aided diagnosis to name a few.^16–21 In echocardiography, machine learning methods have been applied for 2-D cardiac view classification,²² LV boundary segmentation,²³ the measurement of cardiac parameters in M- and B-mode echocardiography,²⁴ fully automated 3-D segmentation of the cardiac chambers, valves, and leaflets.^25,26 Machine learning methods have also been applied to ultrasound image data for detection of breast lesions,^27,28 detection and evaluation of atherosclerosis,²⁹ staging of chronic liver disease,³⁰ and so on. However, we are not aware of any methods or applications designed for the detection of congenital heart diseases in newborns from ultrasound or from other imaging modality data.

Machine learning involves the construction and analysis of algorithms that can learn from data. This involves building models from a representative set of training data that can be used to make predictions on previously unseen data sampled from the same unknown distribution.³¹ Given a collection of consistent datasets, the first step in the learning process usually involves the extraction of a set of features/predictors that are relevant for performing the task at hand. The next step consists of using the extracted features to model the desired input–output relationship and the final step involves validating the trained model on unseen data. In the feature extraction step, the algorithm designer can introduce a priori information regarding aspects of the data that may be beneficial in enhancing the model’s performance.^31,32 Otey et al.²² used a set of specifically engineered features to build a classifier that discriminates between four 2-D echocardiographic views. However, knowing a priori the relevant features of interest may be a difficult problem when designing a learning algorithm. In computer vision, a popular and efficient method for feature engineering was introduced by Viola and Jones³³ for face detection where a multitude of features from face image data was extracted using simple scale space filters. A feature selection algorithm was then used to pick out a subset of the most relevant ones by optimizing a predefined measure of classification performance. Variants of this approach have successfully been used in developing automated algorithms for image recognition and feature detection tasks using medical images.³⁴

Recently, deep learning methods^35–37 have gained much attention for producing state-of-the-art results on a variety of learning problems, including large-scale object detection problems in computer vision.^38–40 Deep learning methods are implemented using multilayer neural networks and employ a two-stage learning process. In the first stage, the hidden layers of the network are pretrained layerwise in an unsupervised manner using the output of one layer as input to the next. In this stage, each layer essentially attempts to learn a hidden representation of the data that can reconstruct the input with minimum expected error. Once all layers have been pretrained, the network is fine-tuned using supervised learning to best approximate the desired input–output mapping. Deep neural networks (DNNs) are capable of learning a rich set of features that are optimal for the defined task. Since explicit feature engineering is a time-consuming activity, the deep learning formalism provides a principled methodology for efficiently constructing machine learning-based applications in medical imaging.

In this work, we describe a fully automated algorithm for the detection of CCHD from 2-D echocardiographic images obtained in standard echo view planes. We use feature sets obtained from a set of stacked denoising autoencoders (SDAE),^41,42 each trained to extract features from a predefined image region and develop a methodology to automatically detect coarctation of aorta (CoA), which is considered as one of the most challenging CCHD detection tasks clinically, and discriminate it from normal 2-D echocardiographic data.

The rest of the paper is organized as follows. In Sec. 2, we present a short description of CoA focusing primarily on its 2-D echocardiographic presentation. In Sec. 3 we provide a detailed description of the algorithmic framework for detection of CCHDs. In Sec. 4, we discuss the experimental setup to detect CoA using the clinically acquired data. Results and statistical analysis are next presented in Sec. 5. Finally, in Sec. 6, we conclude with a discussion on our approach and future directions of our CCHD detection efforts.

2. Two-Dimensional Echocardiography of Coarctation of Aorta

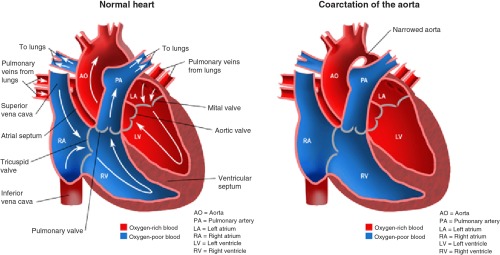
CoA is a critical congenital heart defect that occurs in 6% to 8%^43,44 of patients born with critical congenital heart defects. In CoA, the aorta usually narrows in the area where the ductus arteriosus inserts (Fig. 1). However, rarely, a coarcted segment is present in the lower thoracic or abdominal aorta. The narrowing is due to localized medial thickening with some infolding of the medial and superimposed neointimal tissue. The localized constriction may form a discrete shelf-like membrane in the posterolateral aspect of the descending aorta, distal to the left subclavian artery, or it may manifest as the narrowing of a long segment of the aorta.¹⁴

Fig. 1.

In aortic coarctation, the aorta usually narrows where the ductus arteriosus inserts resulting in obstruction of normal blood flow. However, rarely, a coarcted segment can be present in the lower thoracic or abdominal aorta.

The constriction blocks normal blood flow to the body, which can back up flow into the left ventricle of the heart, making the muscles in this ventricle work harder to get blood out of the heart. The extra work on the heart can cause the walls of the heart to become thicker in order to pump harder. Unless the aorta is widened, coarctation can ultimately lead to heart failure. Aortic coarctation may occur as an isolated defect or in association with various other lesions, most commonly bicuspid aortic valve and ventricular septal defect. In our work, however, we consider pure coarctation only, since it is considerably more challenging to detect.

Blood oxygen saturation measurement via pulse oximetry is currently one of the clinically approved methods to screen from among seven listed CCHDs and several large-scale studies have been performed worldwide to assess the clinical effectiveness of this method.^10,11 While having high sensitivity for many of the target CCHDs, pulse oximetry, however, does not perform well for detection of aortic coarctation. In a clinical study performed in China⁴⁵ (Zhao et al.), pulse oximetry was able to correctly detect three out of seven CoA cases to give a detection rate of 43%. Interestingly, in the same study, pulse oximetry with clinical assessment was able to detect 71% of the CoA cases, while, clinical assessment alone detected 57%. In a similar study performed in Sweden,⁴⁶ the detection rate was 33% over nine cases with CoA. For these reasons, aortic coarctation is not listed as a primary target for pulse oximetry. These results also illustrate the difficulty of detecting CoA using existing screening protocols.

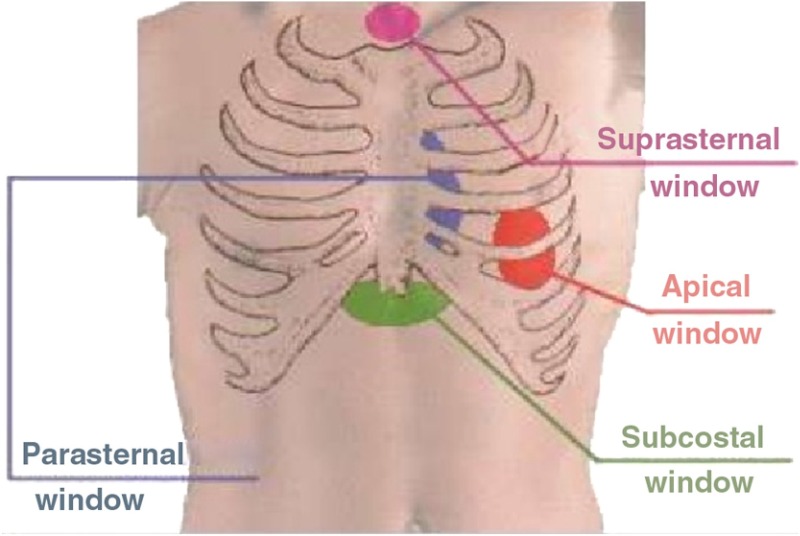
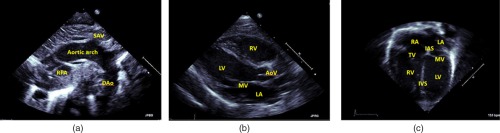
In 2-D transthoracic echocardiography four standard transducer positions, also known as “acoustic windows,” are employed to scan the heart. These are the parasternal window, the apical window, the suprasternal window, and the subcostal window. Figure 2 shows these locations with respect to the human thoracic cage. The standard 2-D transthoracic echo views are defined by positioning the transducer at these locations and orienting it appropriately.¹⁵ Figures 3(a)–3(c) show the 2-D echocardiographic views of the heart that we utilize in our work. They are the suprasternal notch view (SSNA), the parasternal long axis view (PSLAX), and the apical four chamber view (AC4), respectively. Note that the different views highlight different aspects of the heart. However from among these views, the aortic arch can is visible in the SSNA view only. Hence to make a definitive diagnosis of aortic coarctation from 2-D echocardiography, the suprasternal window must be utilized to image. Since, however, CoA imposes significant afterload on the left ventricle, resulting in increased wall stress, which causes compensatory ventricular hypertrophy,⁴⁶ it may be possible to deduce a diseased state from the other views as well, though such a deduction is not definitive.

Fig. 2.

The transthoracic acoustic windows used to obtain ultrasound images of the heart.

Fig. 3.

The standard echocardiographic views used in our study: (a) SSNA view, (b) PSLAX view, and (c) the AC4 view. The significant anatomical parts in these views have been labeled as follows: right pulmonary artery (RPA), supra-aortic vessels, descending aorta (DAo), right/left ventricle (RV/LV), mitral/aortic/tricuspid valve (MV/AoV/TV), right/left atrium (RA/LA), and intra-atrial/ventricular septum (IAS/IVS).

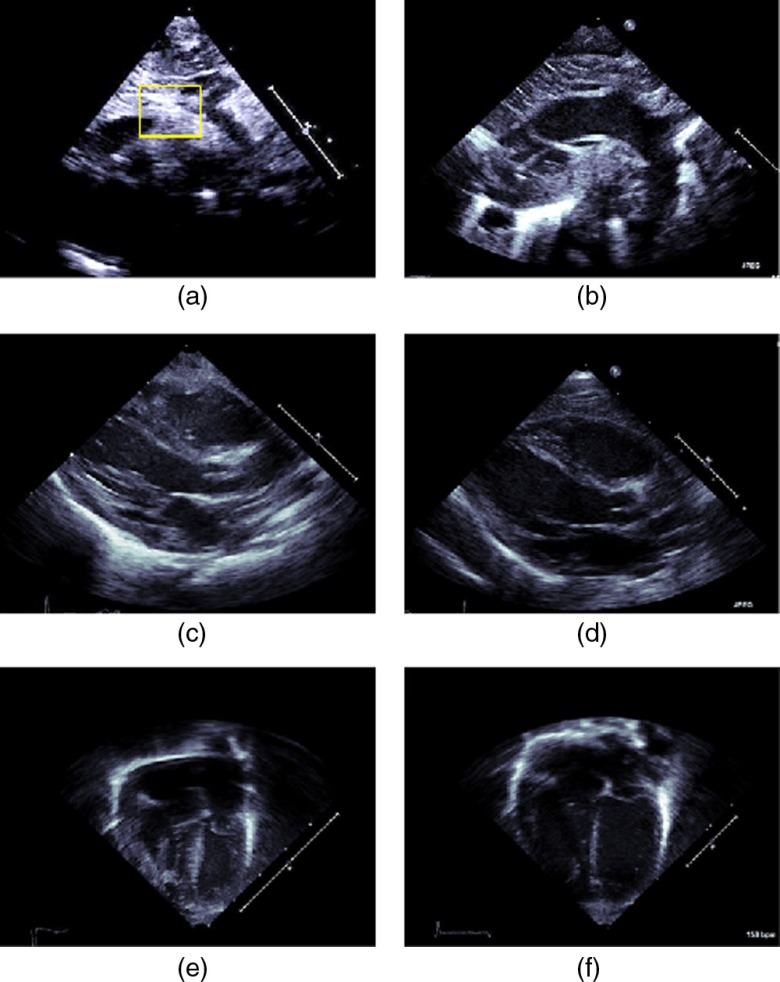
Figures 4(a) and 4(b) show the SSNA view of a coarcted artery and a normal artery, respectively. Note that for the SSNA view, considerable skill is required to obtain the appropriate plane of the aortic arch that shows coarctation unambiguously. Partly, this is because, by the very nature of the sternal notch, the corresponding imaging window is relatively small due to the presence of cartilage, and often, in trying to obtain this view, an inexperienced sonographer might push the tendons inward possibly causing restriction of the airway.

Fig. 4.

Standard 2-D echocardiographic views of the heart. SSNA view of (a) coarcted aorta and (b) normal aorta (right). The SSNA view can be used to diagnose CoA definitively since in this view the narrowing of the aorta can be observed. A rectangle has been overlaid to indicate the region where the coarctation occured for this case. PSLAX view of the heart having (c) coarcted aorta and (d) normal aorta (right). The AC4 view of a heart having (e) coarcted aorta and (f) normal aorta. Aortic coarctation cannot be unambiguously determined from the latter two views, since, in these views the aortic arch cannot be seen. However, secondary effects of coarctation such as wall thickening might be viewed and these can lead to a suspicion of a diseased condition of the heart.

Often, the sonographer therefore will move the transducer to the left or to the right of the sternal notch. This, however, compromises the angle of incidence and may result in foreshortening and partial imaging of the aorta. Since, in principle, aortic coarctation can happen anywhere along the aorta, a compromised view can lead to the lesion being missed. Foreshortening also can lead to a narrowing appearance of the aorta for healthy subjects.

Figures 4(c) and 4(d) show the PSLAX view of a diseased heart that has a coarcted aorta and of a normal heart, respectively. Figures 4(e) and 4(f), likewise, show a diseased and normal heart imaged in the AC4 view. Note that neither in the PSLAX view nor in the AC4 view can the aorta can be directly seen. Hence these views cannot be used to unambiguously diagnose aortic coarctation.

3. Framework for Automated Detection of CCHD

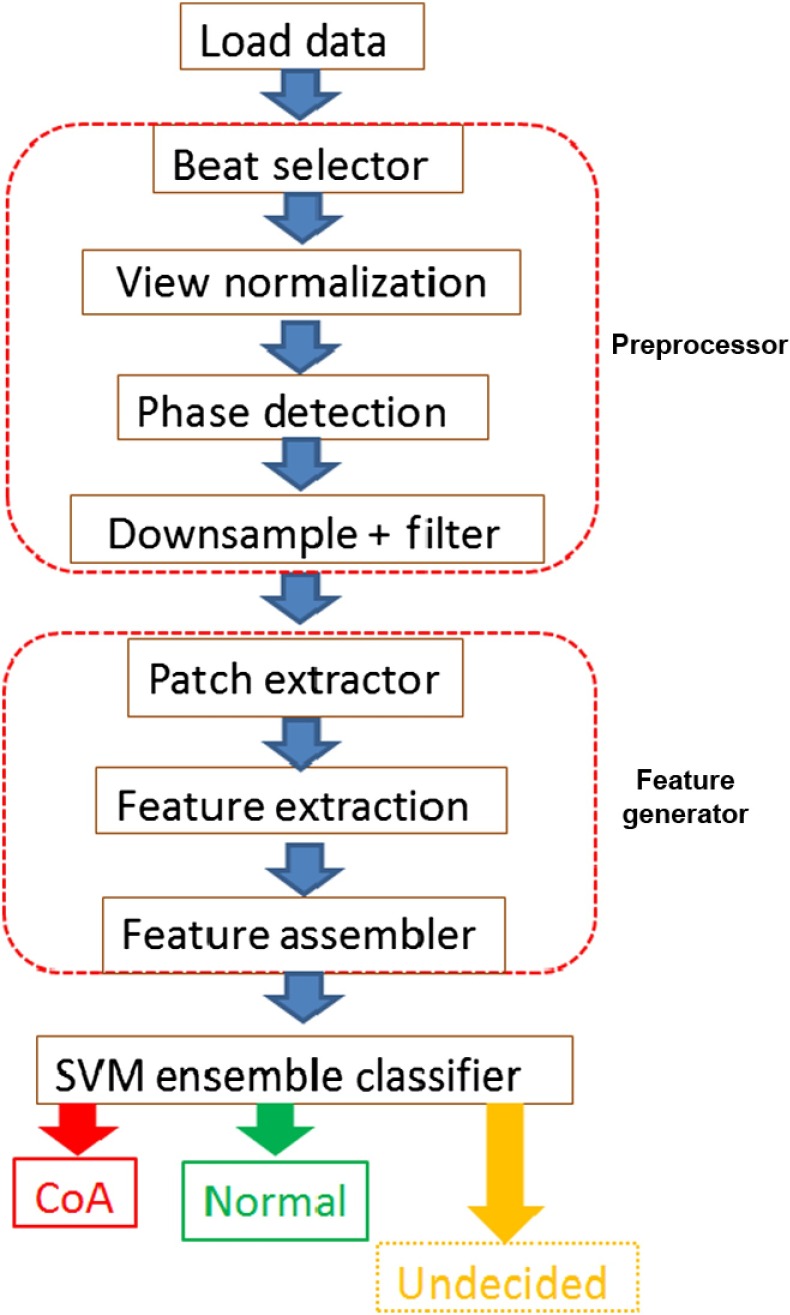
We now describe our method for automated detection of CCHD from 2-D ultrasound images. We employ machine learning-based approaches to train a classifier to perform the detection task. Note that, while describing the algorithm in this section, we do not specify numeric values of the various parameters used. We list these values in Sec. 4 where details of the experimental setup are provided. This was done to keep the algorithmic description general. Figure 5 shows a diagram of the overall algorithm. It consists of an input module, a preprocessing module, a feature extraction module, and a classifier module.

Fig. 5.

The CoA detection framework. After loading the data, a number of preprocessing steps are applied to it in the preprocessor module. In the feature generator module, the image region is next divided into predefined sectors and from each of these sectors, image patches of prespecified dimensions are extracted in the patch extraction module. In the feature extraction unit, neural networks trained for each sector, are then used to extract features from their corresponding sector image patches. In the feature assembler unit, the sector feature vector is constructed by taking a featurewise maximum of the patch feature vectors. The frame feature vector is constructed by concatenating the sector feature vectors and the data feature vector are constructed by taking the feature wise mean of the frame feature vectors. The frame feature vector is finally fed to an ensemble of trained SVM classifiers. Majority voting is used to decide whether the input dataset is of type CoA or normal.

3.1. Input Module

Since the input data are stored in DICOM format, this module consists of a DICOM file reader. The data itself are stored as a temporal sequence of 2-D image frames as an $N_{\mathrm{R}}\times N_{\mathrm{C}}\times 3\times N_{\mathrm{T}}$ array of bytes. Here, $N_{\mathrm{R}}$ and $N_{\mathrm{C}}$ refer to the number of rows and columns, respectively, and $N_{\mathrm{T}}$ is the number of temporal frames acquired. The number of employed channels is indicated by three in the array dimensions representation (RGB). The image data stored are essentially scan-converted B-mode ultrasound data prepared for display on the monitor of the acquisition device.

The three channels therefore contain identical intensity data information quantized to 8 bits and represented in the interval [0, 255]. The full capability of the RGB representation is however used to display various nonimage data and information in specific colors. This information includes standard or user-supplied annotations, traces of the ECG wave forms (if ECG recording capabilities of the system are used), any caliper markings corresponding to user-specified manual measurements, patient-specific information, and information on other vital sign readings that the clinical user might include for later reference. Note that all patient-specific identification information was removed on-site by a clinician as per IRB regulations. In addition to the standard public information stored in specific tags, the DICOM representation¹⁶ can also contain other relevant data in vendor-specific private tags that may be useful for the operation of protected vendor-specific applications.

3.2. Data Preprocessing Module

Data preprocessing consists of the following steps.

3.2.1. Cardiac cycle selection

As the input data can contain multiple cardiac cycles, this step consists of approximately identifying a temporal segment of data corresponding to one full cardiac cycle. This is done by cross correlating the first data-frame with subsequent frames and then finding the maxima on the resulting correlation curve. The frames between two subsequent maxima roughly correspond to one cardiac cycle.

3.2.2. View normalization and data clean-up

The relative shape, size, and location of the acquired image region vary over datasets. The view normalization step employs translation and scaling of a given dataset in order to maximize the correlation between its acquisition mask and a predefined standard acquisition mask. The acquisition mask corresponds to the wedge-shaped region of the scan converted ultrasound data that contains the region imaged. The acquisition region parameters are stored as meta-data under private tags in the DICOM file and with proprietary parser software this information can be obtained.

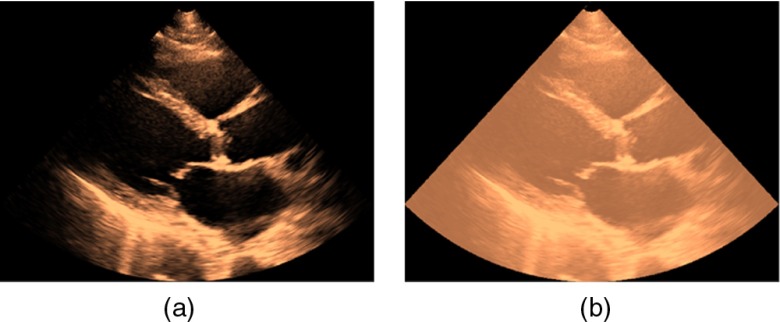
Figure 6(a) shows an image frame corresponding to the PSLAX view, while Fig. 6(b) shows the same image data with its acquisition mask superimposed. If the vendor-specific parser software is not available, or, if the image data stored in the DICOM file is just the data prepared for the display device, which usually has various annotations overlaid on it, then image processing methods can be used to obtain an estimate of the acquisition mask. We provide details of one such method that assumes that 2-D temporal loop data are available.

Fig. 6.

(a) Ultrasound image data in the PSLax view with its (b) wedge-shaped mask region superimposed.

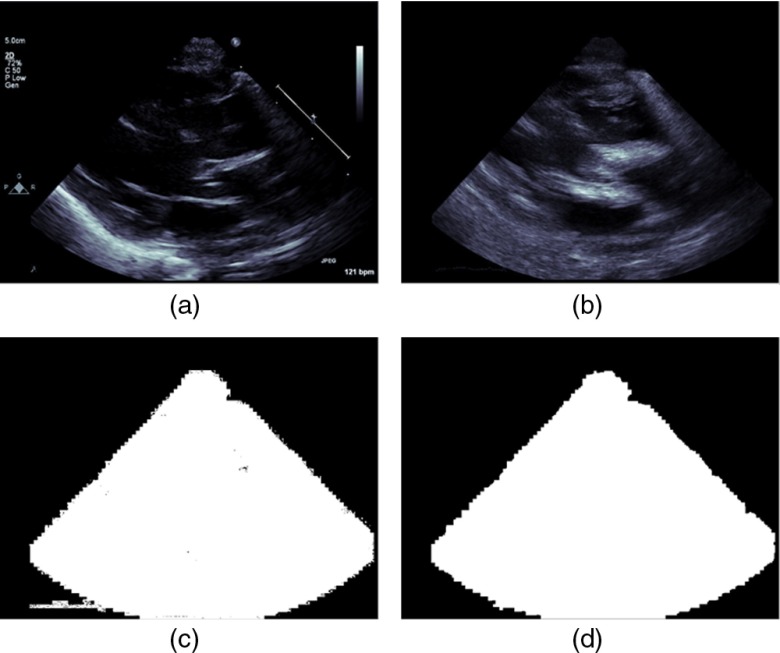
Select an even number, $N_{\mathrm{f}}$, of consecutive frames from the temporal loop and compute the pixelwise sum, $S$, of absolute values of the pixelwise differences between each frame and its previous one [Fig. 7(b)].

$$S=\sum _{n=2}^{N_{\mathrm{f}}}|I_n-I_{n-1}|.$$

Here, $I_n$ and $I_{n-1}$ are two consecutive image frames of the temporal loop data. Note that, static annotations, if any, will cancel out in the sum-frame, $S$, after this operation. Now construct a binary mask by thresholding every pixel of the sum-frame, $S$, and setting all pixels having nonzero values to the value 1 [Fig. 7(c)]. This binary mask will contain the cardiac view region, as well as, regions corresponding to nonstatic annotations, such as the trace of the ECG signal and so on. Usually, the nonstatic annotations are located outside the image region. However, sometimes they can overlap with the view data. The morphological opening operation⁴⁷ is applied to separate out such overlapping regions following which, the connected components algorithm⁴⁷ is used to find pixel locations corresponding to the maximally connected component. All pixels in the mask not belonging to this maximal component are zeroed out. The final image acquisition mask is then obtained by applying the morphological closing operation⁴⁷ to it [Fig. 7(d)].

Fig. 7.

Process for obtaining the image acquisition mask from annotated image data: (a) frame of 2-D echocardiographic temporal loop data in the PSLax view (b) the sum of the frame-wise differences are then computed over an even number of frames, (c) the binary mask corresponding to the nonzero locations of the sum image are then determined, (d) pixels corresponding to the maximal component of the connected components algorithm applied to (c) to get the data specific acquisition mask.

To obtain the standard acquisition mask, we first compute a sum-mask obtained by adding the individual acquisition masks of each dataset in the training cohort. This sum mask is then converted to a binary mask by thresholding each pixel value against a predetermined threshold. In our work, the threshold value was set at 0.95 of the maximum value of the sum-mask. The resulting binary mask is the standard acquisition mask.

3.2.3. Image-based detection of diastolic and systolic cardiac phases

Data frames corresponding approximately to the end diastolic (ED) and the end systolic (ES) cardiac phases are then detected. This is necessary because we have found that it can be beneficial to use data frames in the neighborhood of either one of these phase frames for CCHD detection. If available, the ECG signal can be used to select frames corresponding to the ED and ES phases. In our case, the ECG signal was not available in most cases. Hence, we employ an image-based method proposed by Gifani et al.,⁴⁸ for phase detection. In this approach, the embedded information in sequential images is represented on a 2-D manifold using the locally linear embedding algorithm whereby each image frame corresponds to a point on the manifold. The dense regions on this manifold correspond to three key phases of the cardiac cycle, notably, the isovolumetric contraction phase, isovolumetric relaxation phase, and the reduced filling phase. By characterizing these three regions, the ED and ES phases are determined.

The final preprocessing step consists of downsampling the dataset, denoising using a smoothing filter and normalizing each data frame to zero mean with unit variance. The last step reduces intensity scaling effects in the image data. Downsampling is performed so that we can use moderate size image patches as input to the neural networks, which yet contains information at length scales that are anatomically meaningful. From the perspective of the network learning problem, this in turn translates to a smaller network, and therefore, smaller number of weights and biases to be estimated from the training data.

3.3. Feature Extraction Module

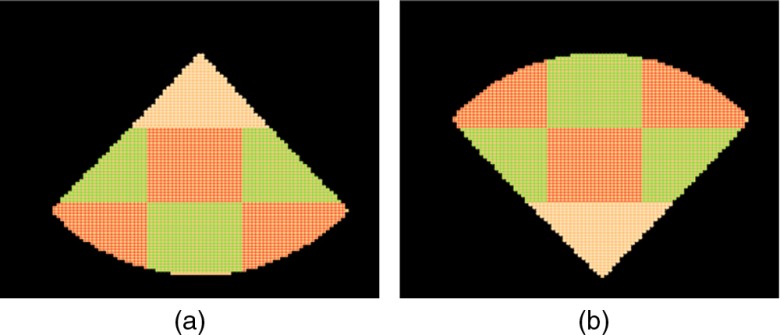
The feature extraction module consists of a bank of stacked denoising autoencoder neural networks (SDAE–NN)^41,42 trained to extract features over predefined image regions in the standard acquisition mask. We term each such region as a sector. Figure 8(a) shows the sectors for the PSLax and the SSNA view and Fig. 8(b) shows it for the AC4 view.

Fig. 8.

Sector map corresponding to the (a) PSLax/SSNA view and the (b) AC4 view. A neural network is trained for each sector to extract relevant features for the classification task.

To train an SDAE–NN for a given view, phase, and sector, data frames within a prespecified temporal neighborhood of the phase frame are selected. Rigid transformations consisting of small randomly selected scaling factors and rotation angles are then applied to each frame. Rectangular image patches of predefined dimensions are then extracted from randomly selected locations within the sector. Each frame is used multiple times by using different random transformations on the original frame. Introducing such transformations in the training data was found to allow the feature detectors to perform more robustly in the presence of mild acquisition variability. Using the extracted image templates, each sector SDAE–NN is then trained following the deep learning methodology. After completing the fine-tuning stage, the classification layer of each SDAE–NN is discarded.

In order to apply the trained network to extract sector features for a given dataset, image templates are extracted from a regular array of, $N_{\mathrm{p}}$, sampling points within a prespecified neighborhood of the center of that sector. The templates are fed to the truncated SDAE–NN to produce a set of feature vectors. The sector feature vector is then constructed by taking a featurewise maximum over the template feature vectors. The resulting vectors of all sectors are concatenated to give the frame feature vector. The process is repeated for each frame within a prespecified neighborhood of the phase frame. The data feature vector is finally obtained by taking the featurewise means over the frame feature vectors. Symbolically the process of obtaining the data feature vector can be expressed as follows:

Let ${\mathbf{T}}^i=[{\mathbf{T}}_1,{\mathbf{T}}_2,\dots {\mathbf{T}}_{N_{\mathrm{p}}}]$ denote the matrix of template patches, each represented as a column vector, extracted from the, $N_{\mathrm{p}}$, locations of the sector, $i$. Let ${\mathbf{F}}^i=[{\mathbf{F}}_1,{\mathbf{F}}_2,\dots {\mathbf{F}}_{N_{\mathrm{p}}}]$ denote the matrix of the feature vectors obtained from these template vectors using the sector-specific neural network ${\mathrm{\Phi }}_i$.

$${\mathbf{F}}^i={\mathbf{\Phi }}_i({\mathbf{T}}^i).$$

The overall sector feature vector, ${\mathbf{F}}_{\mathrm{Sec}}^i$, is then obtained from the matrix, ${\mathbf{F}}^i$, by applying the columnwise maximum operator

$${\mathbf{F}}_{\mathrm{Sec}}^i=\underset{k}{\max }{\mathbf{F}}_{jk}^i.$$

The frame feature vector, ${\mathbf{F}}_{\mathrm{Frm}}^j$, for the $j$’th data frame is constructed by concatenating the, $N_{\mathrm{S}}$, sector feature vectors for that frame

$${\mathbf{F}}_{\mathrm{Frm}}^j=\left[\begin{array}{c}{\mathbf{F}}_{\mathrm{Sec}}^1\\ {\mathbf{F}}_{\mathrm{Sec}}^2\\ ⋮\\ {\mathbf{F}}_{\mathrm{Sec}}^{N_{\mathrm{S}}}\end{array}\right].$$

Let ${\mathbf{D}}^k=[{\mathbf{F}}_{\mathrm{Frm}}^1,{\mathbf{F}}_{\mathrm{Frm}}^2,\dots {\mathbf{F}}_{\mathrm{Frm}}^{N_{\mathrm{F}}}]$ denote the matrix obtained by stacking the, $N_{\mathrm{F}}$, frame feature vectors of the $k$’th dataset along the column dimensions. The data feature vector, ${\mathbf{D}}_k$, for the $k$’th dataset is then obtained by taking the rowwise mean of the matrix ${\mathbf{D}}^k$

$${\mathbf{D}}_k=\underset{i}{\text{mean}}{\mathbf{D}}_{ij}.$$

The feature pooling steps so outlined are done in order to reduce the dimensionality of the input feature space and hence, control overfitting of our final layer classifier.^49,50 The mean pooling over the frame feature vectors additionally reduces statistical noise for each feature.

3.4. Classification Module

Our classification module consists of an ensemble of support vector machine (SVM) classifiers^51,27 each trained on a random subset of the training data feature vectors. In the context of feature learning, the use of SVMs as a final layer classifier has been demonstrated to produce state of art results in a number of studies.^52,53 Note that the random subsets are constructed over the data space and not over the feature space. Majority voting of the ensemble is used to decide the output class label of a test dataset.

4. Experiments

We now discuss experiments conducted to develop and test the CCHD detection method described in Sec. 3. All parts of our algorithm were implemented in the MATLAB^® technical computing language (MATLAB^® and Statistics Toolbox Release 2012b, The Mathworks, Inc., Natick, Massachusetts).

4.1. Data Acquisition

We used 2-D echocardiographic temporal sequences (also termed here as, 2-D-US sequence) of normal neonates and neonates born with CoA, obtained in the three standard views that we investigate, to train and test the classifiers used in our CoA detection algorithm. The datasets were collected from the clinical archives of Boston Children’s Hospital. They were acquired between January 2008 and December 2014 using one of the Philips 5500, the Philips 7500, or, the Philips IE 33 2-D ultrasound systems with either the S8, or, the S12 high frequency imaging probes (Philips Ultrasound, Bothell, Washington). As our work involves data from human subjects, the study protocol was reviewed by the IRB and given exemption status, since, all patient datasets were deidentified prior to use. The mean age of the neonates at the time when the ultrasound data were acquired was 7 days. The CoA datasets selected were those that were adjudged by experts to have isolated aortic coarctation and no secondary lesions. In the clinical setup, the image acquisition protocol suggests, but does not require, that a given patient be imaged in all of standard views. Hence, although for most of the patient records we had datasets corresponding to the three views of interest for each patient case, there were a few records that had one or more of the view datasets missing. Given the paucity of clinical data, we included these as well in our study. Note also that since our datasets were acquired to perform a diagnosis for a particular patient at a particular point of time, they vary in terms of the various acquisition settings, such as depth, resolution, sector width, and so on. Therefore, to minimize the effects of any systematic acquisition bias between diseased and normal patient cases, a clinical expert visually inspected each of the datasets selected to ensure that they were of comparable appearance, had no gross movement of the transducer for at least one cardiac cycle, and had no annotations superimposed on the regions corresponding to the imaging field of view. The clinical expert also performed all required anonymization. The Merge Cardio clinical reporting and analytics system (Merge Healthcare, Chicago, Illinois) was used for this purpose.

The datasets were then separated into two parts: (1) a training set used for training and optimizing the machine learning algorithm and (2) a test set used to validate the algorithm. Table 1 lists the number of training and test sets for each of the cardiac views. Note, that in the test set, the studies corresponding to the 26 diseased patients are complete patient studies, meaning that each patient was imaged in each of the three cardiac views studied in this paper. For the normal test set, we started with 59 complete patient records. However, as more normal datasets became available later, they were added to the test set. Note also that the patient records corresponding to the test set were randomly chosen from the patient pool. The only requirements we set were (i) that at least 75 datasets per category (CoA or normal) be used for training and (ii) the difference between the numbers of datasets in each category used for training is not excessively large, since training classifiers with grossly unbalanced classes is challenging.

Table 1.

Number of training and validation datasets used for each of the views.

	AC4		PSLax		SSNA
	CoA	Normal	CoA	Normal	CoA	Normal
Train	77	86	75	85	75	76
Test	26	65	26	64	26	70

4.2. Training

For each dataset, the preprocessing steps described in Sec. 3.2 were then applied to give a set of view normalized data frames and the final frame dimension was set at $100\times 100\text{pixels}$ after the downsampling step. To train the cardiac phase-specific feature detectors for each sector, data-frames within three frames of the phase-frame were used. As explained in Sec. 3.3, during training, each data frame was used multiple times by randomly scaling and rotating the image data about the acquisition mask center by small scaling factors and rotation angles. Uniform scaling was used with scaling factors selected from the range [0.8, 1.2]. The rotation angle likewise was randomly selected from the range $[-5\mathrm{deg},5\mathrm{deg}]$. The resulting 2-D image data frames were then filtered using a seven-tap separable Gaussian filter of standard deviation (sigma), 0.75, to reduce image intensity interpolation artifacts introduced in the downsampling and the rigid transformation steps. For each transformed frame, 50, training templates of size, $25\times 25$, pixels were then extracted from randomly selected locations at a distance no greater than 9 pixels from the center point of each sector. Using the extracted templates, the sector-specific feature detectors consisting of a four-layer deep SDAE having sigmoidal activation units were then trained. The unsupervised learning phase for each SDAE was performed using 20,000 templates each from the normal and the CoA population in randomly drawn minibatches of size 100. Prior to presenting to the input layer of the autoencoder (AE), each template was normalized by scaling the intensity to be in the interval [0,1]. The input data to that layer were then corrupted with white noise of variance, 0.1, and the uncorrupted version was used as the training signal. 30 noise realizations were generated per minibatch iteration following which the network weights were updated. Stochastic gradient descent using the error back propagation algorithm⁵⁴ was used and adaptive learning rates for the weights were determined using the ADA-Delta algorithm.⁵⁵ A term involving the $L_2$ norm of the weights was also used in the network cost functional for weight regularization.^32,56 In the supervised learning phase, the network parameters were left unaltered, except for the number of training epochs, which were varied for the training error to converge. Table 2 lists values of parameters used to train each sector network. Optimization of the metaparameters of neural networks is a known difficult problem⁵⁷ and the values shown were selected manually after limited experimentation on a small sample set chosen from the training data.

Table 2.

Neural network parameters.

SDAE architecture parameters
Number of layers	4
Hidden layer node numbers	[600, 300, 150, 50]
$L_2$ weight parameter ($\lambda$)	$1\times {10}^{-5}$
ADADelta parameters
${ϵ}_{\mathrm{adel}}$	$1\times {10}^{-6}$
${\rho }_{\mathrm{adel}}$	0.95
Convergence criteria
Unsupervised learning number of iterations/layer	30
Error threshold during supervised fine tuning	0.01

After completing the training process for the neural networks, sector-specific features were extracted from the training and validation dataset as described in Sec. 3.3. For each sector, templates at distance no greater than 7 pixel units from the sector center were used to compose the sector feature vector. For the data feature vector, 3 frames on either side of the phase frame were used. Each feature was then normalized to have zero mean and unit standard deviation by subtracting the mean and dividing by the standard deviation of that feature. Robust means and standard deviations obtained using the bootstrap method⁵⁸ were used in the process. The normalized feature set corresponding to the training data was then used to train the final layer of the classification module, which consisted of an ensemble of 101 $\nu$-SVM classifiers.⁵⁹ The individual classifiers in the ensemble were obtained by training on randomly selected subsets of the input training data. Gaussian kernels were used for each SVM and the kernel width and SVM margin parameters were optimized using 100 runs of fivefold nested cross validation strategy.⁶⁰

4.3. Validation

In the validation phase, the feature vectors extracted from the test datasets were evaluated by the trained classifier ensemble. For each test case, a probability score for the dataset to be of type CoA was obtained by normalizing the number of SVMs in the ensemble that classified it as CoA. By suitably thresholding this raw probability score, the final class of the dataset was determined to be of type CoA whenever the raw score was equal to or exceeded this threshold. In our work, the mean of the ROC cutoff values of the probability scores obtained on the training feature set using fivefold cross validation was selected as the detection threshold. We also tested the following decision combination strategies:

• 1.Combine decisions of the CoA–normal classifier ensembles corresponding to the ED and ES phases for each view: majority voting decides the class label for a given case. Records with tied votes are treated as “undecided.”
• 2.Combine decisions of the CoA–normal classifier ensembles corresponding to the views for each phase: majority voting decides the class label for a given case. For paired views, tied decisions are treated as “undecided.” Table 3 summarizes the number of patient studies in the test set available for the view combination studies.

Table 3.

Number of common patient test datasets among the views used in the CoA–normal detection study.

	CoA	Normal
PSLAX—AC4	26	64
PLAX—SSNA	26	59
AP4—SSNA	26	59
PSLAX—PSAX—AP4	26	59

5. Results and Analysis

For each strategy investigated, we determined the false-negative (CoA) error rate, the false-positive (normal) error rate, and the total error rate on the test set. The 95% exact (Clopper–Pearson) binomial confidence interval^61,62 for each of error type was also determined. To assess the significance of the differences among the strategies, bootstrap resampling⁵⁸ was used on the classifier output labels to generate multiple sample sets. For each strategy studied, these resampled sets essentially provide a distribution on the means of the performance metrics. One way analysis of variance (ANOVA) using the nonparametric Kruskal–Wallis test⁶³ was then performed on the boot-strapped means corresponding to the strategies. To assess the significance of pairwise differences between strategies, the ANOVA tests were followed by post hoc multiple comparison analysis using Bonferroni corrections.⁶⁴

Table 4 shows the false-negative error rates, the false-positive error rates, and the total error rates for the single view-single-phase strategy and corresponding to the three cardiac views used in our study. The 95% binomial confidence intervals corresponding to each error type have also been shown. Note that, the PSLAX view has the lowest CoA error rate as well as the lowest total error rate, while, the SSNA view has the lowest error rates on the normal population. However, the CoA error rate for the SSNA view is surprisingly the highest.

Table 4.

Error rates and their 95% binomial confidence intervals for the single view-single-phase strategy corresponding to the three cardiac views.

View	Phase	CoA error rate	Normal error rate	Total error rate
PSLAX	ED	7.7 [6.1, 10.5]	23.4 [22.4, 24.7]	18.9 [18.2, 19.8]
	ES	11.5 [9.8, 14.3]	23.4 [22.5, 24.7]	20.0 [19.3, 20.9]
AC4	ED	19.2 [17.3, 22.0]	20.0 [19.1, 21.2]	19.8 [19.1, 20.7]
	ES	15.4 [13.5, 18.2]	20.0 [19.1, 21.2]	18.7 [17.9, 19.6]
SSNA	ED	19.2 [17.2, 22.0]	35.7 [34.7, 36.9]	31.3 [30.5, 32.2]
	ES	23.1 [20.8, 25.6]	40.0 [39.1, 41.3]	35.4 [34.7, 36.4]

Table 5 lists the performance of the various strategies studied. The false-negative error rate, false-positive error rate, the total error rate, as well as, their corresponding 95% confidence intervals have been listed for the best performing cases in each strategy. Note that, for the single view-single-phase strategy, the PSLax view in the ED phase was found to have the best overall performance. Additionally, its difference with the ES phase case, as well as, with the AC4 and SSNA views were found to be statistically significant. The PSLax view was also found to have the best performance in the phase combination strategy. Combining phases was found to significantly reduce the error rates for both type-1 and type-2 errors, although, this was at the cost of having a significant fraction of the CoA and normal cases undecided.

Table 5.

Error rates and their 95% binomial confidence intervals for the various strategies studied. Only the best performing cases corresponding to each strategy are shown.

Strategy	Best case	CoA error rate (%)	Normal error rate (%)	Total error rate (%)	% CoA undecided	% normal undecided	% Total undecided
Single view	PSLAX (ED)	7.7 [6.1, 10.5]	23.4 [22.4, 24.7]	18.9 [18.2, 19.8]	0	0	0
Single view-combined phase	PSLAX	3.9 [2.5, 6.7]	18.8 [17.9, 20.1]	14.4 [13.8, 15.3]	11.5	9.4	10.0
Two-view combination	PSLAX + AC4 (ED)	3.8 [2.4, 6.7]	7.8 [7.0, 9.0]	6.7 [6.1, 7.6]	19.2	28.1	25.6
Three-view combination	PSLAX + AC4 + SSNA (ED)	11.5 [9.8, 14.4]	13.6 [12.7, 14.9]	12.9 [12.3, 13.9]	0	0	0

For the view combination studies using two views, the combination for the PSLax and AC4 view in ED was found to have the best performance. The error rate for this particular case was also significantly lower than for the single views cases. However, the percentage of cases undecided was found to be significantly higher than the best single view-combined phase strategy. Note that, although the three view combination strategy was found to have a higher CoA error rate than the best two view combination strategy, the normal and total error rates are still significantly lower than strategies employing a single cardiac view. Additionally, this strategy has no undecided cases.

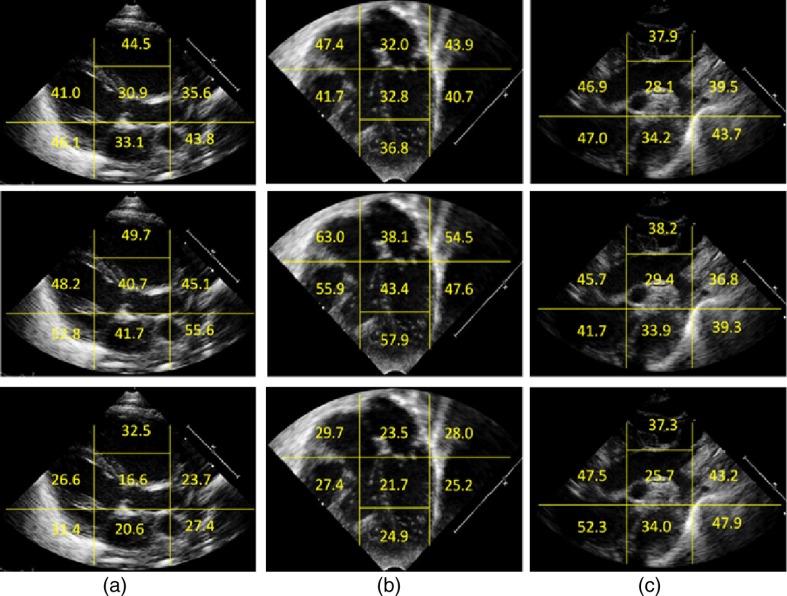
For each view, we also assessed the importance of individual sector features on the error rates. For a given sector, this was done by replacing the remaining sector features with random numbers drawn from a standard normal distribution to make those sector features uninformative. The resulting feature vectors were then classified by the SVM ensemble classifiers. This process was repeated a number of times, each time with a different set of random number draw. The resulting mean values of the error rates provide information regarding the importance of the individual sector in the classification task. Figure 9(a) shows results of the sector importance analysis for the three cardiac views in terms of the total error rate, Fig. 9(b) the false-negative error rate, and Fig. 9(c) the false-positive error rates.

Fig. 9.

Importance analysis of the sector features for (a) the PSLAX view, (b) the AC4 view and (c) the SSNA view. The sector-wise error rates are shown for the total error (top row), the false negative error (middle row) and the false negative error (bottom row). For each sector, the feature vectors corresponding to all other sectors except that sector were made uninformative and the output of the SVM ensemble detector evaluated.

For the PSLax view (top row), the sector in the center and the sector vertically below it containing the mitral valve plane and the left atrium (LA), respectively, are the most important sectors for the CoA–normal discrimination task. For the AC4 view (middle row), the sector in the center and sector above it containing the left atrium and left ventricle, respectively, are most important, while, for the SSNA view (bottom row) the sector in the center containing the aortic arch is maximally informative.

Finally, Table 6 shows the runtime statistics of the MATLAB^® code for the CoA detection algorithm run for a single view-single-phase classifier. The datasets corresponding to the test set were used in obtaining these statistics. Note that the mean run time will linearly scale up for multiple view, multiple phase strategies. Note also that the variability in runtime is primarily due to the data loading and data preprocessing stages of the algorithmic pipeline, since, these parts deal with varying number of the input data frames.

Table 6.

Runtime performance of the MATLAB^® code for a single view and single-phase classification strategy.

$N$	Mean (s)	Standard deviation (s)
90	0.5327	0.1952

6. Discussions and Conclusions

In this paper, we proposed a fully automated algorithm for the detection of CCHDs and applied it to the detection of CoA from 2-D echocardiographic image data acquired in three standard acquisition view planes. To our knowledge, this is the first published work that applies state of art machine learning methods to detect a challenging congenital heart defect from 2-D ultrasound. Our goal was to determine if such learning methods can be used to reliably determine the presence of a difficult-to-diagnose cardiac abnormality from 2-D ultrasound image data acquired in appropriate standard acquisition planes. Intuitively, anatomical, structural and temporal information present in image data loops provide a rich repository for arriving at inferences on interesting questions about the object being imaged. As many abnormalities have definitive spatiotemporal, or, structural signatures that can be observed in image sequences, the inferences arrived at can be expected to have good sensitivity and specificity as well.

Note that, although abnormal motion of cardiac structures can constitute important cues for the expert radiologist in detecting many cardiac abnormalities, in our work, we do not attempt to analyze motion information present in the ultrasound temporal sequences. Although, recurrent neural networks^65,66 might be employed in such a context, we have not explored this in our work. This, however, is an interesting direction for further research.

Our results demonstrate that on single view data, the algorithm achieves false-negative (CoA) error rates that are considerably lower than those reported in a number of clinical studies.^45,67 The gold standard, however, would be to compare results from an appropriately designed clinical study involving human observers evaluating the same test datasets. We plan on performing such a study in the near future.

Among the combination strategies studied here, those involving an even number of classifier ensembles resulted in some undecided cases. These can be flagged for further review. An alternate approach to majority voting would be to have a separate classification layer that would combine the individual classifier-ensemble outputs and provide unambiguous decisions for all cases. However, in cross validation studies, we found this approach to yield inferior performance.

We found that the PSLax view yielded the lowest total error rate on the test dataset for the single view-single-phase strategy. It also had the lowest false-positive error rate and the lowest number of undecided cases for the single view-combined phase strategy. In view combination studies, the PSLax + AC4 combination had the lowest total error rates. The superior performance of the PSLax view may appear surprising since neither the PSLax view, nor, the AC4 view can be used to infer aortic coarctation unambiguously. While it may be the case that the obstruction at the level of the aortic arch causes worse LV systolic function resulting in a dilated left ventricle, or, dilated left atrium, or even, a relative shift in the position of the inter ventricular septum; the distributed nature of nonlinear multilayered neural network systems make it hard to pinpoint the exact factors driving the selection, and the possibilities that we have listed are therefore speculative. Our results suggest that for purposes as a screening tool to detect critical congenital heart defects in the newborn, the use of these views may be very useful. We, however, plan on performing a clinical study in the near future to understand this better.

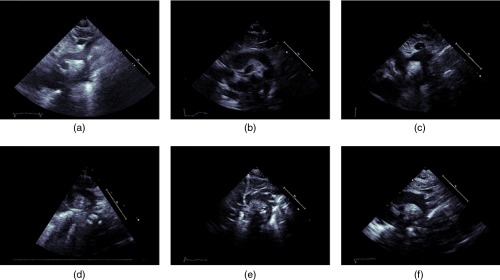
Although, the SSNA view is clinically used to diagnose CoA definitively, it is also a difficult view to consistently image in. Moreover, foreshortening and through plane motion are more pronounced in this view. The combined effects of these factors result in considerable variations in appearance for data acquired in the SSNA view, which may have adversely impacted the performance of classifiers trained on this view. Figure 10 shows that the top row contains image frames of corresponding to three CoA datasets while the bottom frame contains image frames corresponding to normal cases. Note that, on the CoA images, the aorta does not appear to be narrowing while it does on the normal images. For the normal images, the narrowing is more likely due to view foreshortening.

Fig. 10.

Images from the SSNA view illustrating challenges inherent in detecting aortic coarctation in this view: (a)–(c) are images of CoA datasets where the aorta does not seem to be constricting, while (d)–(f) are images of normal subjects where the aorta appears to be narrowing. For the normal cases especially, the narrowing appearance is more likely due to not obtaining the appropriate cross-sectional plane for imaging.

Complex machine learning methods such as DNNs typically employ a large parameter space to achieve desired performance on complex, high-dimensional data. Ideally, the training dataset size should be proportional to the number of parameters estimated. Regularization methods can be used to reduce effective model complexity. However, when the effective number of modes of variability of the data is low, such as when data are acquired in a standardized manner or when the population from which the data is extracted is constrained in some manner, deep learning methods have been shown to be more efficient, in terms of the number of datasets required to learn a given problem, than methods that employ ad-hoc feature generation strategies.²³ Returning to our case, we pose the CoA detection problem as a binary classification problem, the datasets we use consist of images acquired in a standardized manner, and finally, our patients consist of babies between 1 and 7 days of age. These constraints do reduce the complexity of the training problem. However, to ensure an unbiased estimate of model performance, the test set should ideally be large as well. For cases such as aortic coarctation, obtaining a large number of diseased cases is challenging due to the relatively low prevalence of the abnormality. Although in our study we were able to obtain a significantly larger number of diseased cases than reported in the literature,^45,46 we are aware that our classifier models should be tested on a larger population of both diseased and normal cases.

Note that, in the view normalization step (Sec. 3.2.2), we use a relatively simple registration process that aligns the image acquisition mask to a standard prespecified mask instead of performing a more complex anatomic registration that would align specific regions of the image (such as the major cardiac chambers). Such anatomic registration would require an additional learning layer prior to the detection phase. While this is a valid approach, it would be applicable to abnormalities that do not distort the anatomical appearance significantly. Since our aim was to design an algorithm that can be applied for other congenital heart diseases apart from aortic coarctation, we use the simpler approach and equivalently account for the anatomical variability in the training set by letting the neural networks learn that variability as described in Sec. 3.3. This aim also guided our decision not to explore any specific segmentation approach (such as segmenting the aortic arch in the SSNA view) and use that information in the detection task.

Given the relatively small prevalence of CCHDs among newborns, the false-positive error rates of our algorithm would still yield a significant number of false positives over a large enough patient population and this may be a matter of concern when economic costs of patient care are taken into consideration. However, this may be alleviated by combining information obtained from other pertinent sources/modalities, such as pulse oximetry, clinical examination, cardiac chamber wall strain analysis, patient reports, and so on. Such fusion of information is likely to positively impact the performance of machine learning-based approaches. Note that, for pulse oximetry to be used for newborn screening, and in the published literature requires a specific protocol consisting of obtaining measurements in upper and lower limbs at two time points after birth, separated typically by 24 h. This specific protocol, however, was not followed in most of the infants that had newborn echocardiography data available in our patient cohort. We are considering performing a prospective study in the near future comparing oximetry from newborn screening protocol to standard view echocardiography.

Finally, the generality of our algorithm allows it to be applied to detect other congenital heart diseases in addition to CoA and we plan on investigating these various avenues in the near future.

Biographies

Franklin Pereira received his PhD in physics (nuclear medicine physics and imaging) from University of Massachusetts, Amherst, USA, in 2008. He was a postdoctoral fellow at Brigham and Women’s Hospital/ Harvard Medical School between 2008-2010 and has been working as a research engineer at Philips Ultrasound R&D since then. His present work includes developing solutions for ultrasound imaging, image processing, image-based classification and quantification, motion tracking, and image quality enhancement.

Alejandra Bueno received her medical degree from Autonomous University of Chihuahua, Mexico, in 2011. She finished a postdoctoral cardiology research fellowship at Boston Children’s Hospital, under supervision of Dr. del Nido (2015). Some of her publications are “Outcomes and Short-Term-Follow-Up in Complex Ross Operations in Pediatric Patients Undergoing DKS Takedown” in the Journal of Thoracic and Cardiovascular Surgery, “UV, Light Transmitting Device for Cardiac Septal Defect Closure” in Science Translational Medicine. She is currently a pediatric resident at Bronx-Lebanon Hospital.

Andrea Rodriguez received her medical degree from Autonomous University of Guadalajara, Mexico, in 2012. She did a postdoctoral cardiovascular surgery research fellowship at Boston Children’s Hospital, under the supervision of Dr. del Nido, which ended earlier in the year (2016).

Douglas Perrin received his PhD from the University of Minnesota Artificial Intelligence, Robotics and Computer Vision Laboratory. He is currently an instructor in surgery at the Harvard Medical School with a joint appointment at Boston Children's Hospital. He has over 13 years of experience in translating advances in computer science into medicine. He has published research is the areas of robotics, computer vision, user interfaces, image guided cardiac intervention, and ultrasound enhancement and analysis.

Gerald Marx received his medical degree at the University of California, Los Angeles Medical School. He completed his pediatric residency and fellowship at Boston Children’s Hospital. He is currently a senior associate in cardiology at Boston Children’s hospital, and associate professor in pediatrics at Harvard School of Medicine. His research interests are in the development and application of three-dimensional echocardiography in congenital heart disease.

Michael Cardinale is presently a Systems Intergration Testing Engineer at Philips Healthcare. He has a BS in Science for Ultrasound and is registered with ARDMS for Adult Echo/Adbomen/and Ob-Gyn since 1984. He has been working as a clinical research sonographer at Philips for 30+ years, collaborating with Philips Research in the development of advanced imaging and analysis tools for 2-D and 3-D ultrasound including speckle tracking, Heart Model™, mitral/aortic valve quantification etc.

Ivan Salgo received his BS and MS degrees from Columbia University and MD degree from the Mount Sinai School of Medicine. He is a associate chief medical officer for Philips. He oversees medical device technology strategy and new business models. He did his residency and fellowship at the University of Pennsylvania in Cardiothoracic Anesthesiology, where he later joined the faculty. He also received his MBA degree from the Massachusetts Institute of Technology Sloan School of Management in 2012.

Pedro del Nido received his medical degree at the University of Wisconsin Medical School. He completed Cardiothoracic Surgery at the University of Toronto in 1985. He is currently the William E. Ladd professor of Child Surgery at Harvard Medical School and Chief of Cardiac Surgery at Boston Children’s Hospital. His research interests include development of tools and techniques for beating heart intracardiac surgery, and image guided surgery.

Disclosures

The authors declare that they have no conflict of interest, financial or otherwise.