Mesoscale imaging with cryo-light and X-rays: Larger than molecular machines, smaller than a cell

Abstract

In the context of cell biology, the term mesoscale describes length scales ranging from that of an individual cell, down to the size of the molecular machines. In this spatial regime, small building blocks self-organise to form large, functional structures. A comprehensive set of rules governing mesoscale self-organisation has not been established, making the prediction of many cell behaviours difficult, if not impossible. Our knowledge of mesoscale biology comes from experimental data, in particular, imaging. Here, we explore the application of soft X-ray tomography (SXT) to imaging the mesoscale, and describe the structural insights this technology can generate. We also discuss how SXT imaging is complemented by the addition of correlative fluorescence data measured from the same cell. This combination of two discrete imaging modalities produces a 3D view of the cell that blends high-resolution structural information with precise molecular localisation data.

Introduction

Across scientific disciplines, the term mesoscale is used to indicate ‘intermediate’, or ‘middle-ground’ ranges of measures, such as energy, length or time (Laughlin et al. 2000). As a result, mesoscale means different things to different people. Before we go any further, it is important we define the term mesoscale in the context of biology and as used throughout this paper. The accepted definition is that the biological mesoscale begins at length scales larger than the molecular machines, and extends up to the dimensions of an individual cell (Sear et al. 2015). The cellular mesoscale, therefore, typically spans length scales from a few tens of nm, up to 10 µm, although some individual cells can, of course, be much larger (Sear et al. 2015). In this paper, we will describe imaging methods for characterising the cellular mesoscale. Before detailing these methods, we will explain why the mesoscale is fundamentally important in biology, and why it cannot be imaged effectively using well-established, existing modalities.

Importance and characteristics of the biological mesoscale

One could argue that the most important sub-cellular action occurs at the molecular level, for example, gene transcription, protein synthesis and receptor signalling and thus that the mesoscale is simply a reflection of these events. The response to such statements is relatively simple but profound. At the molecular level, cell biology is governed by the established laws of chemistry and physics (Laughlin et al. 2000). In which case, a particular molecular interaction can be characterised in vitro, and predicted, with some certainty, in cellulo by taking into account factors such as temperature, pH or degree of molecular crowding (Laughlin et al. 2000, Laughlin and Pines 2000). Predictions arising from the knowledge of molecular level events are routinely tested by a plethora of biophysical techniques, with theory and experiment frequently being closely aligned. As an example, blocking a specific protein–protein interaction using small molecule has long been the path towards development of new therapeutic drugs (Scapin 2006). If the molecule blocks the interaction of isolated molecules in a test-tube, the chances are high that it will function similarly in the cell, provided, for example, that the drug can be delivered effectively, and is not bound by competing molecules (Rudin and Weissleder 2003). However, when it comes to predicting the mesoscale characteristics of a cell, the situation is markedly more complicated. Mesoscale self-organisation presumably conforms to a set of rules and guiding principles, but, for the most part, these rules and principles remain largely unknown (Laughlin et al. 2000). In a ground-breaking paper on the mesoscale,Laughlin et al. (2000) wrote, ‘rules that are dreamt up without the benefit of physical insight are nearly always wrong, for correct rules are natural phenomena and, therefore, must be discovered, not invented’. This statement still holds true today. Characterising the mesoscale cell must still be done experimentally, most effectively by imaging cells. Some imaging techniques will be better suited to the task of visualising the mesoscale than others. At this point, the reader may reasonably think, ‘surely, the mesoscale can be imaged readily by light and electron microscopy’. To a limited extent, the answer is yes it can, but not adequately. Let us explore the option of using familiar imaging methods as mesoscale visualisation tools.

Extending molecular methods into the mesoscale

For the past few decades, characterising cellular components up to the size of the molecular machines has been something of a global industry (Campbell 2002). An army of researchers have applied techniques such as electron microscopy (EM) (Nogales 2016), nuclear magnetic resonance (NMR) (Dutta et al. 2015) and macromolecular X-ray crystallography (Dauter and Wlodawer, 2016) to determine the tertiary structures of nucleotides, proteins, and even viruses. The effort in this area is on-going, and rapidly expanding in the case of cryo-EM, where a resurgence in the technique has a focus on determining the structure of ever more complex molecules, including multi-component molecular machines at near-atomic resolution (Nogales 2016). Since we would like to get the highest possible resolution views of the mesoscale, EM and macromolecular crystallography seem like obvious choices for this task. Unfortunately, crystallography is limited to imaging many repeats of the object held in the rigorously ordered lattice of a crystal (Dauter and Wlodawer, 2016). There is, however, some optimism that a new generation of coherent light sources, for example, the Linear Coherent Light Source at Stanford and the European XFEL in Hamburg, Germany, could image cells with molecular or even atomic resolution (van der Schot et al. 2015). Whether or not this become a routine process in the future remains to be seen.

Transmission electron microscopes (TEM) produce very high spatial resolution images of the specimen, and can image the mesoscale organisation. Unfortunately, there is a trade-off in TEM between spatial resolution and specimen thickness. In general, the thicker the specimen, the lower the achievable resolution. As a ballpark figure, the sweet spot for imaging biological specimens is a thickness of less than 500 nm (Leis et al. 2009). Of course, there are many instances where excellent work has been done using much thicker specimens (Hohmann-Marriott et al. 2009, Wolf et al. 2014, Trepout et al. 2015). Of course, one could rightly argue there is huge value in visualising even a single, well-chosen 500 nm thick section of a cell using EM (Leis et al. 2009). Both history and the literature have shown this to be the case. Indeed, our knowledge of organelle structures is almost entirely due to decades’ worth of EM. However, visualising a complete cell in 3D using EM is technically difficult and time-consuming (Höög et al. 2007). Moreover, there are technical challenges in tracing fine structural details across the boundaries between sections, due to a loss of specimen, or specimen integrity at the junction between sections (Al-Amoudi et al. 2003). That said, some truly Herculean work is underway to image large regions of brain tissue for connectomics (the creation of maps showing the connections between neurons) (Cao et al. 2016, Mikula 2016, Ohno et al. 2016, van den Heuvel et al. 2016).

EM can be carried out on cryopreserved or chemically fixed cells. The former is considered the ‘gold standard’ for retaining the native state of the specimen (Dubochet and McDowall, 1981, Dubochet and Lepault, 1984, Dubochet et al., 1984, Dubochet et al. 1988). Chemical fixation, no matter how well done, is believed to still result in some alteration of the specimen ultrastructure from its true native state. In short, EM can clearly make a strong contribution to mesoscale imaging. However, inherent technical limitations of the technique make it a less than satisfactory solution.

Fluorescence microscopy is the other major contributor to our understanding of the sub-cellular organisation, and can be applied to imaging the location of individual molecules inside a cell, or identifying and quantifying the size and shape of organelles (Tsien 2003, Tsien 2005, Giepmans et al. 2006). Fluorescence microscopy has also undergone a technology driven resurgence in recent years, due to the development of ‘super-resolution’ methods (Huang et al. 2010). Although these instruments and methods have pushed the achievable spatial resolution of fluorescence imaging far higher than once thought possible, super-resolution microscopy can only image fluorescently labelled molecules, and not the surrounding cell environment. For a complete picture of the mesoscale, fluorescence imaging data must be combined with structural data. Since we have just argued EM is not a satisfactory solution, the question becomes ‘What are the viable alternatives?’

Specimen illumination is primarily the parameter that differentiates microscopy methods from each other. This is perhaps stating the obvious, but in most regards, the way visible light, electrons and X-rays interact with biological specimens could not be more different. Since we have argued that light and electron microscopes are not good choices for mesoscale imaging, the obvious answer is X-rays. Of course, ‘hard’ X-rays have been put to work imaging biology since their discovery by W.C. Röentgen in 1895 (Stark 1935, Santin 1995). More than a century later, few people in the developed world live their lives without having a medical or dental X-ray taken at some point. Regarding imaging individual cells, the characteristics of hard X-rays that make them so good at imaging broken bones – passing unfettered through the skin and soft tissue, but absorbed by bone – clearly, render them less easy to use for imaging cells. Recently, significant effort has been put towards this challenge, and resulted in some very promising results, particularly using the method of ptychography (Wilke et al. 2012) (Bartels et al. 2012) (Bartels et al. 2015).However, the X-ray regime extends far beyond the energies used in clinical imaging. A clinical or dental X-ray source typically produces photons with energies in the tens of keV range. At the opposite end of the X-ray spectrum lies the so-called ‘soft’ X-ray region, measured in hundreds of eV (Le Gros et al. 2014). Photons within the soft X-ray region interact strongly with all matter, and cannot penetrate deeper than a layer or so of skin; a property that makes soft X-rays well-suited to imaging cells. Absorption by the cell contents is the basis for image contrast in a soft X-ray transmission microscope. But it gets better. Within the soft X-ray regime, there is a specific range of energies – between the K-absorption edge of oxygen at a wavelength of 2.34 nm and the K-absorption edge of carbon at 4.4 nm – known as the ‘water window’ (Falcone et al. 2011). As the name suggests, in this energy regime, water is relatively transparent towards water window illumination and biomolecules containing carbon are an order of magnitude more strongly absorbing (Attwood 1999). Since cells are a heterogeneous mix of biomolecules and water, differences in cellular composition at each point in the cell, that is relative concentrations of carbon and water, result in differences in attenuation of the soft X-ray illumination as it passes through the cell. In other words, a highly solvated region, for example a vacuole, will transmit most of the illumination since it has a relatively high water content. On the other hand, a membrane bilayer will be strongly absorbing due to the high concentration of carbon, and relatively low water content. In practice, soft X-rays can readily penetrate cells that are up to 10 µm thick, or thicker if the cell has a high water content (Larabell and Nugent 2010). This means a soft X-ray microscope can image the largest length scale in the biological mesoscale. How about the opposite end of the mesoscale, the size of a molecular machine? Soft X-ray microscopy (SXM) also has that covered. The current generation of soft X-ray microscopes can image down to a spatial resolution of 35 nm, or even better (Figure 1A).We will now describe the characteristics of SXM in more detail, beginning with the most important aspect, methods used to ensure the imaged specimen truly represents the in vivo cell.

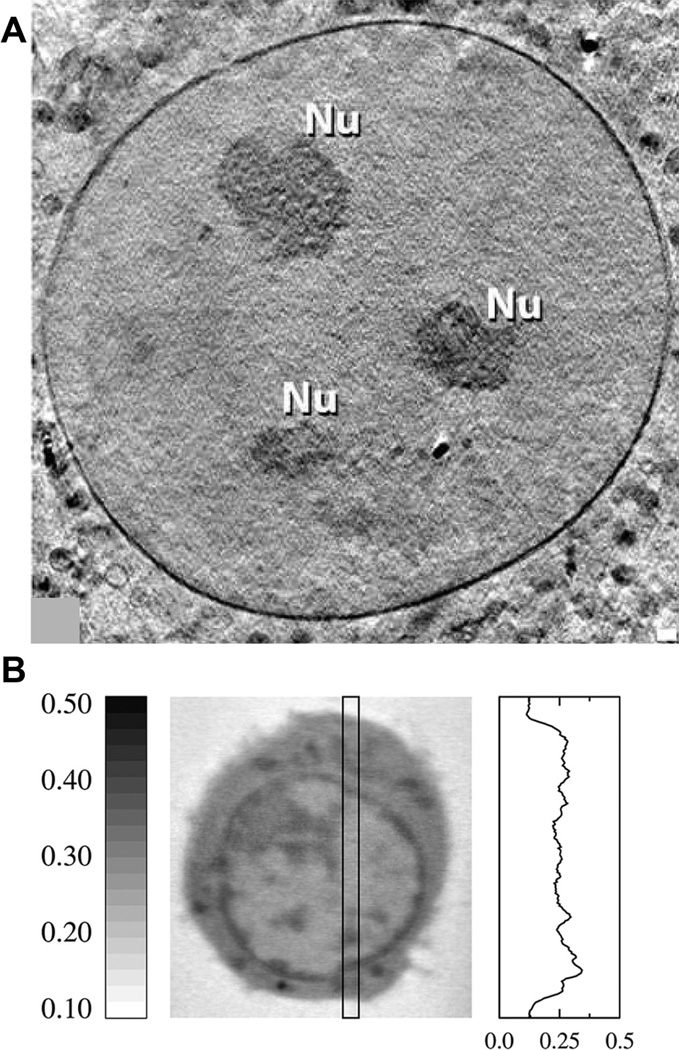
Figure 1. SXT imaging and resolution.

(A) An overview of a nucleus containing three nucleoli (Nu) showing the clarity with which the nuclear membrane can be visualized using a 25nm zone plate objective. Image taken from (Muller et al. 2012). (B) An orthoslice from a SXT reconstruction of a B-cell (center) and a representative profile of the variation of LAC within a cell (right). Dark features in the image correspond with structures containing higher concentration of carbon and thus have higher LAC values. LAC values are in units of µm⁻¹.

Soft X-ray microscopy

Soft X-ray microscopes have existed for many years, but it is only relatively recently that they have been successfully applied to imaging the cellular mesoscale (Weiß et al. 2000, Denbeaux et al. 2001, Meyer-Ilse et al. 2001, Schneider et al. 2002). The reasons for this change are twofold. Firstly, a combination of technical advances – specifically, in the areas of detectors, X-ray sources, and optics – made soft X-ray microscopes capable of imaging cells more rapidly, and with higher spatial resolution. Secondly, cryogenic specimen rotation stages became available on soft X-ray microscopes, making tomographic data collection possible (Weiß et al. 2000, Larabell and Le Gros, 2004a,b). Adopting a tomographic approach is essential for imaging the mesoscale organisation using a soft X-ray microscope. Without it, the microscope can only generate 2D projection images of the cell. In these projections, internal structures are superimposed on each other, making interpretation of the images virtually impossible (McDermott et al. 2012a,b).

Retaining the native structure by cryopreservation

Cells imaged by SXM must be immobilised, or ‘fixed’ at the molecular level. Otherwise, the constant movement of sub-cellular objects would result in blurred details, a bit like taking a photograph of a fast moving object in low light without using a flash (Smith et al. 2014a,b). Moreover, as with any high-intensity illumination, soft X-rays have the potential to cause dose-dependent specimen damage (Parkinson et al. 2013). Fixation, in addition to restricting motion, can also mitigate the effects of radiation damage. As a fixation method, cryogenic temperature preserves the subtle architecture of biological specimens better than chemical fixation. The fact that cells are routinely deep-frozen and then cultured once thawed can be taken as evidence that properly executed cryopreservation does not irreversibly damage the delicate sub-cellular balance and organisation (Morrison 1977, Witt and Bousquet, 1987). Of course, these observations are based on the viability of large cell populations or cell aggregates that may be able to tolerate significant damage through sheer force of numbers. In many cases, if a small percentage of cells survive freezing, this may be sufficient to start exponential growth. In this case, we must look for direct evidence that freezing does not damage cells. In this regard, additional evidence can be drawn from cryogenic EM (cryo-EM), and the ground breaking work of Dubochet (Dubochet and McDowall, 1981, Dubochet et al. 1984, Dubochet et al. 1988, Al-Amoudi et al. 2004, Bouchet-Marquis et al. 2006). In cryo-EM, the specimen is rapidly frozen to 77 K, or lower, usually under high-pressure (2000 atm). Specimens fixed in this manner show few signs of structural damage as a result of preservation, even when examined at ultra-high resolution (Mcdowall et al. 1984, Dubochet et al. 1988, Al-Amoudi et al. 2004, Leis et al. 2005). Consequently, cryopreservation is universally regarded as the ‘gold standard’.

Virtually all cells imaged by SXM, at least in the past decade, have been cryogenically fixed – either by rapidly plunge freezing the specimen on an EM grid or encased in a thin-walled glass capillary or by high-pressure freezing specimens mounted on a thin EM style grid – and maintained at low temperature throughout data acquisition. Since the spatial resolution of a soft X-ray microscope is much lower than that of a TEM, little to no radiation damage is visible in images of the specimen. However, since some investigators have reported high-pressure freezing results in a more uniform cooling rate across the entire specimen, this method may be required in the future, as the resolution of X-ray microscopes increases (Hagen et al. 2012).

Rotating the specimen to add an extra dimension to SXM

You are probably familiar with the role of computed tomography (CT) in clinical diagnosis and have undoubtedly seen the iconic instrument featured at some point in every present day medical drama. The instrument is recognisable as a large circular structure with a hole in the centre, through which the patient is moved on a table. Inside the outer casing, there is an X-ray source on one side of the ring, with X-ray detectors in the opposite. Both are rotated in tandem around the central axis occupied by the patient. 2D projection images through the patient are taken from multiple angles (Canigiani and Imhof, 1979). The projections can be described as a transform of the sample volume, and a 3D reconstruction of the patient is calculated by ‘simply’ solving the inverse of this transform. The resultant tomographic reconstruction is enormously more informative than a simple 2D image. In 2D, all of the internal structures of the body are superimposed on top of one another, making it very difficult to view soft tissue if bone surrounds it. Similar problems translate to SXM of cells. In a 2D projection image, the sub-cellular organisation appears ‘flat’ and very difficult to interpret. To overcome this issue, similar principles applied to human-scale clinical imaging are put to work imaging cells by soft X-ray tomography (SXT). Of course, there are a few technical differences, together with some advantages to imaging small cells versus a live human. In SXT, it would be very difficult to rotate the X-ray source/detector pair, so the cell is rotated around a central axis during tomographic data acquisition. Since the specimen is held at 77 K from the instant it is cryopreserved, until the moment it is discarded at the end of an experiment, it can tolerate significant radiation dose without the appearance of artefact in the image, allowing collection of tomographic data with excellent signal-to-noise ratio. Of course, eventually all biological specimens exhibit radiation damage if the dose is high enough. In general, this results in gas bubbles being present in the reconstructed image of a cell. In the next section, we will expand on the attributes of SXT in some greater detail.

Soft X-ray tomography

Let us consider the main attributes of SXT as a cell imaging method. It is a non-invasive, 3D imaging technique that visualises and quantifies volumes, surfaces, interfaces, membranes and organelle connectivity within intact, fully hydrated cells. That is quite a skill set for any imaging modality, so we will now justify and expand on each of these attributes.

Near-native state imaging

Soft X-ray photons have significantly greater penetration depth through biological specimens than electrons. This is a critical factor in transmission mode imaging, where the image formation is created by the attenuation of the illumination as it passes through the specimen. Greater penetration depth means soft X-rays can image comparatively thick specimens with good signal to noise ratio. In practice, this means soft X-ray microscopes have the capacity to image intact cells up to 15 µm thick. This eliminates the need for invasive, time-consuming processes, such as sectioning or ion-milling, that may be required for other imaging methods.

3D reconstructions

Projection images are the primary output of a soft X-ray microscope. As a standalone piece of data, 2D representations of a cell, especially a larger eukaryotic cell, are of limited use. In projection, internal structures are confusingly superimposed on top of each other, similar to the way bones in a 2D clinical X-ray get superimposed on top of soft tissue, making diagnosis difficult. A 2D clinical X-ray image is, therefore, great for identifying a broken leg, but poor for viewing the thorax, where attenuation by the breastbone and spine would cause issues. Of course, in the clinical case, the solution is to collect X-ray images from different perspectives, ideally covering all angles around a central axis.

However, data collected in this way can be computed to generate a 3D tomographic reconstruction. CT instruments are iconic in healthcare tomography as a well-established method for reconstructing the interior of an object in 3D from its 2D projections (Derosier and Klug, 1968, Crowther et al. 1970). It is based on the mathematical description of the projections, the Radon transform (Radon 1917), or more specifically, on the existence of its inverse, that is the internal structure of an object is defined by its (continuous) projections. In practice, however, CT is restricted by both the finite number of projections and by the discrete nature of the sampling making a direct inverse of the Radon transform highly unstable.

The most widely used reconstruction is the Filtered Back Projection (FBP), which follows naturally from the relation between the Radon transform and the Fourier Slice Theorem (Kak and Slaney, 1988). The Fourier Slice Theorem states that the Fourier transform of the projection is equivalent to an extracted 1D line from the 2D Fourier transform of the object. The Radon transform does not provide an equal sampling of the frequency data. Thus, a naïve back-projection of the data will overestimate low-frequency signals. The word ‘filtered’ stems from this weighting of the frequencies as it can be accounted for by applying a filter on the projected image, in the either the spatial or frequency domain by a convolution or point-wise multiplication, respectively.

This method is very quick, and can calculate a reconstruction of a cell in near real time using very modest computational resources and has remained the canonical method for tomographic reconstruction for over three decades. As an example, a common laptop has sufficient computational power to calculate a FBP reconstruction of SXT data in a reasonable timeframe.

Regardless of the specific algorithm chosen for the reconstruction of the sample, the setup of the problem requires that the relative locations of the camera and the sample are known. In many applications of µCT and medical imaging, the engineering of the devices can be made with accuracy sufficient to keep mechanical stability within the limit of the resolution, and thus, these locations can be assumed to be known a priori. However, with increasing resolution, these inaccuracies become substantial, and both random and systematic movement can be significant and require correction to enable a proper reconstruction of the sample.

Although this is a fairly new problem for X-ray microscopy, the problem has been dealt with for quite some time in EM (Mastronarde 2007) and many tools and methods are readily available and directly suitable for SXT. In principle, it is sufficient to only determine the positions and orientation of the projection with respect to the object, but it is usually computationally beneficial to correct the measured projection images (rotation, translation, skew etc.) so that it conforms to a chosen symmetry of the reconstruction algorithm. The current standard way to deduce and correct for these errors is by fiducials, that is a set of easily detectable markers that can be identified from each projection image. The paths of the markers, either partial or full, can be used to deduce the optimal corrections of the images (Jing and Sachs 1991, Lawrence 1992).

Although the fiducial alignment produces the most reliable and robust way to align the projection images, it suffers from severe drawbacks. The need to attach the fiducials on the sample requires an extra step in the sample preparation limiting the range of different samples. The manual alignment (although it can be eased with programs (Larabell and Le Gros, 2004a,b, Parkinson et al. 2013) is slow, labour-intensive and prone to human error. The high contrast markers also often cause artefacts in the reconstructed image.

The simplest way to try to circumvent these problems is by cross correlating (Jing and Sachs 1991, Frank and McEwen, 1992). The basic idea is that with small enough angular difference in the tilt between successive projections, the images can be matched by similarity measures. This method has proven, however, to be problematic (Brandt 2007) as errors easily accumulate and produce drifting in the aligned stack. A relatively recent method is the model based methods or projection matching (Penczek et al. 1994, Winkler and Taylor, 2003, Brandt and Kolehmainen, 2004, Yang et al. 2005, Brandt and Kolehmainen, 2007). This approach uses an initial alignment for a tomographic re-construction of the sample which is then iteratively refined by aligning the experimental projection images to computational projections of the reconstruction. These model-based approaches are indeed promising in SXT imaging (Parkinson et al. 2012) and may provide a suitable solution to the problem. A similar method, using fiducial free image registration, has been developed for electron tomography (Sorzano et al. 2009). In principle, this technique could also be adopted for alignment of SXM projection images.

Tomographic reconstruction is the process of using these aligned 2D projection images to calculate a 3D representation of the specimen (Natterer 1986). In an idealised experiment, the image series would contain an infinite number of noiseless, perfectly aligned images, in which the choice of reconstruction algorithm would be moot since all competent algorithms would generate the same reconstruction. However, real world measures can contain only a finite number of images and additionally, suffer from both statistical noise and imperfections in their alignment. In many of these cases, especially for low-dose imaging, where either the number of images or the photon count per image is limited, analytic reconstructions such as FBP are often unsuitable. For many such occasions, iterative reconstruction (Beister et al. 2012) methods result in superior reconstruction quality as they allow for more flexible model adjusting. This can be done for example by accounting for known statistical behaviour of the signal (Sauer and Bouman, 1993, Fessler 2000, Thibault et al. 2007), or by assumptions of smoothness in the imaged sample (Candes et al. 2006, Ramani and Fessler, 2011, Vandeghinste et al. 2011, Ramani and Fessler, 2012, Charbonnier et al., 1997). The choice of best algorithm to use for the reconstruction of a given data set is often a matter of trial and error and also an optimisation of the image quality with respect to the available computational resources.

Quantitative imaging: The power of the LAC

High-resolution imaging studies, SXT included, have the potential to cause accumulated photon damage to the specimen, which in turn leads to artefacts in the images. Fixation, in most instances, can mitigate this damage to undetectable levels and is, therefore, an essential step in most studies that require repeated exposure of the specimen to harsh illumination (whether in the form of light, electrons or X-rays). Instead of chemical fixation, which again inflicts damage on the structural integrity of the cell, we turned to cryo-preservation. However, this presented a significant technical challenge: cryogenic microscopes suitable for cell imaging all used air lenses that were not refractive-index matched to the specimen and were therefore only capable of producing relatively low-resolution images that contain aberrations.

The reconstructed volume of the imaged sample in CT results in a 3D density map of the sample describing the local linear absorption coefficient (LAC) of the sample. SXT illumination for use in biological imaging is typically tuned to lie in a spectral region between the K-edges of carbon (E = 284 eV, λ = 4.4 nm) and oxygen (E = 543 eV, λ = 2.34 nm) (Weiß et al. 2000, Larabell and Le Gros, 2004a,b). In this region, more commonly known as the ‘water window’, the LAC of organic material is typically about an order of magnitude higher than that of water. This means that the chemical composition of the biological structure provides sufficient contrast for its identification without the need for labelling. For example, for illumination of wavelength 2.4 nm ice has a theoretical LAC value of 0.109 µm⁻¹, whereas a model protein with chemical composition C₉₄H₁₃₉N₂₄O₃₁ has a calculated LAC value of 1.35 µm⁻¹ (Weiß et al. 2000).

In reality, the measured LAC values correspond closely with theoretical values, with the LAC for each structural component in the cell falling within the values for ice and dry protein. For example, densely packed lipid droplets have a high concentration of carbon and relatively little water content, resulting in a LAC value of ≈0.7 µm⁻¹, whereas water-filled organelles such as vacuoles have lower LAC values, around 0.22 ± 0.07 µm⁻¹ (Uchida et al., 2011). LAC values of specific cellular components in both single cell populations, and across different cell types across many eukaryotic species, consistently fall within a certain range. For example, mammalian nuclear heterochromatin typically ranges from 0.23 to 0.36 µm⁻¹, and euchromatin from 0.13 to 0.25 µm⁻¹ (Smith et al. 2014a,b). Similarly, the LAC of nuclear chromatin in yeast is 0.26 ± 0.01 µm⁻¹. Other LAC value examples include the nucleolus, 0.33 ± 0.01 µm⁻¹, and mitochondria, 0.36 ± 0.02 µm⁻¹ (Figure 1B). In recent work, Kapshnikov et al. (2013) distinguished between hemozoin crystals and lipid droplets in the digestive vacuole of the malaria parasite Plasmodium falciparum. In this case, the LAC values were directly correlated with chemical composition, reinforcing the argument that SXT is a quantitative imaging technique.

Figures 2A–2B show a slice through a reconstruction of an adherent cell. As one can see, there is excellent contrast differentiating the various sub-cellular organelles. Not only does this contrast allow the organelle to be segmented, that is computationally isolated from the other cell contents, there are structure revealing contrasts within the organelle itself, revealing the sub-organelle organisation. Given the scope of this paper, we will not describe the segmentation process in detail; interested readers can find more information in Parkinson et al. 2013.

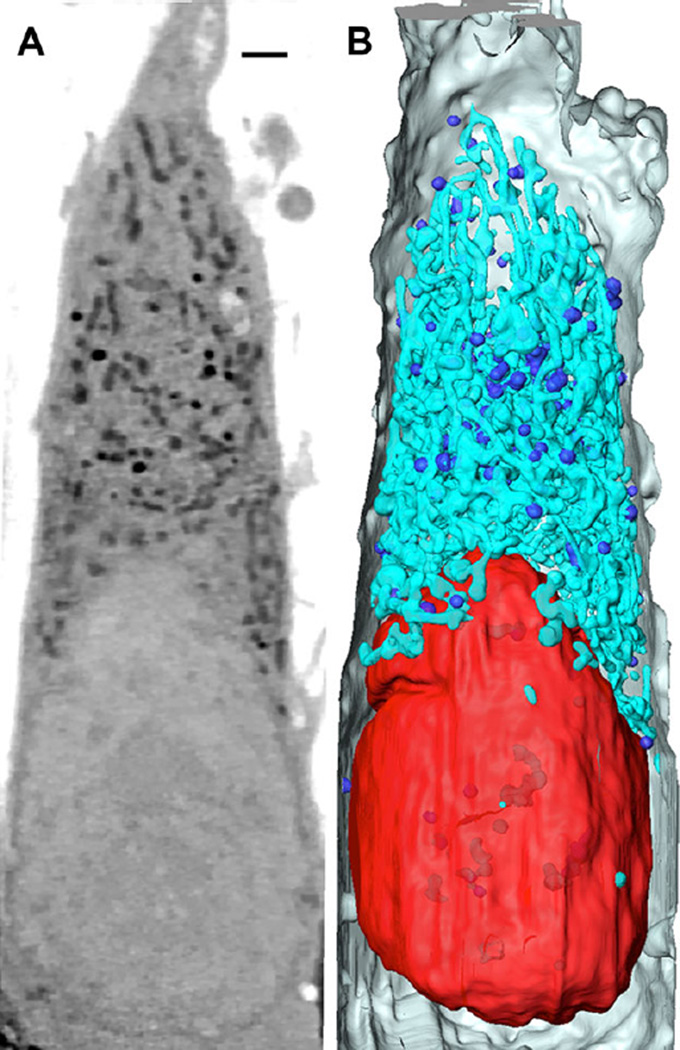
Figure 2. SXT of a fibrosarcoma cell.

(A) An orthoslice through a SXT reconstruction of a HT1080 fibrosarcoma cell. (Nu, Nucleus; >, Lipid; *, Mitochondria). Image is comprised of tomographic reconstructions from two adjacent fields computationally stitched together. (B) 3D volume rendering based on organelles’ linear absorption coefficient (LAC) and morphology. Red: Nucleus, Turquoise: Mitochondria, Blue: Lipids, Gray: cell membrane. Scale bar = 1.5 µm.

Hopefully, by this point, we have convinced you SXT is an excellent tool for mesoscale imaging, but it is, however, not all encompassing. SXT reconstructions do not contain molecular localisation data. Not unless molecules of interest have been labelled with an electron-dense tag, for example a titanium nanoparticle that is visible in the data (Ashcroft et al. 2008) or a quantum dot (Alivisatos et al. 2005). Although this sounds like a viable method for localising molecules in an SXT reconstruction, in practice it is not very satisfactory. To add a metal tag, the specimen must be chemically fixed and permeated to allow ingress of antibodies that bind the target molecule. There are other steps in the process, but we feel this first step is a show stopper. Chemical fixation/permeation is an invasive process that potentially causes changes in the mesoscale organisation (Lucic et al. 2008, Leis et al. 2009). In which case, an alternative method was sought and found; correlated fluorescence microscopy.

Combining dots with blobs: Putting molecules into their cellular context

The fundamental criteria for correlated fluorescence microscopy-SXT are similar to those for correlated light and electron microscopy (CLEM). Ideally, the fluorescence method must be (i) reproducible, (ii) have a well-defined localisation error, (iii) be capable of detecting signal from low numbers of fluorescent tags, (iv) cover the spectrum of available fluorescent labels, and be carried out on specimens mounted in a support suitable for subsequent imaging in another modality.

CLEM is a well-established technique for combining data from two distinct modalities to generate a composite view of the specimen (Ellisman et al. 2012). After more than 40 years of effort, CLEM is a highly evolved technique and commonplace in the literature. In CLEM, fluorescence microscopy data are used to locate specific features within the specimen, with EM/tomography providing detailed information on the cellular ultrastructure (Martone et al. 2000). A significant review of this procedure is beyond the scope of this manuscript. However, interested readers can find a wealth of information in the literature, including some stunning examples where ‘super-resolution’ fluorescence data are correlated with EM data from the same specimen (Kopek et al. 2012, Kopek et al. 2013). Kaufman et al. (2014) have also demonstrated the capability of using standard room temperature fluorescent proteins under cryogenic conditions.

Applying the concept of CLEM was a next logical step after the successful development of SXT. Of course, given SXT images cryopreserved specimens, the fluorescence imaging component must also be carried out at low temperature (Cinquin et al. 2014). If fluorescence microscopy were carried out at room temperature, and then the cell was frozen, the internal organisation would have time to change, perhaps even dramatically, making the combination of data moot (Smith et al. 2013). As a result, cells must be first cryopreserved and then imaged in both the SXM and the fluorescence microscope. Naturally, this requires the cell is to be maintained at low temperature throughout (McDermott et al. 2012a,b). Le Gros et al. addressed this need by developing a new, low-temperature microscope, more details of this work can be found here (Le Gros et al. 2009). In the interest of completeness, we will now give a very brief overview of this development.

The cryogenic light microscope images specimens at liquid nitrogen temperature, using liquid propane (refractive index, RI = 1.32) or iso-pentane (RI = 1.35) as an immersion fluid (Le Gros et al. 2009). Using RI-matched immersion fluid increases light collection efficiency by lowering the amount of light reflected at the interface between different RI (Le Gros et al. 2009). Collecting fluorescence data at cryogenic temperatures has several inherent advantages over room temperature. Firstly, the fluorescence emission spectra of many fluorophores are narrower at low temperature compared with room temperature (Smith et al. 2014a,b). Secondly, and perhaps more importantly, the average working lifetime of fluorescent proteins is extended by a factor of 30 or more at cryogenic temperatures (Moerner and Orrit, 1999). Longer working lifetime allows acquisition of many more images before the fluorescence becomes photo-bleached, and the signal is lost (Smith et al. 2013). This opportunity to collect more images opened up the possibility of adopting a tomographic approach to data acquisition, with the specimen being rotated around a central axis (Cinquin et al. 2014, Smith et al. 2014a,b, Elgass et al. 2015). Reconstructed fluorescence tomography data can achieve isotropic spatial resolution instead of the approximately threefold reduction in resolution that usually occurs along the optical axis (Heintzmann and Cremer, 2002). Tomographic fluorescence imaging, therefore, produces a 3D reconstruction of the fluorescence signal (McDermott et al. 2012a,b, Smith et al. 2014a,b). Since the high numerical aperture optics results in a shallowing of the depth-of-field, at each angular increment, a number of images were collected at varying focal lengths and deconvolved. The result was a deconvolution/tomographic data set that sampled information along the optical axis very well. The only challenge that remained was how to overlay the fluorescence and soft X-ray volumetric data accurately. Fortunately, fluorescence polystyrene beads are visible in both types of data. Simply by adding such beads to the specimen mount the two data types can be aligned independently, and coaligned with great accuracy and precision (Hagen et al. 2012, Smith et al. 2013, Cinquin et al. 2014, Duke et al. 2014, Hagen et al. 2014, Smith et al. 2014a,b, Elgass et al. 2015). As a result, correlated imaging using soft X-rays is the optimal way to locate the position of molecules within the context of a high-resolution 3D reconstruction of a cell and the cellular mesoscale (Figures 3A and 3B).

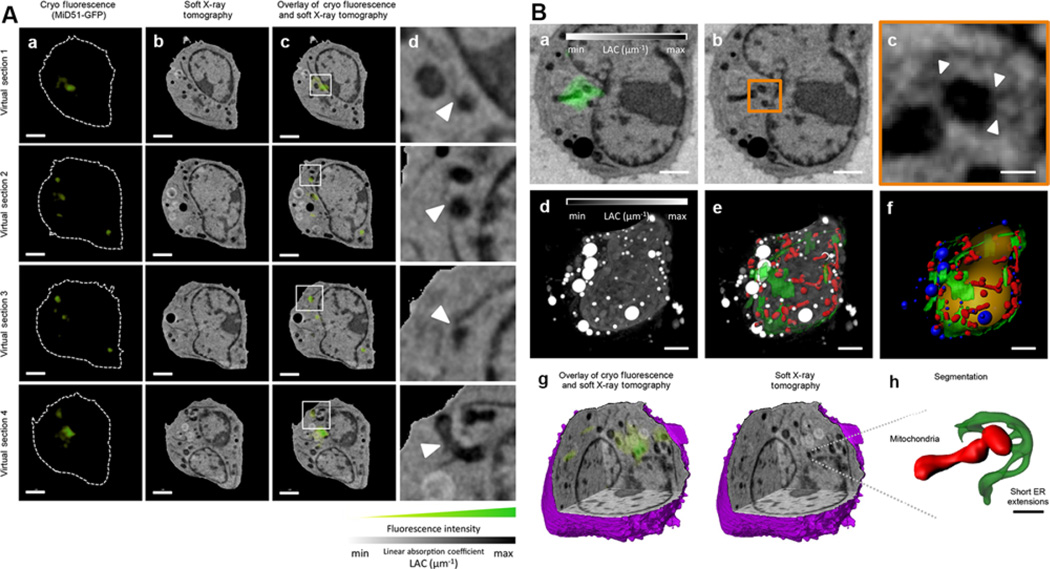
Figure 3. Recent example of correlated CFT-SXT.

Taken from Elgass et al. (2015) (A) (a) Fluorescence confocal slice, (b) virtual section of the SXT-generated reconstruction and (c) correlative CFT–SXT overlay are shown at four different planes, or virtual sections, within the cell volume. (d) The rightmost panels show magnifications of the boxed areas in c, which indicate ER–mitochondria contact sites that overlap with MiD51–GFP fluorescence foci (white arrowheads). Scale bars: 2 µm (a–c).

(B) (a) Two-dimensional computer-generated slice from a reconstruction of a mouse lymphoblastoid cell expressing MiD51–GFP (green), generated using correlated CFT–SXT. (b) The same computer-generated slice from the SXT reconstruction as presented in a without fluorescence overlay. The orange rectangle outlines the area of concentrated MiD51–GFP fluorescence. (c) Magnification of the area shown in a and b containing a concentration of MiD51–GFP. White arrowheads indicate positions of ER–mitochondria contact sites. (d) Maximum intensity projection of the full 3D SXT reconstruction with the contrast reversed so that features that are low-absorbing are shaded black and features that are highly absorbent are shaded white. (e) ER (green) and mitochondria (red) segmented out and overlaid with the reconstruction. (f) Surface-rendering of segmented cellular features, including the nucleus (orange), lipid droplets (blue), ER (green) and mitochondria (red). (g) Three-dimensional cutaway of the SXT-generated reconstruction reveals the same 3D location of the MiD51–GFP fluorescence of that shown in a. (h) Detailed view of small ER extensions contacting the mitochondria at the MiD51 foci. Scale bars: 2 µm (a, b, d–f); 400 nm (c); 1 µm (h).

Reckoning the cellular contents on the mesoscale

Different microscope techniques provide us with different types of information. Fluorescence microscopy, for example is typically used to identify sub-cellular structures based on the incorporation of fluorescent stains, or fluorescently tagged proteins onto the surface or localised to the interior of organelles (Shaner et al. 2005, Giepmans et al. 2006). However, the disadvantages of this technique are the inaccuracy in quantifying the labelled molecules or proteins of interest and the invisibility of cell contents surrounding the fluorescent labels (McDermott et al. 2012a,b). On the other hand, EM and SXT can produce detailed visuals of the cellular ultrastructure but cannot identify specific molecules without significant treatment of the cell. Consequently, a major challenge in microscopy in recent years has been building bridges between modalities that image cell structure and those that locate specific molecules. One recent success story in this regard was the combination of cryogenic fluorescence tomography (CFT) with SXT (Hagen et al. 2012, Smith et al. 2013, Cinquin et al. 2014, Duke et al. 2014, Hagen et al. 2014, Smith et al. 2014a,b, Elgass et al. 2015). The correlation of data from these two modalities effectively overcomes the constraints of each respective technique. For example, CFT–SXT combines detailed cellular context with molecular localisation data. Although fluorescence microscopy visually tracks molecules, it does not account for the compartmentalisation that exists in individual cells. For example, two fluorescently tagged molecules can appear to be in proximity but, in reality, are located in different cellular compartments.

Conclusions

You probably have vivid memories of your first time viewing living cells through a simple microscope. For most of us, this experience was a profound introduction to biological science, and firmly etched the power of microscopy in our mind. In addition to seeing external features of the cell, such as flagella, our first foray into imaging also revealed that cells, even relatively simple cells, have internal structure and organisation. As a nascent scientist, you probably wondered what all that stuff inside a cell is, and why it is moving? Is it the same in every cell? What does it all do? Questions like these still motivate biological scientists to this day, particularly since the answers have huge implications in areas such as human health. Of course, we do not mean to infer imaging the cell mesoscale is only just changing from a childhood fascination to fuelling medical insights and cures. As long ago as 1860, Lionel Beale used a basic microscope to observe variations in nuclear size and shape in cells from patients with cancer of the pharynx (Zink et al. 2004). More recently, George Papanicolaou established a staining technique that revealed the mesoscale nuclear and cytoplasmic changes due to cervical cancer (Zink et al. 2004). Visualising the mesoscale organisation of the nucleus using Papanicolaou’s technique has saved countless lives, and is still the ‘gold standard’ for detecting cervical cancer and pre-cancer via the well know ‘Pap test’ (DeMay 1996). Mesoscale imaging is, therefore, a major need in biology and medicine. At this point, you could argue ‘we have the Papanicolaou and similar stains that tell us everything we need to know about the nuclear mesoscale in cancer cells’. And to some limited extent, you would have a valid argument. However, basic staining only provides us with limited information – namely the global organisation of the sub-cellular entities that bind the stain. It does not tell us anything about the mesoscale organisation of the other cell contents, which may be a considerable fraction of the cell (McDermott et al. 2009, Ellisman et al. 2012). This is why techniques such as SXT are not just a nice addition to the cell biologist’s toolbox; they are a necessary addition. SXT images the entire mesoscale at a resolution commensurate with the smallest and largest objects in that spatial regime, that is to say, from larger than a molecular machine to the cell itself.

The latest generation of soft X-ray microscopes are ideally suited to imaging the cellular mesoscale. For soft X-ray imaging, cells are simply taken from their growth media or tissue explant, mounted on a grid or in a capillary, and instantly cryo-preserved. The cells are imaged intact, fully hydrated, and unstained (Parkinson et al. 2013, Do et al. 2015). The resultant images do not contain artefacts due to procedures such as sectioning, chemical fixation or dehydration.

As with simple light microscopes, the spatial resolution of a soft X-ray microscope image is determined by the objective lens. In the case of Fresnel objective lenses, the width of the outer zone dictates the maximum spatial resolution contained in an image of the specimen (Attwood 1999). Making such an X-ray microscope capable of imaging at higher resolution is conceptually simple, just install an objective with finer structuring in the outer zone. Today, soft X-ray microscopes are typically equipped with objectives that produce images with a spatial resolution of 35–50 nm (Le Gros et al. 2014). However, there are no technological reasons why the imaging resolution cannot be increased higher, due to recent improvements in nanoscale fabrication technologies (Chao et al. 2005, Chao et al. 2009, Chao et al. 2012). Taking advantage of higher resolution zone plates for imaging requires some developments, such as ensuring the microscope specimen stage is capable of collecting data at different focal lengths to overcome the shallower depth of field that comes with increased zone plate resolution. The depth of field of a 10 nm zone plate is in the region of 1–2 µm, smaller than most specimens of interest. Adopting a deconvolution with tomography approach to data collection allows thicker cells to be imaged in 3D with the full resolving power of the microscope.

The advantage of accessing the molecular level attenuation of X-rays comes at the cost of both an increased difficulty reconstructing the image and by possibly introducing radiation damage. In fact, the radiation dose is quite strongly linked to the resolution; the greater the resolution, the greater the dose. This general rule is difficult, if not impossible to circumvent our current understanding of signal processing and physics. However, there is optimism that techniques such as dose fractionation, developed for electron tomography (McEwen et al. 1995), can be applied to SXT equally effectively in the future. To get a certain minimally detected signal above the background noise needs a certain number (Weiß et al. 2000) of photons impinging on the specimen. In 2D it is not a major issue, certainly not compared with the 3D case where a significantly larger number of images are required.

In summary, SXT reconstructions of large cells contain information that spans the entire mesoscale. Of course, SXT alone does not address the functional aspect of the mesoscale organisation; that requires images from other imaging modalities together with data from other biochemical/biophysical techniques. Fluorescence microscopy is an excellent partner for SXT in correlated imaging experiments (this is equally true regarding correlated fluorescence with EM). Both SXT and CFT image the same cryopreserved specimen and do so with similar spatial resolution. Once the two types of data have been coaligned and accurately overlaid, CFT adds molecular identities to the sub-cellular features in a 3D SXT reconstruction of the cell. The combination of data allows unambiguous assignment of mesoscale structures, together with the position of molecular interactions in their cellular context. Naturally, an added benefit to imaging fluorescently is the ability to select particular cells by their fluorescence signatures and capture them using microfluidics or devices such as laser tweezers. Thus making it possible to compare rare, but highly significant, cellular phenotypes against the bulk cell population, for example, similar to the work described in Cruz-Adalia et al. (2014) andSherman et al. (2016).

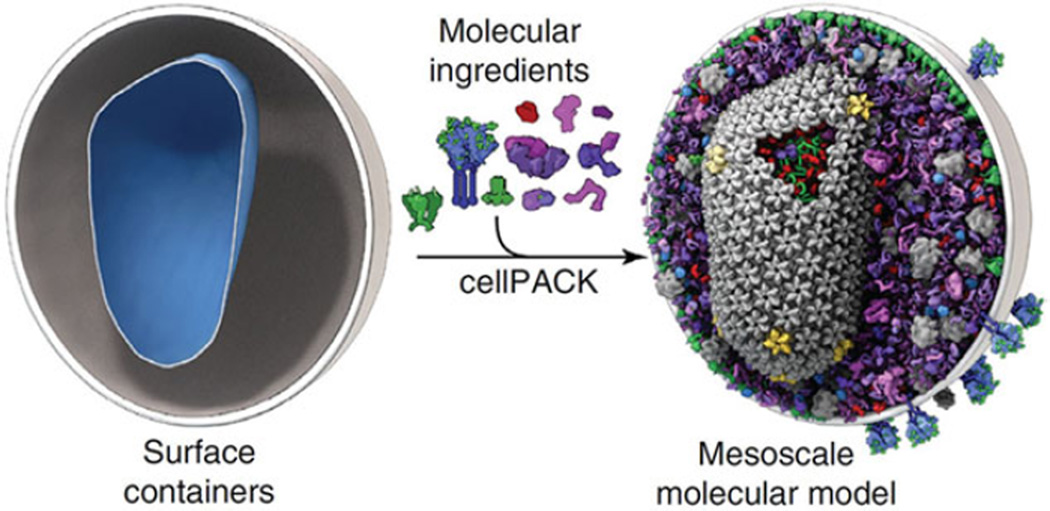
Looking towards the future, we can predict with confidence the direction mesoscale imaging will take. Biology occurs on a continuum of size scales, from atomic level interactions, through molecular to mesoscale, and then onto tissue scale and then organismal level. It is clear there are cause and consequence events that span this entire range. A single mutation in a protein can lead to cell dysfunction, which in turn causes tissue malfunction, eventually resulting in a disease. Imaging from an atomic/molecular level interaction up to a sick patient is an astronomic range of scale, more than 25 orders of magnitude difference in size. Although this is achievable by using a collection of imaging tools, we will focus on going from the atomic to the size of a single cell. We envision SXT and CFT being part of a story, where the complete narrative begins on the smallest scale by using macromolecular crystallography, NMR or single particle cryo-EM to image the atomic structure of molecules and assemblies up to the size of the molecular machines. Ultra-high resolution structural motifs, imaged by EM, NMR or X-ray crystallography can be localised using cryogenic fluorescence and combined with a SXT mesoscale reconstruction of the cell. This concept was envisioned in a paper by Johnson et al. (2015) describing the software package cellPACK (Figure 4). The advent of high specimen throughput correlated cryo-fluorescence with SXT makes this vision not just a possibility, but a reality.

Figure 4. A comprehensive view of the mesoscale.

Image taken from Johnson et al. (2015) shows the potential end-result of merging various types of data with a SXT mesoscale reconstruction of a cell.

Abbreviations

CFT

cryogenic fluorescence tomography

CFT–SXT

correlated cryo-fluorescence and soft X-ray tomography

CLM

cryo-light microscope

CLEM

correlated light and electron microscopy

EM

electron microscopy

FBP

Filtered Back Projection

LAC

linear absorption coefficient

NMR

nuclear magnetic resonance

RI

refractive index

SXM

soft X-ray microscopy

SXT

soft X-ray tomography

TEM

transmission electron microscope.