Molecular dynamics simulations of spontaneous fibril formation by random-coil peptides

Abstract

Assembly of normally soluble proteins into amyloid fibrils is a cause or associated symptom of numerous human disorders, including Alzheimer's and the prion diseases. We report molecular-level simulation of spontaneous fibril formation. Systems containing 12-96 model polyalanine peptides form fibrils at temperatures greater than a critical temperature that decreases with peptide concentration and exceeds the peptide's folding temperature, consistent with experimental findings. Formation of small amorphous aggregates precedes ordered nucleus formation and subsequent rapid fibril growth through addition of β-sheets laterally and monomeric peptides at fibril ends. The fibril's structure is similar to that observed experimentally.

The pathological manifestation of the so-called amyloid diseases, including Alzheimer's, Parkinson's, and the prion diseases, is the slow coming together of specific proteins to form fibrillar plaques or tangles rich in β-sheet structure (1-3) within a specific organ in the body. Although progress toward understanding the molecular-level mechanisms driving protein fibrillization has been made through in vitro studies of particular proteins, concomitant atomic-resolution computer simulation studies have been impossible due to the large system sizes required and the long timescales involved. As a consequence, to date, most atomic-resolution simulation studies of spontaneous fibril formation (4-8) have been limited to consideration of small model systems containing only a few peptides, too small to model the nucleation and subsequent growth of the large β-sheet complexes that are observed in experiments. Recent suggestions (1, 9, 10), however, that fibrils are stabilized by forces common to all proteins, hydrophobic interactions and backbone hydrogen bonding, and not by forces particular to a specific sequence imply that: (i) progress toward understanding the etiology of the various amyloid diseases can be made by examining the fibrillization of systems containing model proteins that are less complex than the specific amyloidogenic protein, and (ii) in silico examination of fibril formation is possible using low- to- intermediate-resolution protein models provided that such models faithfully capture the essential features of protein geometry, hydrophobicity, and hydrogen bonding. We have developed an intermediate-resolution protein model to meet the latter requirements.

In this work, we simulate the formation of fibrils using an intermediate-resolution protein model originally introduced by Smith and Hall (11), which we now call PRIME (Protein Intermediate-Resolution Model). PRIME is simple enough to allow the simulation of multiprotein systems over relatively long timescales yet contains sufficient detail to mirror real protein dynamics when used with discontinuous molecular dynamics (DMD), a fast alternative to conventional molecular dynamics. We are able to simulate the spontaneous formation of fibrils in systems containing up to 96 16-residue alanine-based peptides starting from the random-coil state. PRIME is an off-lattice unbiased implicit-solvent protein model based on a four-sphere united atom representation (three backbone spheres and one side-chain sphere) with realistic bond lengths and bond angle constraints; it has the ability to interact both intra- and inter-molecularly via hydrogen bonding and hydrophobic interaction potentials. This model was designed for use with DMD (12), a variant of traditional molecular dynamics that is applicable to systems of molecules interacting via discontinuous potentials, e.g., hard-sphere and square-well potentials. The great speed of this algorithm allows us to sample much wider regions of conformational space, longer timescales, and larger systems than in traditional molecular dynamics. The model peptide chosen for study is the polyalanine peptide Ac-KA₁₄K-NH₂, which has been shown by Blondelle and coworkers (13, 14) to undergo a transition from α-helical structures to β-sheet complexes in vitro. Because these simulations take only days on a workstation, we are able to conduct runs at a wide variety of concentrations and temperatures and thereby explore how peptide concentration and temperature affect the formation of various Ac-KA₁₄K-NH₂ structures including α-helices, β-sheets, amorphous aggregates, and fibrils.

Three types of simulations are performed, each highlighting a different aspect of the fibrillization process. (i) Slow-cooling simulations allow us to explore the exquisite sensitivity of fibrillization on system temperature and peptide concentration; in these simulations, a system of random coils equilibrated at a high temperature is cooled very slowly to the temperature of interest to minimize kinetic trapping in local free energy minima. (ii) Constant-temperature simulations give us the best opportunity to monitor fibrillization dynamics; in these simulations, a system of random coils equilibrated at a high temperature is quickly cooled to the temperature of interest and then monitored over time. (iii) Seeded constant-temperature simulations allow us to support the hypothesis that fibrillization is a nucleated process; in these simulations, a previously created single fibril is immersed in a sea of denatured chains and then monitored over time.

Methods

Model Peptide and Forces. The model peptide sequence PH₁₄P, where H and P are hydrophobic and polar amino acid residues, respectively, was chosen to mimic Ac-KA₁₄K-NH₂ peptides, which have been found to form stable soluble β-sheet complexes in vitro (13, 14). The geometry of the PRIME protein model is illustrated in Fig. 1. Each amino acid residue is composed of four spheres: a three-sphere backbone comprised of united atom NH, C_αH, and CO, and a single-bead sidechain R (CH₃ for alanines). Ideal backbone bond angles, C_α—C_α distances, and residue l-isomerization are achieved by imposing pseudobonds, as shown in Fig. 1. Details of the model are given in our earlier papers (11, 15, 16).

Fig. 1.

Geometry of the intermediate-resolution protein model, PRIME, for polyalanine. Covalent bonds are shown with gray lines connecting united atoms. At least one of each type of pseudobond is shown with a color line. Pseudobonds are used to maintain backbone bond angles, consecutive C_a distances, and residue l-isomerization. The united atoms are not shown full size for ease of viewing.

All forces are modeled by either hard-sphere or square-well potentials to ensure compatibility with DMD. The solvent is modeled implicitly; its effect is factored into the energy function as a potential of mean force. The excluded volumes of the four united atoms are modeled by using hard-sphere potentials with realistic diameters. Interactions between hydrophobic sidechains are represented by a square-well potential of depth ε_HP; interactions between polar sidechains or between polar and hydrophobic sidechains are represented by a hard-sphere interaction. Hydrogen bonding between amide hydrogen atoms and carbonyl oxygen atoms is represented by a directionally dependent square-well attraction of strength ε_HB between NH and CO united atoms. The strength of a hydrophobic contact, ε_HP, is fixed at 1/10th the strength of a hydrogen bond, ε_HB.

DMD. Simulations are performed by using the DMD simulation algorithm (12, 17-19), an event-driven variant of traditional molecular dynamics applicable to systems of molecules interacting via discontinuous potentials, e.g., hard-sphere and square-well potentials. Unlike soft potentials such as the Lennard-Jones potential, discontinuous potentials exert forces only when particles collide, enabling the exact (as opposed to numerical) solution of the collision dynamics. For details on DMD simulations, see papers by Alder and Wainwright (12) and Smith, Hall, and Freeman (20).

Simulations are performed in the canonical ensemble with periodic boundary conditions imposed to eliminate artifacts due to box walls. Constant temperature is achieved by implementing the Andersen thermostat method (21). Simulation temperature is expressed in terms of the reduced temperature, T^* = k_BT/ε_HB, where k_B is Boltzmann's constant, and T is the temperature. Reduced time is defined to be t^* = t/σ(k_BT/m)^1/2, where t is the simulation time, and σ and m are the average bead diameter and mass, respectively.

The slow-cooling simulations are started from a random coil configuration equilibrated at high temperature and then cooled to the temperature of interest (T^* = 0.08-0.15) to minimize kinetic trapping. The peptide concentrations considered are c = 0.5, 1, 2.5, 5, 10, and 20 mM. Although simulations are conducted on systems containing 12, 24, 48, and 96 peptides, most of our analysis focuses on the 48-peptide system. These simulations take between 40 h for 8 billion events at T^* = 0.08 and 160 h at T^* = 0.15 for 32 billion events on a single processor of an AMD (Beckeln, Germany) Athlon MP 2200+ workstation.

The unseeded constant-temperature simulations are started in a random coil configuration equilibrated at high temperature and then quickly cooled to the temperature of interest, T^* = 0.08-0.15. In the seeded constant-temperature simulations, 48 denatured chains are added randomly to a simulation box containing a fibrillar structure taken from the end of a previous unseeded 48-peptide simulation at c = 1.0 mM and T^* = 0.13. The resulting 96-peptide system at c = 2.0 mM is quickly heated to T^* = 0.14 and maintained there for 32 billion events.

The results presented in this paper are averages from at least 10 simulations at each temperature and concentration with error bars taken from the standard deviations at each time. The structures are defined in the following way. If 12 intrapeptide α-helical hydrogen bonds (bonds between N_i+4 and C_i) are formed, the structure is an α-helix. If each peptide in a group of peptides has at least seven interpeptide β-hydrogen bonds to a particular neighboring peptide in the group, this group is a β-sheet. If at least two β-sheet structures form intersheet hydrophobic interactions (at least four hydrophobic interactions per peptide per β-sheet), and the β-sheet structures are at an angle <35°, this is a fibril; otherwise, this and isolated β-sheets are classified as nonfibrillar β-sheet structures. If each peptide in a group of peptides has at least two interpeptide hydrogen bonds or hydrophobic interactions with a neighboring peptide in the same group, that group is an aggregate. Aggregates that are not fibrils or nonfibrillar β-sheets are amorphous aggregates. Single-peptide structures that are not α-helices or β structures are random coils.

Results

Fibril Formation Is Preceded by the Formation of Amorphous Aggregates. The initial formation of a small fibril (or protofilament) in our simulations involves a process in which the appearance of fluid-like amorphous aggregates precedes the appearance of β-sheets and then of a fibrillization nucleus. Fig. 2 shows snapshots of the fibrillization process taken at various reduced times, t^*, for the 48-peptide unseeded constant-temperature simulation at T^* = 0.14 and a peptide concentration of c = 10 mM. Starting in random coil conformations at reduced time t^* = 0, the chains begin to form small amorphous aggregates almost immediately. These amorphous aggregates have grown by t^* = 10.0 and have collapsed into one big amorphous aggregate by t^* = 12.0. This big amorphous aggregate disperses by t^* = 14.6 into smaller aggregates, one of which is a two-peptide β-sheet (Fig. 2 Middle Left, purple sheet at the middle right side of the box). By t^* = 36.1, the other amorphous aggregates have converted into three three-peptide β-sheets (Fig. 2 Middle Center, light-blue sheet in box middle, white sheet behind light-blue sheet, and dark-blue sheet in upper right corner); in addition, the purple sheet has grown into a six-peptide β-sheet. By t^* = 40.2 (Fig. 2 Middle Right), the light-blue sheet has associated with the white sheet, creating a two-sheet fibrillar structure. By t^* = 49.7 (Fig. 2 Bottom Left), this two-sheet fibrillar structure has been joined by the purple and dark-blue sheets, the latter of which is at an oblique angle. By t^* = 92.7 (Fig. 2 Bottom Center), the dark-blue sheet has realigned itself, docking to create a four-sheet fibril, which itself has grown by adding peptides to the ends of the β-sheets. Even after a long equilibration time, t^* = 205.9 (Fig. 2 Bottom Right), the fibrillar structure remains stable and grows by adding more peptides to the ends of the β-sheets.

Fig. 2.

Snapshots of the 48-peptide system at various reduced times, t^*, during a simulation (see Movie 1, which is published as supporting information on the PNAS web site) at c = 10 mM and T^* = 0.14 that results in a fibril. Hydrophobic sidechains are red; colors of backbone atoms on different peptides are assigned to make it easy to distinguish the various sheets in the resulting fibril. United atoms are not shown full size for ease of viewing.

The fibrillization process just described is typical of most of our simulations at different peptide concentrations and temperatures. In the beginning, the denatured peptide system stays in a lag phase, during which some amorphous aggregates form. These aggregates then convert into small β-sheets containing aligned β-strands. The sheets eventually align one by one, creating a small fibril, which grows gradually into a longer fibril. These features are reminiscent of the nucleation steps seen by Serio et al. (22), who observed that yeast prion protein Sup35 forms small amorphous aggregates containing 20-80 protein monomers followed by critical nuclei and finally by rapid growth of large fibrils. The amorphous aggregates seen in our simulations may be akin to the micelles observed by Glabe and coworkers (23) during the initial formation of Aβ fibrils; in that case, the micelles were thought to mediate the nucleation events by producing a high local concentration of Aβ peptides. Disordered aggregate formation may also precede fibril formation in Alzheimer's and light chain diseases (24).

Fibril Growth Proceeds by Both β-Sheet Elongation and Lateral Addition. There are two fibril growth mechanisms in our simulations: β-sheet elongation, in which the fibril grows by adding individual peptides to the end of each β-sheet, and lateral addition, in which the fibril grows by adding already-formed β-sheets to its side. Both mechanisms are seen in the snapshots in Fig. 2. Initially, the fibrils are relatively small, containing two β-sheets, each consisting of two peptides. The number of β-sheets per fibril increases over time, indicating that already-formed β-sheets are being added to the fibril's side. In addition, the number of peptides per β-sheet increases gradually with time, indicating that peptides are being added to the ends of each β-sheet, thereby lengthening the fibril along the fibril axis. Even after the fibril reaches its final size of four β-sheets and the number of β-sheets per fibril remains constant, the number of peptides per β-sheet per fibril continues to increase from six to nine peptides. When the number of peptides that are added to the fibril via either the β-sheet elongation or lateral addition mechanism over time is plotted (not shown), both mechanisms are found to play equally important initial roles in fibril growth. However, once the fibril structure contains six β-sheets, the β-sheet elongation mechanism takes over. These two growth mechanisms, which are characteristic of all our simulations, are similar to those observed in experiments by Green et al. (25), who found two distinct phases in human amylin fibrillogenesis where lateral growth of oligomers is followed by longitudinal growth into mature fibrils.

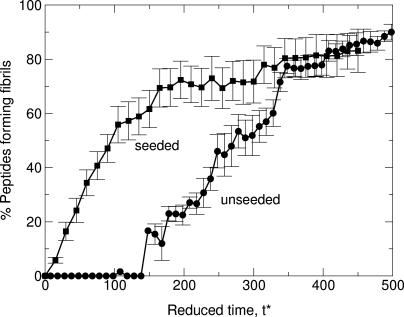
Fibril Formation Is Nucleation-Dependent. Fibril formation in our simulations involves a nucleation event, as has been suggested in the experimental literature (21, 26-28). Evidence for this comes from our seeded simulations, which show that denatured chains exposed to a previously created fibril add to the fibril immediately, bypassing the slow fibril nucleation step. Fig. 3 plots the percentage of the 48 initially random-coil peptides inserted into the seeded system that become attached to the fibril seed (resulting in fibril growth) as a function of the reduced time, t^*, at c = 2.0 mM and T^* = 0.14. For comparison, the percentage of peptides in fibrils during the unseeded 96-peptide simulations at the same condition is also plotted. The lag time for fibril formation from the unseeded simulations is ≈135 reduced time units compared with a lag time of zero for fibril formation in the seeded simulations.

Fig. 3.

The percentage of peptides in fibril structures versus reduced time, t^*, in the seeded and unseeded simulations at c = 2.0 mM and T^* = 0.14.

Fibril Formation Is a Function of Temperature and Peptide Concentration. The populations of α-helices and fibrils depend strongly on temperature and peptide concentration, as shown in Fig. 4, which plots the percentage of peptides at the end of those 48-peptide slow-cooling simulations in which these structures are formed versus the temperature at different peptide concentrations, c. Fig. 4a shows that the percentage of peptides that form α-helices (the Ac-KA₁₄K-NH₂ native state) decreases with increasing concentration and ceases at concentrations ≥5 mM. At c <5 mM, there is an optimal temperature range for forming α-helices centered about a maximum at T^* = 0.09. At lower temperatures, the system is kinetically trapped and forms either nonfibrillar β structures or amorphous aggregates. At higher temperatures, the driving force for α-helix formation diminishes and disappears at the isolated chain's folding temperature, T^* = 0.11. Fibril formation is seen primarily at high temperatures and high concentrations, as indicated in Fig. 4b. At high concentrations, c = 5, 10, and 20 mM, fibril formation increases as the temperature increases up to T^* = 0.13 and then decreases. The maximum in the percentage of peptides in fibrils as a function of temperature broadens and shifts to lower temperatures as the concentration is increased from c = 5 mM to 20 mM. This observation reveals that the critical temperature for forming fibrils decreases with increasing peptide concentration.

Fig. 4.

The percentage of peptides in α-helices (a) and fibrils (b) versus the reduced temperature T^* at different peptide concentrations: 0.5 mM (black circles), 1.0 mM (red circles), 2.5 mM (green diamonds), 5 mM (blue triangles), 10 mM (purple triangles), and 20 mM (orange triangles).

The results described above agree qualitatively with the experimental findings of Blondelle and coworkers (13, 14) on Ac-KA₁₄K-NH₂ peptides, that the critical fibril formation temperature decreases with peptide concentration. They observed monomeric α-helical structures at low concentrations (100 μM) and temperatures (25°C). As the peptide concentration increased to 1 mM, β-sheet complex formation increased with increasing temperature, exhibiting an S shaped dependence on temperature with a critical temperature of 65°C. As the peptide concentration increased to 1.8 mM, the critical temperature at which β-sheet complexes started to form decreased to 45°C.

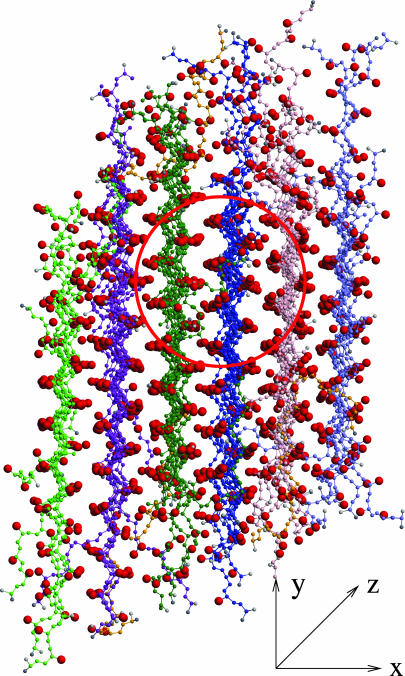
Fibril Structure. The fibrils observed in our simulations mimic the structural characteristics of fibrillar aggregates currently described in the literature. Most peptides within a β-sheet on simulated fibrils are arranged in a parallel orientation. The percentage of peptides whose C terminus is on a particular side of its β-sheet in the fibril (with the N terminus on the other side) relative to the total number of peptides in all β-sheets in the fibril is 93.3 ± 5.7%. In addition, adjacent peptides within each β-sheet are usually in register, as has been observed in experiments on fibrils formed by β-amyloid proteins (29-31). A snapshot of the 96-peptide fibril formed at c = 5.0 mM and T^* = 0.13 is shown in Fig. 5; it reveals that the alanine sidechains within a particular β-sheet (e.g., green sheet in red circle) are aligned (stacked on top of one another in Fig. 5) and alternate from one side of the sheet to the other. Alanine sidechains on an adjacent sheet (e.g., dark-blue sheet) also alternate from side to side but shift so that they fit into the “pockets” on the neighboring sheet. The peptides in our fibrils are almost fully extended, with an average end-to-end distance of 40.81 ± 4.76 Å), which can be compared with 51.24 Å for the completely stretched-out peptide conformation and 29.05 ± 0.39 Å) for a random-coil conformation.

Fig. 5.

A close-up snapshot of the 96-peptide fibrillar structure formed at c = 5.0 mM and T^* = 0.13 viewed down the fibril (z) axis.

The β-sheets in the fibrillar structures resulting from our simulations are stabilized primarily by intrasheet backbone-backbone hydrogen bonds and secondarily by intrasheet hydrophobic interactions, all running parallel to the length of the sheet. These intrasheet hydrophobic contacts are a consequence of the tight packing in the complex and serve to lower its overall internal energy. The adjoining β-sheets are held together by intersheet sidechain-sidechain hydrophobic interactions oriented nearly perpendicular to the length of the sheet.

The packing of fibrillar structures mimics the close packed sheets found in experiments on a variety of peptides (26, 32, 33). The typical fibrillar complex in our simulations is a dense ordered structure with tightly packed side chains. The average intrasheet C_α—C_α distance is 5.05 ± 0.07 Å, which is slightly larger than the experimentally determined value of 4.7-4.8 Å for close-packed sheets of different peptides (26, 32, 33). In addition, the average intersheet C_α—C_a distance is 7.5 ± 0.5 Å, which is comparable to the low end of the experimental values of 8-10 Å for transthyretin fragments (34) and significantly smaller than the experimentally determined value of ≈9-10 Å for close-packed sheets of Alzheimer's peptides (26, 32, 33). This difference is not surprising, because both transthyretin fragments and β-amyloid peptides have big bulky sidechains, whereas our model peptides consist mostly of alanine residues, which are among the smallest of sidechains.

The fibrils in our simulations contain four to six sheets, depending upon the system size. As the system size is increased from 12 to 24, 48, and 96 peptides, the number of β-sheets asymptotes to a value near six. Once the fibrillar structure reaches its critical β-sheet number, monomeric peptides tend to attach to the ends of the fibrillar structure rather than create a new β-sheet. The number of sheets per fibril that we observe is similar to that in real fibrils, which tend to contain four to six β-sheets, but with 1,000 or more peptides per sheet (33, 35-37).

Conclusion

We hope to have convinced the reader that computer simulations offer unique opportunities to observe and analyze molecular-level events in the protein fibrillization process that are difficult or impossible to observe experimentally. By combining the very fast DMD technique with our intermediate-resolution protein model, PRIME, we have been able to simulate the spontaneous formation of fibrils in large systems of polyalanine peptides starting from the random-coil state. Polyalanine was chosen for this study because it is the simplest peptide known to form fibrils; its simple sidechain structure makes it relatively easy to model. Our simulations support the notion that fibril formation at concentrated conditions is a direct consequence of the interplay between backbone hydrogen bonding, hydrophobic interaction, and protein geometry (1, 9). As a result of this research, we have come to think that the question to be asked is not why some proteins form fibrils but rather why more proteins do not form fibrils. We have been able to quantify the conditions that promote fibrillization by examining fibril formation at a variety of temperatures and peptide concentrations. Our simulation method allows the direct observation (via snapshots taken from simulation videos) of peptide configurations during the fibril assembly process, which is of course impossible in experiment. The results we have presented on the thermodynamics and kinetics of fibril formation and on fibril structure are in good qualitative agreement with experiments on many proteins (13, 14, 22, 25-28).

It is important to point out that our model and analysis are subject to a number of limitations. First, we do not include charged residues at the ends of the model peptide chains, which have been shown to be important in experimental systems for reducing amorphous aggregation and precipitation. Second, it is possible that a more elaborate model force field is required to adequately represent peptides and their environment. Specifically, we have neglected solvent effects by incorporating solvent as a potential of mean force mainly in the form of the hydrophobic interactions between nonpolar sidechains. The strength of the hydrophobic interactions plays an important role in fibrillization. When the strength of the hydrophobic interaction is relatively weak, between 1/10th and 1/8th the strength of the hydrogen bonding, fibrils are formed. As the strength of the hydrophobic interactions increases from 1/10th or 1/8th to 1/6th the strength of the hydrogen bond, hydrophobic interactions prevent peptides from forming fibrils; instead, amorphous structures are formed.

Based on this initial success in simulating the formation of fibrils, we believe that computer simulation is now on the brink of becoming a creditable partner with experiment in efforts to identify the sources of fibril stability and better understand the fundamental mechanisms driving fibril formation, information vital to the rational design of therapeutic strategies in amyloid diseases.