Earthquake rates in Oklahoma should significantly decrease by the end of 2016 and approach historic levels within the next years.
Keywords: Earthquake forecasting, induced seismicity, saltwater injection, seismic hazard
Abstract
In response to the marked number of injection-induced earthquakes in north-central Oklahoma, regulators recently called for a 40% reduction in the volume of saltwater being injected in the seismically active areas. We present a calibrated statistical model that predicts that widely felt M ≥ 3 earthquakes in the affected areas, as well as the probability of potentially damaging larger events, should significantly decrease by the end of 2016 and approach historic levels within a few years. Aftershock sequences associated with relatively large magnitude earthquakes that occurred in the Fairview, Cherokee, and Pawnee areas in north-central Oklahoma in late 2015 and 2016 will delay the rate of seismicity decrease in those areas.
INTRODUCTION
In 2015, approximately 900 widely felt M ≥ 3 earthquakes occurred in north-central Oklahoma (1). Before 2009, about one M ≥ 3 earthquake occurred in Oklahoma on average each year (Fig. 1). It is now widely recognized that this almost 900-fold increase is related to widespread disposal of saltwater that is being coproduced with oil in the seismically active areas (2–5). Most of the oil wells in Oklahoma produce more water than oil. Because the produced water is too saline to be put to beneficial use, it is usually recycled back into the producing formation as part of water flooding operations. However, in the past few years, extremely large volumes of produced saltwater were injected into the highly permeable Arbuckle group (Fig. 2). This formation is in hydraulic communication with faults in the crystalline basement, where natural geologic processes have accumulated stress on preexisting faults (4). The increase in pressure resulting from injection reduces the frictional resistance to sliding and can trigger the release of the accumulated stress in earthquakes. Although this basic physical mechanism is well understood (6–8), the evolving short-term earthquake hazard is difficult to forecast or manage (9).
Fig. 1. Tectonic and induced earthquakes (M ≥ 3) in Oklahoma (1979 to September 2016).
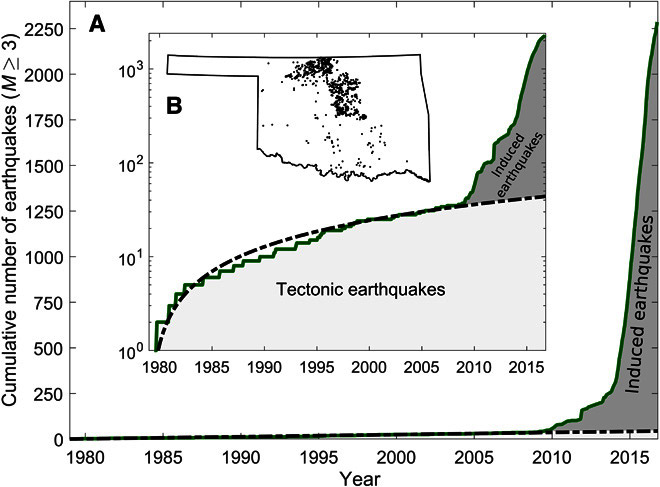
The cumulative number of earthquakes is presented in linear (A) and logarithmic scales (B). The map shows the epicenters of the earthquakes in Oklahoma. In 2009, the cumulative number of earthquakes (M ≥ 3) (green line) starts to exceed the constant tectonic earthquake activity (black dashed line). All earthquakes that are inconsistent with a constant tectonic background rate are classified as induced earthquakes (gray shaded area).
Fig. 2. Saltwater disposal and earthquakes in Oklahoma.
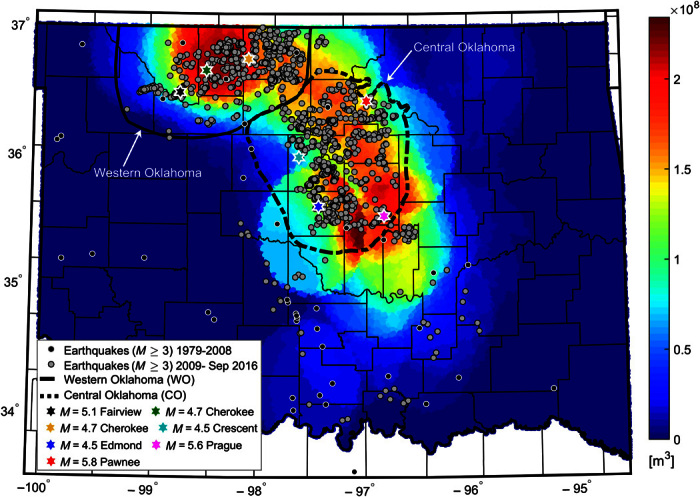
The background color shows the cumulative volume (m3) of saltwater injected into the Arbuckle formation between 2009 and December 2015 in different areas of Oklahoma. The saltwater injection volume has been calculated within a radius of 0.5° around a given location on the map and is plotted at the center of the areas (≈8000 km2). Historic earthquakes (1979–2008) are shown as black circles, and recent earthquakes (2009 to September 2016) are presented as gray circles. Areas affected by volume reductions mandated in February and March 2016 are shown as solid (WO) and dashed (CO) lines, respectively. Colored stars show the locations of recent M ≥ 4.5 earthquakes (see main text and table S1).
In response to the marked increase in seismicity since 2009, in February and March 2016, Oklahoma regulators called for a 40% reduction in the injection volume for 2016 compared to the volume injected in 2014 (10, 11). The directives affect two large areas in north-central Oklahoma (Fig. 2). Operators were requested to complete the injection rate reduction by the end of May 2016. Here, we present a statistical model of injection-related seismicity in Oklahoma that links changes of saltwater injection rates to seismicity rates. As described below, the model is based on an approach developed to evaluate fluid injection–induced earthquakes at geothermal and hydrocarbon reservoirs that are usually associated with a single injection well (12–16). By adapting this model to hundreds of large-volume injection wells and thousands of injection-related earthquakes in Oklahoma, we first calibrate the model with the observed earthquakes and reported injection volumes in the areas covered by the directives and then go on to predict how induced seismicity in Oklahoma will respond to the mandated injection rate reduction.
RESULTS
Relating earthquake rates to injection rates
As shown in Fig. 1, seismicity in north-central Oklahoma began to increase rapidly in 2009. For the purpose of this analysis, we classify all earthquakes that are not consistent with a constant tectonic background rate as induced earthquakes. The number of induced earthquakes increases almost exponentially, with about 2250 induced M ≥ 3 earthquakes recorded by the end of September 2016. The strain energy release of the past 8 years is the equivalent of more than 1900 years of naturally occurring energy. The total number of the induced earthquakes in Oklahoma is far above any other documented cases of induced seismicity (17). The volume of injected saltwater is correspondingly much larger than the injected fluid volumes for any other cases. The three largest earthquakes that have occurred to date are the M = 5.6 earthquake near Prague in November 2011, the M = 5.1 event in the Fairview earthquake sequence that occurred in February 2016, and the recent Pawnee M = 5.8 earthquake in September 2016. The Pawnee M = 5.8 event is the largest earthquake in instrumented history in Oklahoma. A M = 5.8 earthquake is only slightly below the maximum magnitude (Mmax = 6) expected during 1900 years of tectonic background activity (see fig. S1).
Almost all recent M ≥ 3 earthquakes in Oklahoma have occurred where very large volumes of saltwater have been injected into the Arbuckle group (see Fig. 2). The number of earthquakes outside the area of high-volume injection in north-central Oklahoma is generally consistent with the tectonic background activity. It suggests that the distance over which injected fluids have affected surrounding faults is limited to the size of the areas analyzed in Fig. 2 (≈50-km radius around a well). Although there are a number of recent earthquakes in south-central Oklahoma, the saltwater injection rate there has been appreciable (20 million m3 to 30 million m3 within areas of ≈8000 km2), albeit much less than the injection rates in north-central Oklahoma, which are as large as 200 million m3 within areas of ≈8000 km2.
We restrict our analysis to the two areas covered by the February and March directives (10, 11) as western (WO) and central (CO) Oklahoma (Fig. 2). These regions have been defined by the Oklahoma Corporation Commission on the basis of the large number of earthquakes that occurred in the last few years. Each region covers approximately 13,000 km2. Combined, the two areas contain almost all recent earthquakes. Figure 3 presents the combined monthly saltwater injection and M ≥ 3 earthquake rates in WO and CO. The “spikes” of earthquake activity are usually associated with aftershocks of relatively large magnitudes, such as the Prague, Fairview, and Pawnee earthquakes. In the Supplementary Materials, we present earthquake and injection rates separately for WO and CO (figs. S2 and S3).
Fig. 3. Combined monthly Arbuckle saltwater injection and induced earthquake rate in CO and WO.
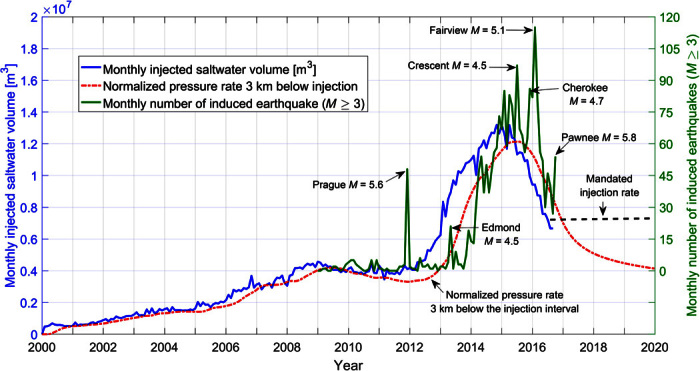
Monthly Arbuckle saltwater injection (2000 to July 2016) (blue line) and earthquake rate (2009 to September 2016) (green line). Earthquake rate changes follow changes of the injection rate with a time delay of several months. Aftershock sequences are visible in the monthly earthquake rates for the largest magnitudes. The red dashed line shows the normalized pressure rate, which arrives delayed at a depth of 3 km below injection (the average depth of the earthquake hypocenters) (see the Supplementary Materials for more details).
The monthly volume of produced saltwater injected into the Arbuckle formation steadily increased from 2001 to 2009, followed by a phase of approximately constant injection through the end of 2011 (see Fig. 3). Note that, before 2012, almost all saltwater was injected in CO (fig. S2). Monthly saltwater injection rates in WO did not exceed 1 million m3 before 2012 (fig. S3). However, in 2012, the rate of saltwater injection markedly increased in both areas because of large-scale production from several oil reservoirs with unusually high water/oil ratios (4). As oil prices began to markedly decline in late 2014, saltwater injection rates started to decrease significantly in early 2015.
It is important to note that Fig. 3 illustrates a lower threshold of monthly injection rates below which no M ≥ 3 earthquakes were triggered in the noted areas. Almost all earthquakes, with the exception of the Prague sequence in the southeastern corner of CO, occur after the saltwater disposal volume markedly increased throughout CO and WO in early 2012. As shown in Fig. 3, there is a delay of several months between the increase of saltwater disposal volume and earthquake activity. This time delay makes physical sense and corresponds to the time the pressure increase takes to propagate from the injection wells in the Arbuckle group to the critically stressed faults in the crystalline basement (4). A time lag of several months between the injection of fluid and the occurrence of earthquakes is not unexpected. It has been observed in cases of earthquakes associated with reservoir impoundment that time lags of several years between impoundment of the reservoir and earthquake occurrence are common (18). The time lag observed in Oklahoma is controlled by factors such as the distance between injection intervals and preexisting faults in the crystalline basement, the permeability of the Arbuckle group and the crystalline basement, as well as the pressure increase needed for fault reactivation.
The red dashed line in Fig. 3 shows the normalized pressure rate 3 km below the injection interval [corresponding to the average depth of the earthquake hypocenters (19)]. It has been computed according to three-dimensional diffusion and reported saltwater injection rates for all Arbuckle injection wells in CO and WO (see the Supplementary Materials for details). The shape of the pressure rate is similar to the injection but delayed by several months due to the time pressure takes to diffuse down from the injection wells.
In summary, we observe that seismicity markedly increases in 2013 throughout CO and WO, several months after the abrupt increase in saltwater disposal. At this point, we have made no attempt to remove aftershocks, or “decluster” the seismicity catalog (20), to avoid accidentally introducing any artifacts into the data. In the next section, we present a statistical model of injection-related seismicity in Oklahoma that links changes of saltwater injection rates to seismicity rates.
A seismic hazard model for Oklahoma based on saltwater injection rates
The classical magnitude/frequency (Gutenberg-Richter) relation has been modified for fluid injection–induced earthquakes at hydrocarbon and geothermal reservoirs to relate the expected cumulative number N≥M(t) of earthquakes above magnitude M induced until the time t to the cumulative injected fluid volume VI(t) (12)
| (1) |
In this equation, a and b are the a and b values of the Gutenberg-Richter law (21), and Σ is termed the seismogenic index (SI). Fundamentally, the SI incorporates the volume concentration of preexisting faults and the state of stress (termed the seismotectonic state) (14). In contrast to the Gutenberg-Richter relation associated with natural earthquake sequences, Eq. 1 does not assume stationarity of the a value (as typically used in probabilistic hazard analysis) but relates changes of earthquake activity in time to changes of the fluid injection rate in the crustal volume affected by the injection: a(t) = log10[VI(t)] + Σ. In agreement with the conceptual model of other studies analyzing induced seismicity in Oklahoma (2–5), Eq. 1 has been derived from the understanding that induced seismicity is triggered by pore pressure diffusion in the pore and fracture space of rocks from the injection wells to preexisting faults near failure.
Equation 1 states that both the injected fluid volume and the seismotectonic state of the affected region determine the seismogenic response to the fluid injection rate. Whereas temporal changes of seismicity are described by changes of the injection volume, the SI quantifies the number of earthquakes induced by injection for a unit volume of fluid. It has been shown that Σ is constant over time at single injection sites but varies from one region to another (12, 15, 16). The SI can be computed from observations of injection volume and seismicity. This means that, once calibrated for a region, the SI can be used to forecast the number of future earthquakes induced by future fluid injection volumes. The approach defined above has been applied to single injection wells. Here, we are extending its application to earthquakes occurring in a broad region in response to widely distributed injection.
Calibrating the model
On the basis of the relationship between seismicity and injection rates shown in Fig. 3, we introduce a triggering threshold of the injection rate and a time delay between injection and earthquake occurrence in the SI model and determine the best-fitting parameters by applying a least-squares fit between the model and the cumulative number of earthquakes (M ≥ 3) (more details are included in Methods). We vary the temporal endpoint of the calibration phase between June 2014 and December 2015 to analyze the influence of the time scale used for calibration and the predictive capability. The models are separately calibrated in CO and WO. The seismicity rates resulting from the different calibration time scales are presented in Fig. 4 for the combined area of CO and WO (see figs. S4 and S5 for rates specific to WO and CO individually and parameters of the calibrated SI models).
Fig. 4. Observation and prediction of induced seismicity in CO and WO.
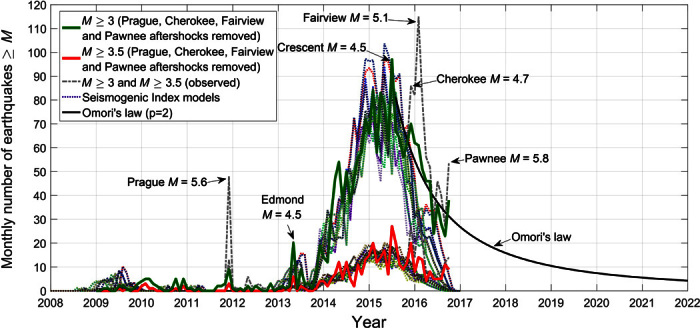
Solid colored lines show the combined monthly number of observed earthquakes (green, M ≥ 3; red, M ≥ 3.5) in CO and WO (aftershocks of M ≥ 4.7 events have been removed). The gray dashed lines present the complete earthquake catalog. The colored dotted lines present SI models calibrated through different times between June 2014 and December 2015. Separate figures for CO and WO and the parameter of the SI models are included in the Supplementary Materials (see figs. S4 and S5). The black solid line shows a decay of M ≥ 3 earthquakes according to Omori’s law (see the Supplementary Materials).
We find that, after a sufficiently large number of earthquakes are included in the calibration phase to determine b values, the parameters of the calibrated models are relatively stable. Calibration of the model through December 2015 results in an SI of Σ = −0.47 in CO and Σ = −0.63 in WO. The value of the SI in Oklahoma is in the range of the SI reconstructed from fluid injection–induced seismicity at enhanced geothermal systems in the crystalline basement (1 ≥ Σ ≥ −3) (15). The maximum likelihood estimate of the b values results in a b value of 1.41 in CO and 1.33 in WO. As reported for induced seismicity at enhanced geothermal systems (15) and hydrocarbon reservoirs (16), b values of induced seismicity tend to be larger than the b value of about 1, which is widely observed for natural earthquakes. In agreement, we find that the b value of the tectonic earthquake activity in all of Oklahoma before 2009 is 1.09.
The sporadic occurrence of induced earthquakes starts in CO in 2009 after the monthly injected volume in this area exceeded the seismicity-triggering threshold determined by the model calibration (3.6 × 106 m3 per month). With the exception of the mainshock/aftershock sequences related to the M = 5.6 earthquake in November 2011 near Prague, the earthquake rate remains low until 2013. Moreover, no M ≥ 3 earthquakes occurred in WO until 2013 when the saltwater injection rates exceeded the triggering threshold in WO (5.6 × 106 m3 per month). Fundamentally, the triggering threshold represents the rate of injection (throughout a region of interest) that can be accommodated by the hydrologic system with minimal, or only localized, pressure changes.
Note that we removed the aftershocks of the Prague M = 5.6 earthquake for model calibration, because they increased fluctuations of the model parameter obtained for different calibration times. Because the Prague sequence does not fit our overall model, it does not allow us to conclude whether it was triggered by injection or not, as our model characterizes the general relationship between an injected volume and seismicity in a crustal volume as a whole. A localized pressure increase in a limited area could always trigger seismicity on a given fault. In the three 5000-km2 seismically active areas in north-central Oklahoma analyzed by Walsh and Zoback (4), it was clear that there was very little induced seismicity until injection rates exceeded approximately 1.2 × 106 m3 per month. Note that CO and WO are each about three times the size as the areas analyzed by Walsh and Zoback (4). Although CO and WO cover similar areas, further analysis is needed to clarify which parameters influence the triggering threshold in different regions. Similarly, different time delays between the injection of fluid and earthquake occurrence were found in CO and WO. A delay of 5 months was found for CO and 2 months for WO. Because the time lag results from the time pressure increases take to reach faults stressed nearly to failure in the crystalline basement, differences of hydraulic transport properties and the distance between injection intervals and preexisting fractures can result in variations of the time lag in different regions.
The most significant change in the 2013 seismic activity rate is caused by the marked increase of saltwater injection rates throughout CO and WO starting mid-2012. During the period of nondecreasing injection rates, seismicity rates in CO and WO increase proportionally to the saltwater injection rates above the triggering threshold.
Predicting the response of seismicity to decreasing injection rates
In Fig. 3, we show the 2016 mandated injection rate (60% of 2014 volumes). Although the mandated injection rate after May 2016 remains almost twice as high as it was in 2009 when the induced earthquake sequence started, it is now distributed over an area twice as large as it was in 2009. Thus, by mandating a 40% reduction in injection rates for both the CO and WO areas relative to 2014 levels, the average injection volume per unit area in the two combined areas is similar to that in 2009. One can see that the actual saltwater injection rates decrease to a value slightly below the mandated injection rate level after May 2016.
Taking into account the observed proportionality of earthquake rates and saltwater disposal rates above the triggering threshold, Eq. 1 suggests that, after the saltwater injection rates began to decrease in 2015, the earthquake rates should start to decrease within several months. As seen in Fig. 3, the highest earthquake rates to date are observed several months after peak saltwater injection rates have been reached. After February 2016, the earthquake activity markedly decreased, and in May 2016, the combined earthquake rate in CO and WO is as low as in early 2014.
Figure 4 compares CO and WO earthquake rates with the predictions of our SI models calibrated through different times between June 2014 and December 2015. The seismicity rates resulting from the models are predictions for times greater than the calibration time. Despite the different time scales used for calibration, the seismicity rates resulting from all models are comparable. All models fit the seismicity rates generally well through the end of 2015 when injection rates start to decrease significantly. Even after removing the aftershocks of the Cherokee and Fairview sequences our models (dotted lines) tend to slightly underestimate the actual number of earthquakes.
To describe the decay of seismicity after injection rates significantly decreased, we follow Langenbruch and Shapiro (13) and use a modification of Omori’s law, describing the decay of aftershock sequences of large tectonic earthquakes (for more details, see the Supplementary Materials). Whereas the pressure close to an injection well starts to decrease immediately after the injection rate has been decreased, pressure at larger distances can still be increasing and could trigger slip on critically stressed preexisting faults. Consequently, the seismicity rate is no longer proportional to the injection rate after injection rates start to decrease significantly. At enhanced geothermal systems and hydrocarbon reservoirs, a significant number of earthquakes have been observed even after complete shut-in of injection wells.
The modification of Omori’s law is used to describe the decay of the seismicity after the injection rate starts to decrease significantly (and falls below the triggering threshold), as shown in Fig. 4. Taking into account the fact that saltwater has been injected above the triggering threshold for years, Omori’s law suggests that it will take several years to return to the background level of seismicity. Moreover, aftershock sequences associated with the Fairview, Cherokee, and Pawnee earthquakes delay the overall decrease in the number of induced earthquakes in those areas. After the aftershocks of all M ≥ 4.7 earthquakes were removed, the decay of the combined earthquake rate in CO and WO agrees with Omori’s law presented in Fig. 4.
Magnitude exceedance probability
Although most of the recent Oklahoma earthquakes of the past 8 years have posed little danger to the public, the possibility of damaging earthquakes on potentially active basement faults cannot be discounted (9). Of particular concern, are earthquakes associated with sufficiently long faults capable of producing earthquakes large enough to cause significant ground shaking (M ≥ 5), as occurred in the Prague, Fairview, and Pawnee areas. This is especially true in areas with critical industrial facilities such as the Cushing oil terminal (19). Here, we show how our model can be used to predict occurrence probabilities of potentially damaging earthquakes.
Because large magnitudes are rare events, it is important to analyze their possible occurrence in a probabilistic sense. Observations of injection-induced earthquakes at geothermal and hydrocarbon reservoirs suggest that, in agreement with natural earthquakes, a Poisson process can be used to describe the occurrence of induced seismicity (14, 16). Because tectonic background activity is driven by constant tectonic loading, a Poisson process describes the occurrence times of natural earthquakes that are homogeneous in time. Fluid injection–induced earthquakes are driven by the time-dependent fluid injection rate (above the triggering threshold), and the Poisson process has to be considered in the injection volume domain (14, 16). For instance, to compute annual occurrence probabilities of induced earthquakes, we have to consider not only the time of 1 year but also the volume of fluid injected within the year. The annual probability PE(M) to exceed magnitude M, that is, the probability to observe one or more earthquakes above magnitude M within 1 year, can be computed on the basis of annual injected saltwater volume VIa above the determined seismicity-triggering threshold, the SI, and the b value (12)
| (2) |
The above relation corresponds to the probability of one minus the probability that no earthquake above magnitude M occurs during injection of the fluid volume VIa. Equation 2 states that the probability of exceeding potentially damaging magnitudes increases with the volume of injected fluid. Because the seismicity rates in Oklahoma are proportional to the fluid injection rate above the observed triggering threshold, higher saltwater injection volumes cause more earthquakes. Consequently, because earthquakes follow a Gutenberg-Richter relationship, higher injection volumes cause larger magnitudes.
Figure 5A presents combined annual probabilities to exceed magnitude M in CO and WO (see figs. S6 and S7 for CO and WO only). Probabilities have been computed according to Eq. 2, and parameters were determined by model calibration until December 2015. Because of the stability of SI models calibrated over different time scales, during the period of nondecreasing injection rate, the probabilities shown in Fig. 5 could have been estimated in early 2014 (see fig. S8). The tectonic earthquake activity between 1979 and 2009 in Oklahoma is characterized by a nontrivial annual probability of exceeding widely felt magnitudes. For instance, there is an annual likelihood of 28% of exceeding M = 3.5. However, the annual probability to exceed potentially damaging magnitudes (M ≥ 5) is extremely low (0.73%). To compute the magnitude exceedance probability for the tectonic background activity, the expression VIa10Σ−bM in Eq. 2 (that is, the annually expected number of earthquakes above magnitude M) can be replaced by the average annual number of earthquakes observed between 1979 and 2009 in all of Oklahoma (1.16 earthquakes of magnitude 3 and larger and 1.16 10−b(M−3) earthquakes of magnitude M and larger) (see also Fig. 1). We used the b value of 1.09 determined for the tectonic background seismicity in all of Oklahoma between 1979 and 2009 to compute tectonic occurrence probabilities.
Fig. 5. Annual magnitude exceedance probability and maximum magnitude in CO and WO.
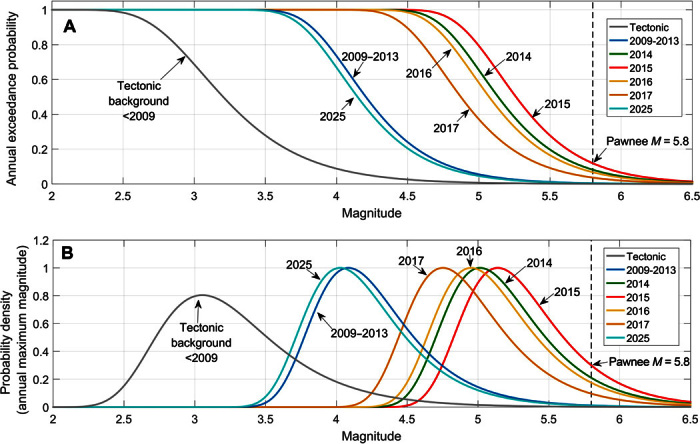
The figure shows combined annual probabilities of exceeding magnitude M (A) and the maximum magnitude (B) in the combined area of CO and WO. Magnitude exceedance probabilities have been computed according to Eq. 2 as well as assuming the applicability of Omori’s law to describe the decay of seismicity following injection. The probability of potentially damaging earthquakes is enhanced compared to the tectonic background and critically high in 2014 to 2016.
Figure 5A shows that, after the injection rate exceeded the seismicity-triggering threshold and the induced earthquake sequence started in 2009, the annual exceedance probability of potentially damaging magnitudes is significantly enhanced. The time lags between injection of fluid and earthquake occurrence for 5 months in CO and 2 months in WO are considered in the computations as well as assuming the applicability of Omori’s law to describe the decay of seismicity following injection. Between 2009 and 2013, the annual probability of exceeding M = 5 increased to 3.8%. Note that this probability corresponds to a 5.5-fold increase compared to the background level in all of Oklahoma. The probability of M ≥ 5 earthquakes increased further to 65% in 2014 after the injection rates throughout CO and WO markedly increased.
Our model predicts the highest probability of potentially damaging earthquakes in 2015. Six of the 10 M ≥ 4.5 earthquakes observed to date occured in 2015 and 2016, where our model predicts a high probability of potentially damaging earthquakes. During peak injection rates in 2015, annual exceedance probabilities of M = 5 are as high as 80%. This means that, without the reduction of saltwater injection rates in 2015 and 2016, there would likely have been an 80% chance to exceed M = 5 every year. Compared to the natural tectonic activity in all of Oklahoma the combined injection rates in CO and WO caused a 110-fold increase in the probability of potentially damaging earthquakes.
However, because of economic factors and mandated volume reductions, the injection rates throughout CO and WO significantly decreased in 2015 and continued to decrease in 2016. Our model predicts that the probability of potentially damaging earthquakes will significantly reduce after the injection rates start to decrease. Nevertheless, there is still a 58% probability of exceeding an M = 5 (7% to exceed M = 5.8) quake where the M = 5.8 Pawnee earthquake occurred in 2016. Considering the decay according to Omori’s law, the probability of potentially damaging earthquakes should approach the tectonic background probability during the next few years. However, in 2017, there is still a 37% chance to exceed M = 5. We note that the assumption of the decay according to Omori’s law and a p value of 2 represents a conservative decay rate. The decay of seismicity observed after injection at enhanced geothermal systems is usually characterized by larger p values. The results in Fig. 5 can be updated during the next year or two if the seismicity decays faster than assumed.
We observe that decreasing the injection rates in only WO or CO would not have been sufficient to mitigate the occurrence of larger magnitudes because, in 2015, the exceedance probabilities of M = 5 in both CO (50%) and WO (58%) are critically high (see figs. S6 and S7). The results show that our model has the potential to assess how injection rates have to be managed to reduce the occurrence probability of potentially damaging injection-induced earthquakes in an area of interest to an acceptable level.
We introduce the probability of a given magnitude to be the annual maximum magnitude as another useful indicator of the induced seismic hazard. The probability distribution of the maximum magnitude can be determined by taking the magnitude derivative of the annual magnitude exceedance probability shown in Fig. 5A. The probability distribution of the annual maximum magnitude for the tectonic earthquake activity between 1979 and 2009 and its increase caused by the high rates of saltwater injection during the recent years are presented in Fig. 5B. The maximum of the probability distribution shifts from M = 3.1 for the natural earthquake rate between 1979 and 2009 to its highest level of M = 5.1 in 2015. Without reduction of the saltwater injection rates in 2015 and 2016, a maximum magnitude of M ≈ 5.1 would have been expected each year. Note that the energy radiated from an earthquake as seismic waves scales logarithmically with the magnitude (21). An increase of two magnitude units corresponds to a 1000-fold increase of the energy released by the expected maximum magnitude. The induced seismic hazard rapidly changes within time periods of only 1 year if injection rates increase or decrease. Our model predicts that, because of the saltwater injection rate decrease in 2015 and 2016, the maximum magnitude should approach the tectonic background level in a few years. However, assuming a decay according to Omori’s law, the maximum magnitude in 2017 is still expected to be about M = 4.8.
DISCUSSION
Our study presents an important step toward the development of a predictive seismic hazard model for induced and triggered seismicity in Oklahoma. The current assumption in hazard models, such as the U.S. Geological Survey 1-year hazard map for induced and triggered seismicity (9), is that earthquake rates within 1 year remain relatively stationary and can be used to forecast earthquake hazard and damage intensity for the next year. Overall, we observe that the induced seismic hazard in Oklahoma rapidly changes within time periods of less than 1 year if injection rates increase or decrease. We propose to incorporate the SI in a seismic hazard model in the central and eastern United States to allow forecasting of the evolving short-term hazard by considering future saltwater injection rates.
Ideally, to be able to incorporate the SI into seismic hazard models, not only the temporal, but also the spatial occurrence of induced earthquakes have to be predictable. However, the spatial scale which we applied our model to was predefined by the two broad areas for the volume reduction mandated by the Oklahoma Corporation Commission. Thus, the determined model parameter corresponds to the bulk properties in all of CO and WO. Our model averages over all the heterogeneity within the two analyzed regions. It will be interesting to analyze how the SI, the triggering threshold, and the time delay between injection and earthquake occurrence fluctuate in different subregions of Oklahoma and other regions of the central and eastern United States. The main physical causes of these fluctuations should be variations of the volume concentration of preexisting fractures and the state of stress. A map of the SI might provide insights into the fluctuation of these physical properties, which are unknown in the crystalline basement, where most of the induced earthquakes occur in Oklahoma. This will help in understanding why certain regions are prone to induced seismicity, whereas injection of the same fluid volume in other regions can be accomplished completely aseismic.
A requirement for the application of the SI model is a complete earthquake catalog and a sufficient number of earthquakes above the completeness magnitude to determine reliable b values. The calibration of our models shows that at least 150 events above the completeness magnitude have to be included in the calibration phase to estimate the model parameter. However, the application of the SI model is not restricted to magnitudes greater than M = 3 as used in this study. In the ideal case, the earthquake catalog is complete down to smaller magnitudes that, according to the Gutenberg-Richter law, should occur in a sufficiently large number to calibrate model parameters before the occurrence of widely felt magnitudes. On the basis of the calibrated model, injection rates could potentially be limited to a level above which the occurrence probabilities of larger magnitudes exceed an acceptable limit.
Sensitive seismic monitoring and efficient earthquake detection algorithms using waveform similarity can be useful to refine earthquake catalogs in different parts of the central and eastern United States (22). This will help in applying the SI model in regions where the number of earthquakes above the completeness magnitude is currently not large enough to reliably calibrate the SI model. We note that our model has the potential to be updated in near real time after injection volumes are reported and earthquakes are recorded. Moreover, although earthquake size is formulated in terms of magnitudes in the SI model, it could be expressed in terms of seismic moments by considering the scaling relations given by Kanamori and Anderson (23).
In general, it has been observed that fluid injections into hydrocarbon reservoirs in shallow sedimentary formations are characterized by a lower SI (−3 ≥ Σ ≥ −10) than injections at enhanced geothermal systems in the crystalline basement (1 ≥ Σ ≥ −3) (15, 16). By increasing the distance between injection intervals and the top of the crystalline basement, it might be feasible to inject higher fluid volumes without inducing widely felt earthquakes. High-rate fluid injection close to or into the crystalline basement, where tectonic processes can accumulate high energy on long preexisting faults, should be avoided.
The main purpose of this paper was to clarify whether the mandated injection reductions are expected to cause seismicity to decrease in the future. We did not intend to present a final and reliable seismic hazard model for Oklahoma. The number of earthquakes outside the area of high-volume injection in north-central Oklahoma does not exceed the tectonic background activity. Moreover, we find a lower threshold of the injection rate in CO and WO below which no induced earthquakes (M ≥ 3) occur. Thus, it should be possible to dispose a limited volume of produced saltwater into the Arbuckle formation aseismic. On the basis of our results, the mandated saltwater injection rate reduction in 2016 was an effective step in mitigating the seismic hazard associated with the occurrence of triggered and induced earthquakes in Oklahoma because injection rates in both CO and WO drop below the observed triggering thresholds. Consequently, widely felt M ≥ 3 earthquakes in the affected areas, as well as the probability of potentially damaging events, should significantly decrease by the end of 2016 and return to tectonic levels within the next few years.
We observe that relatively large magnitudes occur shortly after the injection rate started to decrease. Aftershock sequences related to these earthquakes appear to delay the decay of the number of induced earthquakes. It has been observed that, during hydraulic stimulation of enhanced geothermal systems in the crystalline basement, the largest magnitudes tend to occur shortly after injection has been terminated (24). Geometric (25), pore pressure (26), and poroelastic (27) effects have been considered to explain these observations. Similar processes might be responsible for the increasing earthquake rates observed in Oklahoma several months after the injection rates start to decrease, which cannot be explained by our model. However, our model could have been used as early as 2014 when critically high exceedance probabilities would have been predicted based on the injection rates in the following years (fig. S8). For example, the M = 5.1 Fairview earthquake in February 2016, the two M = 4.7 earthquakes in the Cherokee area in November 2015, and the M = 4.5 Crescent earthquake in July 2015 are within the high probability range of the maximum magnitude predicted by our model (see Fig. 5B) and can be attributed to the injection of saltwater. In contrast, the M = 5.6 earthquake near Prague in November 2011 occurred unexpectedly early in the induced earthquake sequence. On the basis of our model, it remains unclear whether this earthquake was caused by injection of saltwater or whether it would also have been released without anthropogenic influence. The M = 5.8 Pawnee earthquake appears to have a higher magnitude than predicted by our model, because the annual maximum magnitude in 2016 is expected to be around M = 5. However, the cumulative probability of exceeding M = 5.8 by injection of the saltwater volume between 2009 and September 2016 is 25% (see fig. S9).
Our model predicts that earthquakes in Oklahoma will return to tectonic background levels. However, the occurrence of potentially damaging earthquakes cannot be ruled out during the next few years. A decay of the induced earthquake sequence according to Omori’s law (p = 2) results in a 37% chance to exceed M = 5 in 2017. Moreover, the M = 5.6 Prague earthquake occurred when the saltwater injection rates in CO were as low as the mandated injection rates after May 2016. Locally, seismicity could be triggered below the triggering threshold determined for CO and WO, because the latter is a parameter determined by the SI model to represent the bulk property of a large area. Consequently, earthquakes could persist in some areas irrespective of the overall rate of injection. Additional localized saltwater injection rate reductions might be required to mitigate the residual risk in these areas. Increased injection of saltwater should be prevented in all the areas in Oklahoma that have experienced increased seismicity in the past few years.
METHODS
Modification and calibration of the SI model
Two major differences between injection-induced seismicity at geothermal and hydrocarbon reservoirs and induced seismicity in Oklahoma require changes of the SI concept (12) to make it applicable to the seismicity in Oklahoma. Induced seismicity at geothermal and hydrocarbon reservoirs usually occurs in the direct vicinity of the injection well. Little or no time lag between injection of fluid and earthquake occurrence is observed. However, induced earthquakes in Oklahoma occur at distances of several kilometers from the injection intervals of the saltwater disposal wells in the Arbuckle formation. It requires the consideration of a time lag between injection of fluid and earthquake occurrence, which corresponds to the specific time the pressure increase needs to propagate from injection intervals in the Arbuckle group to the critically stressed fractures in the crystalline basement. We analyzed injection and seismicity in two large areas, where the hydrologic system seems to be able to accommodate a certain rate of injection with minimal or only localized pressure changes. It requires the introduction of a seismicity-triggering threshold represented by a monthly injection rate because the injection of saltwater below this rate is not triggering any earthquakes.
The equation we used to calibrate the model based on the observed earthquakes and reported injection volumes is
| (3) |
In the above equation, Vseis(t − ts) corresponds to the cumulative saltwater volume injected until the time t − ts above the seismicity-triggering threshold Vmin of the monthly injection rate. ts represents the time lag between injection of fluid and earthquake occurrences. ∑, Vmin, and ts are calibration parameters of the model and are determined by minimizing the residuals resulting from a least-squares fit between the cumulative number of observed earthquakes (M ≥ 3) and Eq. 3. The b values in CO and WO were determined by a maximum likelihood fit.
Supplementary Material
Acknowledgments
This study would not have been possible without the Underground Injection Control injection data provided by the Oklahoma Corporation Commission and the U.S. Geological Survey National Earthquake Information Center earthquake catalog. We thank C. Frohlich and an anonymous reviewer for comments that improved the manuscript. Funding: The Stanford Center for Induced and Triggered Seismicity provided the financial support for this study. Author contributions: C.L. carried out the bulk of detailed analysis, with continual supervision and guidance by M.D.Z. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors. Earthquake catalog: http://earthquake.usgs.gov/earthquakes/search/. Injection well location and saltwater injection data: www.occeweb.com/og/ogdatafiles2.htm.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/11/e1601542/DC1
Supplementary Methods
fig. S1. Maximum magnitude expected during 1900 years of tectonic earthquake activity in Oklahoma.
fig. S2. Saltwater injection and earthquake rate in CO.
fig. S3. Saltwater injection and earthquake rate in WO.
fig. S4. Observation and prediction of induced seismicity in CO.
fig. S5. Observation and prediction of induced seismicity in WO.
fig. S6. Annual magnitude exceedance probability and maximum magnitude in CO.
fig. S7. Annual magnitude exceedance probability and maximum magnitude in WO.
fig. S8. Annual magnitude exceedance probability and maximum magnitude.
fig. S9. Cumulative magnitude exceedance probability and maximum magnitude in CO and WO (2009 to September 2016).
table S1. Recent magnitude 4.5 and larger earthquakes in Oklahoma.
REFERENCES AND NOTES
- 1.U.S. Geological Survey, National Earthquake Information Center earthquake catalog; http://earthquake.usgs.gov/earthquakes/search/.
- 2.Ellsworth W. L., Injection-induced earthquakes. Science 341, 1225942 (2013). [DOI] [PubMed] [Google Scholar]
- 3.Keranen K. M., Weingarten M., Abers G. A., Bekins B. A., Ge S., Sharp increase in central Oklahoma seismicity since 2008 induced by massive wastewater injection. Science 345, 448–451 (2014). [DOI] [PubMed] [Google Scholar]
- 4.Walsh F. R. III, Zoback M. D., Oklahoma’s recent earthquakes and saltwater disposal. Sci. Adv. 1, e1500195 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Weingarten M., Ge S., Godt J. W., Bekins B. A., Rubinstein J. L., High-rate injection is associated with the increase in U.S. mid-continent seismicity. Science 348, 1336–1340 (2015). [DOI] [PubMed] [Google Scholar]
- 6.Healy J. H., Rubey W. W., Griggs D. T., Raleigh C. B., The Denver earthquakes. Science 161, 1301–1310 (1968). [DOI] [PubMed] [Google Scholar]
- 7.Talwani P., Acree S., Pore pressure diffusion and the mechanism of reservoir-induced seismicity. Pure Appl. Geophys. 122, 947–965 (1984). [Google Scholar]
- 8.Zoback M. D., Harjes H.-P., Injection-induced earthquakes and crustal stress at 9 km depth at the KTB deep drilling site, Germany. J. Geophys. Res. 102, 18477–18491 (1997). [Google Scholar]
- 9.M. D. Petersen, C. S. Mueller, M. P. Moschetti, S. M. Hoover, A. L. Llenos, W. L. Ellsworth, A. J. Michael, J. L. Rubinstein, A. F. McGarr, K. S. Rukstales, 2016 One-Year Seismic Hazard Forecast for the Central and Eastern United States from Induced and Natural Earthquakes (Open-File Report 2016-1035, U.S. Geological Survey, 2016).
- 10.Western Oklahoma Regional Volume Reduction Plan; www.occeweb.com/News/2016/02-16-16WesternRegionalPlan.pdf.
- 11.Central Oklahoma Regional Volume Reduction Plan and Expansion of Area of Interest; www.occeweb.com/News/2016/03-07-16ADVISORY-AOI,%20VOLUME%20REDUCTION.pdf.
- 12.Shapiro S. A., Dinske C., Langenbruch C., Wenzel F., Seismogenic index and magnitude probability of earthquakes induced during reservoir fluid stimulations. Leading Edge 29, 304–309 (2010). [Google Scholar]
- 13.Langenbruch C., Shapiro S. A., Decay rate of fluid-induced seismicity after termination of reservoir stimulations. Geophysics 75, MA53–MA62 (2010). [Google Scholar]
- 14.Langenbruch C., Dinske C., Shapiro S. A., Inter event times of fluid induced earthquakes suggest their Poisson nature. Geophys. Res. Lett. 38, L21302 (2011). [Google Scholar]
- 15.Dinske C., Shapiro S. A., Seismotectonic state of reservoirs inferred from magnitude distributions of fluid-induced seismicity. J. Seismol. 17, 13–25 (2013). [Google Scholar]
- 16.Hajati T., Langenbruch C., Shapiro S. A., A statistical model for seismic hazard assessment of hydraulic-fracturing-induced seismicity. Geophys. Res. Lett. 42, 10,601–10,606 (2015). [Google Scholar]
- 17.National Research Council, Induced Seismicity Potential in Energy Technologies (The National Academies Press, 2012). [Google Scholar]
- 18.Simpson D. W., Seismicity changes associated with reservoir loading. Eng. Geol. 10, 123–150 (1976). [Google Scholar]
- 19.McNamara D. E., Benz H. M., Herrmann R. B., Bergman E. A., Earle P., Holland A., Baldwin R., Gassner A., Earthquake hypocenters and focal mechanisms in central Oklahoma reveal a complex system of reactivated subsurface strike-slip faulting. Geophys. Res. Lett. 42, 2742–2749 (2015). [Google Scholar]
- 20.Gardner J. K., Knopoff L., Is the sequence of earthquakes in southern California, with aftershocks removed, Poissonian?. Bull. Seismol. Soc. Am. 64, 1363–1367 (1974). [Google Scholar]
- 21.B. Gutenberg, C. F. Richter, Seismicity of Earth and Associated Phenomenon (Princeton Univ. Press, ed. 2, 1954). [Google Scholar]
- 22.Skoumal R. J., Brudzinski M. R., Currie B. S., Levy J., Optimizing multi-station earthquake template matching through re-examination of the Youngstown, Ohio, sequence. Earth Planet. Sci. Lett. 405, 274–280 (2014). [Google Scholar]
- 23.Kanamori H., Anderson D. L., Theoretical basis of some empirical relations in seismology. Bull. Seismol. Soc. Am. 65, 1073–1095 (1975). [Google Scholar]
- 24.Majer E. L., Baria R., Stark M., Oates S., Bommer J., Smith B., Asanuma H., Induced seismicity associated with Enhanced Geothermal Systems. Geothermics 36, 185–222 (2007). [Google Scholar]
- 25.Shapiro S. A., Krüeger O. S., Dinske C., Langenbruch C., Magnitudes of induced earthquakes and geometric scales of fluid-stimulated rock volumes. Geophysics 76, WC55–WC63 (2011). [Google Scholar]
- 26.Bachmann C. E., Wiemer S., Goertz-Allmann B. P., Woessner J., Influence of pore-pressure on the event-size distribution of induced earthquakes. Geophys. Res. Lett. 39, L09302 (2012). [Google Scholar]
- 27.Segall P., Lu S., Injection induced seismicity: Poroelastic and earthquake nucleation effects. J. Geophys. Res. Solid Earth 120, 5082–5103 (2015). [Google Scholar]
- 28.H. S. Carslaw J. C. Jaeger, Conduction of Heat in Solids (Oxford Univ. Press, 1959). [Google Scholar]
- 29.Townend J., Zoback M. D., How faulting keeps the crust strong. Geology 28, 399–402 (2000). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/11/e1601542/DC1
Supplementary Methods
fig. S1. Maximum magnitude expected during 1900 years of tectonic earthquake activity in Oklahoma.
fig. S2. Saltwater injection and earthquake rate in CO.
fig. S3. Saltwater injection and earthquake rate in WO.
fig. S4. Observation and prediction of induced seismicity in CO.
fig. S5. Observation and prediction of induced seismicity in WO.
fig. S6. Annual magnitude exceedance probability and maximum magnitude in CO.
fig. S7. Annual magnitude exceedance probability and maximum magnitude in WO.
fig. S8. Annual magnitude exceedance probability and maximum magnitude.
fig. S9. Cumulative magnitude exceedance probability and maximum magnitude in CO and WO (2009 to September 2016).
table S1. Recent magnitude 4.5 and larger earthquakes in Oklahoma.


