A Probabilistic Analysis of Completely Excised High-Grade Soft Tissue Sarcomas of the Extremity: An Application of a Bayesian Belief Network

Abstract

Background

It is important to understand the relative importance of prognostic variables in patients with soft tissue sarcomas. The purpose of this study was to describe the hierarchical relationships between features inherent to completely excised, localized high-grade soft tissue sarcomas of the extremity and compare the associations to those previously reported.

Methods

Data were collected from the Memorial Sloan-Kettering Cancer Center Sarcoma Database. All adult patients with high-grade extremity soft tissue sarcomas who underwent complete excision (R0 margins) at our institution between 1982 and 2010 were included in the analysis. Bayesian belief network (BBN) modeling software was used to develop a hierarchical network of features trained to estimate the likelihood of disease-specific survival. Important relationships depicted by the BBN model were compared to those previously reported.

Results

The records of 1318 consecutive patients met the inclusion criteria, and all were included in the analysis. First-degree associates of disease-specific survival were the primary tumor size; presence of and time to distant recurrence; and presence of and time to local recurrence. On cross-validation, the BBN model was sufficiently robust, with an area under the curve of 0.94 (95% CI, 0.93–0.96).

Conclusions

We successfully described the hierarchical relationships between features inherent to patients with completely excised high-grade soft tissue sarcomas of the extremity. The relationships defined by the BBN model were similar to those previously reported. Cross-validation results were encouraging, demonstrating that BBN modeling can be used to graphically illustrate the complex hierarchical relationships between prognostic features in this setting.

SYNOPSIS

We used a Bayesian Belief Network (BBN) to describe the hierarchical relationships between features inherent to patients with completely excised high-grade soft tissue sarcomas of the extremities. The relationships defined by the BBN model were similar to those previously reported, demonstrating that BBN modeling can be used as an adjunct to existing nomograms to graphically illustrate the complex hierarchical relationships between prognostic features.

INTRODUCTION

Accurate, personalized survival estimates are important in the treatment of soft tissue sarcomas (STS). Since the development of our institution’s prospectively collected soft tissue sarcoma database, we have evolved from the descriptive characterization^1–4 of prognostic factors for outcome⁵ to the development of generic,⁶ disease-specific,⁷ and therapy-related⁸ nomograms. These nomograms, however, require that specific outcomes be defined a priori, are limited by the number of specific categories in each variable (i.e., histology), and, more importantly, can be hampered by missing or outlying data points.

Bayesian classification, which includes Bayesian belief network (BBN) modeling, is an inductive statistical method that allows for rational learning from experimental data. For a given set of data, probabilistic relationships between features can be characterized by defining conditional probabilities in terms of joint events: P(A,B) = P(A /B) · P(B), which allows one to estimate the probability of “A” given a frame of knowledge “B.” Repeated application of this formula enables the development of a graphical n-dimensional model that codifies all related features within a single hierarchical network. When used as prognostic models, Bayesian classifiers can also account effectively for data multidimensionality and uncertainty—a quality that enables prognostic BBN models to maintain their robustness in the setting of incomplete or outlying clinical data.^{9, 10} Importantly, BBN models are capable of codifying even the most complex data into clear, graphical representations of hierarchical relationships—a quality that may interest physicians and surgeons. For instance, this technique has been used to better understand relationships between variables in a variety of oncologic settings,^11–14

The purpose of this study was to develop a BBN model to describe the hierarchical relationships between features inherent to completely-excised localized high-grade soft tissue sarcomas of the extremity. In doing so, we illustrate the power of BBN modeling as a clinical tool that can aid clinicians in codifying complex hierarchical relationships between prognostic variables into clear graphical representations.

MATERIALS AND METHODS

The Memorial Sloan-Kettering Cancer Center (MSKCC) Sarcoma Database contains prospectively collected clinical, pathologic, and treatment-related variables for all adult patients (age >16 years) with primary and recurrent STS treated at our institution since 1982. After obtaining approval from the MSKCC institutional review board, which issued a waiver of informed consent, we searched the MSKCC Sarcoma Database for all patients with high-grade STS of the extremity who underwent complete resection (R0 margins). This homogeneous patient population was chosen in an effort to control for tumor grade and resection margin status prior to performing the initial probabilistic analysis.

Twenty-seven candidate features were chosen based on their current clinical or historical association with disease-specific outcomes in patients with high-grade STS, as well as their availability within the MSKCC Sarcoma Database (Table 1). These included the following: age at the time of surgical excision; sex; size, depth, and location of the tumor; histology and, if applicable, histologic variant; oncologic procedures prior to referral, if any; whether the sarcoma was thought to be radiation-induced; the patient’s home zip code at the time of referral; the surgeon and surgical service of record; need for tumor bed excision following referral; type of surgical procedure performed; presence of bone, nerve, or vascular invasion by the tumor; bone or nerve resection with the tumor; history of chemotherapy or radiotherapy; timing of chemotherapy or radiotherapy, if applicable; presence of and time to local recurrence (LR); presence of and time to distant recurrence (DR); and death from disease.

TABLE 1.

Candidate features considered for inclusion in the Bayesian belief network model

Candidate feature	Label	Description	States
Agea	AGE	Patient age, at the time of surgery	CV
Sex	SEX		Male Female
Sizea	PRIMARY SIZE CATEGORY	Size category of tumor in maximum dimension	≤5 cm 5–10 cm >10 cm
Deptha	DEPTH	Depth of primary tumor compared to investing fascia of limb	Superficial Deep
Sitea	SITE		Upper extremity Lower extremity
Subsite	SUBSITE	Extremity tumors distal to the vertical plane made by the axillary fold and horizontal plane made by the inguinal ligament were considered.	Hand Forearm Elbow Arm Axilla Shoulder Groin Hip Thigh Knee Leg Ankle Foot
Histologya	HISTOLOGY	Final histology following excision, review by 3 pathologists	MFH/HGPS Synovial Liposarcoma Leiomyosarcoma MPNST Fibrosarcoma Other
Varianta	VARIANT	Histologic variant, if applicable	Monophasic Biphasic…etc.
Presentation statusa	PRESENTATION STATUS	Oncologic procedures performed prior to referral (if any)	None Biopsy only Marginal excision Wide excision
Radiation-induced	RT INDUCED	Whether the sarcoma is considered radiation induced	Yes No
Referring zip code	FIRST 3 DIGITS ZIP	First 3 digits of patient’s home zip code at the time of referral	CV
Surgeona	SURGEON CODE	31 surgeons, listed anonymously	A-EE
Servicea	SERVICE CODE	2 surgical services	GMT Orthopaedic Surgery
Re-excisiona	RE EXCISION	Whether the patient, upon referral, required a tumor bed excision	Yes No
Procedurea	PROCEDURE	Type of procedure performed	Limb sparing Amputation
Bone invasiona	BONE INVASION		Yes No
Bone resectiona	BONE RESECTED		Yes No
Nerve invasiona	NERVE INVASION		Yes No
Nerve resectiona	NERVE RESECTED		Yes No
Vascular invasion	VASC INVASION		Yes No
Chemotherapy
Preopa	PREOP CHEMO		Yes No
Postopa	POSTOP CHEMO		Yes No
Radiotherapy
Preopa	PREOP RT		Yes No
Postopa	POSTOP RT		Yes No
Time to LRa	TIME TO LR	In months	CV None
Time to DRa	TIME TO DR	In months	CV None
Death from diseasea	DOD	Whether the patient died of disease, a reflection of disease-specific survival	Yes No

^aCandidate feature included in the final model.

CV = continuous variable; MFH/HGPS = malignant fibrous histiocytoma/high-grade pleomorphic sarcoma; MPNST = malignant peripheral nerve sheath tumor; GMT = Gastric & Mixed Tumor; LR = local recurrence; DR = distant recurrence.

The following definitions were used in this study. As mentioned above, only completely excised high-grade STS of the extremity were considered in this analysis. Specifically, tumors distal to the vertical plane made by the axillary fold in the upper extremity or distal to the inguinal ligament in the lower extremity were considered. A sarcoma was considered to be radiation-induced if it was histologically dissimilar from the original tumor and occurred within an irradiated field more than 6 months after irradiation. For histology, only histologic diagnoses comprising more than 2% of cases were included. Those comprising less than 2% of cases were combined and categorized as “other.” Patients were considered to have undergone a re-excision if they required, in the opinion of the treating surgeon, a tumor bed excision after referral for local control. Bone adherence/invasion was considered present if, on imaging, the tumor exhibited any effect on an adjacent bone, including periosteal reaction. Nerve and vascular invasion were determined histologically. The presence of and time to first DR were determined based on imaging, and calculated from the date of initial operation. Local recurrences were diagnosed by physical examination and/or imaging, and were confirmed histologically. Time to LR was calculated from the date of initial surgical excision to the date of histologic diagnosis of recurrence. Deaths confirmed to be sarcoma-related were considered disease-related.

Bayesian Statistical Analysis and Model Development

The training data set included all cases identified from the MSKCC Sarcoma Database during the study period. All 27 candidate features were considered for inclusion in the preliminary models. The BBN models were developed using commercially available machine-learning algorithms (FasterAnalytics, DecisionQ Corp., Washington, DC, USA) that automatically learn network structures and priors from the training data, thus, priors were not specified a priori.^{15, 16} Prior to Bayesian analysis, features containing continuous variables required conversion to categorical variables,^{17, 18} We used equal-area binning based on prior distributions learned from the training set. In an effort to balance goodness-of-fit against robustness, a parsimony metric was used to reduce the risk of overfitting the final model to the training data.^{9, 18} Using a step-wise process, unrelated and redundant features were pruned from the preliminary models to produce the final model.^{9, 18}

To account for missing data within the training set, we used a passive, truncation-based imputation algorithm.⁹ We imputed values for those features in which missing data represented less than 30% of the total record count, and for which there was no adequate substitute feature. The imputation algorithm was applied to six features within the training set: bone invasion (missing in 5.4% of records), bone resection (7.9%), nerve invasion (11.6%), nerve resection (12.2%), vascular invasion (12.4%), and re-excision (27.5%). Thus, no features were pruned from the model because of missing data. Most patients had neither LR (85.3%) nor DR (68.3%). Therefore, a “missing” value in each of these features was defined as no LR or DR.

We trained the BBN model to specify network structure and prior probability distributions in order to develop classifiers of estimated disease-specific survival (DSS). The network structure was then portrayed graphically to illustrate the conditional interdependence and hierarchy of the features. First-degree associates were defined as those nodes that share edges with the outcome of interest (death from disease, in this case), while second-degree associates were those nodes that share edges with the first-degree associates. Inference tables were calculated depicting posterior estimates of probability for each possible permutation with respect to the outcome.

Cross-validation

Ten-fold cross-validation was performed to assess the robustness of the final BBN model. Data were randomized and divided into 10 matching train-and-test sets. Each train-and-test set consisted of a training set composed of 90% of the patient records and a test set composed of the remaining 10%. Each matching set was unique, without overlap. A BBN model was trained, using each training set, by applying the same parameters as the final BBN model, then tested on the corresponding test set. This was repeated 10 times on each of the ten unique train and test groups. Using the generated predicted probabilities, a receiver operating characteristic (ROC) curve, which is a graphical plot of sensitivity versus 1-specificity at all discrimination threshold levels, was generated considering DSS as the outcome. The area under the ROC curve (AUC) was then calculated to assess the model’s overall accuracy and robustness.

RESULTS

We identified a total of 1318 patients who met the inclusion criteria. All records were included in the analysis. The clinical characteristics and demographics of the patient population are shown in Table 2. These data comprised the training set for model development. The median age was 54 years (interquartile range [IQR], 38, 58). Most patients were male (55.2%), and most had lower-extremity lesions (73.1%). Tumor size was less than 5 cm (35.5%), 5–10 cm (32.5%), and greater than 10 cm (31.6%); it was unknown in six patients (0.5%). The most common histology was malignant fibrous histiocytoma/high-grade pleomorphic sarcoma (39.6%) followed by synovial sarcoma (15.8%), liposarcoma (12.7%), leiomyosarcoma (10.8%), malignant peripheral nerve sheath tumor (3.9%), and fibrosarcoma (2.6%).

TABLE 2.

Clinical characteristics and demographics for all patients with completely excised high-grade soft tissue sarcomas of the extremity (N = 1318)

Feature	No.	%	Median	IQR
Age (years)			54	38, 58
Sex
Male	728	55.2
Female	590	44.8
Tumor size category
≤5 cm	468	35.5
5–10 cm	428	32.5
>10 cm	416	31.6
Unknown	6	0.5
Depth
Superficial	265	20.1
Deep	1053	79.9
Site
Upper extremity	354	26.9
Lower extremity	964	73.1
Subsite
Hand	37	2.8
Forearm	99	7.5
Elbow	26	2.0
Arm	91	6.9
Axilla	33	2.5
Shoulder	68	5.2
Groin	43	3.3
Hip	12	0.9
Thigh	607	46.0
Knee	73	5.5
Leg	149	11.3
Ankle	22	1.7
Foot	58	4.4
Histology, variant
MFH/HGPS	522	39.6
Pleomorphic	200	38.3
Myxofibrosarcomatous	171	32.8
Giant Cell	10	1.9
Inflammatory	2	0.4
NOS	139	26.6
Synovial sarcoma	208	15.8
Monophasic	136	65.4
Biphasic	70	33.7
NOS	2	0.9
Liposarcoma	168	12.7
Myxoid/round cell	83	49.4
Pleomorphic	57	33.9
Dedifferentiated	21	12.5
NOS	7	4.2
Leiomyosarcoma	142	10.8
MPNST	51	3.9
Fibrosarcoma	34	2.6
Other	193	14.6
Presentation Status
No prior treatment	260	19.7
Biopsy only	555	42.1
Marginal excision	371	28.1
Wide excision	132	10.0
Radiation-induced
Yes	19	1.4
No	1299	98.6
Zip code upon referral
First 3 digits			112	087, 125
Surgeon
A	318	24.2
B	245	18.6
C	146	11.1
D	123	9.3
E	116	8.8
F	103	7.8
G	102	7.8
Other	165	12.4
Surgical Service
GMT	798	60.6
Orthopaedic Surgery	512	38.8
Other	8	0.6
Tumor bed excision
Yes	457	34.7
No	498	37.8
Missing	363	27.5
Procedure
Amputation	106	8.0
Limb-sparing surgery	1212	92.0
Bone invasion
Yes	51	3.9
No	1196	90.7
Missing	71	5.4
Bone resected
Yes	183	13.9
No	1031	78.2
Missing	104	7.9
Nerve invasion
Yes	27	2.1
No	1137	86.3
Missing	154	11.6
Nerve resected
Yes	156	11.8
No	1001	78.0
Missing	161	12.2
Vascular invasion
Yes	73	5.5
No	1081	82.0
Missing	164	12.4
Chemotherapy
Preop	164	12.4
Postop	202	15.3
None	952	72.2
Radiotherapy
Preop	51	3.9
Postop	579	43.9
None	688	52.2
LR	194	14.7
Time to LR (months)			15	6, 29.5
DR	419	31.8
Time to DR (months)			11	5, 24
Death from disease	349	26.5
Follow-up time (months)			39	14.6, 96.8

IQR = interquartile range; MFH/HGPS = malignant fibrous histiocytoma/high-grade pleomorphic sarcoma; NOS = not otherwise specified; MPNST = malignant peripheral nerve sheath tumor; GMT = Gastric & Mixed Tumor; LR = local recurrence; DR = distant recurrence.

Chemotherapy was administered preoperatively in 12.4% of patients and postoperatively in 15.3%. Radiotherapy was given preoperatively in 3.9% of patients and postoperatively in 43.9%. In 34.7% of patients, re-excision was performed after a previous marginal excision (28.1%) or wide excision (10.0%). LR occurred in 14.7% of patients, with a median time to LR of 15 months (IQR, 6.0, 29.5). DR occurred in 31.8% of patients, with a median time of 11 months (IQR, 5.0, 24.0). Overall survival for the entire group was 54.4%, and DSS was 73.5%, at a median follow-up of 39.9 months (IQR, 14.6, 96.8). Median survival was not reached.

Bayesian analysis revealed strong, hierarchical associations between the various features (Figure 1). As shown, there were three first-degree associates of DSS: primary tumor size, time to DR, and time to LR. Second-degree associates of DSS were: the anatomic site and depth of the tumor, any oncologic treatment prior to referral, and a history of preoperative chemotherapy.

Figure 1.

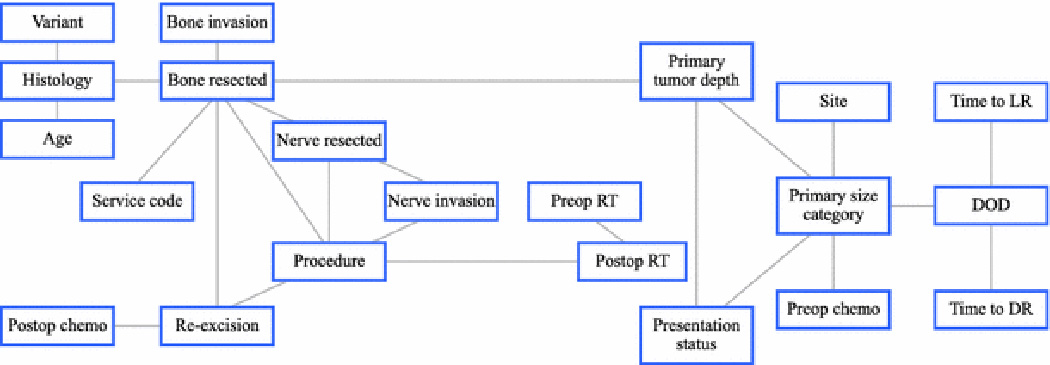
Bayesian belief network constructed using the records of 1318 patients with completely excised high-grade soft tissue sarcomas of the extremity. As shown, there are three first-degree associates of death from disease (“DOD”): primary tumor size (“PRIMARY SIZE CATEGORY”); time to distant recurrence (“TIME TO DR”); and time to local recurrence (“TIME TO LR”).

On cross-validation, ROC curve analysis demonstrated that the model was robust. With DSS as the predicted outcome, the AUC was 0.94 (95% CI, 0.93–0.96). Inference tables were calculated based on the three first-degree associates, and posterior estimates of probability of death from disease ranged from 0.1% to 97.7%. The 41 most likely inferential cases are presented (Table 3), out of 144 potential permutations for this model.

TABLE 3.

Inference table describing the 41 most likely scenarios, out of a total of 144 potential permutations. The outcome of interest was the predicted probability of death from disease

Probability of case based on training data (%)	Primary size category (cm)	Time to LR (months)	Time to DR (months)	Predicted probability of death from disease (%)
24.5	≤ 5	No LR	No DR	0.1
18.6	5–10	No LR	No DR	0.4
14.6	> 10	No LR	No DR	0.7
2.4	> 10	No LR	≤ 4	83.3
2.3	> 10	No LR	14–28	83.9
2.3	> 10	No LR	9–14	85.3
2.2	> 10	No LR	> 28	75.0
2.1	> 10	No LR	4–9	84.1
1.9	5–10	No LR	≤ 4	72.4
1.8	5–10	No LR	> 28	61.2
1.8	5–10	No LR	14–28	73.3
1.8	5–10	No LR	9–14	75.4
1.6	5–10	No LR	4–9	73.5
1.4	≤ 5	No LR	> 28	35.8
1.3	≤ 5	No LR	≤ 4	48.1
1.2	≤ 5	No LR	14–28	49.3
1.2	≤ 5	No LR	9–14	52.0
1.1	≤ 5	No LR	4–9	49.5
0.8	≤ 5	18–37	No DR	0.2
0.7	≤ 5	> 37	No DR	0.2
0.6	5–10	18–37	No DR	0.6
0.6	5–10	> 37	No DR	0.6
0.5	≤ 5	≤ 5	No DR	0.6
0.5	> 10	18–37	No DR	1.2
0.4	> 10	> 37	No DR	1.1
0.4	> 10	> 37	No DR	1.1
0.4	≤ 5	11–18	No DR	0.9
0.4	5–10	≤ 5	No DR	1.7
0.4	≤ 5	5–11	No DR	1.0
0.3	5–10	11–18	No DR	2.5
0.3	> 10	≤ 5	No DR	3.1
0.3	5–10	5–11	No DR	2.7
0.3	> 10	11–18	No DR	4.7
0.2	> 10	11–18	≤ 4	97.1
0.2	> 10	11–18	9–14	97.5
0.2	> 10	11–18	14–28	97.2
0.2	> 10	5–11	No DR	5.0
0.2	> 10	5–11	≤ 4	97.3
0.2	> 10	5–11	9–14	97.7
0.2	> 10	5–11	14–28	97.4
0.2	> 10	5–11	No DR	5.0

LR = local recurrence; DR = distant recurrence

For locally recurrent tumors, the model showed a difference in survival based on the original size of the primary tumor. From the BBN model, we generated case-specific examples of LR for the three size categories (Table 4). The predicted probability of disease-related death was 28.6% for tumors 5 cm or smaller, but increased to 52.5% for tumors 5–10 cm and to 67.9% for tumors larger than 10 cm. Importantly, death from disease became the most likely scenario following a LR if the size of the primary tumor was greater than 5 cm, but only in the presence of DR (Table 3).

TABLE 4.

Association between the size category of the primary tumor and disease-specific survival in cases of local recurrence

Local Recurrence	Size category of primary tumor (cm)	Predicted probability of death from disease (%)	Change in probability above baseline (%)
N/A	N/A	26.8	0
Yes	≤ 5	28.6	+1.9
Yes	5–10	52.5	+25.7
Yes	> 10	67.9	+41.2

N/A = not applicable

An association between DSS and the time to LR was also shown. Again, from the BBN model, we created five case-specific examples in which LR occurred prior to and after 18 months (Table 5). If LR occurred prior to 18 months after surgery, the predicted probability was 59.6%– 68.2% and death from disease was 55.8%–65.9%. However, if LR occurred 18 months after surgery, the predicted likelihood of DR and death from disease decreased substantially to 37.4%–39.8% and 29.7%–32.4%, respectively. Thus, time to LR affected both the likelihood of DR and the likelihood of death from disease.

TABLE 5.

Time-dependent association between local recurrence and disease-specific survival

LR	Time to LR (months)	Predicted probability of death from disease (%)	Change in probability above baseline (%)
N/A	N/A	27.5	0
Yes	≤ 5	55.8	29.1
Yes	5–11	67.5	40.8
Yes	11–18	65.9	39.2
Yes	18–37	32.4	5.8
Yes	> 37	29.7	3.0

LR = local recurrence; N/A = not applicable

DISCUSSION

Using readily available clinical data, we successfully described the hierarchical relationships between features inherent to patients with completely excised high-grade STS of the extremity. In doing so, we illustrated the ability of Bayesian statistics to codify the complex relationships that exist between prognostic variables in STS into a simple hierarchical model. In the broader sense, we hope that by incorporating the use of BBN modeling in oncology, clinicians can improve their understanding of the complex relationships between various features and offer personalized estimations of any outcome of interest based on prior information. For example, the BBN model constructed in the present study confirmed several important relationships between prognostic features related to the treatment of STS (Figure 1). First-degree associates, or primary determinants, of DSS in this case, were the size of the primary tumor, time to DR, and time to LR.

Using a series of regression-derived nomograms, we have previously shown that a personalized estimation of outcomes in patients with STS is possible.^1–8 Canter et al. demonstrated that the primary tumor size and the tumor site (upper or lower extremity) were the two variables most strongly associated with DSS in patients with synovial sarcoma, the majority of whom had undergone R0 resections. ¹⁹ In the present BBN model, both the primary tumor size and site of the tumor (upper vs lower extremity) also emerged as dominant features; the former was identified as a first-degree associate of DSS and the latter as a second-degree associate. Elsewhere, Canter et al. acknowledged that using tumor grade alone to classify patient outcomes was inadequate; in high-grade tumors, other variables such as histology need to be included for accurate outcome prediction. ²⁰ They found a statistically significant difference in DSS by discretizing histologic diagnoses into “favorable,” “intermediate,” and “unfavorable” groups. We chose not to group histologic diagnoses in this fashion, but in an effort to improve the generalizability of the BBN model, we represented the dominant histologies comprising more than 2% of cases as individual categories. In the present study, which is based on a relatively homogeneous patient population, the BBN model structure revealed that the specific histologic diagnosis is a fourth-degree associate of DSS, and that knowledge of the size category (first-degree associate) or depth of the primary tumor (second-degree associate) renders DSS independent of the individual histologic diagnosis. Stojadinovic et al. previously described the relationship between LR, including the disease-free interval, and DSS. ²¹ In the present study, by examining the prior distributions within the BBN model, we observed not only an association between LR and a higher probability of death from disease (22.7% vs 27.0%), but also that patients who experienced an LR within 18 months were twice as likely to die from disease than those who experienced an LR after 18 months (63.6% vs 31.6%).

Preoperative chemotherapy was identified as a second-degree associate of DSS in this patient population. This is an important observation considering that only 27.8% of patients received adjuvant chemotherapy and 12.4% received neoadjuvant chemotherapy. Although it varies between treating oncologists, preoperative chemotherapy is typically offered at our institution for larger tumors (>7.5 cm) in which the risk of metastatic disease is believed to be higher. As such, this relationship may represent an institutional selection bias. Evaluation in other independent data sets is thus needed to confirm this observation.

We believe that a Bayesian classifier is well suited for analyzing outcomes in patients with STS for a variety of reasons. First, we have previously shown that there are verifiable relationships between features in the setting of patients with extremity STS ^{5–7, 20, 22} and that the nature of and time to LR influence these relationships.²³ Studying the effect(s) of one variable at a time while holding all others constant is generally not possible in clinical research, nor does it adequately represent conditional interdependence. The Bayesian method not only generates a joint distribution function describing these relationships, but it also displays them graphically in an intuitive, transparent, and comprehensive manner. For the purpose of the current study, this is considered a major advantage over other, popular machine learning approaches such as Artificial Neural Networks (ANNs), which do not represent data graphically. The BBN method also depicts important relationships within one cohesive model (as opposed to a series of nomograms), which allows the clinician to better understand the hierarchy and relative importance of each feature as it pertains to an individual clinical scenario. Second, Bayesian networks can account for uncertainty within the data, ^{9, 10} and can thus be used effectively in the setting of reasonable amounts of incomplete or missing input data. This is a significant advantage over traditional nomograms and ANNs which require that input data be complete. As we have recommended with nomograms, clinicians may first conceptualize the model structure, then compute personalized estimations of outcomes for a given clinical scenario. As an analytical tool, Bayes’ theorem is inductive, updating beliefs (H) in response to evidence (e)— P(H/e)—something clinicians do every day. Thus, like other modeling techniques, Bayesian models can be updated (improved) from time to time as new evidence presents itself, be it emerging patterns of disease, new prognostic variables, or more effective treatment modalities. We acknowledge that prospectively collected data are ideally suited for this purpose; however, to establish the basis of this analysis in this patient population and improve the ability for other populations to be treated similarly, we encourage participation in multi-institutional prospective trials.

This study has several limitations. First, the BBN model was developed using only patients with localized high-grade STS of the extremity resected with negative margins. Thus, it is not applicable to all patients with STS, particularly those with low-grade lesions or those who have positive margins. Our inclusion of institution-specific features, such as “SURGEON,” “SERVICE,” and “REFERRING ZIP CODE,” further limits the model’s applicability and were included simply as a description of our current patient population. Second, like other machine-learning techniques, Bayesian methods have imperfections, especially when trained using censored observations.²⁴ Other methods such as proportional hazard regression²⁵ may better describe the likelihood of disease-specific death in the presence of censored data. However, graphically representing the hierarchical relationships between features (the purpose of this study) is not possible, by this method. We recognize this limitation and in lieu of developing a prognostic model, we performed an initial, descriptive Bayesian analysis designed to compare our results to previously reported data. The relationships described by the current model are similar to those previously reported; and cross-validation, which was performed as a general metric of overall robustness, yielded encouraging results. Nevertheless, the effect of censoring on Bayesian analysis is the subject of continued research, and future studies that include broader populations of patients with extremity sarcomas are under way to better define the role of Bayesian modeling in these patients. Next, feature selection was performed prior to cross validation, which could theoretically result in overstatement of model robustness. As such, adoption of the model structure depends on similarities between it and BBN models developed in other, independent datasets. Finally, this cohort is from a highly selected, relatively homogeneous referral population and the generalizability of subsequent Bayesian models depends on their performance in a variety of centers with differing institutional biases and treatment philosophies. Other variables that are potentially important, such as compartmentalization,²⁶ were not available; these variables may be as important as other variables included in this model. Thus, development and validation of future models in other, more diverse patient populations is required and has already been planned.

The present analysis demonstrates that Bayesian modeling, an inductive statistical method, can be used to illustrate the complex hierarchical relationships between features and can thus function as an adjunct to existing nomograms. Controlling for tumor grade and resection margin status, as we did in this study, helps to easily visualize the relative importance of time to LR, primary tumor size, histology, and other features with respect to DSS. Perhaps most importantly, this type of modeling can provide insights into the interrelationships between various prognostic features that can then be explored further either by more restrictive Bayesian models or by defined population nomograms.