Abstract
Electroencephalogram shortly termed as EEG is considered as the fundamental segment for the assessment of the neural activities in the brain. In cognitive neuroscience domain, EEG-based assessment method is found to be superior due to its non-invasive ability to detect deep brain structure while exhibiting superior spatial resolutions. Especially for studying the neurodynamic behavior of epileptic seizures, EEG recordings reflect the neuronal activity of the brain and thus provide required clinical diagnostic information for the neurologist. This specific proposed study makes use of wavelet packet based log and norm entropies with a recurrent Elman neural network (REN) for the automated detection of epileptic seizures. Three conditions, normal, pre-ictal and epileptic EEG recordings were considered for the proposed study. An adaptive Weiner filter was initially applied to remove the power line noise of 50 Hz from raw EEG recordings. Raw EEGs were segmented into 1 s patterns to ensure stationarity of the signal. Then wavelet packet using Haar wavelet with a five level decomposition was introduced and two entropies, log and norm were estimated and were applied to REN classifier to perform binary classification. The non-linear Wilcoxon statistical test was applied to observe the variation in the features under these conditions. The effect of log energy entropy (without wavelets) was also studied. It was found from the simulation results that the wavelet packet log entropy with REN classifier yielded a classification accuracy of 99.70 % for normal-pre-ictal, 99.70 % for normal-epileptic and 99.85 % for pre-ictal-epileptic.
Keywords: Electroencephalogram, Entropy, Recurrent Elman neural network, Wavelet packets, Log energy entropy, Norm entropy
Introduction
Electroencephalogram shortly referred as EEG is used as a physiological indicator to assess the continuous neuronal activities of the brain. Of specific, epileptic seizures are considered as a chronic neurological disorder that occurs due to abnormal excessive or synchronous neuronal activity in the brain of patients suffers from epilepsy (Fisher et al. 2005; Gao et al. 2011; Pippa et al. 2016). Continuous monitoring of EEG is essential for the recognition/detection of seizures and such a procedure is tedious for the neurologist through qualitative visual inspection. Designing an automated system to detect epilepsy on time would be helpful and time-saving for the neurologist. Lately, numerous mechanized frameworks have been proposed for the forecast and recognition of epilepsy with distinctive time and frequency domain features, non-linear features with pattern classifiers (Gotman and Deng 1991; Acharya et al. 2012a, b, c; Bajaj and Pachori 2013; Wang et al. 2013; Venkataraman et al. 2014; Samiee et al. 2015; Faust et al. 2015; Du et al. 2016).
It is well known that the computerized seizure detection merely relies on the selection of appropriate EEG feature. Time domain, frequency domain, time–frequency, non-linear domain features were applied for deriving these feature from EEG recordings. Specifically, entropy based related studies have shown significant specificity and sensitivity quantitative measures for the recognition of epileptic seizures. Any EEG-based quantitative study towards epileptic seizure detection requires the appropriate application of filtering, segmentation, features selection and pattern classifier techniques. Although several attempts have been made by make use of entropy as a feature pattern to detect epileptic seizures from EEG recordings (Aydin et al. 2009; Pravin et al. 2010; Guo et al. 2010; Wang et al. 2013), there are still unsolved issues related to computational complexity and overall performance. The appropriate selection of feature and pattern classifier by considering its relative performance will confirm its suitability for the real time seizure detection. This specific research study makes use of wavelet packet based log and norm entropies along with recurrent Elman neural network (REN) for the classification of normal versus pre-ictal, normal versus epileptic and pre-ictal versus epileptic. The proposed work makes use of the University of Bonn, Germany, database (Andrzejak 2001) and three different entropies, log energy entropy, wavelet packet log energy and norm entropies were applied to extract entropy features from EEG recordings. The time–frequency characteristic of the EEGs and its non-linear nature is well exploited by making use of wavelet packet based on Haar mother wavelet with 5th level decomposition and entropy measure respectively. It has been reported that the physiological signals with disorders (abnormality) tend to yield high entropy values (Natwong et al. 2006; Wang et al. 2011; Das and Bhuiyan 2016). The features considered in our work were based on energy present in the signal which relatively increases the magnitude of the entropy value and shows a distinguishable difference between normal, pre-ictal and pure epileptic EEG. Further relative performance in terms of classification accuracy and computational complexity confirms the suitability of this proposed scheme for real-time seizure detection compared to the other techniques reported in the literature (Srinivasan et al. 2007; Pravin et al. 2010; Wang et al. 2011; Acharya et al. 2012a; Xiang et al. 2015).
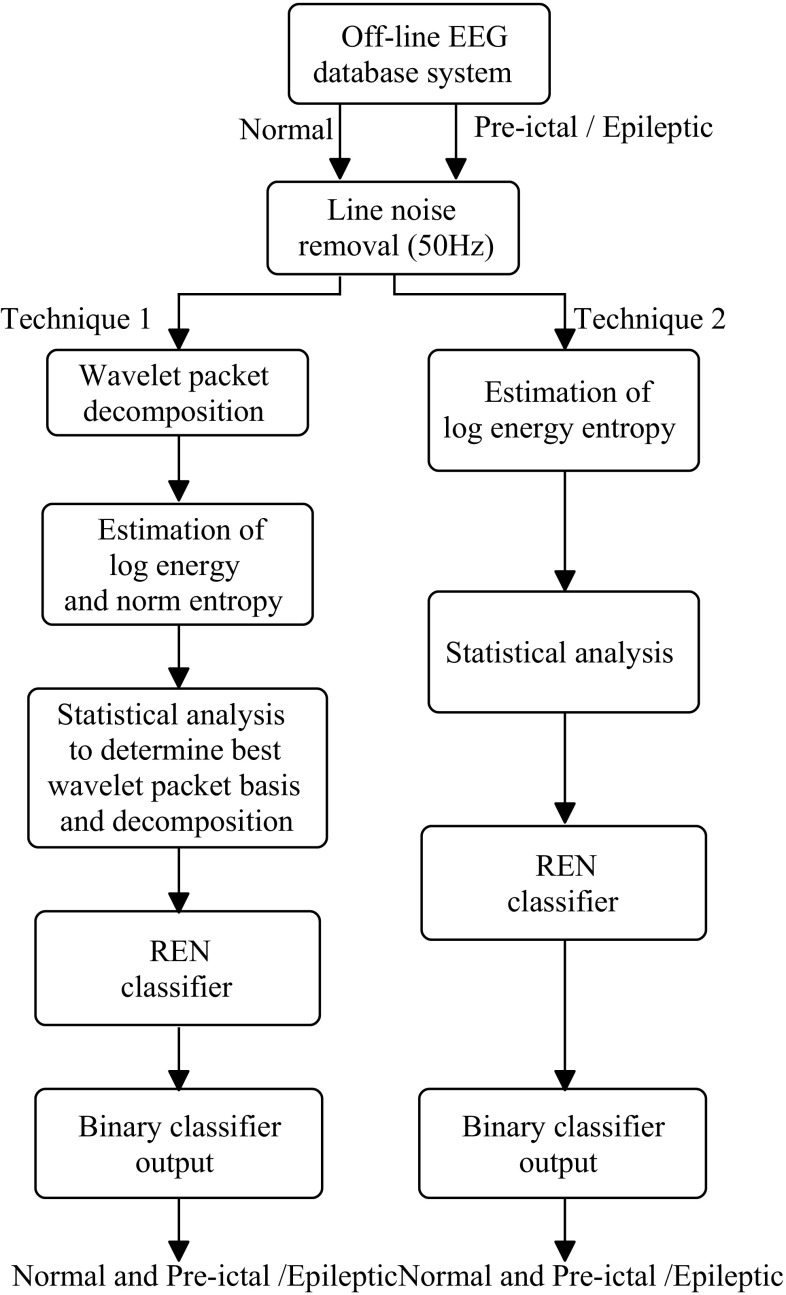
Figure 1 shows the proposed approach schematic diagram.
Fig. 1.
Block diagram of the proposed epileptic detection system
During the visual inspection by the local specialist, the presence of line noise in the Bonn database was observed and same was evident through the periodogram and spectrogram analysis. An adaptive least mean square (LMS) algorithm was applied to remove the power line noise from the raw EEGs and then wavelet packet based entropies were estimated. The best basis was confirmed by the statistical analysis and the identified features were then applied as the input to REN classifier to perform the binary classification: normal-pre-ictal, normal-epileptic and pre-ictal-epileptic. The performance of the WPE- REN was compared with log energy entropy feature with REN classifier.
Related literature review
In early 1980’s, Gotman initiated an automated procedure for long duration EEG recordings (Gotman 1982). In 2007, Srinivasan et al. showed an attainment of 100 % classification accuracy by making use of approximate entropy (ApEn) with a REN classifier. A study proposed by Pravin et al. (2010) making use of sample, spectral and wavelet entropies with REN network showed a classification accuracy of 94.5 %. Zhou et al. (2013) have applied Lacunarity feature with Bayesian linear discriminant analysis (BLDA) classifier for epileptic seizure detection and showed a classification rate of 96.25 %. Samiee et al. (2015) introduced rational discrete short time Fourier transforms (DSTFT) with multilayer perception (MLP) neural network for classification of epileptic seizures from normal EEGs. Bajaj and Pachori (2013) have applied the Hilbert transformation of intrinsic mode functions to detect the focal temporal lobe epilepsy. Kumar et al. (2014) have investigated the discrete wavelets transform (DWT) based ApEn and multilayer back propagation neural network to discriminate normal and epileptic seizures. Koren et al. (2015) have done a detailed clinical investigation towards the recognition of non-convulsive seizures and non-convulsive status epileptics. Venkataraman et al. (2014) proposed an automated seizure detection algorithm by making use of adaptive short-term maximum Lyapunov exponent and adaptive Teager energy. Kelly et al. (2010) have made use of scalp based electrodes for the assessment of epileptic seizures. Three significant features, pattern-match regulation static, local maximum frequency and amplitude variation were used to quantify the seizures.
Pippa et al. (2016) proposed a clinical study to investigate the effect of psychogenic non epileptic seizures and vasodepressor syncope. Several time and frequency domain features with different pattern classifier were employed. The study revealed a classification accuracy of 95 % was achieved. Abualsaud et al. (2015) have proposed an EEG-based epileptic seizure framework that makes use of compressed sensing phenomenon and encoding technique for transmission of data followed by automated detection of seizure at the receiver side using linear and non-linear classifier. An attempt has been made by making use of smoothed pseudo-Wigner-Ville distribution to recognize the seizure from normal EEGs (Tzallas et al. 2007). Zeng et al. (2016) have employed compressive sensing principle for recognizing inter-ictal, pre-ictal and ictal EEG-based epileptic seizures. Sample and permutation entropies with Hurst index features were applied along with four variant classifiers. The performance results obtained were quite promising and confirm it’s suitable for tele-monitoring of epileptic patients. Best result was achieved using discriminant analysis (DA) for compressed sensing structure similarity feature (CS-SSIM). A focused study that makes use of four entropies namely ApEn, sample entropy (SampEn), phase entropy 1 (S1), and phase entropy 2 (S2) for automated detection of normal, pre-ictal and ictal conditions derived from EEGs was proposed. Seven different classifiers were employed and an overall accuracy of 98.1 % was achieved (Acharya et al. 2012a). A specific work that makes use of fuzzy entropy for epileptic seizures recognition was reported (Xiang et al. 2015). The fuzzy entropy was estimated based on the working principle of ApEn and the results were compared with the sample entropy. A grid optimization method was proposed to train the features using support vector machine (SVM) classifier. Gajic et al. (2014) have proposed classification algorithm using wavelets and statistical pattern recognition for the detection of epileptic seizures. Wang et al. (2010) have applied principal component analysis for dimension reduction to the décorrelation of epileptic and normal EEG. Then DWT combined with ApEn is performed and found distinct difference between the ApEn values of epileptic and normal EEG.
Faust et al. (2015) reported a detailed review of wavelet based technique for epileptic seizure detection. The study included wavelet decomposition followed by non-linear dynamic based entropy features. The importance of supervised and unsupervised pattern classifiers were also reported. Acharya et al. (2012c) have applied two entropies namely ApEn and SampEn along with fractal dimension and Hurst exponent as features with fuzzy classifier for the classification of normal and epileptic seizures from EEG recording. It was shown classification accuracy of 99.7 % attained using combined non-linear features. Srinivasan et al. (2007) and Pravin et al. (2010) have applied ApEn and SampEn, achieved 100 and 94.5 % classification accuracy respectively. It can be inferred that all such procedures yields good classification rate with high classification cost. Acharya et al. (2012c) make use of wavelet packet decomposition to extract Eigen values from the wavelet coefficient using principal component analysis. Significant features were selected using ANOVA test and 99 % classification accuracy was obtained using Gaussian mixture model (GMM) classifier with tenfold cross validation. Aydin et al. (2009) make use of log energy entropy with a multilayer neural network for distinguishing epileptic EEGs from normal. Our work makes use of WPT followed by log energy entropy to explore the low-frequency components during epileptic EEG signal and recorded best results compared to work done by Aydin et al.
It can be observed from the recent literature (Srinivasan et al. 2007; Pravin et al. 2010; Acharya et al. 2012a; Kumar et al. 2014) that the time–frequency domain features ensures good classification accuracy at extreme computational cost. Specifically, approximate entropy (Srinivasan et al. 2007) and sample entropy (Pravin et al. 2010) features showed a good classification accuracy but their computational cost related to feature estimation found to be very high and hence had its own limitation for real-time seizure detections. One can infer from the literature that the entropy-based features ensure good classification results compare to the other time–frequency domain features, there is a need to perform detailed research study to determine the trade-off between classification accuracy and computational complexity by making a selection of appropriate entropy-based features.
While considering the University of Bonn database for the experimental study, there is a symptom of the presence of line noise and to the best of authors knowledge, attempts have not been made for the removal of line noise as a preprocessing procedure.
To solve the above mentioned issues, the proposed approach make use of an adaptive filter, wavelet packet transform, log energy entropy, norm entropy, REN classifier and relative performance methods. The major contribution of this research work is the removal of line noise in the EEGs with appropriate recognition of the statistical variations during normal, pre-ictal and epileptic activities through wavelet based log and entropy features. Then, the relative performance in terms of classification accuracy and computational complexity ensures the suitability of the proposed method for real-time automated seizure detection.
Materials and methods
EEG dataset
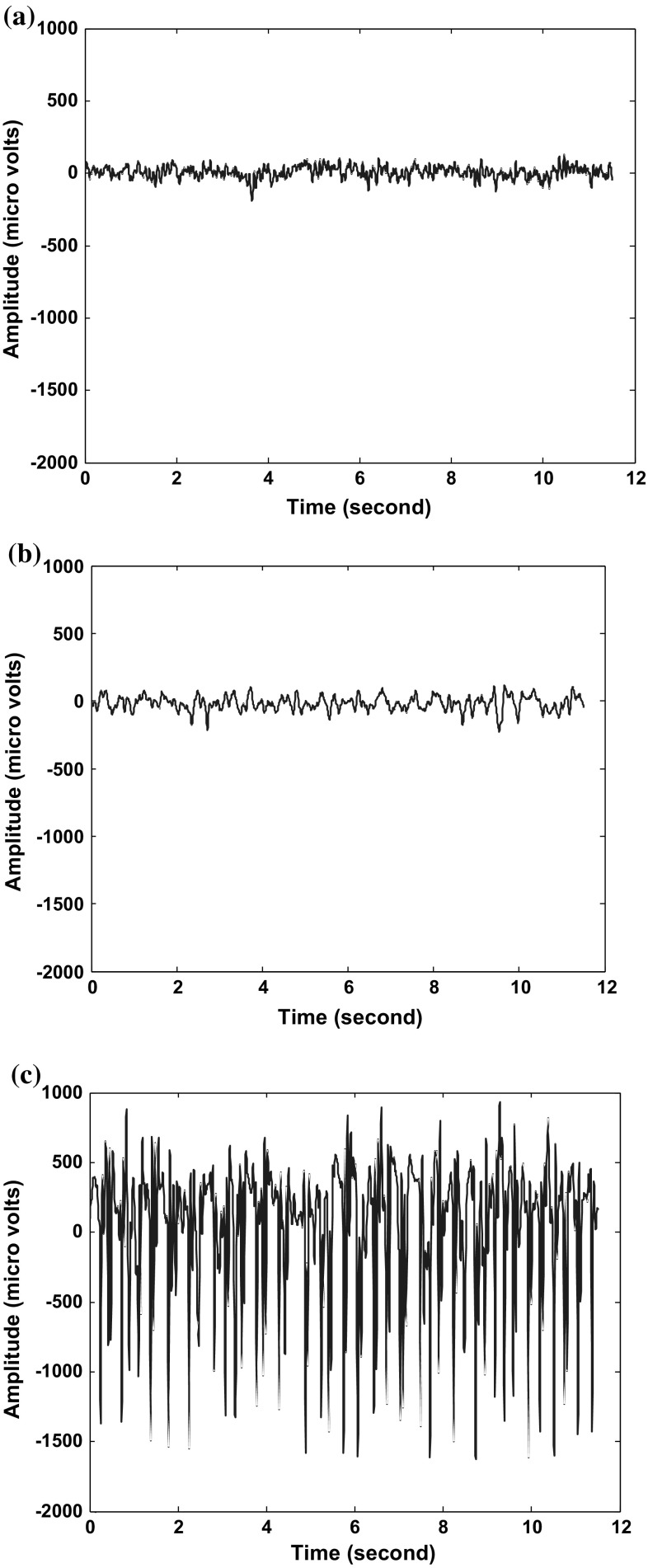
For the proposed study, EEG datasets were obtained from University of Bonn, Germany. Three conditions, normal (set A), pre-ictal (set C) and epileptic seizures (set E) were considered and corresponding datasets were used. For further details, one can refer the work reported (Andrzejak 2001). Figure 2 shows the sample recording of sets A–C–E respectively. As reported earlier (Andrzejak 2001; Srinivasan et al. 2007; Kumar et al. 2014) the entire datasets were divided into 100 single channel segments with a total duration 23.6 s with a sampling rate of 173.6 Hz.
Fig. 2.
Sample recordings of a Normal EEG b Pre-ictal EEG c Epiliptic EEG
Line noise removal
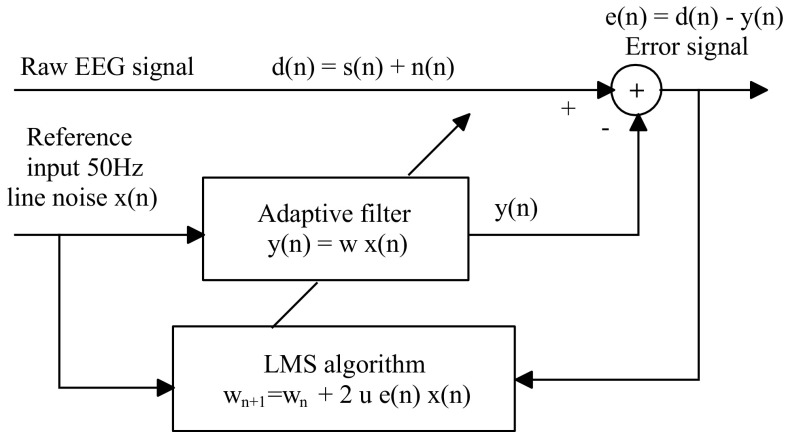
It is well-known fact that the artifacts such as 50 Hz power line noise are added during EEG recordings. Such artifact leads to the wrong diagnosis during the clinical inspection by a specialist. In the proposed study, line noise was observed during the clinical interpretation by the specialist, which was also in evident through periodogram and spectrogram analysis. To eliminate the line noise, an adaptive Weiner filter was employed. (Tan and Jiang 2008). The filter removes the 50 Hz power line noise from the raw EEGs by making use of LMS algorithm (Haykin 1996). Figure 3 shows the structure used for the current study.
Fig. 3.
Structure of adaptive filter using LMS algorithm
The LMS algorithm is defined as below:
The corrupted EEG signal can be expressed as (Tan and Jiang 2008)
| 1 |
An error signal is expressed as
| 2 |
An error signal is approximately equal to desired line noise free EEG signal.
Output of the filter is
| 3 |
And filter coefficients by LMS algorithm is given by (Tan and Jiang 2008)
| 4 |
where n = sample index; s[n] = Actual signal (EEG signal); n[n] = Noise signal (power line noise); d[n] = Corrupted signal (EEG + power line noise); e[n] = Error signal (desired signal); x[n] = Reference input (50 Hz sinusoidal signal); y[n] = Adaptive filter output; μ = Convergence factor (step size); w n = Filter coefficients.
Step size μcontrols how fast and how well the algorithm converges to the optimum filter coefficients so it needs to be selected properly to reach the best performance of the adaptive filter. If μis too larger, the algorithm will not converge, if μ is too small the algorithm converges slowly.
Wavelet packet decomposition
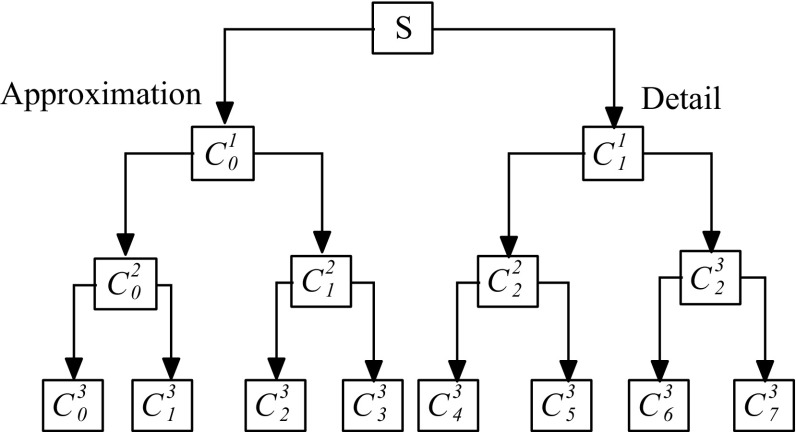
The wavelet packet transform (WPT) is considered as a classical derivative of wavelet transform (WT). Both satisfy the orthogonality condition. Given a non-stationary signal applying these transforms emphasizing the low pass and high pass filtering operations yields the sub-band tree decomposition to some desired level. It is well-known fact that the WT decomposes only approximation coefficients of the signal and successive detail are never considered and taking information located at higher frequency will be lost on the other hand WPT decomposes successive details and approximation, taking good and adjustable frequency resolutions at high frequencies (Adeli et al. 2003; Yang et al. 2006; Ocak 2009). It retains the key information located in higher frequency than WT for certain applications. The bottom level of WPT has better frequency resolution, whereas top level is considered as the time representation of the signal.
A typical 3-level WPT decomposition sub-band tree is depicted in Fig. 4. The two infinite filters shown correspond to wavelet, i.e. a low pass filter h(k) and high pass filter g(k) (Han et al. 2013). Using these two filters the wavelet packet function can be defined as (Mallat 1989)
| 5 |
| 6 |
where ψ(t) is the mother wavelet function. The recursive relation between jth level and the (j + 1)th level for signal s(t)are (Mallat 1989)
| 7 |
| 8 |
Fig. 4.
Decomposition tree for three-layer WPT
Thus, wavelet coefficients c jk at position k of level j can be expressed as (Mallat 1989)
| 9 |
In our study, wavelet packet transform is implemented by using Haar function as mother wavelet with 5th level decomposition from the previous study (Raghu et al. 2015).
Feature extraction
Log energy entropy
Entropy is a common in many fields, mainly in signal processing and communication. In biomedical signal processing, lengthy EEGs recording needs more time to do analysis and these lengthy data or signals can be viewed as entropy to differentiate seizures from normal EEGs. Entropy gives a measure of signal disorder or complexity and provides distinctive features about the signal (Shannon 1948). There are many types of entropy such as Shannon entropy, log energy entropy, norm entropy, threshold entropy, fuzzy entropy and approximation entropy that are employed in estimating information from signals. The two entropies, log energy and norm entropy investigated in this proposed study were not based on concept of a probability. These two entropies are estimated based on the energy present in the signal and entropy may result in higher values. The normalization of the signals is not performed in the case of wavelet entropy and this fact is well exploited in this proposed work.
EEG signal can be defined as the variation in amplitude w.r.t. time. The best way to acquire entire information from the signal is to square the signal. Squaring the EEG time series doesn’t lead to a decrement of signal energy instead, it results in higher values (Selik et al. 2001). s = (s 1, s 2, s 3,….., s n), where s is a wavelet packet decomposed EEG signal with n samples, energy of the signal is calculated in following way
The log energy entropy is defined as (Coifman et al. 1990),
| 10 |
| 11 |
E1(s) gives a log energy entropy value for a 1 s segment. The same procedure was employed for rest of the EEGs to estimate log energy entropy.
Norm entropy
The norm entropy neither uses normalization nor log function and it is based on the value ofpin the power. The norm entropy is defined as the concentration inl pnorm entropy with p ≥ 1
| 12 |
| 13 |
In this work, p value is chosen as 1.
Artificial neural network classification
Recurrent Elman neural network (REN) also referred as Elman neural network found to be a potential candidate for the pattern classification problems (Elman 1990; Srinivasan et al. 2007; Tang and Li 2011; Sriraam 2013). The typical architecture of that has been considered for the proposed study is shown in Fig. 5. The neural nodes 1-90-90-1 were considered with three additional context nodes for establishing feedback from hidden to input layers. Two hidden layers with ninety hidden neurons were found to be sufficient to train the network for attaining the convergence during the experimental study. For the input hidden layer, tan-sigmoidal activation function and hidden output layer, log sigmoidal activation function was employed. A resilient back-propagation (RP) learning algorithm with an adaptive learning rate of 0.6 was used to train the REN network. Table 1 shows the recurrent Elman neural network setting parameters. Nguyen- Windrow algorithm was employed during the initialization of hidden layer weights.
Fig. 5.
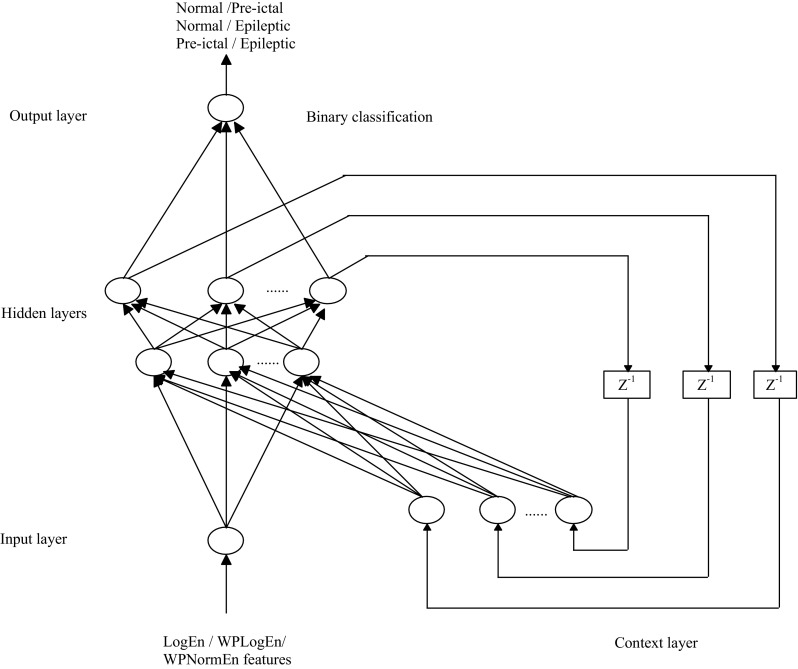
Recurrent Elman neural network architecture
Table 1.
REN training parameters
| Training parameters | Value |
|---|---|
| Initial learning rate | 0.6 |
| Learning rate increase (LRI) | 1.06 |
| Learning rate decrease (LRD) | 0.8 |
| Performance goal (MSE) | 0.01 |
The classification performance of REN classifier was evaluated by in terms of four parameters namely, specificity (SP), sensitivity1 (SE1), sensitivity2 (SE2) and classification accuracy (CA) (Srinivasan et al. 2007).
| 14 |
| 15 |
| 16 |
| 17 |
Three cases were considered for classification purpose.
Case A: Normal-Pre-ictal
Case B: Normal-Epileptic
Case C: Pre-ictal-Epileptic
Performance evaluation
For the experimental study, set A, set C and set E reflecting normal eye open, pre-ictal and epileptic seizure EEG recordings were considered from University of Bonn database (Andrzejak 2001). An adaptive filter reported earlier was applied to remove line noise from raw EEGs. The convergence factor μ = 0.005 and order N = 3 was selected for adaptive filter implementation. The estimation of periodogram clearly reveals the presence and removal of noise as depicted in Fig. 6a–d respectively.
Fig. 6.
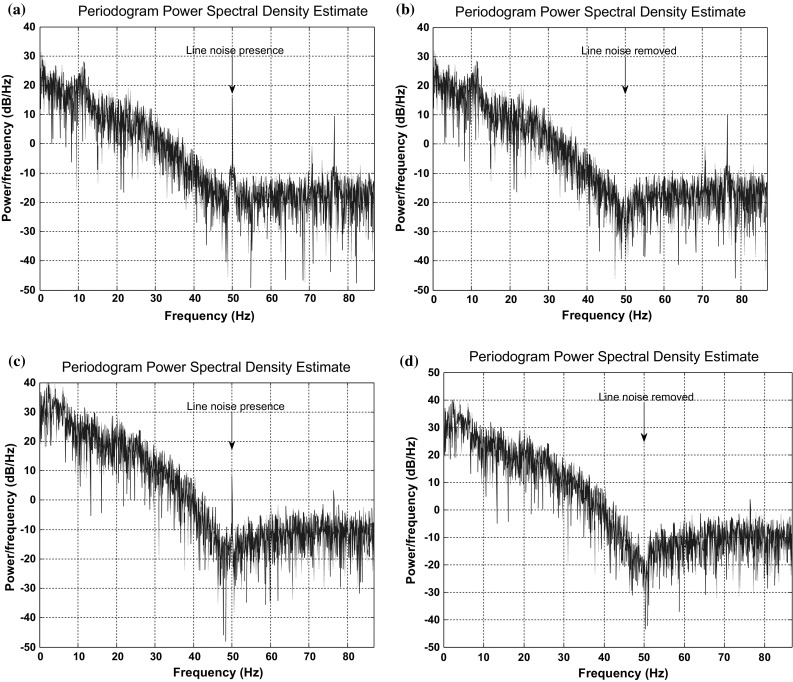
Power spectral density of a Normal EEG with line noise b Normal EEG without line noise c Epileptic EEG with line noise d Epileptic EEG without line noise
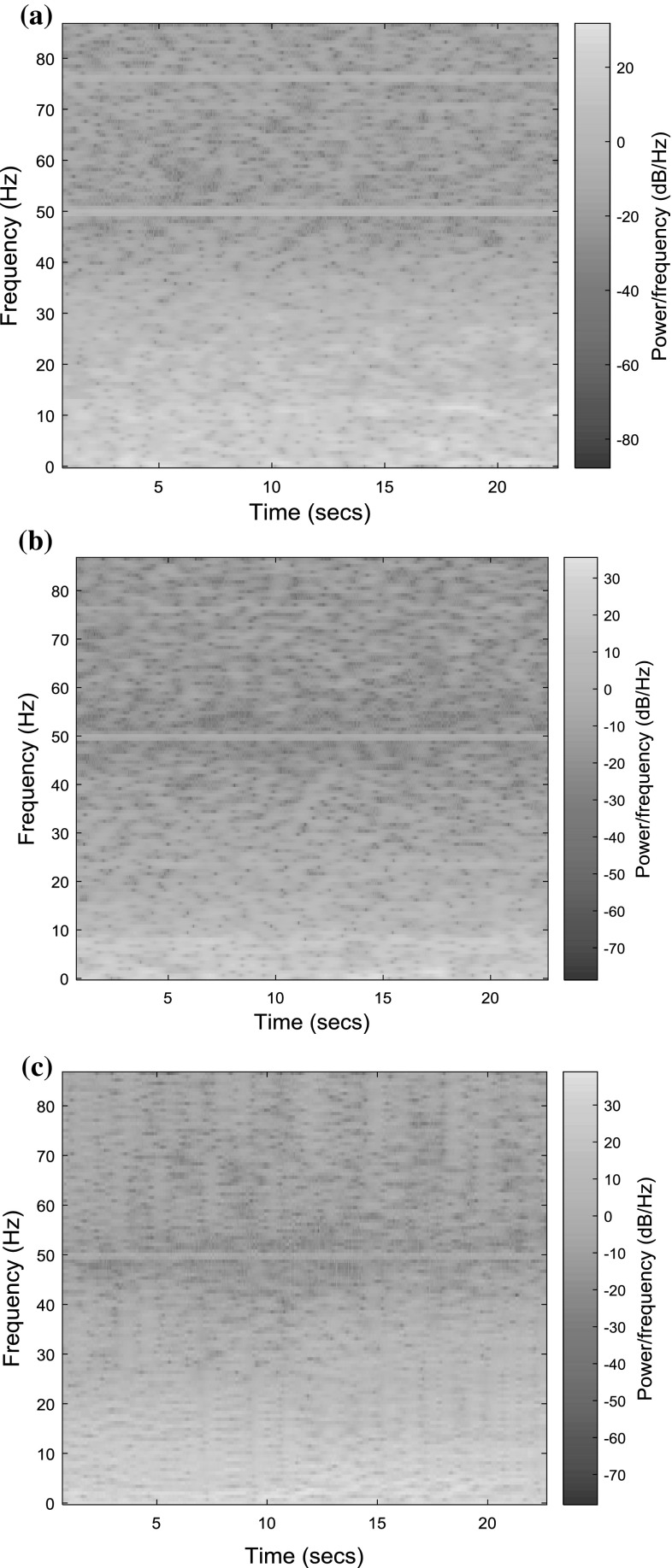
The spectrogram analysis also ensures the presence of line noise as shown in Fig. 7a–c. The spectrogram shows the time–frequency components of the EEG signal using short-term Fourier transform.
Fig. 7.
Spectrogram of a Normal EEG b Pre-ictal EEG c Epileptic EEG
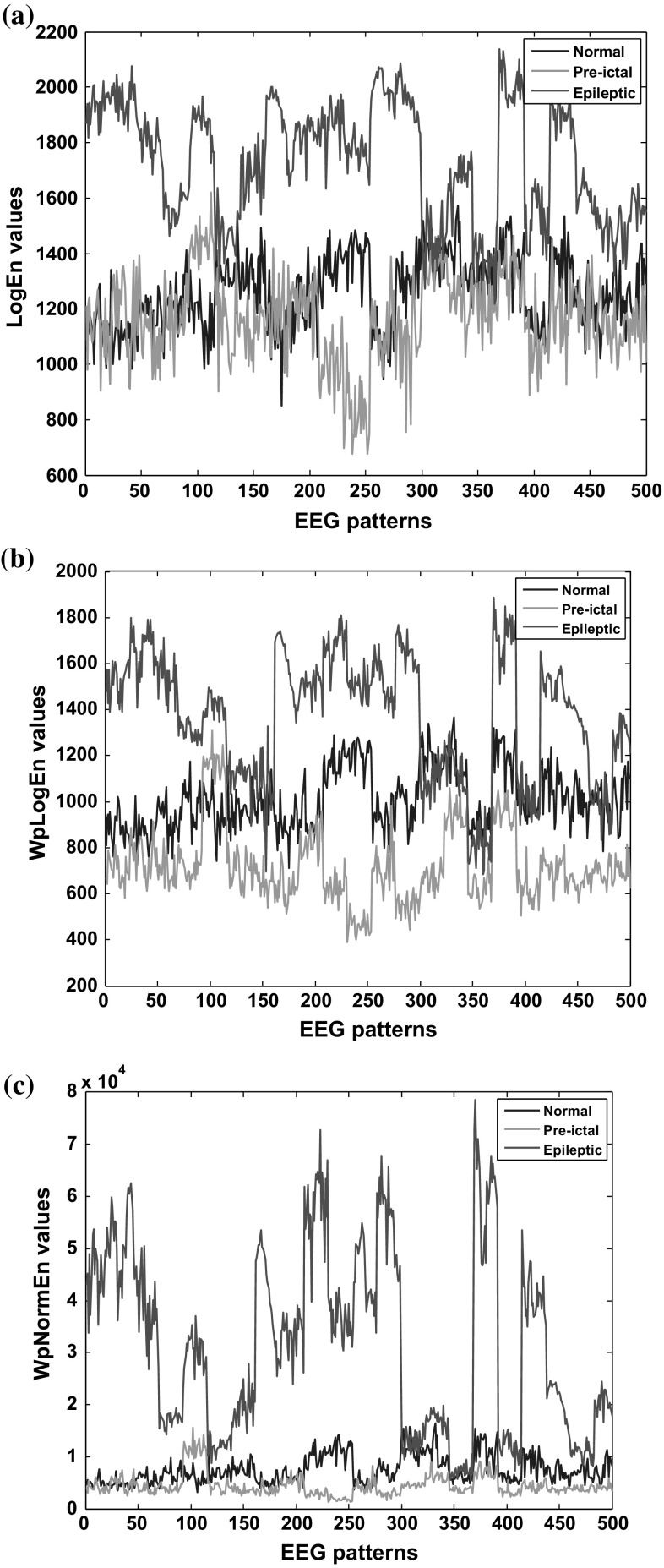
In order to preserve the stationarity for non-linear EEGs, a 1 s windowing was introduced to the filtered recordings. For each 1 s segmented time series (say, EEG pattern) three entropies namely, log energy entropy (LogEn), wavelet packet log energy entropy (WPLogEn) and wavelet packet norm entropy (WPNormEn) were estimated. In this proposed study, Haar wavelet with 5th level decomposition has been applied to decomposed EEG (Raghu et al. 2015). Figure 8a–c show the pattern distribution for the different conditions using three entropy features.
Fig. 8.
Entropy values for normal, pre-ictal and epileptic EEGs using a Log En features b WPLogEn features c WPNormEn features
It can be observed from Fig. 8a–c that the entropies provide significance variation under the three conditions. LogEn values are higher in epileptic states than in normal and pre-ictal states. But these values are in same range for normal and pre-ictal states, it would be difficult to achieve good classification accuracy (refer Fig. 8a). A good discrimination was obtained by applying wavelet decomposition on EEGs before estimating entropy values. The influence of wavelet packet decomposition on EEG signals can be seen in Fig. 8b. Among the three features, WPLogEn feature shows a clear band difference compared to other features.
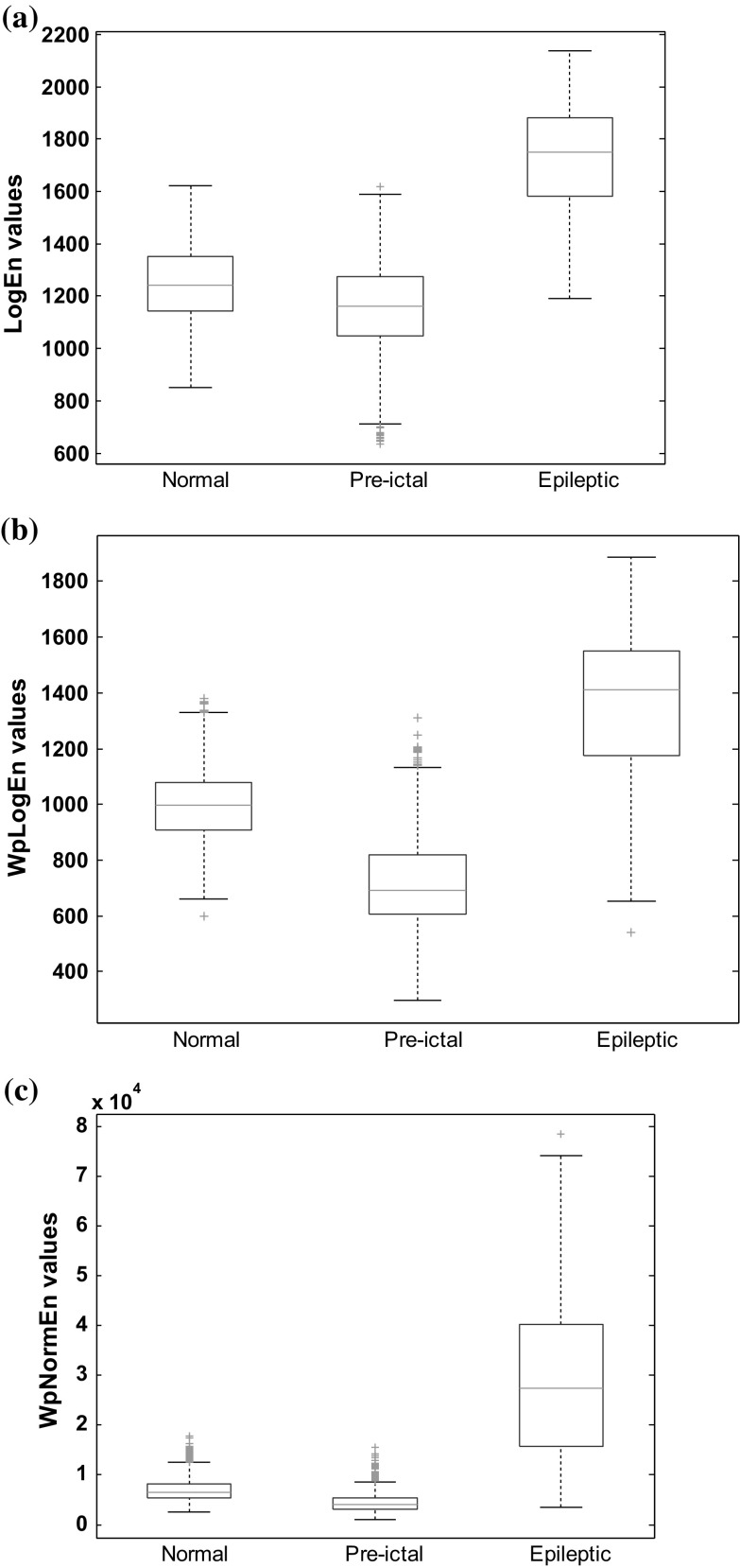
To recognize the importance of selected feature for its significance for the pattern classification, statistical analysis using ANOVA and Wilcoxon model was employed. Since EEG signal is a non-stationary signal, the Wilcoxon non-parametric test was applied for the analysis. Further Box plot analysis demonstrates the median value with interquartile distances with skewed distribution. The typical box plot has lines at the upper median and lower quartile values. Further Boxplot analysis (refer Fig. 9) confirms the suitability of the feature for pattern classification. The significance of wavelet packet decomposition on EEGs for WPLogEn gives good discrimination between normal and pre-ictal (refer Fig. 9a, b).
Fig. 9.
Box plot for normal, pre-ictal and epileptic EEGs using a LogEn features b WPLogEn features c WPNormEn features
The interesting observation made from Table 2 is that the mean value for pre-ictal EEGs is lower than normal EEGs for all three types of entropies. The WPLogEn is lower than LogEn due to the influence of wavelet packet decomposition on EEGs. Standard deviation is an increasing quantity for LogEn and WPLogEn from normal to pre-ictal to epileptic EEGs, whereas standard deviation for WPNormEn in pre-ictal is lesser than in normal EEGs. A p value is used for testing statistical hypothesis and it found to be less than 0.01 for all combinations of EEG cases except for Case B for LogEn. Decomposition of EEGs using wavelet packet transform results in p value lesser than 0.01 for Case B.
Table 2.
Range (mean ± standard deviation) of entropy features and p value for normal, pre-ictal, and epileptic EEGs
| Normal | Pre-ictal | Epileptic | p value | |||
|---|---|---|---|---|---|---|
| Case A | Case B | Case C | ||||
| LogEn | 1245.01 ± 135.31 | 1154.32 ± 171.51 | 1726.23 ± 197.34 | <0.01 | <0.05 | <0.01 |
| WPLogEn | 991.12 ± 125.45 | 711.79 ± 164.32 | 1367.01 ± 242.31 | <0.01 | <0.01 | <0.01 |
| WPNormEn | 7076.43 ± 2400.9 | 4329.53 ± 1879.01 | 29362.22 ± 15835.02 | <0.01 | <0.01 | <0.01 |
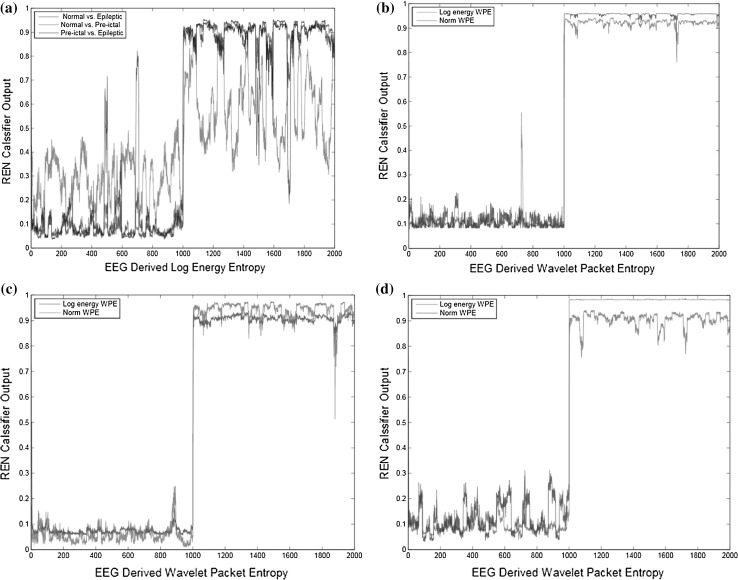
In order to introduce the automated seizure detection procedure, REN classifier was employed with entropy features as input. By considering the typical generalization characteristics of the artificial neural network, only 58 % of the patterns were applied for training using the REN architecture. With the available 2360 patterns (for each condition), 1360 were used for training and 1000 for testing. Figure 10a–d show the performance of REN classifier and Tables 3, 4 and 5 shows the overall classification results using REN classifier with LogEn, WPLogEn, and WPNormEn. The REN classifier gives high CA rate of 99.70 % using WPLogEn with less time and number of iterations as compared to other two features for Case A (refer Table 3). The CA was found very less i.e. 67.10 % using LogEn and maximum CA obtained using WPLogEn for Case B (refer Table 4). For Case C the best accuracy recorded using WPLogEn and it uses less time and iterations to train REN classifier. Among all three entropies WPLogEn shows best results for all the cases.
Fig. 10.
REN classifier output for a LogEn for Case A, Case B, Case C b WPLogEn and WPNormEn for Case A c WPLogEn and WPNormEn for Case B d WPLogEn and WPNormEn for Case C
Table 3.
Classification results using LogEn, WPLogEn and WPNormEn for Case A
| Training | Testing | ||||
|---|---|---|---|---|---|
| No. of iterations | Time (s) | SP (%) | SE1 (%) | CA (%) | |
| LogEn | 1296 | 17 | 0 | 34.20 | 67.10 |
| WPLogEn | 65 | 5 | 100 | 99.40 | 99.70 |
| WPNormEn | 168 | 14 | 99.30 | 99.40 | 99.35 |
Table 4.
Classification results using LogEn, WPLogEn and WPNormEn for Case B
| Training | Testing | ||||
|---|---|---|---|---|---|
| No. of iterations | Time (s) | SP (%) | SE2 (%) | CA (%) | |
| LogEn | 961 | 13 | 99.40 | 100 | 99.70 |
| WPLogEn | 53 | 9 | 100 | 99.40 | 99.70 |
| WPNormEn | 101 | 16 | 99.55 | 99.30 | 99.42 |
Table 5.
Classification results using LogEn, WPLogEn and WPNormEn for Case C
| Training | Testing | ||||
|---|---|---|---|---|---|
| No. of iterations | Time (s) | SE1 (%) | SE2 (%) | CA (%) | |
| LogEn | 76 | 11 | 98.30 | 95.10 | 96.70 |
| WPLogEn | 38 | 4 | 100 | 99.70 | 99.85 |
| WPNormEn | 68 | 8 | 100 | 99.30 | 99.60 |
Discussion
The time varying behavior and non-linear characteristics of EEG signals is well exploited for the studies related to epileptic seizure detection (Adeli et al. 2003; Srinivasan et al. 2007; Tzallas et al. 2007; Panda et al. 2010). The proposed study makes use of log energy, wavelet packet based log energy and norm entropies for the seizure detection. Following were the inference derived from the proposed study.
Although several works using the University of Bonn, Germany, database for EEG-based seizure detection was reported (Andrzejak 2001; Srinivasan et al. 2007; Pravin et al. 2010; Kumar et al. 2014; Chaurasiya et al. 2015), none of the work emphasize on the removal of power line noise from raw EEGs. The application of adaptive LMS algorithm showed a 2 % improvement in terms of classification accuracy compared to the raw EEGs without removal of line noise.
Entropies based detection of an epileptic seizure using EEGs have been studied and well reported in the recent past (Srinivasan et al. 2007; Pravin et al. 2010; Aydin et al. 2009; Wang et al. 2011; Gopan et al. 2015). Srinivasan et al. (2007) have employed ApEn feature with REN network as a classifier and have achieved 100 % CA. The computation cost for estimating ApEn by varying the parameters m, r and N were found to be very high and thus had constraints for real-time seizure detection. For REN, Gradient descent learning algorithm was applied to train the network. The proposed study makes use of RP algorithm and it was found to yield better results in terms of computation time. Attempts have been made using Gradient descent learning algorithm for training REN network and it was observed during the experimental study that the computation time was large compared to RP learning algorithm. Similarly, Pravin et al. (2010) have shown the influence of spectral, sample and wavelet entropies.
In the proposed study, the application of wavelet packet based log and norm entropies found proven for seizure detection due to the nature of WPT and its ability to detect varying component at a lower frequency. Figure 8a–c confirms these results. Further, the efficiency of wavelet packet based entropy found to show band variation compared to log entropy.
During the experimental study, it was observed that LogEn and norm entropy yielded the same result. Hence comparison analysis was given only with LogEn.
A preliminary study on the wavelet packet decomposition levels (Raghu et al. 2015) on trial and error basis provided the optimal selection of wavelet basis and decomposition level. The proposed study makes use of Haar wavelet basis with 5th level decomposition.
To confirm the suitability of the proposed features for classification problem, Wilcoxon non-linear statistical model was employed. Both p value and Box plot results show the significance of the wavelet packet features than log entropy features.
The selection of pattern classification is very important for the development of automated medical expert system. The proposed study makes use of the REN for classification. Being the feedback network, REN ensures effective training with early convergence and then ensuring the low computational requirement. With the MATLAB R13 environment, the network further yielded less computational time compared to the work reported earlier (Srinivasan et al. 2007; Pravin et al. 2010; Sriraam 2012, 2013). It can be inferred from the results shown in Fig. 10a–d show the wavelet packet entropy with REN proven to be excellent pattern recognition compared to the other neural network including SVM where computational burden found to be large.
-
The performance of the proposed method was evaluated in terms of new index parameter called relative performance (RP), which is defined as (Sriraam and Eswaran 2008; Sriraam and Shyamsunder 2011):
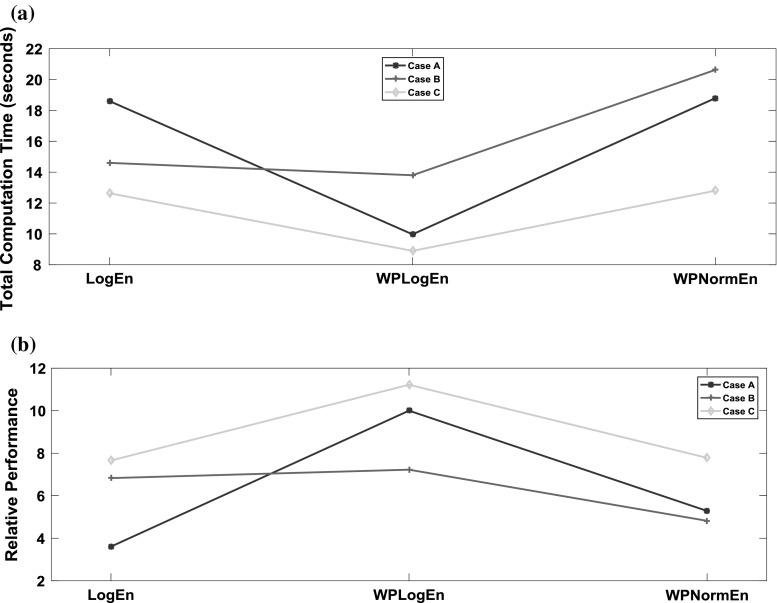
18 The computation time was calculated based on the preprocessing, feature extraction, training and testing phase of the REN classifier. Higher the RP value shows the efficiency of the technique. Figure 11a–b show the plots for computational time and relative performance index using all the three feature parameters employed in the proposed study.
It can be inferred from Fig. 11a–b that the RP clearly indicates the overall performance of the feature extraction parameter along with recurrent Elman neural network. Among the three entropies, WPLogEn outperforms compared to the other two techniques. The study reported by Srinivasan et al. (2007), Acharya et al. (2012a, c) have employed ApEn and SampEn where the computational cost of feature estimation were found to be high. The proposed technique overcomes such limitations (computational complexity and classification accuracy.
-
A similar work reported using non-normalization based Shannon entropy features obtained from best basis wavelet packet decomposition (Wang et al. 2011). The study was based on wavelet packet entropy computations using the Eq. (18) (Shannon 1948).
where s i is coefficient of a signal in an orthonormal basis.19 Compared to the results obtained using Shannon entropy, the proposed wavelet packet log energy and norm entropies found to be superior in terms of computational complexity. The Shannon entropy based wavelet packet coefficients possess large value and due to this computational time were found to be large. The proposed technique overcomes this problem.
-
An overall comparison of the work proposed in the literature with the proposed study is shown in Table 6. All the work has made use of the University of Bonn, Germany, database for the seizure detection. From the Table 6, it can be observed that the proposed technique outperforms results reported by Srinivasan et al. (2007), Pravin et al. (2010).
But due to the excellent computational processing facilities (Intel® core ™ i5) with R2013a MATLAB version, the proposed algorithm required less computational time with an overall classification accuracy of 99.70 %. It can be concluded that the proposed wavelet packet entropies with recurrent Elman network classifier classifier can be considered as the potential candidate for epileptic seizure detection problems. As a future step multi-classification will be considered between normal, pre-ictal and epileptic as future work with different mother wavelets and classifiers. The entire methodology will be implemented using SCILAB platform due to its open source availability option for clinical implementation.
Fig. 11.
a Total computation time b Relative performance of the proposed method
Table 6.
A Comparison of overall classification accuracy obtained by proposed method and other’s method for EEG classification problems
| Author (s) | Year | Features | Classifier | EEG Bonn Data | CA (%) |
|---|---|---|---|---|---|
| Panda et al. | 2010 | Wavelet based energy, Standard deviation and entropy | SVM | A–E | 91.2 |
| Srinivasan et al. | 2007 | ApEn | REN | A–E | 100 |
| Ocak | 2009 | WT based relative wavelet energy | Surrogate data analysis | A–E | 98 |
| Guo et al. | 2010 | DWT based relative wavelet energy | MLP | A–E | 95.2 |
| Pravin et al. | 2010 | Wavelet entropy | REN | A–E | 99.75 |
| Wang et al. | 2011 | Best basis wavelet packet entropy | K-NN | A–E | 100 |
| Acharya and Molinari et al. | 2012 | ApEn, SampEn, phase entropy 1, phase entropy 2 | Fuzzy | A–E | 98.1 |
| Acharya and Sree et al. | 2012 | Eigen values | GMM | A–E | 99 |
| Acharya and Alvin et al. | 2012 | ApEn, SampEn, fractal dimension Hurst exponent |
Fuzzy | A–E | 99.7 |
| Zhou et al. | 2013 | Lacunarity | BLDA | A–E | 96.25 |
| Kumar et al. | 2015 | One-dimensional local binary pattern | K-NN | A–E | 98.33 |
| Samiee et al. | 2015 | DSTFT | MLP | A–E | 98.1 |
| Chaurasiya et al. | 2015 | Hilbert huang transform | SVM | A–E | 96.25 |
| Alotaiby et al. | 2015 | Original common spatial pattern | SVM | A–E | 93.15 |
| Gopan et al. | 2015 | Entropy | Fuzzy K-NN |
A–E | 89.8 |
| Zeng et al. | 2016 | CS-SSIM | DA | A–E | 76.7 |
| Pippa et al. | 2016 | Time and frequency domain features | Bayesian network | A–E | 95 |
| Proposed work | 2016 | WPLogEn | REN | A–C A–E C–E |
99.70 99.70 99.85 |
| WPNormEn | REN | A–E A–C C–E |
99.35 99.42 99.60 |
Set A refers normal, Set C refers pre-ictal and Set E refers epileptic EEG
Conclusion
The proposed research study suggested a combinational variant feature, wavelet packet log energy and norm entropies that possess time–frequency domain and non-linear domain characteristics to investigate the EEG time series. In order to distinguish normal, preictal and epileptic seizures, wavelet packet log energy and norm entropies based feature were deployed and its performance was compared with log energy entropy. Periodogram and spectrogram techniques were employed on EEG to test the presence of line noise and it was eliminated by applying Weiner adaptive filter. A recurrent Elman neural network classifier was employed to perform binary pattern classification. From the experimental study, ANNOVA test, Wilcoxon statistical test and Box plot results showed the distinguishable variation using the wavelet packet entropy features for normal, pre-ictal and epileptic conditions. It was found from the simulation results that the wavelet packet log entropy with REN classifier yields a good classification accuracy of 99.70 % for normal-pre-ictal, 99.70 % for normal-epileptic and 99.85 % for pre-ictal-epileptic respectively. The overall effectiveness of the proposed technique was evaluated in terms of relative performance index which proved wavelet packet log energy entropy feature with recurrent Elman network as the potential candidate for epileptic seizure classification from normal EEG as compared to the earlier methods reported in the literature.
Acknowledgments
The authors would like to acknowledge Dr. R.G. Andrzejak of University of Bonn, Germany, for providing permission to use the EEG data available in the public domain. The authors would like to thank Dr. A.S. Hegde, Centre for Neuro Science, M.S. Ramaiah Memorial Hospital, Bangalore, India for the useful discussion. The authors would also like to thank the anonymous reviewers for their helpful comments and suggestions that greatly improved the quality and clarity of the manuscript.
Compliance with ethical standards
Conflict of interest
There is no conflict of interest involved in the proposed study.
References
- Abualsaud K, Massudi M, Saleh M, Mohamed A. Ensemble classifier for epileptic seizure detection for imperfect EEG data. Sci World J. 2015 doi: 10.1155/2015/945689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Acharya UR, Molinari F, Vinitha SS, Chattopadhyay S, Kwan-Hoong N, Suri JS. Automated diagnosis of epileptic EEG using entropies. Biomed Signal Process Control. 2012;7(4):401–408. doi: 10.1016/j.bspc.2011.07.007. [DOI] [Google Scholar]
- Acharya UR, Alvin AP, Sree SV, Yanti R, Suri JS. Application of non-linear and wavelet based features for the automated identification of epileptic EEG signals. Int J Neural Syst. 2012;22(2):1250002. doi: 10.1142/S0129065712500025. [DOI] [PubMed] [Google Scholar]
- Acharya UR, Sree SV, Suri JS, Alvin AP. Use of principal component analysis for automatic classification of epileptic EEG activities in wavelet framework. Exp system Appl. 2012;10(39):9072–9078. doi: 10.1016/j.eswa.2012.02.040. [DOI] [Google Scholar]
- Adeli H, Zhou Z, Dadmehr N. Analysis of EEG records in an epileptic patient using wavelet transform. J Neurosci Methods. 2003;123(1):69–87. doi: 10.1016/S0165-0270(02)00340-0. [DOI] [PubMed] [Google Scholar]
- Alotaiby N, El-Samie EA, Alshebeili SA, Aljibreen KH, Alkhanen E (2015) Seizure detection with common spatial pattern and support vector machines. In: Proceedings of information and communication technology research, 52–155. doi:10.1109/ICTRC.2015.7156444
- Andrzejak RG (2001) Indications of nonlinear deterministic and finite dimensional structures in time series of brain electrical activity: dependence on recording region and brain state. Phys Rev E. doi:10.1103/PhysRevE.64.061907 [DOI] [PubMed]
- Aydin S, Saraoglu HM, Kara S. Log energy entropy-based EEG classification with multilayer neural networks in seizure. Ann Biomed Eng. 2009;37(12):2626–2630. doi: 10.1007/s10439-009-9795-x. [DOI] [PubMed] [Google Scholar]
- Bajaj V, Pachori RB. Epileptic seizure detection based on the instantaneous area of analytic intrinsic mode functions of EEG signals. Biomed Eng Lett. 2013;3:17–21. doi: 10.1007/s13534-013-0084-0. [DOI] [Google Scholar]
- Chaurasiya RK, Jain K, Goutam S, Manisha (2015) Epileptic seizure detection using HHT and SVM. In: Proceedings of international conference electrical electronics signals communication and optimization, pp 1–6. doi:10.1109/EESCO.2015.7253660
- Coifman R, Meyer Y, Quake S, Wickerhauser MV. Signal processing and compression with wavelet packets. J Byres, Wavelets and their applications. Netherland: Springer; 1990. pp. 363–379. [Google Scholar]
- Das AB, Bhuiyan MH. Discrimination and classification of focal and non-focal EEG signals using entropy based features in the EMD-DWT domain. Biomed Signal Process Control. 2016;29:11–21. doi: 10.1016/j.bspc.2016.05.004. [DOI] [Google Scholar]
- Du M, Li J, Wang R (2016) The influence of potassium concentration on epileptic seizures in a coupled neuronal model in the hippocampus. Cogn Neurodyn 10(5):405–414 [DOI] [PMC free article] [PubMed]
- Elman JL. Finding structure in time. Cognit Sci. 1990;14:179–211. doi: 10.1207/s15516709cog1402_1. [DOI] [Google Scholar]
- Faust O, Acharya UR, Adeli H. Wavelet-based EEG processing for computer-aided seizure detection and epilepsy diagnosis. Seizure. 2015;26:56–64. doi: 10.1016/j.seizure.2015.01.012. [DOI] [PubMed] [Google Scholar]
- Fisher RS, Boas EW, Blume W, Elger C. Epileptic seizures and epilepsy: definitions proposed by the international league against epilepsy (ILAE) and the international bureau for epilepsy (IBE) Epilepsia. 2005;46(4):470–472. doi: 10.1111/j.0013-9580.2005.66104.x. [DOI] [PubMed] [Google Scholar]
- Gajic D, Zeljko D, Stefano DG, Fredrik G. Classification of EEG signals for detection of epileptic seizure based on wavelet and statistical pattern recognition. Biomed Eng Appl Basis Commun. 2014;26(2):1450021. doi: 10.4015/S1016237214500215. [DOI] [Google Scholar]
- Gao J, Hu J, Tung W. Complexity measures of brain wave dynamics. Cogn Neurodyn. 2011;5(2):171–182. doi: 10.1007/s11571-011-9151-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gopan GK, Sinha N, Babu DJ (2015) Statistical features based epileptic seizure EEG detection—an efficacy evaluation. In: Proceedings of advances in computing, communications and informatics (ICACCI), pp 1394–1398. doi:10.1109/ICACCI.2015.7275808
- Gotman J. Automatic recognition of epileptic seizures in the EEG. Electroencephalogr Clin Neurophysiol. 1982;99:530–540. doi: 10.1016/0013-4694(82)90038-4. [DOI] [PubMed] [Google Scholar]
- Gotman J, Deng L. State-dependent spike detection: concepts and preliminary results. Electroencephalogr Clin Neurophysiol. 1991;70:11–19. doi: 10.1016/0013-4694(91)90151-S. [DOI] [PubMed] [Google Scholar]
- Guo L, Riveero D, Pazos A. Epileptic seizure detection using multi wavelet transform based approximate entropy and artificial neural networks. J Neurosci Methods. 2010;193:156–163. doi: 10.1016/j.jneumeth.2010.08.030. [DOI] [PubMed] [Google Scholar]
- Han CX, Deng J, Yi GS, Che YQ. Investigation of EEG abnormalities in the early stage of Parkinson’s disease. Cogn Neurodyn. 2013;7(4):351–359. doi: 10.1007/s11571-013-9247-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haykin SS. Adaptive filter theory. 3. Prentic Hall: Upper Saddle River; 1996. [Google Scholar]
- Kelly KM, Shiau DS, Kern RT, et al. Assessment of a scalp EEG-based automated seizure detection system. Clin Neurophysiol. 2010;121(11):1832–1843. doi: 10.1016/j.clinph.2010.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koren J, Herta J, Draschtak S. Prediction of rhythmic and periodic EEG patterns and seizures on continuous EEG with early epileptiform discharges. Epilepsy Behav. 2015;49:286–289. doi: 10.1016/j.yebeh.2015.04.044. [DOI] [PubMed] [Google Scholar]
- Kumar K, Dewal ML, Anand RS. Epileptic seizures detection in EEG using DWT-based ApEn and artificial neural network. SIViP. 2014;8:1323–1334. doi: 10.1007/s11760-012-0362-9. [DOI] [Google Scholar]
- Kumar TS, Kanhangad V, Pachori RB. Classification of seizure and seizure-free EEG signals using local binary patterns. Biomed Sig Proc Control. 2015;15:33–40. doi: 10.1016/j.bspc.2014.08.014. [DOI] [Google Scholar]
- Mallat S. A theory for multi-resolution signal decomposition: the wavelet representation. IEEE Pattern Anal Mach Intell. 1989;11(7):674–693. doi: 10.1109/34.192463. [DOI] [Google Scholar]
- Natwong B, Sooraksa P, Pintavirooj C, Bunluechokchai S, Ussawawongaraya W (2006) Wavelet entropy analysis of the high resolution ECG. In: Proceedings of IEEE industrial electronics and applications, Singapore, pp 1–4
- Ocak H. Automatic detection of epileptic seizure in EEG using discrete wavelet transform and approximate entropy. Expert Syst Appl. 2009;36(2):2027–2036. doi: 10.1016/j.eswa.2007.12.065. [DOI] [Google Scholar]
- Panda R, Khobragade PS, Jambhule PD, Jengthe S, Pal PR, Gandhi TK (2010) Classification of EEG signal using wavelet transform and support vector machine for epileptic seizure detection. In: Proceedings of systems in medicine and biology (ICSMB), 405–408. doi:10.1109/ICSMB.2010.5735413
- Pippa E, Zacharaki IE, Mporas I, Vasiliki T, et al. Improving classification of epileptic and non-epileptic EEG events by feature selection. Neurocomputing. 2016;171:576–585. doi: 10.1016/j.neucom.2015.06.071. [DOI] [Google Scholar]
- Pravin SK, Sriraam N, Benakop PG, Jinaga BC. Entropies based detection of epileptic seizures with artificial neural network classifiers. Expert Syst Appl. 2010;37:3284–3291. doi: 10.1016/j.eswa.2009.09.051. [DOI] [Google Scholar]
- Raghu S, Sriraam N, Pradeep KG. Effect of wavelet packet log energy entropy on electroencephalogram (EEG) signals. Int J Biomed Clin Eng. 2015;4(1):32–43. doi: 10.4018/IJBCE.2015010103. [DOI] [Google Scholar]
- Samiee K, Kovacs P, Gabbouj M. Epileptic seizure classification of EEG time-series using rational discrete short-time Fourier transform. IEEE Trans Biomed Eng. 2015;62(2):541–552. doi: 10.1109/TBME.2014.2360101. [DOI] [PubMed] [Google Scholar]
- Selik M, Baraniuk R, Blair A (2001) Signal energy versus signal power. Openstack-CNX Module: m10055, http://cnx.rice.edu/content/m10055/2.4
- Shannon CE. A mathematical theory of communication. Bell Syst Tech J. 1948;27:379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x. [DOI] [Google Scholar]
- Srinivasan V, Eswaran C, Sriraam N. Approximate entropy-based epileptic EEG detection using artificial neural networks. IEEE Trans Inf Technol Biomed. 2007;11(3):288–295. doi: 10.1109/TITB.2006.884369. [DOI] [PubMed] [Google Scholar]
- Sriraam N. EEG based automated detection of auditory loss: a pilot study. Expert Syst Appl. 2012;39(1):723–731. doi: 10.1016/j.eswa.2011.07.064. [DOI] [Google Scholar]
- Sriraam N. EEG based thought translator: a BCI model for paraplegic patients. Int J Biomed Clin Eng. 2013;2(1):50–62. doi: 10.4018/ijbce.2013010105. [DOI] [Google Scholar]
- Sriraam N, Eswaran C. An adaptive error modeling scheme for the lossless compression of EEG signals. IEEE Trans Inf Technol Biomed. 2008;12(5):587–594. doi: 10.1109/TITB.2007.907981. [DOI] [PubMed] [Google Scholar]
- Sriraam N, Shyamsunder R. 3-D medical image compression using 3-D wavelet coders. Digit Signal Proc. 2011;21:100–109. doi: 10.1016/j.dsp.2010.06.002. [DOI] [Google Scholar]
- Tan L, Jiang J. Digital signal processing, fundamentals and applications. 2. New York: Academic Press; 2008. [Google Scholar]
- Tang Z, Li R. An improved neural network model and its applications. J Inf Comput Sci. 2011;8(10):1881–1888. [Google Scholar]
- Tzallas AT, Tsipouras MG, Fotiadis DI. Automatic seizure detection based on time-frequency analysis and artificial neural networks. Comput Intell Neurosci. 2007;2007:80510. doi: 10.1155/2007/80510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venkataraman V, Vlachos I, Faith A, Krishnan B (2014) Brain dynamics based automated epileptic seizure detection. doi:10.1109/EMBC.2014.6943748 [DOI] [PubMed]
- Wang C, Zou J, Zhang J. Feature extraction and recognition of epileptiform activity in EEG by combining PCA with ApEn. Cognit Neurodyn. 2010;4(3):233–240. doi: 10.1007/s11571-010-9120-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang D, Miao D, Xie C. Best basis-based wavelet packet entropy feature extraction and hierarchical EEG classification for epileptic detection. Expert Syst Appl. 2011;38(11):14314–14320. [Google Scholar]
- Wang S, Chaovalitwongse WA, Wong S. Online seizure prediction using an adaptive learning approach. IEEE Trans Knowl Data Eng. 2013;25(12):2854–2866. doi: 10.1109/TKDE.2013.151. [DOI] [Google Scholar]
- Xiang J, Ci L, Li H, Cao R, Wang B, Han X, Chen J. The detection of epileptic seizure signals based on fuzzy entropy. J Neurosci. 2015;243:18–25. doi: 10.1016/j.jneumeth.2015.01.015. [DOI] [PubMed] [Google Scholar]
- Yang BH, Yan GZ, Yan RG, Wu T. Feature extraction of EEG-based brain computer interface by wavelet packet best basis decomposition. J Neural Eng. 2006;3(4):251–256. doi: 10.1088/1741-2560/3/4/001. [DOI] [PubMed] [Google Scholar]
- Zeng K, Jiaqing Y, Yinghua W. Automatic detection of absence seizures with compressive sensing EEG. Neurocomputing. 2016;171:497–502. doi: 10.1016/j.neucom.2015.06.076. [DOI] [Google Scholar]
- Zhou W, Liu Y, Yuan Q, Li X. Epileptic seizure detection using lacunarity and Bayesian linear discriminant analysis in intracranial EEG. IEEE Trans Biomed Eng. 2013;60(12):3375–3381. doi: 10.1109/TBME.2013.2254486. [DOI] [PubMed] [Google Scholar]