Weak electric fields detectability in a noisy neural network

Abstract

We investigate the detectability of weak electric field in a noisy neural network based on Izhikevich neuron model systematically. The neural network is composed of excitatory and inhibitory neurons with similar ratio as that in the mammalian neocortex, and the axonal conduction delays between neurons are also considered. It is found that the noise intensity can modulate the detectability of weak electric field. Stochastic resonance (SR) phenomenon induced by white noise is observed when the weak electric field is added to the network. It is interesting that SR almost disappeared when the connections between neurons are cancelled, suggesting the amplification effects of the neural coupling on the synchronization of neuronal spiking. Furthermore, the network parameters, such as the connection probability, the synaptic coupling strength, the scale of neuron population and the neuron heterogeneity, can also affect the detectability of the weak electric field. Finally, the model sensitivity is studied in detail, and results show that the neural network model has an optimal region for the detectability of weak electric field signal.

Introduction

Noise is ubiquitous in both natural and engineered systems. Intensive studies have revealed the enhanced effects of noise on weak signals transmission, transduction and detection, which is known as stochastic resonance (SR) (Gammaitoni et al. 1998; Kanamaru et al. 2001; Zhou et al. 2003; Cubero et al. 2007; Yu et al. 2011; Weber and Waldman 2016). It is a phenomenon based on the cooperative effect between the stochastic dynamical system and the external forcing (Wiesenfeld and Jaramillo 1998). The phenomenon is first proposed as a plausible mechanism for almost periodic occurrences of ice ages on earth during the last 700,000 years (Benzi et al. 1981). The birth of SR as an experimentally controlled physical phenomenon occurred in 1983, after its first laboratory demonstration in Schmitt triggers (Fauve and Heslot 1983). Since then SR has grown into a rapidly developing field with interdisciplinary research. It has been extended to many other bistable systems, such as Josephson junctions (Bryant et al. 1987), ring laser (McNamara et al. 1988). SR was also studied in threshold triggered monostable systems, where the addition of noise may lead to the stochastic crossing of a threshold, thus resulting in temporary excitation; the system then relaxes to the equilibrium state awaiting the next trigger event.

In particular, a well-known monostable system is the neuron, which is fundamental element constituting biological neural networks. The main function of neurons is to generate electrical signals in response to chemical and other inputs, and transmit them to other neurons (Dayan and Abbott 2005). The neuronal environment is noisy, this is mainly due to conduction influence, membrane fluctuations, channels stochastic gating and synaptic background activity (Guo 2011; Neishabouri and Faisal 2014). The constructive effects of noise on signal transmission among neurons have been extensively studied from both theoretical and computational approaches (Moss et al. 2004; Zheng et al. 2013). Array-enhanced SR has been verified in Refs. (Stacey and Durand 2002; Kawaguchi et al. 2011), where the results show that transmission and detection of subthreshold signal can be enhanced with increased coupling strength or neuron numbers in the network, and the noise characteristics also play key roles in SR performance. Besides, a close relationship between the neurons’ sensitivity and the frequencies of input signal is found, suggesting that the performance of SR is determined by both the external modulation and neurons’ properties (Yu et al. 2001a, b). Furthermore, the dependence of noise intensity on weak input signal is investigated with Hodgkin–Huxley (HH) neuron model, evidencing the enhancement effects of noise on the firing time reliability of neurons (Tanabe and Pakdaman 2001; Lindner et al. 2002).

Recently, low-intensity electrical stimulation has attracted more and more attentions, and its effects have been investigated widely (Deans et al. 2007; Anastassiou et al. 2010; Gordon and English 2016). Some studies have proposed SR as a key mechanism in optimizing the performance of specific functional electric stimulation devices, such as hearing implants (Morse and Roper 2000; Zeng et al. 2000). Beside this specific application, the functional electric stimulation technique covers a huge class of application fields (Russell et al. 1999; Lin et al. 2000; Fraccalvieri et al. 2015). Transcranial electrical stimulation (TES) with weak currents is actively investigated to treat a range of neurological and psychiatric disorders (Fregni et al. 2006; Liebetanz et al. 2006), and there is evidence that low-intensity TES can affect ongoing brain activity (Kirov et al. 2009; Iliopoulos et al. 2014). Animal studies indicate that electric fields with intensities below synaptic background activity can incrementally polarize somatic membranes (Bikson et al. 2004). Increasing attention in the therapeutic potential of weak transcranial direct current (DC) and alternating current (AC) stimulation to treat a range of neuropsychiatric disorders (Knotkova and Cruciani 2010; Loo et al. 2010) necessitates a quantitative framework for understanding and optimizing electrotherapeutic strategies, and exploring a cooperative role of noise seems to be of particular significance.

Following this motivation, the detectability of weak electric field is studied detailedly in a special neuronal environment (a randomly connected network with similar conduction delays, connection probability, and ratio between excitatory and inhibitory neurons as that in mammalian neocortex). We impose weak electric fields on the randomly connected network model, and the signal properties and noise intensity that may influence the electric field detectability are investigated with the network model. Moreover, the effects of network parameters on the electric field detectability are investigated systemically.

The rest of the paper is organized as follows: In “Mathematical model and methods” section, the construction of the neural network model is presented together with the introduction of the electric field and the linear response Q. In “Weak electric field detectability” section, the effects of network properties on the detectability of weak electric field are investigated in detail. Frequency sensitivity of the network model will also be demonstrated in this part. Finally, discussion of this investigation is given in “Discussion” section,

Mathematical model and methods

Each neuron in the randomly coupling network is described by the simple spiking model-lzhikevich model, which is computationally efficient and capable of reproducing rich firing patterns similar with the real biological neurons (Izhikevich 2003). The neural model has the following form

$$\begin{array}{cc}& \dot{v}=0.04v^2+5v+140-u+I\hfill \\ \hfill & \dot{u}=a(bv-u)\hfill \\ \hfill \end{array}$$ 1

with the auxiliary after-spike resetting

$$\begin{array}{c}\hfill ifv\ge 30\text{mV},then\left\{\begin{array}{c}v\leftarrow c\hfill \\ u\leftarrow u+d\hfill \end{array}\right.\end{array}$$ 2

Here, variable v and u are dimensionless variables. v represents the membrane potential of the neuron and u represents a membrane recovery variable, which accounts for the activation of $K^{+}$ ionic currents and inactivation of ${N_a}^{+}$ ionic currents, and it provides negative feedback to v. Synaptic currents or injected currents are delivered via the variable I. a, b, c and d are dimensionless parameters. The parameter a describes the time scale of the recovery variable u, b describes the sensitivity of the recovery variable u to the subthreshold fluctuations of the membrane potential v, c describes the after-spike reset value of the membrane potential v caused by the fast high-threshold $K^{+}$ conductances and d describes after-spike reset of the recovery variable u caused by slow high-threshold ${N_a}^{+}$ and $K^{+}$ conductances. According to Eq. (2), the membrane voltage and the recovery variable are reset when the spike reaches its apex at $+30\text{mV}$. Depending on the values of the parameters, the model can exhibit many properties of biological neurons (Izhikevich et al. 2004). The model does not have a fixed threshold and its resting potential is between −70 and −60 mV according to the value of b. We use $(b,c)=(0.2,-65)$ for all neurons in the network. For excitatory neurons, we use the values $(a,d)=(0.02,8)$, which corresponds to regular spiking neurons according to its firing pattern. For inhibitory neurons, we use the values $(a,d)=(0.1,2)$, which corresponds to fast spiking neurons.

In this paper, we simulated an anatomically realistic network model that composed by excitatory (80 %) and inhibitory 20 % neurons with conduction delay. The ratio of excitatory to inhibitory neurons is 4 to 1, similar as that in the mammalian neocortex. Any two neurons are connected with the probability near 0.1, which is again similar with the neocortex. The connections of the neurons in the network belong to the pulse-coupled type, where the firing of the presynaptic neuron instantaneously changes the membrane potential v of the postsynaptic neurons by the synaptic weights $s_{ij}$. Here, we assign excitatory synaptic weights to distribute randomly in the range of [0, 6] and inhibitory weights in the range of [0, 8]. The synaptic connections among neurons have fixed conduction delays, which are random integers between 1 and 20 ms. We assign 1 ms delay to all inhibitory connections, and 1–20 ms delay to all excitatory connections.

Inhibitory neurons were not polarized by the weak electric field, assuming a typical symmetric morphology (Radman et al. 2009). For excitatory neurons and weak uniform electric fields, the change of membrane voltage is linear with the applied field magnitude, and the polarization of the Izhikevich neuron model to a current injection exhibits low-pass characteristics (Deans et al. 2007; Reato et al. 2010). So the electrical stimulation in the model is implemented as low-pass-filtered current $I_E$ that is proportional to the applied electrical field (Reato et al. 2010):

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\mathit{\tau }}_E\frac{\mathit{\partial }{I}_E}{\mathit{\partial }t}=-I_E+k_{E}E(t),}\hfill \end{array}\end{array}$$ 3

where $k_E$ is the sensitivity of the membrane to the field and it depends on cell geometry and field orientation. We use $I_{E0}=k_{E}E(t)$, which has the form of $I_{E0}=A_{s}sin(2\mathit{\pi }{f}_{s}t)$. In order to achieve a better match with experimentally obtained magnitude response, the sensitivity $k_E=0.1$ m/V and time constant ${\mathit{\tau }}_E=10$ ms, the same as in Ref. (Reato et al. 2010). To account for the ensemble of possible noise sources, a white Gaussian current $D\mathit{\xi }(t)$ has been considered, where D represents its intensity. Here for Eq.1, we take $I=I_E(t)+D\mathit{\xi }(t)+I_{syp}(t)$, where $I_{syp}(t)$ is the synaptic currents from other neurons.

To evaluate the effects of SR on the neural network, the Fourier coefficient Q is calculated as a function of the input frequency. The parameter Q is used instead of the power spectrum because we are interested in the transport of the information by the neural network. For this task, the Q parameter is a much more compact tool than the power spectrum (Gammaitoni et al. 1998),

$$\begin{array}{cc}\hfill Q_{sin}& =\frac{\mathit{\omega }}{2n\mathit{\pi }}{\int }_0^{2\mathit{\pi }n/\mathit{\omega }}2x(t)sin(\mathit{\omega }t)dt,\hfill \\ \hfill Q_{cos}& =\frac{\mathit{\omega }}{2n\mathit{\pi }}{\int }_0^{2\mathit{\pi }n/\mathit{\omega }}2x(t)cos(\mathit{\omega }t)dt,\hfill \\ \hfill Q& =\sqrt{Q_{sin}^2+Q_{cos}^2},\hfill \end{array}$$ 4

Here, n is the number of periods, and $\mathit{\omega }=2\mathit{\pi }{f}_s$ where $f_s$ is the frequency of the weak signal $I_{E0}$. x(t) is the average firing rate of the network. The maximum of Q shows the best phase synchronization between input signal and output firing rate. It should be noted that one could expect a response of the Q measure in the case of phase synchronization but not vice versa. Other parameters used in this paper are given in each case.

Weak electric field detectability

Network responses to different noise intensities

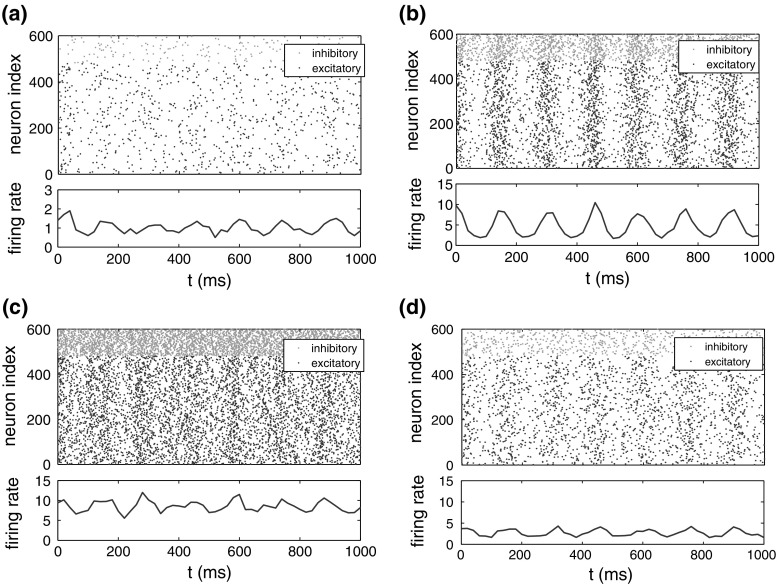
The effects of noise intensities on the detectability of weak electric field are investigated firstly with the neural network constructed above. We use white Gaussian noise to represent the noise that may exist in neuronal environment. Figure 1 shows the spike raster and firing rates of the neural network under different noise intensities. The network activities corresponding to the same external electric field and different noise intensities are shown in Fig. 1a–c. When the noise intensity is lower (Fig. 1a), fewer neurons in the network fire and the firing rate is low. But when the noise intensity is too high (Fig. 1c), the phase sychronization between the applied field and the spikes of the network is damaged. The optimal case is represented by Fig. 1b, which shows obvious coherence of network activities with the applied field. This was consistent with previous investigations that noise can modulate the phase synchronization between the firing activities of the network and weak electric field (Qin et al. 2014).

Fig. 1.

Spike raster diagrams and firing rates of the neural network subjected to the same external electric field for different noise intensities of D. Red dots denote inhibitory spikes and blue ones denote excitatory spikes. The frequency of applied field is 6.7 Hz. a $D={10}^{0.4}$; b $D={10}^{0.66}$; c $D={10}^{0.85}$; d $D={10}^{0.66}$, the network is in the decoupled state and subjects to synaptic currents which are recorded without the electric field application before decoupled. (Color figure online)

In order to distinguish the effects of single neuron and neural network on SR, we recorded the synaptic currents without electric field applied to the neurons in the decoupled network. Then those currents are replayed to the same neurons in the decoupled network with the electric field together. The results are shown in Fig. 1d, where the coherence phenomenon of the network with the applied electric field is not so obvious as in Fig. 1b. Thus, the amplification effect of the network plays a key role in the resonance phenomenon.

Detectability for different weak signals

Frequency and amplitude are two essential factors of alternating electric field. To study the detectability of various weak electric fields in the neural network, the linear response Q of the network is calculated as a function of noise intensity under the two factors respectively.

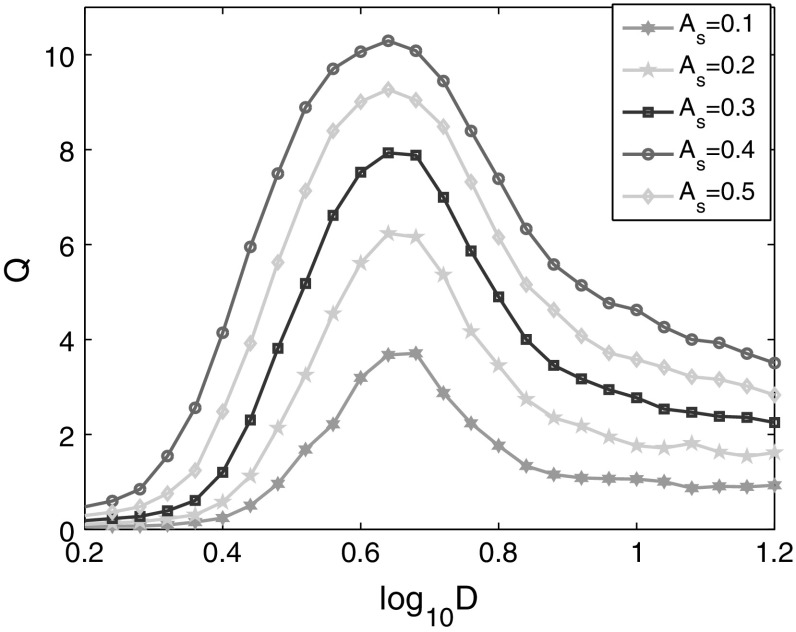
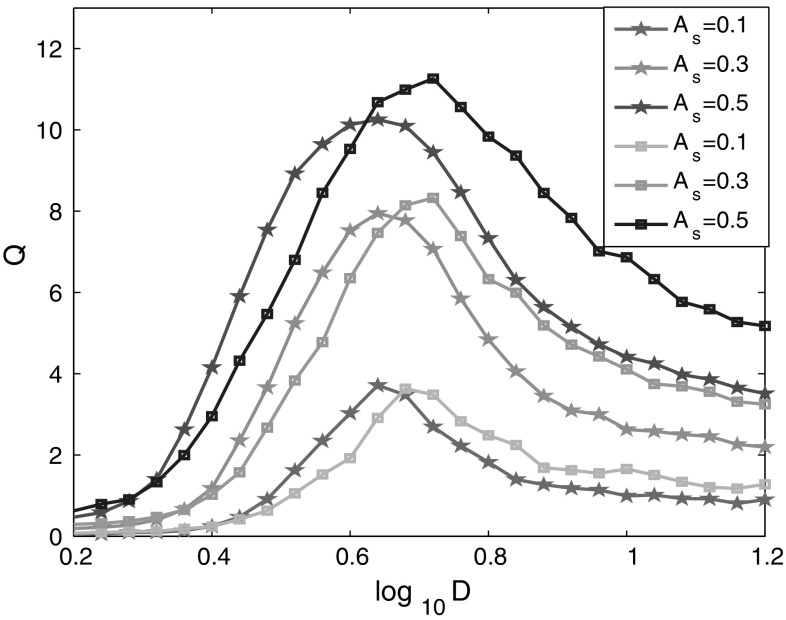
As shown in Fig. 2, bell-shaped curves for different signal amplitudes are observed, which indicates that there exists an optimal noise intensity corresponding to the maximal Q for each signal amplitude. The maximal Q implies that the phase synchronization between the spiking activities of the network and the external electric field is optimal. It’s also found that the maximum Q increases with the amplitude of input signal, which is consistent with the previous investigation of mammalian brain (Gluckman et al. 1996). Furthermore, the optimal intensity of noise is shifted left slightly with the increase of the amplitude of external electric field. The effects of signal amplitudes can be illustrated as follows. The increased amplitude of external electric field elevates the potentials of neurons and makes the neurons more easily fire, which further leads to the decrease of optimal noise intensity.

Fig. 2.

Linear response Q of the neural network versus noise intensity for different signal amplitudes. The frequency of weak signals is f _s = 6.7 Hz

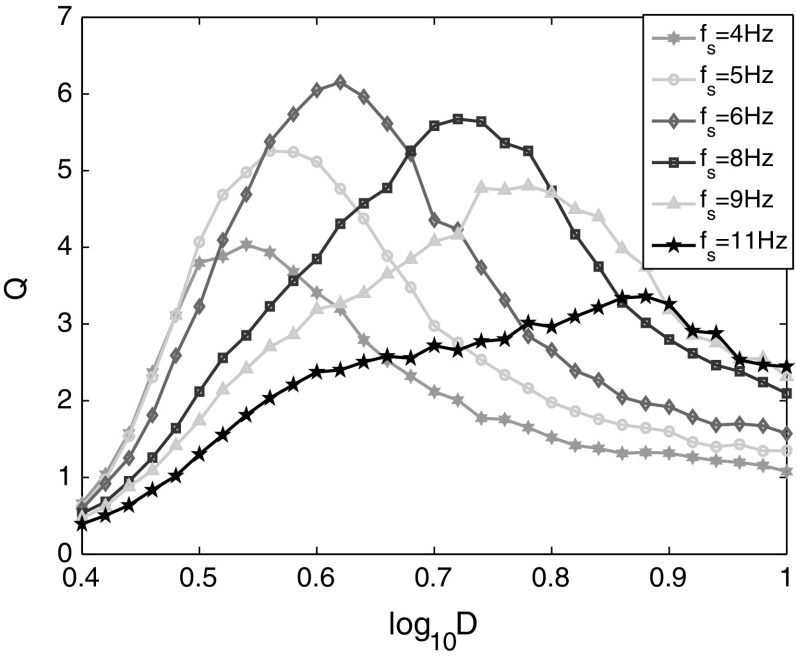
The detectability of the weak signal with different frequencies is also investigated. It shows clearly in Fig. 3 that each curve has a maximal Q value corresponding to the optimal SR between the network and the weak signal. Different from the effects of signal amplitudes on SR, the optimal noise intensity increases obviously with the increase of signal frequency. When the signal frequency is increased gradually, the maximal Q corresponding to different signal frequencies are increased firstly then decreased. The variation trends of maximal Q should be related with the frequency sensitivity of the network model, where there is a finite time (the refractory time) for neurons after excitation. When the signal frequency is lower than the network’s intrinsic frequency, a reminiscent duration with longer time is needed. When the signal frequency is higher than the network’s intrinsic frequency, the network becomes more difficult to resonate with noise at original intensity. And this makes the optimal noise intensity shift right, in which the network can resonate with noise of higher intensity. The sensitive frequency of the network model will be studied in the following part.

Fig. 3.

Linear response Q of the neural network versus noise intensity for different signal frequencies. The amplitude of weak signals is A _s = 0.2

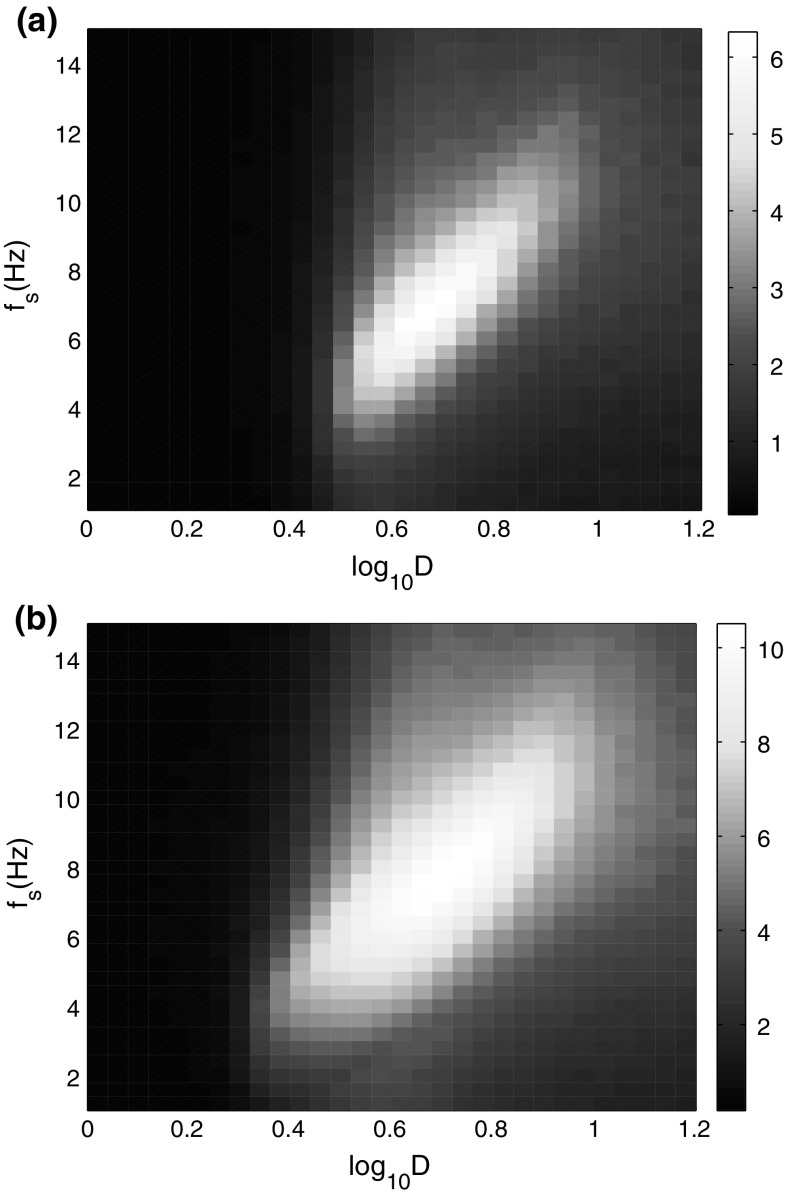
To gain more insights into the effects of the signal frequency on weak signal detectability, the linear response Q is calculated as a function of the signal frequency and noise intensity (Fig. 4). It can be seen that the signal detectability relates to both of the noise intensity and signal frequency. Specially, a bright elliptic area of Q is found, which indicates that the firing rates of neural network are more consistent with the signal when the parameters of signal frequency and noise intensity are in that area. Slightly increasing the amplitude of the input signal will result in better response of SR and make the weak signal detection more easily, which is shown clearly by comparing Fig. 4a, b.

Fig. 4.

Linear response Q of the neural network as a function of signal frequency and noise intensity. The color denotes the value of Q. a A _s = 0.2; b A _s = 0.5. (Color figure online)

Effects of network parameters on weak signal detectability

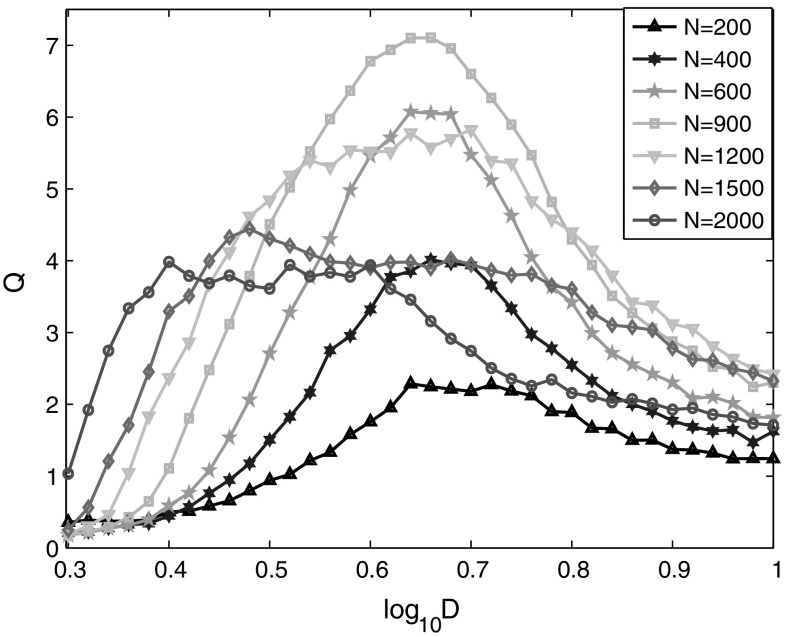
In the following, we will study the typical network parameters that may influence the detectability of weak signal, which includes the neuron population, the synaptic coupling strength and the connection probability between neurons. The effect of neuron population on SR is shown in Fig. 5, where the dependence of Q on the noise intensity is calculated for different neuron populations. Obviously, there exists an optimal noise intensity corresponding to maximal Q for each neuron population, and the optimal noise intensity decreases with the increase of neuron population of the network. This should be related with the increase of positive current that each neuron received. As the connection probability is constant, the increase of neuron population will make each neuron link with more excitatory neurons, which further increases the synaptic current from excitatory neurons. It also shows that the variation trends of the optimal Q value for different neuron populations first increase then decrease. Thus, there should have an optimal neuron population and noise intensity for the detectability of a fixed weak signal.

Fig. 5.

Linear response Q of the neural network versus noise intensity for different neuron populations

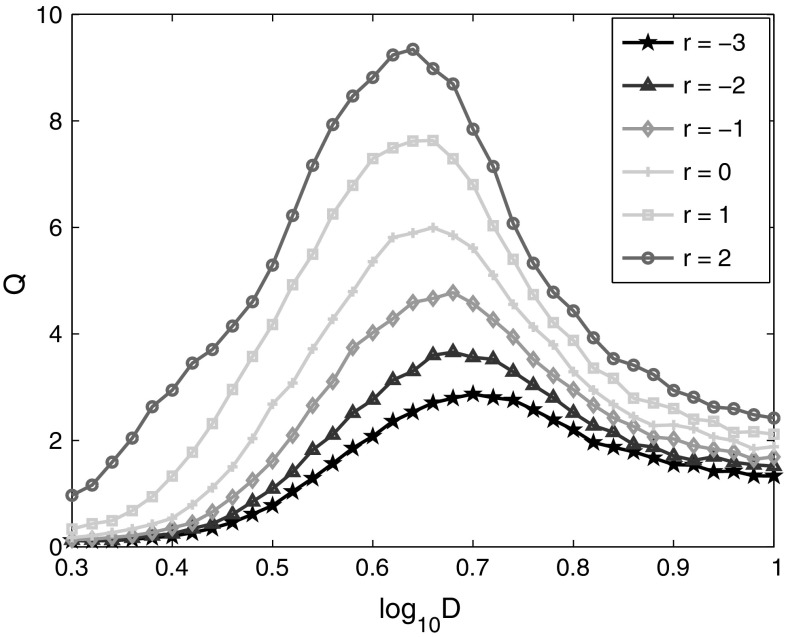
Besides the neuron population, the synaptic coupling strength is another factor that may affect the weak signal detectability in the neural network. In order to explore this, the linear response Q for different synaptic strength is shown in Fig. 6. The value of r is used to change the range of synaptic distribution. It is found that the maximal Q increases with the coupling strength between neurons. The range that SR happens is also enlarged with the increase of synaptic coupling strength, and the optimal noise intensity for weak signal detection shifts leftward slightly. After examining the changes of the network during this circumstance, it is found that the firing rates of the network are elevated with larger coupling strength between neurons, which further leads to the occurrence of SR more easily.

Fig. 6.

Linear response Q of the neural network versus noise intensity for different ranges of synaptic coupling strength. The excitatory synaptic weights are distributed randomly in the range of $[0,6+r]$, and the inhibitory synaptic weights are distributed in $[0,8+r]$

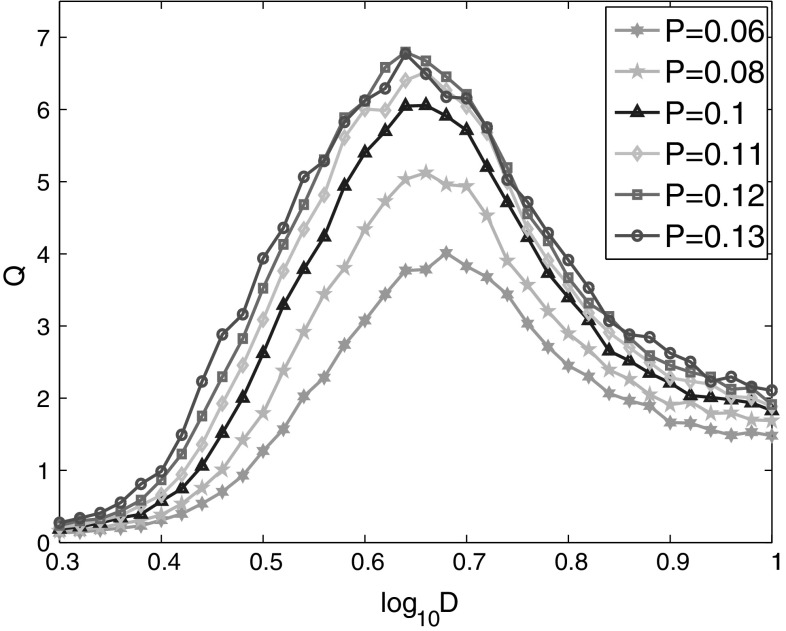
Finally, the effects of connection probability on the detectability of weak signal are investigated. As the network we concerned has similar connection probability as that in the mammalian neocortex, we just focus on the probability distributed around 0.1. Figure 7 is the linear response Q of the network against the noise intensity for different connection probabilities. With the increase of connection probability P, the linear response Q increases first, then it reaches a saturate state. The range of noise intensity that enhances signal detectability becomes wider with the increase of connection probability. This should be related with the ratio of excitatory and inhibitory neurons in the network as more excitatory neurons can be connected to each neuron when the connection probability is increased, which further leads to the enhancement of positive synaptic currents to neurons. It makes the neuron more easily fire than the circumstance that the connection probability between neurons is low. It should be noticed that either the increase of coupling strength or connection probability can enhance the detectability of weak signal, and their reasons are all related with the increase of firing rates of the neural network.

Fig. 7.

Linear response Q of the neural network versus noise intensity for different connection probabilities P. The detectability of the weak signal increases with the increasing connection probability until it reaches a saturate state

Therefore, the detectability of weak signal can be affected by the network parameters, such as the neuron population, the coupling strength and the connection probability of the network. These results may have implications for the applications of electrical stimulation device to cortical neural network in vivo as the network parameters we choose here are similar as that in mammalian neocortex.

Effects of neuron heterogeneity on weak signal detectability

As heterogeneity is ubiquitous in real world and closely related with several collective behaviors of neural networks, the effects of it on weak signal detectability are studied here. The best way to achieve heterogeneity for Izhikevich neural model has been introduced in Ref.(Izhikevich 2003). Here, we deal it with the same method by assigning the parameters of each excitatory neuron as $(a_i,b_i)=(0.02,0.2)$ and $(c_i,d_i)=(-65,8)+(15,-6)\ast k_i^2$, where $k_i$ is a random variable uniformly distributed on the interval [0, 1], and i is the neuron index. Thus, $k_i=0$ corresponds to the regular spiking (RS) neuron, and $k_i=1$ corresponds to the chattering (CH) neuron. We use $k_i^2$ to bias the distribution toward RS neurons. Similarly, the parameters for each inhibitory neuron are $(a_i,b_i)=(0.02,0.25)+(0.08,-0.05)\ast k_i$ and $(c_i,d_i)=(65,2)$. Thus, $k_i=0$ corresponds to the low-threshold spiking (LTS) neuron, and $k_i=1$ corresponds to the fast spiking (FS) neuron. The neural network with the same structure as above is constructed using the heterogeneous neurons.

The effects of neuron heterogeneity on the detectability of weak signal are shown in Fig. 8, where pentagram mark is used to denote the case with fixed neuron parameters (named case 1), and square mark is used to denote the case with randomized neuron parameters (named case 2). A _s is the amplitude of weak signal. It can be noticed that the bell curve of linear response Q is still presented in case 2, which verifies the reliability of the results above in this paper. The optimal noise intensity corresponding to the maximal Q shifts a little right compared with case 1, meaning larger noise intensity is needed for the optimal detection of weak signal in neural network with heterogeneous neurons. The neuron heterogeneity makes their firing patterns diversity, which further hinders the phase synchronization between the firing of neurons and external weak signal. Thus, stronger noise is needed to induce the appearance of SR for the neural network.

Fig. 8.

Linear response Q of heterogeneous/homogeneous neurons as a function of noise intensity for different amplitudes of weak signals. Here, the frequency of the weak signal is 6.7 Hz. Pentagram mark denotes case 1 with fixed neuron parameters, and square mark denotes case 2 with randomized neuron parameters

Frequency sensitivity

SR is a phenomenon typically exhibited in nonlinear systems for the detection, transmission and processing of weak input signal, and the occurrence of it is strictly related to the model sensitivity. So the weak signal detection is easier when model sensitivity increases. On the other hand, when the signal frequency is away from sensitive frequency of the network model, higher amplitudes of the input signals will be needed for detection with the same noise intensity.

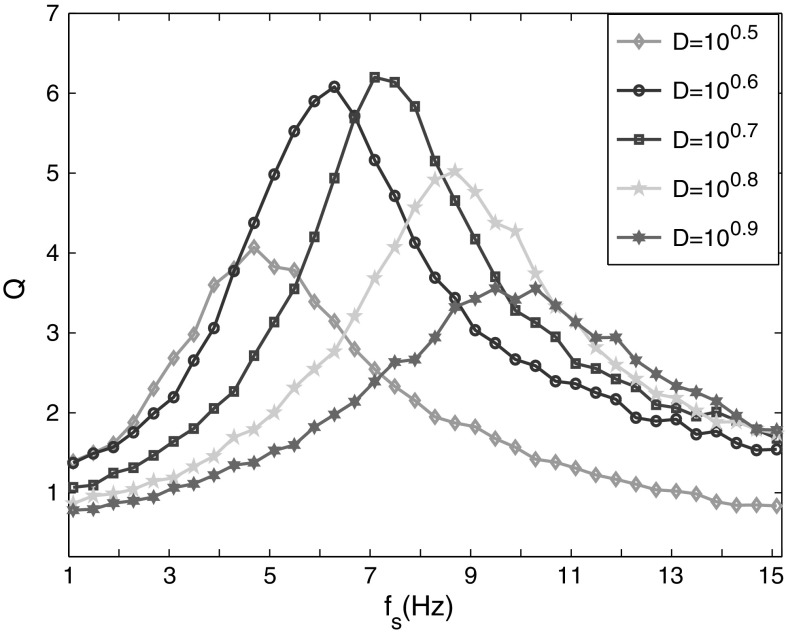
Therefore, a preliminary study on frequency sensitivity of network model should be carried out to confirm the range for the detectability of weak electric field. The linear response Q is calculated as a function of signal frequency for different noise intensities and the same signal amplitude A _s, which is shown in Fig. 9. It can be found that the optimal signal frequency is enhanced with the increase of noise intensity in the network. The variation trends of the maximal Q for different noise intensities first increase then decrease, indicating that there is an optimal signal frequency which can lead to more obvious SR phenomenon than any other signal frequencies.

Fig. 9.

The frequency sensitivity of the model. Curves represent the linear response Q versus signal frequency. The neural network has different optimal frequencies for different noise intensities. Here, A _s = 0.2

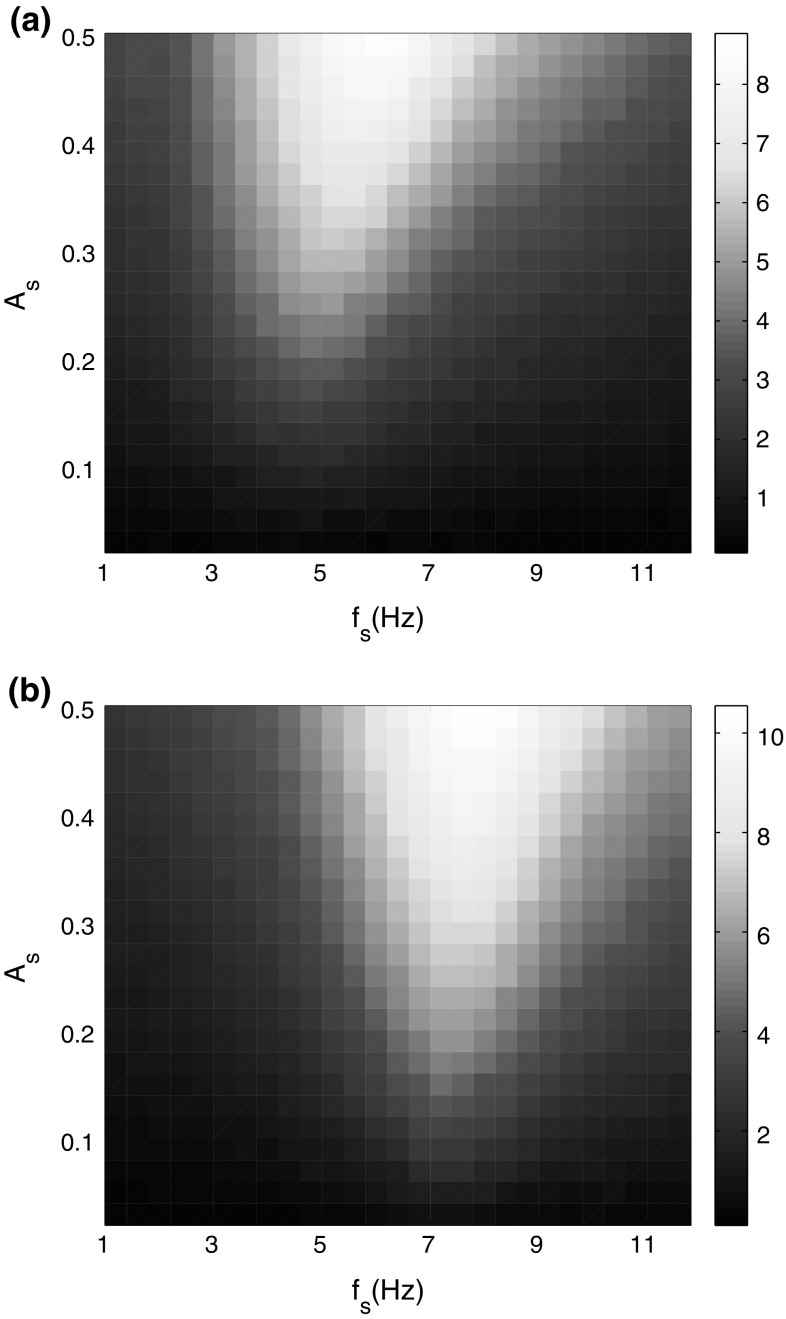
To further understand the mechanism underlying the frequency sensitivity of network model and weak signal detectability, signals with different frequencies and amplitudes are investigated. Figure 10 is the linear response Q of the network as a function of the signal frequency and amplitude. Each point in the heat map represents the value of Q. It’s found that the linear response Q relates to both of the signal amplitude and frequency. When the amplitude and the frequency are chosen at a proper range, the optimized response of the network (the bright region) is obtained, which corresponds to the most sensitive region of the network for input signal. Comparing Fig. 10a, b, it is found that the bright region expands and shifts rightward with proper increase of noise intensity, which is also consistent with the above investigations of the effects of frequency and noise on the detectability of weak signal.

Fig. 10.

Linear response Q as a function of noise intensity and weak signal amplitude. The color denotes the value of Q. a $D={10}^{0.5}$; b $D={10}^{0.7}$. (Color figure online)

Therefore, frequency sensitivity of network model plays an important role in weak signal detectability. When the signal frequency is in the range of sensitive frequency of the network model, it can be easily detected with noise at certain intensity.

Discussion

Throughout the paper, the capability of neural network to detect weak electric fields is discussed for different neuron populations, neuron types, coupling strength, connection probabilities and noise intensities. Results show that the noise can improve the detectability of weak electric field in the randomly connected network, which is strictly related with the occurrence of SR. Moreover, the weak signal detection is found to be dependent on the parameters of neural network, such as the neuron heterogeneity, the coupling strength, the sensitive frequency of the network and so on.

We have systemically investigated the factors of the neural network that may affect the detectability of the weak signal. It is found that the linear response Q of the network increases with the coupling strength between neurons, indicating that better detectability of weak signal is attained. The effects of coupling strength on SR have been investigated previously. Mahmut et al. constructed small-world networks with HH neurons and found that SR is intensively associated with the coupling strength among neurons (Ozer et al. 2009). Yu et al. further studied SR with the spike-time-dependent plasticity (STDP) rule in small-world neural network constituted by FitzHugh–Nagumo (FHN) neural model, and found that SR can be further improved via fine-tuning of the average coupling strength between neurons (Yu et al. 2014). Our investigation shows that SR will be more obvious with the increased coupling strength between neurons, which extends the previous results although different network structures and neural models are used. The effects of neuron population are also investigated, where the detectability of weak signal first increases then decreases obviously with the enlargement of neural population, and the optimal noise intensity corresponding to each neuron population shifts leftward. Similar results have also been found in small-world network with both chemical and electrical synaptic couplings between FHN neurons, where the optimal noise intensity of SR shifted left slightly when the neuron number of the network is increased (Wei et al. 2015). Stacey et al. simulated noisy neural networks with CA1 neurons by NEURON software and found that detection of subthreshold signal is improved when the neuron number or the coupling strength in the network is increased (Stacey and Durand 2002). Furthermore, the investigation here found that increasing connection probability between neurons can elevate the maximal value of Q to a saturated state and make the optimal noise intensity shift left slightly. This is also consistent with the results of SR in small-world network with STDP, where an optimal probability of adding shortcuts is convenient for the noise-induced transmission of weak periodic signal (Yu et al. 2014). It should be noticed that the new shortcuts also increase the connection probability of the neural network. Heterogeneity is also essential to the mathematical simulation of neural networks as the neurons in real-world should be different with each other. The investigation indicates that noise with higher intensity is needed in the neural network with heterogeneous neurons to synchronize the weak signal than the neural network with homogeneous neurons. However, the maximal Q of the network with heterogeneous neurons are larger than the network with homogeneous neurons, suggesting the network activities are more synchronous with weak signal than that of homogeneous neurons. The improvement of SR with neuron heterogeneity has also been reported by previous investigation with scale-free network, where the maxima of SR measurement are enhanced as the heterogeneity is increased (Wang et al. 2012). The heterogeneity here is set as constant, but an enhancement effect on SR corresponding to different signal amplitudes is still found by comparing SR with homogeneous neurons. In short, it is concluded that the network parameters mentioned above play key roles in determining the detectability of the weak signal.

Low-intensity electrical stimulation has led to many achievements in recent years. The effects of TES should be cumulative as multiple consecutive sessions are often needed to make it become effective for subjects (Charvet et al. 2015). Although it has been verified effective in improving sensory, cognitive and psychiatric processes, there still has not unified illustration for its principles. How and what kind of neural plasticity are induced by weak electric stimulation is still unclear. It is also difficult to investigate the mechanism of TES due to the absence of techniques to observe microscopic changes of subject’s cortex together with the application of TES. A well established tool for TES investigation is the hippocampal slice of rat, where the network activity under weak electrical field can be obtained with intracellular recording technique (Fröhlich and McCormick 2010). Weak electrical fields can incrementally polarize somatic membranes and further affect the firing rates and spike timing of neural network in hippocampal slices (Reato et al. 2010). As SR is a possible mechanism for the illustration of TES, a randomly connected neural network that utilizes the structural parameters of anatomical mammalian cortex is constructed with Izhkevich neural model in this investigation, where the effects of different parameters of neural networks on SR can be studied detailedly. The investigation here indicates that the frequency and amplitude of weak electrical field play key roles in modulating the cortical activities, and weak electrical field with suitable frequency can be effective even at a small amplitude. The application region of TES is also important as it is related with the network properties investigated above, where suitable neuron populations and coupling strength between neurons can aid the performance of TES. Recently, the importance of endogenous field on network activities is emphasized (Fröhlich and McCormick 2010; Wei et al. 2015). Investigations indicate that endogenous field also interacts with the external electrical field and local field potentials of neural network. Thus, further investigations will focus on the effects of endogenous field on TES performance. Moreover, the effects of STDP on the evolution of cortical network can also be investigated, which is more vivid to simulate the effects of TES on subjects.

The results shown in this paper should be significant to the field of neuroscience. Since there is not clear interpretation for the functional mechanism of weak electric stimulation devices, studies of weak signal detectability here may be helpful to understand the interaction mechanisms between the weak electric stimulation and the activity of a biological system. It also makes sense to use this network model to investigate how the endogenous field affects the network activities and the neural coding and encoding.