Force Responses and Sarcomere Dynamics of Cardiac Myofibrils Induced by Rapid Changes in [P_i]

Abstract

The second phase of the biphasic force decay upon release of phosphate from caged phosphate was previously interpreted as a signature of kinetics of the force-generating step in the cross-bridge cycle. To test this hypothesis without using caged compounds, force responses and individual sarcomere dynamics upon rapid increases or decreases in concentration of inorganic phosphate [P_i] were investigated in calcium-activated cardiac myofibrils. Rapid increases in [P_i] induced a biphasic force decay with an initial slow decline (phase 1) and a subsequent 3–5-fold faster major decay (phase 2). Phase 2 started with the distinct elongation of a single sarcomere, the so-called sarcomere “give”. “Give” then propagated from sarcomere to sarcomere along the myofibril. Propagation speed and rate constant of phase 2 (k_+Pi(2)) had a similar [P_i]-dependence, indicating that the kinetics of the major force decay (phase 2) upon rapid increase in [P_i] is determined by sarcomere dynamics. In contrast, no “give” was observed during phase 1 after rapid [P_i]-increase (rate constant k_+Pi(1)) and during the single-exponential force rise (rate constant k_−Pi) after rapid [P_i]-decrease. The values of k_+Pi(1) and k_−Pi were similar to the rate constant of mechanically induced force redevelopment (k_TR) and Ca²⁺-induced force development (k_ACT) measured at same [P_i]. These results indicate that the major phase 2 of force decay upon a P_i-jump does not reflect kinetics of the force-generating step but results from sarcomere “give”. The other phases of P_i-induced force kinetics that occur in the absence of “give” yield the same information as mechanically and Ca²⁺-induced force kinetics (k_+Pi(1) ∼ k_-Pi ∼ k_TR ∼ k_ACT). Model simulations indicate that P_i-induced force kinetics neither enable the separation of P_i-release from the rate-limiting transition f into force states nor differentiate whether the “force-generating step” occurs before, along, or after the P_i-release.

Introduction

Muscle contraction is driven by the cyclic ATPase activity of the cross-bridges. To understand how cross-bridges convert chemical into mechanical energy, the force-generating transitions in this ATPase cycle, i.e., the force-generating steps, have to be clarified. It is generally accepted that the first and major force-generating step is not coupled to the cleavage of ATP into ADP and inorganic phosphate (P_i) but rather to the subsequent, reversible release of P_i, e.g., through the backdoor of the myosin molecule (1, 2, 3, 4). To explore the chemo-mechanical coupling, force changes were induced in muscle fibers by rapid length changes (5, 6, 7, 8, 9, 10), temperature jumps (5, 11), pressure jumps (12), or photolytic release of caged-P_i (13, 14, 15, 16, 17), and the kinetics of these force changes were interpreted in terms of cross-bridge models. The rapid change in [P_i] provides a well-defined approach because it specifically perturbs the reversible equilibrium of the P_i-release. Analysis of force transients induced by photolytic release of caged-P_i led to the perception that the first force-generating step is an isomerization of an ADP.P_i-binding state that precedes the P_i-release (13, 14, 16). However, other models and recent evidence from novel crystal structures support a more direct coupling of the first force-generating step to P_i-release (3, 18, 19, 20). Furthermore, force transients induced by length steps were often interpreted in terms of this force-generating step occurring independently or after P_i-release (9, 10). Thus, it is controversial whether the first major force-generating step occurs before, along, or after P_i-release, while a second force-generating step is associated with the release of ADP from the active site (21).

Force kinetics after rapid change of [P_i] were first explored in skinned skeletal muscle fibers (14, 17) and cardiac myocyte bundles (16). Flash photolysis of caged-P_i in these preparations enabled the investigators in these studies to study the kinetics of the force decay induced by rapid increase of [P_i]. The rate constant k_Pi of the major force decay was found to be markedly faster than k_TR, the rate constant of force redevelopment. k_TR is determined by rate-limiting transitions in the cross-bridge cycle (22, 23). In experiments with cardiac trabeculae and with myofibrils, k_TR is similar to k_ACT, the rate constant of force development upon a stepwise increase in free Ca²⁺-ion concentration (24, 25, 26). k_Pi being larger than k_ACT and k_TR had important implications for the assignment of the first force-generating step in the cross-bridge cycle. In contrast to k_TR and k_ACT, which were interpreted to reflect rate-limiting transitions in the cross-bridge cycle, k_Pi was interpreted to report the kinetics of the force-generating isomerization. Forward and reverse rate constants of this isomerization were determined from the hyperbolic relation of k_Pi versus the [P_i] (13, 14, 15, 17) and from the hyperbolic [P_i]-dependence of the force kinetics induced by sinusoidal length changes (6, 7). Former cross-bridge models (3, 18) were revised by adding a force-generating ADP.P_i-binding state to the cross-bridge model. Force generation was attributed to an isomerization between two ADP.P_i-binding states whose kinetics can be separated from a preceding slower rate-limiting step that is regulated by thin filament activation and is reported by k_ACT and k_TR (13, 14, 27).

However, the use of caged-P_i in the larger muscle preparations has some limitations. The limited capacity of caged-P_i does not allow switching over a large [P_i]-scale from the same initial [P_i] to a different final [P_i], or from a different initial [P_i] to the same final [P_i]. Furthermore, caged-P_i does not enable a force rise as in k_ACT- and k_TR-measurements, because this requires the rapid decrease in [P_i]. Both limitations might be crucial, because the P_i-induced transitions between preforce and force-generating states might not only depend on the final [P_i] but also on the magnitude and the direction of the force change. For example, force kinetics induced by positive and negative length steps have been shown to exhibit a [P_i]-dependent asymmetry (8). Different interpretations of length-induced asymmetric force kinetics exist (9, 28, 29), but none of them explains an asymmetry involving the P_i-release/binding equilibrium. Thus, the chemo-mechanical coupling between P_i-release and the force-generating step remains unclear.

The limitations given by caged-P_i can be overcome by using myofibrils or thin myofibril bundles (diameter of 1 to a few μm) that rapidly equilibrate within 1 ms with the surrounding solution. In contrast to skinned fibers, myofibrils are therefore well suited to measure force kinetics with rate constants <1000 s⁻¹ induced by a rapid solution change without limitation by diffusion. Rapid solution changes allow both rapidly stepping up and stepping down [P_i]. Thus, with myofibrils we can determine not only the rate constant k_Pi of the force decay upon rapid increase in [P_i] which is from now on termed k_+Pi to specify the increase (+) in [P_i], but also the rate constant k_−Pi upon rapid decrease (−) in [P_i] belonging to a force response in same direction, i.e., to a force rise, as in the case of k_ACT- and k_TR-measurements. Such experiments had been performed by Tesi et al. (26) using myofibrils from skeletal muscle. Interestingly, when turning to the same final [P_i], they found that the k_−Pi upon a decrease in [P_i] was approximately fourfold lower than the k_+Pi upon an increase in [P_i]. Furthermore, k_−Pi was similar to k_TR, indicating that a force rise upon a [P_i]-change yields similar kinetics as the classical mechanically induced force redevelopment. The authors (26) noted that the difference between k_+Pi and k_−Pi, and the similarity of k_−Pi and k_TR, are unexpected from the models evolved from P_i-jump studies on muscle fibers. However, the reason for the asymmetry of k_+Pi and k_−Pi remained unexplained.

In this study, the P_i-induced force kinetics of cardiac myofibrils were investigated to test whether the asymmetry between k_+Pi and k_−Pi is similar to the one reported for skeletal myofibrils (26). In addition, the reason for the previously observed asymmetry was explored. One reason could be that the force decay upon [P_i]-increase is accelerated by organized sarcomere dynamics similar to the “give” that we had previously shown to occur during the fast phase of muscle relaxation. This sarcomere “give” is responsible for the asymmetric force kinetics observed with myofibrils when free Ca²⁺-ion concentration is stepped up and stepped down in a contraction-relaxation cycle (30, 31). Thus, together with the force changes, the length of individual sarcomeres was monitored in response to rapid changes in [P_i]. Furthermore, the values of k_+Pi and/or k_−Pi might not only be affected by the final [P_i] after the [P_i]-change, but also by the magnitude of the [P_i]-change. This can be tested by switching from a different initial [P_i] to the same final [P_i]. Therefore, not only the relation of k_+Pi and k_−Pi on the final [P_i] but also their relation on the initial [P_i] was investigated.

Here, it is found that the force decay upon an increase in [P_i] consists of two phases, an initial slow force decay (phase 1) followed by a major fast force decay (phase 2). Onset of phase 2 coincides with onset of rapid lengthening (“give”) of a single sarcomere. The kinetics of phase 2 depends not only on the final [P_i] but also on the magnitude of the [P_i]-change. In contrast, phase 1 and the force rise upon a rapid decrease in [P_i] occur without sarcomere “give”, do not depend on the initial [P_i], and exhibit symmetric kinetics, i.e., at same final [P_i] their rate constants are similar and furthermore indistinguishable from k_ACT and k_TR. This indicates that in the absence of sarcomere “give”, P_i-induced force responses simply report the rate-limiting transitions in the cross-bridge cycle.

Materials and Methods

Myofibrillar preparation and solutions

Myofibrils were prepared from left ventricles of the guinea pig as in Stehle et al. (30). Relaxing/activating standard solutions without added P_i contained either 3 mM K₄Cl₂CaEGTA (activating) or 3 mM K₄Cl₂EGTA (relaxing solution), 10 mM imidazole, 1 mM K₂Cl₂Na₂MgATP, 3 mM MgCl₂, 47.7 mM Na₂CrP, 2 mM DTT, pH 7.0 at 10°C, ionic strength (μ) = 0.17 M. The standard solutions contained 0.16 ± 0.04 mM (mean ± SD) contaminant P_i as determined by a phosphate assay kit (E-6646; Molecular Probes, Eugene, OR). To keep a constant μ for all solutions, in solutions with additional P_i for each mM of added P_i, the [Na₂CrP] was reduced by 0.65 mM.

Apparatus and myofibril experiments

The mechanical setup for simultaneous measurements of forces, force transients, and lengths of individual sarcomeres of myofibrils upon rapid changes in [Ca²⁺] and [P_i] was mounted on a model No. IX-70 microscope (Olympus, Melville, NY) and previously described in detail in Stehle et al. (25, 30). All experiments were performed at 10°C using thin bundles of few myofibrils with bundle diameters ranging from 1.5 to 3.0 μm and bundle lengths from 28 to 96 μm. Slack sarcomere length was 2.02 ± 0.04 μm (mean ± SD). Before activation, bundles were stretched to a sarcomere length (SL) of 2.3 μm. For a detailed description of setup components, solution change technique, and data acquisition, see the Supporting Material.

Signal conditioning for movement of actuators and acquisition of force and length signals were performed with a PCI6110-E device (National Instruments, Austin, TX) under self-written programs in LabVIEW 4.0 (National Instruments). During the force measurements, video images of the myofibril bundles were recorded with the ORCA-ER camera (Hamamatsu Photonics, Herrsching, Germany) under 90-fold magnification. The physical pixel size of the camera charge-coupled device sensor corresponded to a square of 6.45 × 6.45 μm². Thus, an individual pixel represented a 71.7 × 71.7 nm² square in the object plane.

Data analysis

To obtain the rate constants k_ACT, k_TR, and k_−Pi, force transients were fitted by single-exponential functions. Kinetic parameters of force changes upon rapid increases in [P_i] were obtained by fitting transients by the biphasic function described for relaxation (25). The function consists of a linear term to obtain the rate constant k_+Pi(1) and the duration t_+Pi(1) of the initial slow force decline (phase 1) and an exponential term with the rate constant k_+Pi(2) for the subsequent rapid exponential force decay (phase 2).

To obtain SL transients, the video images recorded during force measurement were processed using the AquaCosmos 1.3.0.1 (Hamamatsu Photonics). A rectangular region of interest (ROI) enclosing the sarcomeres selected for quantitative analysis of length changes was defined (see the Supporting Material for examples of ROI) and the pixel intensities were integrated perpendicular to the bundle axis to create a one-dimensional intensity profile along the myofibrils. Individual SLs were determined by fitting the centers of the intensity peaks along the profile using the subroutine peak detector.vi in LabVIEW 4.0. The mean SL was obtained by applying Fourier analysis to the same profile.

Results

Experimental protocols

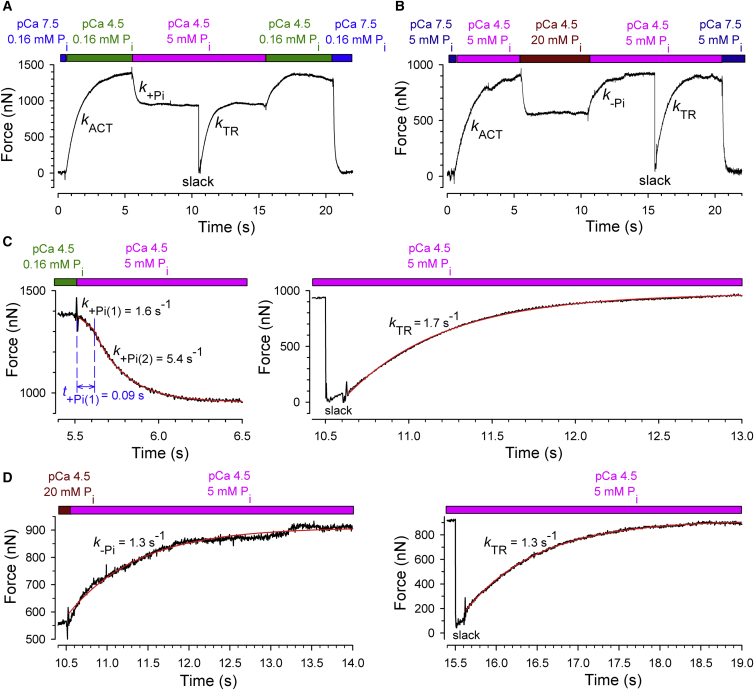
Fig. 1 shows original traces of the experimental protocols together with expanded parts to illustrate the force transients with the curve fitting used to derive the different kinetic parameters explored in this study. Force transients were initiated by rapidly increasing the [Ca²⁺] (k_ACT-measurement) and by stepping up or stepping down the [P_i] when force had reached a steady state. These transients were compared to the force transient in response to a slack-restretch maneuver to initiate force redevelopment (k_TR-measurement). The k_TR-measurement was performed directly after recording the force kinetics induced by a rapid increase in [P_i] (Fig. 1, A and C) or decrease in [P_i] (Fig. 1, B and D) so that the kinetics in response to changes in [P_i] and k_TR were obtained at the same concentrations of P_i and Ca²⁺-ions.

Figure 1.

Examples of experimental protocols and analysis of force transients. (A) Whole force records of an experiment designed for comparing k_+Pi with k_TR. (B) Same as in A for comparing k_−Pi and k_TR. (C) Expanded segments of force transients from (A) (black lines) and corresponding fits (red lines). A biphasic function is fitted to the force decay after rapid increase in [P_i] and a single-exponential function to the k_TR measurement. (D) Single-exponential functions (red lines) were fitted to segments of the force transient (black lines) shown in (B). The force rise upon the decrease in [P_i] and that after the slack-restretch yield similar rate constants.

Kinetics of force transients induced by increases in [P_i]

After a jump increase in [P_i] to 5 mM P_i, the overall force decay is faster than its rise in the k_TR-measurement at the same [P_i] (Fig. 1 A). This result is in agreement with previous studies on skinned fibers (13, 14, 27) and skeletal myofibrils (26). Concerning detail, however, the P_i-induced force decay appears biphasic, starting with a slow decline (called here “phase 1”) followed by a major, fast decay (i.e., “phase 2”) (Fig. 1 C). To assign rate constants to the two phases, the force decays were fitted using the biphasic function previously described for force relaxation after rapid Ca²⁺-removal (25). This function is sectioned into an initial linear term and a subsequent exponential term. The fit yields the rate constant k_+Pi(1) and the duration t_+Pi(1) of phase 1, and the rate constant k_+Pi(2) of phase 2. As shown in Fig. 1 C, the values of k_+Pi(1) and k_TR are similar while k_+Pi(2) is substantially higher than k_TR.

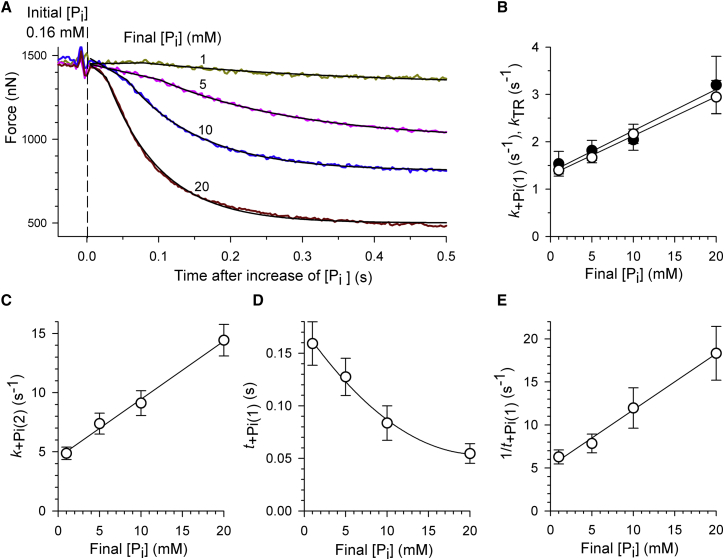
Fig. 2 A illustrates force transients induced by changing from standard activating solution to activation solutions with different concentrations of added P_i. The contaminant [P_i] measured in the standard activating solution was 0.16 mM. With increasing the final [P_i] after the [P_i]-jump, the second phase starts earlier and during both phases the force decays faster. Comparison of the individual rate constants reveals that at the same [P_i], the values of k_+Pi(1) and k_TR are very similar (Fig. 2 B). In contrast, k_+Pi(2) (Fig. 2 C) is 3–5-fold higher than k_TR at corresponding [P_i] (Fig. 2 B). Notably, none of the three rate constants levels off at high [P_i], which would point to a hyperbolic relationship of k_TR, k_+Pi(1), or k_+Pi(2) on [P_i]. Instead, all three [P_i]-dependencies can be described by linear relationships (Fig. 2, B and C). A hyperbolic relationship would indicate saturation of force kinetics at high [P_i]. Saturation would be expected if force kinetics at high [P_i] were determined by intrinsic rate constants of a force-generating isomerization that can be separated by its kinetics from P_i-binding (13, 15). The duration of the initial slow phase, t_+Pi(1), becomes shorter with increasing [P_i] (Fig. 2 D). If t_+Pi(1) is regarded to be a lag phase for delayed onset of phase 2 like in previous studies on fibers (13), the rate constant of the lag phase equals the reciprocal of t_+Pi(1). A plot of 1/t_+Pi(1) versus [P_i] yields a linear relation (Fig. 2 E). In summary, neither the delay nor the rate constant of phase 2 exhibit saturation kinetics that would allow us to separate force generation from P_i-release.

Figure 2.

Effect of the final [P_i] on force kinetics upon rapid increases in [P_i]. (A) Force transients (colored traces) of a myofibril bundle after increase of [P_i] from 0.16 mM to different final [P_i]. (Black lines) Biphasic functions fitted to force transients yielding the values at 1 mM P_i of k_+Pi(1) = −0.47 s⁻¹, t_+Pi(1) = 0.080 s, k_+Pi(2) = 3.0 s⁻¹; at 5 mM P_i of k_+Pi(1) = 2.0 s⁻¹, t_+Pi(1) = 0.101 s, k_+Pi(2) = 5.1 s⁻¹; at 10 mM P_i of k_+Pi(1) = 3.6 s⁻¹, t_+Pi(1) = 0.056 s, k_+Pi(2) = 9.8 s⁻¹; and at 20 mM P_i of k_+Pi(1) = 3.6 s⁻¹, t_+Pi(1) = 0.027 s, k_+Pi(2) = 14.1 s⁻¹. Note that the negative value for k_+Pi(1) at 1 mM P_i results from the positive slope of phase 1 in this particular transient. The values obtained from fitting the transients of six myofibril bundles were averaged to obtain the relations of kinetic parameters (presented in B–D as means ± SE) versus the final [P_i]. (B) The rate constant of the initial force decay (phase 1) upon a P_i-jump (k_+Pi(1), solid circles) closely matches the rate constant of mechanically induced force redevelopment (k_TR, open circles) measured at same [P_i]. (C) The rate constant of the major second phase of the force decay after a P_i-jump linearly increases with the [P_i]. (D) The duration of phase 1 is plotted versus the [P_i]. (E) If phase 1 is considered to be a delay of phase 2, the rate constant of the delay (1/t_+Pi(1)) linearly increases with the [P_i]. To see this figure in color, go online.

Sarcomere dynamics induced by rapid increases in [P_i]

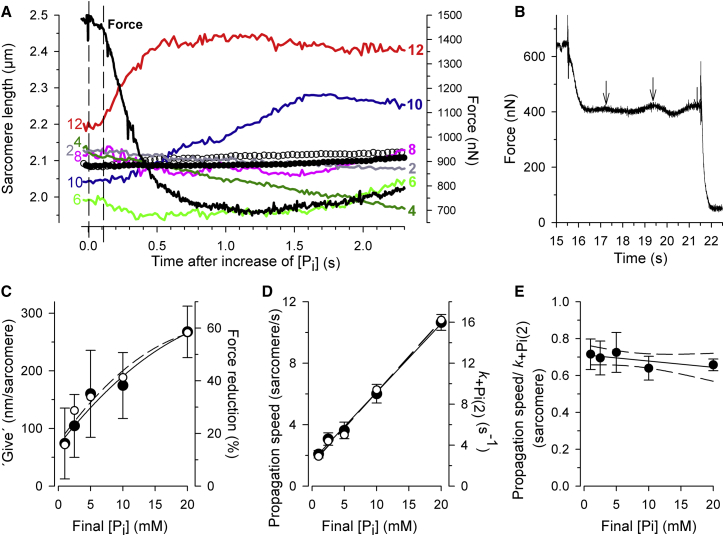
Fig. 3 A shows force and SL changes induced by a rapid increase of [P_i] from 0.16 to 5 mM P_i occurring in a myofibril consisting of ∼15 sarcomeres in total, of which 12 could be analyzed for their length dynamics. Movies S1A and S1B show the sarcomere dynamics in the experiment and are described in the Supporting Material. After the solution change there is a period (from 0 s to ∼0.11 s) during which no significant changes of SLs are observed (SL traces in Fig. 3 A). This period coincides with the duration of the slow phase 1, t_+Pi(1), fitted to the force transient. At the onset of the major, fast phase 2, a single sarcomere (sarcomere 12) near the cantilever started to rapidly lengthen (red trace in Fig. 3 A). In most (∼80% of total) cases, “give” initiates in a weak sarcomere near the cantilever, most likely because of the deterioration of this end during the mounting procedure. This rapid lengthening has been termed “give” according to its description for the sudden rapid lengthening of segments in relaxing intact muscle fibers (32). The pronounced “give” of sarcomere 12 then slowly propagates along the myofibril toward sarcomere 1. This propagation lasts much longer than the force decay (black trace in Fig. 3 A), i.e., the time of phase 2 relates to the “give” of only few sarcomeres. The “give” of sarcomere 12 during phase 2 amounts to 200 nm, i.e., 100 nm per half-sarcomere, while the mean of all individual SL changes by <10 nm. This is also because the large “give” of the few sarcomeres (e.g., 12–10) during phase 2 is partly compensated by slow shortening of other sarcomeres (e.g., 6–2). Mean SL calculated by Fourier analysis changes even only by ∼2 nm. Thus, the pronounced dynamics that can occur at the single sarcomere level during phase 2 would be hardly detected, e.g., by measuring mean SL using laser diffraction.

Figure 3.

(A) Changes in force and sarcomere dynamics of a myofibril bundle after a rapid increase in [P_i] from 0.16 to 5 mM. Mean sarcomere length (circles) and individual sarcomere lengths (colored lines) were analyzed from video images of the myofibril (see Movies S1A and S1B and description for Supporting Movies), simultaneously recorded with the force (black transient). The bundle contained ∼15 sarcomeres, of which 12 were analyzed for sarcomere dynamics, starting with sarcomere 1, located at the side of the mounting needle up to sarcomere 12, located at the side of the cantilever. For clarity, only the individual SL change of every second sarcomere is displayed. Pronounced “give” starts in sarcomere 12 (red trace) at t = 0.10–0.12 s, close to the onset of phase 2 in the force signal, t_+Pi(1) = 0.112 s (black vertical dashed line). The “give” then propagates with decreasing amplitude along the myofibril toward sarcomere 1, indicated by the delayed onsets of “give” in sarcomeres 10, 8, and 6. (Solid circles) Mean SL derived from Fourier analysis of sarcomere profiles along the whole myofibril that mimics a similar type of SL signal obtained using laser diffraction in fiber experiments. (Open circles) Mean SL calculated from the average of individual SLs. Note that in particular the Fourier-derived SL signal remains very stable during phase 2 and changed only by ∼2 nm in the first second after the [P_i], i.e., ∼100-fold less than the SL change of sarcomere 12. (B) Force oscillations occurring after phase 2 in a P_i-jump experiment. (Arrows) Transitions from rise to fall in force. (C–E) Comparison of force and sarcomere changes obtained in an experiment on a myofibril bundle consisting of 22 sarcomeres in which the [P_i] was switched from 0.16 mM P_i to different final [P_i]. (C) The averaged amount of lengthening of the first three sarcomeres performing “give” after onset of phase 2 (solid circles represent the mean and error bars the SD of the three individual values) and the force reduction during phase 2 relative to initial force at 0.16 mM P_i (open circles) are plotted versus the final [P_i]. (D) Force kinetics of phase 2 expressed by k_+Pi(2) (open circles) and sarcomere dynamics expressed by the average propagation speed of “give” (solid circles) increase in same proportion with the final [P_i]. Average propagation speed was obtained from the first three propagation times of “give”, each defined by the time shift of the onset of “give” in the neighboring sarcomere. Error bars represent SD. (E) The ratio of the propagation speeds to k_+Pi(2) remains constant with the [P_i] indicating a close correlation of sarcomere dynamics and force kinetics (see Results text for details and for correlation statistics).

Sarcomere dynamics are not finished after “give” once spreads across all sarcomeres. We previously demonstrated (33) that repeated waves of sarcomere “give”, so-called spontaneous oscillatory contraction (SPOC), initiate in cardiac myofibrils during Ca²⁺-activation in the presence of P_i. Such P_i-dependent SPOC (P_i-SPOC) often occurred in our experiments during the force plateau at [P_i] ≥ 2.5 mM and occasionally at 1 mM P_i. The P_i-SPOC manifests in a continuous force oscillation (Fig. 3 B; for sarcomere dynamics of P_i-SPOC, see Movie S2). Noteworthy, P_i-SPOC does not initiate during a force rise, i.e., before force reaches the plateau, neither during Ca²⁺-induced, nor mechanically or P_i-induced force development (for the latter see Fig. 4 C and Movies S3A and S3B).

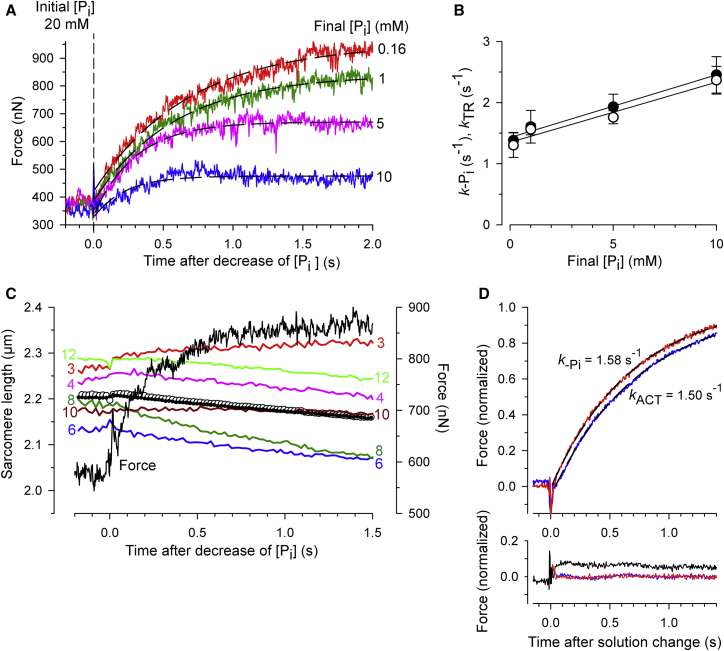
Figure 4.

Force kinetics and sarcomere dynamics induced by rapid decreases in [P_i]. (A) Force transients (colored lines) upon switching from 20 mM P_i to the different [P_i] indicated next to each force trace. (Black dashed lines) Single exponentials fitted to force transients yielding values for k_−Pi of 1.5 s⁻¹ (0.16 mM P_i), 1.7 s⁻¹ (1 mM P_i), 3.3 s⁻¹ (5 mM P_i), and 4.5 s⁻¹ (10 mM P_i). (B) Dependence of the rate constant k_−Pi (solid circles) of the force rise upon a rapid decrease in [P_i] and the rate constant k_TR (open circles) on the final [P_i]. Data are means ± SE of nine myofibrils. (C) Changes in individual SL (colored traces) in a part of a myofibril bundle (ROI) during the force rise (black trace) after a rapid decrease in [P_i] from 20 to 5 mM. Numbers next to each trace indicate the position of the sarcomere in the ROI (see description for Movies S3A and S3B). (Open and solid circles) Means of individual SL and the mean SL computed via the Fourier transform of the sarcomere profile, respectively. (D) (Upper part) Force transients averaged from experiments of eight myofibrils. At a constant pCa of 4.6, the [P_i] was rapidly decreased from 20 to 0.16 mM (red trace) or at constant [P_i] of 0.16 mM, the [Ca²⁺] rapidly increased from pCa 7.5 to 4.6 (blue trace). Before averaging, all force transients were aligned by the peak of the solution change artifact, i.e., the time of effective solution change at the myofibril was set to t = 0. (Dashed black lines) Single exponentials. (Lower part, black line) Difference between the two force transients in the upper part. (Colored lines) Residuals, i.e., the deviation of the single-exponential fit from the corresponding force transient (red line, [P_i]-change; blue line, [Ca²⁺]-change). The short initial peak in the residual for the [P_i]-change amounts to 7% of the total force change. It represents the margin of the solution change artifact rather than a real initial fast phase, because the exponential function fitted to the averaged P_i-induced force transient (see upper part) intersects with the initial force at t = 0. This suggests that there is neither a detectable lag, nor a significant initial fast change, nor an offset in the force response.

To explore whether the P_i-induced force decay in phase 2 is related to the amplitude and the propagation speed of sarcomere “give”, force kinetics and sarcomere dynamics of a myofibril consisting of 22 sarcomeres were analyzed (Fig. 3, C–E). The [P_i] was switched from the same initial [P_i] of 0.16 mM to different final [P_i]. For each final [P_i], the sarcomere dynamic parameters were averaged from the first 3–4 sarcomeres participating in the “give” process. Both the average amplitude of “give” per sarcomere (Fig. 3 C) as well as the average speed by which “give” propagated from sarcomere to sarcomere along the myofibril (Fig. 3 D) increased with the final [P_i], i.e., with the magnitude of the P_i-jump. Remarkably, the average amplitude of “give” and the force reduction during phase 2 exhibit very similar [P_i]-dependencies (Fig. 3 C), and linear regression analysis (not illustrated) yields a strong correlation of average amplitude of “give” and force reduction (r = 0.983, p = 0.0026). Also, the propagation speed of “give” and the force kinetics of phase 2 (k_+Pi(2)) changed in parallel with the [P_i] (Fig. 3 D) with a very strong correlation of propagation speed and k_+Pi(2) (r = 0.999, p = 3.8 × 10⁻⁵). Thus, both the amplitude and the kinetics of the force decay of phase 2 are closely correlated with the amplitude and dynamics of sarcomere “give”. To estimate how far “give” propagates in relation to the force decay, the propagation speed was multiplied by the lifetime of the fast force decay τ = 1/k_+Pi(2), i.e., the time when force decays by (1 – 1/e) = 63% = 0.63 during phase 2. The product yields a [P_i]-independent value of 0.6–0.7 sarcomeres (Fig. 3 E). This small number indicates that “give” of a single sarcomere is already sufficient to cause a large part of the force decay during phase 2.

Kinetics of force transients and sarcomere dynamics induced by rapid decreases in [P_i]

Force transients after rapid decreases in [P_i] can be fitted like the mechanically induced force redevelopment by a single-exponential function with the rate constant k_−Pi (compare to Fig. 1 D). To obtain the dependence of k_−Pi on the [P_i], force transients were induced by decreasing [P_i] from 20 mM P_i to different final [P_i]. The set of transients in Fig. 4 A illustrates that the time required for reaching the force plateau becomes longer the lower the final [P_i]. The value of k_−Pi increases linearly with the [P_i] and the value of k_−Pi is very similar to that of k_TR measured at the same [P_i] (Fig. 4 B).

Fig. 4 C shows changes of individual SL occurring in a part of a myofibril bundle during the force rise after rapidly decreasing the [P_i] from 20 to 5 mM. The bundle consisted of 19 sarcomeres from which 13 could be quantitatively analyzed (for details, see description for Movies S3A and S3B). Most sarcomeres slowly shorten; some few, for example sarcomere 3 near the attached end, slowly lengthen. However, no fast “give”, i.e., no rapid lengthening of sarcomeres and no organized propagation of “give” along the myofibril, is observed (see also Movie S3A).

As the force response after a rapid decrease in [P_i] is not confounded by “give”, it was of interest whether it consists of an initial lag phase or a fast change before the single-exponential force rise. The lifetime of a lag would indicate the lifetime of a transient cross-bridge state between P_i-release and force-generation, which could be either a force-generating state before P_i-release or a pre-force-generating state after P_i-release. A fast force change would indicate a fast force-generating step adjacent to fast P_i-release, both apart from a rate-limiting transition (see model simulations in the Supporting Material). To minimize the noise, an averaged force transient after a large, rapid decrease in [P_i] from 20 to 0.16 mM was produced and plotted together with the corresponding averaged Ca²⁺-induced force transient (Fig. 4 D). Whereas the Ca²⁺-induced force transient exhibits a lag of ∼30 ms that most likely results from the time needed from Ca²⁺-binding to troponin C to the buildup of force-generating cross-bridges, the P_i-induced transient has neither an initial lag nor a significant fast initial change. A single-exponential fit with a rate constant k_−Pi similar to k_ACT fully describes the time course of the force signal. Hence, the P_i-induced force transient exhibits no further significant kinetic information than the one already reported by k_ACT and k_TR.

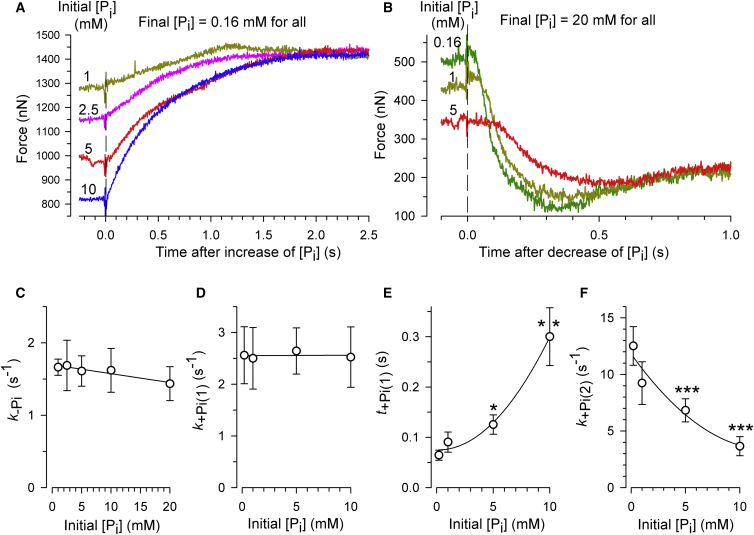
Dependence of force kinetics on the initial [P_i]

Fig. 5 summarizes the effects of changing the initial [P_i] on force kinetics. Fig. 5 A shows force transients induced by decreasing the [P_i] from different initial [P_i] to 0.16 mM. The rate constant k_−Pi of the exponential force rise was not significantly affected by the initial [P_i] (Fig. 5 C), indicating that the force prehistory does not affect P_i-induced force development kinetics.

Figure 5.

Effect of initial [P_i] on P_i-induced force kinetics. (A) Force rises upon decreasing [P_i] from different initial [P_i] to the same final [P_i] of 0.16 mM. (B). Force decays upon increasing [P_i] from different initial [P_i] to the same final [P_i] of 20 mM. (C–F) Means ± SE of the kinetic parameters derived from six experiments of the types depicted in (A) and (B). Neither the rate constant of the force rise (k_−Pi shown in C), nor the rate constant of the initial slow force decay (k_+Pi(1) in D) is significantly altered by the initial [P_i]. With increasing the initial [P_i], the onset of the major force decay (phase 2) is highly significantly prolonged (t_+Pi(1) in E) and the rate constant of phase 2 is highly significantly reduced (k_+Pi(2) in F). Asterisks in (E) and (F) indicate p-values < 0.05 (^∗), < 0.01 (^∗∗), or < 0.001 (^∗∗∗) compared to 0.16 mM initial [P_i]. To see this figure in color, go online.

Fig. 5 B shows force transients induced by increasing the [P_i] from different initial [P_i] to 20 mM. With increasing initial [P_i], the overall amplitude of the force change becomes smaller. The rate constant of the initial slow phase (k_+Pi(1)) was independent of initial [P_i] (Fig. 5 D), and the second phase of the force decay initiates later, i.e., t_+Pi(1) becomes prolonged (Fig. 5 E). The fast phase 2 becomes slower, i.e., k_+Pi(2) becomes decreased (Fig. 5 F). It is tempting to speculate that for the limiting case of a minimal force change if the initial [P_i] approaches the final [P_i], phase 2 vanishes and force decays by a single exponential with rate constant k_+Pi(1). This idea is supported by the fact that k_+Pi(1) is not altered by the initial [P_i] (Fig. 5 D). Furthermore, the findings that k_+Pi(1) and k_−Pi at the same final [P_i] have similar values (Fig. 2 B versus Fig. 4 B) and are both independent of the initial [P_i] (Fig. 5, C and D) corroborates the conclusion that P_i-induced force kinetics behave symmetrically, i.e., do not depend on the force prehistory and the direction of the force change as long as there is no “give”.

Discussion

Synthesis

Rapid increase of [P_i] in cardiac myofibrils induces an initial slow force decay (phase 1, rate constant k_+Pi(1)) before the “give” of the first sarcomere induces the major fast force decay (phase 2, rate constant k_+Pi(2)). At same final [P_i], k_+Pi(1) is identical to k_TR and k_ACT and to the rate constant k_−Pi of the single-exponential force rise in response to a rapid drop in [P_i]. k_+Pi(2) but not k_+Pi(1) nor k_−Pi is altered by the initial [P_i], thus by the prehistory of contraction. These results suggest that the major force decay upon rapid increase in [P_i] does not reflect the kinetics of the “force-generating step” but is determined by sarcomere dynamics whereas in the absence of “give”, P_i-induced force kinetics simply report the kinetics of rate-limiting transitions in the cross-bridge cycle.

Comparison of force kinetics with previous studies and implications of sarcomere “give”

Photolytic release of P_i from caged-P_i in skeletal muscle fibers results in a force transient with up to four, subsequent phases (13, 14, 15): an initial lag phase (phase 1); a major, exponential force decay (phase 2); a minor force increase (phase 3); and a minor force decay (phase 4). The rapid increase in [P_i] induces rebinding of P_i and backward cycling of cross-bridges. Thus, the transient lag has been interpreted to indicate the transient formation of an AM.ADP.P_i-state before the P_i-release step that is still generating force. Consequently, the force-generating step was attributed to an isomerization between two different AM.ADP.P_i-states. The kinetics of this force-generating isomerization was assigned to the rate constant k_+Pi (originally abbreviated as k_Pi) of the major force decay (phase 2). Phase 3 and 4 were difficult to explain in terms of cross-bridge transitions and had been suggested to present artifacts from photolytic side products of the caged-P_i.

In former studies, most attention has been paid to the rate constant of the second phase, k_+Pi, because it is the major phase upon [P_i]-increase in fibers (13, 14). In some studies, the minor phase 1 was not examined (15, 26). In this study, it is found that phase 1 also yields a rate constant (k_+Pi(1)), thus the rate constant of the second phase is termed k_+Pi(2). Interestingly, k_+Pi(1) is very similar to k_TR. Therefore, in this study, phase 1 is not considered to be a lag but the beginning of an exponential force decay reflecting the type of cross-bridge turnover kinetics that has been described for k_TR (22). However, this force decay is truncated by the onset of sarcomere “give” at the beginning of phase 2 (compare to Fig. 3 A).

Considering the lower temperature and the higher amount of the slow myosin heavy chain in the guinea pig compared to the rat heart, the value of k_+Pi(2) of 7.5 s⁻¹ at 5 mM P_i and 10°C obtained in this study using cardiac myofibrils from guinea pig is in close agreement with the value of k_+Pi of 19 s⁻¹ at same [P_i] and 15°C obtained in a study on rat cardiac myocytes (16). Most caged-P_i studies were performed with skinned fibers from the fast rabbit psoas muscle (13, 14, 15). After correcting k_+Pi for temperature by using a Q₁₀ of 3.4 (15), the values for k_+Pi for rabbit psoas muscle fibers are slightly (∼1.5-fold) higher than the ones for myofibrils from this muscle (26) and approximately fourfold higher than the ones for the cardiac myofibrils used in this study. Furthermore, the approximately fourfold difference in k_+Pi between rabbit psoas myofibrils (26) and cardiac myofibrils in this study is slightly higher than the ∼2–3-fold difference in other kinetic parameters between the two myofibril preparations (31, 33). It is difficult to decide whether these slight disparities reflect experimental errors or mechanistic differences. In the latter case, the fast force decay upon [P_i]-increase in myofibrils and fibers of fast skeletal muscle might involve more mechanisms than the ones described here for cardiac myofibrils.

The forward and the reverse rate constants of the force-generating isomerization were determined from the hyperbolic relation of k_+Pi versus the final [P_i] obtained by flash photolysis of caged P_i in fast skeletal muscle fibers (6, 13, 14, 15). There is a tendency for the k_+Pi-[P_i] relation to become more hyperbolic with increasing temperature (13). In contrast, P_i-jump studies on slow skeletal muscle fibers (17) and skinned cardiac myocyte bundles (16) revealed linear relations. Similarly, here with cardiac myofibrils, k_+Pi(2) increased linearly with the final [P_i]. Using myofibrils from fast skeletal muscle and rapid solution change, Tesi et al. (26) also failed to obtain a hyperbolic k_+Pi-[P_i] relation. Therefore, the observation of a hyperbolic relation cannot be simply explained by the fast muscle type. Noteworthy, only the use of myofibrils enables us to obtain the k_+Pi-[P_i] relation over a wide range in [P_i] by always starting from the same initial [P_i]. This is because with the caged-P_i technique used for skinned fibers it is difficult to induce large changes in [P_i] so that the k_+Pi values for higher final [P_i] were determined by starting from higher initial [P_i]. However, the results in this study reveal that k_+Pi(2) becomes significantly decreased with increasing the initial [P_i] (compare to Fig. 5 F). Thus, having to start from higher initial [P_i] to determine k_+Pi(2) values at high final [P_i] would change a linear toward a hyperbolic-shaped relation. In line with this idea, an exploration of the k_+Pi-[P_i] relation over a small [P_i]-range (1–3 mM), by inducing P_i-jumps from same initial [P_i] with the caged-P_i technique, also yielded a linear relation (17). In summary, when initiated from the same [P_i], P_i-induced force kinetics depend linearly on the [P_i]. However, a linear k_+Pi-[P_i] relation cannot reveal intrinsic rate constants of the force-generating isomerization as has been derived from the hyperbolic relation of force kinetics in fast skeletal muscle fibers upon P_i-jumps (13, 14). On the other hand, it can be argued that at smaller perturbations, i.e., when smaller amounts of P_i are released, like in the studies using caged-P_i, the system is closer to the equilibrium and this might minimize the effect of sarcomere “give” on the force response. Whether force kinetics become fully symmetric and whether [P_i]-dependence of parameters are linear or hyperbolic at minimal force changes is difficult to explore in myofibrils, because solution flow artifacts can dominate the force response under this condition. In particular, the error of k_+Pi(1) can be large at small force changes because of the minor amplitude of phase 1.

This study, using cardiac myofibrils, indicates that the major phase 2 is initiated by “give” of a single sarcomere and that the force kinetics of this phase is closely correlated to the speed by which “give” propagates along the myofibril. Sarcomere “give” also occurs during the second and major, so-called fast phase of relaxation upon rapid Ca²⁺-removal from myofibrils (30) and after the end of tetanic activation of intact muscle fibers (32). The process of “give” initiates in the longest, weakest sarcomere of a myofibril that had shortened least during the preceding contraction and in which cross-bridges bear higher strain than on average (30, 31). Furthermore, the “give” during relaxation is sensitively promoted by P_i, an effect that can be attributed to the accelerated detachment of highly strained cross-bridges via rebinding of P_i (30). In line with this explanation for the rapid relaxation phase, the fast force decay of phase 2 after [P_i]-increase might be explained by synchronized fast detachment of highly strained cross-bridges in a weak sarcomere. In summary, the speedup of force kinetics from phase 1 to the phase 2 reflects the increase from slow cross-bridge detachment existing during isometriclike cross-bridge turnover to the fast detachment resulting from sarcomere “give”.

Beside the phase 1 and 2 discussed above, two further phases consisting of a minor force rise (phase 3) and a minor force decay (phase 4) had been described in P_i-jump studies on skinned fibers (13, 17). Phase 3 has been ascribed to a loss of inhibition of force arising from caged-P_i (13, 17). Here with cardiac myofibrils and with no caged-P_i, jump increases in [P_i] frequently induced P_i-SPOCs that manifest in continuous force oscillations around the new force level. Thus, an alternative explanation for phases 3 and 4 observed upon P_i-jumps in fibers might be the reflection of the first period of a force oscillation. Because a long fiber contains more than a single SPOC region, the force oscillations in a fiber likely diminish quickly when the different SPOCs become desynchronized. Notably, “give” of sarcomeres and P_i-SPOC were never observed during force developments, regardless of the [P_i] and whether the force rise was induced by Ca²⁺, slack-restretch, or decrease in [P_i] and a simple single-exponential function was sufficient to describe the time course of the force increase.

Asymmetry of P_i-induced force kinetics and implications for chemo-mechanical coupling

Although this study is the first, to our knowledge, to show that the major second phase upon a step increase in [P_i] results from “give” of single sarcomeres, the asymmetry between k_+Pi and k_−Pi was already described in a study with skeletal myofibrils (26). In the latter study, however, no sarcomere dynamics had been recorded. By changing from low (0.1 mM) or high (10 mM) [P_i] to the same final [P_i] (5 mM), these authors found approximately fourfold higher values of k_+Pi compared to k_−Pi in fast psoas and twofold higher values in slow soleus myofibrils, respectively. Whether sarcomere “give” also accounts for the asymmetry between k_+Pi and k_−Pi reported for skeletal myofibrils (26), remains to be tested by imaging individual sarcomeres. However, our measurements on ventricular myofibrils from guinea pig that mainly contain the slow β-MHC isoform (34) indicate a ∼3–5-fold difference, similar to the one found in fast psoas myofibrils. Thus, it is unlikely that sarcomere “give” explains the observed asymmetry only for the slow MHC isoform. Furthermore, if sarcomere “give” would only influence k_+Pi in cardiac and not in skeletal myofibrils, there is still the unsolved question why k_−Pi in skeletal myofibrils is identical to k_TR (26). So far, no other mechanistic explanation had been given to explain the asymmetry between k_+Pi and k_−Pi and the similarity of k_−Pi to k_TR in skeletal myofibrils and even recent, more complex models could not explain this asymmetry (29). Furthermore, no study exists in which force kinetics after [P_i]-changes were conducted at temperatures close to mammalian body temperature. In summary, future studies will be required to investigate how temperature affects the asymmetry between k_+Pi and k_−Pi in skeletal and cardiac myofibrils and how the individual sarcomeres in skeletal myofibrils behave after rapid [P_i]-changes.

This study reveals that as long as sarcomeres do not “give”, [P_i]-induced force changes describe the reapproach of steady-state distributions among force- and non-force-generating states. Their kinetics are therefore dominated by the same slow reactions that determine k_TR and k_ACT. Simulations show that the force kinetics after rapid [P_i]-changes can be explained by a simplified model in which the P_i-release and the force-generating step are intrinsic parts of a reversible, rate-limiting transition (forward rate constant f) from a non-force-generating AM.ADP.P_i to a force-generating AM.ADP state (Fig. S1, model version 1). Because both the P_i-release and the force-generating step occur during this transition, not only their kinetics but also their sequence remains unclear. Attempts to separate the P_i-release- and/or the force-generating step from a slow transition that limits f reveal only a few model scenarios consistent with the slow single-exponential force kinetics observed upon rapid decrease in [P_i]. Possible scenarios are a slow, rate-limiting force-generating step that occurs before or after a rapid P_i-release (Fig. S1, model versions 2 and 3) or a fast force-generating step that occurs before or after a slow, rate-limiting P_i-release (Fig. S1, model versions 4 and 5). Noteworthy, model versions 1, 2, and 3 imply slow force responses upon any kind of perturbation and are thus not consistent with rapid force recovery upon step length changes (8, 9, 10) unless the latter reflects a mechanism of force generation subsequent to the slow force generation seen in k_TR-experiments or upon rapid decrease of [P_i] (35).

The classical model scenarios of a fast force-generating step preceding or following a rapid P_i-release are reflected by the model versions 6 and 7 (see Fig. S1). Simulations by these models result in a force rise upon [P_i]-decrease that is faster than the force rise in k_TR-experiments. This is neither observed in cardiac myofibrils (compare to Fig. 4 D) nor in fast skeletal muscle myofibrils (26). Thus, the classical scenario of an intermediate to fast force-generating isomerization before rapid P_i-release that has been derived from the fast kinetics of phase 2 in fiber studies using caged-P_i (13, 14) is incompatible with the slow force kinetics observed in cardiac and fast skeletal muscle myofibrils. In searching for sequential models with intermediate-fast force-generating and P_i-release steps yielding similar rates of k_−Pi and k_TR, either the two steps have to be placed before the transition limiting f (Fig. S1, model versions 8 and 9) or the two steps have to be separated from each other by the rate-limiting transition (Fig. S1, model versions 10 and 11). However, all these models cause problems. As indicated by the high initial force values of k_TR-simulations (note the different y axes in Fig. S1), the model versions 8, 9, 10, and 4, in which a fast force-generating step occurs before the step limiting f, all result in a high occupancy of force-generating states during unloaded shortening that is inconsistent with the low duty ratio found at v_max (36). Furthermore, model versions 10 and 11 fail to describe the sensitivity of force or force kinetics to the [P_i].

In summary, model version 1 in which the P_i-release and the force-generating step are both merged with f yields the highest modulation of force and kinetics by [P_i] and account for the observed high modulation of force by [P_i]. On the other hand, model version 5 is the most straightforward to be also combined with the rapid force recovery after length-step and a low duty ratio at v_max. In both these models, the P_i-release is merged with the transition limiting f, which implies that the release of P_i from the cross-bridge is coupled to a slow structural transition. Needless to say, even the seemingly single-exponential force transients after rapid decreases in [P_i] do not exclude the possibility that more than one step might limit the overall rate of cross-bridge cycling to force-generating states (37). However, regardless of the exact nature of the slow structural transition(s), the observed slow single-exponential force kinetics upon a rapid change in [P_i] rule out a mechanism in which P_i-release/P_i-binding to/from the cross-bridge presents a rapid equilibrium followed or following a fast force-generating step.

Finally, force kinetics observed upon [P_i]-changes per se cannot differentiate whether the first force-generating step occurs before, along, or after P_i-release because all model versions 1–5 are consistent with slow, single-exponential force kinetics. Only in combination with other findings, like length-step-induced rapid force recovery and low duty ratio at v_max, a rate-limiting P_i-release preceding a fast force-generating step (model version 5) is the most consistent sequential model. Recently, a novel crystal structure of myosin was found that possesses a fully formed actin interface and opened a backdoor for P_i-release with minimal rotation of the lever arm (20). This structure implies that the P_i-release can occur before the power stroke, different from kinetic analysis of P_i liberated from myosin and structural changes by FRET that indicate the power stroke can occur before P_i-release (38). The conclusion from this myofibril study is that force transients in response to stepwise changes in [P_i] cannot differentiate between these two scenarios. Altogether, this raises the question whether for P_i-release and the first force-generating step a truly mandatory sequence exists, or else the sequence can be both ways.

Editor: James Sellers.

Supporting Citations

References (39, 40, 41) appear in the Supporting Material.

Supporting Material

Movie S1A. Sarcomere Dynamics after a Rapid Increase of [P_i] from 0.16 to 5 mM

The rectangle (green-red dashed line, also visible in the video) marks the ROI selected for evaluating the data shown in Fig. 3 A (see Materials and Methods in the main text). The black numbers in the image on top (not depicted in the movie) indicate the sarcomeres analyzed for length changes according to the numbering of SL traces in Fig. 3 A. During experiment, frames were sampled at intervals of 17.3 ms. The movie consists of 169 frames and starts three frames before the [P_i]-increase that occurs at frame 4. To better follow the fast sarcomere dynamics in the movie, it was stored in the databank in twofold slow motion, i.e., the original duration of the movie was 2.9 s before it was stretched to 5.8 s.

Movie S1B. Sarcomere Dynamics after a Rapid Increase of [P_i] from 0.16 to 5 mM

For a closer view of sarcomeres analyzed within the ROI, Movie S1A was cut to the ROI and twofold magnified in size. Sarcomere “give” initiates in the movies at sarcomere 12 and propagates to the left.

Movie S2. Sarcomere “Give” and Subsequent SPOC after Increase of [P_i] from 0.16 to 20 mM

During experiment, frames were sampled at intervals of 41.1 ms. The movie consists of 120 frames and starts three frames before the increase of [P_i] that occurs at frame 4 of the movie. The movie stored in the databank shows the sequence in twofold slow motion (i.e., movie time was stretched from 4.9 to 9.8 s). The movie illustrates the pronounced sarcomere dynamics at high [P_i]. Sarcomere “give” initiates at the right side near the cantilever and propagates to the left. When “give” reaches the left end of the bundle, it restarts at the right side, resulting in a continuous SPOC wave.

Movie S3A. Sarcomere Dynamics after a Rapid Decrease of [P_i] from 20 to 5 mM

The rectangle (green-red dashed line, also visible in the movie) marks the ROI selected for evaluating the data shown in Fig. 4 C. The black numbers in the image on top (not depicted in the movie) indicate the sarcomeres analyzed for length changes according to the numbering of SL traces in Fig. 4 C. Note that due to the axial shift of sarcomeres between single myofibrils, only a distal part of the bundle and only 13 of the 19 sarcomeres in total could be quantitatively analyzed. During experiment, frames were sampled at intervals of 19.9 ms. The movie consists of 150 frames and starts three frames before the [P_i]-decrease that occurs at frame 4. The movie stored on the databank shows the sequence in twofold slow motion, i.e., movie time was stretched from 3.0 to 6.0 s.

Movie S3B. Sarcomere Dynamics after a Rapid Decrease of [P_i] from 20 to 5 mM

For a closer view of the sarcomeres, the Movie S3A was cut to the ROI and twofold magnified in size. As seen in the movies, there is inhomogeneous shortening of sarcomeres but neither rapid lengthening of individual sarcomeres (“give”) nor organized sarcomere dynamics.