How Do Gyrating Beads Accelerate Amyloid Fibrillization?

Abstract

The chemical and physical mechanisms by which gyrating beads accelerate amyloid fibrillization in microtiter plate assays are unclear. Identifying these mechanisms will help optimize high-throughput screening assays for molecules and mutations that modulate aggregation and might explain why different research groups report different rates of aggregation for identical proteins. This article investigates how the rate of superoxide dismutase-1 (SOD1) fibrillization is affected by 12 different beads with a wide range of hydrophobicity, mass, stiffness, and topology but identical diameter. All assays were performed on D90A apo-SOD1, which is a stable and wild-type-like variant of SOD1. The most significant and uniform correlation between any material property of each bead and that bead’s effect on SOD1 fibrillization rate was with regard to bead mass. A linear correlation existed between bead mass and rate of fibril elongation (R² = 0.7): heavier beads produced faster rates and shorter fibrils. Nucleation rates (lag time) also correlated with bead mass, but only for non-polymeric beads (i.e., glass, ceramic, metallic). The effect of bead mass on fibrillization correlated (R² = 0.96) with variations in buoyant forces and contact forces (between bead and microplate well), and was not an artifact of residual momentum during intermittent gyration. Hydrophobic effects were observed, but only for polymeric beads: lag times correlated negatively with contact angle of water and degree of protein adhesion (surface adhesion and hydrophobic effects were negligible for non-polymeric beads). These results demonstrate that contact forces (alone) explain kinetic variation among non-polymeric beads, whereas surface hydrophobicity and contact forces explain kinetic variation among polymeric beads. This study also establishes conditions for high-throughput amyloid assays of SOD1 that enable the control over fibril morphologies and produce eightfold faster lag times and fourfold less stochasticity than in previous studies.

Introduction

The ability to accurately and reproducibly measure rates of amyloidogenesis is critical for uncovering mechanisms by which pathogenic mutations and post-translational modifications affect protein fibrillization (1, 2, 3) and for discovering compounds that act upon amyloid-like oligomers (4, 5, 6, 7). Under quiescent conditions, that is, without stirring, neurotoxic polypeptides such as α-synuclein and superoxide dismutase-1 (SOD1) self-assemble into amyloid fibrils at timescales ranging from days to months (8, 9, 10, 11). To accelerate amyloidogenesis and reduce stochasticity (9), solutions are gyrated in microtiter plates at >100 rpm with millimeter-sized stirring beads placed in each sample well (9, 12, 13). Beads are typically composed of polytetrafluoroethylene (Teflon), but borosilicate glass and polymethylmethylacrylate (PMMA) have also been used (8, 9, 12, 14, 15, 16). Establishing a few basic rules of thumb for how different bead types do or do not affect formation rates (and morphologies) of amyloid fibrils will help optimize assays; help discern the growing (and often inconsistent) list of reported rates of amyloid nucleation and elongation (10, 14, 17, 18), and might uncover clues about the mechanical, chemical, and surface forces that drive fibrillization.

In general, the mechanical agitation of protein solutions by a gyrating bead is hypothesized to accelerate aggregation by exposing hydrophobic amino acid residues to the air-water interface (8, 19, 20, 21) and, separately, by inducing the fragmentation of oligomers, which allows secondary nucleation and elongation (8, 22, 23) (stirring also, of course, increases collision frequency and abolishes local gradients of reagents). A complete set of physical and chemical rules by which a gyrating bead affects the rate of amyloid formation—i.e., a set that includes hydrophobic, omniphobic, and electrostatic effects; contact mechanics; shear force; and mass—does not exist. For example, will a Teflon bead of 3.2 mm diameter (used in some studies of SOD1 fibrillization (13)) accelerate fibrillization more or less than a Teflon bead of 2.4 mm diameter (used in other studies (24)), and could these differences explain the disparity in reported rates? In microplate-based assays that commonly employ discontinuous gyration (e.g., gyration for 15 s followed by a 15-s pause), will the momentum of a gyrating bead cause a heavier bead to continue orbiting the well longer than a bead of lower mass? Does this residual momentum produce significant differences in observed rates? Moreover, will a bead with smooth surface topology, for example, borosilicate glass, stainless steel, or silicon nitride ceramic (Fig. 1), increase the reproducibility of measured aggregation rates compared to beads with more irregular surfaces (e.g., polypropylene; Fig. 1)? And do micrometer-scale scratches or crevices on the surface of a bead significantly affect rates of fibrillization by providing nucleation sites (as they do with crystallization in glassware (25))? Will a polyethylene bead accelerate aggregation by the same magnitude as its more commonly used fluorinated analog, Teflon (Fig. 1) (12, 26, 27, 28)? Regarding hydrophobic effects, if hydrophobic effects between bead and protein are so dominant (as reported for α-synuclein fibrillization (8)), why do some research groups report identical rates of fibrillization in the presence of either glass or Teflon beads (14), even though water contact angles for borosilicate glass and Teflon differ by >80° (Table 1)? This study set out to answer a few of these questions.

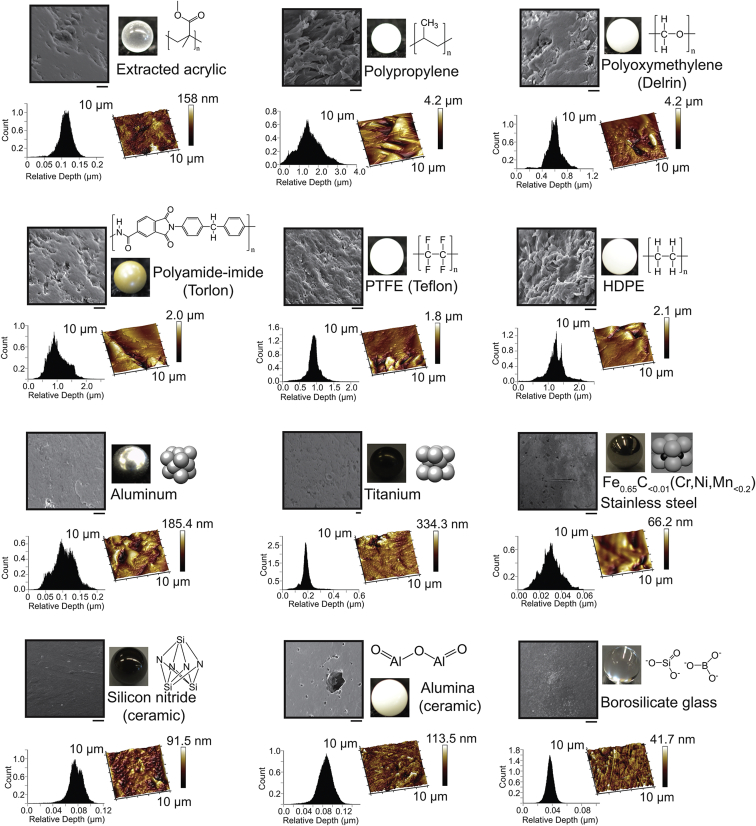
Figure 1.

Chemistry and surface features of beads used in amyloid assays. SEM images of beads show the surface topology. Scale bars, 10 μm. The insets below each SEM micrograph include an AFM image collected across a 10 μm × 10 μm scanned area (lighter color indicates shallower surfaces) and a histogram showing the relative surface depth, calculated from AFM imaging.

Table 1.

Physical and Chemical Properties of Beads Used in This Study

Bead	Mass (mg)a	Surface Roughness; Rq (nm)b	Water Contact Angle (°)c	Lag Time (h)d	Propagation Rate (h−1)d
Polypropylene	15.6 ± 0.6	615	99.0	12.9 ± 1.0 (n = 35)	0.59 ± 0.05
HDPE	15.7 ± 0.2	312	99.1	15.7 ± 1.3 (n = 52)	0.58 ± 0.03
Extracted acrylic	20.8 ± 1.1	19.5	75.0	17.8 ± 1.4 (n = 35)	0.24 ± 0.02
Polyoxymethylene (Delrin)	22.8 ± 0.1	117	73.0	17.7 ± 1.4 (n = 20)	0.29 ± 0.02
Polyamide-imide (Torlon)	23.6 ± 0.2	322	78.0	16.5 ± 0.9 (n = 28)	0.46 ± 0.04
PTFE (Teflon)	35.9 ± 0.1	205	110.0	8.7 ± 0.3 (n = 42)	0.65 ± 0.04
Borosilicate glass	40.8 ± 0.1	5.42	24.0	5.9 ± 0.6 (n = 41)	0.49 ± 0.03
Aluminum	46.9 ± 0.3	30.9	89.2	5.4 ± 0.1 (n = 32)	1.27 ± 0.08
Silicon nitride (ceramic)	54.1 ± 0.01	11.6	26.6	5.7 ± 0.3 (n = 32)	0.72 ± 0.04
Alumina (ceramic)	64.6 ± 0.1	15.5	37.0	4.8 ± 0.5 (n = 32)	0.73 ± 0.04
Titanium	72.9 ± 0.4	48.3	83.0	4.3 ± 0.6 (n = 31)	0.86 ± 0.03
Stainless steel	131.9 ± 0.1	9.23	80.3	3.7 ± 0.1 (n = 31)	1.60 ± 0.07

The bead diameter is 3.2 mm.

^aThe mass of each bead was measured using a sensitive bench-top scale in replicates of four and is reported as the mean ± SD.

^bValues for surface roughness were calculated using AFM.

^cValues for water contact angle were obtained from references (58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69).

^dValues are reported as the mean ± SEM.

Previous investigations into the kinetic effects of different beads have focused on the chemical properties of beads (primarily on hydrophobicity (14, 29, 30)). Those studies have demonstrated the importance of surface-induced changes in protein conformation (30) and oligomer morphology (29), and in induction of fibril fragmentation (14). Very little is known, however, regarding how the basic physical properties of beads—mass and surface roughness, for example—affect the aggregation rate of proteins. The momentum-based and friction forces that emerge from the mass, buoyancy, stiffness (defined as Young’s modulus and Poisson’s ratio), and sleekness (defined as the friction coefficient) of the gyrating bead will alter the contact mechanics between bead and microplate well, and affect shear forces at the water-bead interface. These forces might impact, for example, rates of fibril fragmentation and secondary nucleation (8).

In this investigation, we studied the effect of 12 chemically and physically diverse spherical beads (of identical diameter) on the fibrillization of metal-free (apo) SOD1 in 96-well microtiter plates. Our original intent was to find assay conditions that increased the reproducibility and rate of amyloid assays for SOD1. The amyloidogenesis of SOD1 is slow and notoriously stochastic (13, 15, 24, 31), and morphology of SOD1 aggregates are strongly dependent on reaction conditions (13). The stochastic nature of SOD1 self-assembly is not a property that is unique to SOD1, or to any other protein or macromolecule. Stochastic self-assembly has been observed in all types of living and non-living systems, from the crystallization of water (32) to the aggregation of nucleic acids (33), gene expression (34), and the aggregation of the social amoeba Dictyostelium discoideum (35). We succeeded in this effort: simply using stainless steel beads diminishes much of the stochasticity in fibril nucleation (but not elongation) and accelerates fibrillization. In the course of doing so, we discovered trends between various properties of gyrating beads and fibril lag time and propagation rate. These trends show, for example, that surface chemistry of the bead and protein-surface interactions can only partially explain why some beads accelerate protein fibrillization more than others. In addition to these effects, Newtonian forces (arising from the mass of the bead) significantly affect the kinetics and stochasticity of SOD1 fibrillization. We interpret these Newtonian effects in terms of shear and contact forces between bead and microplate well, which are greater for heavier beads and likely induce fibril fragmentation and secondary nucleation (14) at the bead-microplate and/or bead-solvent interface.

Materials and Methods

SOD1 expression, purification, and demetalation

Human Cu, Zn superoxide dismutase plasmid carrying the D90A mutation was expressed in Saccharomyces cerevisiae. SOD1 was purified and immediately demetalated, as previously described (31). The demetalated state of SOD1 was confirmed to contain <0.05 equivalents of Zn²⁺ or Cu²⁺ per dimer, using inductively coupled plasma mass spectrometry. Protein concentration was determined spectrophotometrically using an extinction coefficient of 10,800 M⁻¹·cm⁻¹ for human apo-SOD1, with λ_max = 280 nm.

Thioflavin-T fluorescence aggregation assay

Fibrillization of D90A apo-SOD1 was monitored and assayed using a microtiter-plate-based thioflavin-T (ThT) aggregation assay, as previously described (13). Briefly, pure D90A apo-SOD1 at a concentration of 30 μM (per dimer) in 10 mM phosphate/5 mM EDTA buffer (pH 7.4) was incubated with 10 mM tris(2-carboxyethyl)phosphine (TCEP) and 150 mM NaCl for 6 h, with gentle shaking at room temperature. The concentration of TCEP is 10 mM in our assays (∼300 times higher than [SOD1]) to mimic intracellular conditions. This concentration of TCEP also prevents the random disulfide cross-linking of SOD1 oligomers. The 96-well microplate that was used to perform the ThT fluorescence aggregation assays was carefully sealed with a polypropylene film. We calculated that throughout the 168 h assay, only 0.02% of TCEP would be oxidized by oxygen, assuming that the rate of O₂ diffusion through the polypropylene seal at 37°C is ≈4.3 × 10⁻⁷ mg/h. After 6 h, 20 μM of ThT was added to the apo-SOD1 solution (filtered with a 200 μm syringe filter), and 200 μL aliquots of this “mother stock” were added to the wells of a 96-well black polystyrene microplate, which contained various types of beads (McMaster-Carr, Elmhurst, IL). Intensity of ThT fluorescence was recorded (for ∼5 days, with circular shaking at 360 rpm) using an Ascent 2.5 fluorescence spectrophotometer (Thermo Scientific, Waltham, MA). The excitation and emission filters were set to be 444 nm and 485 nm, respectively.

Electron microscopy

Surface topology of each bead (under different conditions) was visualized using an FEI (Hillsboro, OR) Versa 3D focused ion-beam scanning electron microscope (SEM). For regular SEM imaging, beads were sputter coated with gold to a thickness of 20 nm.

Morphology of apo-SOD1 fibrils after the termination of aggregation assays was determined with a JEOL JEM 1010 transmission electron microscope (TEM; JEOL, Tokyo, Japan). Sample preparation for TEM imaging was as follows: fibril homogenates from each well were centrifuged at 13,000 × g for 20 min, supernatants were separated, and fibril precipitates were washed five times with pure MilliQ water to remove any residual TCEP. Four microliters of fibril homogenates were then placed on a 200-mesh copper grid and dried after 1 min. By “fibril homogenates,” we simply mean a well-suspended solution of SOD1 fibrils that was prepared via vigorous shaking (without centrifugation). This “homogenization” ensured that a sufficient amount of fibrils was placed on the grid for TEM imaging. Four μL of 3% uranyl acetate solution was placed on the grid for 1 min and dried using a clean filter paper. Samples were then incubated for ∼1 h in a clean, dust-free container and imaged under ∼80 kV.

Atomic force microscopy

Beads were fixed on the atomic force microscopy (AFM) discs using a double-sided tape and imaged using a Dimension Icon AFM equipped with NanoScope V software (Bruker, Santa Barbara, CA). Tapping-mode probes from MikroMasch (NSC35/ALBS, 5.4 N/m; Sofia,, Bulgaria) were used to acquire topography images. The cantilever oscillated at near the resonance frequency (150 KHz) to acquire the images. Images were processed using NanoScope Analysis software. Sample roughness was obtained via analyzing topography frames. Values for surface roughness in Table 1 are reported as the root mean-square average of roughness (R_q), calculated as (36)

$$R_q=\sqrt{\frac{\sum _{i=1}^N{\left(Z_i\right)}^2}{N},}$$ (1)

where N is the number of equally differentiated points (i) along the measured surface and Z_i is the difference between the height of each data point and the mean horizontal line.

Results and Discussion

Rates of amyloid formation vary sevenfold with bead type

In this study, we examined the fibrillization of the ALS-linked D90A variant of apo-SOD1 because this protein was readily available in our laboratory and we are familiar with its fibrillization kinetics in microplate assays (13, 15). ThT fluorescence aggregation assays were performed on D90A apo-SOD1 in 96-well microtiter plates under reducing physiological conditions (10 mM TCEP, 150 mM NaCl (pH 7.4); the well-to-well variation in pH of SOD1 solutions was measured to be <0.1%). We measured rates of fibril nucleation and propagation (elongation) in the presence of the following beads (Fig. 1): polytetrafluoroethylene (PTFE or Teflon), extracted acrylic, polypropylene, polyoxymethylene (Delrin), high-density polyethylene (HDPE), and polyamide-imide (Torlon) (all of which are denoted in this article as “polymeric beads”); and aluminum, titanium, alumina ceramic, silicon nitride ceramic, borosilicate glass, and stainless steel (denoted as “non-polymeric beads”).

The nanoscopic and microscopic topologies of each bead type were visualized using AFM and SEM before the start of assays. All polymeric beads possessed roughness on a micrometer scale according to AFM, except for extracted acrylic, which was smoother on the micrometer scale but showed nanometer-scale roughness (Fig. 1). Accordingly, SEM showed that polymeric beads have a higher degree of “waviness” than non-polymeric beads (“waviness” refers to surface irregularities at the micrometer scale, whereas “roughness” refers to irregularities at the nanometer scale (37)). Surface features on polymeric beads exhibited heights up to 10 μm, with the exception of extracted acrylic beads (Fig. 1). Ceramic, glass, and metallic beads (i.e., non-polymeric beads), on the other hand, possess smoother microscopic surfaces with average depths <400 nm (Fig. 1).

Iterative ThT fluorescence aggregation assays were performed on D90A apo-SOD1 in replicates of ∼40 assays per bead type. Individual (iterative) plots of ThT fluorescence are shown for all beads in Fig. 2. We repeated amyloid assays at this high level of iteration because the fibrillization of apo-SOD1 is intrinsically stochastic and myriad replicates are needed to obtain statistically significant rates (13).

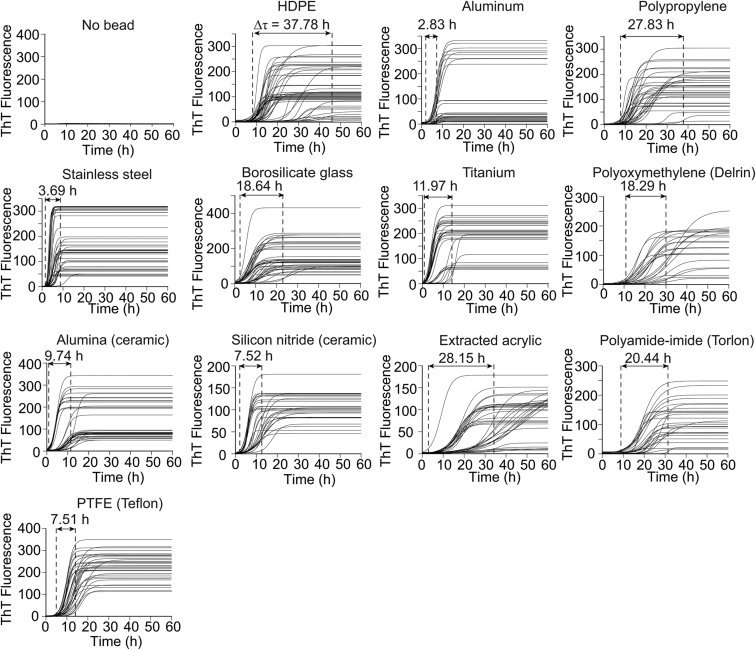
Figure 2.

Replicate ThT fluorescence amyloid assays for D90A apo-SOD1 in the absence and presence of beads with varying chemical and physical properties. The variation in lag time among replicate assays (Δτ) is indicated by numbers above each arrow.

The longitudinal plots of ThT fluorescence are shown for each bead in Fig. 3 A. Plots in Fig. 3 A are averaged, normalized plots of all replicate experiments for each bead type (461 total replicates). A few important trends are immediately observable: in general, non-polymeric beads accelerated the aggregation of D90A apo-SOD1 more than polymeric beads (Fig. 3 A). As expected, the lag time and propagation (elongation) rate derived from each of the 445 iterative experiments (16 replicates were performed for the “No bead” condition, which did not result in any ThT fluorescence) fell along a rational function, regardless of bead type (Fig. 3 B), i.e., α = lag time (τ) × rate (k), where α = 4.21. The α constant is similar to the value previously reported for the aggregation of other variants of apo-SOD1 (13, 24). The distribution of iterate lag times, for each bead type (Fig. S1 in the Supporting Material), suggests that apo-SOD1 aggregation was generally more stochastic in the presence of polymeric beads compared to non-polymeric beads, as shown with a wider range in lag time (i.e., higher Δτ; Figs. 2 and 3 C; Fig. S1). The most reproducible amyloid assays were obtained using stainless steel (Δτ = 3.69 h) and aluminum beads (Δτ = 2.83 h) (Fig. 2). This diminished stochasticity is partially due to the accelerated fibrillization, which by definition narrows any distribution of rates, ceteris paribus, because negative values of time are not real.

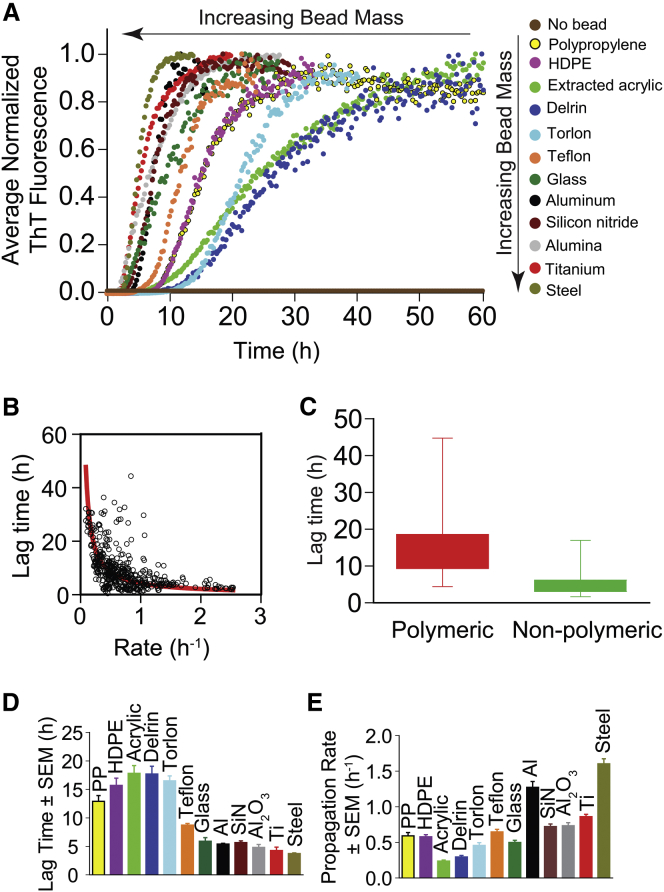
Figure 3.

Kinetics of fibrillization of apo-SOD1 vary with bead type. (A) Average and normalized plots of ThT fluorescence for D90A apo-SOD1 aggregation (from Fig. 2; n_total = 461). Assays were performed in the presence of 10 mM TCEP (pH 7.4) and a physiological concentration of NaCl (150 mM). (B) Correlation plot between lag time and rate of fibril propagation (from all 461 assays). The red line shows the best fit to the data using a rational function. (C) The box-and-whisker plot illustrates stochasticity in lag time for each type of bead. Comparison plots of the (D) lag time and (E) propagation rate of D90A apo-SOD1 aggregation in the presence of different bead types. For visual clarity, error bars in (D) and (E) are depicted as standard error of the mean (SEM), not standard deviation (SD), where SEM = SD/√n.

It is also important to note that the maximal intensity of ThT fluorescence associated with SOD1 aggregation varied by up to 30-fold in the presence of different beads and among replicates of each bead (Fig. 2). We attribute this difference in ThT fluorescence intensity to 1) differences in the number of bound ThT molecules, and 2) differences in the fluorescence intensity (quantum yield) of fibril-bound ThT (38). Differences in the structures, dynamics, and morphologies of fibrils could cause the binding affinity and quantum yield to change. For example, interactions between fibrils, e.g., “fibril matting” (39), could lead to diminished ThT binding via diminished solvent accessibility or to disruptions of secondary structure. Differences in the secondary structure or dynamics of fibrils could also alter the degree to which the C2-C12 bond in ThT is prevented from rotating when bound to a fibril (the absence of rotation is thought to be the cause of ThT fluorescence upon amyloid binding).

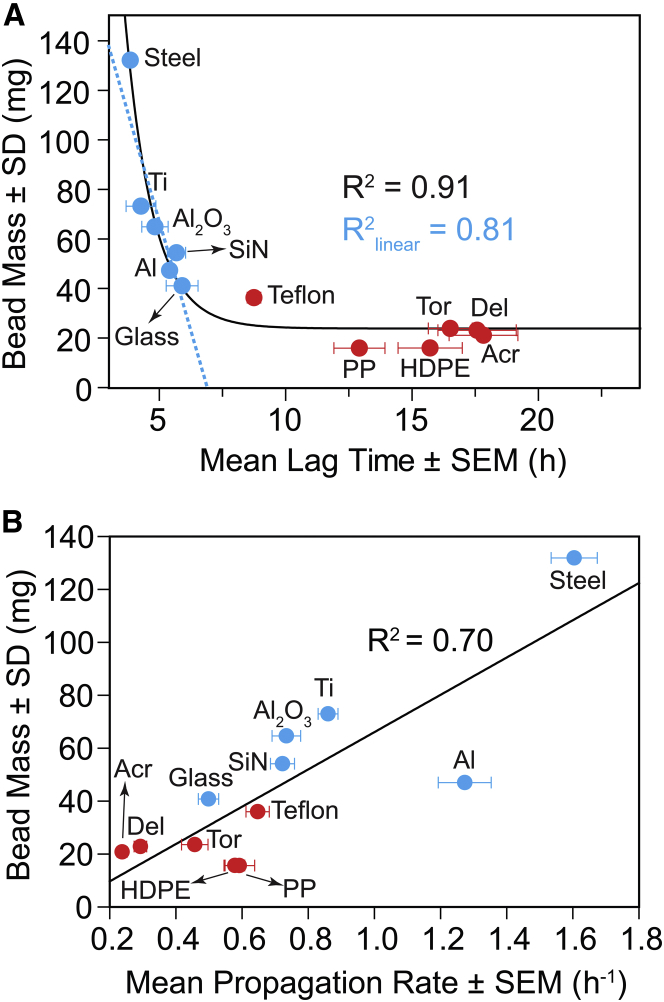
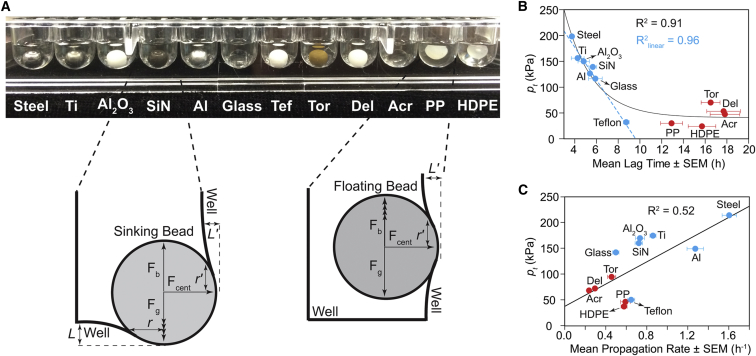
The mass of the beads we chose varied 10-fold, from polypropylene (15.6 ± 0.6 mg) to stainless steel (131.9 ± 0.1 mg). We hypothesized that the mass of each bead type might be one (of perhaps several) causes of the kinetic trend in Fig. 2 and Fig. 3. The lag time correlated exponentially (negatively) with increasing bead mass (Fig. 4 A; R² = 0.91). The rate of fibril propagation correlated linearly (positively) with bead mass (Fig. 4 B; R² = 0.70).

Figure 4.

(A) Correlation between lag time of D90A apo-SOD1 fibrillization and bead mass. The blue dashed line indicates the best fit to the linear portion of the plot (non-polymeric beads). (B) Moderate linear correlation between rate of propagation of D90A SOD1 oligomers and bead mass. PP, polypropylene; Del, Delrin; Acr, acrylic; Tor, Torlon; SiN, silicon nitride ceramic; Al₂O₃: alumina ceramic.

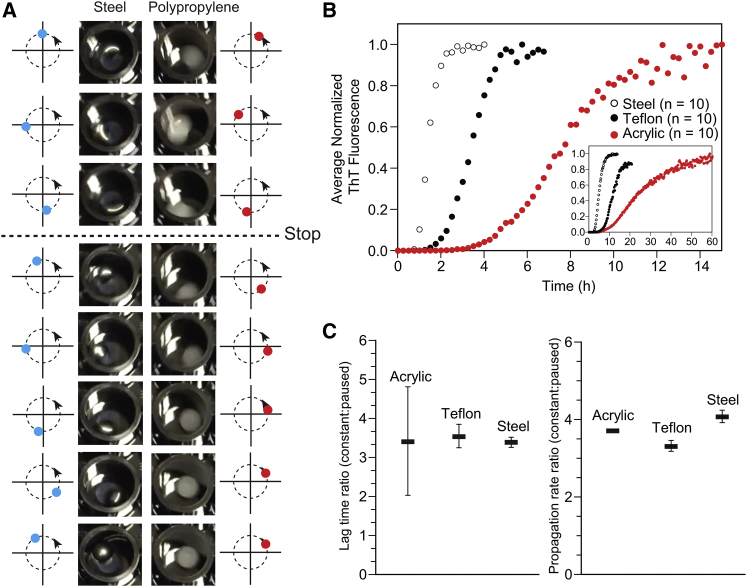
There are a few possible reasons for why the mass of a bead might affect its ability to accelerate amyloid formation during orbital gyration in a microtiter plate, irrespective of the surface charge, hydrophobicity, or topology of the bead (or any other physical or chemical property). First and foremost, the velocities of different beads are approximately equal during orbital gyration of the microplate—regardless of mass—however, heavier beads will acquire more momentum during orbital gyration compared to beads of lower mass (momentum = mass × velocity). Thus, the ∼10-fold greater momentum of a stainless steel bead compared to a polypropylene bead (Table 1) should cause the steel bead to continue orbiting around the microplate well for a longer period of time after the plate reader ceases gyration (in our typical amyloid assay, the Fluoroskan plate reader gyrates the microtiter plate at 360 rpm for 15 s, followed by a pause in gyration for 15 s, and this process repeats continually for 168 h). Therefore, the heavier beads will undergo more revolutions per minute (on average) over the course of the 168 h experiment. To demonstrate this effect visually, polypropylene beads and stainless steel beads were gyrated in a 96-well microtiter plate at ∼180 rpm (Fig. 5 A). The stainless steel beads continued gyrating for 5.2 revolutions after the plate ceased gyrating, whereas polypropylene gyrated for 2.3 revolutions (Fig. 5 A); we did not include water in each well, because doing so interfered with video recording; however, the same qualitative effect was observed in water.

Figure 5.

Residual angular momentum of heavier beads cannot explain the effect of bead mass on amyloid formation. (A) Consecutive images of gyrating steel and polypropylene beads during gyration and after gyration is stopped. Beads were stirred at ∼180 rpm (0.055 m/s) in a black polystyrene microplate. Circular arrows with blue and red dots next to each image show the trajectory of the moving beads inside the well. (B) Average and normalized ThT fluorescence plots of D90A apo-SOD1 aggregation under continuous gyration of steel, Teflon, and acrylic beads. The inset shows plots of D90A apo-SOD1 aggregation in the presence of the same types of bead but with paused gyration, taken from Fig. 3A. (C) Comparison plots of aggregation lag time and propagation rate between two different gyration methods.

To test the “residual momentum” hypothesis, we programmed the Fluoroskan plate reader to gyrate constantly for 40 min, with the only pause occurring for 5 s during spectroscopic measurements of all wells. Thus, the microplate gyrates at 360 rpm for 40 min, followed by 5 s for spectroscopic measurement, and this process repeats for ∼168 h. If residual momentum effects are significant, this increase in the ratio of gyration time and pause time from 1:1 to 480:1, should significantly diminish the measured differences in lag time and propagation rate for different types of beads. ThT fluorescence amyloid assays were performed again for D90A apo-SOD1 in the presence of stainless steel, Teflon, and acrylic beads under continuous gyration (i.e., three beads that produce fast, medium, and slow rates; Fig. 3 A). Continuous gyration did not cause low-mass beads (i.e., acrylic and Teflon) to produce the same lag times as steel beads (Fig. 5 B), and the ratio of lag time at continuous to that at non-continuous gyration was statistically equal for all beads (Fig. 5 C). Continuous gyration accelerated the aggregation of apo-SOD1 in the presence of all three beads (as expected) by ∼3.5-fold compared to paused gyration (Fig. 5, B and C). These results invalidate the “residual momentum” hypothesis of the acceleratory effect of heavy beads on amyloid formation.

Another possible mechanism by which bead mass could affect the aggregation rate of D90A apo-SOD1 is by contact force (pressure) between the bead and bottom and side of the polystyrene microplate. These forces (which we show below are kilopascal in scale) might be sufficient to induce the mechanical fragmentation of oligomers or fibrils, as shear forces have been previously shown to cause oligomer fragmentation and secondary nucleation and elongation (22, 40). Our calculations of these contact forces, below, take into account the stiffness of the bead and polystyrene microplate and the micrometer-scale deformations that the bead introduces upon the microplate.

A bead with mass m and radius R (a hypothetical ideal sphere) is capable, due to its weight, of indenting the surface of the flat polystyrene microplate (a hypothetical elastic half-plate) at all contact points (Fig. 6 A). The radius of this contact area, r, can be expressed as

$$r=\sqrt{RL},$$ (2)

where L is the depth of the displacement on the microplate surface due to indentation (41), as shown in Fig. 6 A (exaggerated for illustration):

$$L=\sqrt[\frac{3}{2}]{\frac{3\left(F_{\text{g}}-F_{\text{b}}\right)}{4E^{\ast }{R}^{0.5}}},$$ (3)

where F_g is the gravitational force exerted by the bead perpendicular to the microplate surface, and F_b is the buoyancy force. Thus, if F_b > F_g, the bead will float and not touch the bottom of the microplate (Fig. 6 A). E^∗ is an interfacial stiffness parameter, defined by the physicomechanical properties of both surfaces as

$$\frac{1}{E^{\ast }}=\frac{1-{\nu }_1^2}{E_1}+\frac{1-{\nu }_2^2}{E_2},$$ (4)

where E₁ and E₂ are the Young’s moduli of the bead and the polystyrene microplate, and ν₁ and ν₂ are the Poisson’s ratios of each bead and the microplate, respectively. The maximum contact pressure on the well surface can be estimated (42) from

$$p_{\text{g}}=\frac{3\left(F_{\text{g}}-F_{\text{b}}\right)}{2\pi r^2}.$$ (5)

Inspecting the bead trajectory inside the gyrating microplate confirmed that all beads stick to the side of each well and gyrate along with the frame of the plate (Fig. 6 A), meaning that contact occurs on the bottom and side of the well (except in the cases of polypropylene and HDPE, which are buoyant). The centrifugal force (F_cent) on the side of wells was used to calculate the parameters of contact mechanics (r′, L′, p_cent; Fig. 6 A), instead of the buoyant and gravitational forces:

$$F_{\text{cent}}=m{\omega }^{2}l,$$ (6)

where ω is the angular velocity of the rotating bead (360 rpm = 0.11 m/s), and l is the radius of gyration, which is 3 mm in the experimental setup used here.

Figure 6.

Contact mechanics between beads and microplate surface can explain the kinetics of amyloid nucleation and propagation. (A) Schematic showing the components of contact forces between the bead and microplate well. Two of twelve beads (i.e., polypropylene and HDPE) did not sink in the solution and contacted only the side of well. Parameters F_g, F_b, F_cent, r, L, r′, and L′, described in the main text, are depicted with arbitrary scales and visually exaggerated for clarity. (B and C) Correlation plots of total contact pressure (p_t) versus lag time and propagation rate, respectively, of D90A apo-SOD1 aggregation. The blue dashed line in (B) indicates the best fit to the linear portion of the plot. We note that a transparent microplate (with a concave bottom) was used to demonstrate buoyancy in (A). Actual experiments were carried out in black polystyrene microplates with flat bottoms (cylindrical wells).

We observed that polypropylene and HDPE beads did not sink when placed in the aggregation solution (i.e., F_b > F_g; Fig. 6 A), and did not touch the bottom of the microplate during the course of the assay (i.e., p_g is a negative value). Thus, in the case of polypropylene and HDPE, we only calculated the contact parameters in terms of F_cent (Fig. 6 A).

Table S1 contains the values of r, r′, E₁, ν₁, E^∗, p_g, and p_cent for all studied beads. We calculated the total contact pressure as p_t = p_g + p_cent for each bead, and plotted it versus the corresponding lag time (Fig. 6 B). We point out that although buoyant beads like polypropylene only contact the sides of wells, these beads can produce almost identical total pressure to heavier polymeric beads that sink (e.g., Teflon). For example, the p_cent value of polypropylene was 4.8 kPa greater than p_cent for Teflon (Table S1); however, the p_g of Teflon (6.9 kPa; Table S1) renders the two p_t values for polypropylene and Teflon similar (Fig. 6). We point out that although the mass of polypropylene is threefold lower than Teflon, the p_cent value for polypropylene is greater than that for Teflon, because polypropylene is more stiff than Teflon (Table S1) and polypropylene will conform less to the surface of the microplate (which provides less surface area, and thus greater pressure, i.e., pressure = force/area).

Similar to the mass-versus-lag time relation (Fig. 4 A), an exponential correlation was observed between p_t and lag time (Fig. 6 B). We note that the linear portion of mass-versus-lag time plots (Fig. 4 A, dashed blue trace) did not include any of the polymeric beads (only non-polymeric beads). Taking into account contact mechanics—calculating contact pressures with mass and stiffness—improved the linear correlation (which contained Teflon beads). Nevertheless, Teflon was the only polymeric bead to fall along this linear portion in plots of p_t and lag time (Fig. 6 B; R² = 0.96). Regarding polymeric beads, there is no general correlation between mass and/or p_t and aggregation lag time (Figs. 4 A and 6 B). A linear correlation was found between the maximum contact pressure of polymeric and non-polymeric beads and the rate of oligomer propagation (Fig. 6 C). These results indicate that contact pressure (mechanical stress) is generally a dominant force in nucleation via non-polymeric beads, but not a generally dominant force in the case of polymeric beads. Polymeric beads accelerate fibrillization to a lesser degree than we would predict based upon their mass and contact pressure, possibly because of hydrophobic effects.

Surface adhesion and hydrophobicity can partially explain the catalytic effect of polymeric beads on SOD1 fibrillization

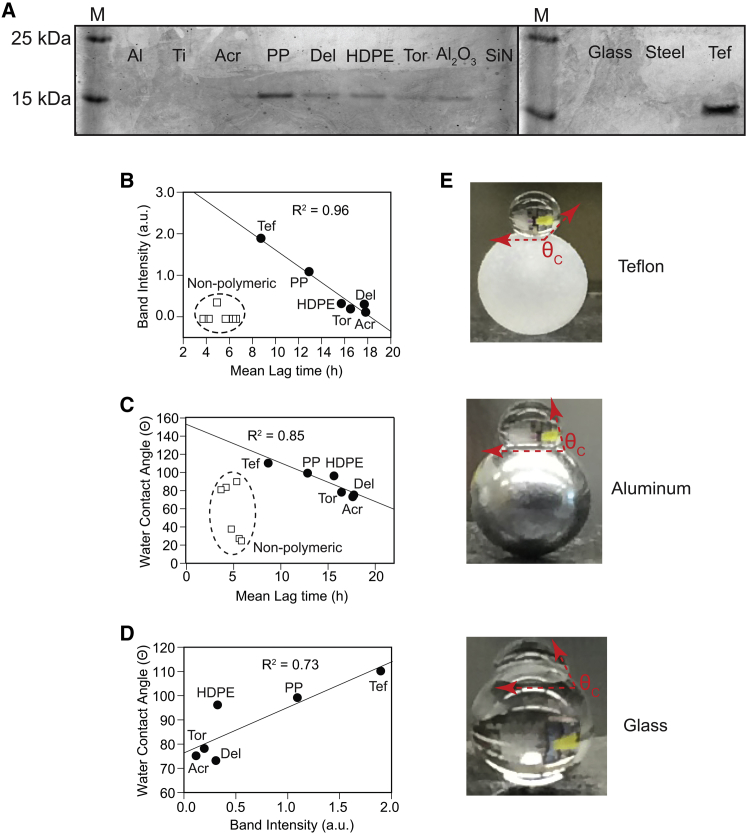
The insufficiency of mass and total contact pressure (p_t) to explain why polymeric beads have such wide-ranging kinetic effects on apo-SOD1 fibrillization suggested that surface chemistry might explain lag times observed with polymeric beads. Polymeric beads might interact with monomeric or oligomeric SOD1 species to a degree that non-polymeric beads do not, and these interactions might be dependent upon surface properties (roughness and hydrophobicity) of each bead. To begin to test these hypotheses, we examined how much protein was attached to each bead surface after the end of the amyloid assay. We extensively washed each bead after completion of an amyloid assay, and we boiled each bead in 2× Laemmli buffer/4% β-mercaptoethanol and performed SDS-PAGE on boiled solutions (Fig. 7 A). The greatest amount of protein adhesion was observed for polymeric beads (except in the case of acrylic beads); negligible adhesion was observed for non-polymeric beads (alumina beads showed moderate affinity for SOD1 polypeptides, which is likely due to their positive ζ potential at pH 7.4 (43)). The concentration of protein that adhered to polymeric beads during amyloid assays (proportional to band intensities in Fig. 7 A) correlated linearly with the lag time of apo-SOD1 fibrillization (Fig. 7 B; R² = 0.96), i.e., greater adhesion correlated with faster nucleation. No correlation was found between the band intensity and the lag time of non-polymeric beads (Fig. 7 B, open squares; R² = 0.02). The correlation between surface adhesion and lag time is interpreted in terms of hydrophobic effects: the surface hydrophobicity (i.e., the water contact angle; Fig. 7 E) of polymeric beads (before amyloid assay) correlated with the lag time of fibrillization (Fig. 7 C) and the quantity of SOD1 that adhered to beads during amyloid assays (Fig. 7 D).

Figure 7.

Surface adhesion and hydrophobicity can explain kinetic variation among polymeric, but not non-polymeric (ceramic, metallic, glass), beads. (A) Sodium dodecyl sulfate polyacrylamide gel electrophoresis of surface-adhered D90A apo-SOD1 recovered from the surface of each washed bead after termination of the ThT aggregation assay (proteins were recovered from the surface by boiling beads in sodium dodecyl sulfate). (B and C) Plots of (B) mean band intensity and (C) water contact angle of the bead (before beginning the assay) versus the mean aggregation lag time of fibrillization for D90A apo-SOD1. (D) Surface hydrophobicity (water contact angle) of the bead correlates with the amount of protein adhered to the surface of polymeric beads. Densitometry analyses were carried out using ImageJ software. (E) Visual demonstration of the variation in hydrophobicity (θ_C, water contact angle) among beads used in this study.

Together, these results demonstrate that kinetic variations among polymeric beads arise (at least in part) from hydrophobic interactions. The mechanism by which these hydrophobic interactions accelerate fibrillization might involve promotion of primary nucleation events (via increasing the local concentration of SOD1 at the bead surface and/or altering the conformation of SOD1 or its oligomers in ways that accelerate nucleation). Hydrophobic effects among non-polymeric beads do not appear to be sufficient to explain the kinetic variations in Fig. 2. Even though some of the non-polymeric beads studied are more hydrophobic than some of the polymeric beads (i.e., aluminum versus Torlon, Delrin, or acrylic, Table 1), non-polymeric beads do not generally bind to SOD1 (Fig. 7 B, open squares), and the contact angle of non-polymeric beads does not correlate in any way with lag time (Fig. 7 C, open squares). Kinetic variations among non-polymeric beads appear to arise not from differences in hydrophobicity, but again from Newtonian mechanical forces. These forces might induce the mechanical breaking of oligomers and fibrils (at the bead-microplate interface), which can promote secondary nucleation processes. Secondary nucleation processes can be induced by mechanical force (22) and are thought to involve the fragmentation of small, intermediate oligomers to create a higher number of “free ends,” which act as nucleation seeds (44) and ultimately result in shorter fibrils (22, 40, 45).

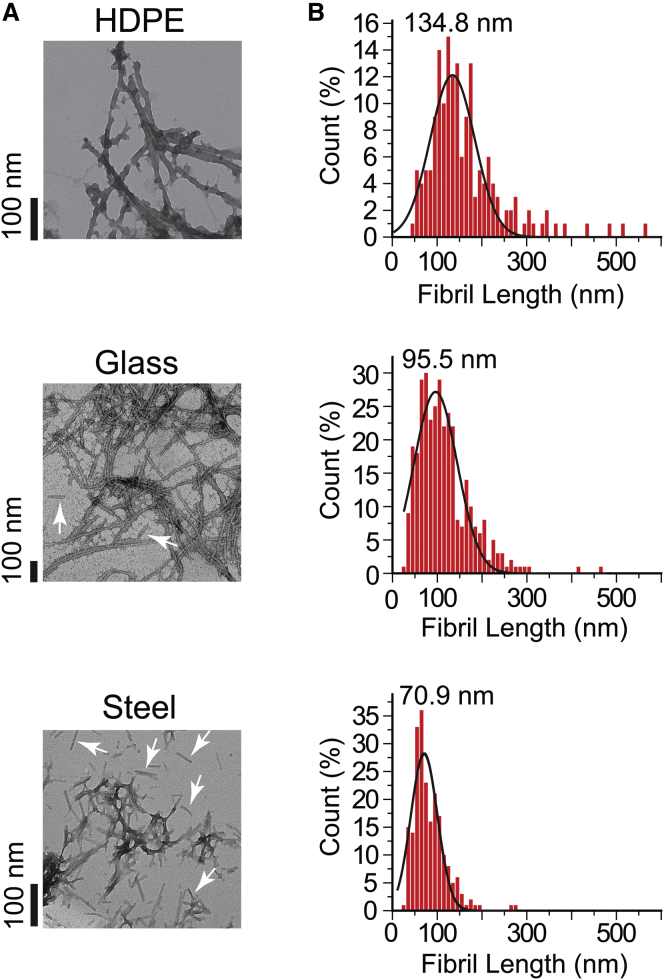
To test whether non-polymeric beads resulted in shorter, more fragmented fibrils than polymeric beads (which we assume would be the end result of greater continuous fragmentation and secondary nucleation), we performed TEM on solutions of fibrils formed in the presence of three different beads: steel, glass, and HDPE (Fig. 8 A). Aggregation of D90A apo-SOD1 resulted in the formation of fibrillar species in the presence of all bead types (Fig. 8 A). Non-polymeric beads caused the formation of a higher number of short, intermittent fibrils (Fig. 8 A, white arrows), where wells with HDPE beads showed mostly long, intertwined fibrils (Fig. 8 A). We also calculated the average fibril length for each bead, which showed that the shortest fibrils exist in the presence of steel beads (median fibril length = 70.9 nm) and longest fibrils are formed with HDPE beads (median fibril length = 134.8 nm) (Fig. 8 B). We attribute this higher quantity of short fibrils (in the presence of steel beads) to increased oligomer fragmentation (22, 40, 45). Similar fragmentation-based mechanisms have been observed for other amyloidogenic polypeptides, such as Aβ_1–42 (46).

Figure 8.

Heavier beads promote shorter SOD1 fibrils. (A) TEM images of D90A apo-SOD1 fibrils in the presence of HDPE, borosilicate glass, and stainless steel beads. White arrows point to the short fibril fragments formed in the presence of stainless steel and borosilicate glass beads. (B) Histograms of fibril length (n_total = 723) for each bead type. Fibril lengths were measured using cellSens software and histograms were fit with a three-parameter Gaussian distribution. The value above each histogram shows the median fibril length.

We observed that bead type also affected the formation of amorphous aggregates (the formation of which competes with fibrillization (13)). In general, a higher population of amorphous aggregates was present for polymeric beads compared to non-polymeric beads according to TEM (Fig. S2 shows representative TEM micrographs for all beads). For example, amorphous SOD1 species were observed to form with HDPE beads (and to a lesser extent glass beads). Amorphous species were not observed in the presence of steel beads, to the point that products of SOD1 aggregation in the presence of steel beads were almost completely fibrillar (Fig. 8; Fig. S2). This observation demonstrates that higher bead mass—which accelerates the formation of fibrillar species—also disfavors the formation of amorphous aggregates. We interpret this effect to be caused by a greater degree of secondary nucleation with heavier beads. For example, we hypothesize that heavier beads (stainless steel) cause a greater degree of fragmentation of amyloid-like oligomers (via increased total contact pressure, p_t), which promotes further fibrillization and by definition disfavors amorphous aggregation.

In summary, these results do not necessarily imply that surface interactions and hydrophobic effects are not involved at all with non-polymeric beads, or that mechanical forces are not involved in SOD1 fibrillization with polymeric beads; rather, they suggest that these forces are not sufficiently dominant to explain the kinetic variation within each set of beads.

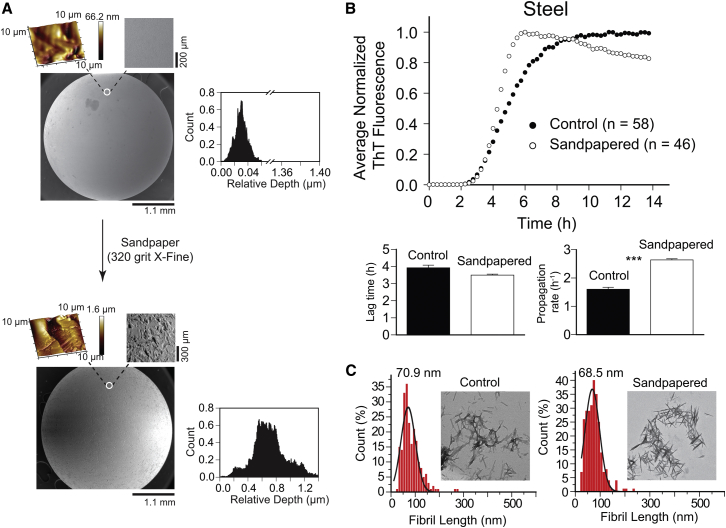
We were also interested in determining whether altering the surface roughness of smooth, non-polymeric beads would influence aggregation kinetics. This type of experiment has theoretical implications, but we were interested in its practical implications. Do scratches on the surface of beads—scratches that could be introduced during manufacturing, shipping, storage, or handling in the laboratory—affect their rates of aggregation? To answer this question, we coarsened the surface of steel beads using commercial sandpaper (320 grit/X-Fine). We chose steel because it presented the smoothest surface (Fig. 1). SEM and AFM imaging showed that the surface roughness of steel beads was significantly increased upon sandpapering (ΔR_q = 220 nm; Fig. 9 A). We then performed ThT fluorescence aggregation assays on both smooth (control) and rough (sandpapered) steel beads (n_total = 104; Fig. 9 B).

Figure 9.

Effect of scratching the surface of beads on rate and morphology of fibrillization. (A) SEM and AFM 3D micrographs of the surface of steel beads before and after sandpapering. Color bars next to the AFM images represent gradual surface roughness, with lighter colors indicating shallower surfaces. The inset next to each graph shows a histogram of the relative surface depth, calculated from AFM imaging. (B) Plots of the average ThT fluorescence during the amyloid assay of D90A apo-SOD1 in the presence of smooth (control) and roughened (sandpapered) steel beads. Bar graphs depict comparison plots of mean lag time and propagation rate (^∗∗∗p < 0.0001). (C) Histograms of fibril length (n_total = 482) for smooth and sandpapered steel beads. Fibril lengths were measured using cellSens software and histograms were fit with a three-parameter Gaussian distribution. The value above each histogram shows the median fibril length. Insets show TEM micrographs of D90A apo-SOD1 fibrils in the presence of control and sandpapered steel beads.

No significant difference was observed between fibril lag times of control and sandpapered steel beads (Fig. 9 B), supporting the hypothesis that variations in surface roughness do not play a major role in amyloid nucleation with non-polymeric beads. We did, however, observe an acceleratory effect on fibril propagation; D90A apo-SOD1 fibrils propagated faster in the presence of sandpapered steel beads (Fig. 9 B). We interpret this result in terms of higher degrees of oligomer fragmentation in beads with rough surfaces. For example, a rougher surface will have, ceteris paribus, fewer contact points with the polystyrene surface of the microplate well, but these fewer contacts will cause greater pressure on points of contact with the polystyrene (as the overall mass of the bead is not greatly affected by roughening). We found that roughening the surface of steel beads upon sandpapering increased the surface roughness by ∼25-fold (i.e., R_q(steel) = 9.23 nm, R_{q(sandpapered)} = 232.0 nm). The average contact pressure that a bead (ideal sphere) exerts on the bottom and sides of a polystyrene plate (ideal half-plate) is directly proportional to the root mean square of the surface slope, i.e., surface roughness (R_q): p_t α R_q. Thus, sandpapering caused an ∼25-fold increase in contact pressure between the bead and the polystyrene plate (42). This increased pressure might promote fibril fragmentation and secondary nucleation processes. This hypothesis was further tested by measuring the length of SOD1 fibrils in the presence of sandpapered steel beads using TEM imaging. SOD1 fibrils that were formed in the presence of sandpapered steel beads were very short, with an average fibril length of 68.5 nm, which is 2.4 nm smaller than the average fibril length in the presence of regular (control) steel beads (Fig. 9 C). These results further demonstrate that increasing contact pressure upon roughening the surface of beads leads to a higher degree of fibril fragmentation.

We also determined whether a correlation existed between the roughness of polymeric beads and aggregation parameters. Values of the surface roughness (R_q) of each bead were plotted against the corresponding lag time and propagation rate (Fig. S3). Polymeric beads with a rougher surface (higher R_q) cause a shorter lag time and faster propagation rate (Fig. S3). No correlation was found between the surface roughness of non-polymeric beads and kinetic parameters of SOD1 aggregation (Fig. S3). The effect of the surface roughness of polymeric beads on SOD1 aggregation can be illustrated especially well by comparing Torlon and Delrin beads. These two beads are approximately similar in mass but have significantly different surface roughness (R_q(Torlon) ≈ 3R_q(Delrin); Table 1). The lag time of SOD1 aggregation is statistically similar in the presence of Torlon and Delrin beads; however, Torlon causes a faster propagation rate than Delrin, possibly due to greater contact pressure, which might promote fibril fragmentation (similar to the results obtained for roughened steel beads).

Omniphobicity and amyloid formation

Fluorinated hydrocarbons such as trifluoroethanol (TFE) have been widely used for years to accelerate the rate of amyloid formation (47, 48, 49) and control fibril morphology (50) during in vitro experiments. The chemical mechanisms of action of fluorinated co-solvents on protein structure, folding, and self-assembly are not clearly understood (51, 52).

The increased rate of fibrillization that we report for a Teflon bead compared to its non-fluorinated analog HDPE might suggest that similar types of acceleration of fibrillization by RC-F groups is occurring at the surface of Teflon beads (which are omniphobic, i.e., resist interactions with polar and non-polar solvents). One additional difference between Teflon and HDPE beads is that Teflon beads are twofold higher in mass than HDPE (Table 1) and HDPE is ∼43% more rigid than Teflon (Table S1). These differences offset to produce similar contact pressures for Teflon and HDPE (Fig. 6 B), which do not seem adequate to explain why SOD1 fibrillizes at ∼16 h in the presence of HDPE beads and ∼8 h in the presence of Teflon beads (Fig. 6 B). Contact mechanics thus seems inadequate to explain why Teflon and HDPE beads produce different fibrillization rates; omniphobic effects between Teflon and the SOD1 protein are of course reasonable explanations.

Hydrodynamic effects during microplate amyloid assays

To what degree can hydrodynamic effects—arising perhaps from changes in bead mass or roughness—explain why different types of beads result in different rates of fibrillization? It is well established that a gyrating bead within a microplate accelerates protein fibrillization via increasing the shear forces upon protein (20, 53). In this study, however, the hydrodynamics and type of flow regime (i.e., laminar, transient, or turbulent) of our system remain generally constant regardless of bead type. For example, the Reynolds number of our system is Re = 328.4, that is, our system exists under a transient hydrodynamic regime. The Reynolds number does not change per bead type because it is independent of the bead’s mass or surface properties:

$$\mathrm{Re}=\frac{\rho vL}{\mu },$$ (7)

where ρ is the fluid density (ρ_{phosphate buffer} = 995 kg/m³), v is the linear gyration speed (0.11 m/s), L is the diameter of circular gyration (0.003 m), and μ is the viscosity of the fluid (μ_{phosphate buffer} = 0.0011 kg/m/s). Furthermore, the drag force of the fluid against each bead does not change for different bead types:

$$F_{\text{D}}=\frac{1}{2}\rho v^2{C}_{\text{D}}A.$$ (8)

C_D (the drag coefficient) and A (the reference area) depend mainly on bead shape, which is constant for the beads used in this study. We note that C_D is also a function of surface roughness, which does differ among the beads used in this study (Table 1). However, C_D is only a function of surface roughness under fully turbulent conditions (i.e., Re > 10⁴). Thus, surface roughness does not have a significant effect on C_D under the transient flow regime of our system.

Conclusion

We originally initiated this study to find reaction conditions that could increase the rate and reproducibly of amyloid assays for the superoxide dismutase protein. We have succeeded in this effort: the continuous gyration of a stainless steel bead at 360 rpm (with only a 5 s pause for measurement) produces the most rapid, reproducible lag time for apo-SOD1 (1.1 ± 0.08 h, compared to 8.7 ± 0.3 h for the intermittent gyration of a Teflon bead at 360 rpm). However, in the course of assay optimization, we have demonstrated the importance of contact mechanical forces (kilopascal scale) on the nucleation and propagation of SOD1 amyloid fibrils. The best illustration of this point is the ≥5-fold difference in both lag time and propagation rate for stainless steel and acrylic beads (i.e., beads of similar hydrophobicity but different mass; Table 1). We attribute the positive correlation between bead mass and rate of amyloidogenesis to the mechanical fragmentation of oligomers by beads (14, 22). We hypothesize that the greater force imparted on oligomers, at the bead-water-polystyrene interface, leads to increased fragmentation and subsequent secondary nucleation (14). Previous studies have shown (at the molecular level) that the fibrillization of proteins can be promoted by imparting mechanical and shear force on existing oligomers (53, 54, 55) (mechanical stress factors have also been identified as risk factors for different types of protein aggregation diseases (56, 57)). Thus, although this study is performed entirely in vitro and would appear to provide little insight into biological processes of SOD1 aggregation, it establishes the importance of shear force and mechanical stress factors on initiating and propagating SOD1 amyloidogenesis of short fibrils. We also point out that the ability to alter the morphology (i.e., length) of fibrils by simply changing bead type offers a simple, practical method for generating different types of oligomers to, for example, test their variable cytotoxicity.

Author Contributions

A.A and B.F.S organized the research. All the authors contributed to the design of the experiments, the analysis of the data, and editing of the manuscript.

Editor: Charles Wolgemuth.